Datastructure tree

Binary Index Tree
Problem:
Give an array A[1], A[2] , … , A[n] and m
queries as follows (n, m ~ 10^6)
type 1: add x to A[k] (1 <= k <= n)
type 2: calculate sum of interval [l , r] of array

Binary Index Tree
Naive solution
type 1: O(1)
type 2: O(n)
→ time complexity O(mn)
m, n ~ 10^6 → impossible

Binary Index Tree
• Fenwick Tree (also called BIT)
• Peter M. Fenwick, "A New Data Structure for
Cumulative Frequency Tables" (1994)
• Support fast operations on array

Binary Index Tree
Support two operations in O(log(n))
[1] Add value x to an element A[k]
A[k] → A[k] + x
[2] Return sum of prefix k
prefix[k] = A[1] + A[2] + ... + A[k]

Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]

Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[1]

Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[3]

Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get prefix[3]

Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get prefix[7]

Binary Index Tree
• Observation
Express k as binary number
1→1 2→10 3→11 4→100
5→101 6→110 7→111 8→1000
Pay attention to number of ‘0’ at the end
add operation : k → k + (last bit 1 of k)
get operation: k → k – (last bit 1 of k)

Binary Index Tree
[1] Add value to element at position index
void add(int index, int value) {
for (int i = index; i <= size; i += i & -i) {
bit[index] += value;
}
} → O(log(n))

Binary Index Tree
[1] Get sum of elements from postion 1 -> index
int get(int index) {
int ans = 0;
for (int i = index; i > 0; i -= i & -i) {
ans += bit[i];
}
return ans;
} → O(log(n))

Binary Index Tree
• Total time complexity for m queries
Naive: O(mn) → BIT: O(mlog(n))
Amazing 🎉 Bravo 👏
Let see some practical uses of BIT

Count Inverse Pair
Give an array A[1], A[2], ..., A[n], n ~ 10^6
Count number of pair (A[i], A[j]) such that
i < j and A[i] > A[j]
Naive solution: scan all pairs (A[i], A[j]) , i < j
→ time complexity O(n^2) → impossible

Another solution
• Using technique of merge sort
Divide and conquer (A[1], ... ,A[n])
→ (A[1], ... ,A[n/2]) ∨ (A[n/2+1], ..., A[n])
solve(A[1], ... ,A[n/2])
solve(A[n/2+1], ..., A[n])
merge(A[1], ... ,A[n/2] ∨A[n/2+1], ..., A[n])
Time complexity O(nlog(n))

Using BIT
Suppose 1 <= A[1], A[2], ..., A[n] <= n and are
integer.
If not, we can make a mapping by sort because
we only consider about magnitude correlation
ex: (1.2, -9.8, 5.0, 3.4) → (2, 1, 4, 3)

Using BIT
int ans = 0;
void solve() {
for (int i = 1; i <= n; ++i) {
ans += i - 1 - get(a[i]);
add(a[i], 1);
}
}

D-Query
Problem:
Given an array n number A[1], A[2], ..., A[n]
and m queries as follows (n ~ 3x10^4, m ~
2x10^5, 1 <= A[i] <= 10^6)
query : (l, r) return number of distinct
elements in subarray A[l], A[l+1], ..., A[r]
→ Cann’t solve with naive solution

D-Query
Solution with BIT
[1] Sort queries based on right value
(l1,r1), (l2,r2), ..., (lm, rm)
→ r1 <= r2 <= ... <= rm
[2] Go through array from left to right, using
index[] to save last position each value
→ index[x] is last position of x in current array

D-Query
Solution with BIT
[3] Current value a[i]
＊if index[a[i]] != i then update index[a[i]] = i
＊if there is some r[j] = i then calculate
answer and go to next queries
＊else go to next postion
[4] Print answers

D-Query
struct queries {
int l, r, id;
};
bool comp(queries x, queries y) {
return x.r < y.r;
}
sort(queries.begin(), queries.end(), comp);

D-Query
for (int j = 0, i = 1; j < num_queries;) {
if (index[a[i]] != i) {
bit.add(index[a[i]], -1);
index[a[i]] = i;
bit.add(i, 1);
}
if (queries[j].r == i) {
ans[queries[j].id] += bit.get(i) – bit.get(queries[j].l – 1);
j++;
}
else i++;
}

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
index[1] = -1
index[2] = -1
index[3] = -1
3 queries
[2, 4]
[1, 5]
[3, 5]

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 1
→ bit.add(-1, -1) , bit.add(1, 1)
index[2] = -1
index[3] = -1

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 2
→ bit.add(1, -1) , bit.add(2, 1)
index[2] = -1
index[3] = -1

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 2
index[2] = 3
→ bit.add(-1, -1) , bit.add(3, 1)
index[3] = -1

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
→ bit.add(2, -1) , bit.add(4, 1)
→ ans[2] = bit.get(4) – bit.get(1)
index[2] = 3
index[3] = -1

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
index[2] = 3
index[3] = 5
→ bit.add(-1, -1) , bit.add(5, 1)

D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
index[2] = 3
index[3] = 5

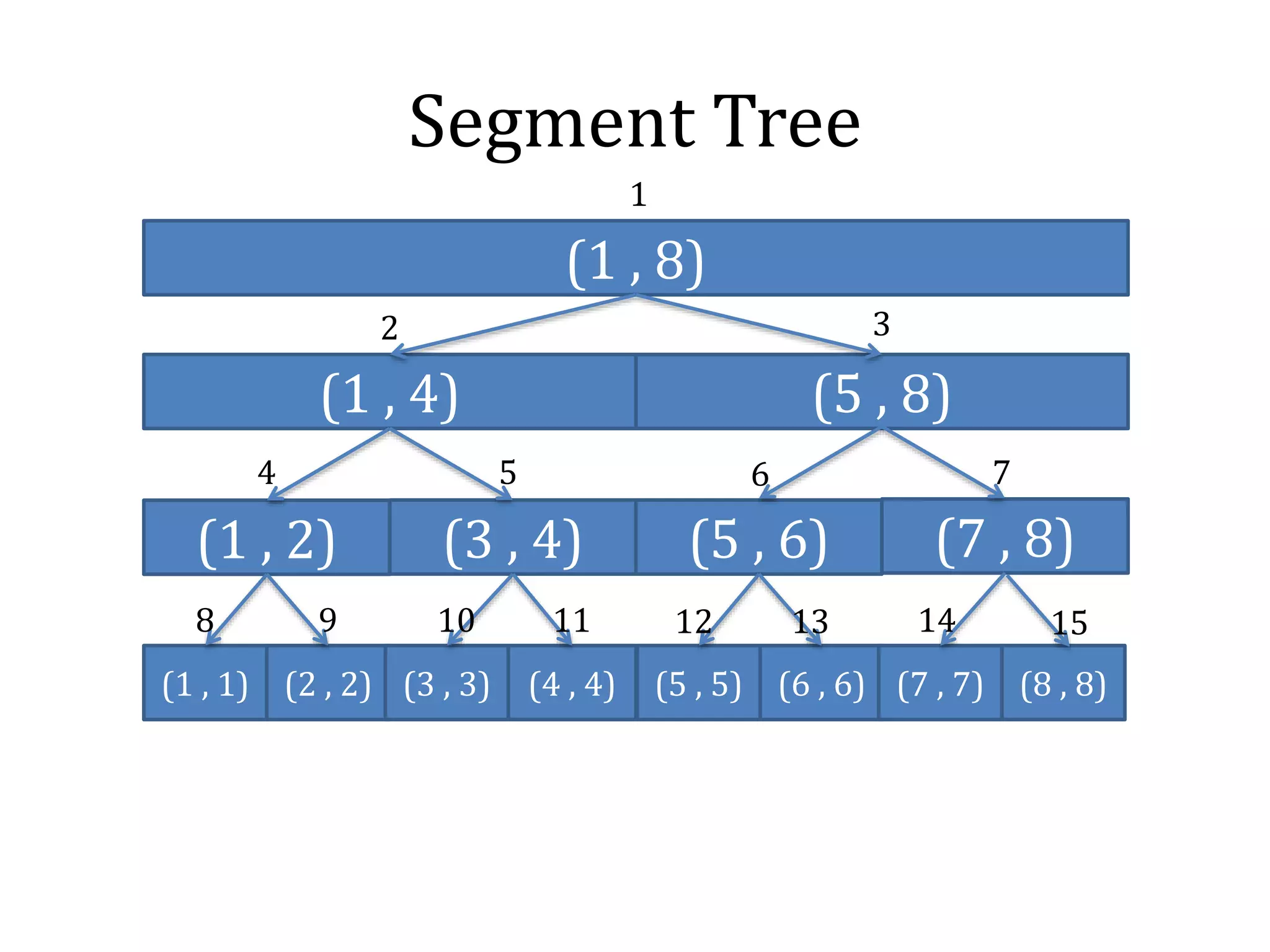
Segment Tree
Problem:
Give an array A[1], A[2], ..., A[n] and m queries
as follows (n, m ~ 10^6)
type 1: add x to A[k]
type 2: calculate max, min on interval [l, r]

Segment Tree
Naive solution
Same as previous one
type 1: O(1)
type 2: O(n)
→ time complexity O(mn)
→ impossible when n, m ~ 10^6

Segment Tree
• Discoverd by Bentley in 1977 in “Solution to
Klee’s rectangle problems”
• Support fast operations on interval

Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]

Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[2]

Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[6]

Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get max on [3,8]

Segment Tree
• Each node of tree is an interval [l, r]
• If l < r, it has two children [l, m] and [m+1, r]
with m = (l + r)/2
• Length of array is n → total node of tree is
1 + 2 + 4 + ... + 2^k = 2^(k+1) – 1
k is smallest number such that 2^k >= n
→ total node <= 4n, memory O(n)

Segment Tree
(1 , 4) (5 , 8)
(1 , 8)
(1 , 2) (3 , 4) (5 , 6) (7 , 8)
(1 , 1) (2 , 2) (3 , 3) (4 , 4) (5 , 5) (6 , 6) (7 , 7) (8 , 8)
1
2 3
4 5 6 7
8 9 10 11 12 13 14 15

Segment Tree
＊Initialize: build(1, 1, n)
void build(int node, int l, int r) {
if (l == r) {sg[node] = A[l]; return;}
int m = (l + r)/2;
build(node * 2, l, m);
build(node * 2 + 1, m + 1, r);
sg[node] = max(sg[node * 2], sg[node * 2 + 1]);
} → O(n)

Segment Tree
＊Add x to A[k]: update(1, 1, n, k, x)
void update(int node, int l, int r, int k, int x) {
if (l == r) {sg[node] = A[k] + x; return;}
int m = (l + r)/2;
if (m >= k) update(node * 2, l, m, k, x);
else update(node * 2 + 1, m + 1, r, k, x);
sg[node] = max(sg[node * 2], sg[node * 2 + 1]);
} → O(log(n))

Segment Tree
＊Get max on interval [l,r]: query(1, 1, n, l, r)
int query(int node, int i, int j, int l, int r) {
if (l<=i && j <= r) {return sg[node];}
int m = (i + j)/2;
if (m >= r) return query(node * 2, i, m, l, r);
else if (m < l) return query(node * 2 + 1, m + 1, j, l, r);
else return max(query(node * 2, i, m, l, r),
query(node * 2 + 1, m + 1, j, l, r));
} → O(log(n))

Treap
• What is treap?
• Combination of tree and heap → treap
• Height of tree is proportional to log(n) with
high probability (n is number of keys in
tree)
• Each node has two attributes: key and
priority number
• Key is binary-tree ordered, priority number
is heap ordered

Treap
• Support search, insertion, deletion, merge
and split
• When insert a key, priority number is
randomed → time complexity of all
operations are expected O(log(n))

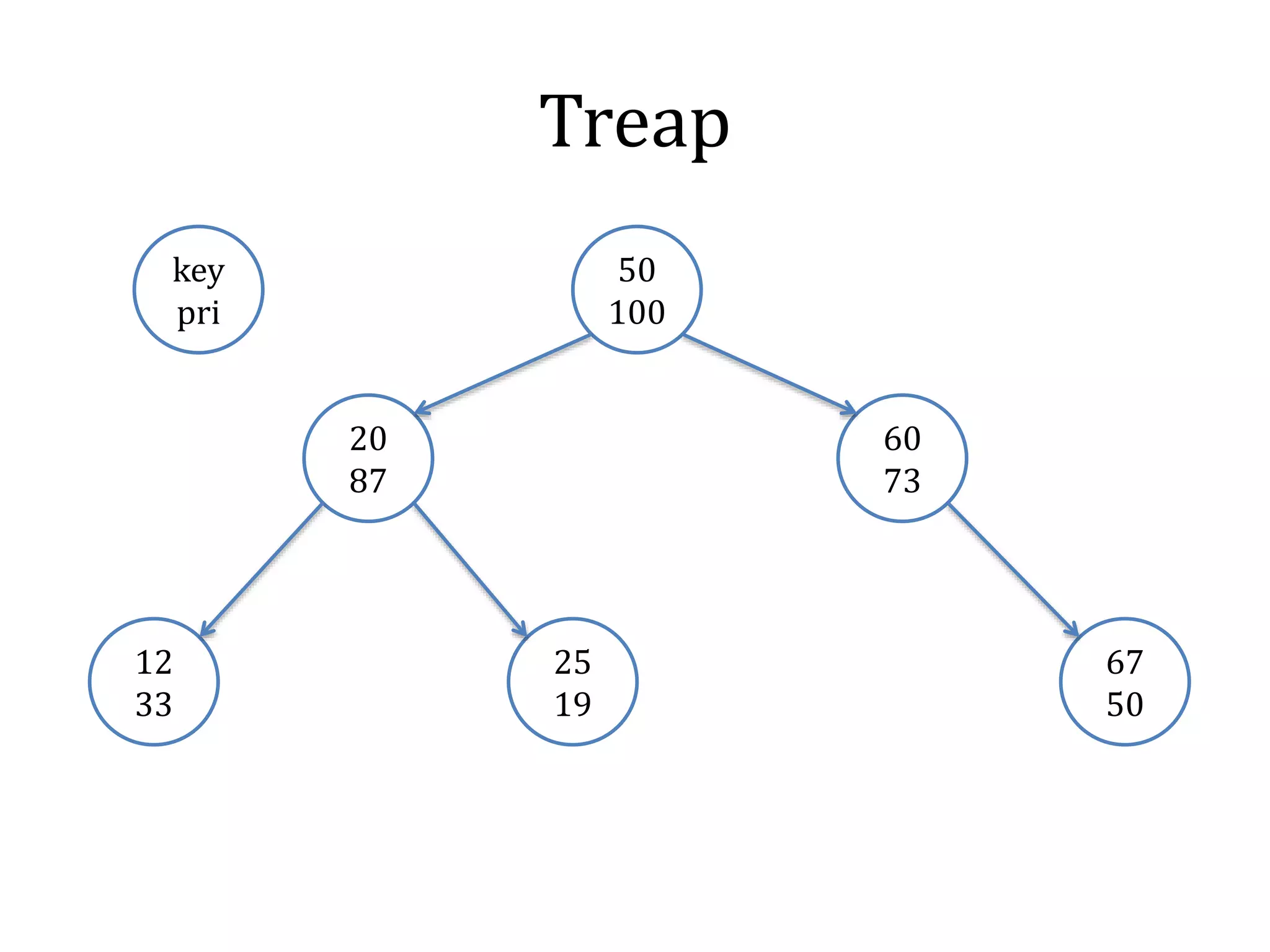
Treap
50
100
67
50
25
19
12
33
60
73
20
87
key
pri

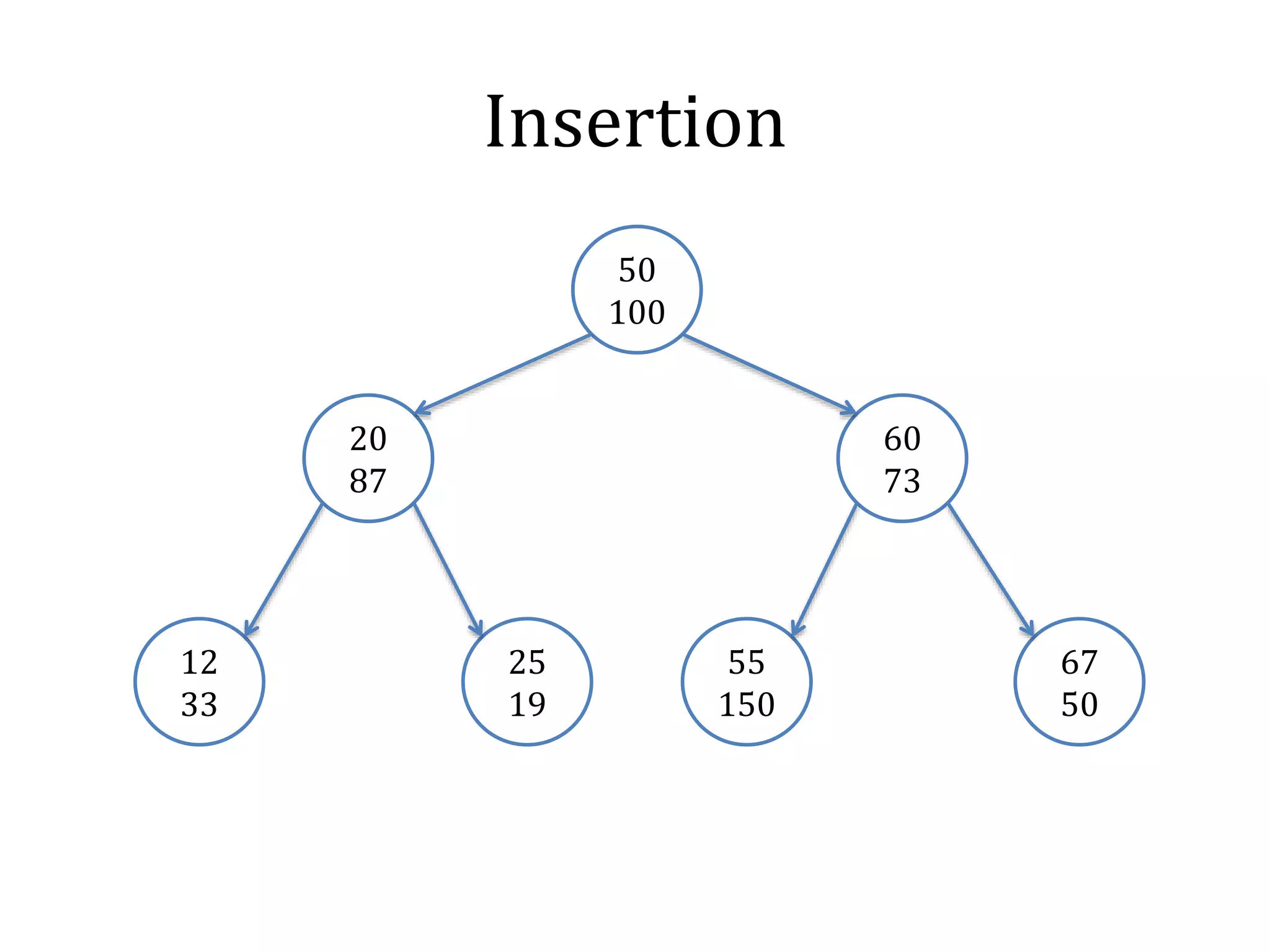
Treap
typedef struct node {
int val, pri, cnt, sum;
struct node * child[2];
node(int v, int p) : val(v), pri(p), cnt(1), sum(v) {
child[0] = child[1] = NULL;
}
} * node_t;

Treap
int count(node_t t) {
return t ? t->cnt : 0;
}
int sum(node_t t) {
return t ? t->sum : 0;
}
node_t update(node_t t) {
t->cnt = count(t->child[0]) + count(t->child[1]) + 1;
t->sum = sum(t->child[0]) + sum(t->child[1]) + t->val;
return t;
}

Insertion
• Randomize a priority number
• Insert node to tree as binary search tree
• Rotate tree until priority number is heap-
ordered
• Expected time complexity: O(log(n))

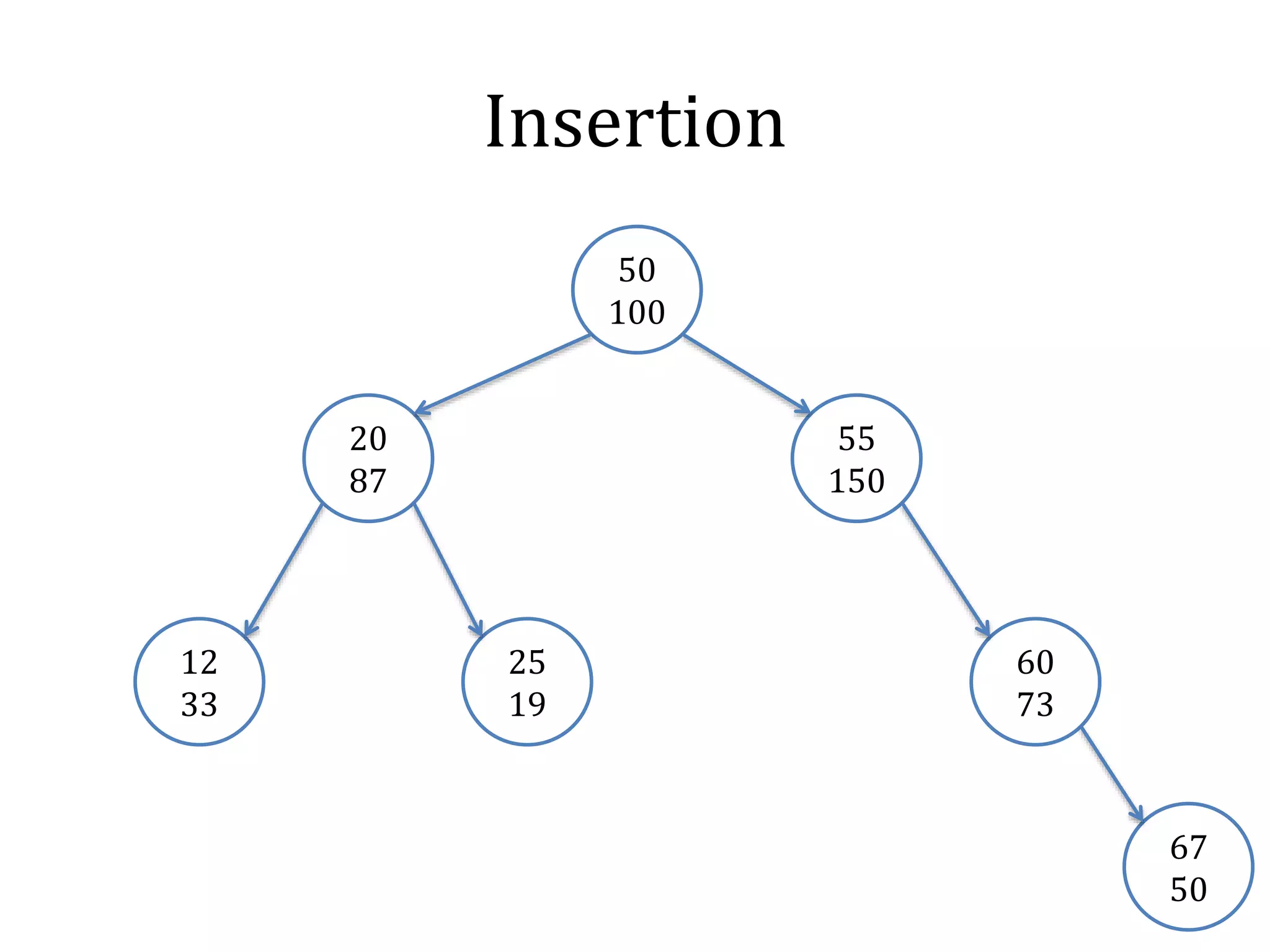
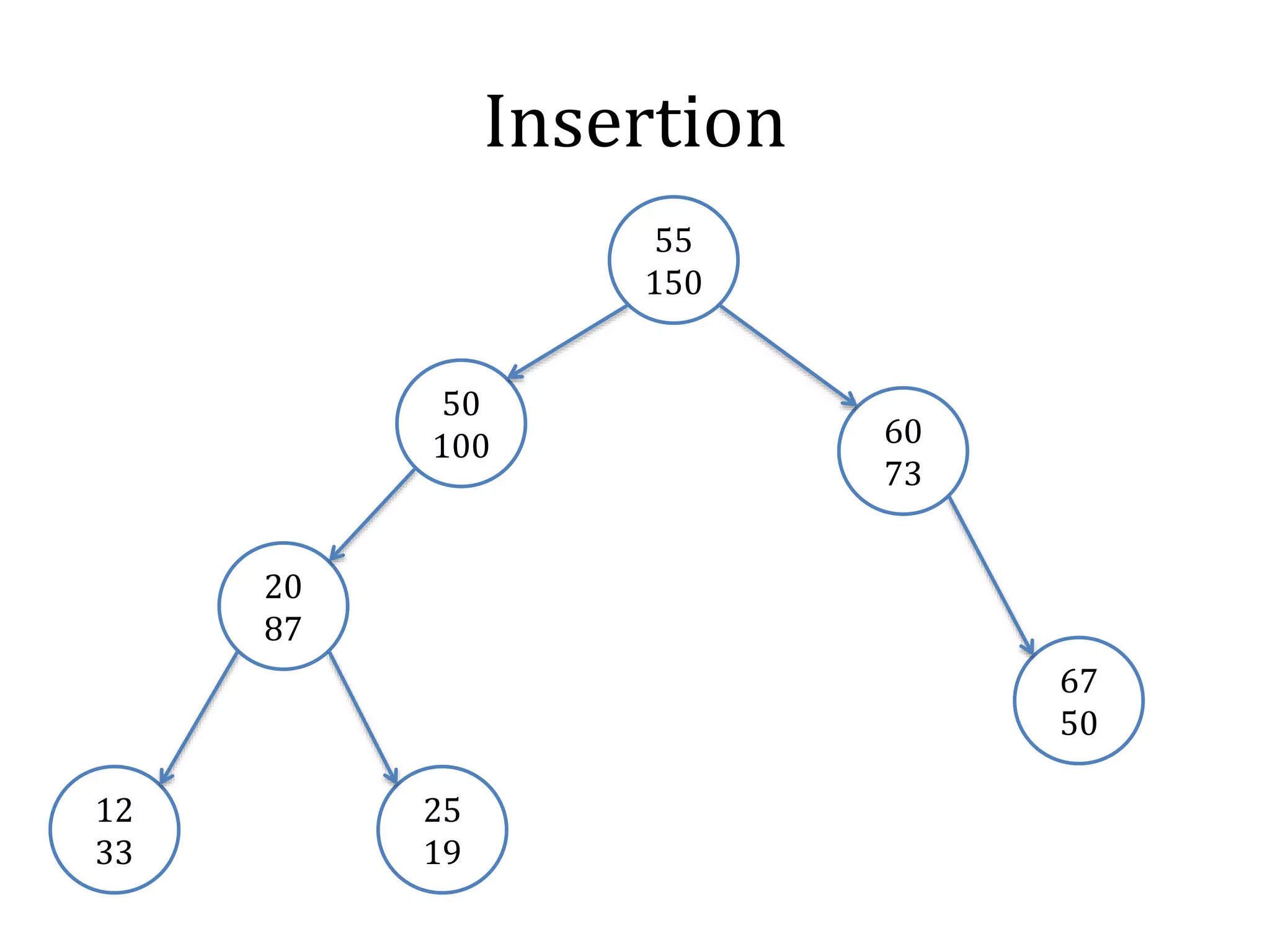
Insertion
50
100
67
50
25
19
12
33
60
73
20
87
55
150

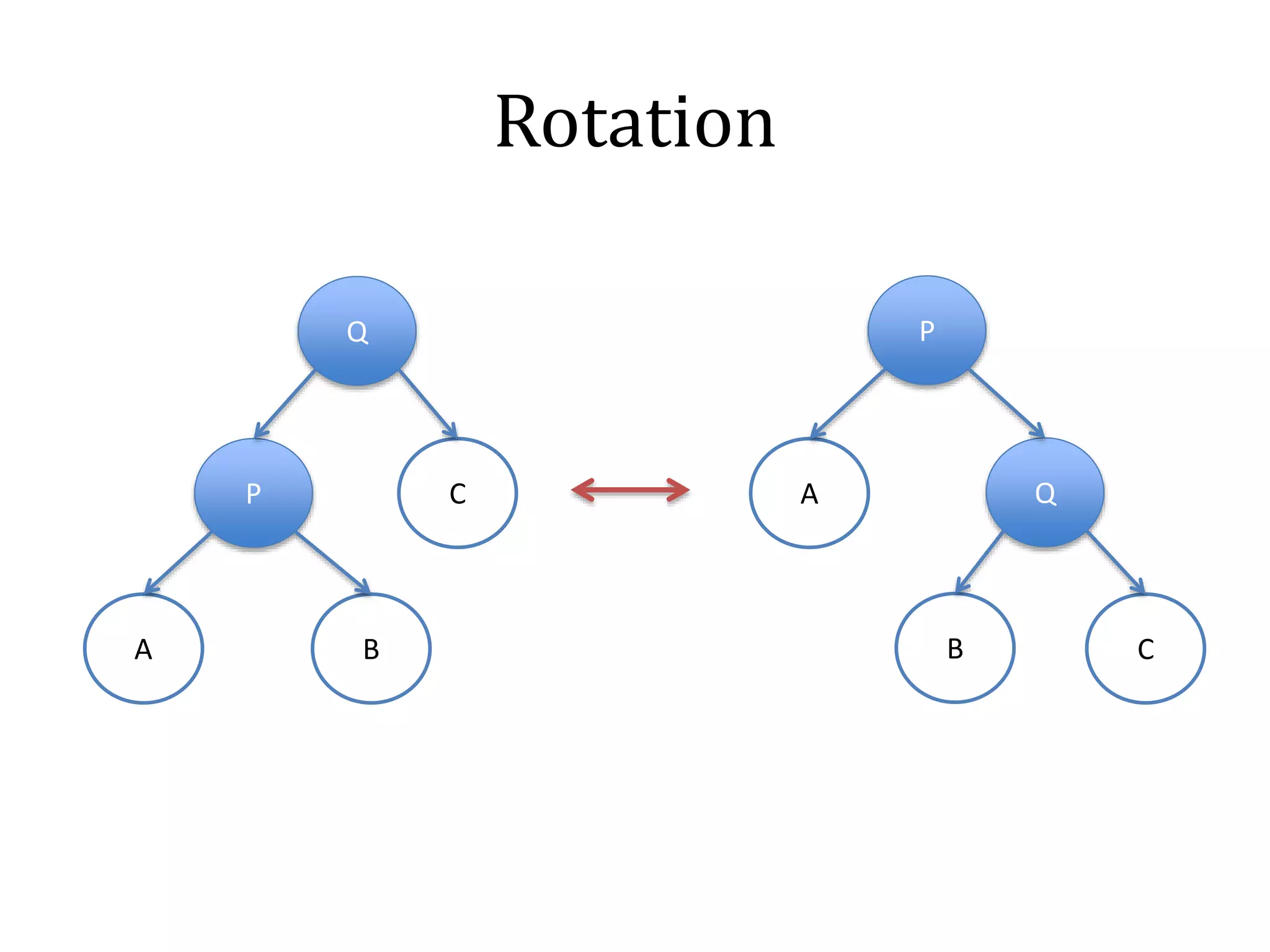
Rotation
node_t rotate(node_t t, int b) {
node_t s = t->child[b];
t->child[1-b] = s->child[b];
s->child[b] = t;
update(t);
update(s);
return s;
}

Deletion
• Find node as binary search tree
• Bring node to leaf and delete
• Rotate tree until priority number is heap-
ordered

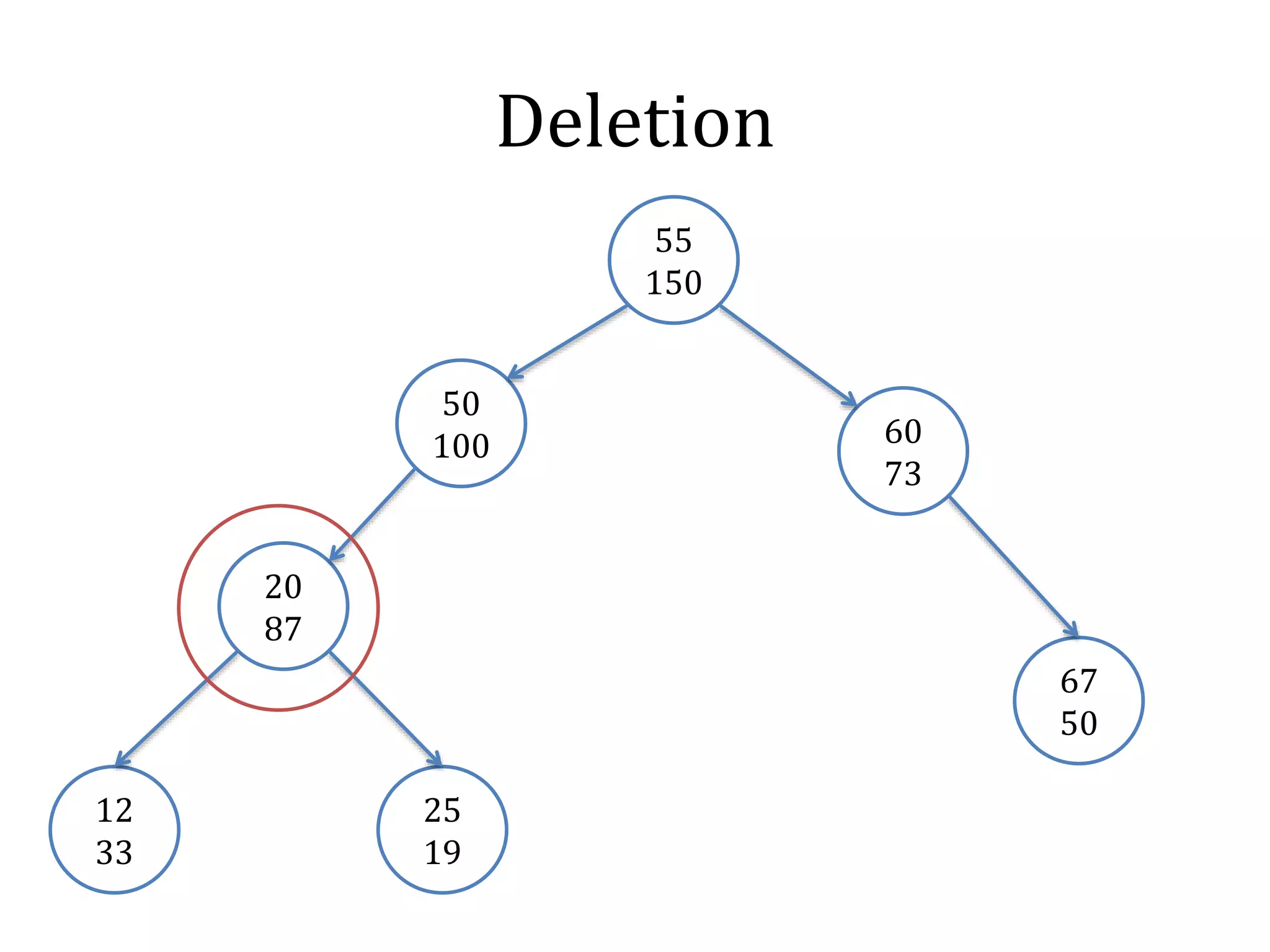
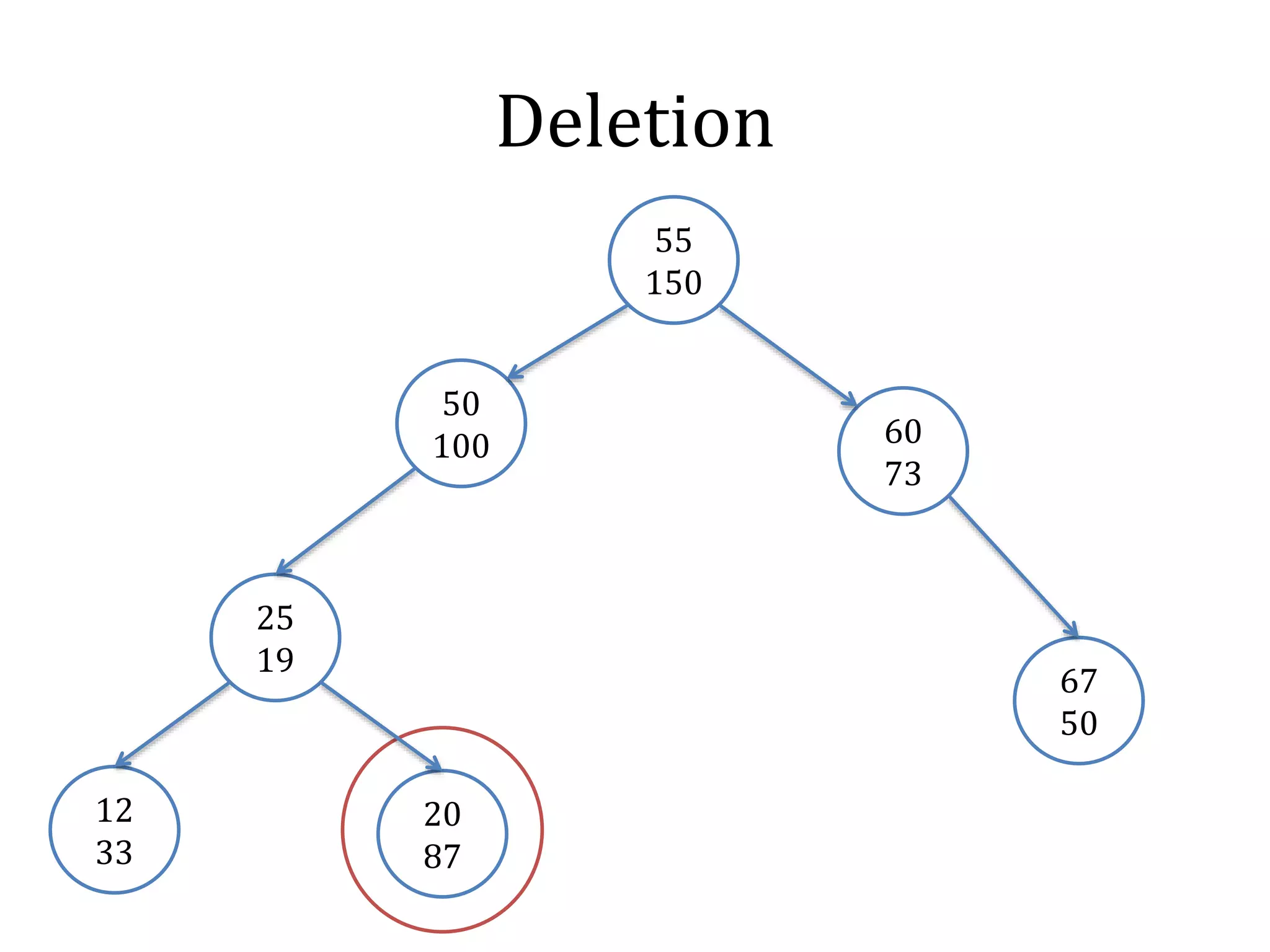
Deletion
50
100
67
50
25
19
12
33
60
73
20
87
55
150

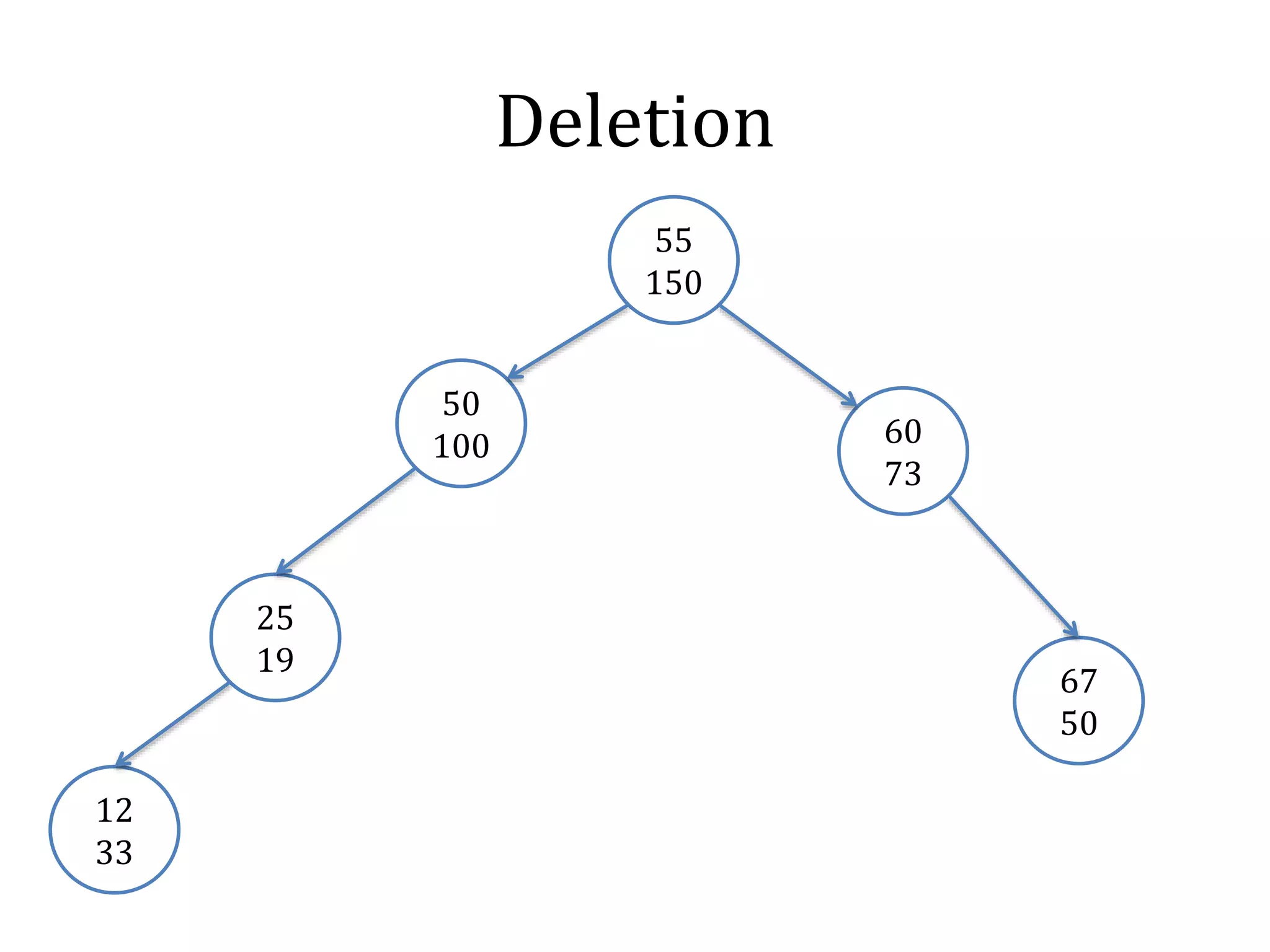
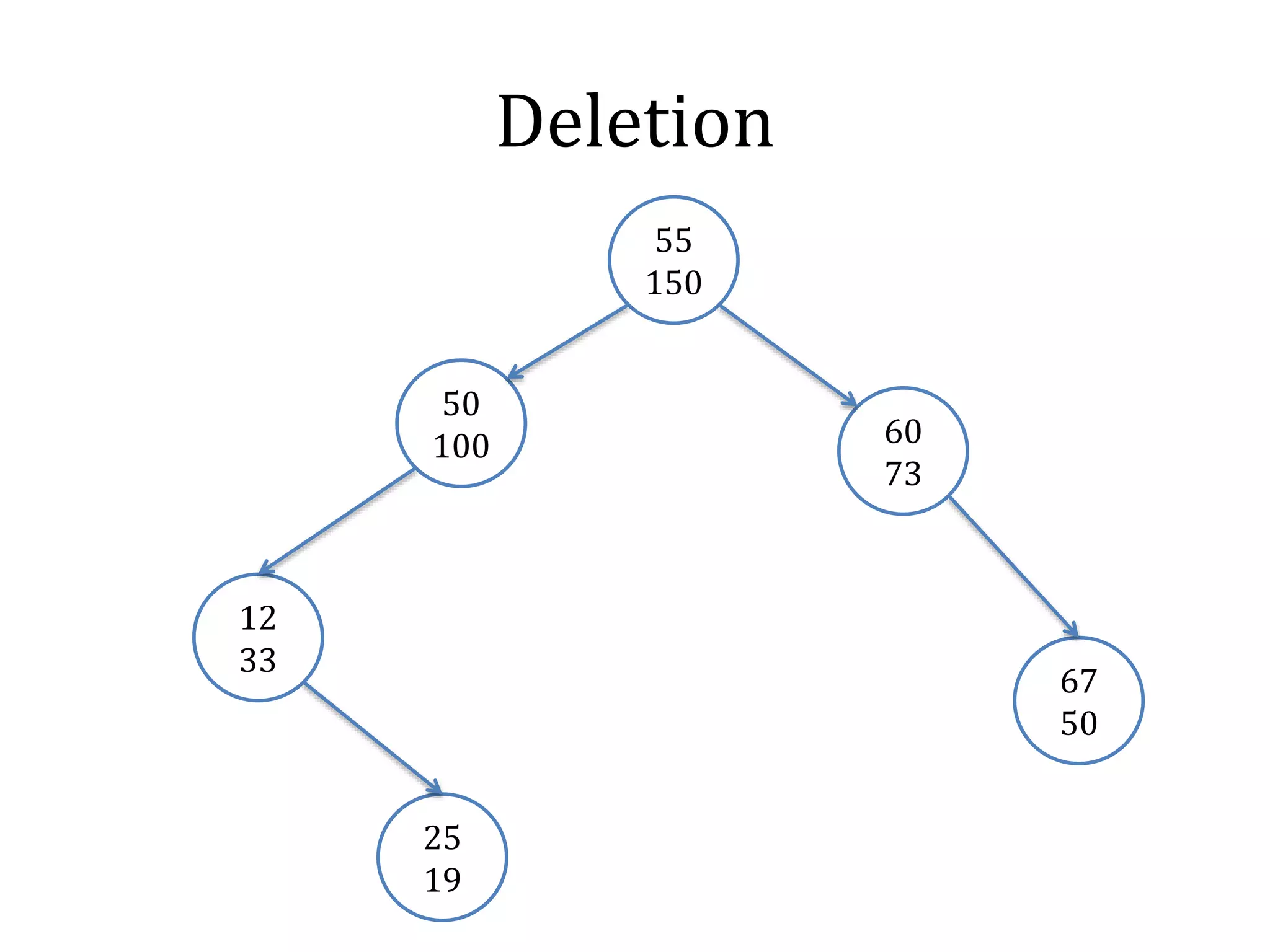
Deletion
50
100
67
50
25
19
12
33
60
73
55
150

Merge-Split
• Merge two treaps into one
• Split treap into two treaps
• Implement indirectly by insertion and
deletion
• Implement directly

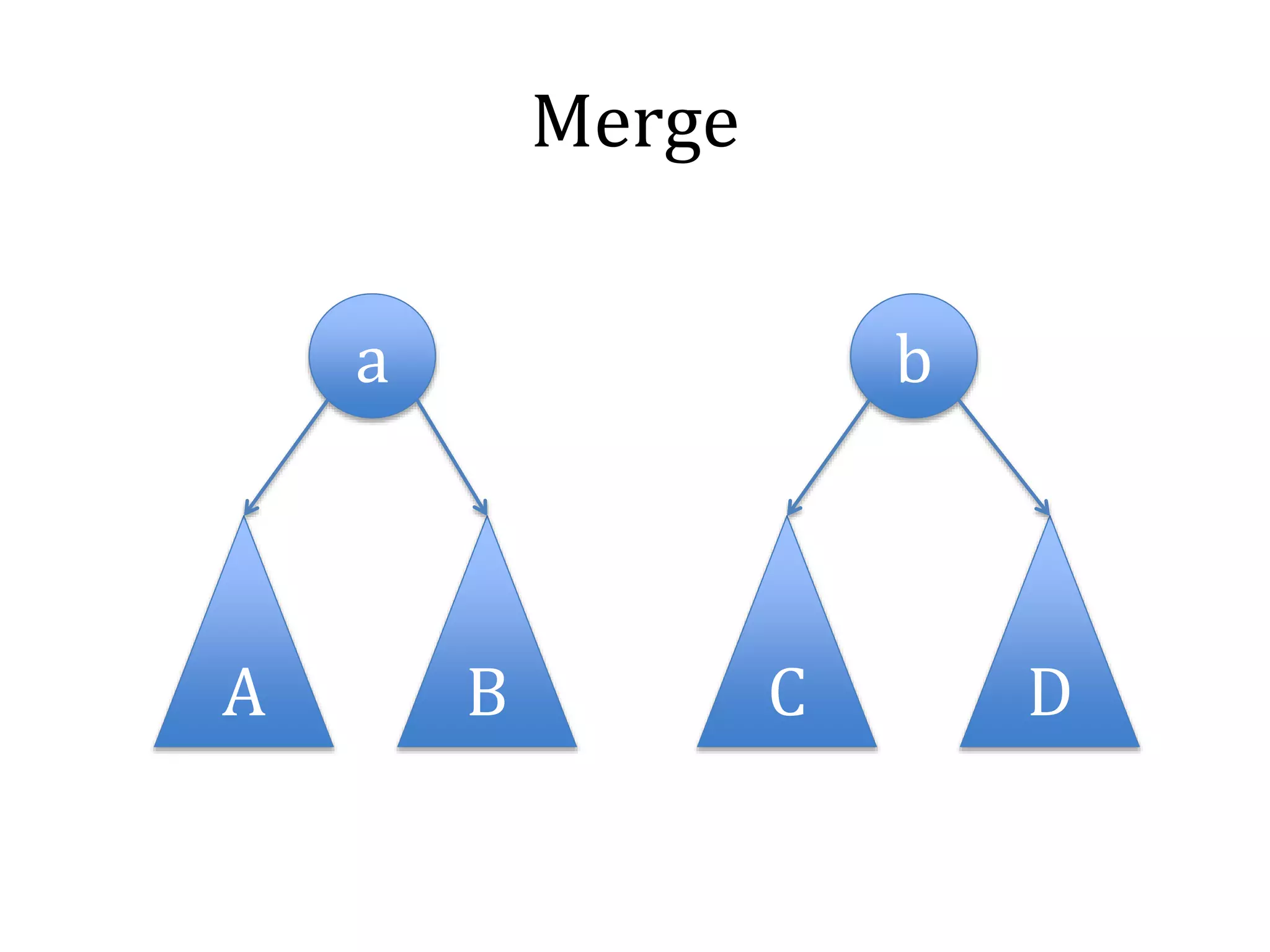
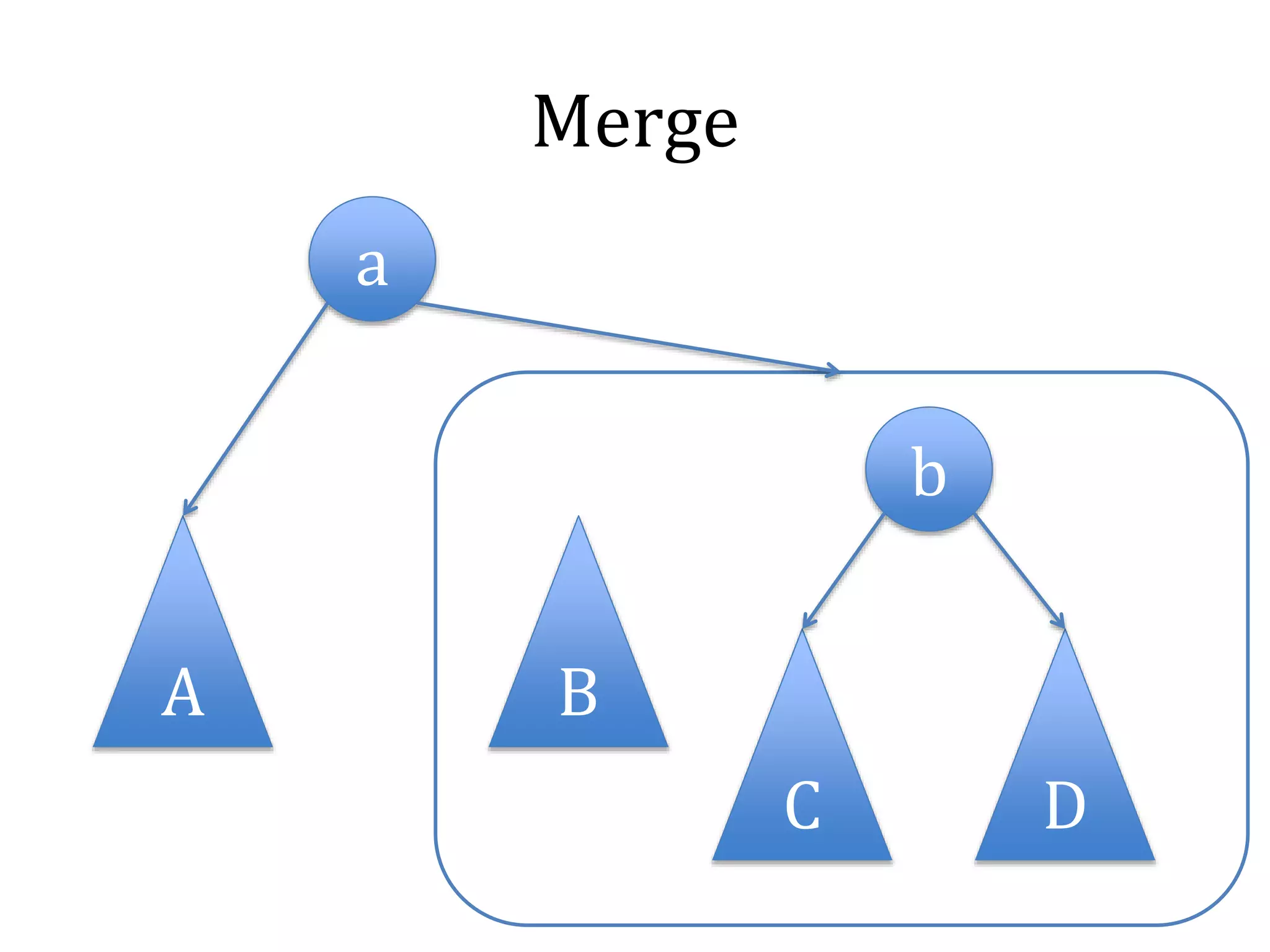
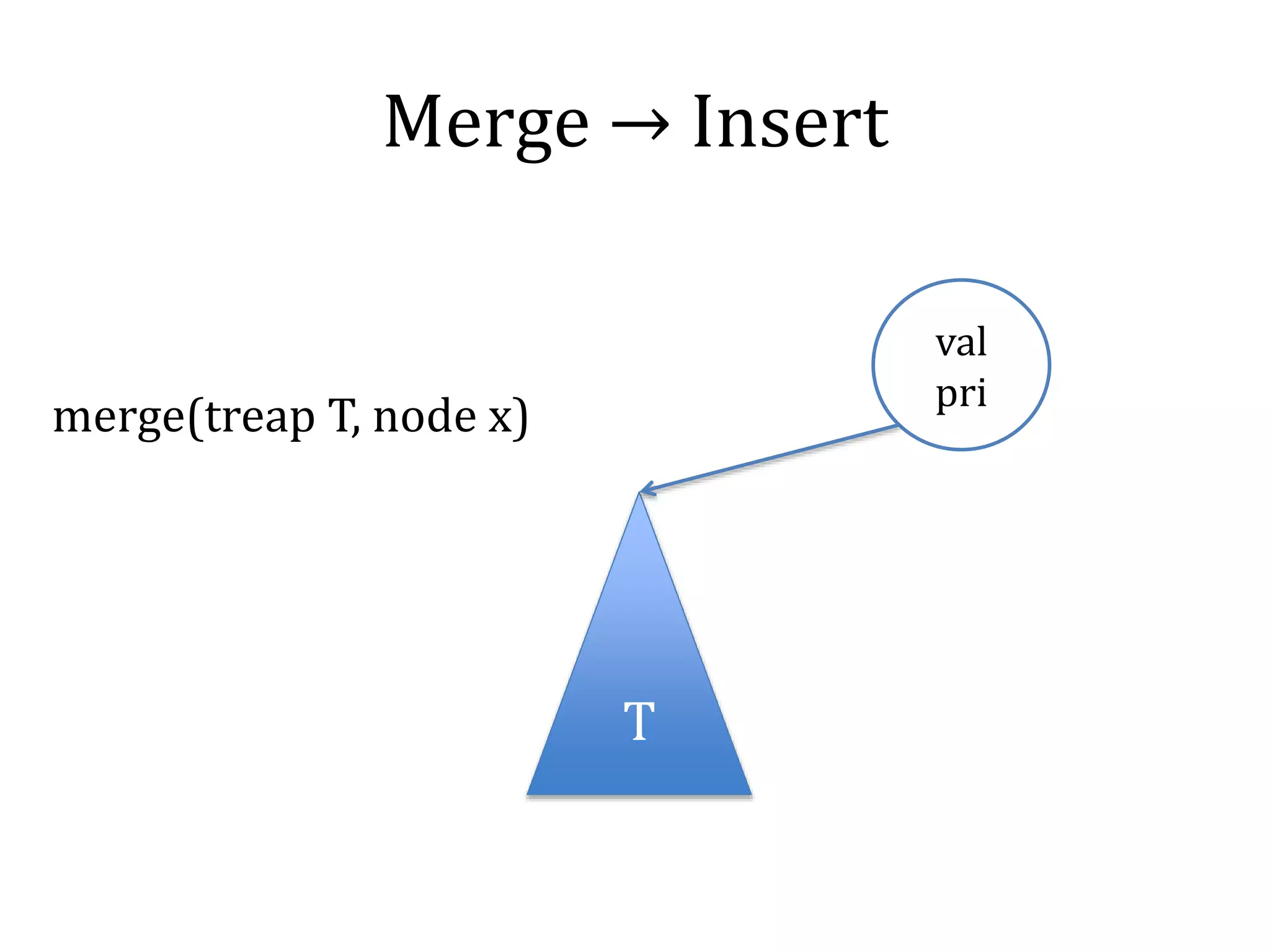
Merge
node_t merge(node_t l, node_t r) {
if (!l || !r) return !l ? r : l;
if (l->pri > r->pri) {
l->child[1] = merge(l->child[1], r);
return update(l);
}
else {
r->child[0] = merge(l, r->child[0]);
return update(r);
}
}

Merge → Insert
T
val
pri
merge(treap T, node x)

Datastructure tree

More Related Content

What's hot

Viewers also liked

Similar to Datastructure tree

Recently uploaded

Datastructure tree