Downloaded 130 times
Uploaded byHimani Solanki
Decision Table Based Testing
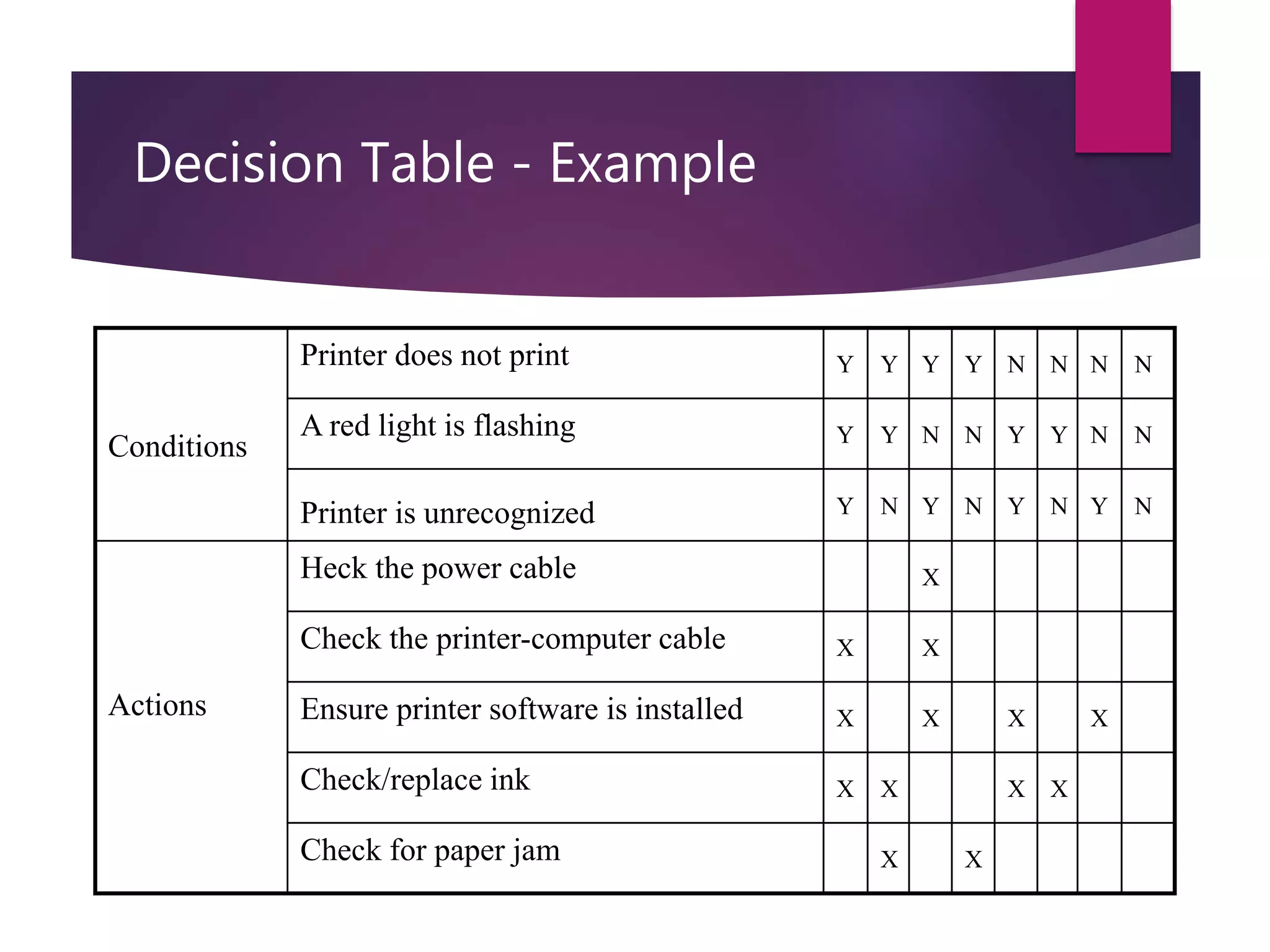
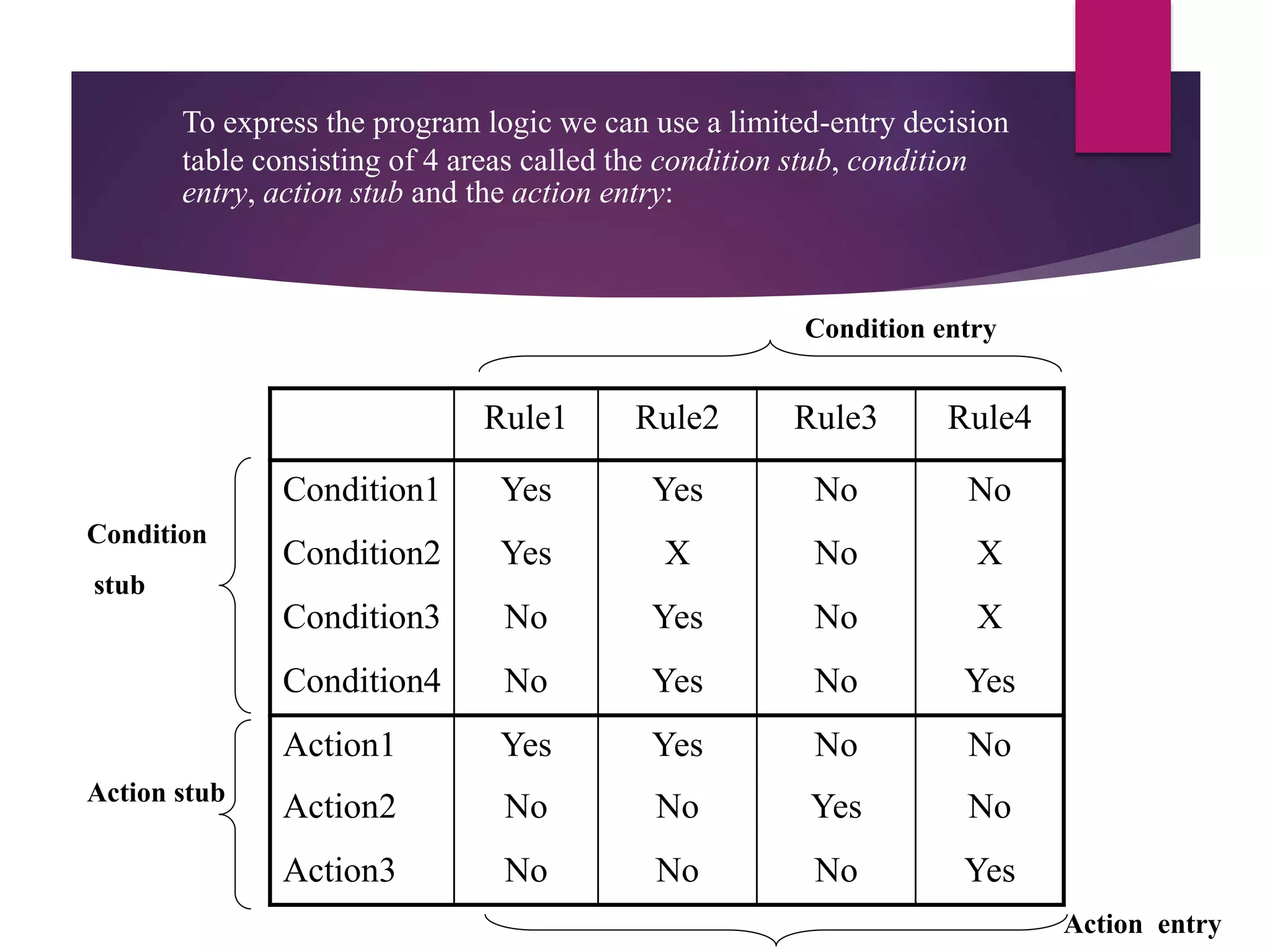
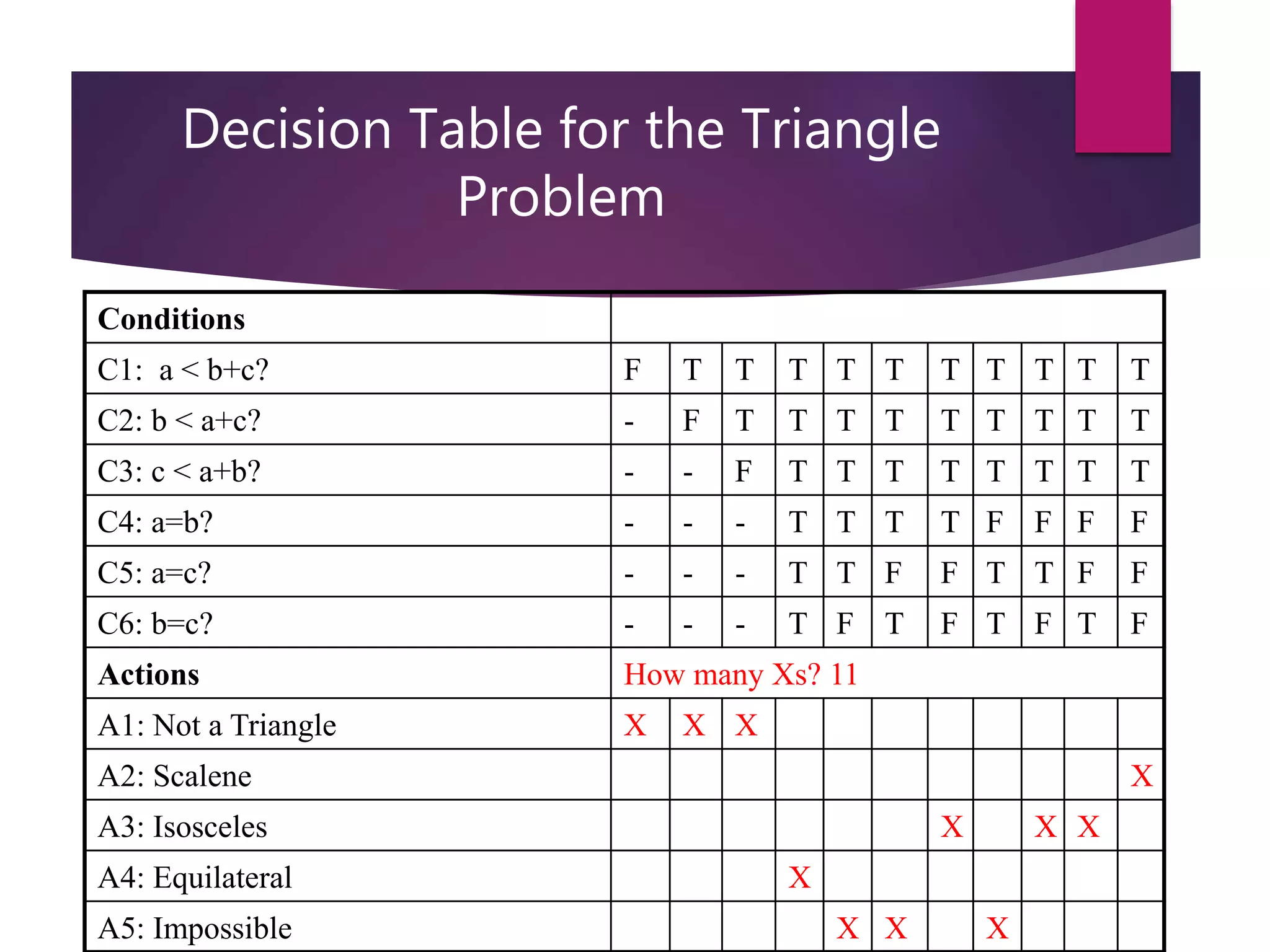
The document discusses decision table-based testing, which models complex logic by providing a set of conditions and corresponding actions. It outlines the structure of decision tables, including condition stubs, action stubs, and various examples, emphasizing their utility in representing logical relationships. Decision tables enable a clear visualization of input/output dependencies and can effectively handle multiple conditions and actions.
More Related Content
Similar to Decision Table Based Testing
Decision Table Based Testing
- 1. DECISION TABLE BASEDTESTING HIMANI SOLANKI IT/8TH SEM 06713503112
- 2. DECISION TABLE DecisionTable provides set of conditions and their corresponding action. O/P may depend on I/P conditions and decision table gives pictorial view of various combination of I/P conditions. Decision tables are a precise yet compact way to model complicated logic. Decision tables can associate many independent conditions with several actions in an elegant way. Decision table are used to represent complex logical relationship.
- 3. Decision Tables -Structure Conditions - (Condition stub) Condition Alternatives – (Condition Entry) Actions – (Action Stub) Action Entries All conditions are represented here which is used to determine a particular action All possible actions are listed here. Values entered here are known as inputs. These are outputs that are dependent on functionality of the program
- 4. Decision Table -Example Conditions Printer does not print Y Y Y Y N N N N A red light is flashing Y Y N N Y Y N N Printer is unrecognized Y N Y N Y N Y N Actions Heck the power cable X Check the printer-computer cable X X Ensure printer software is installed X X X X Check/replace ink X X X X Check for paper jam X X
- 5. To express theprogram logic we can use a limited-entry decision table consisting of 4 areas called the condition stub, condition entry, action stub and the action entry: Rule1 Rule2 Rule3 Rule4 Condition1 Yes Yes No No Condition2 Yes X No X Condition3 No Yes No X Condition4 No Yes No Yes Action1 Yes Yes No No Action2 No No Yes No Action3 No No No Yes Condition stub Action stub Condition entry Action entry
- 6. Decision Table forthe Triangle Problem Conditions C1: a < b+c? F T T T T T T T T T T C2: b < a+c? - F T T T T T T T T T C3: c < a+b? - - F T T T T T T T T C4: a=b? - - - T T T T F F F F C5: a=c? - - - T T F F T T F F C6: b=c? - - - T F T F T F T F Actions How many Xs? 11 A1: Not a Triangle X X X A2: Scalene X A3: Isosceles X X X A4: Equilateral X A5: Impossible X X X