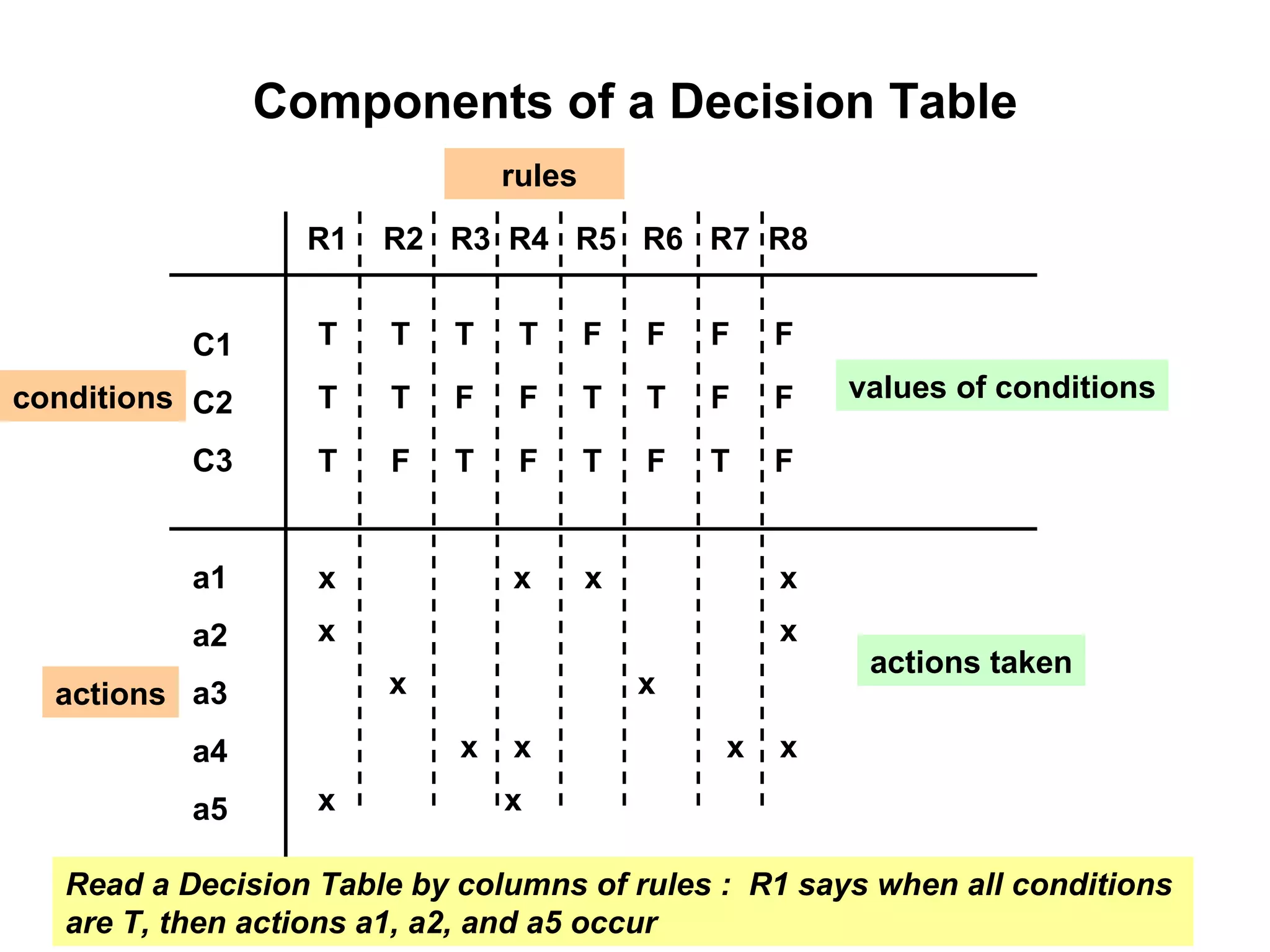
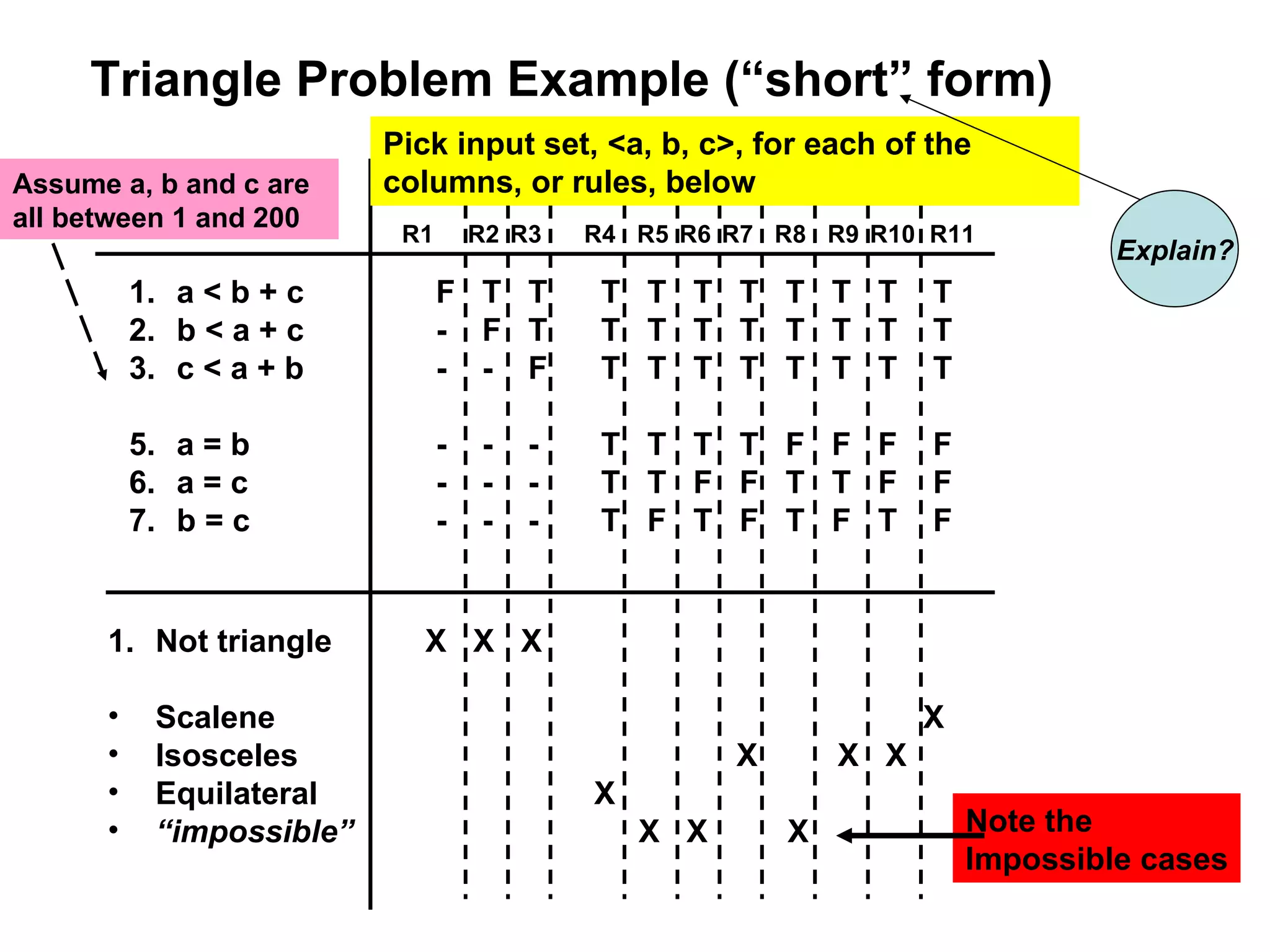
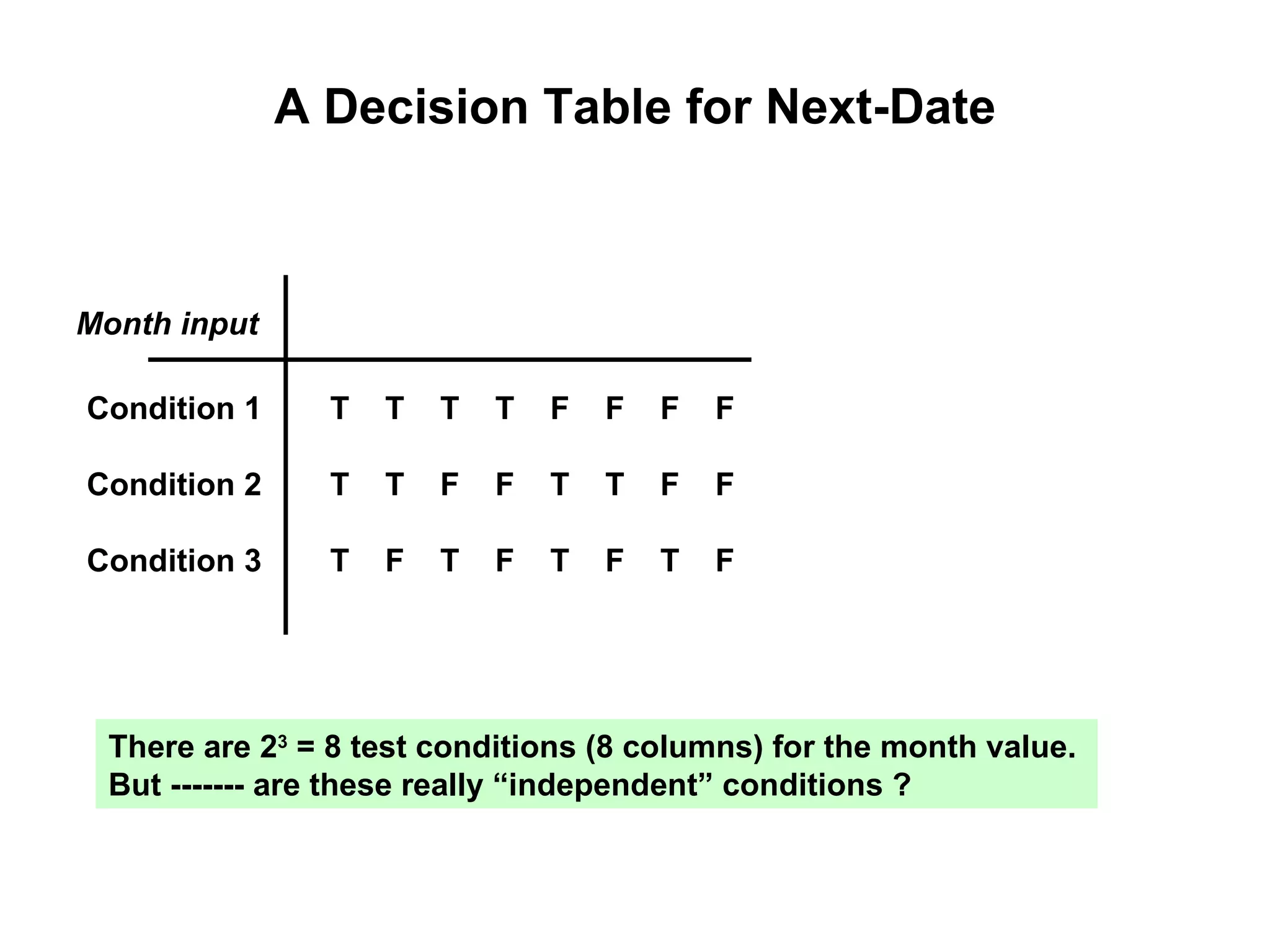
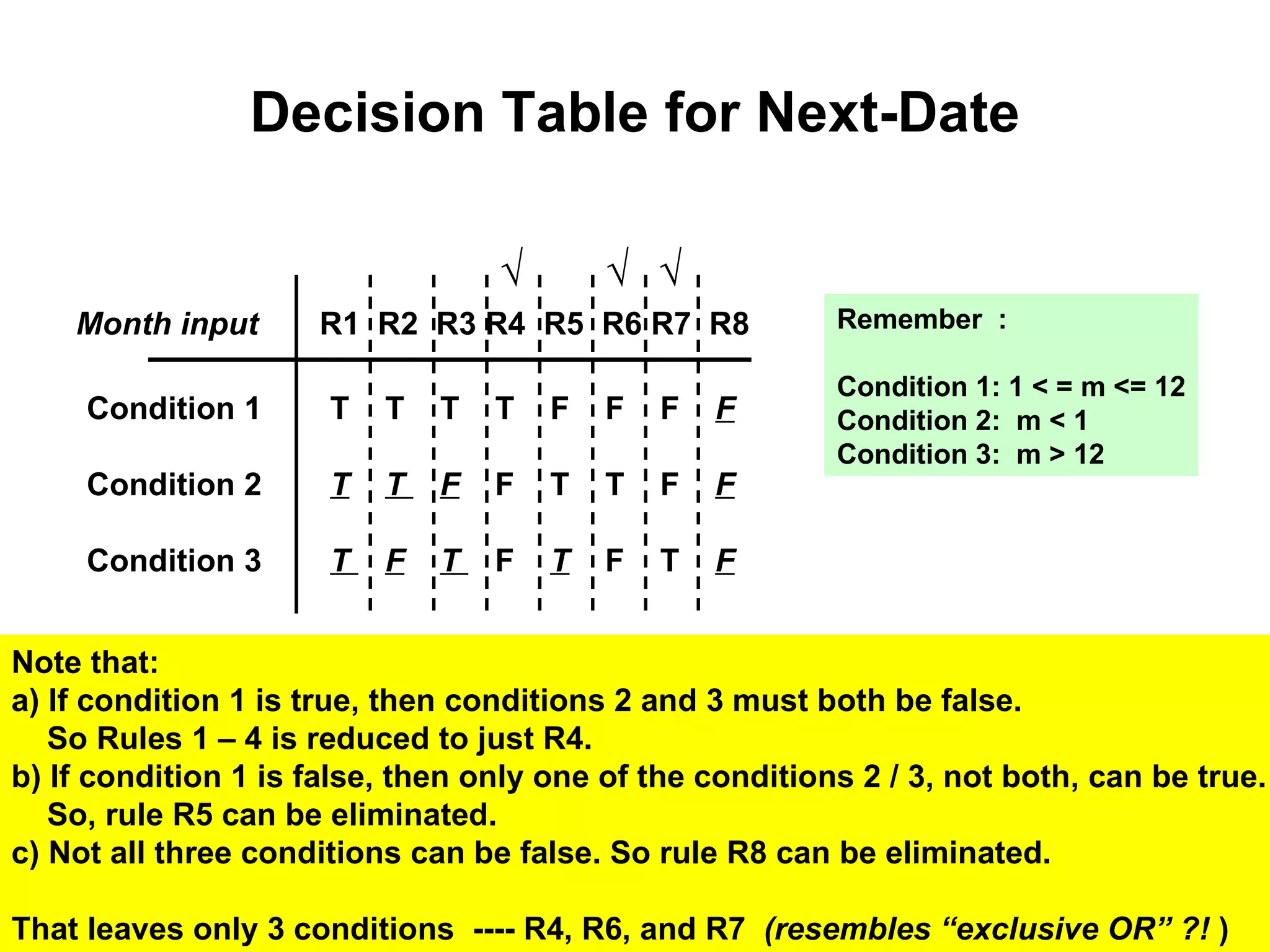
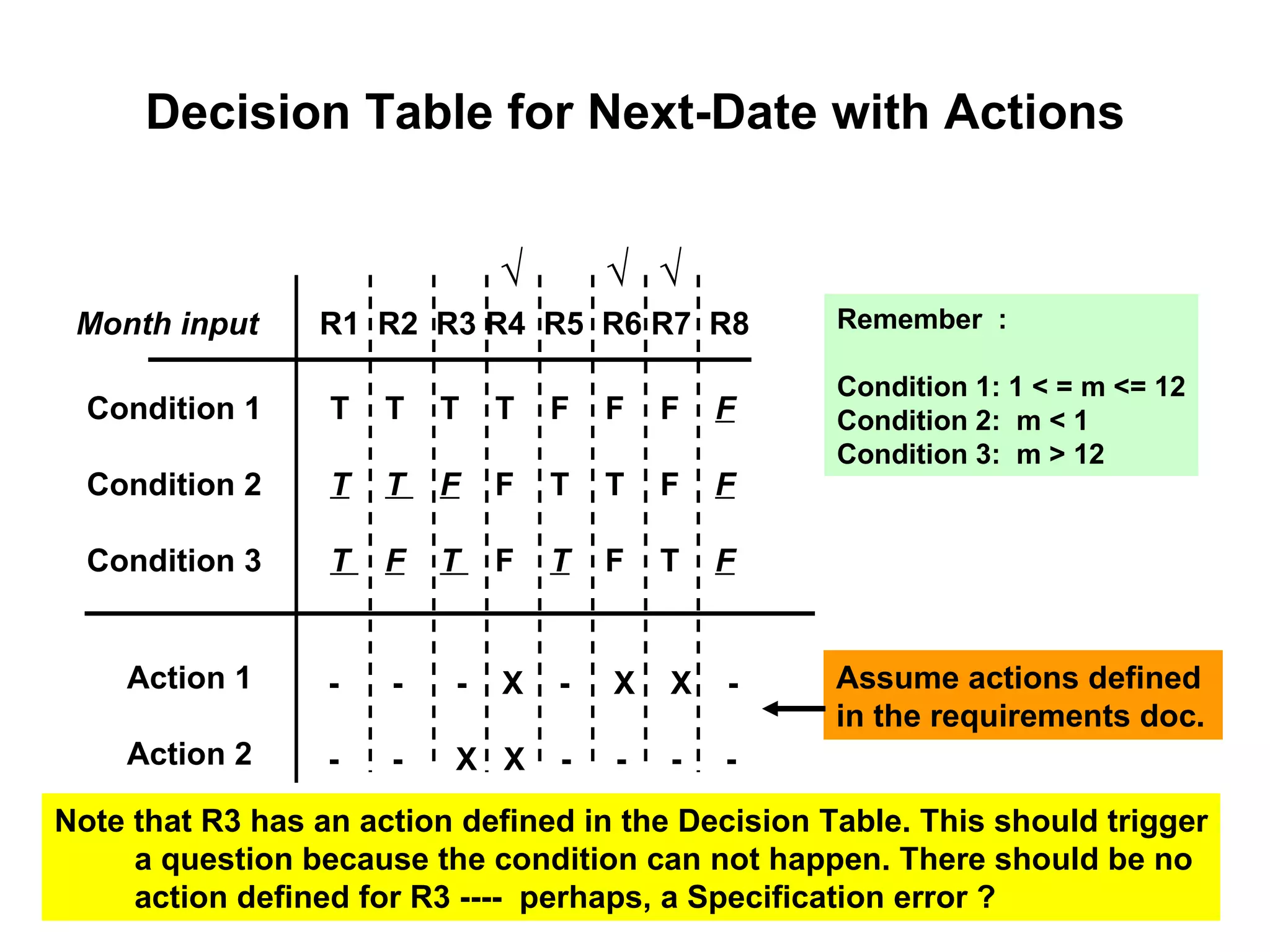
The document discusses decision table-based testing. A decision table lists conditions and their possible values along with corresponding actions. It allows testing all combinations of condition values to check for completeness and inconsistencies. While decision tables initially consider all combinations, some may be dependent or impossible, reducing the number of test cases needed. The document provides examples of using decision tables to test problems like determining triangle types and calculating next dates.