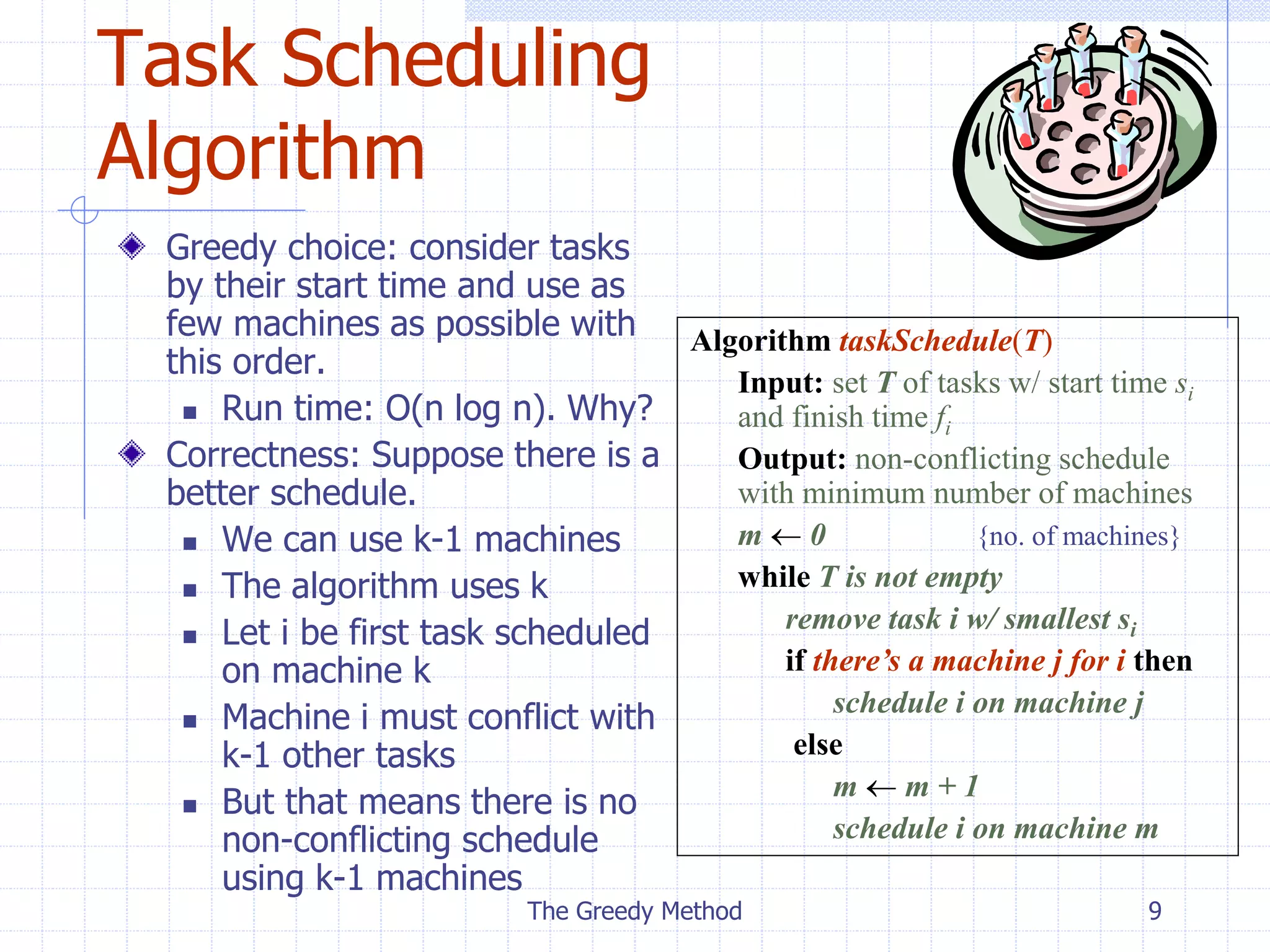
The document outlines the greedy method, an algorithm design paradigm that focuses on making locally optimal choices to find a globally optimal solution. It discusses specific applications of the greedy method, including the fractional knapsack problem and task scheduling, detailing the objective functions and algorithms for each. Examples illustrate the greedy choice property and the effectiveness of the method in achieving solutions with minimal resources.

![The Greedy Method 2
Outline and Reading
The Greedy Method Technique (§5.1)
Fractional Knapsack Problem (§5.1.1)
Task Scheduling (§5.1.2)
Minimum Spanning Trees (§7.3) [future lecture]](https://image.slidesharecdn.com/greedywithtaskschedulingalgorithm-221205041919-b5992690/75/Greedy-with-Task-Scheduling-Algorithm-ppt-2-2048.jpg)






![The Greedy Method 10
Example
Given: a set T of n tasks, each having:
A start time, si
A finish time, fi (where si < fi)
[1,4], [1,3], [2,5], [3,7], [4,7], [6,9], [7,8] (ordered by start)
Goal: Perform all tasks on min. number of machines
1 9
8
7
6
5
4
3
2
Machine 1
Machine 3
Machine 2](https://image.slidesharecdn.com/greedywithtaskschedulingalgorithm-221205041919-b5992690/75/Greedy-with-Task-Scheduling-Algorithm-ppt-10-2048.jpg)