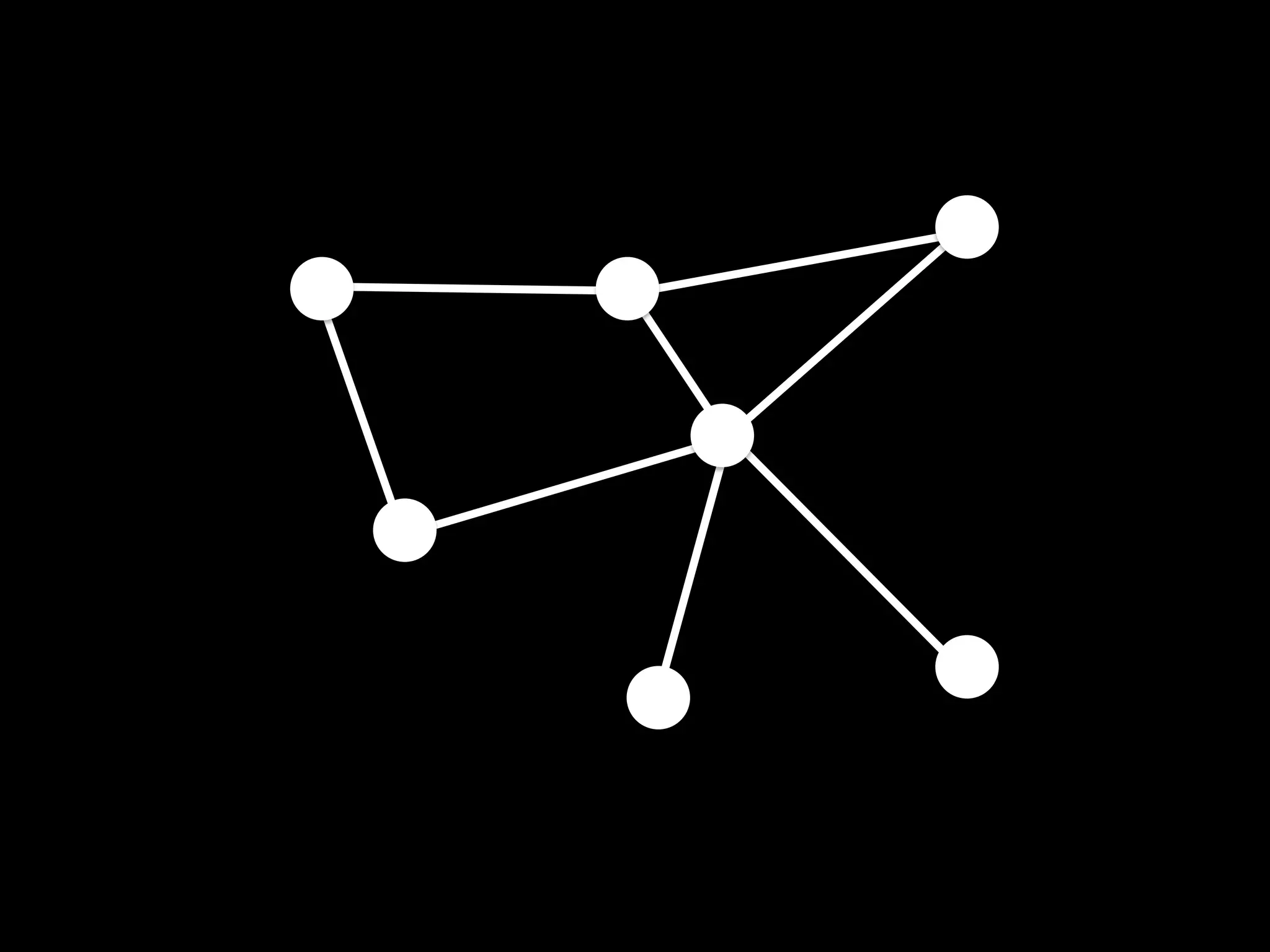
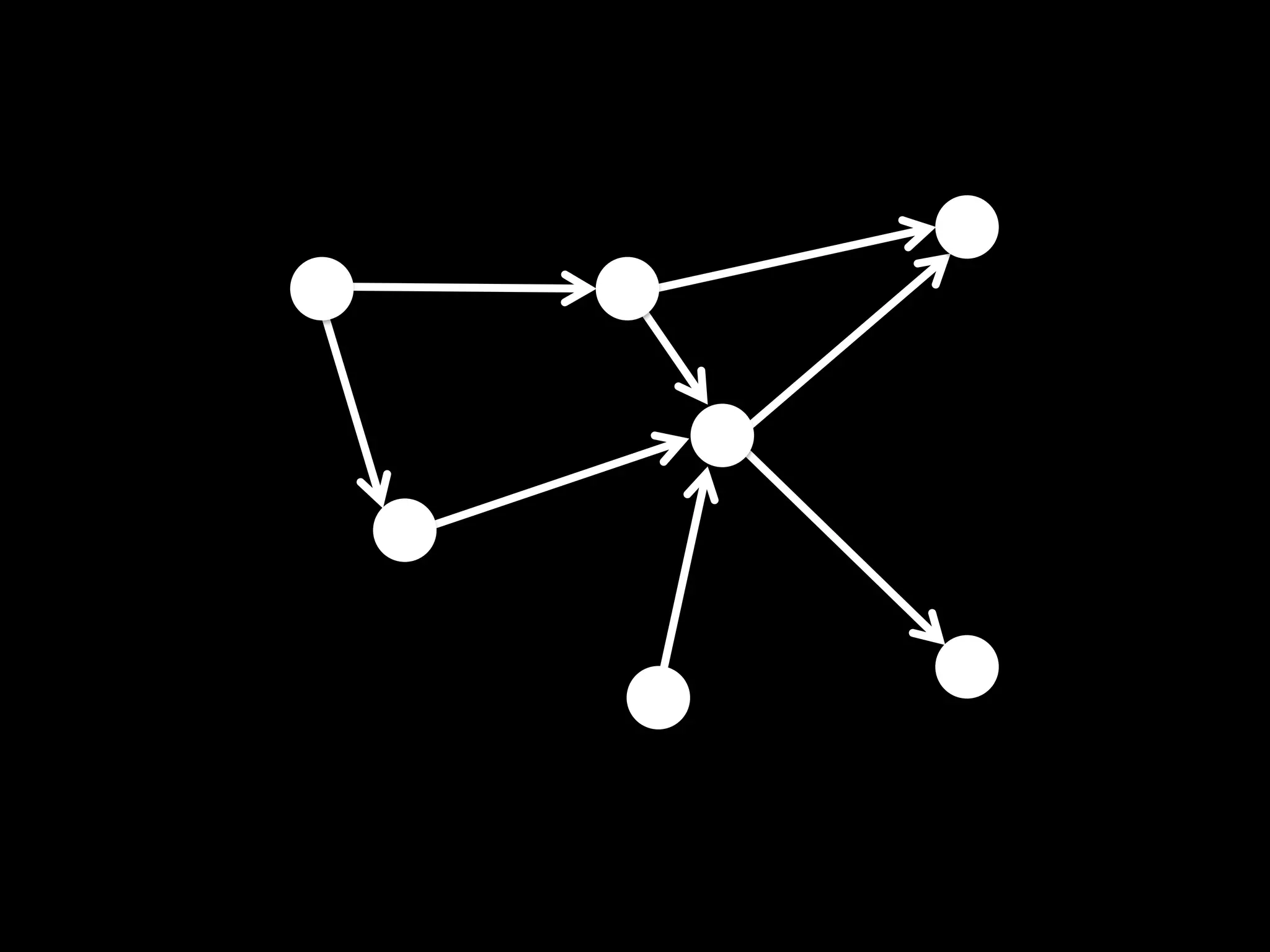
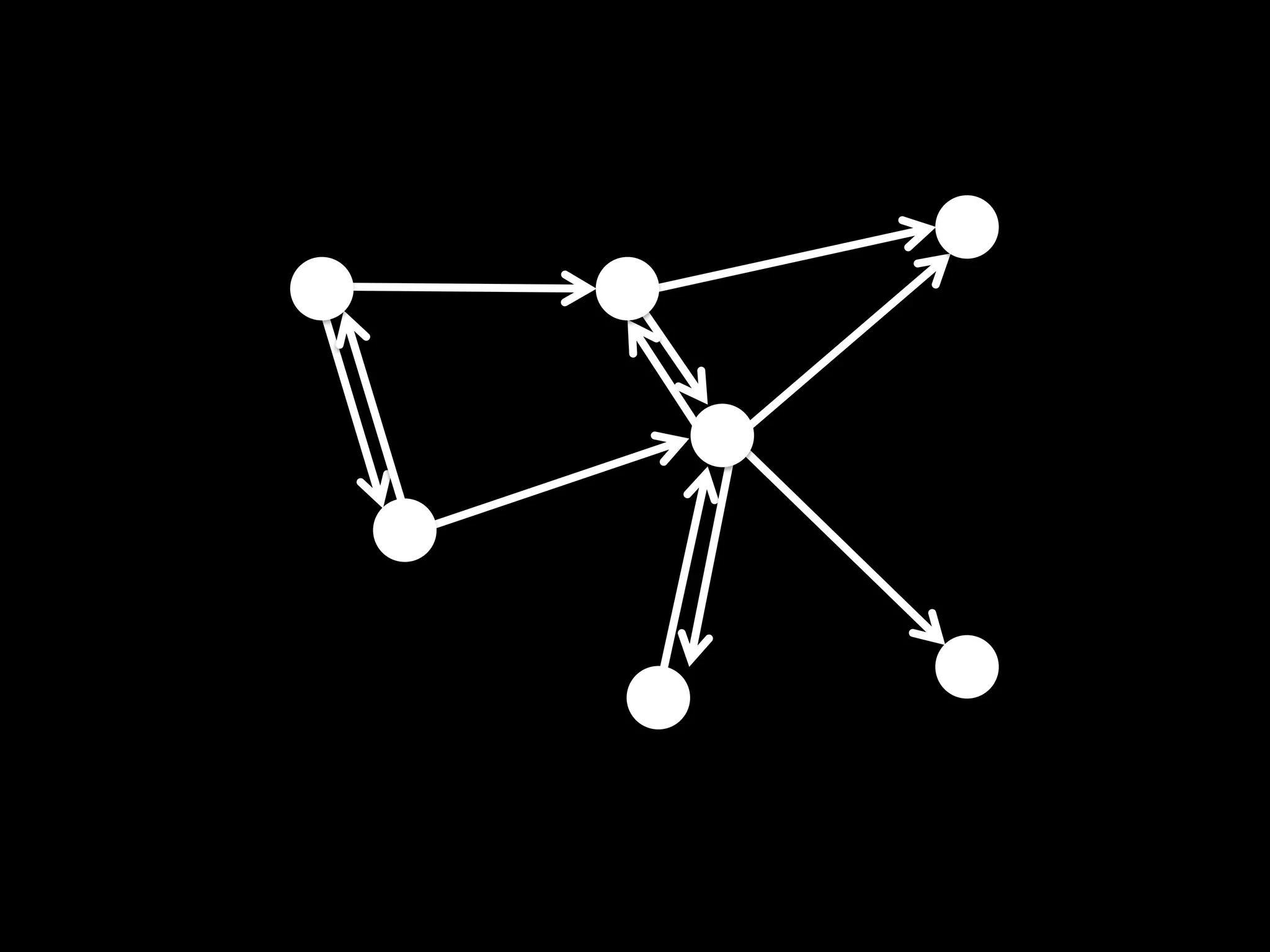
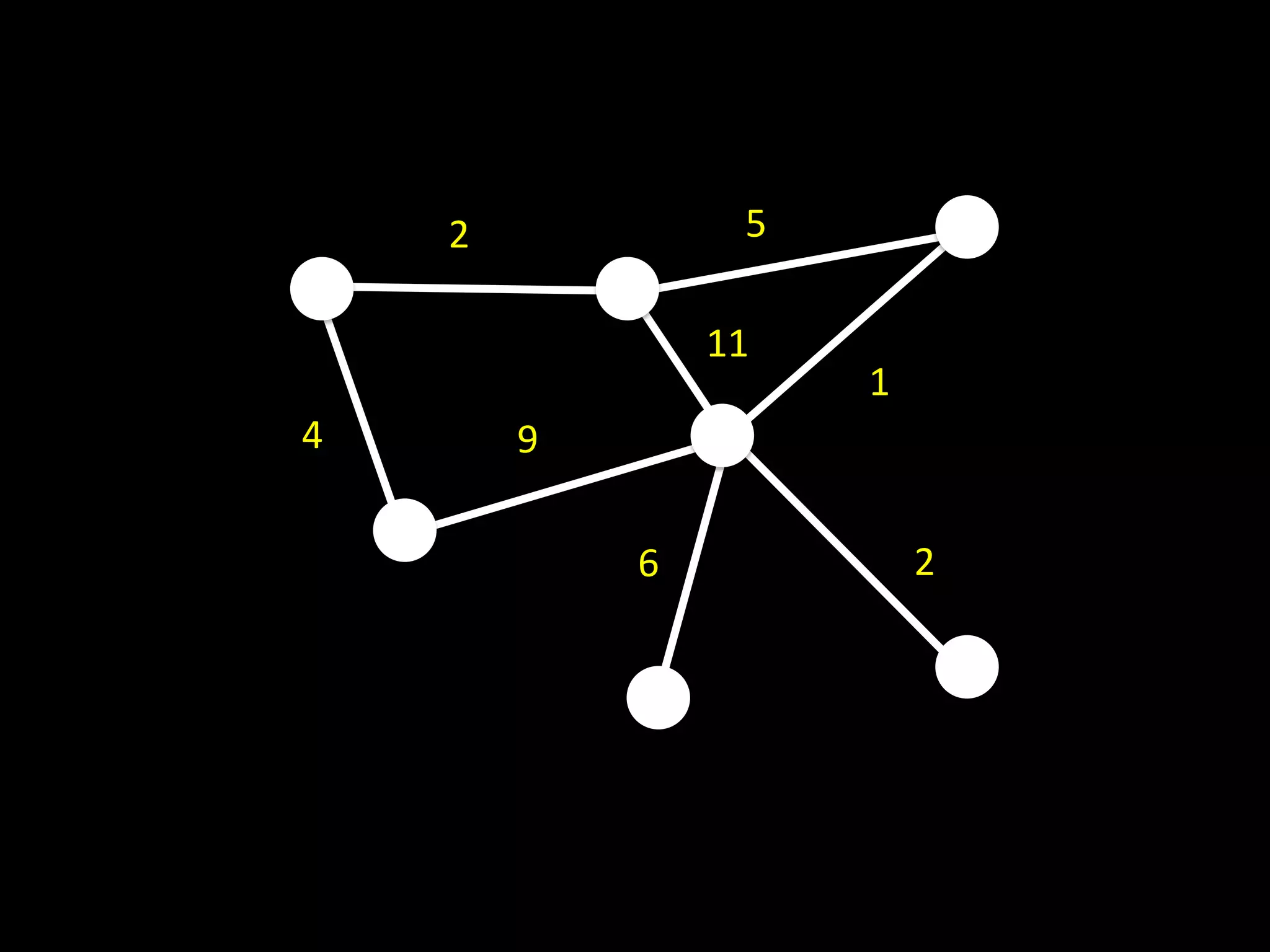
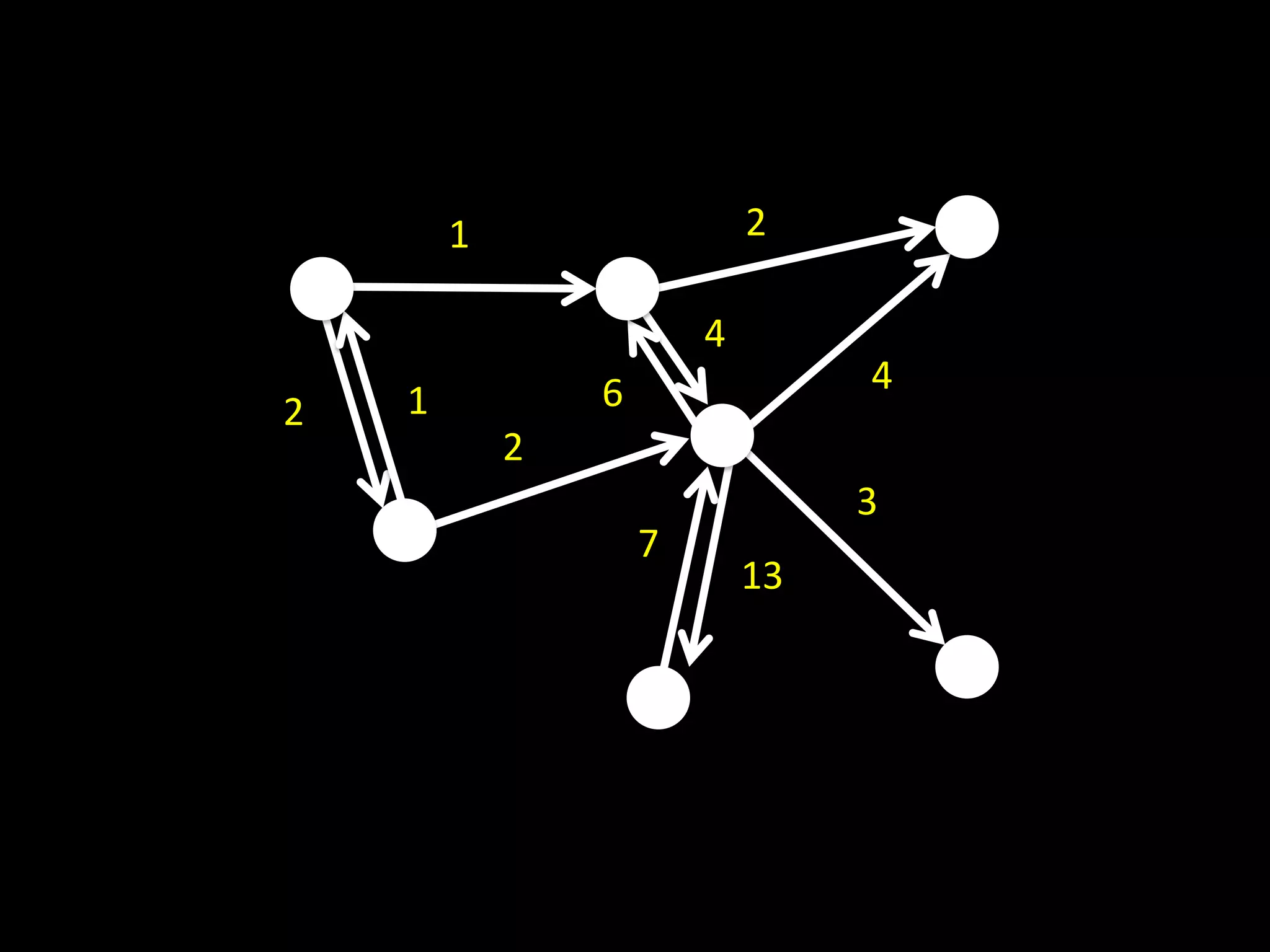
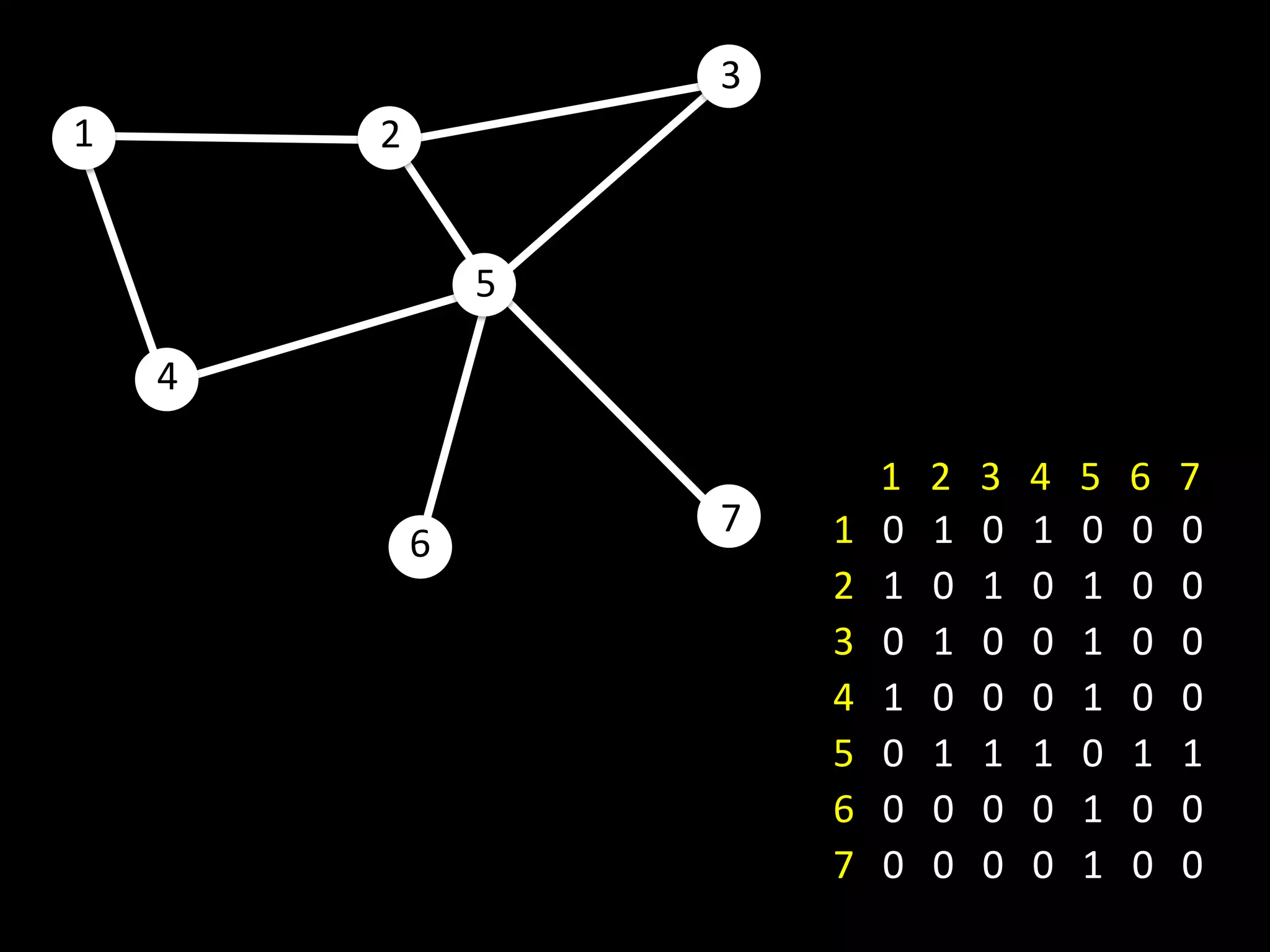
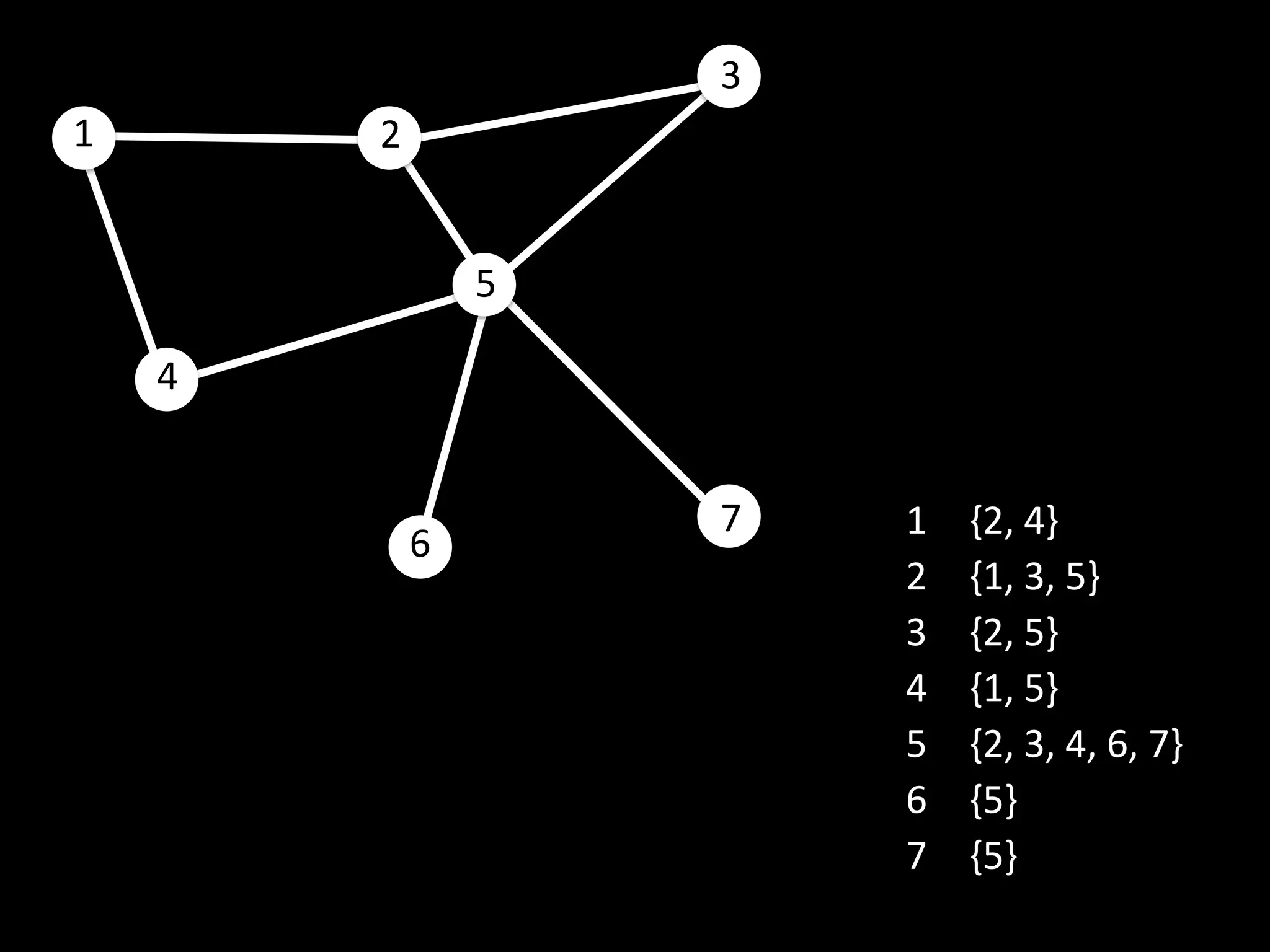
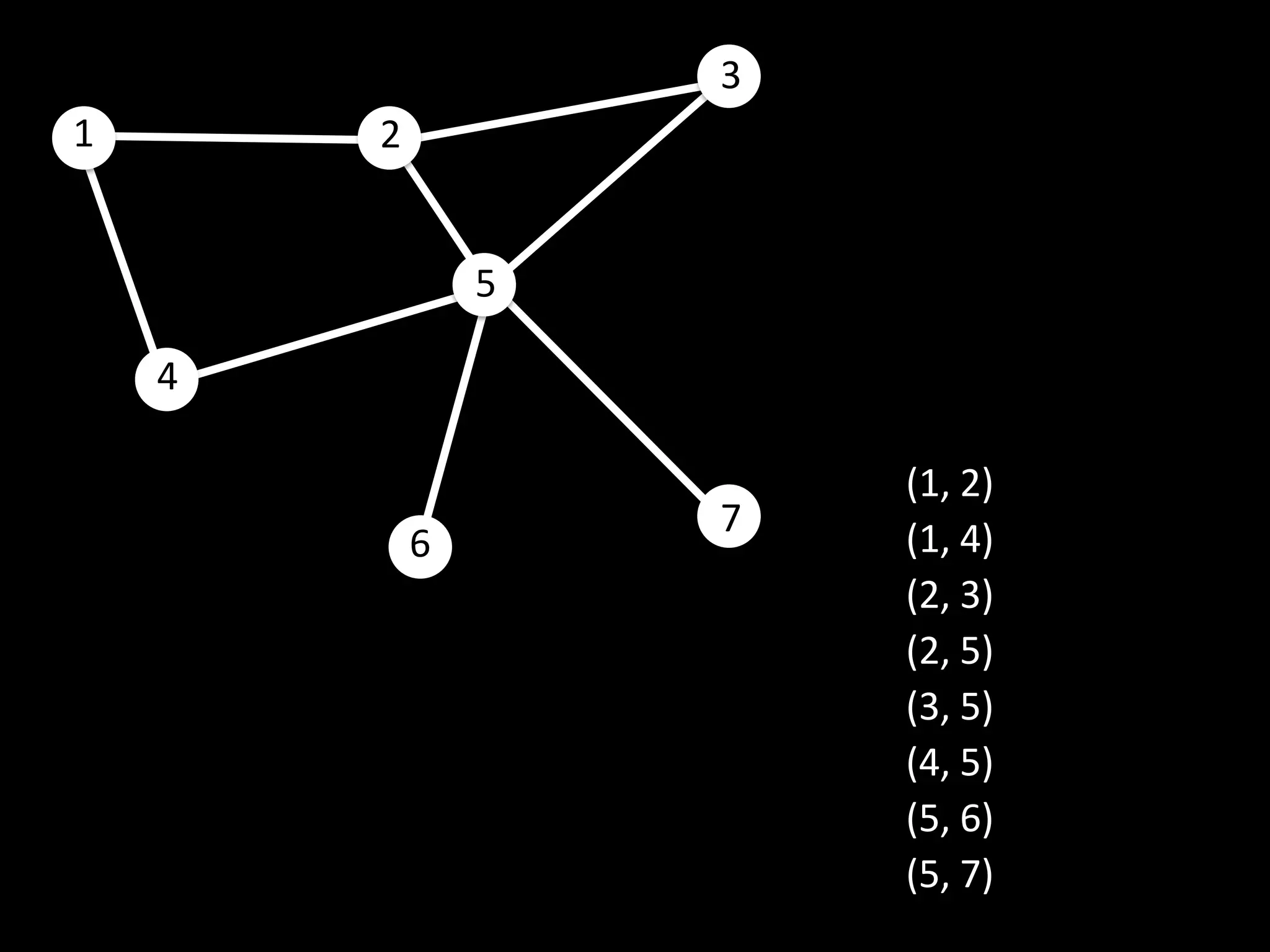
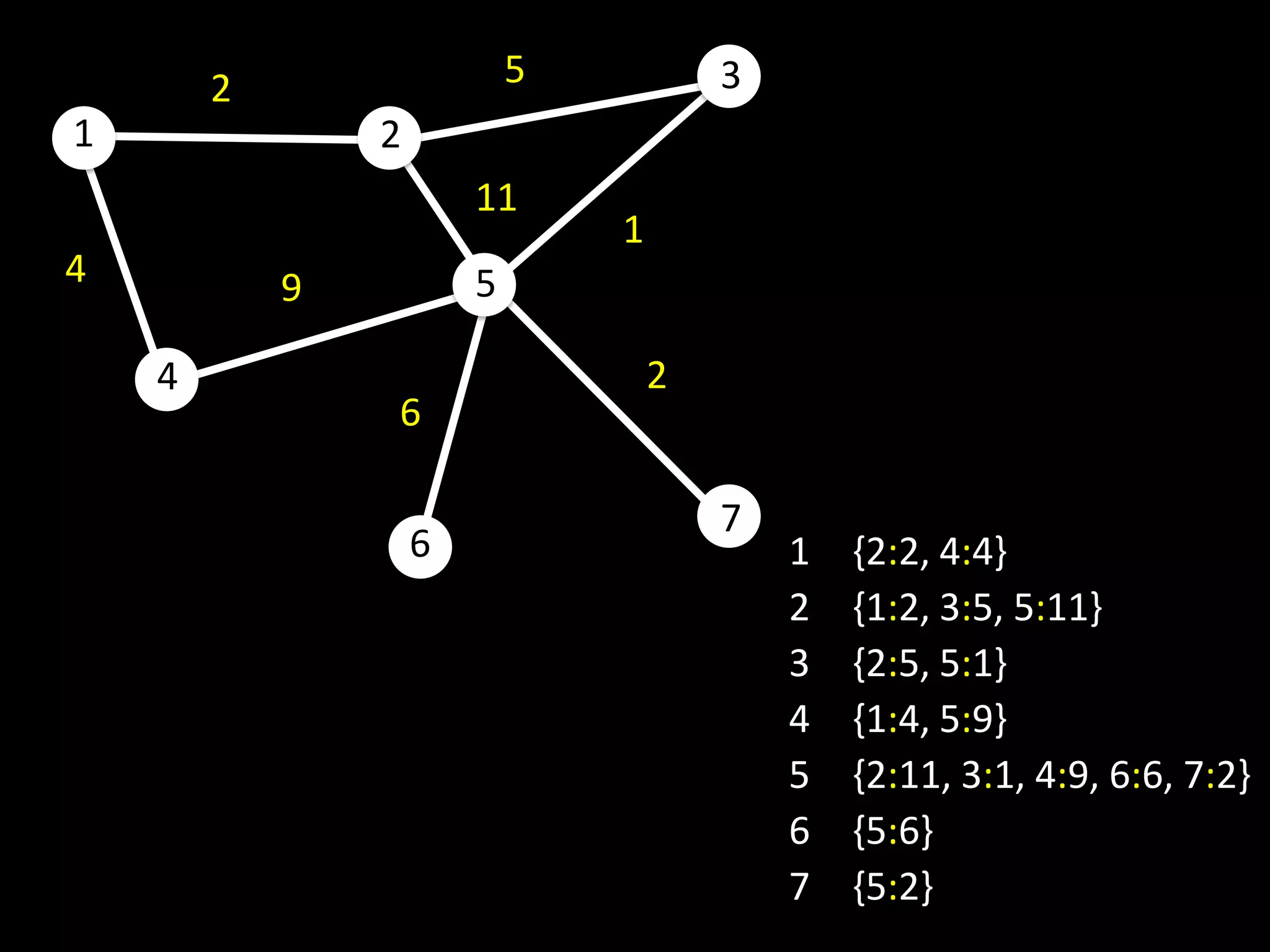
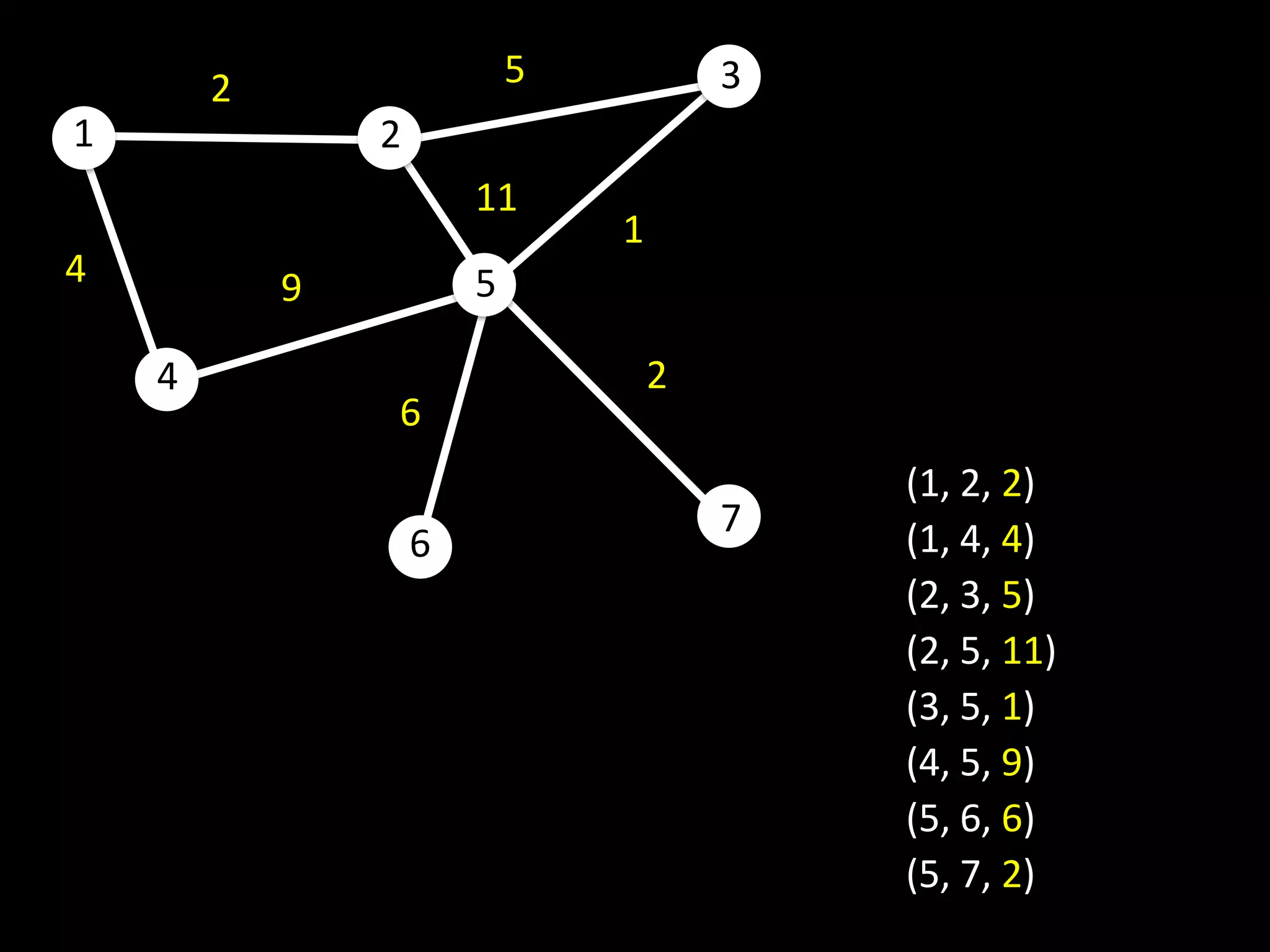
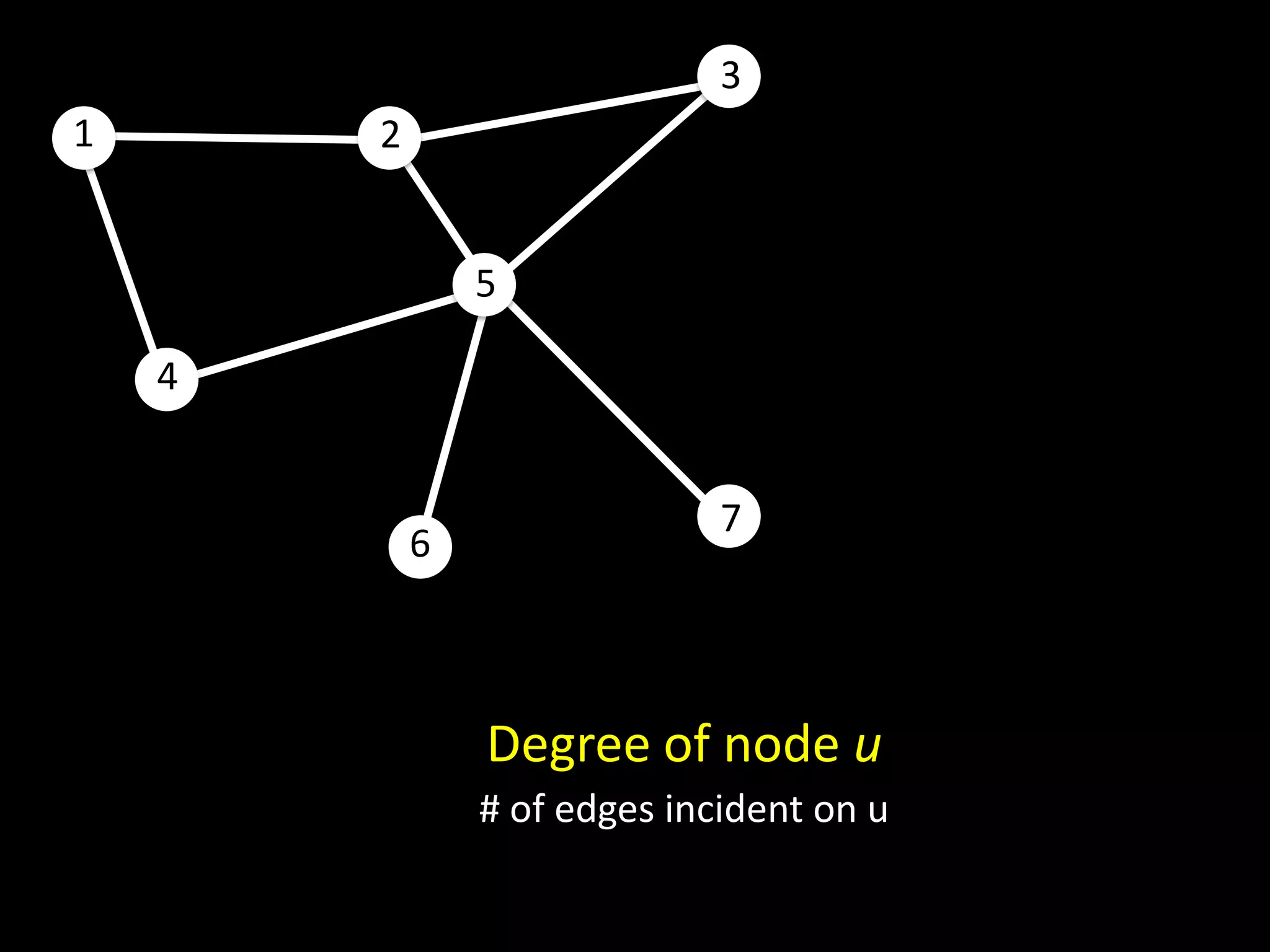
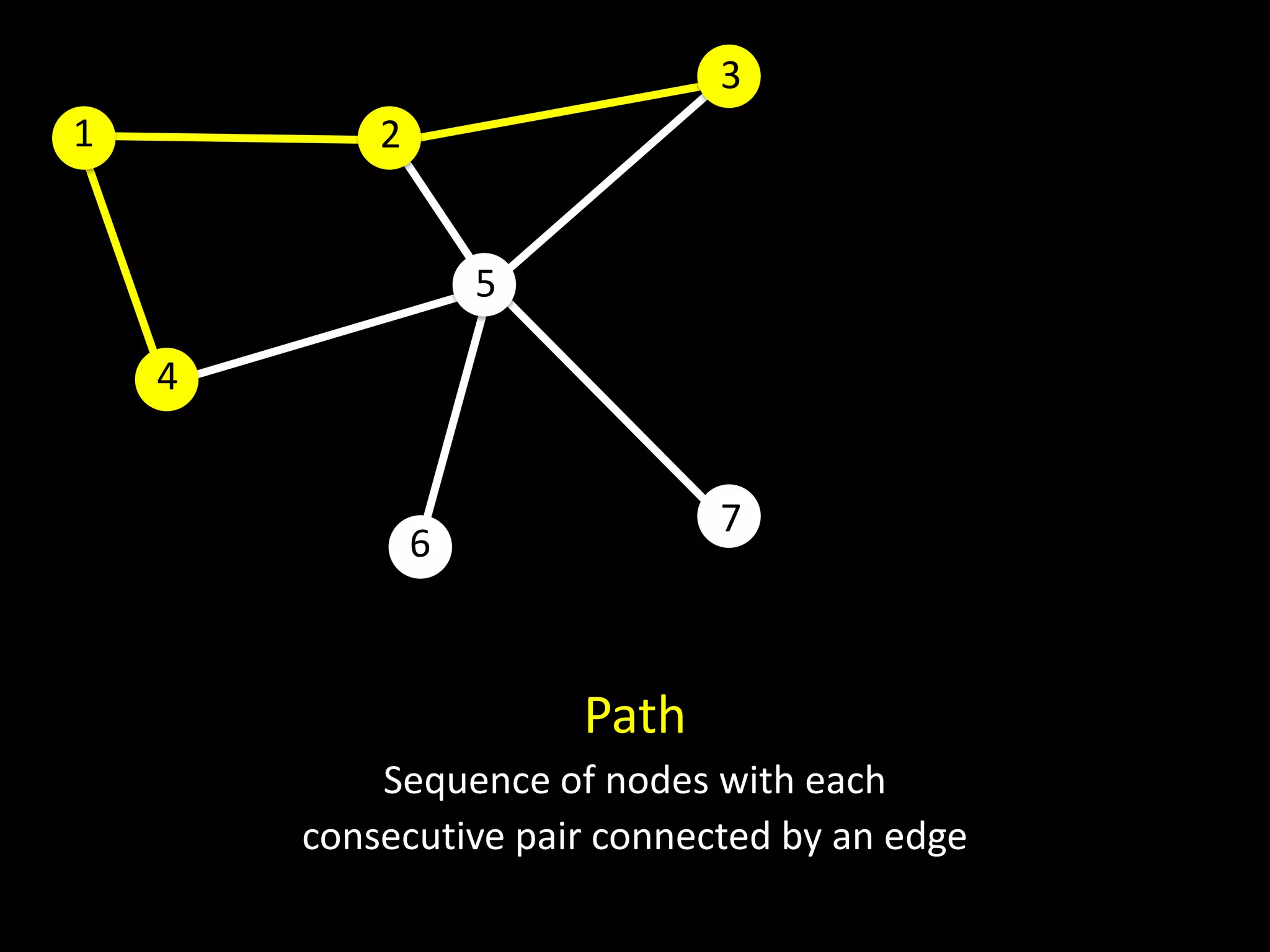
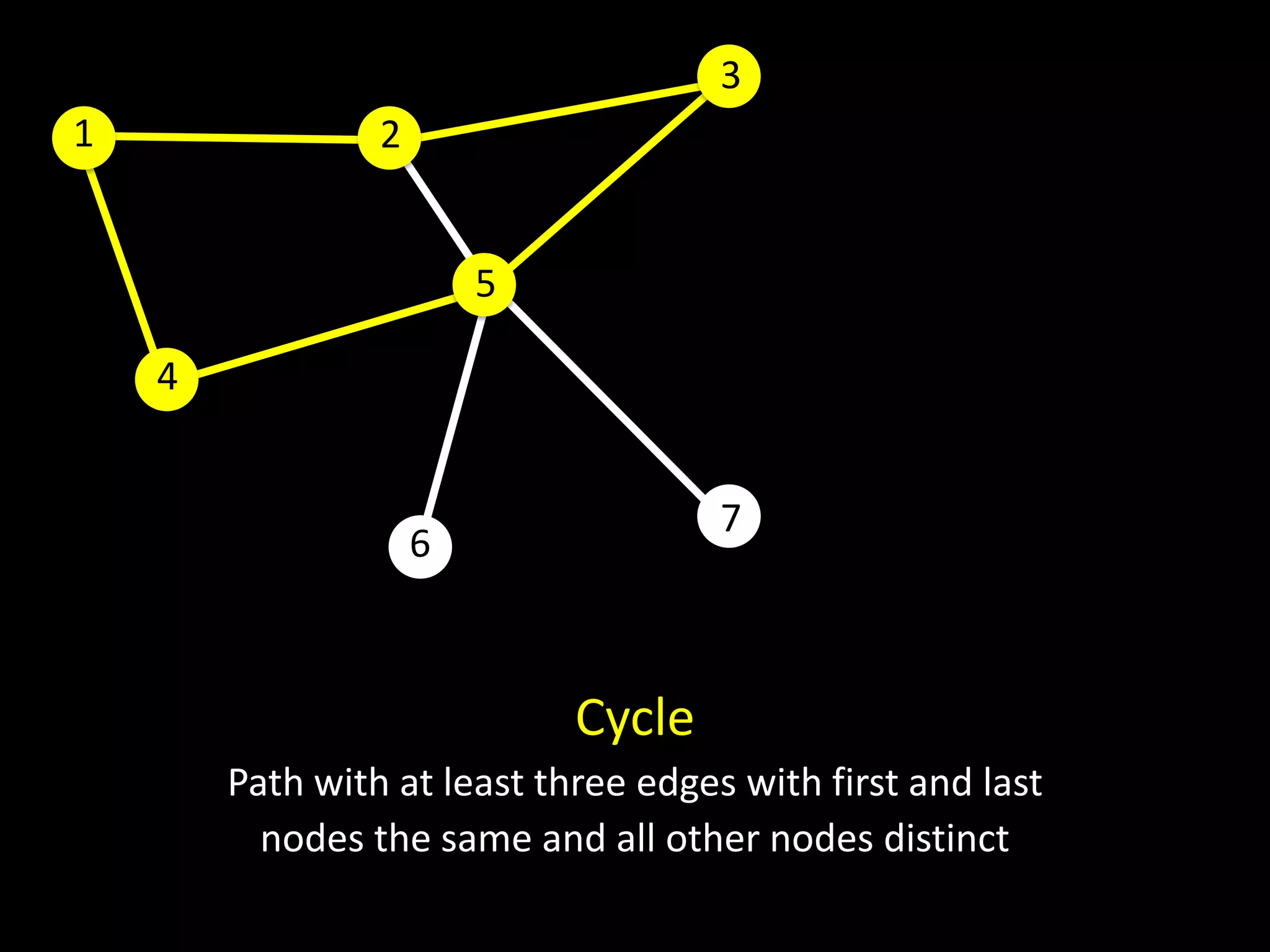
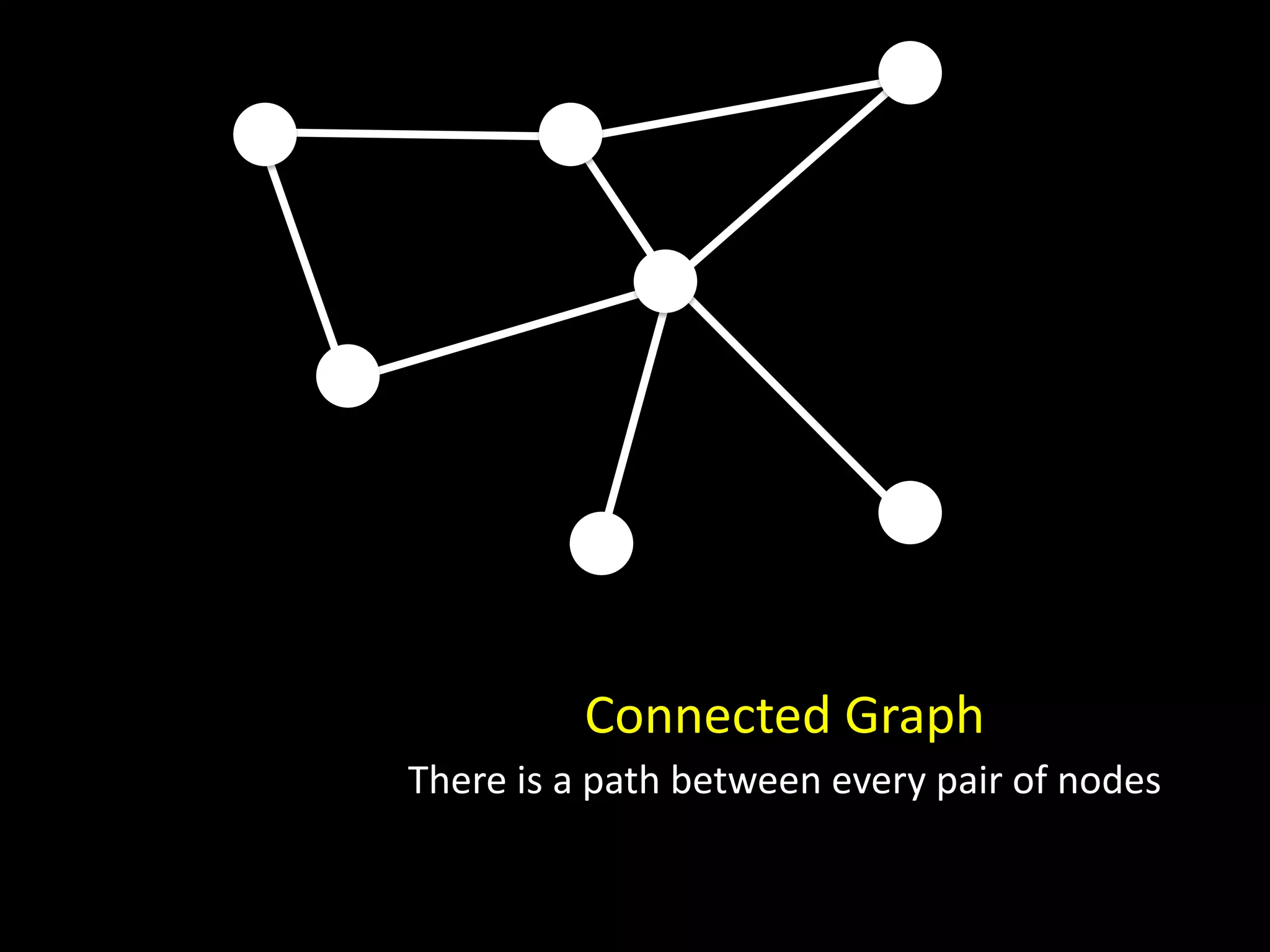
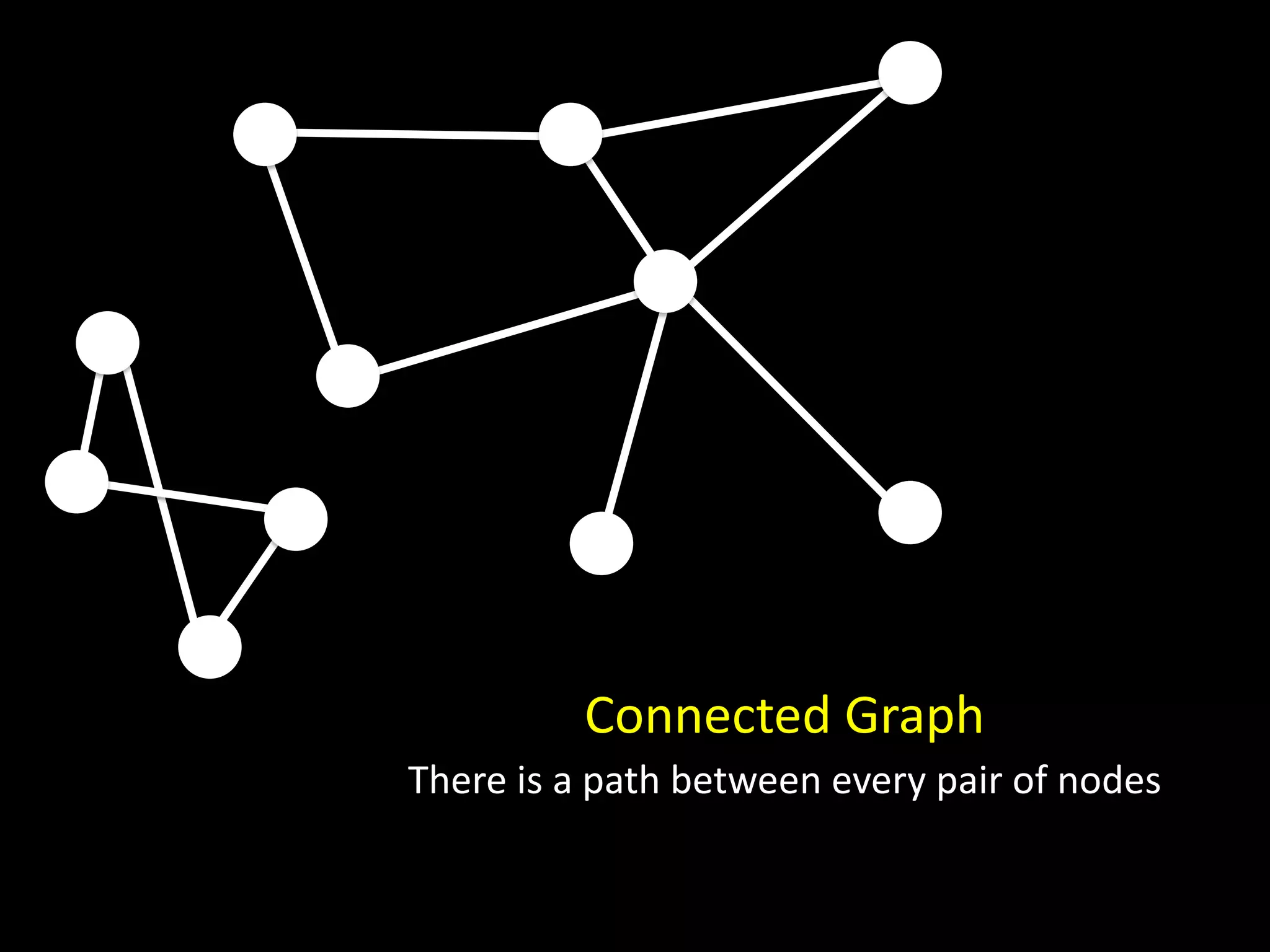
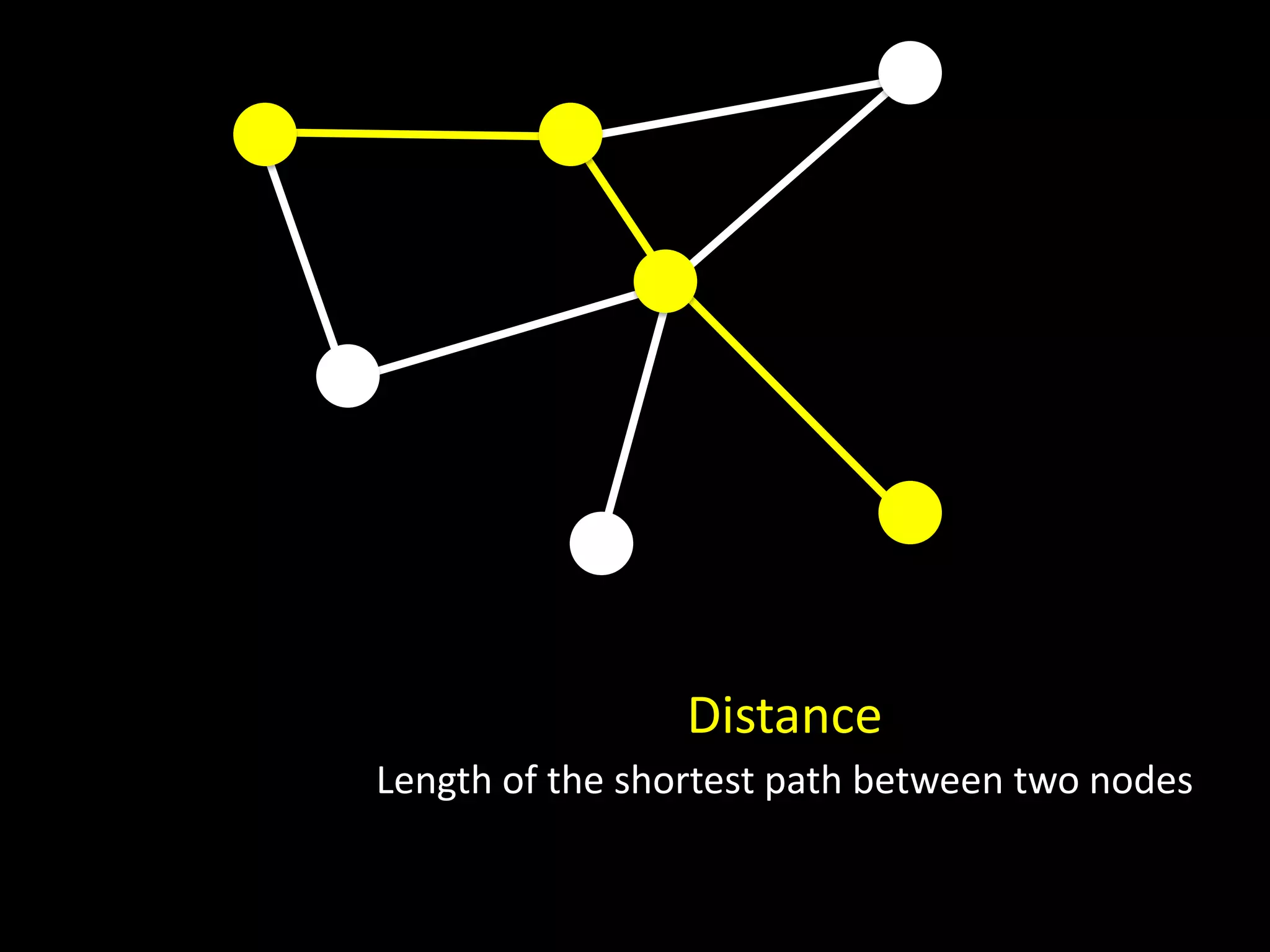
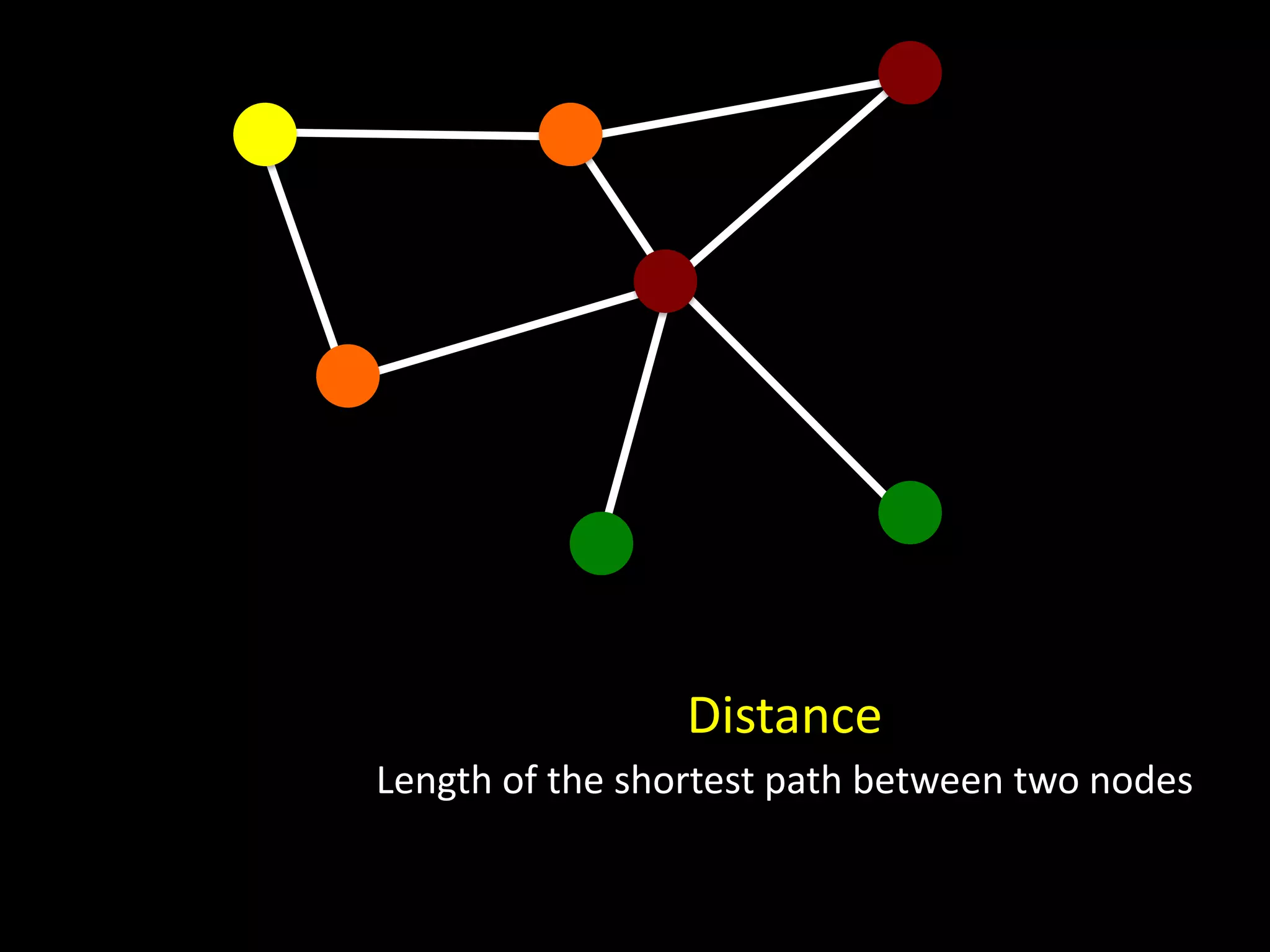
The document discusses networks and graph concepts. It provides examples of social networks and the internet. It defines nodes, edges, and how networks can be represented using adjacency lists and edge lists. It discusses computing properties of networks like degrees, connected components, distances, and performing breadth-first search.

![High School Dating Network
[ Bearman, Moody, & Stovel, 2004 ]
Image by Mark Newman, via Easley & Kleinberg](https://image.slidesharecdn.com/networks1-130312124613-phpapp01/75/Computational-Social-Science-Lecture-05-Networks-Part-I-2-2048.jpg)
![Corporate E-mail Communication
[ Adamic & Adar, 2004 ]
via Easley & Kleinberg](https://image.slidesharecdn.com/networks1-130312124613-phpapp01/75/Computational-Social-Science-Lecture-05-Networks-Part-I-3-2048.jpg)













![# initialize distances
dist = {}
for u in G:
dist[u] = NA
dist [u1] = 0
d=0
periphery = { u1 }
while len(periphery) > 0:
# find nodes one step away from the periphery
next_level = {}
for u in periphery:
next_level += { w for w in neighbors[u] if dist[w] == NA }
# update distances
d += 1
for u in next_level:
dist[u] = d
# update periphery
periphery = next_level](https://image.slidesharecdn.com/networks1-130312124613-phpapp01/75/Computational-Social-Science-Lecture-05-Networks-Part-I-34-2048.jpg)

![BFS @ scale
undirected network
Input: distances (u, d)
1. join distances with edge list
2. foreach (u, d, w) output (w, d+1)
[ also output (u0, 0) ]
3. group by w, and output min d](https://image.slidesharecdn.com/networks1-130312124613-phpapp01/75/Computational-Social-Science-Lecture-05-Networks-Part-I-36-2048.jpg)