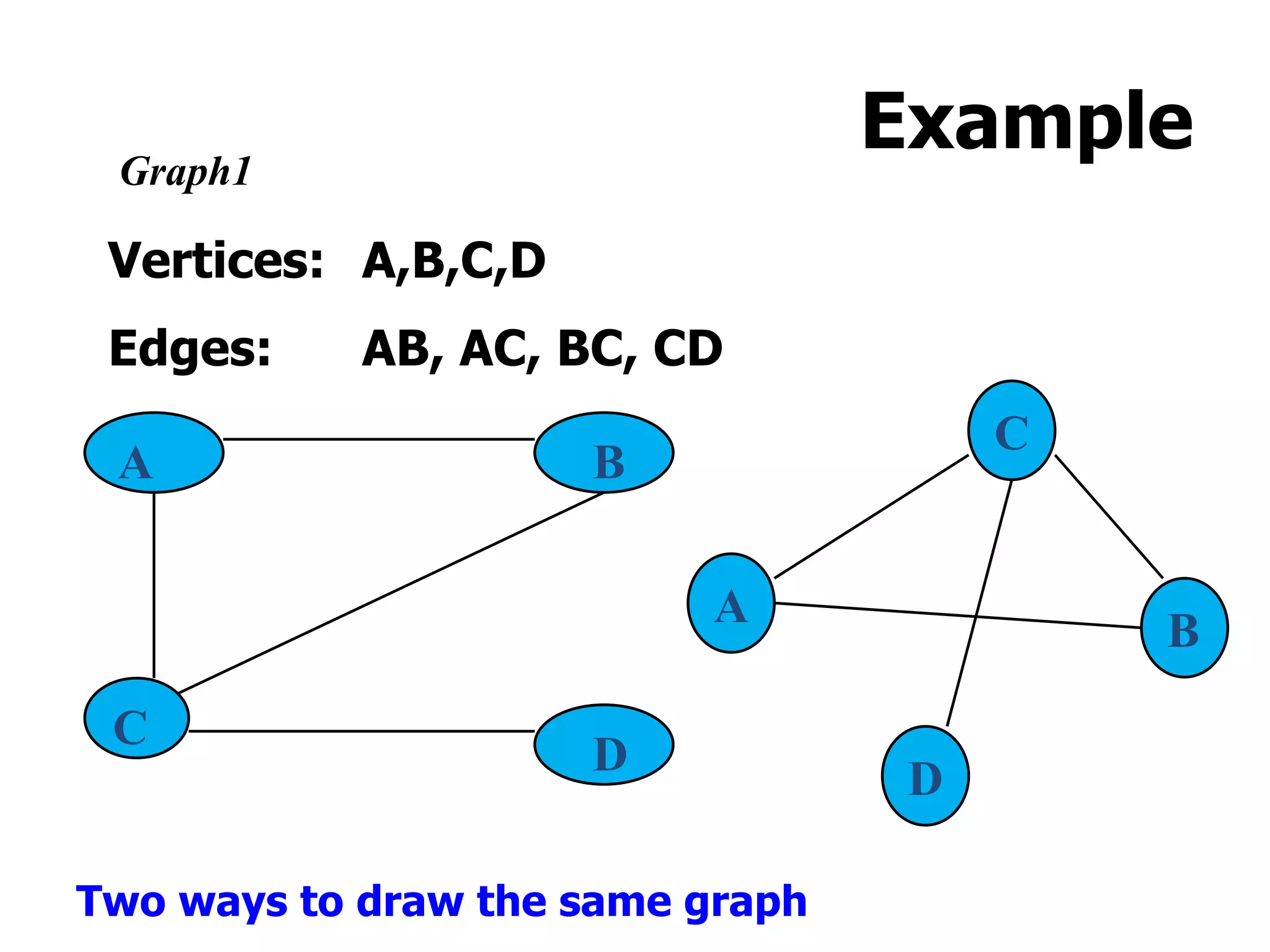
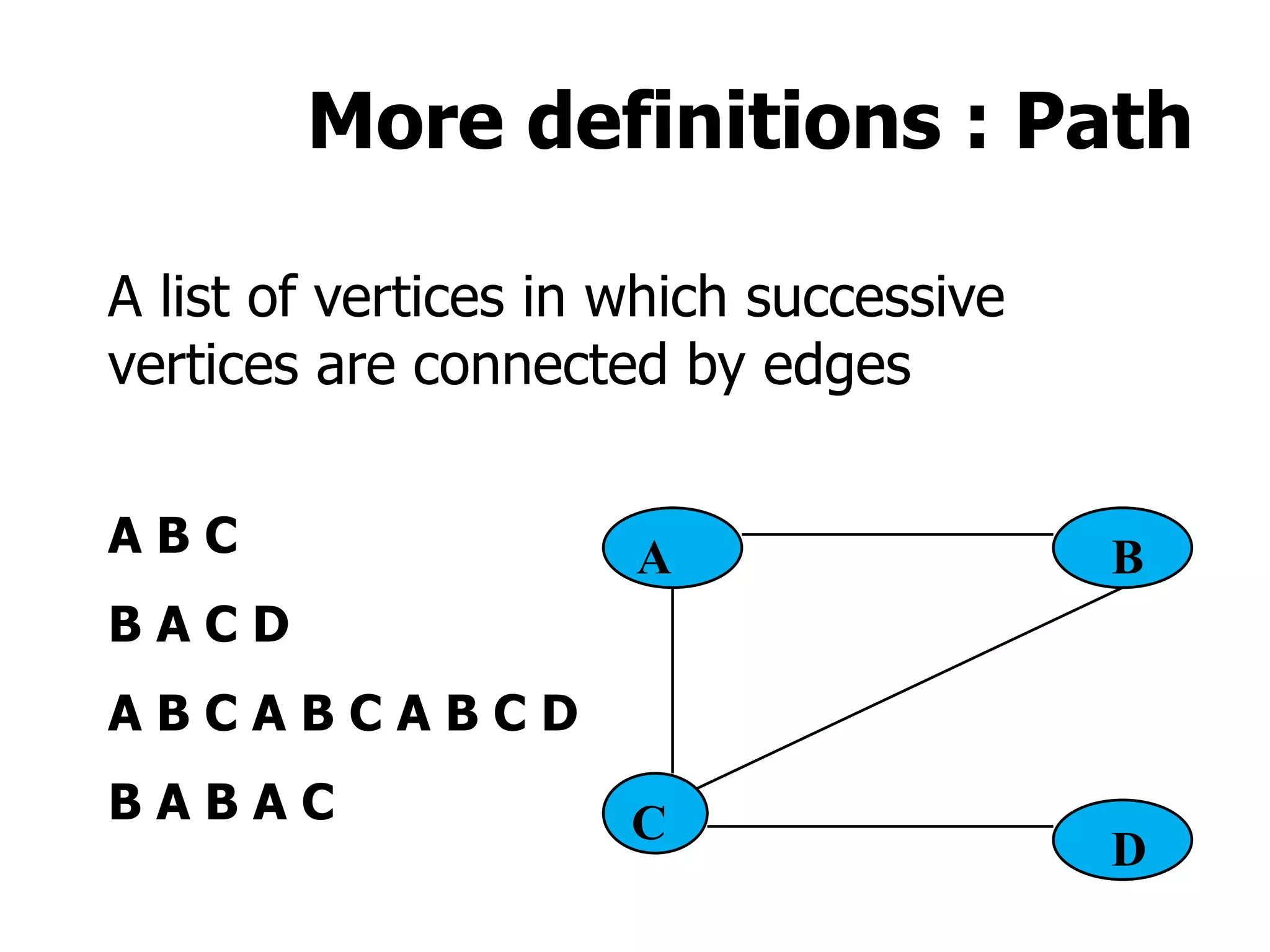
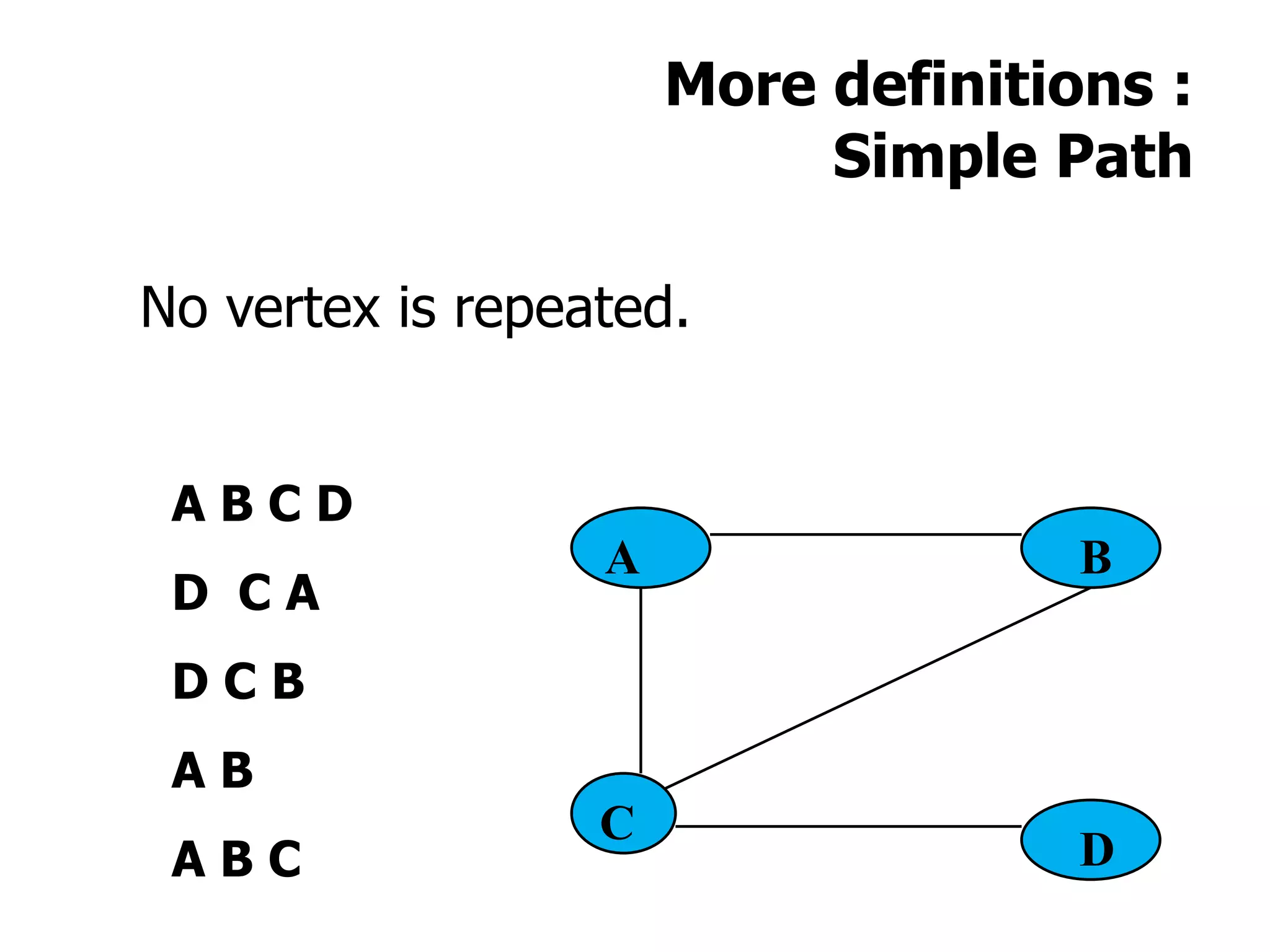
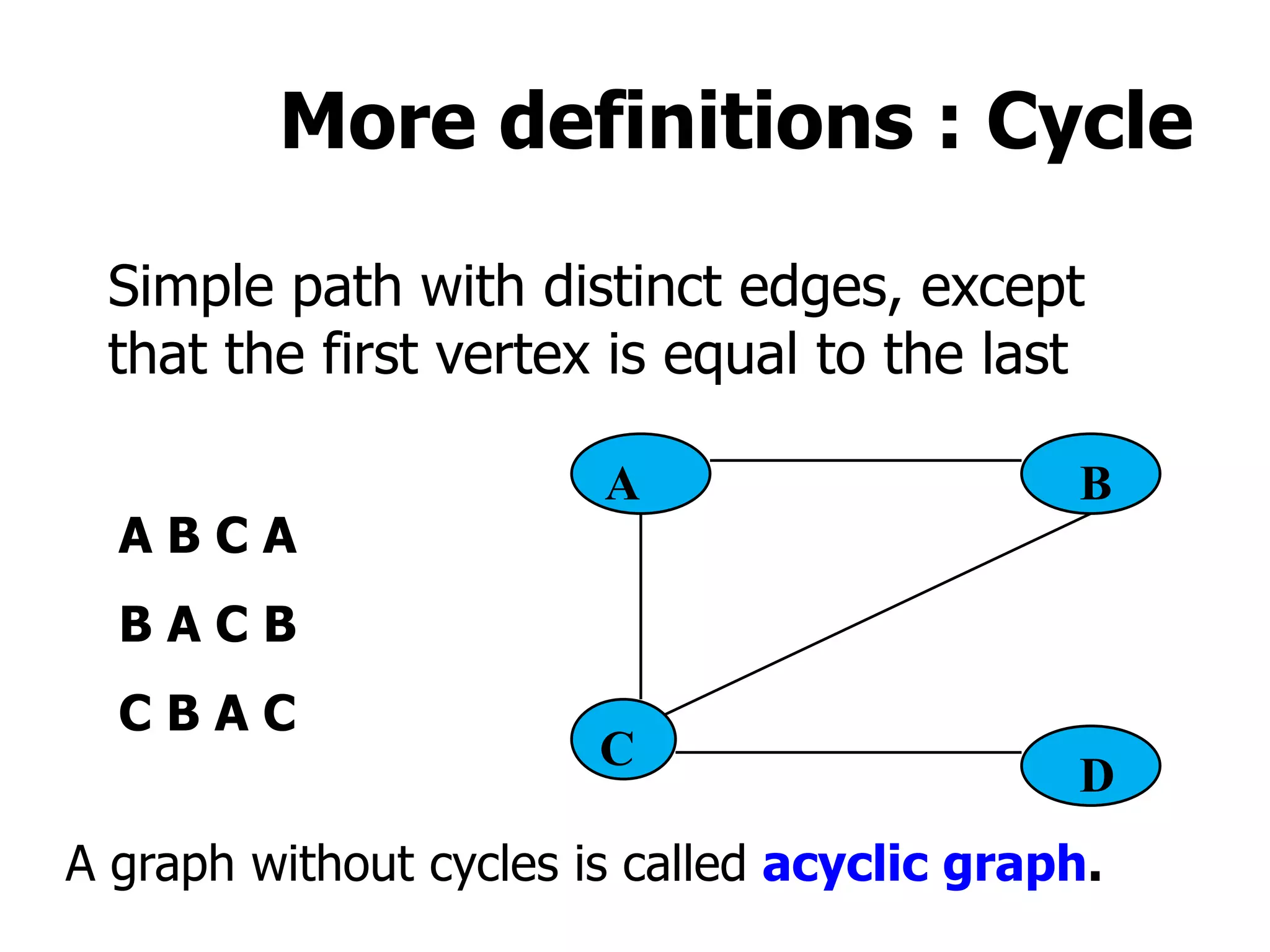
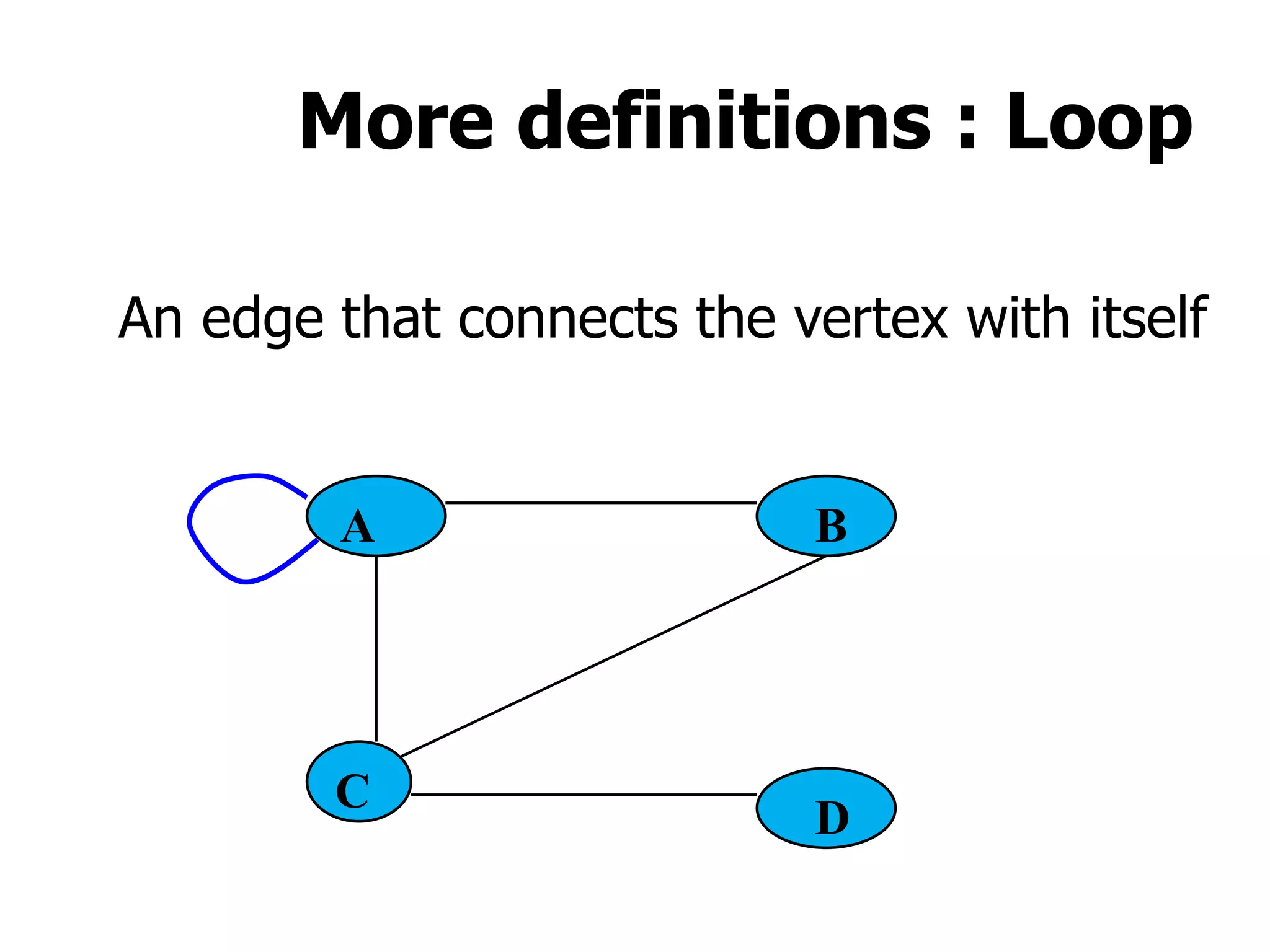
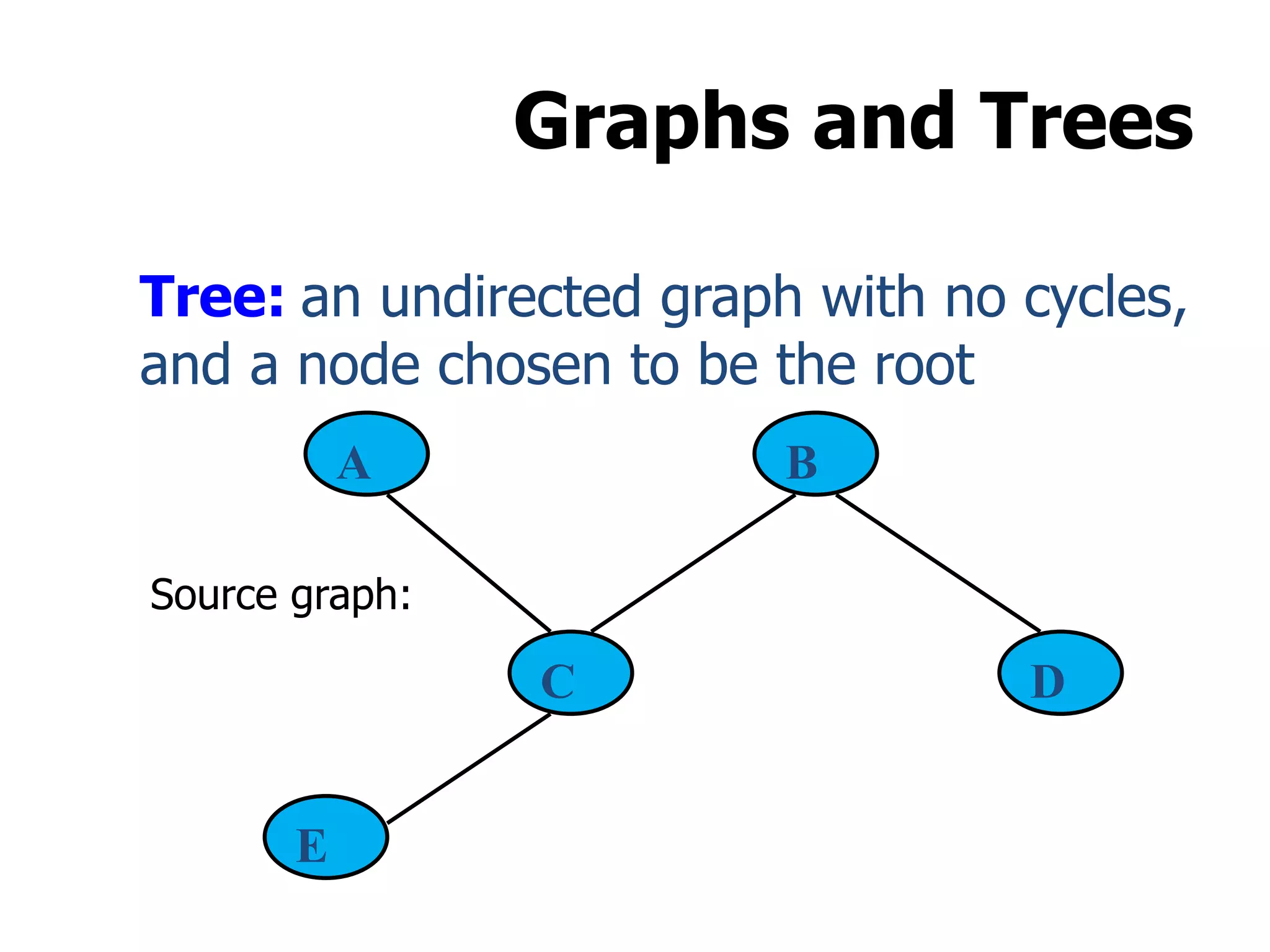
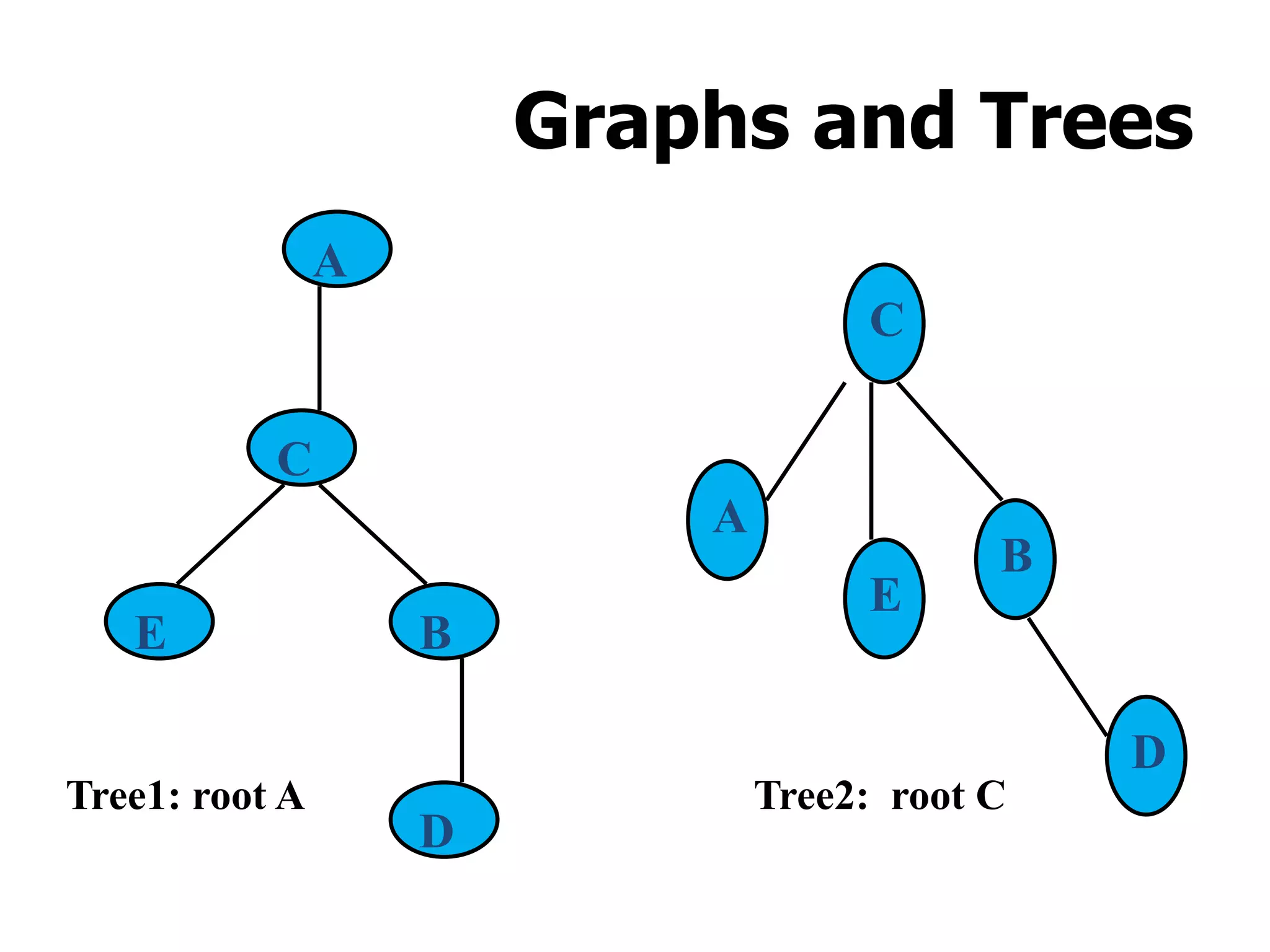
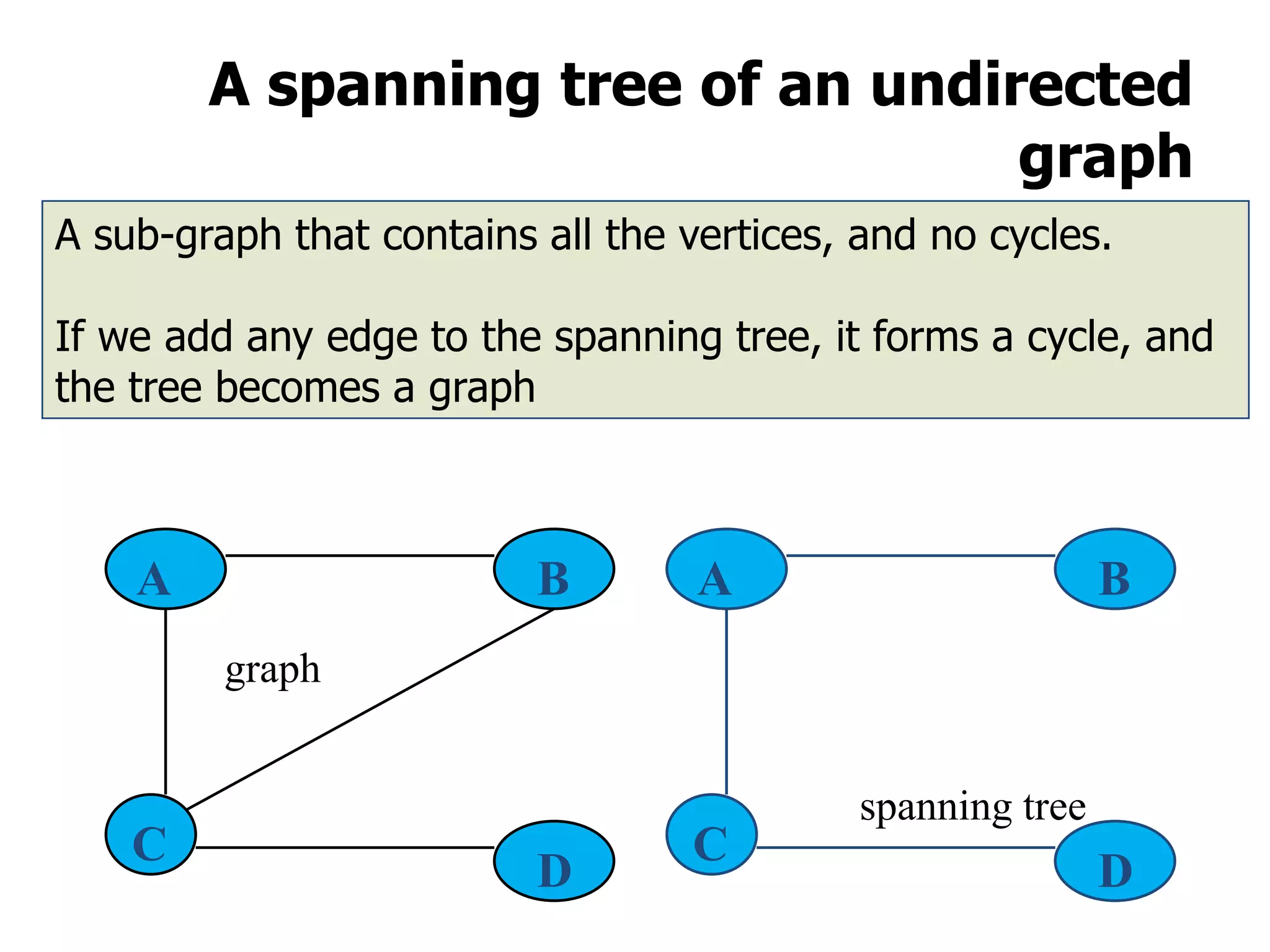
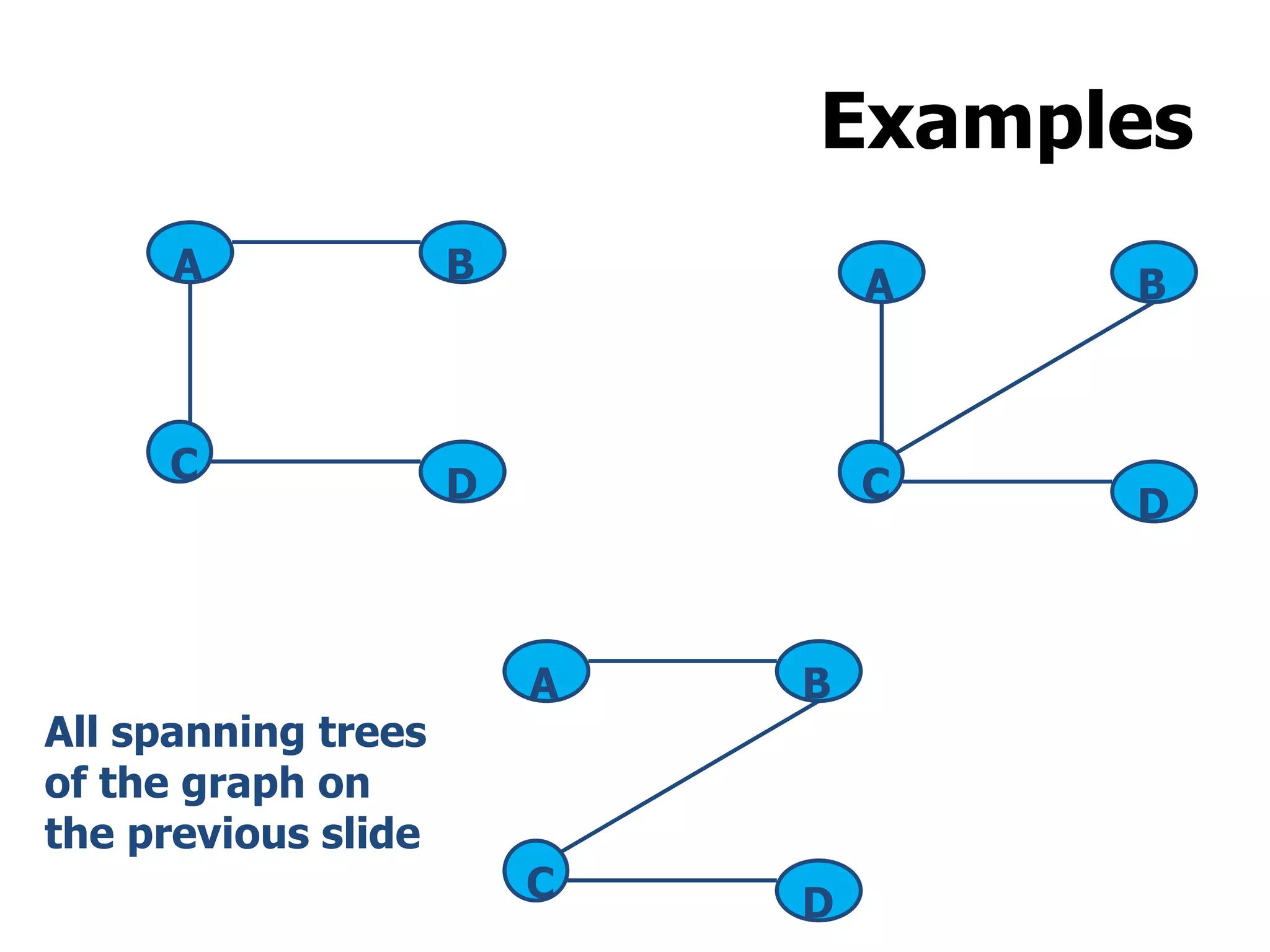
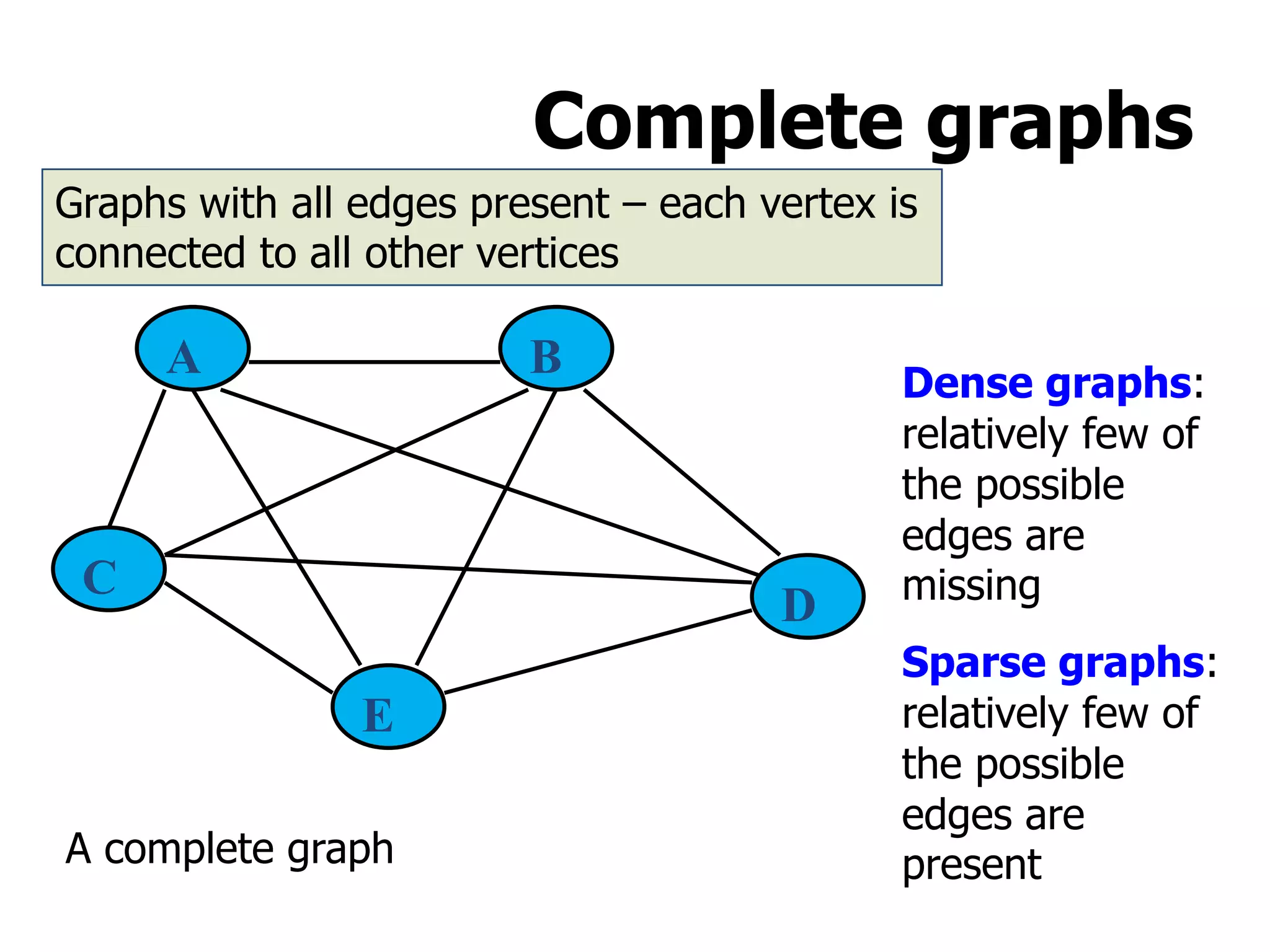
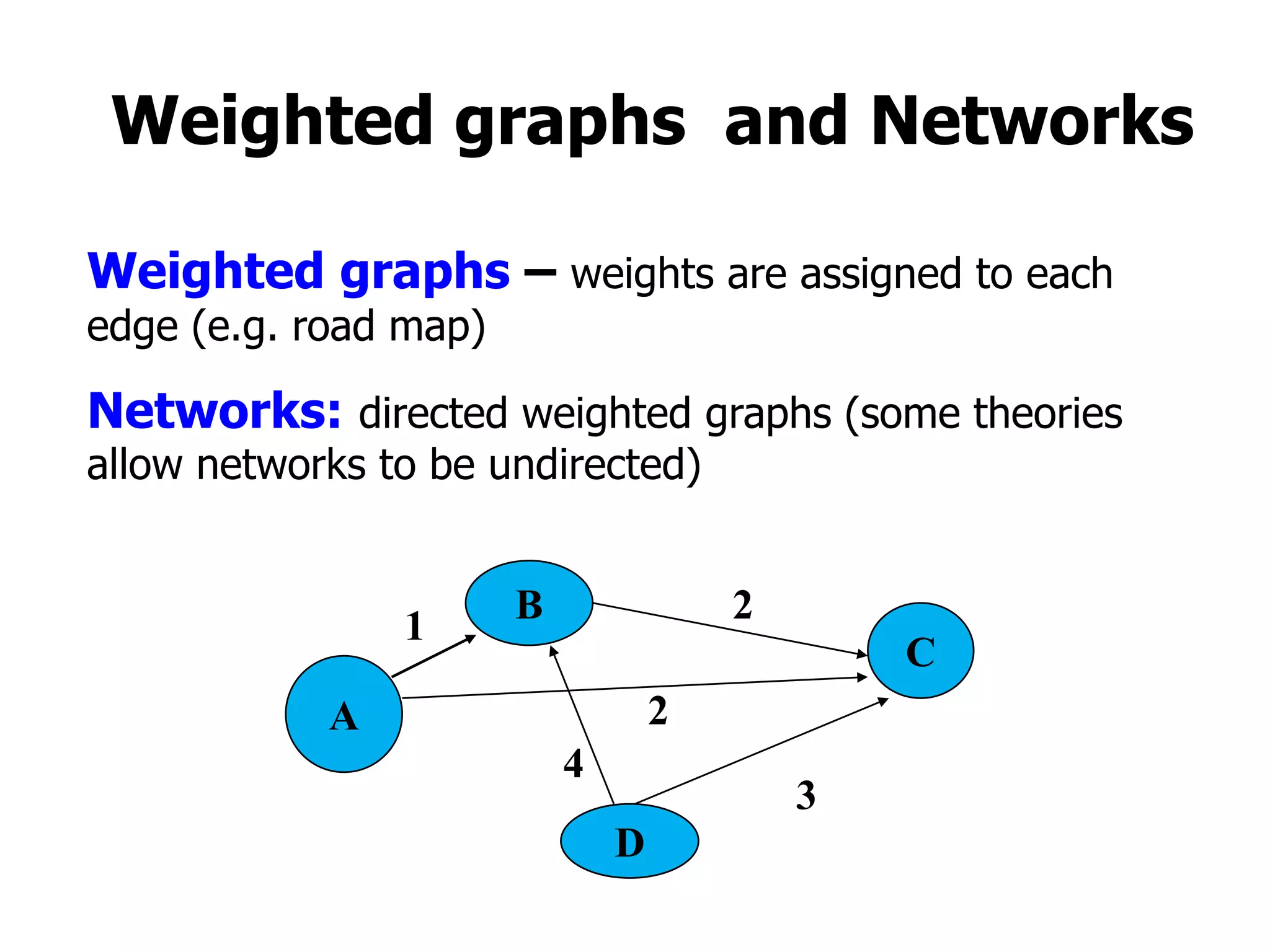
1) A graph is a collection of vertices and edges, where vertices represent nodes and edges connect pairs of vertices.
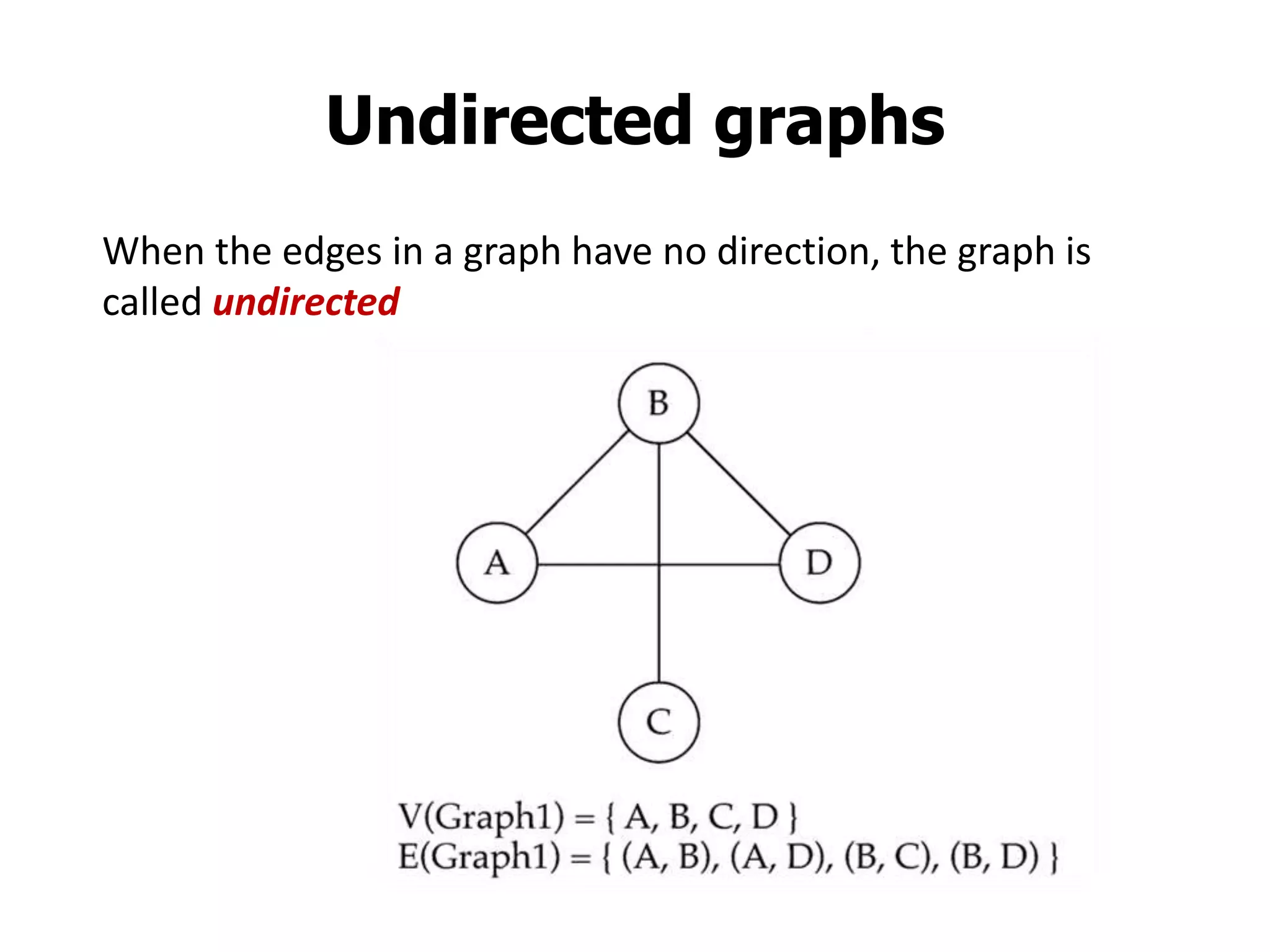
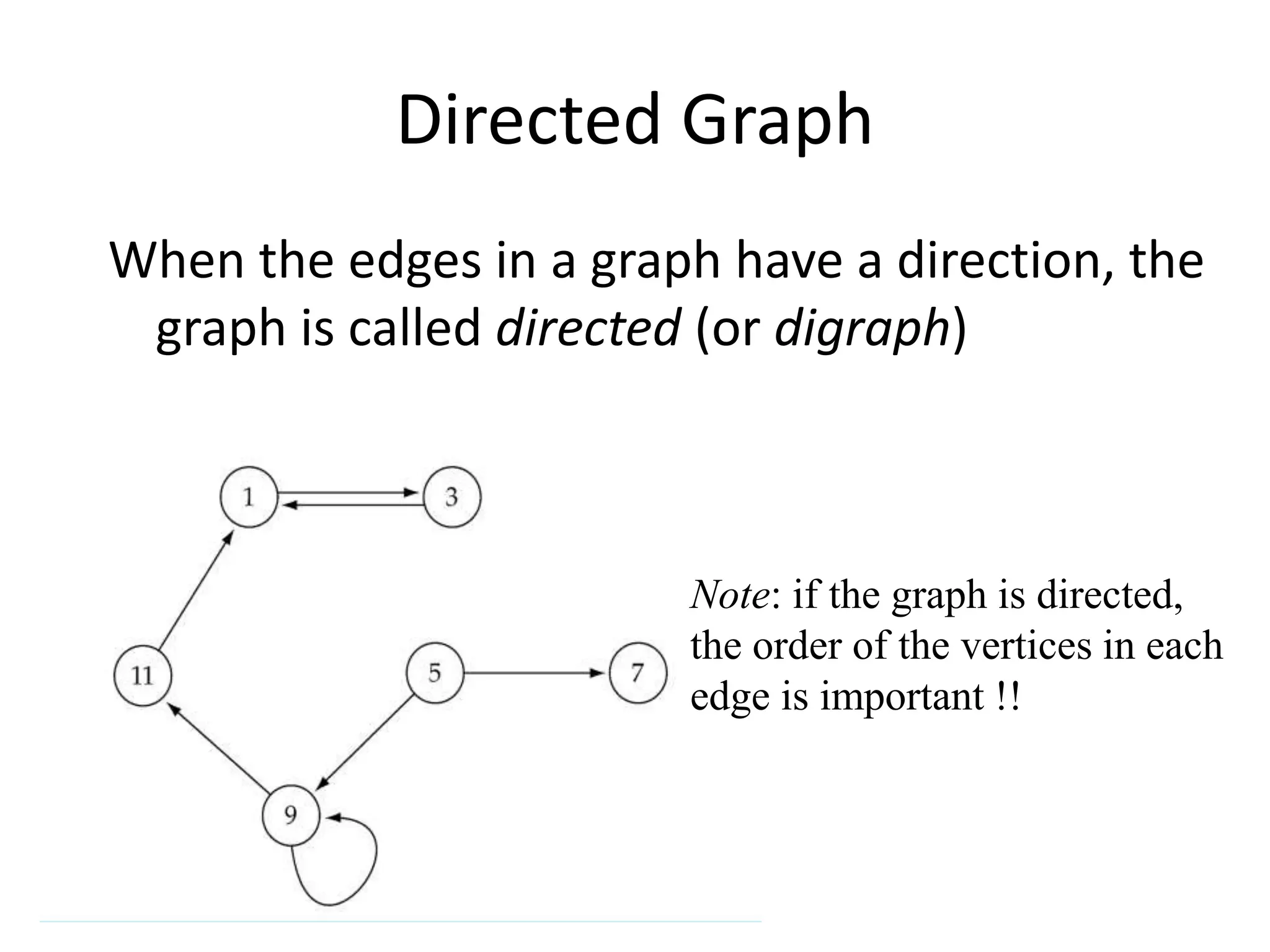
2) Graphs can be undirected, where edges have no directionality, or directed (digraphs), where edges have a direction associated with them.
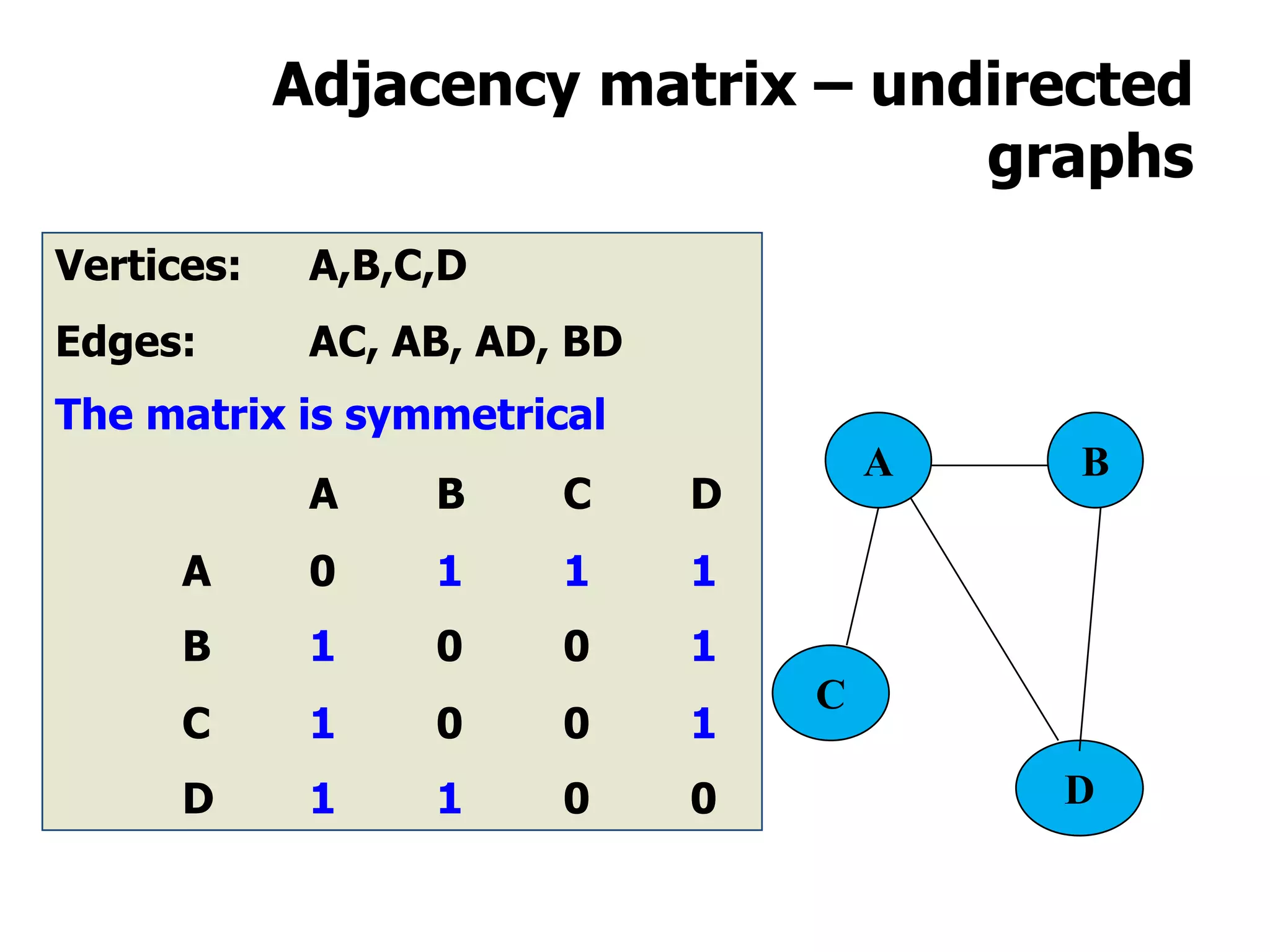
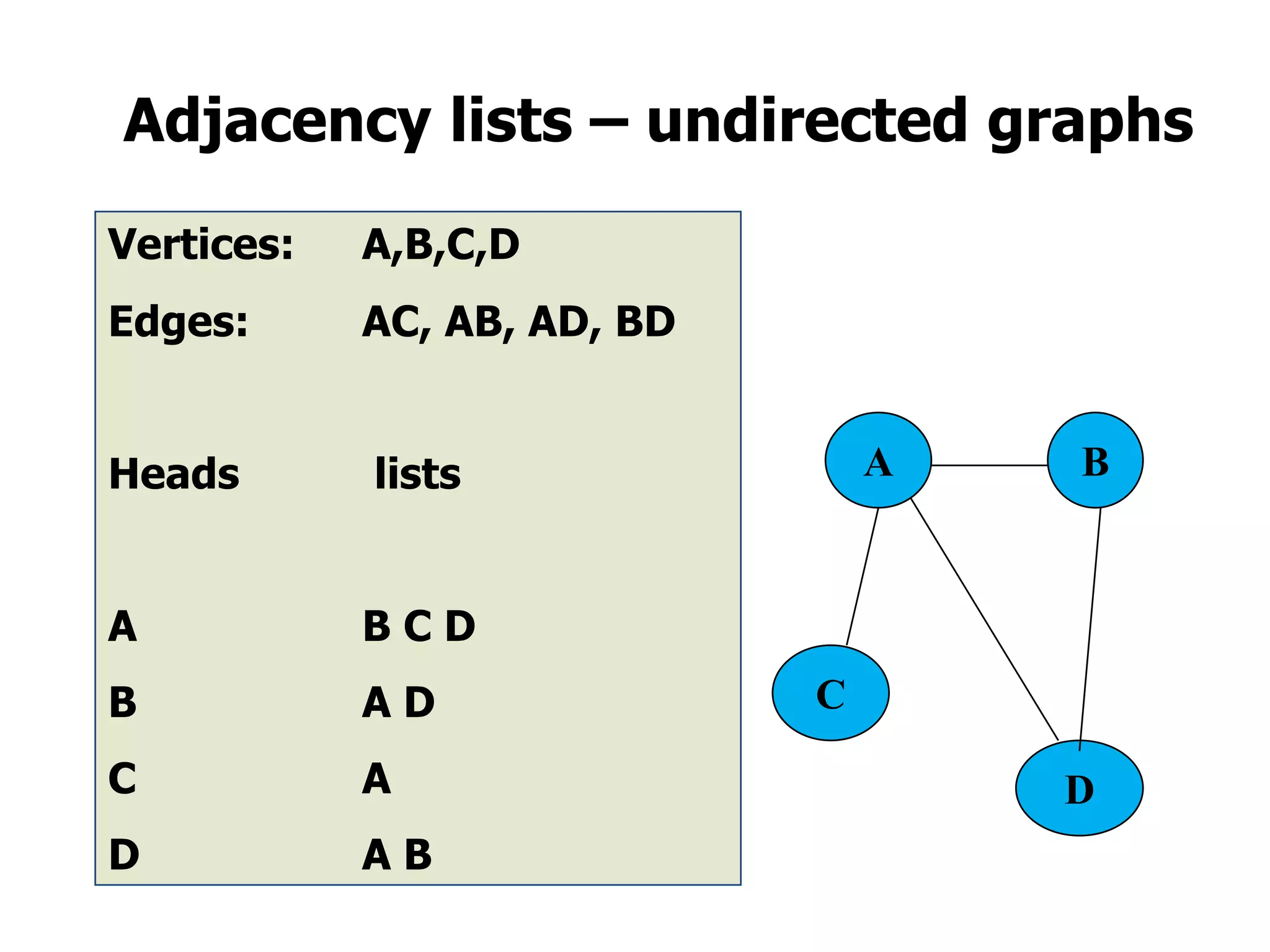
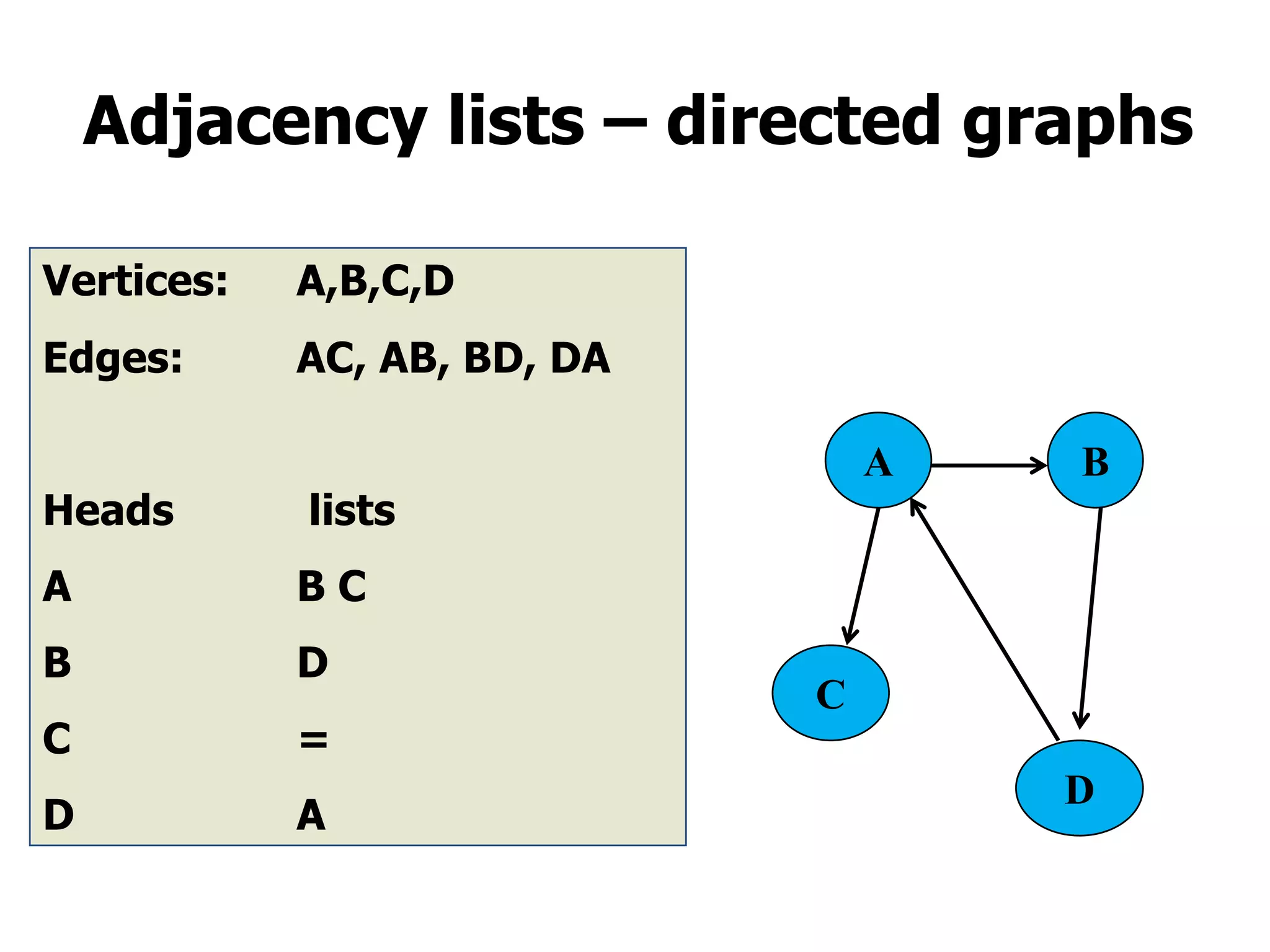
3) Graphs are commonly represented using adjacency matrices, with cells indicating connections between vertex pairs, or adjacency lists, with each vertex listing its connected neighbors.