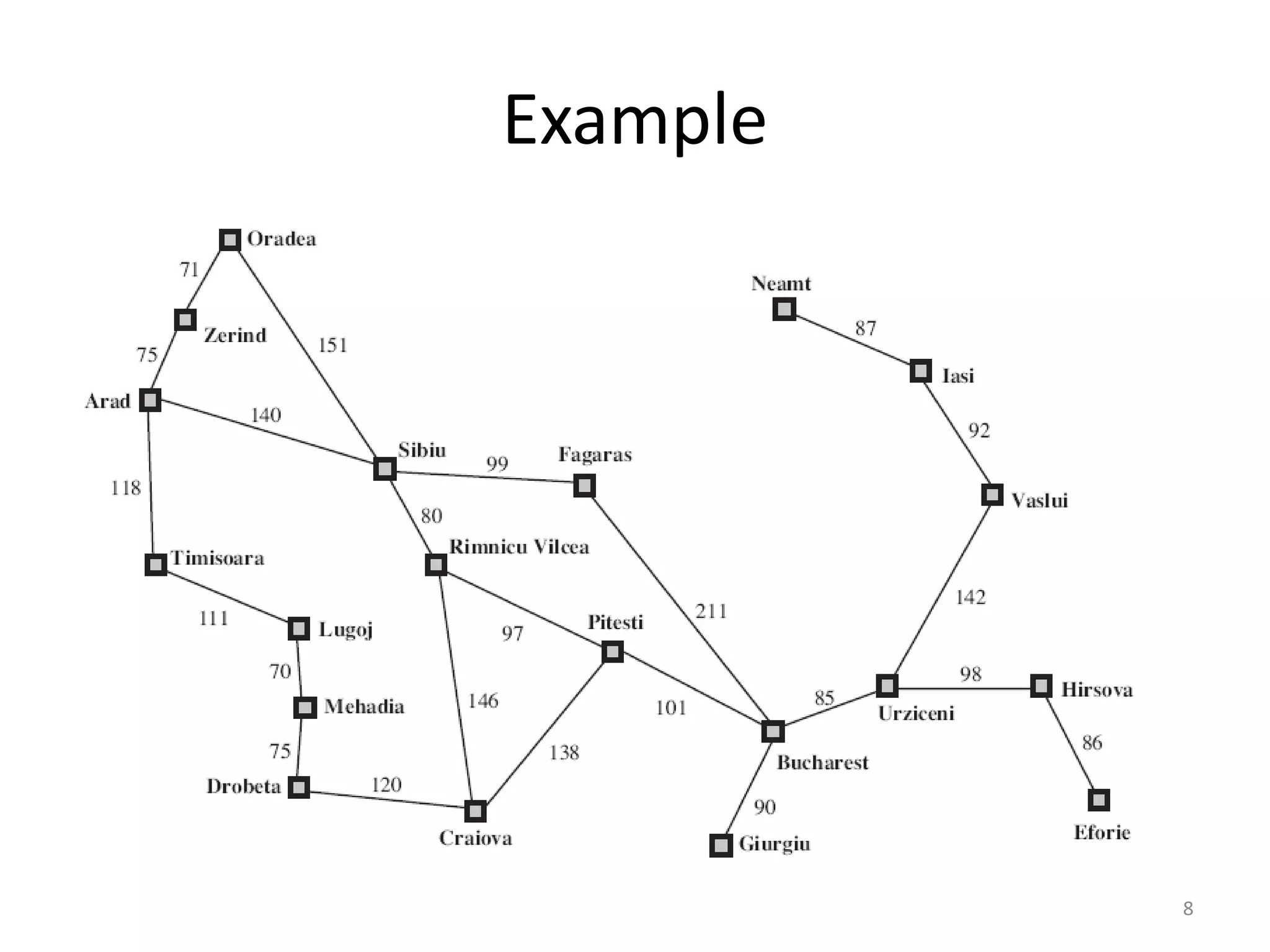
RBFS is a memory bounded search algorithm similar to A* that uses heuristics. It recursively searches the problem space, but only keeps the current search path and sibling nodes in memory at a given time. When exploring a subtree no longer looks promising, it is abandoned to save space. The space complexity of RBFS is linear in the search depth, same as IDA*. RBFS inherits heuristic values h(n) from parent nodes to child nodes to guide the search when reexploring subtrees.






![RBFS-Algorithm
function RECURSIVE-BEST-FIRST-SEARCH(problem) returns a solution, or failure
return RBFS(problem,MAKE-NODE(problem.INITIAL-STATE),∞)
function RBFS(problem, node, f limit ) returns a solution, or failure and a new f-cost limit
if problem.GOAL-TEST(node.STATE) then return SOLUTION(node)
successors ←[ ]
for each action in problem.ACTIONS(node.STATE) do
add CHILD-NODE(problem, node, action) intosuccessors
if successors is empty then return failure,∞
for each s in successors do /* update f with value from previous search, if any */
s.f ←max(s.g + s.h, node.f ))
loop do
best ←the lowest f-value node in successors
if best .f > f limit then return failure, best .f
alternative ←the second-lowest f-value among successors
result , best .f ←RBFS(problem, best , min( f limit, alternative))
if result = failure then return result
7](https://image.slidesharecdn.com/lecture-16memoryboundedsearch-170131122117/75/Lecture-16-memory-bounded-search-7-2048.jpg)