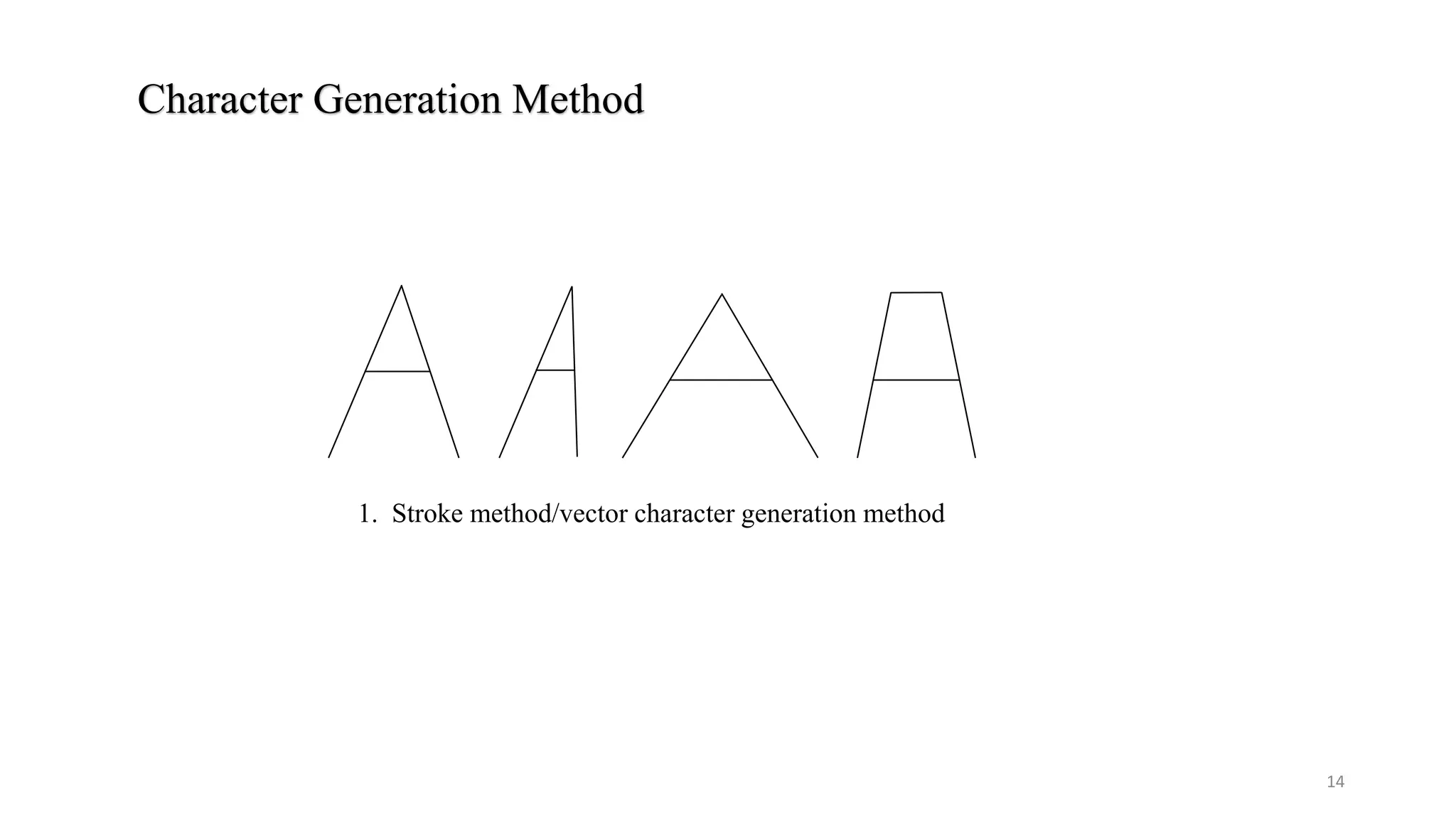
The document describes various algorithms for line and circle drawing in computer graphics, focusing on the Digital Differential Analyzer (DDA) and Bresenham's algorithms. It outlines the steps involved, advantages and disadvantages of each method, and includes examples for clarity. Additionally, it touches on character generation methods such as stroke, dot-matrix, and starburst methods.