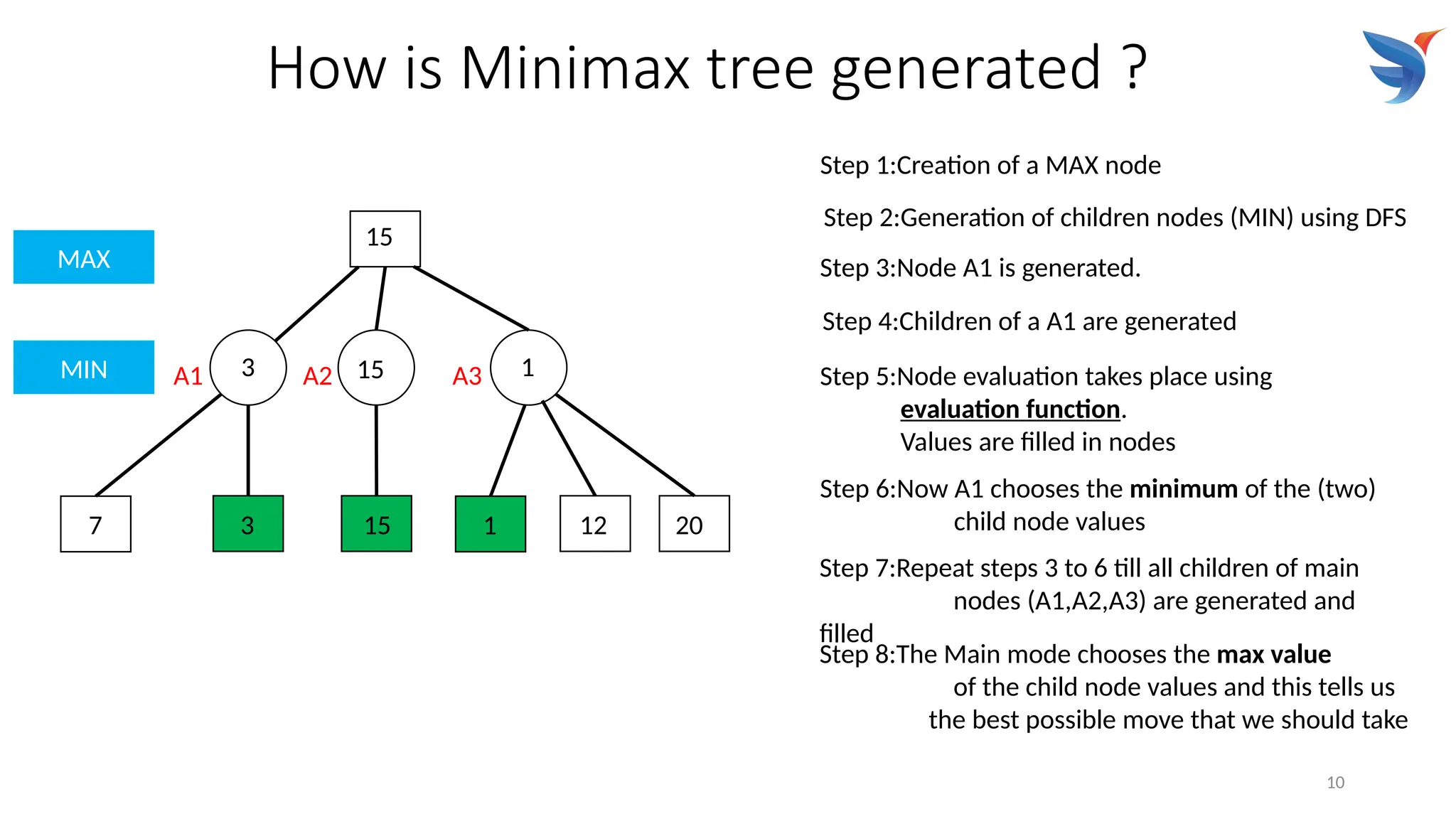
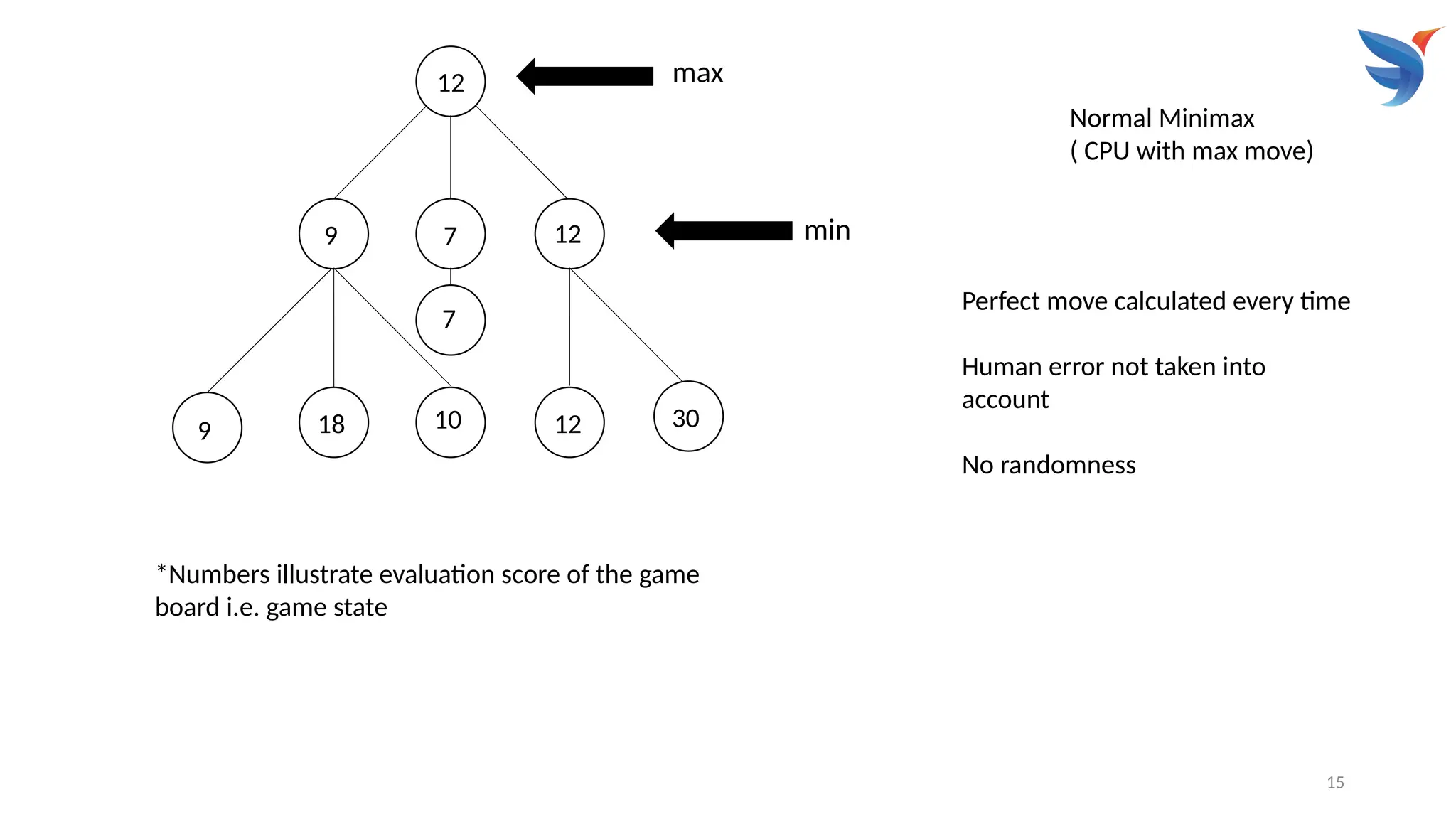
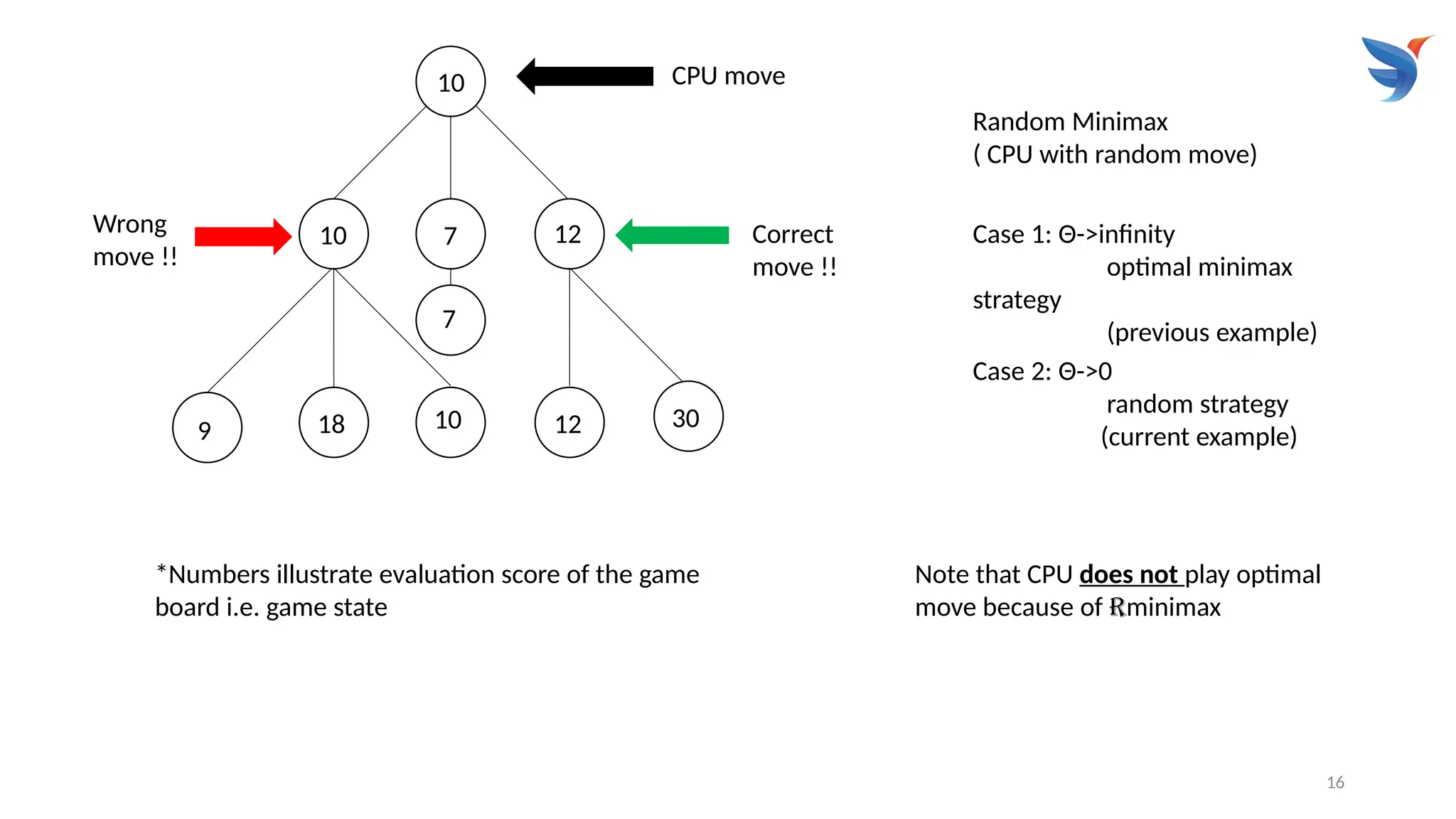
The Mini-Max algorithm is a recursive or backtracking algorithm used in artificial intelligence, particularly for two-player, zero-sum games like chess and tic-tac-toe. It helps determine the optimal move for a player, assuming the opponent will also play optimally to minimize the first player's gains. The algorithm explores a game tree, evaluating potential moves and their consequences to select the best course of action for the "max" player while anticipating the "min" player's (opponent's) optimal response