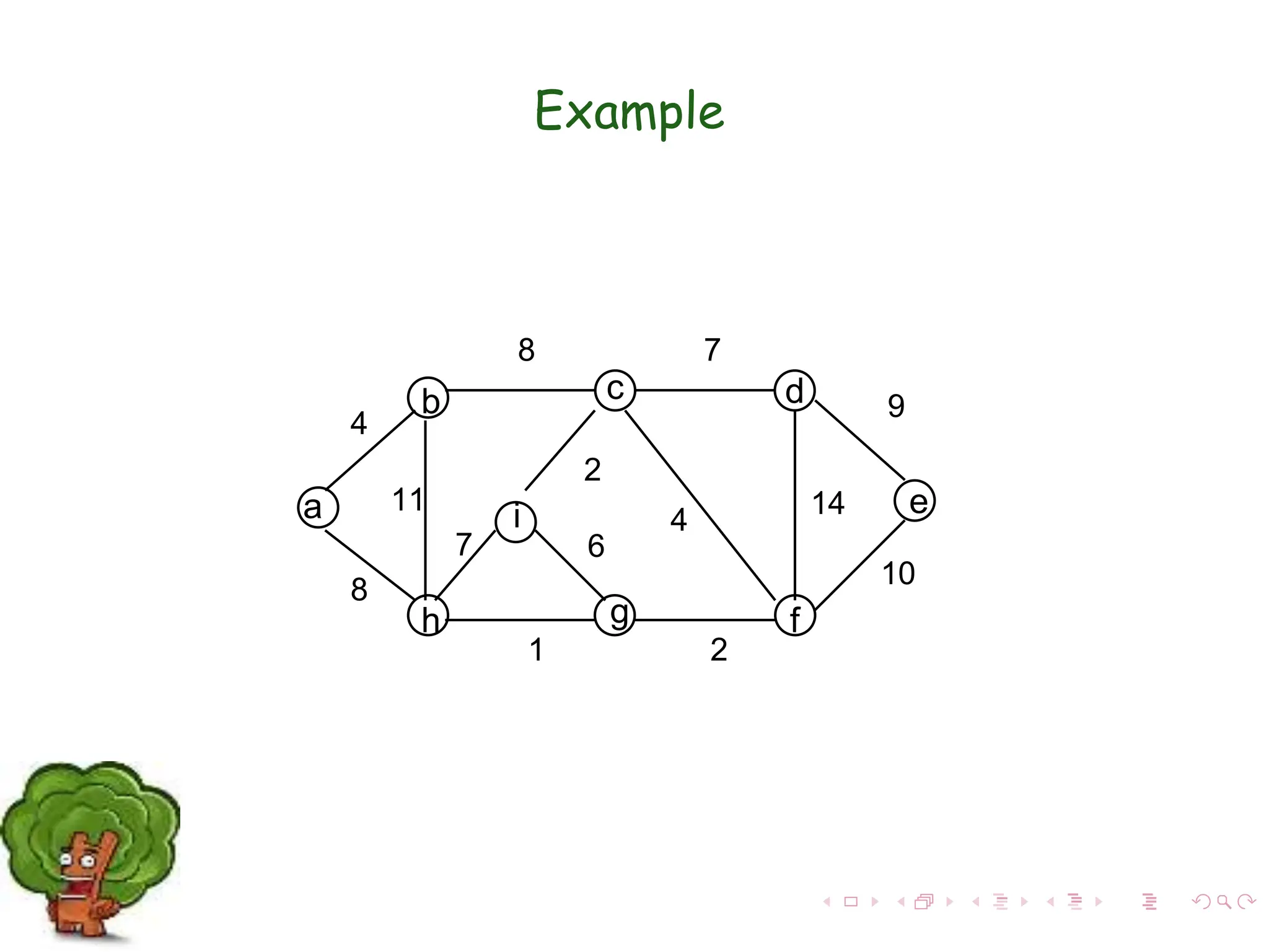
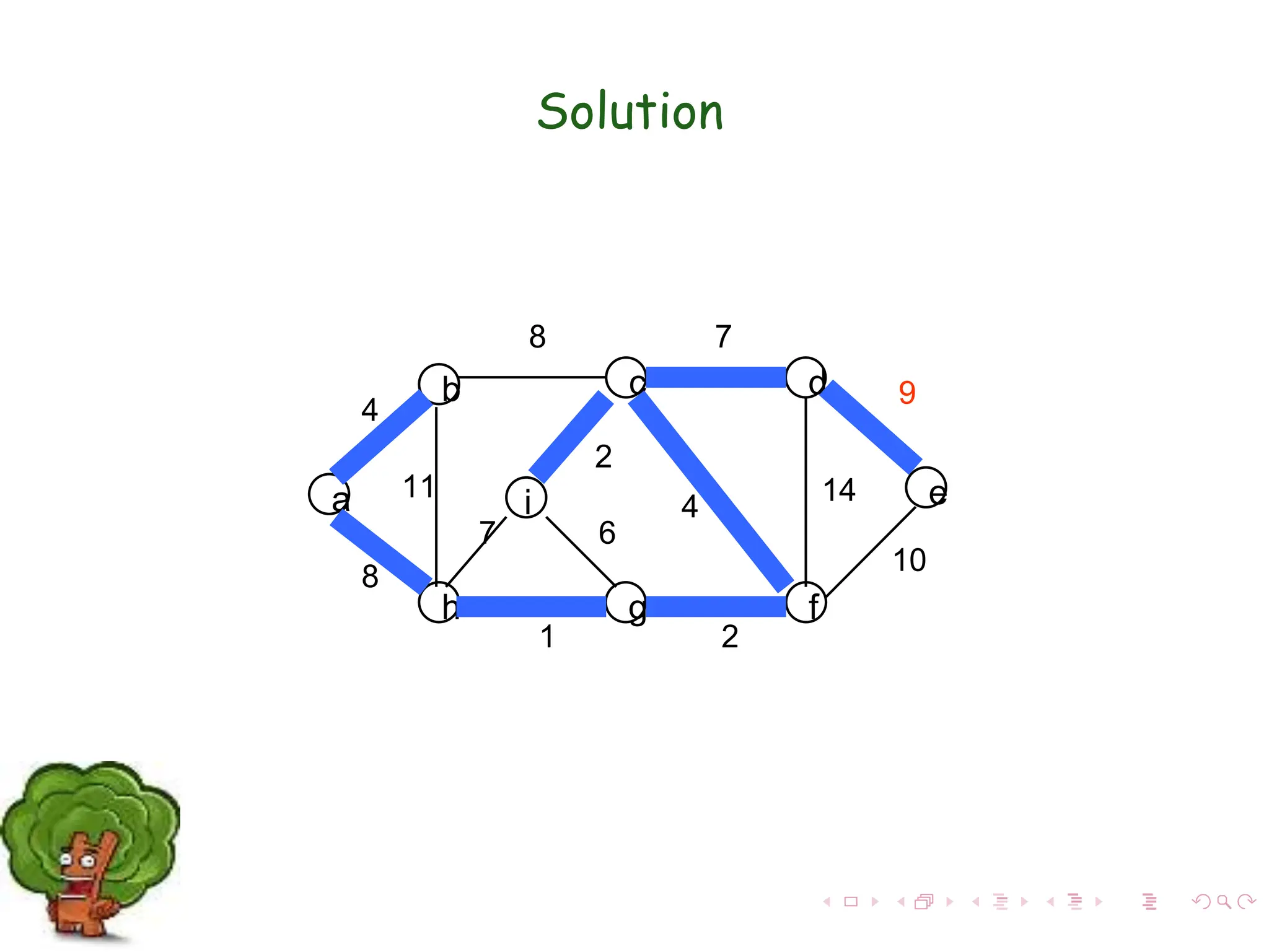
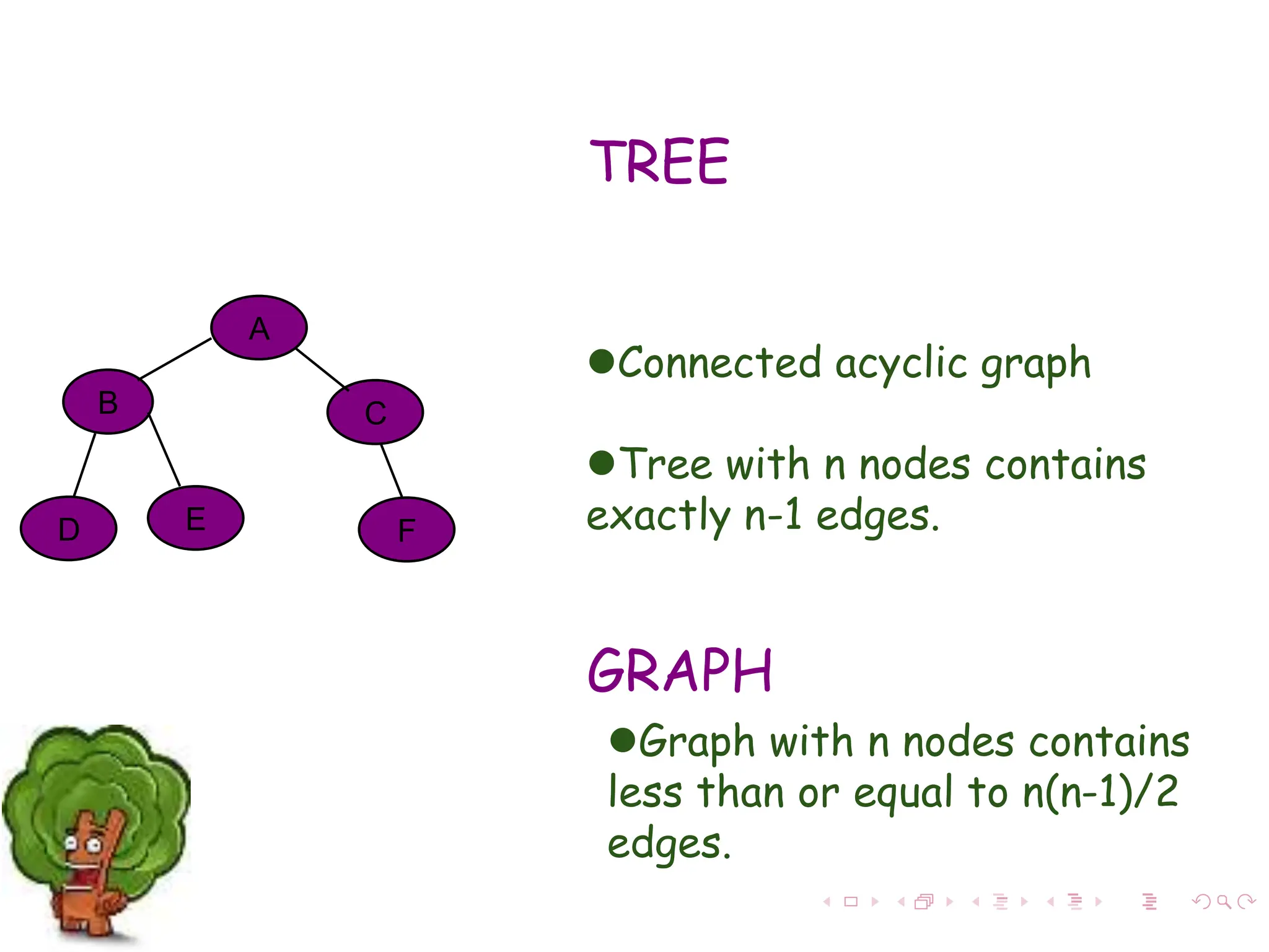
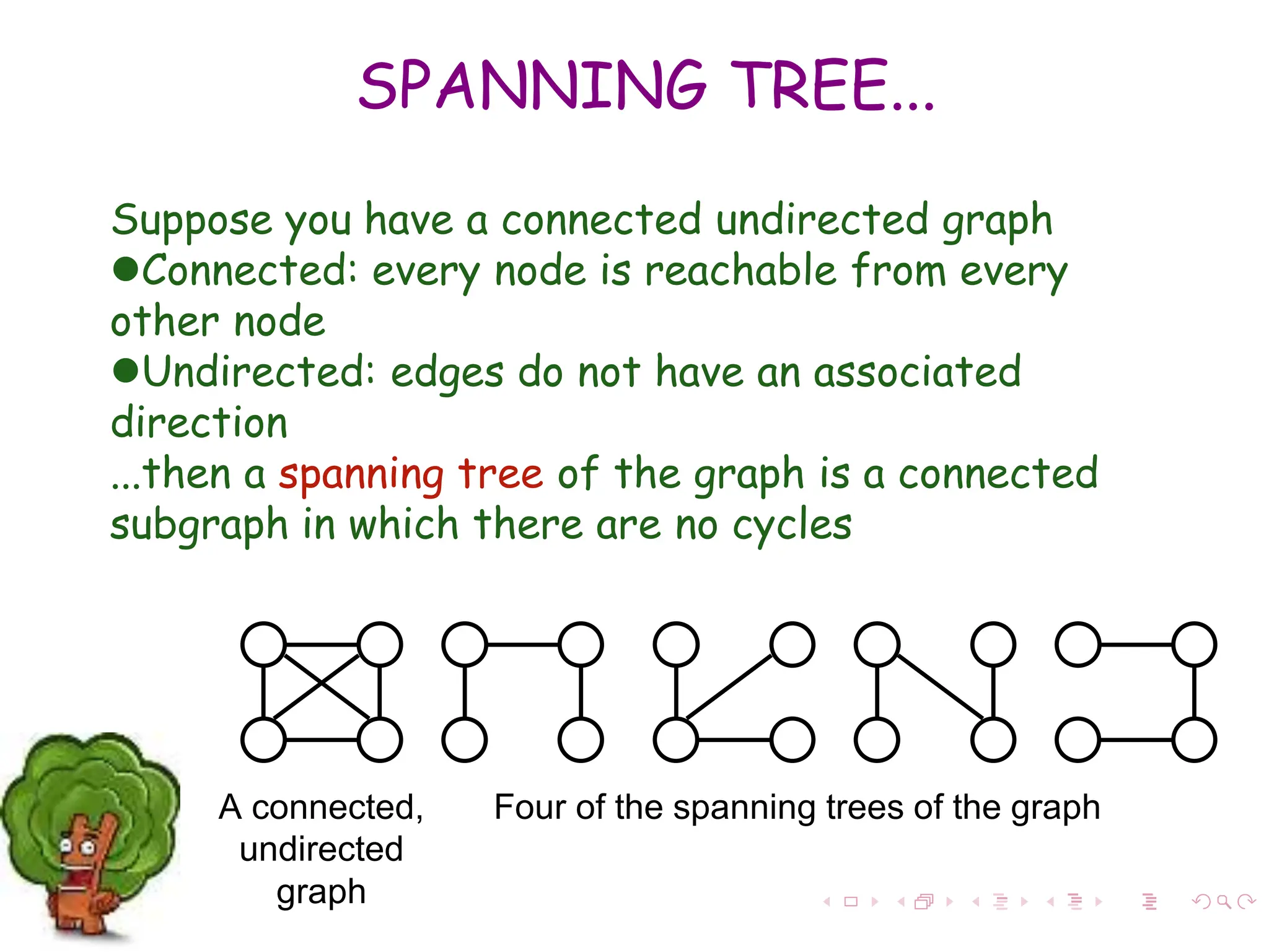
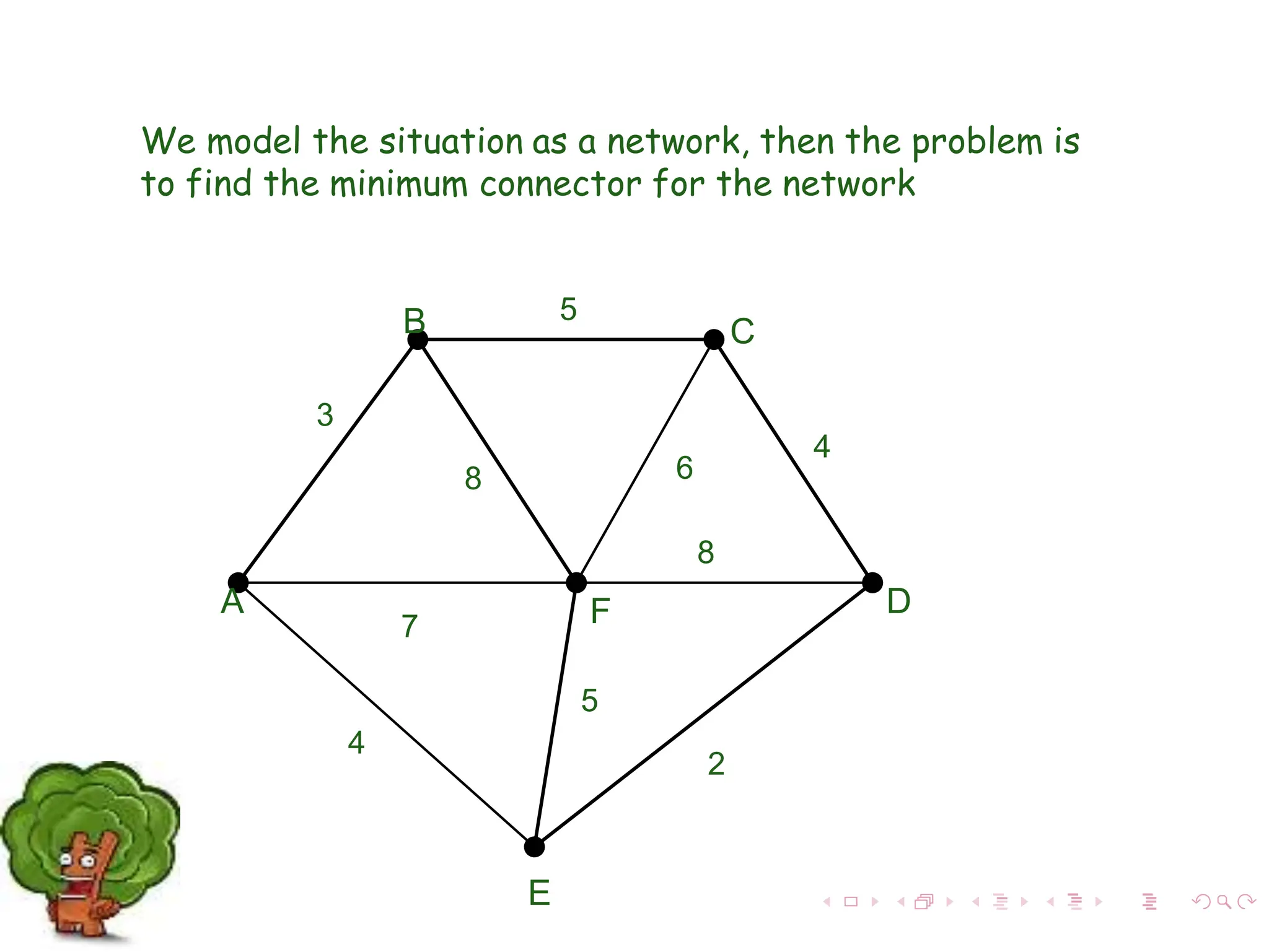
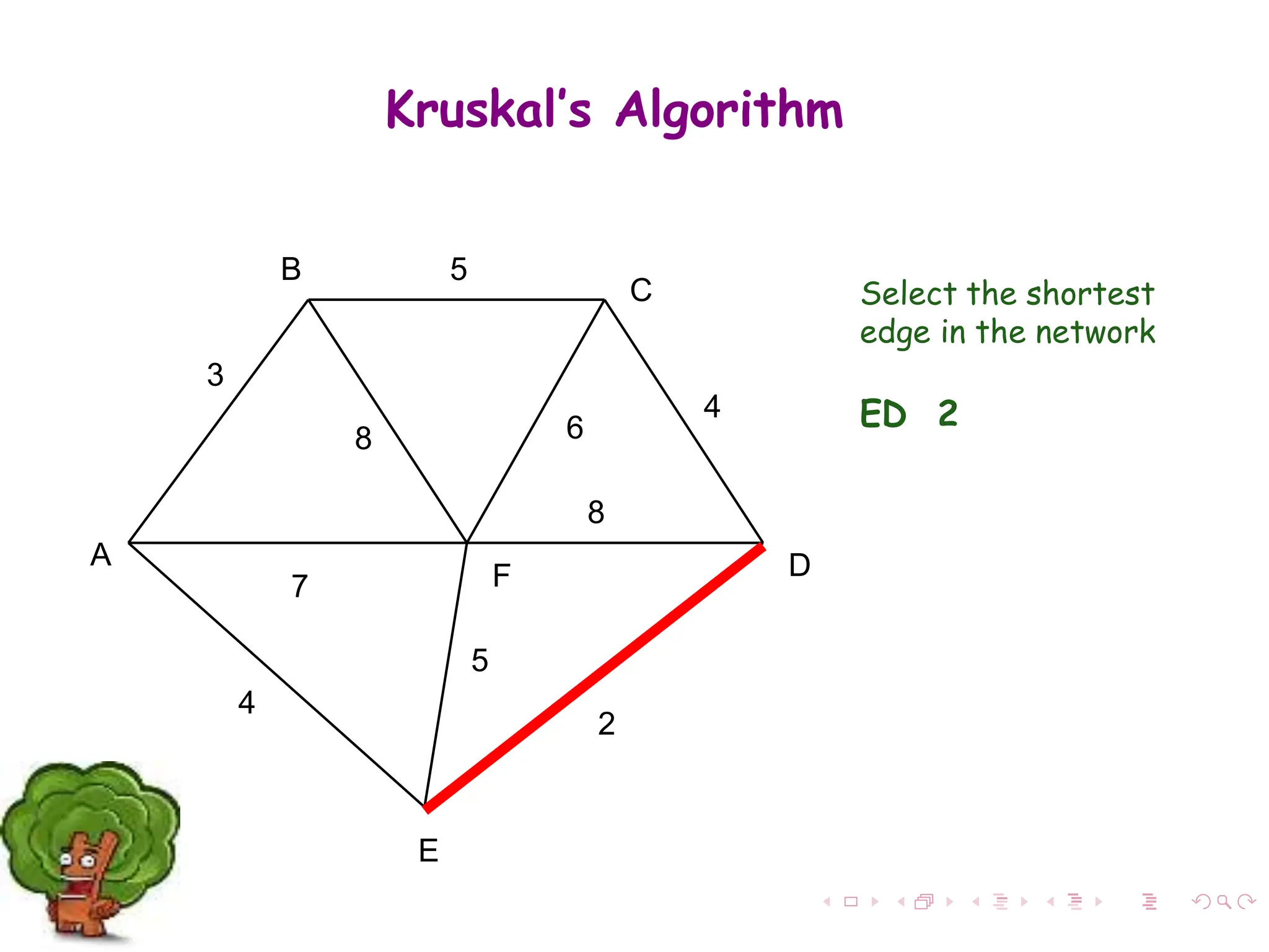
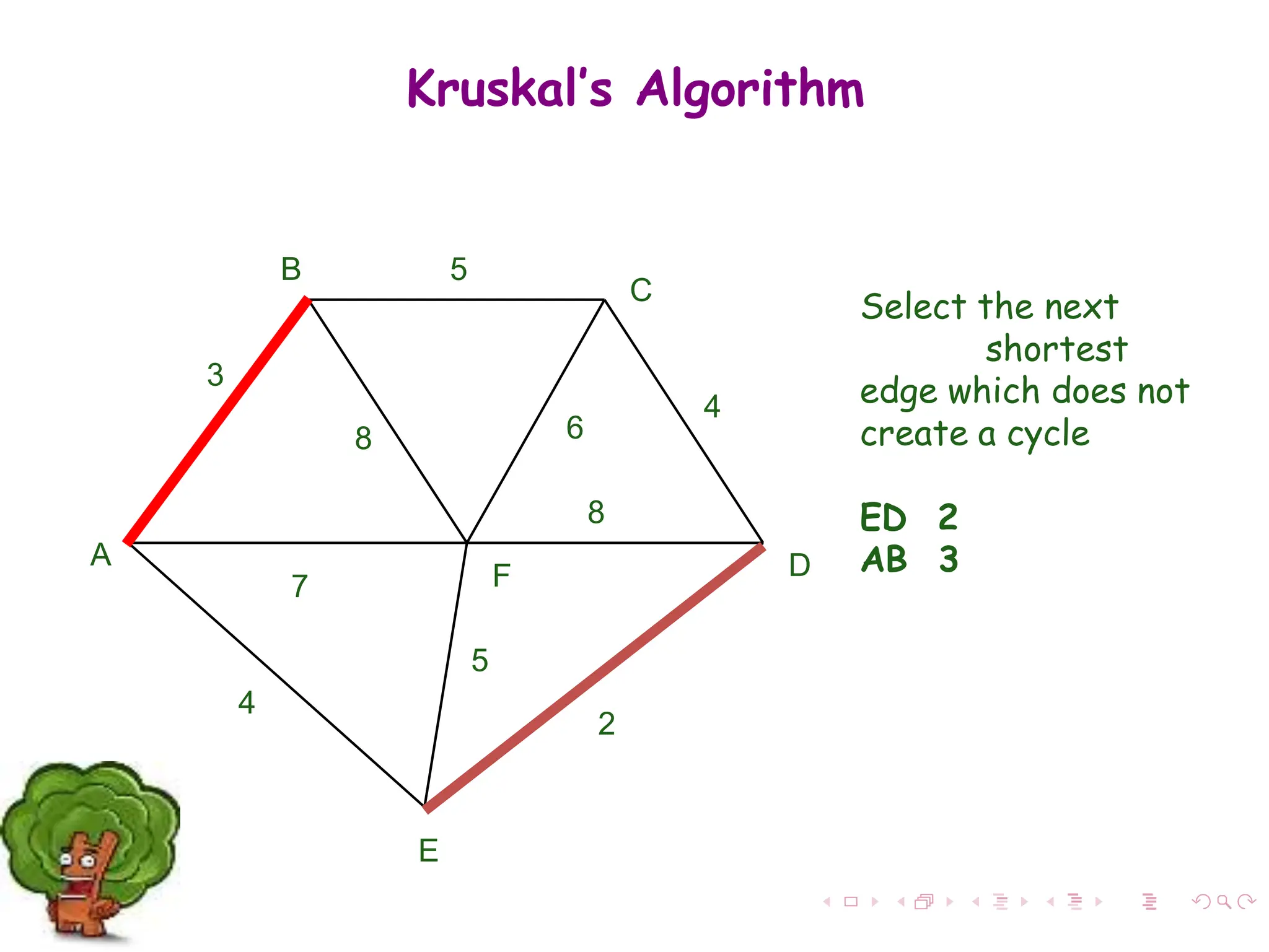
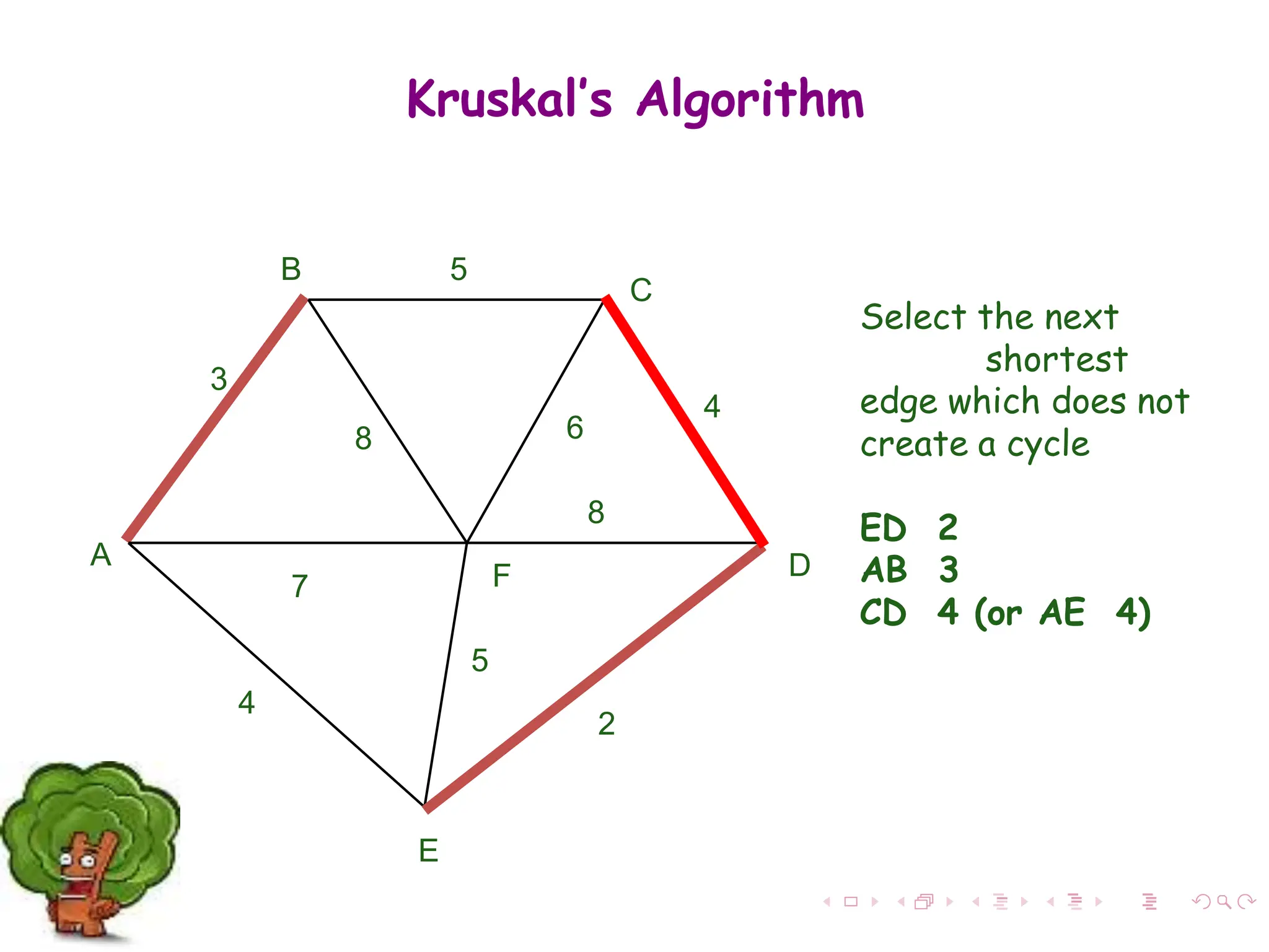
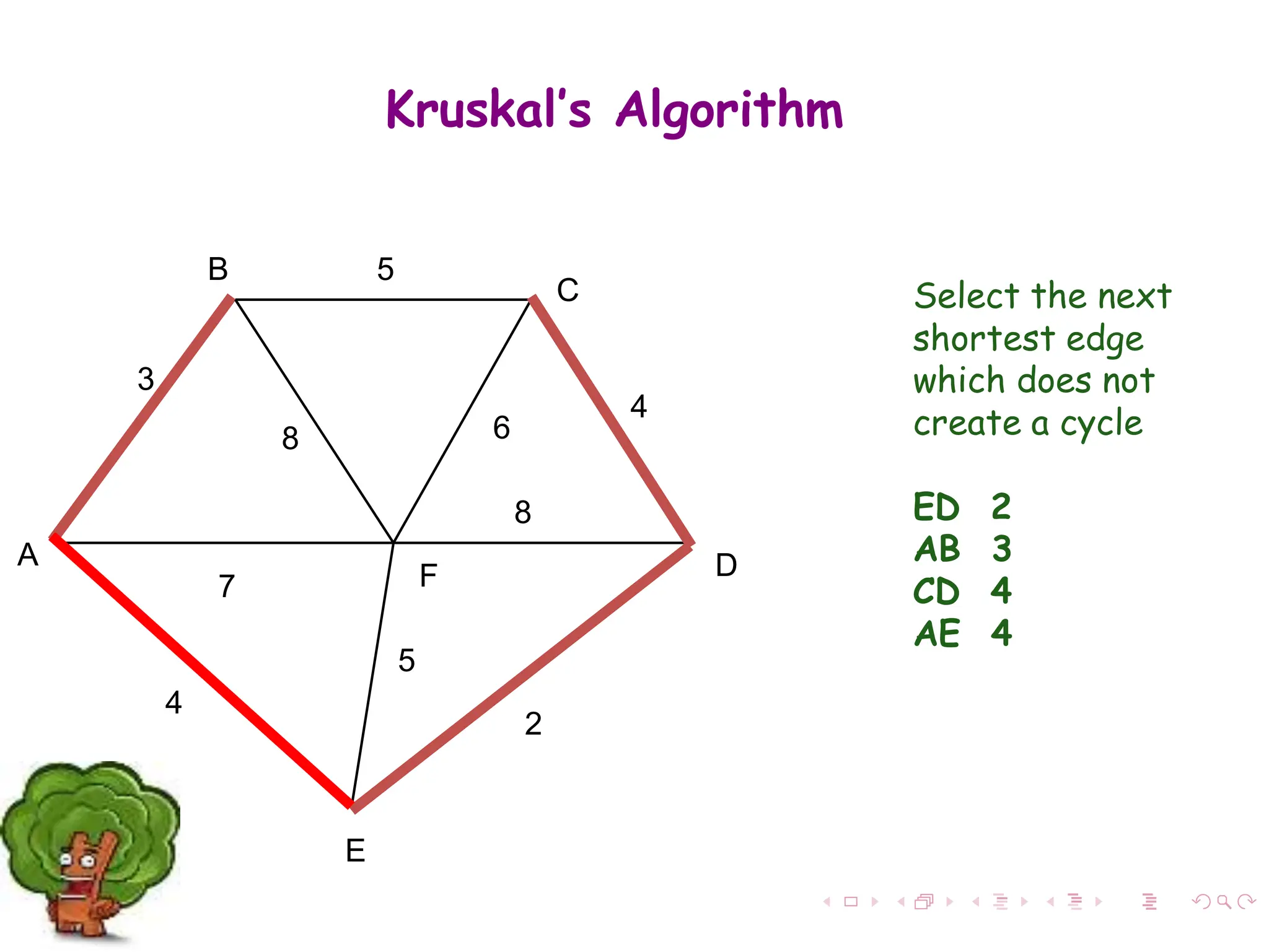
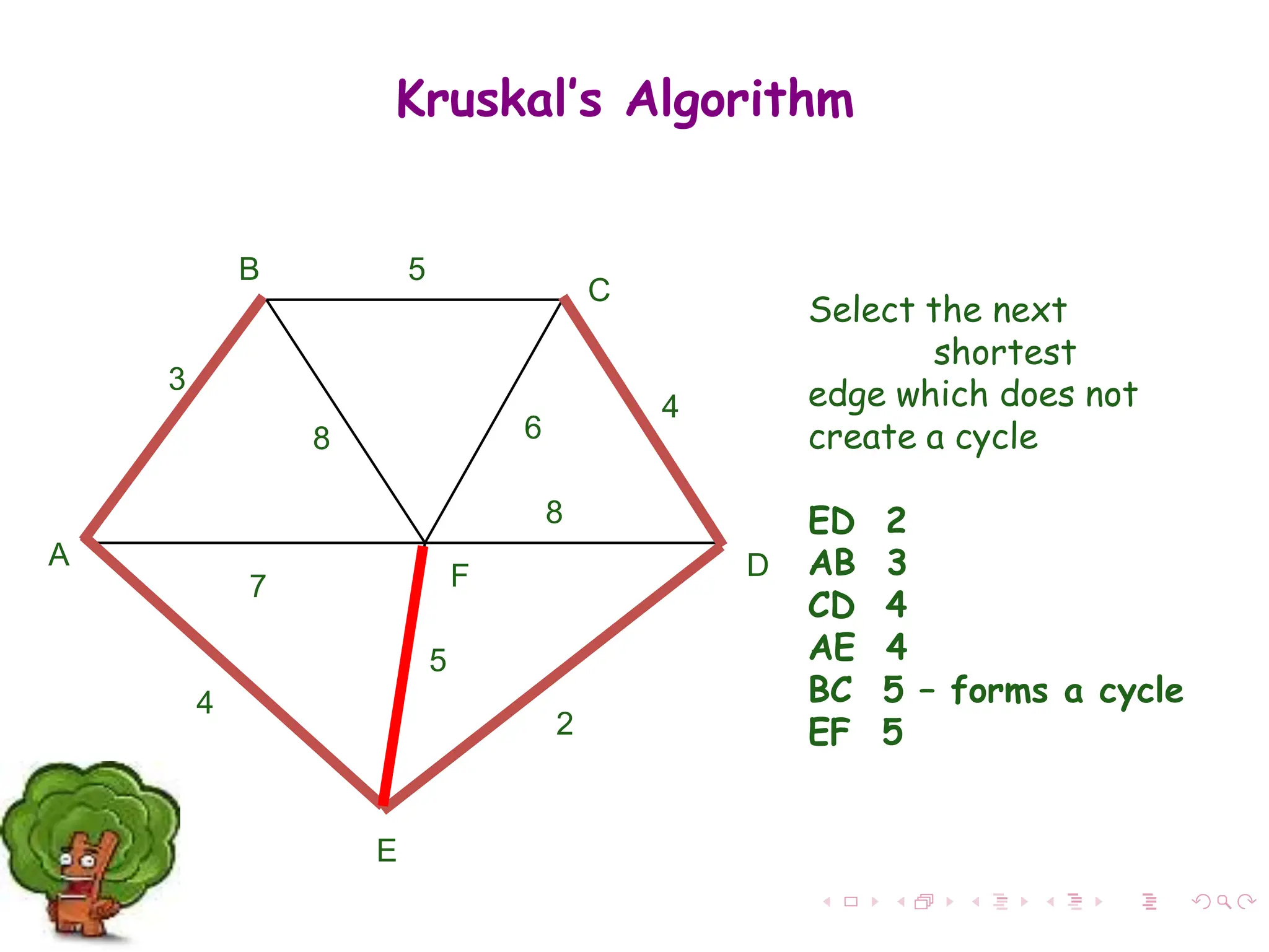
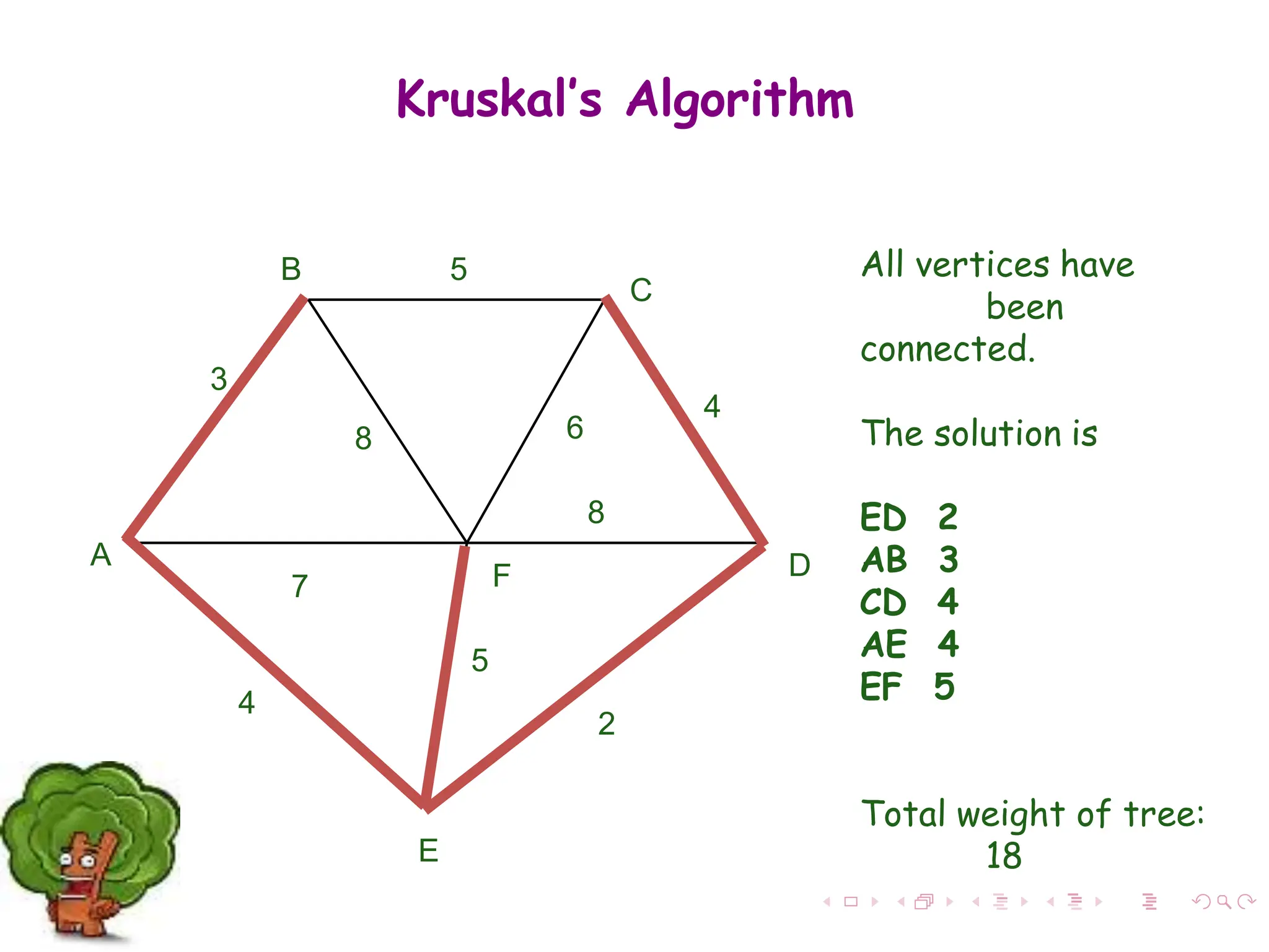
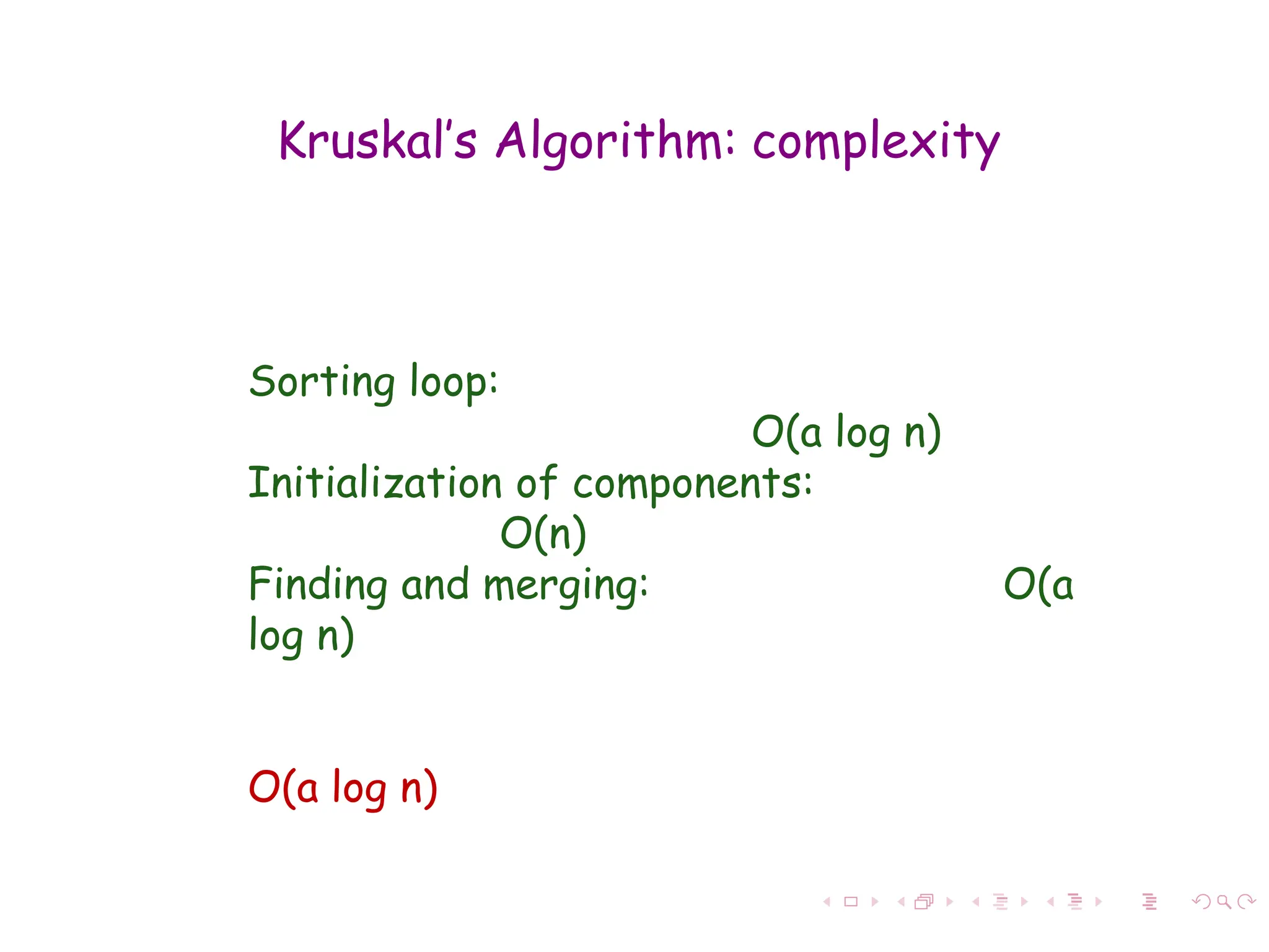
The document discusses minimum spanning trees (MST) in connected, undirected graphs, defining them as trees with n-1 edges containing all nodes. It outlines two primary algorithms for finding MST: Kruskal's and Prim's, both of which are greedy algorithms that aim to connect all nodes with the minimum edge weight. Example scenarios illustrate the application of these algorithms and detail their respective processes and complexities.









![Prim’s Algorithm
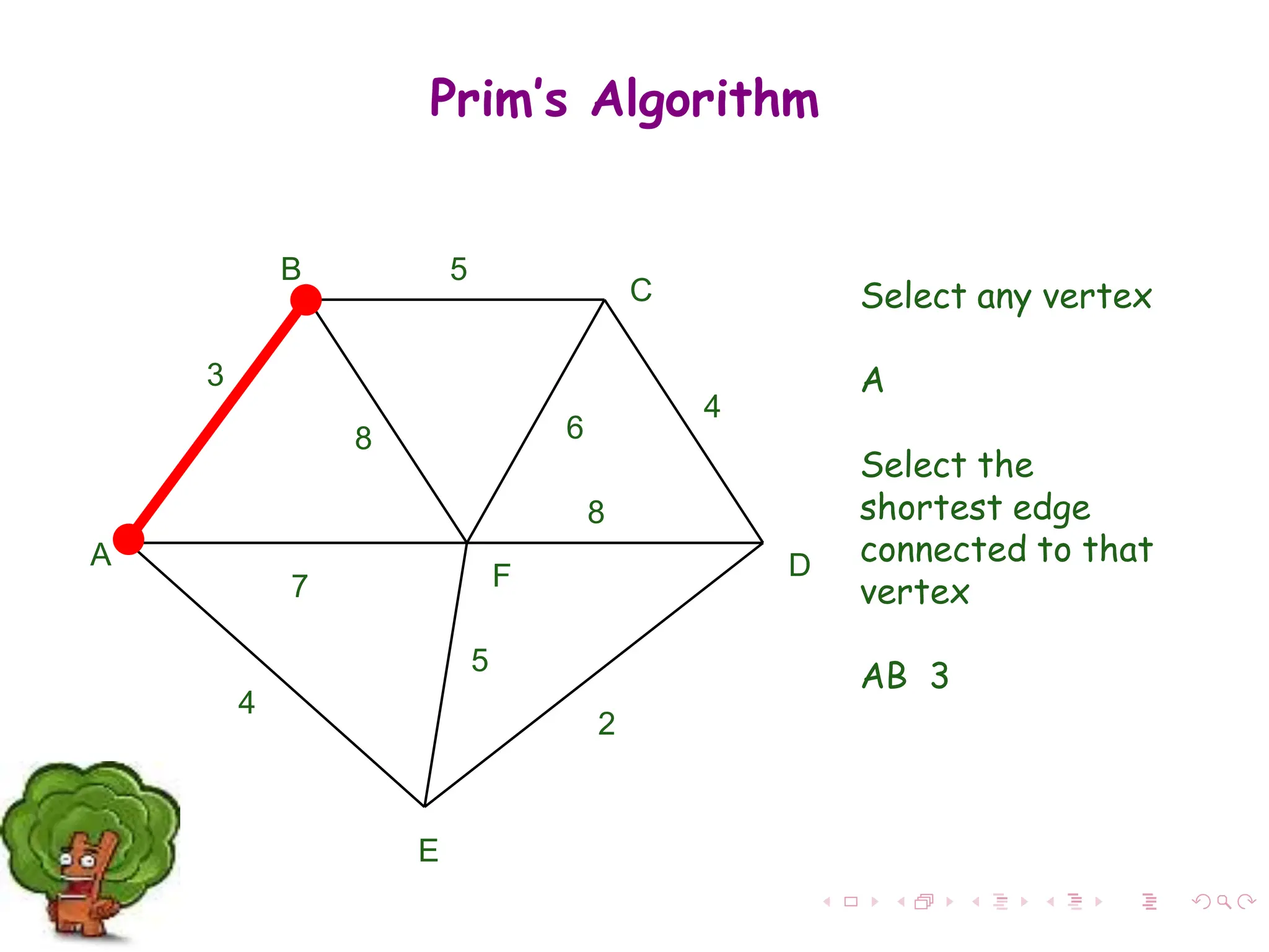
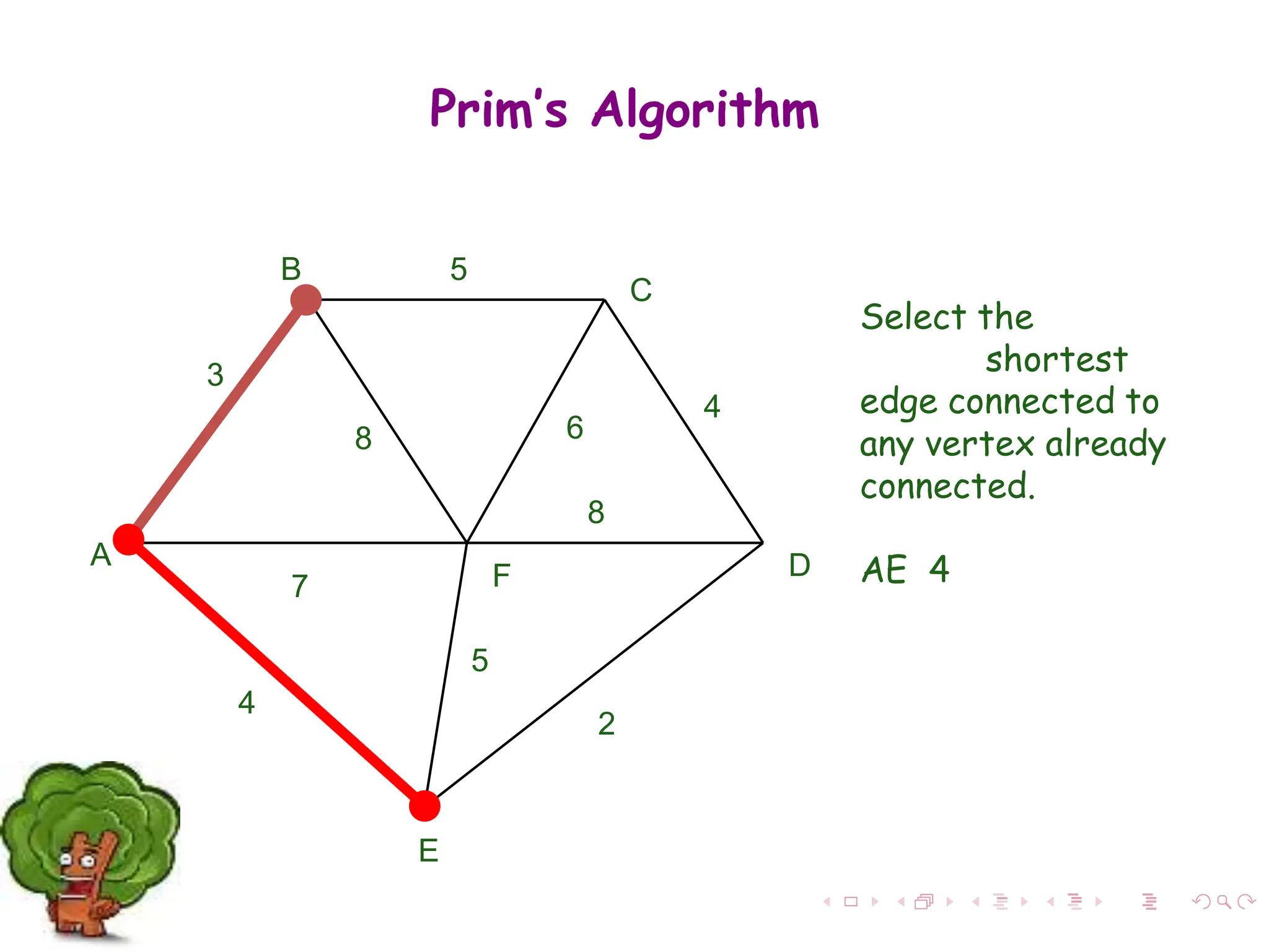
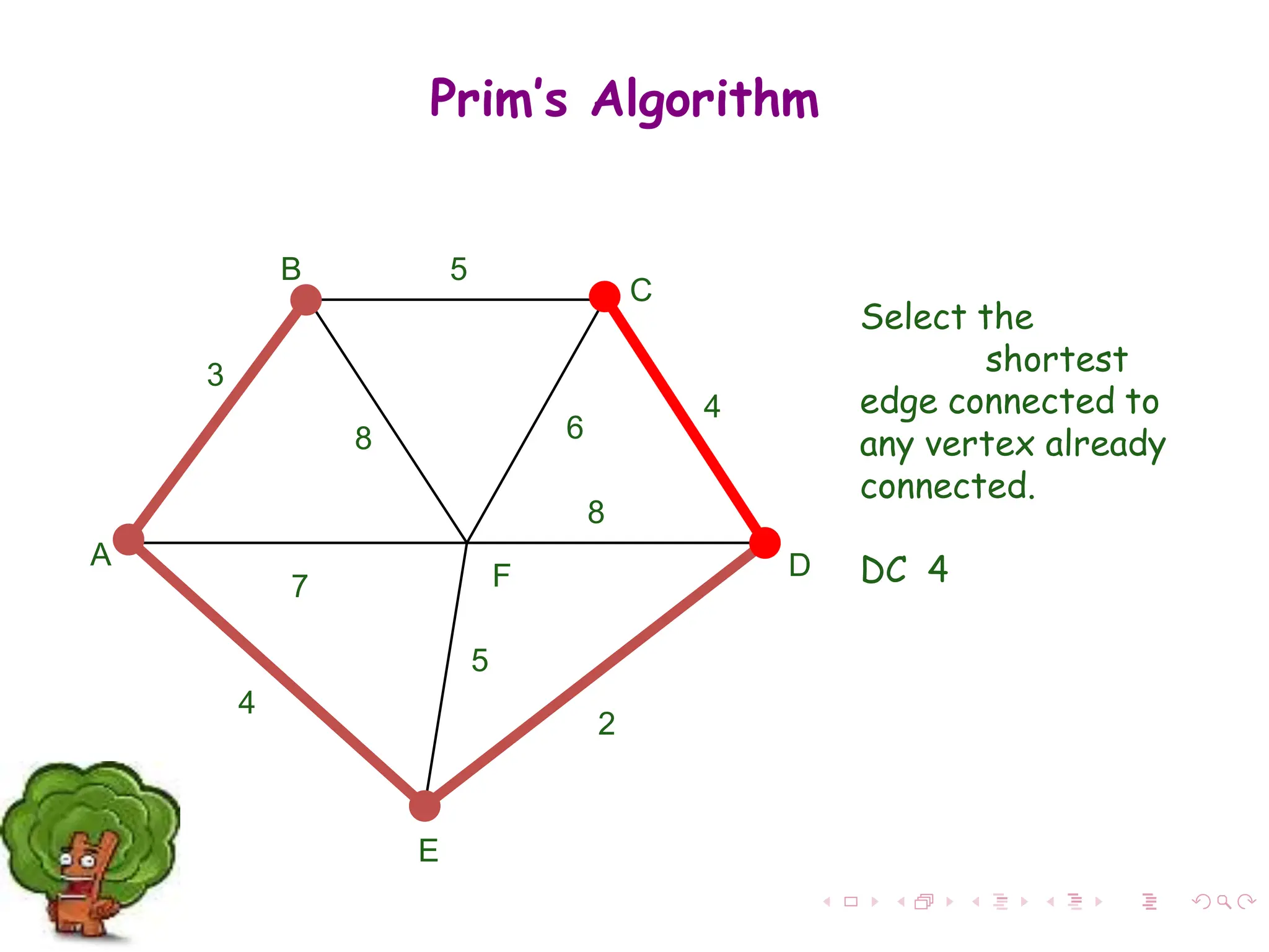
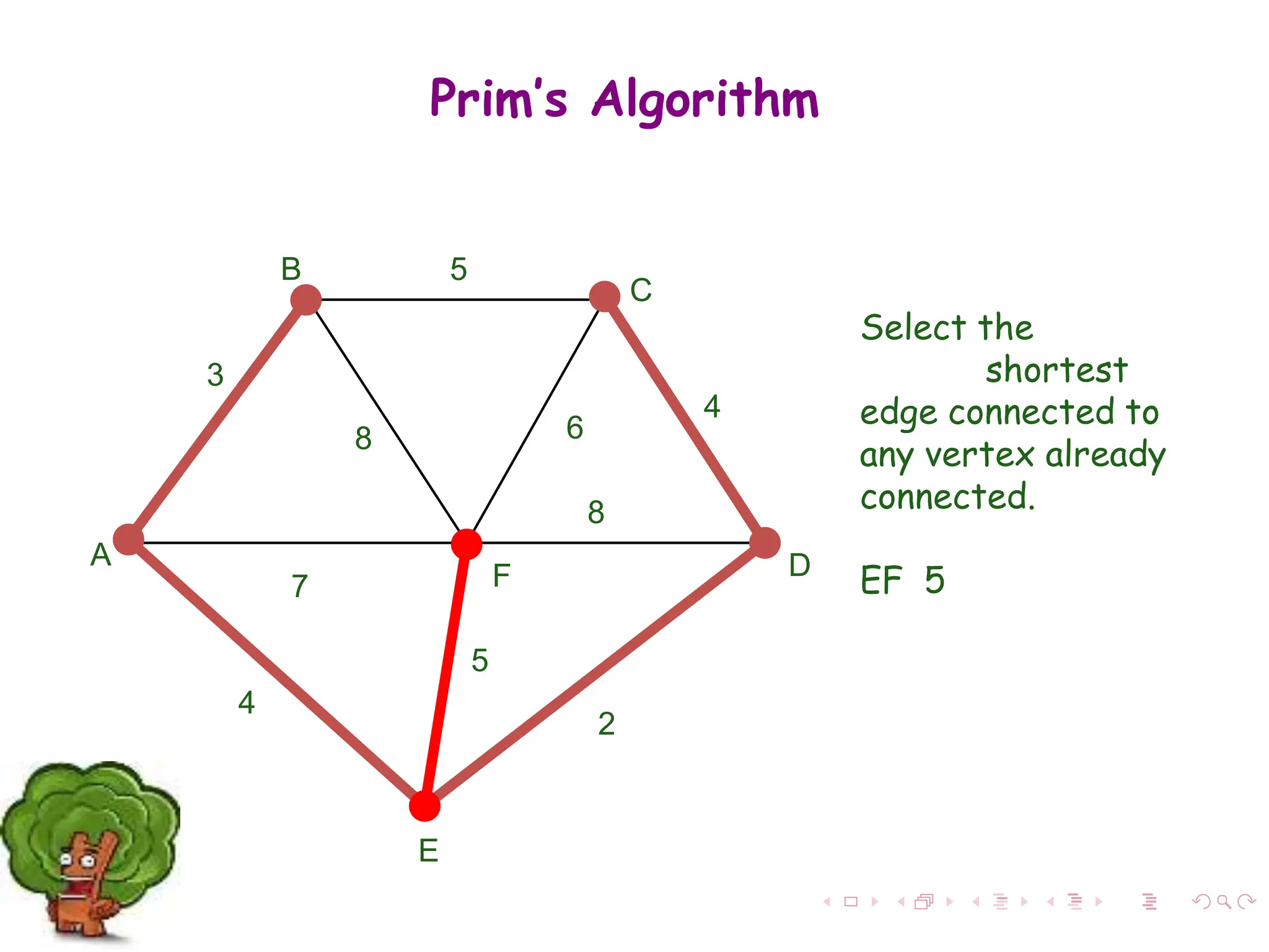
Step 1: Select a starting vertex
Step 2: Repeat Steps 3 and 4 until there are fringe
vertices
Step 3: Select an edge e connecting the tree vertex
and fringe vertex that has minimum weight
Step 4: Add the selected edge and the vertex to the
minimum spanning tree T
[END OF LOOP]
Step 5: EXIT](https://image.slidesharecdn.com/mst-240725141047-6c5fd962/75/Minimum-Spanning-Tree-Data-Structure-and-Algorithm-20-2048.jpg)