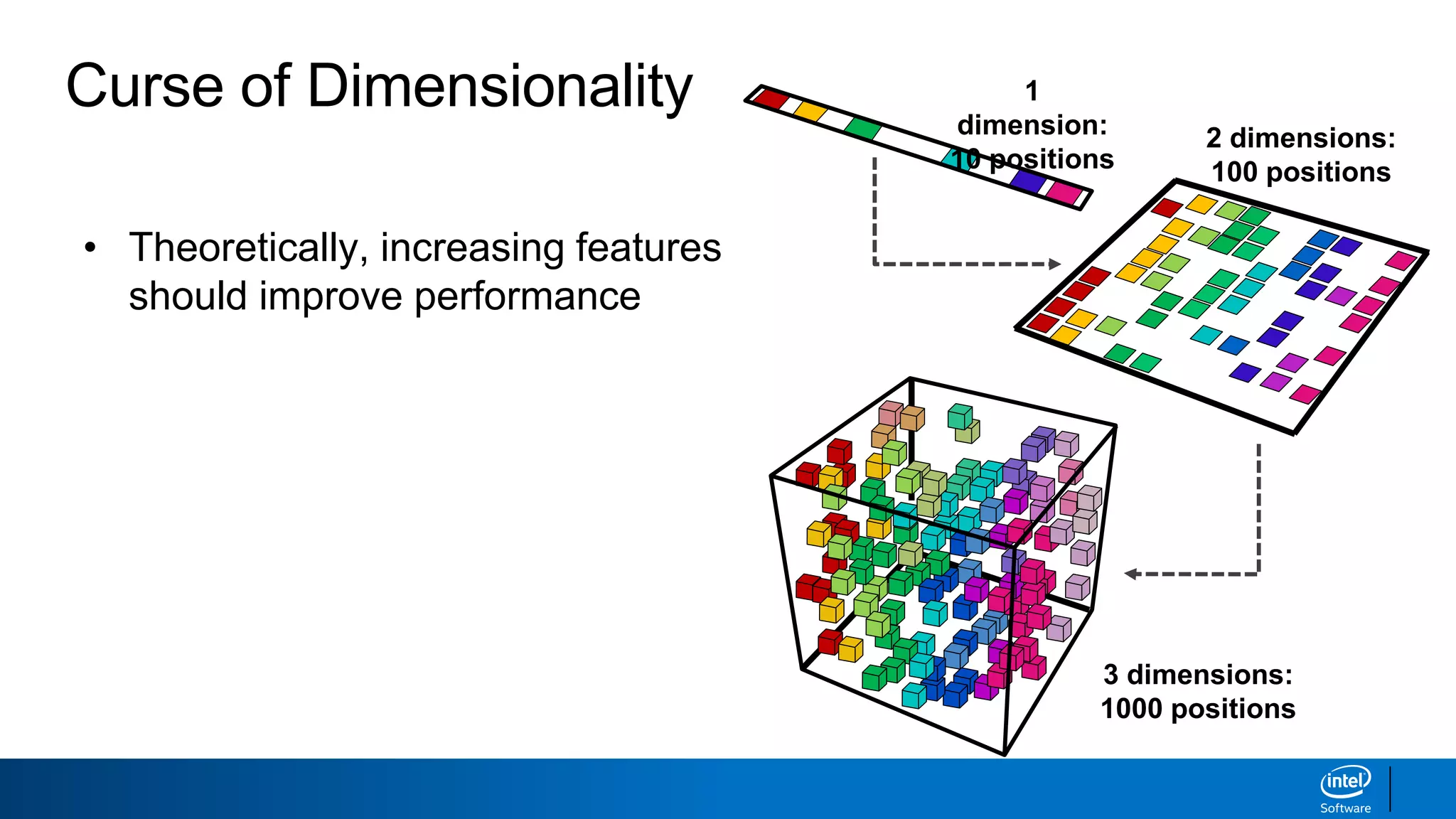
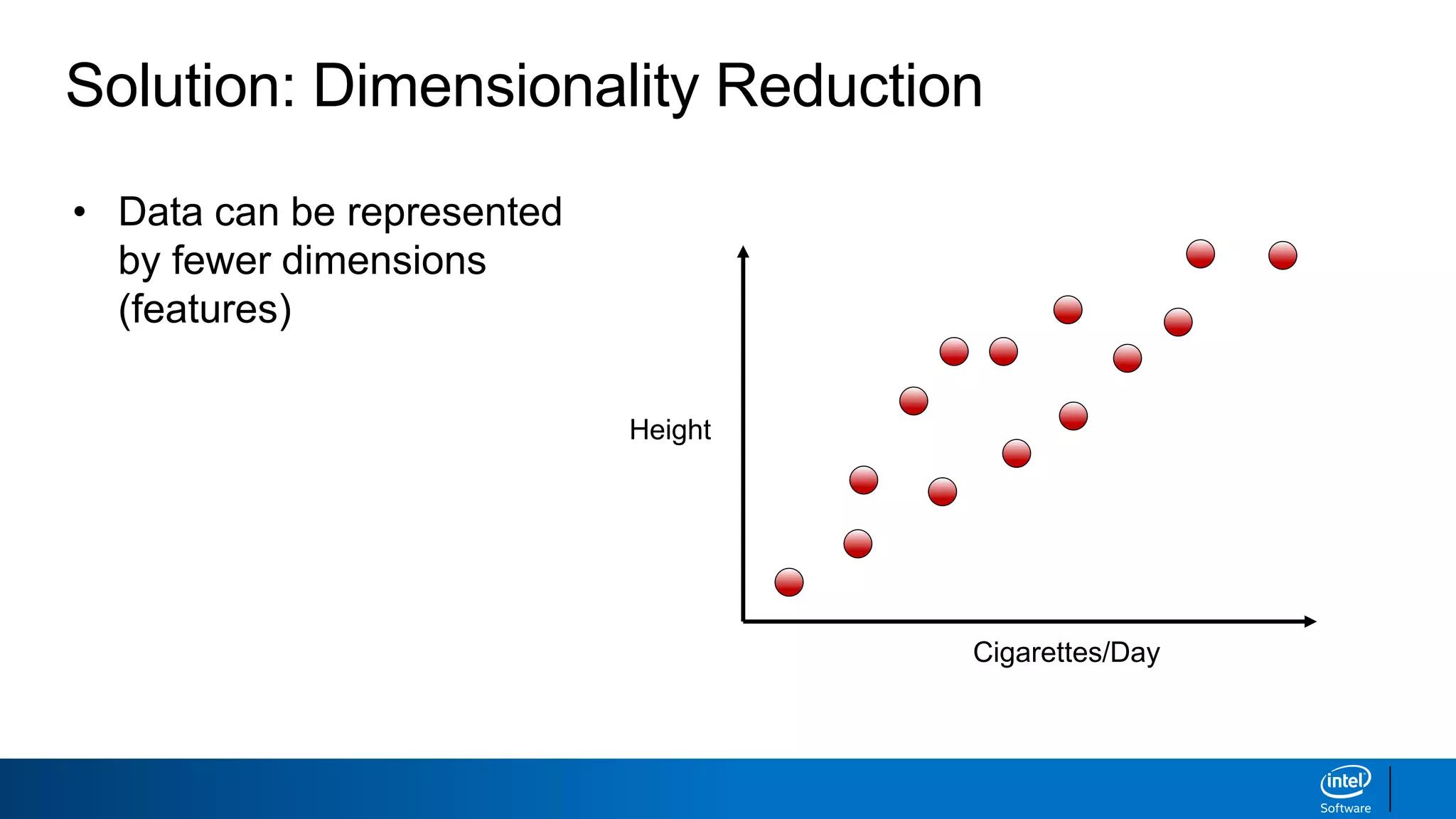
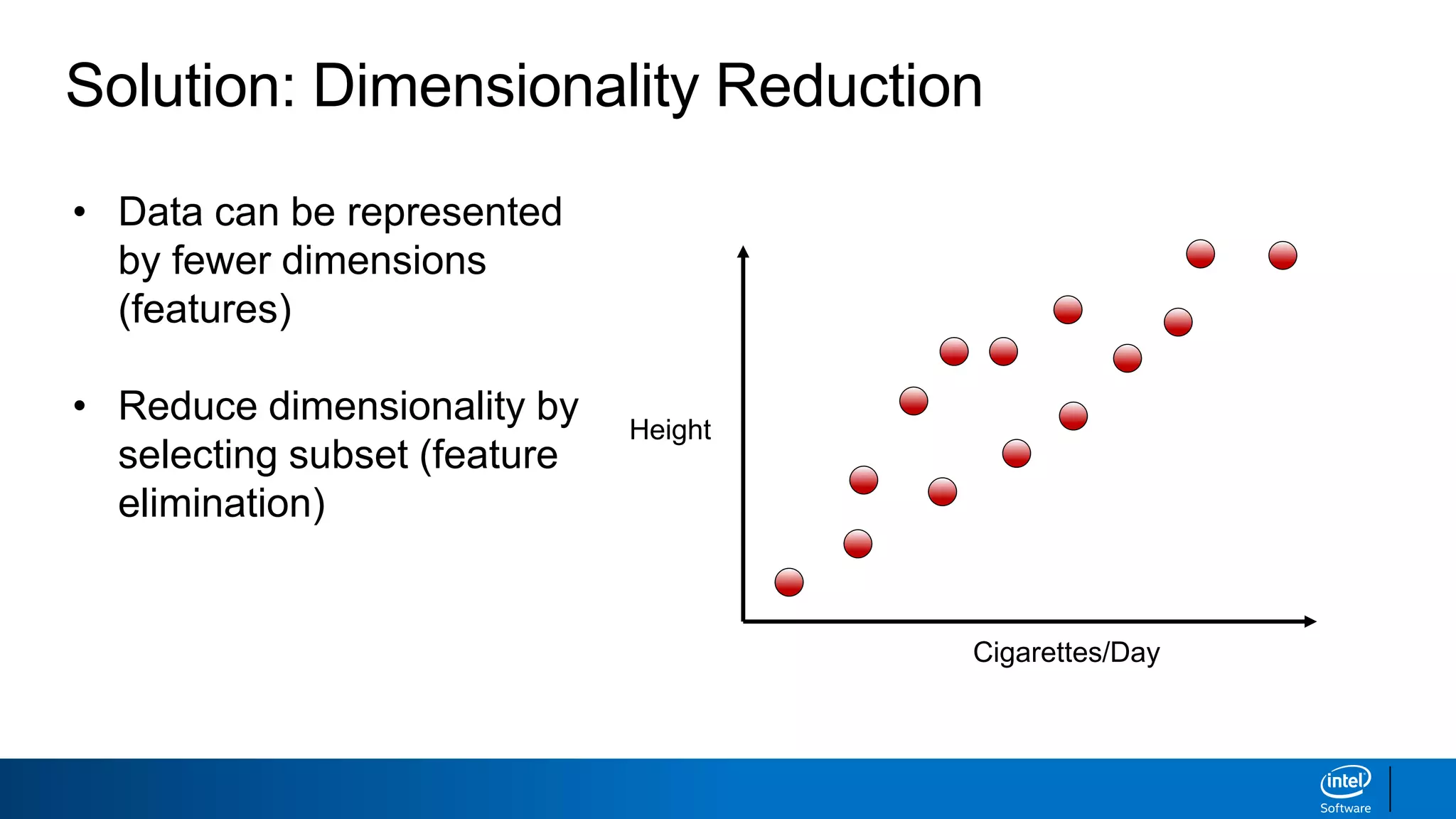
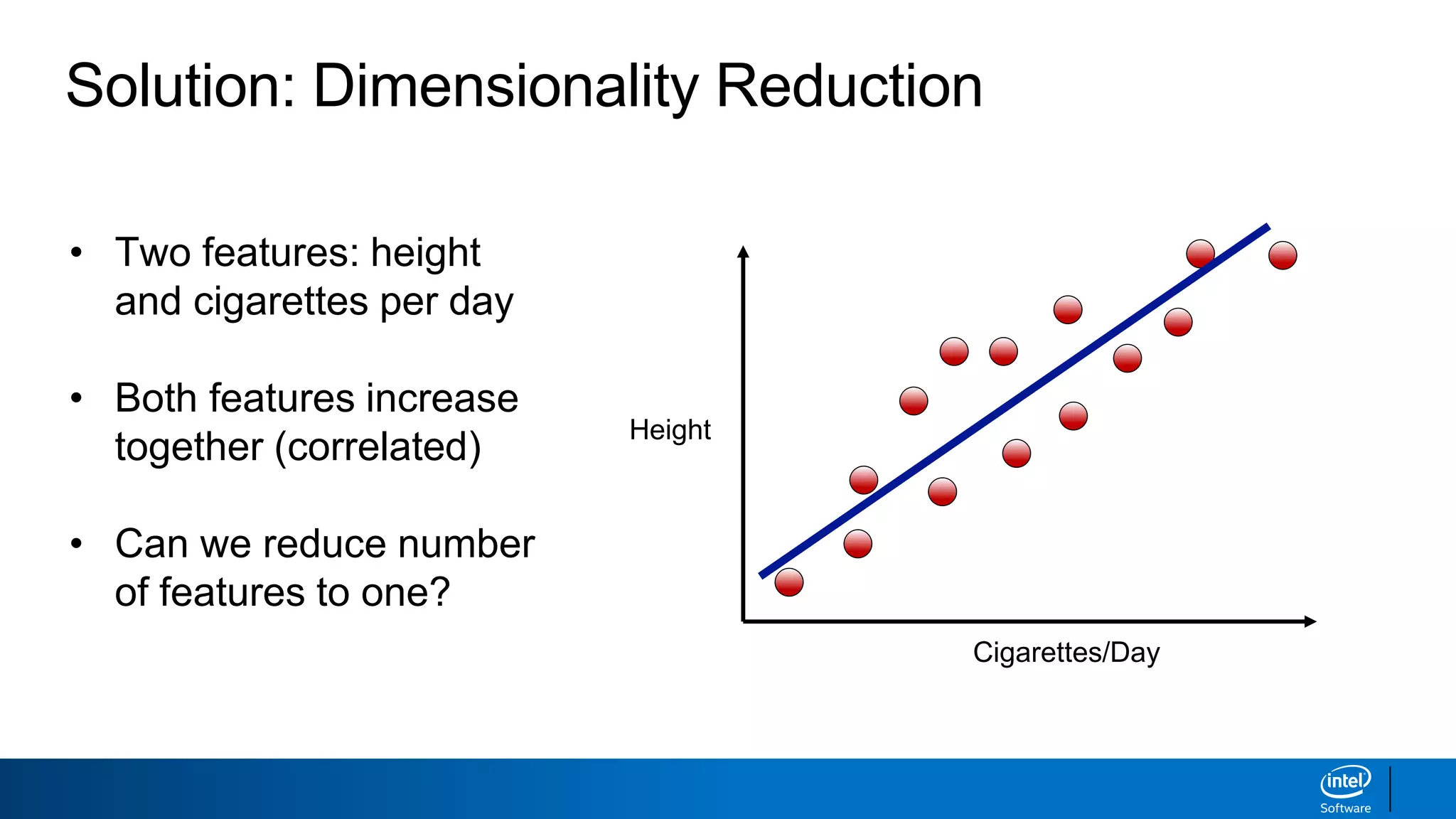
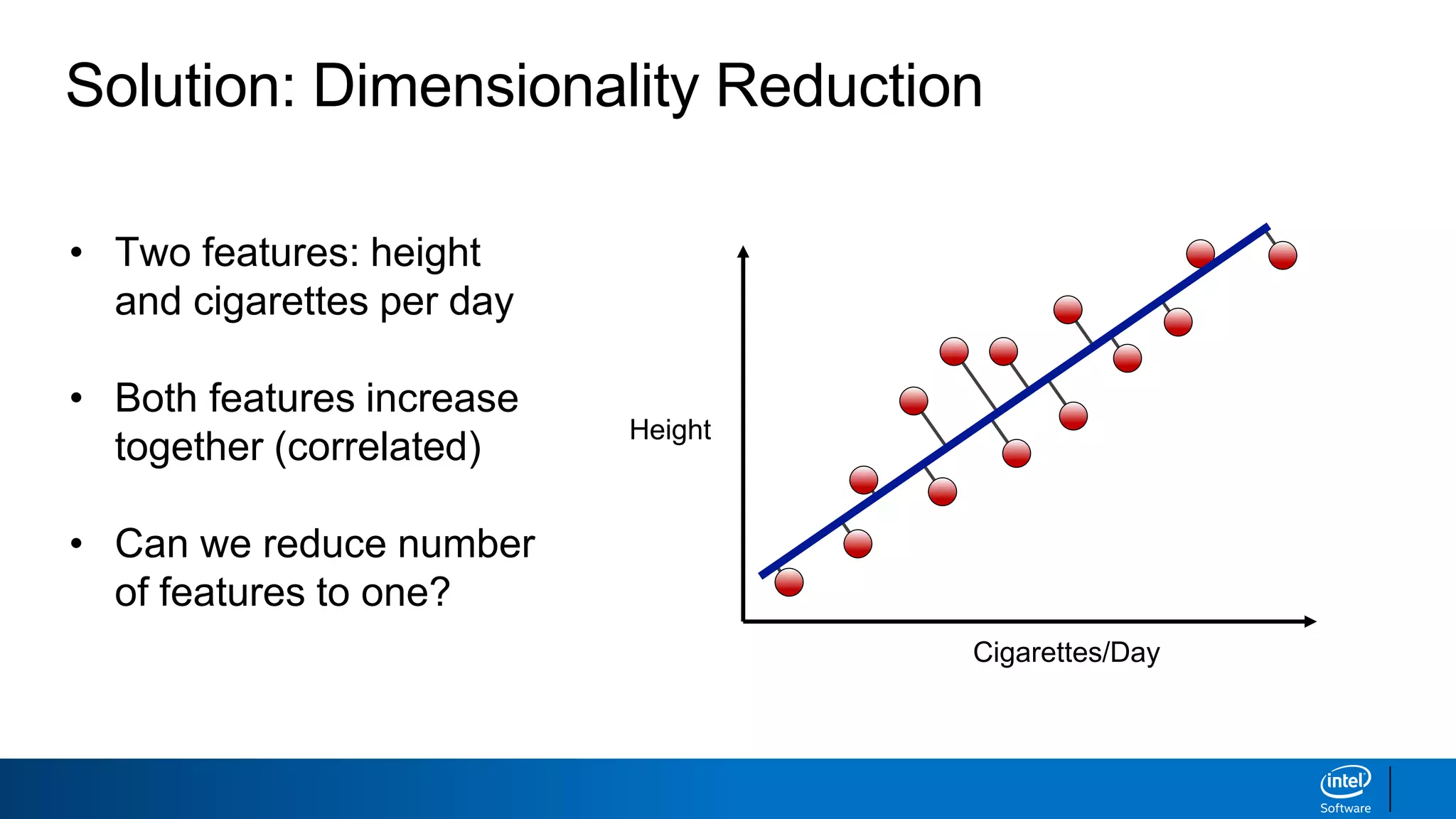
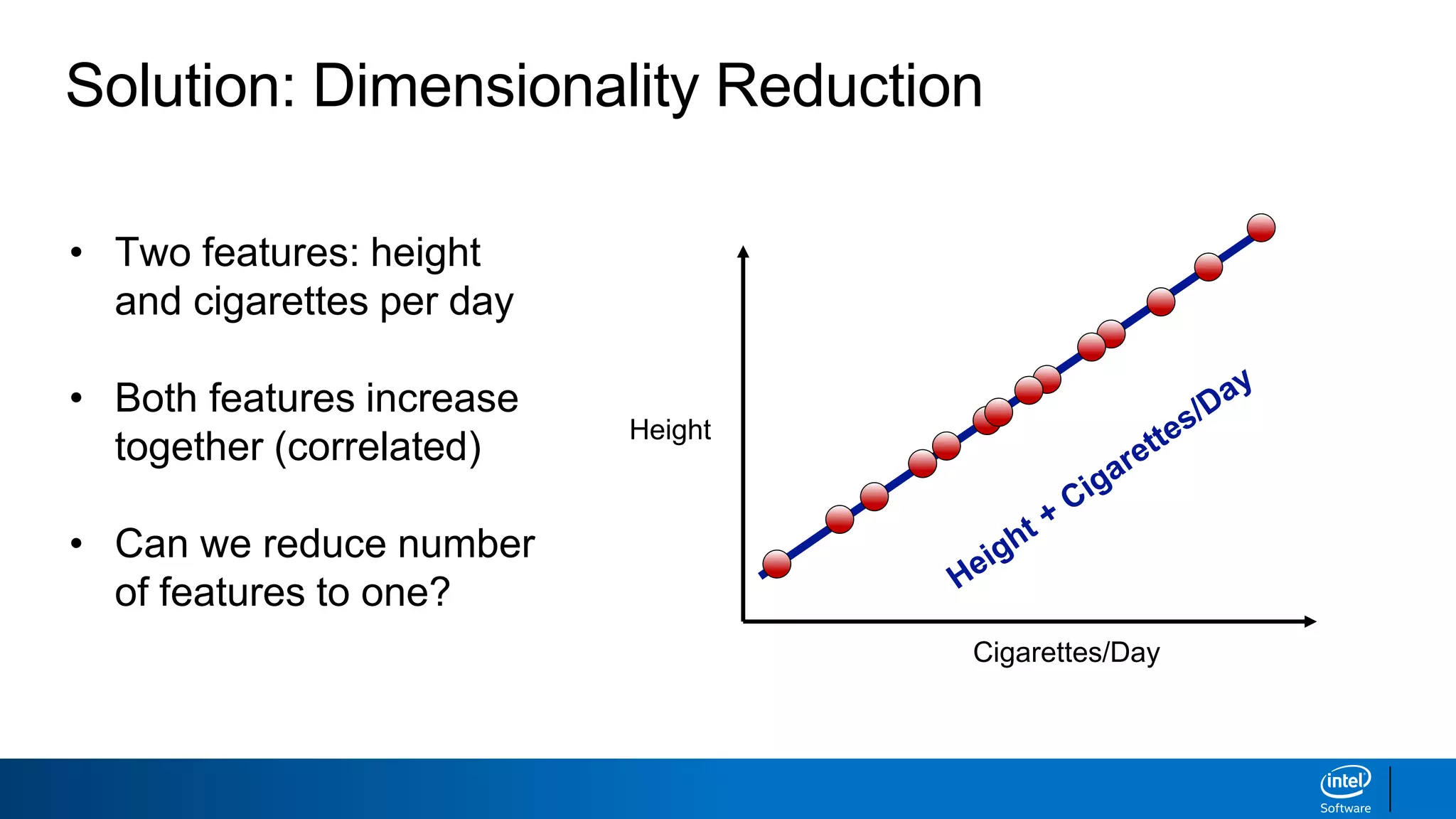
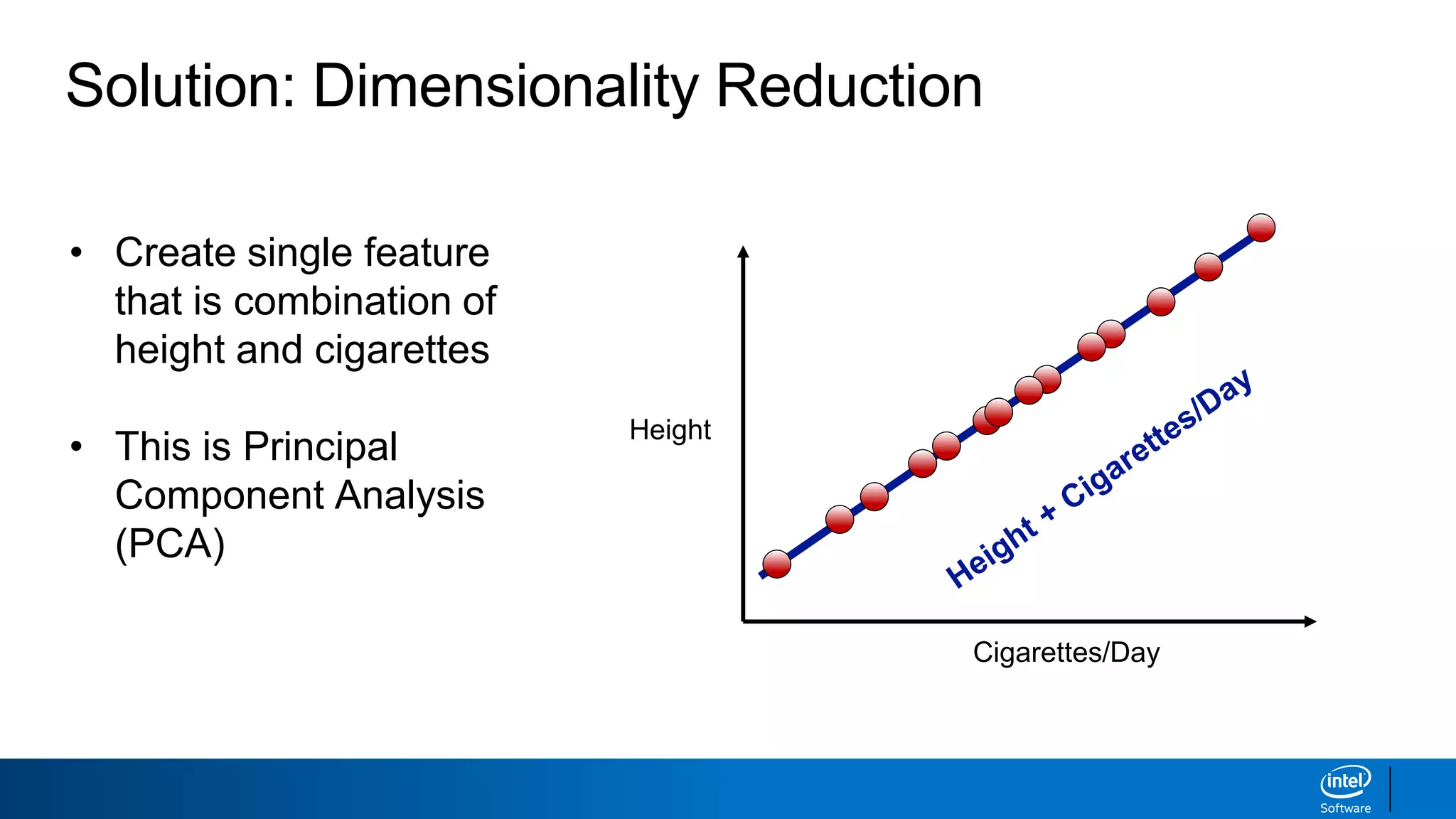
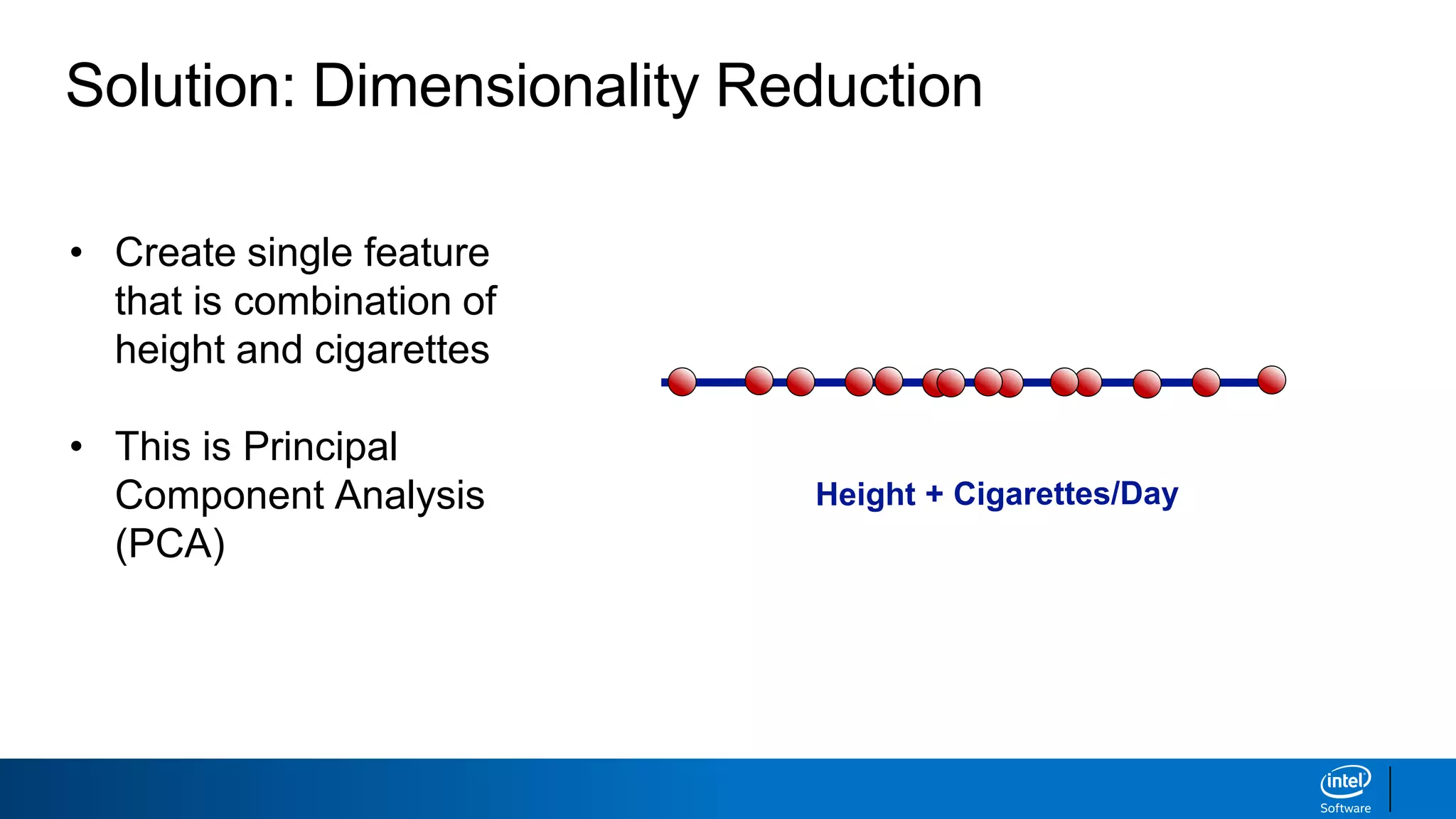
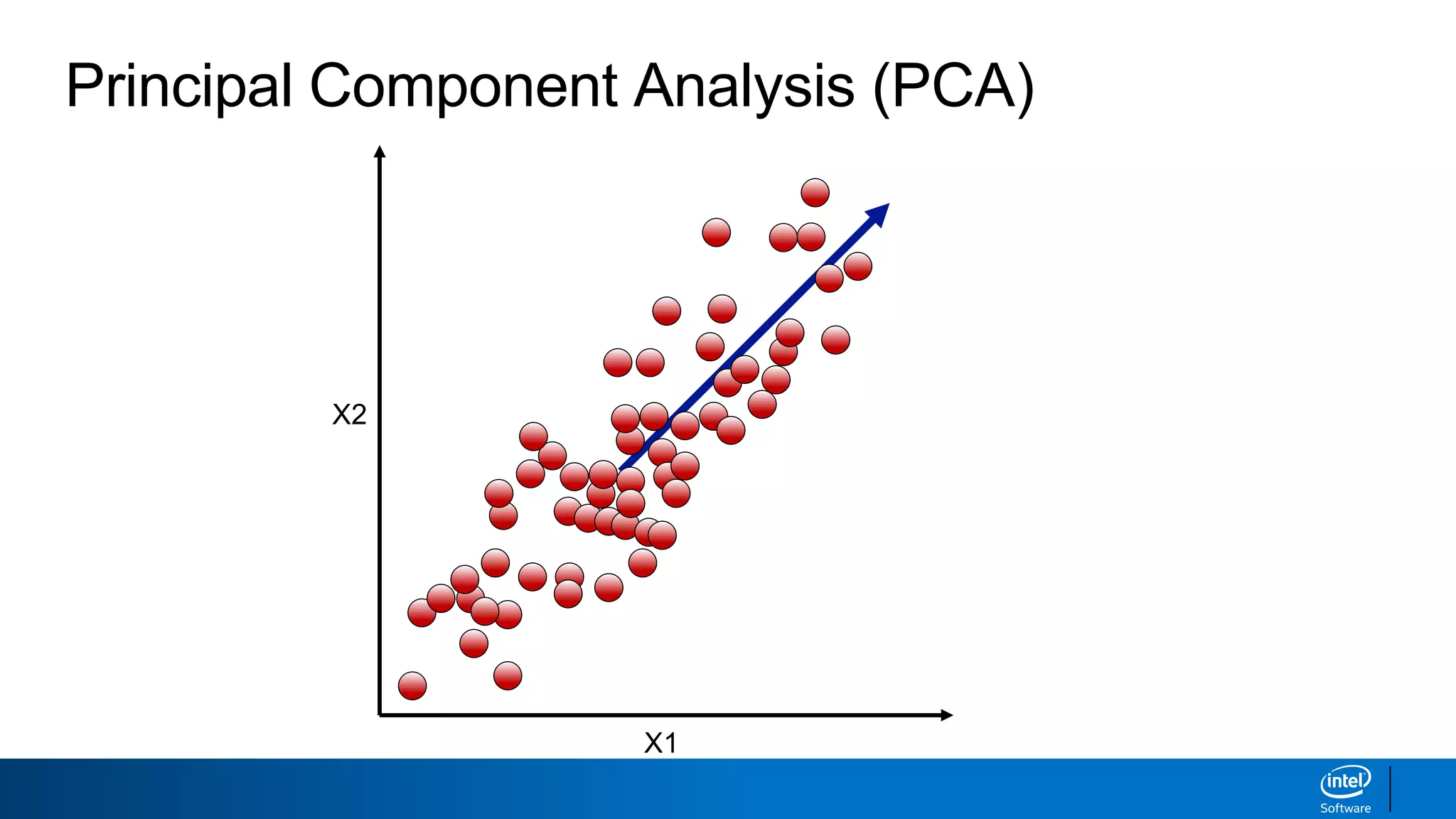
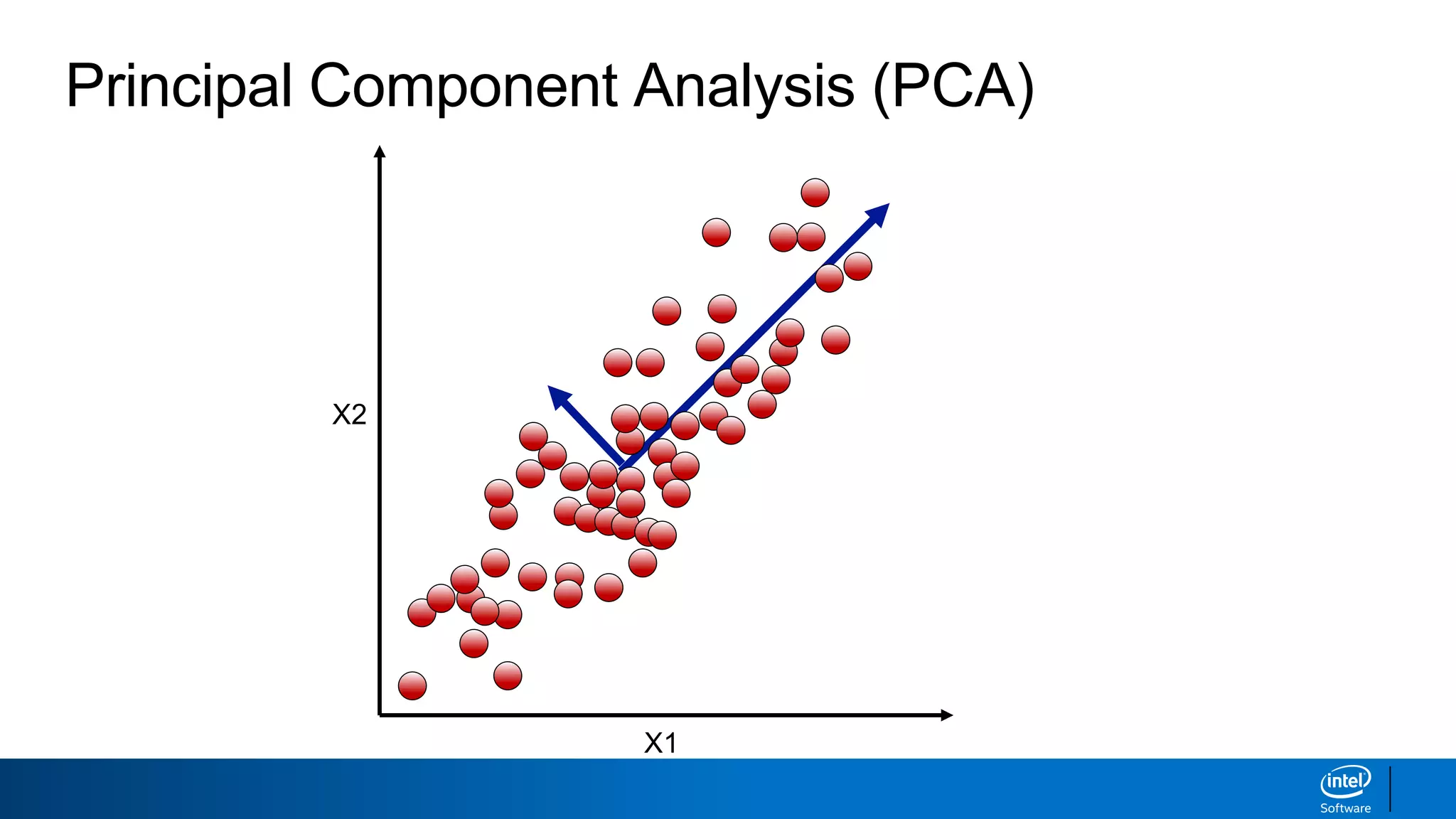
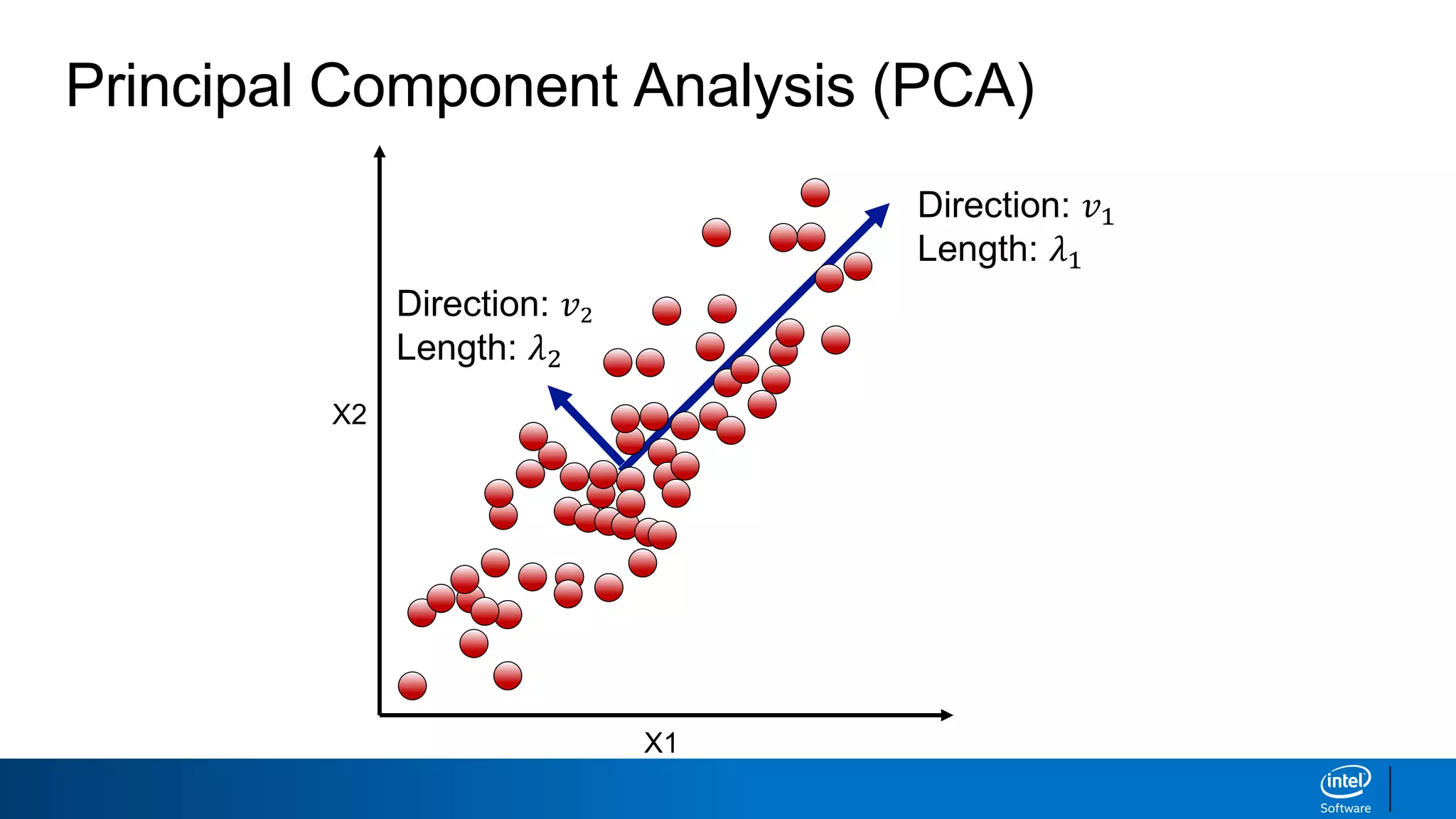
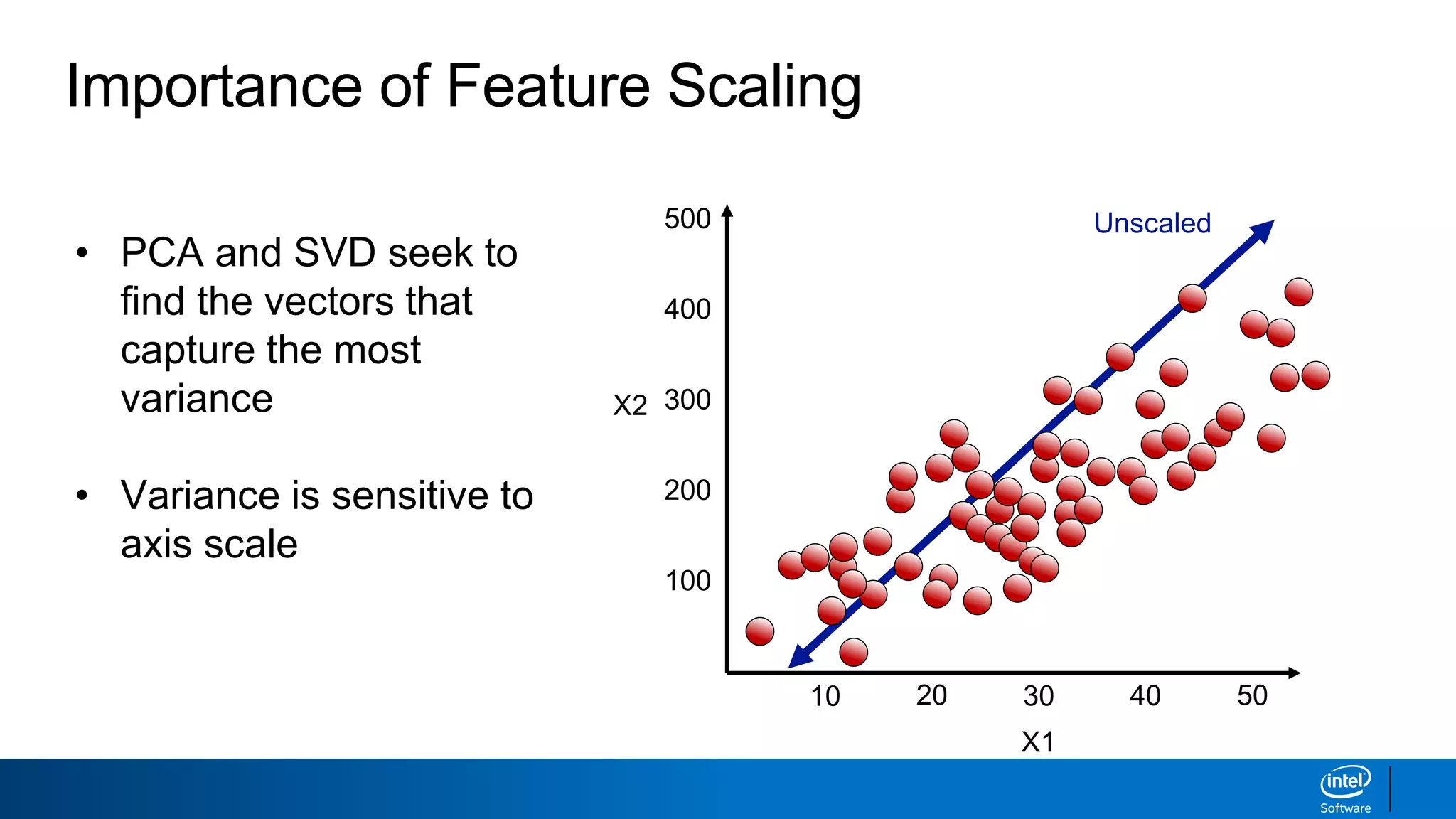
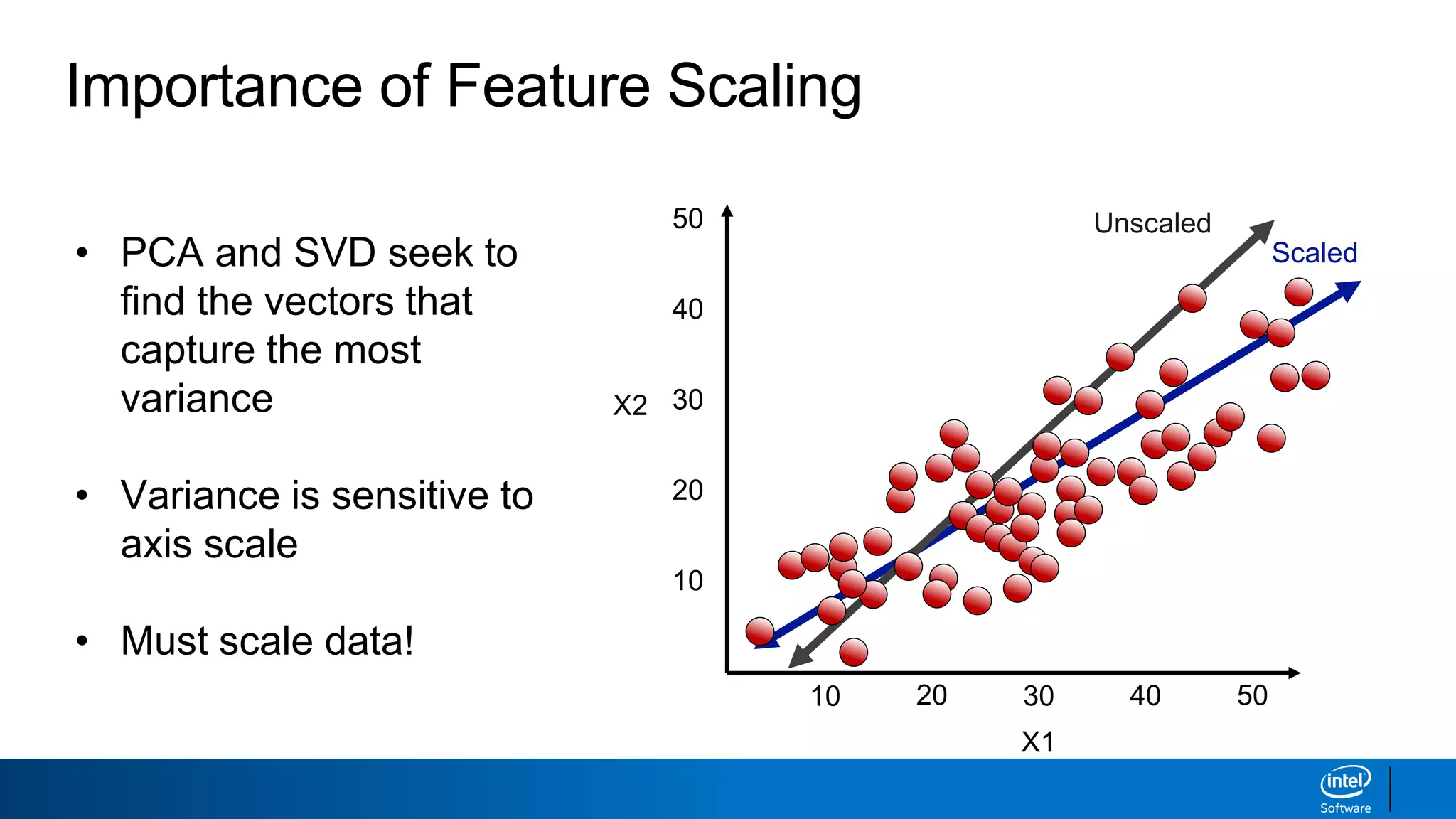
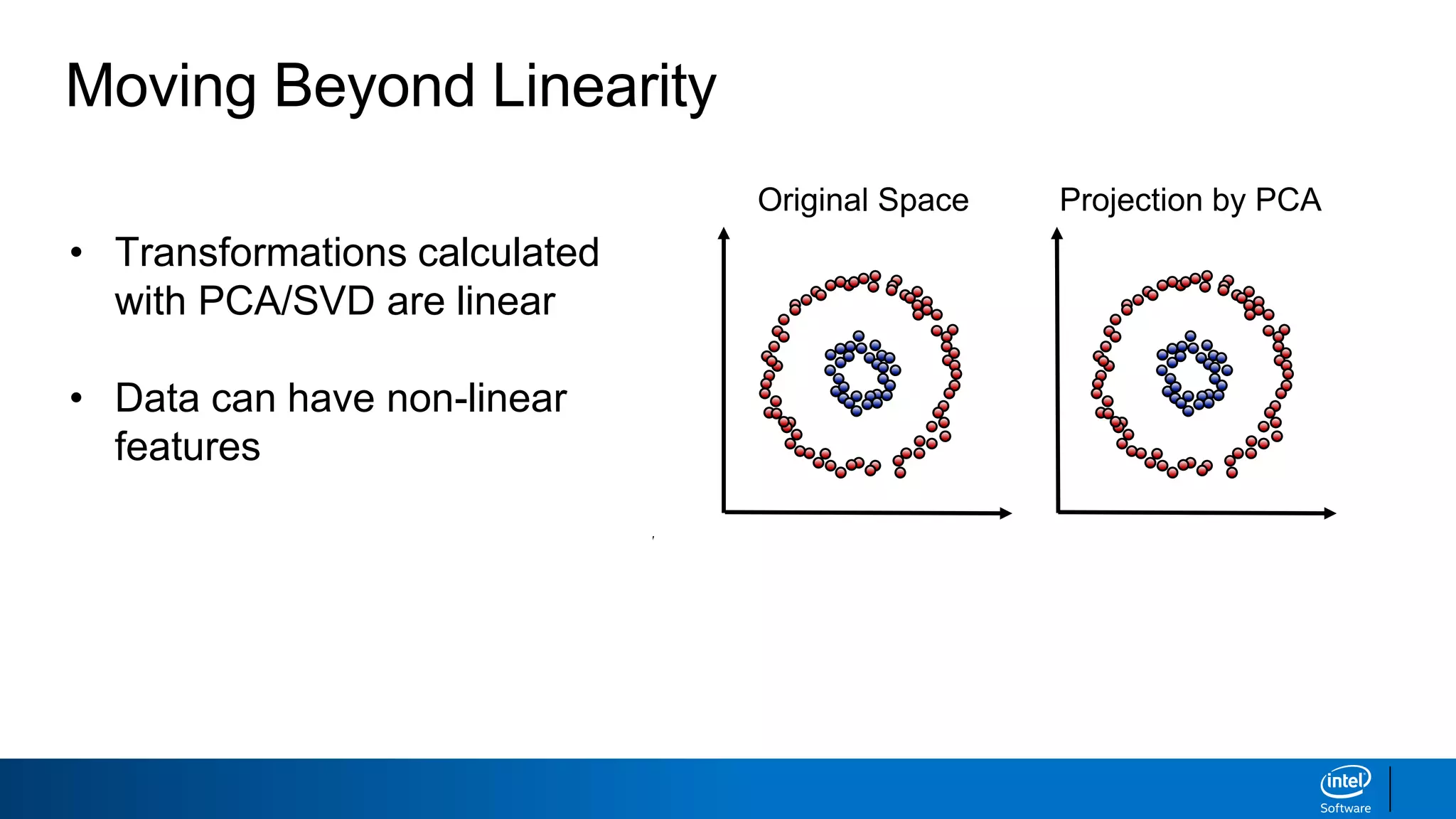
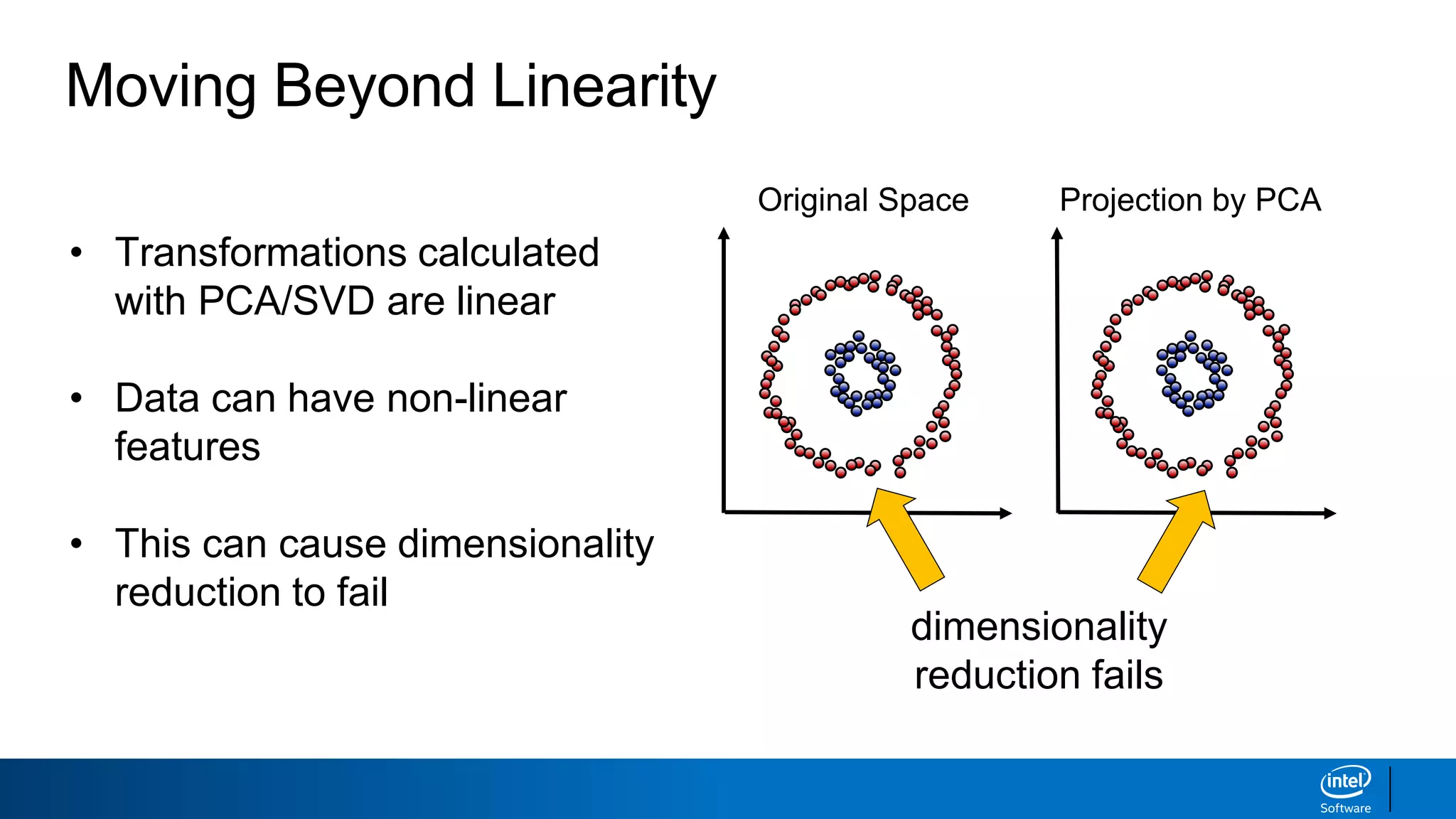
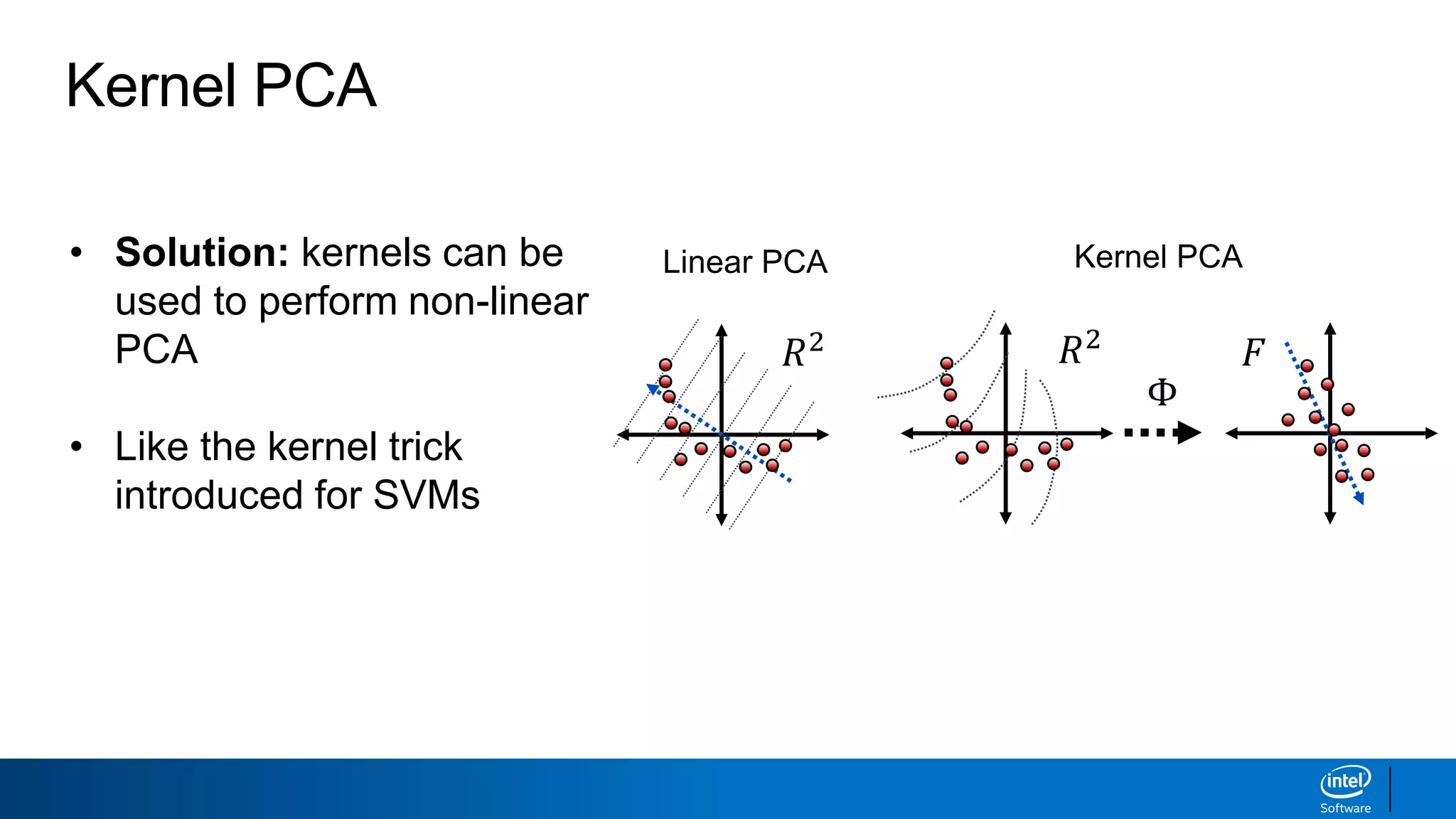
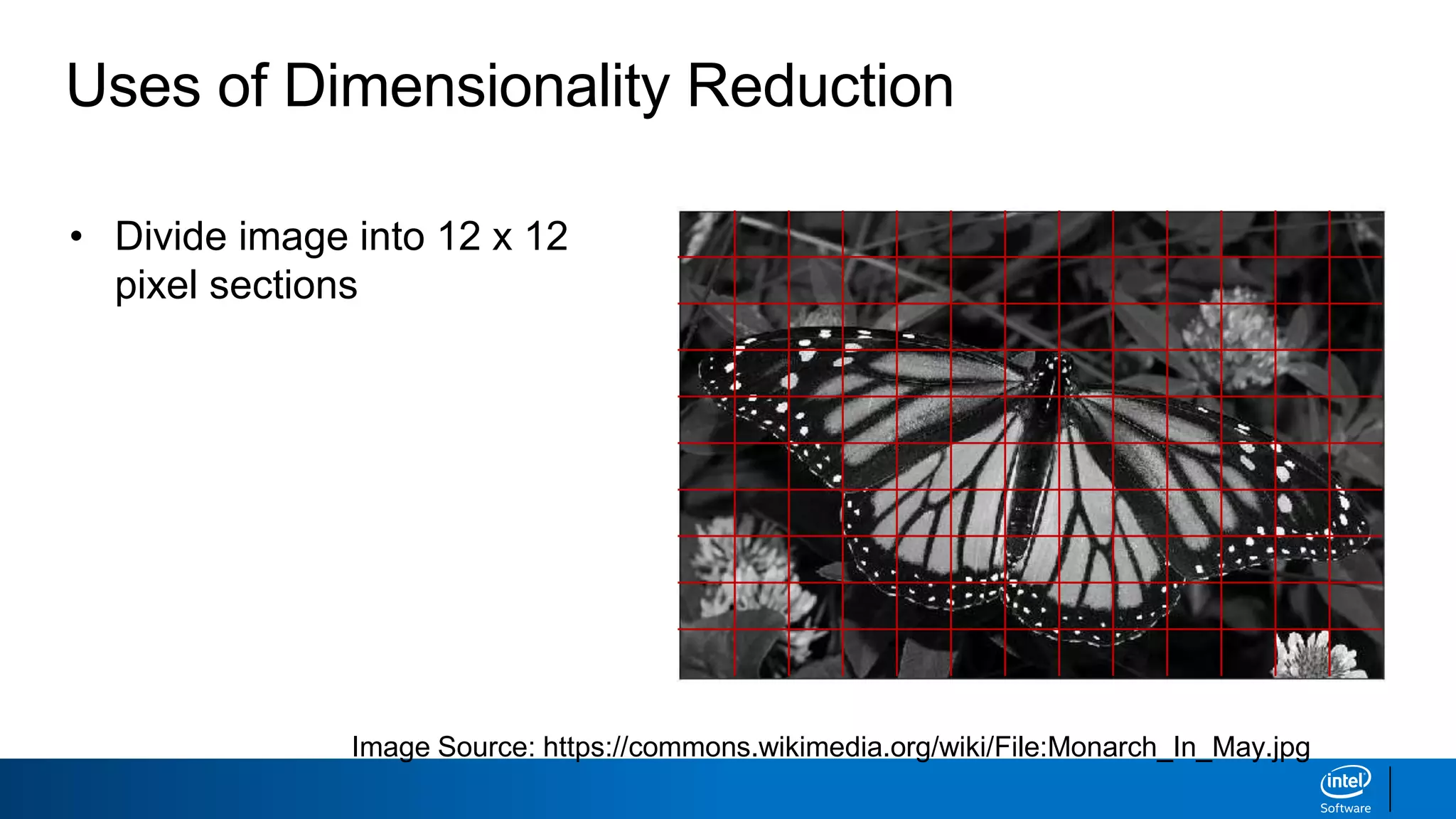
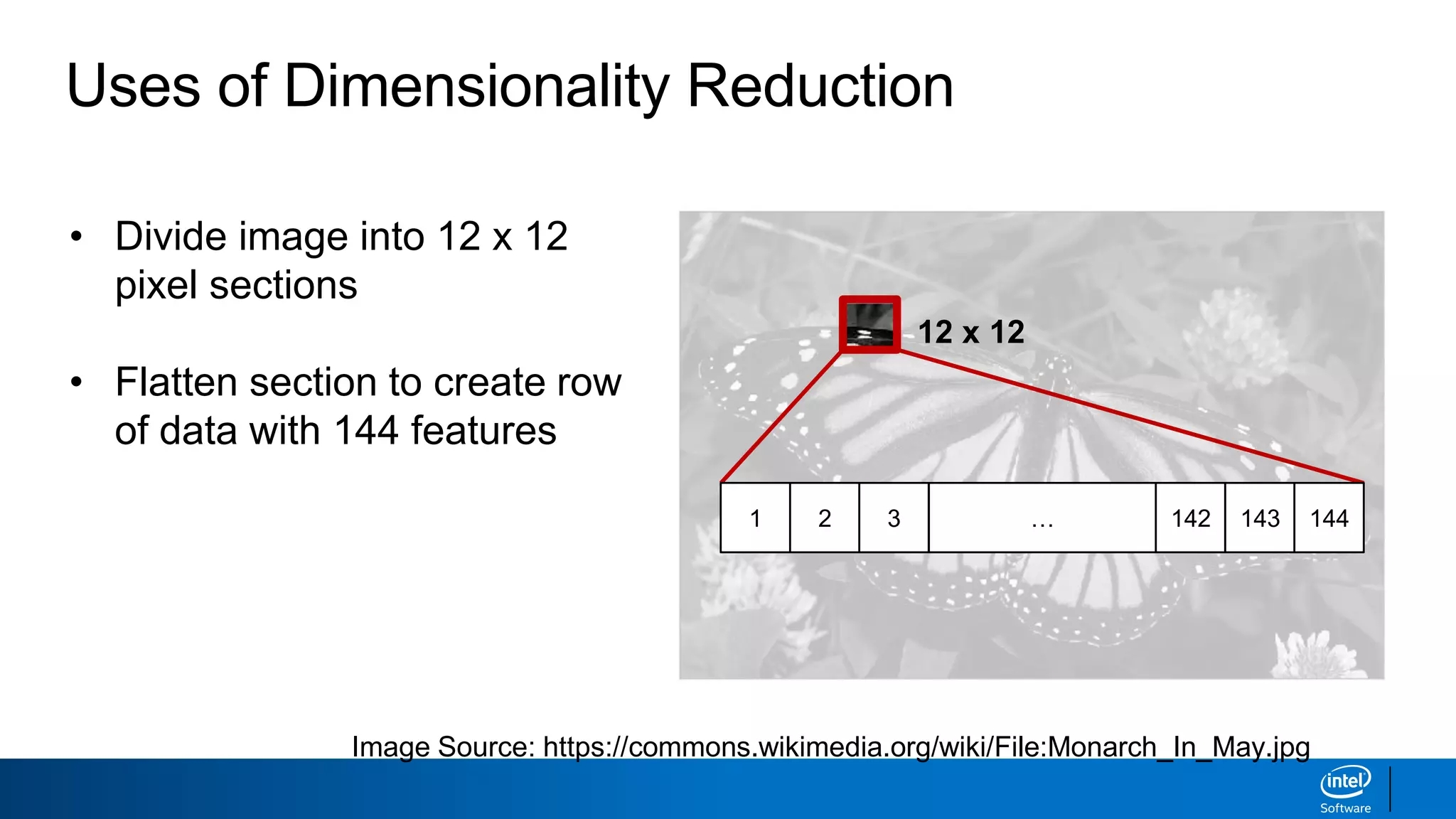
The document discusses dimensionality reduction techniques. It begins by explaining the curse of dimensionality, where adding more features can hurt performance due to the exponential increase in the number of examples needed. It then introduces dimensionality reduction as a solution, where the data can be represented using fewer dimensions/features through feature selection, linear/non-linear transformations, or combinations. Principal component analysis (PCA) and singular value decomposition (SVD) are described as common linear dimensionality reduction methods. The document also discusses nonlinear techniques like kernel PCA and multi-dimensional scaling, as well as uses of dimensionality reduction like in image and natural language processing applications.