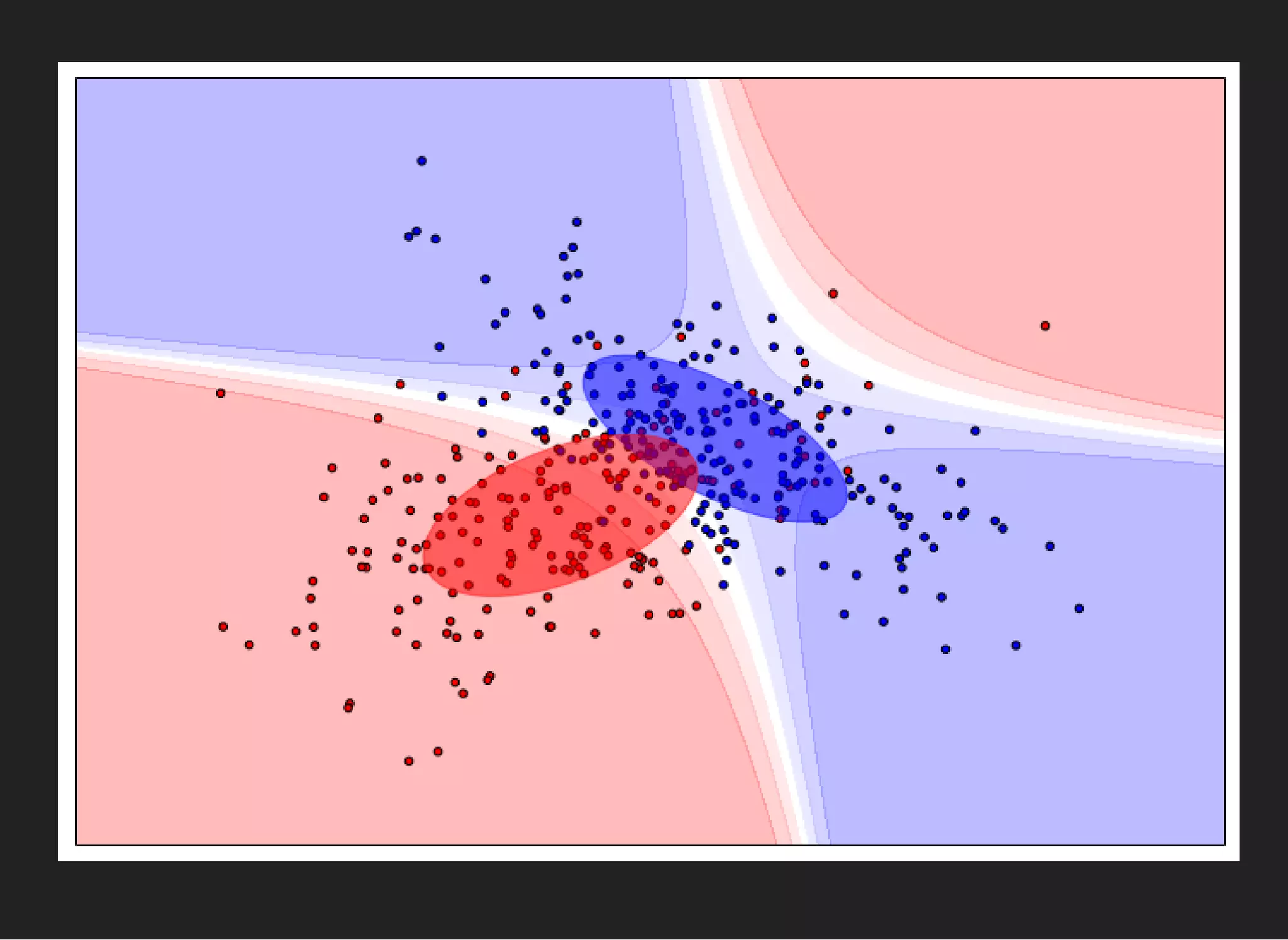
MLHEP 2015: Introductory Lecture #1

MACHINE LEARNING IN HIGH
ENERGY PHYSICS
LECTURE #1
Alex Rogozhnikov, 2015

INTRO NOTES
4 days
two lectures, two practice seminars every day
this is introductory track to machine learning
kaggle competition!

WHAT IS ML ABOUT?
Inference of statistical dependencies which give us ability to
predict
Data is cheap, knowledge is precious

WHERE ML IS CURRENTLY USED?
Search engines, spam detection
Security: virus detection, DDOS defense
Computer vision and speech recognition
Market basket analysis, Customer relationship management
(CRM)
Credit scoring, fraud detection
Health monitoring
Churn prediction
... and hundreds more

ML IN HIGH ENERGY PHYSICS
High-level triggers (LHCb trigger system: )
Particle identification
Tagging
Stripping line
Analysis
40MHz → 5kHz
Different data is used on different stages

GENERAL NOTION
In supervised learning the training data is represented as set
of pairs
,xi yi
is index of event
is vector of features available for event
is target — the value we need to predict
i
xi
yi

CLASSIFICATION EXAMPLE
, if finite set
on the plot: ,
Examples:
defining type of particle (or decay
channel)
— binary classification, 1
is signal, 0 is bck
∈ Yyi Y
∈xi ℝ2
∈ {0, 1, 2}yi
Y = {0, 1}

REGRESSION
y ∈ ℝ
Examples:
predicting price of house by it's positions
predicting number of customers / money income
reconstructing real momentum of particle
Why need automatic classification/regression?
in applications up to thousands of features
higher quality
much faster adaptation to new problems

CLASSIFICATION BASED ON
NEAREST NEIGHBOURS
Given training set of objects and their labels we
predict the label for new observation.
{ , }xi yi
= , j = arg ρ(x, )ŷ yj min
i
xi

VISUALIZATION OF DECISION RULE

NEAREST NEIGHBOURSk
A better way is to use neighbours:k
(x) =pi
# of knn events in class i
k

OVERFITTING
what is the quality of classification on training dataset when
?
answer: it is ideal (closest neighbor is event itself)
quality is lower when
this doesn't mean is the best,
it means we cannot use training events to estimate quality
when classifier's decision rule is too complex and captures
details from training data that are not relevant to
distribution, we call this overfitting (more details tomorrow)
k = 1
k > 1
k = 1

KNN REGRESSOR
Regression with nearest neighbours is done by averaging of
output
=ŷ
1
k ∑
j∈knn(x)
yj

COMPUTATIONAL COMPLEXITY
Given that dimensionality of space is and there are
training samples:
d n
training time ~ O(save a link to data)
prediction time: for each samplen × d

BALL TREE
training time ~
prediction time ~ for each sample
O(d × n log(n))
log(n) × d
Other option exist: KD-tree.

OVERVIEW OF KNN
1. Awesomely simple classifier and regressor
2. Have too optimistic quality on training data
3. Quite slow, though optimizations exist
4. Hard times with data of high dimensions
5. Too sensitive to scale of features

SENSITIVITY TO SCALE OF FEATURES
Euclidean distance:
ρ(x, y = ( − + ( − + ⋯ + ( −)
2
x1 y1 )
2
x2 y2 )
2
xd yd )
2
Change scale fo first feature:
ρ(x, y = (10 − 10 + ( − + ⋯ + ( −)
2
x1 y1 )
2
x2 y2 )
2
xd yd )
2
ρ(x, y ∼ 100( −)
2
x1 y1 )
2
Scaling of features frequently increases quality.

DISTANCE FUNCTION MATTERS
Minkowski distance
Canberra
Cosine metric
(x, y) = ( −ρp
∑i
xi yi )
p
ρ(x, y) = ∑i
| − |xi yi
| | + | |xi yi
ρ(x, y) =
< x, y >
|x| |y|

RECAPITULATION
1. Statistical ML: problems
2. ML in HEP
3. nearest neighbours classifier and regressor.k

MEASURING QUALITY OF BINARY
CLASSIFICATION
The classifier's output in binary classification is real variable
Which classifier is better?
All of them are identical

ROC CURVE
These distributions have the same ROC curve:
(ROC curve is passed signal vs passed bck dependency)

ROC CURVE
Contains important information:
all possible combinations of signal and background
efficiencies you may achieve by setting threshold
Particular values of thresholds (and initial pdfs) don't
matter, ROC curve doesn't contain this information
ROC curve = information about order of events:
Comparison of algorithms should be based on information
from ROC curve
s s b s b ... b b s b b

TERMINOLOGY AND CONVENTIONS
fpr = background efficiency = b
tpr = signal efficiency = s
→

where are predictions of
random background and signal events.
ROC AUC
(AREA UNDER THE ROC CURVE)
ROC AUC = P(x < y) x, y

Which classifier is better for triggers?
(they have the same ROC AUC)

STATISTICAL MACHINE LEARNING
Machine learning we use in practice is based on statistics
1. Main assumption: the data is generated from probabilistic
distribution:
2. Does there really exist the distribution of people / pages?
3. In HEP these distributions do exist
p(x, y)

The best classification quality is provided by
(optimal bayesian classifier)
p(y = 0 | x)
OPTIMAL BINARY CLASSIFICATION
Optimal bayesian classifier has highest possible ROC curve.
Since the classification quality depends only on order,
gives optimal classification quality too!p(y = 1 | x)
=
p(y = 1 | x)
p(y = 0 | x)
p(y = 1) p(x | y = 1)
p(y = 0) p(x | y = 0)

FISHER'S QDA (QUADRATIC DISCRIMINANT
ANALYSIS)
Reconstructing probabilities from
data, assuming those are multidimensional normal
distributions:
p(x | y = 1), p(x | y = 0)
p(x | y = 0) ∼  ( , )μ0 Σ
0
p(x | y = 1) ∼  ( , )μ1 Σ
1

QDA COMPLEXITY
samples, dimensionsn d
training takes
computing covariation matrix
inverting covariation matrix
prediction takes for each sample
O(n + )d
2
d
3
O(n )d
2
O( )d
3
O( )d
2
f (x) = exp
(
− (x − μ (x − μ)
)
1
(2π |Σ)
k/2
|
1/2
1
2
)
T
Σ
−1

QDA
simple decision rule
fast prediction
many parameters to reconstruct in high dimensions
data almost never has gaussian distribution

WHAT ARE THE PROBLEMS WITH
GENERATIVE APPROACH?
Generative approach: trying to reconstruct , then use
it to predict.
p(x, y)
Real life distributions hardly can be reconstructed
Especially in high-dimensional spaces
So, we switch to discriminative approach: guessing p(y|x)

This is (finding parameters ).
LINEAR DECISION RULE
Decision function is linear:
d(x) =< w, x > +w0
{
d(x) > 0,
d(x) < 0,
class + 1
class − 1
parametric model w, w0

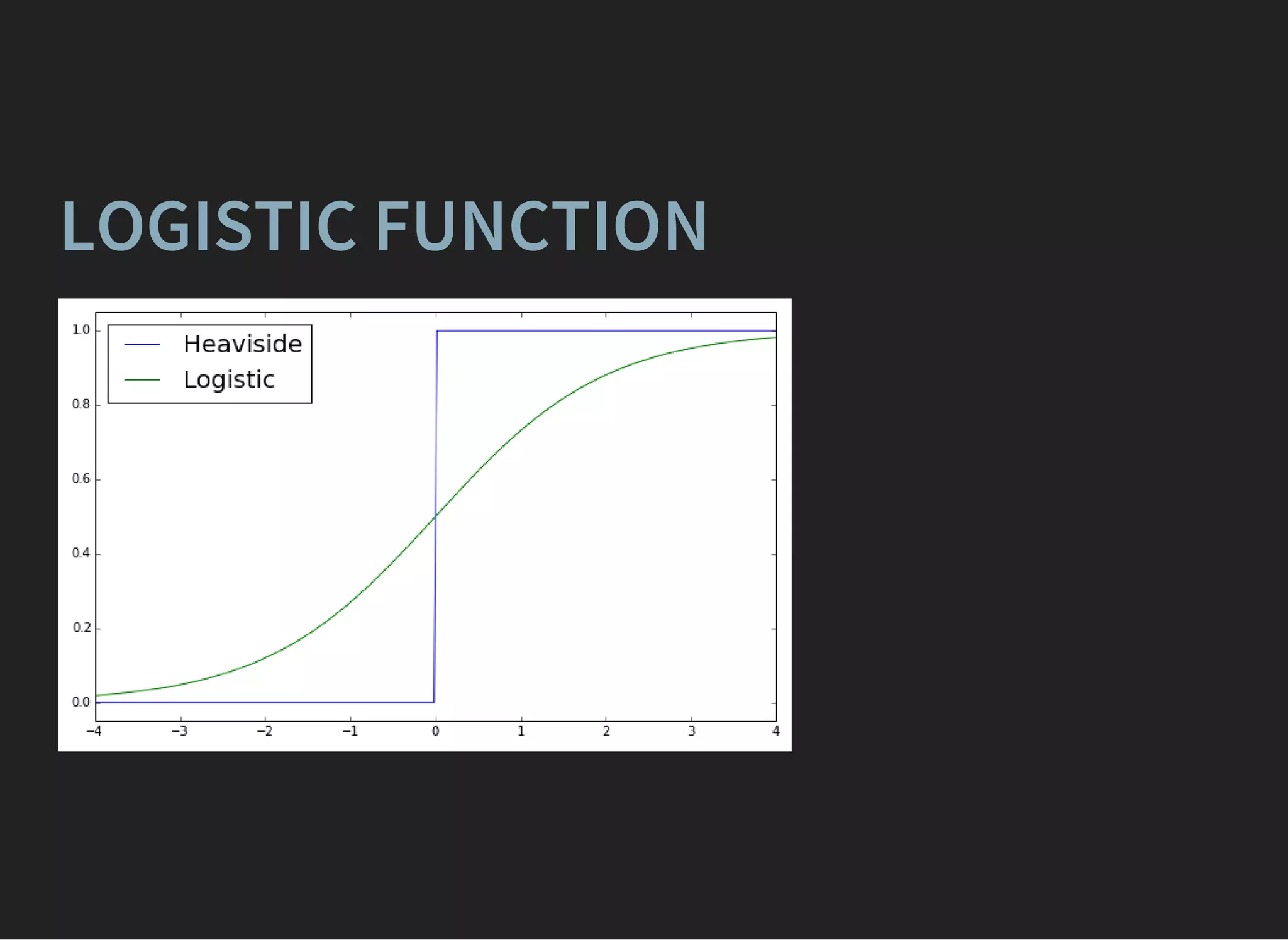
FINDING OPTIMAL PARAMETERS
A good initial guess: get such , that error of
classification is minimal ([true] = 1, [false] = 0):
Discontinuous optimization (arrrrgh!)
Let's make decision rule smooth
w, w0
 = [ ≠ sgn(d( ))]
∑
i∈events
yi xi
(x)p+1
(x)p−1
= f (d(x))
= 1 − (x)p+1
⎧
⎩
⎨
⎪
⎪
f (0) = 0.5
f (x) > 0.5
f (x) < 0.5
if x > 0
if x < 0

LOGISTIC FUNCTION
a smooth step rule.
σ(x) = =
e
x
1 + e
x
1
1 + e
−x
PROPERTIES
1. monotonic,
2.
3.
4.
σ(x) ∈ (0, 1)
σ(x) + σ(−x) = 1
(x) = σ(x)(1 − σ(x))σ′
2 σ(x) = 1 + tanh(x/2)

Optimizing log-likelihood (with probabilities obtained with
logistic function)
LOGISTIC REGRESSION
d(x)
(x)p+1
(x)p−1
=
=
=
< w, x > +w0
σ(d(x))
σ(−d(x))
 = − ln( ( )) = L( , ) → min
1
N ∑
i∈events
pyi
xi
1
N ∑
i
xi yi

Exercise: find expression and build plot for L( , )xi yi
DATA SCIENTIST PIPELINE
1. Experiments in appropriate high-level language or
environment
2. After experiments are over — implement final algorithm in
low-level language (C++, CUDA, FPGA)
Second point is not always needed.

SCIENTIFIC PYTHON
NumPy
vectorized computations in python
Matplotlib
for drawing
Pandas
for data manipulation and analysis (based on
NumPy)

SCIENTIFIC PYTHON
Scikit-learn
most popular library for machine learning
Scipy
libraries for science and engineering
Root_numpy
convenient way to work with ROOT files

MLHEP 2015: Introductory Lecture #1

More Related Content

What's hot

Similar to MLHEP 2015: Introductory Lecture #1

Recently uploaded

MLHEP 2015: Introductory Lecture #1