Data Structures- Part3 arrays and searching algorithms

Data Structures I (CPCS-204)
Week # 3: Arrays & Searching Algorithms

Data Structures
 Data structure
 A particular way of storing and organising data in a
computer so that it can be used efficiently
 Types of data structures
 Based on memory allocation
o Static (or fixed sized) data structures (Arrays)
o Dynamic data structures (Linked lists)
 Based on representation
o Linear (Arrays/linked lists)
o Non-linear (Trees/graphs)

Array: motivation
 You want to store 5 numbers in a computer
 Define 5 variables, e.g. num1, num2, ..., num5
 What, if you want to store 1000 numbers?
 Defining 1000 variables is a pity!
 Requires much programming effort
 Any better solution?
 Yes, some structured data type
o Array is one of the most common structured data types
o Saves a lot of programming effort (cf. 1000 variable names)

What is an Array?
 A collection of data elements in which
 all elements are of the same data type, hence
homogeneous data
o An array of students’ marks
o An array of students’ names
o An array of objects (OOP perspective!)
 elements (or their references) are stored at
contiguous/ consecutive memory locations
 Array is a static data structure
 An array cannot grow or shrink during program
execution – its size is fixed

Basic concepts
 Array name (data)
 Index/subscript (0...9)
 The slots are numbered sequentially
starting at zero (Java, C++)
 If there are N slots in an array, the
index will be 0 through N-1
 Array length = N = 10
 Array size = N x Size of an element = 40
 Direct access to an element

Homogeneity
 All elements in the array must have the same
data type
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Index:
0 1 2 3 4
Value: 5.5 10.2 18.5 45.6 60.5
Index:
0 1 2 3 4
Value: ‘A’ 10.2 55 ‘X’ 60.5
Not an array

Contiguous Memory
 Array elements are stored at contiguous memory
locations
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
 No empty segment in between values (3 & 5 are
empty – not allowed)
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 45 60 65 70 80

Using Arrays
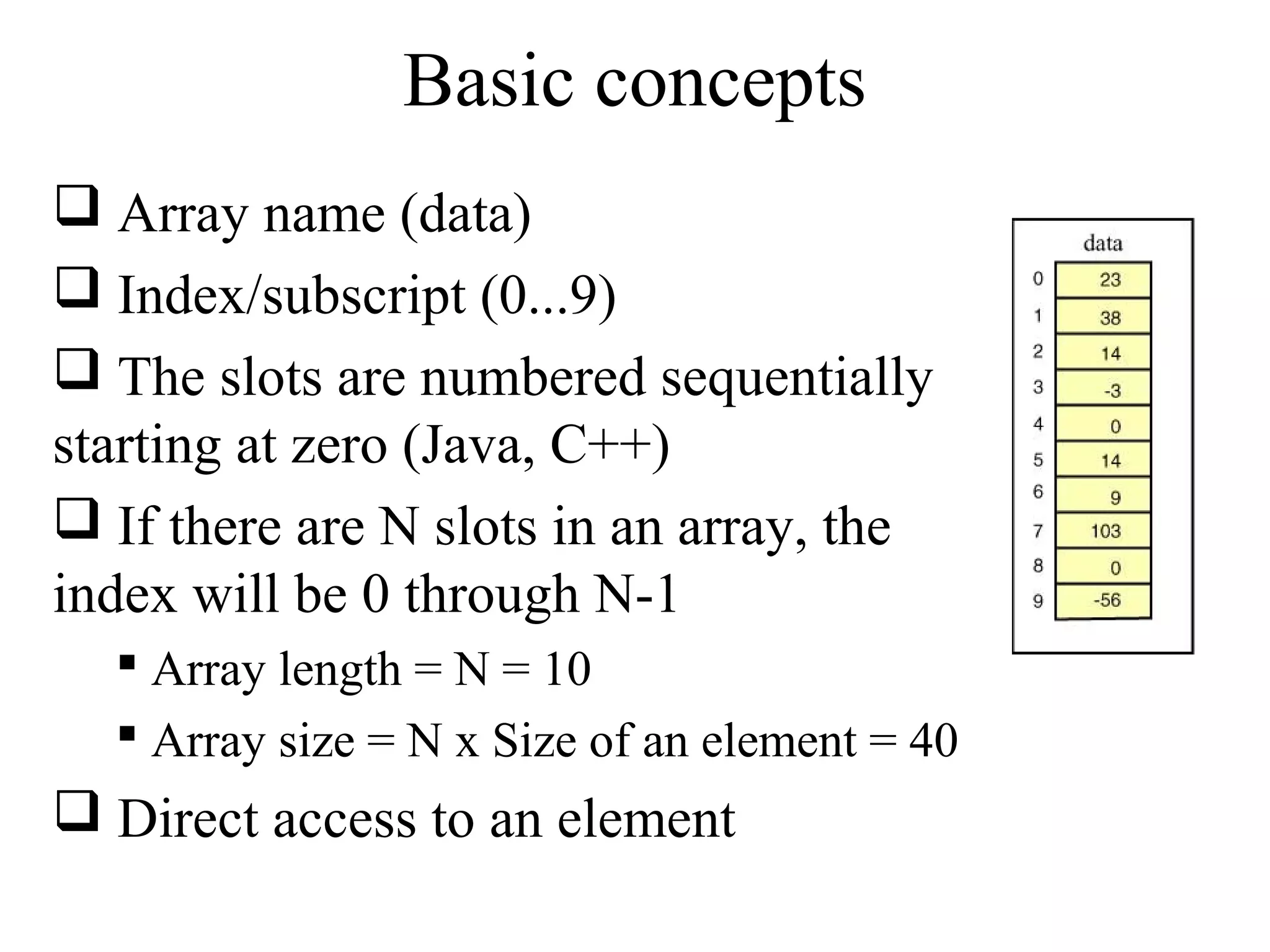
 Array_name[index]
 For example, in Java
 System.out.println(data[4]) will display
0
 data[3] = 99 will replace -3 with 99

Some more concepts
data[ -1 ] always illegal
data[ 10 ] illegal (10 > upper bound)
data[ 1.5 ] always illegal
data[ 0 ] always OK
data[ 9 ] OK
Q. What will be the output of?
1.data[5] + 10
2.data[3] = data[3] + 10

Array’s Dimensionality
 One dimensional (just a linear list)
 e.g.,
 Only one subscript is required to access an individual
element
 Two dimensional (matrix/table)
5 10 18 30 45 50 60 65 70 80
 e.g., 2 x 4 matrix (2 rows, 4 columns)
Col 0 Col 1 Col 2 Col 3
Row 0 20 25 60 40
Row 1 30 15 70 90

Two dimensional Arrays
 Let, the name of the two dimensional array is M
20 25 60 40
30 15 70 90
 Two indices/subscripts are required (row,
column)
 First element is at row 0, column 0
 M0,0 or M(0, 0) or M[0][0] (more common)
 What is: M[1][2]? M[3][4]?

Array Operations
 Indexing: inspect or update an element using its index.
Performance is very fast O(1)
randomNumber = numbers[5];
numbers[20000] = 100;
 Insertion: add an element at certain index
– Start: very slow O(n) because of shift
– End : very fast O(1) because no need to shift
 Removal: remove an element at certain index
– Start: very slow O(n) because of shift
– End : very fast O(1) because no need to shift
 Search: performance depends on algorithm
1) Linear: slow O(n) 2) binary : O(log n)
 Sort: performance depends on algorithm
1) Bubble: slow O(n2) 2) Selection: slow O(n2)
3) Insertion: slow O(n2) 4)Merge : O (n log n)

One Dimensional Arrays in Java
To declare an array follow the type with (empty) []s
int[] grade; //or
int grade[]; //both declare an int array
In Java arrays are objects so must be created with the new
keyword
 To create an array of ten integers:
int[] grade = new int[10];
Note that the array size has to be specified, although it can be
specified with a variable at run-time

Arrays in Java
 When the array is created memory is reserved for its contents
 Initialization lists can be used to specify the initial values of an
array, in which case the new operator is not used
int[] grade = {87, 93, 35}; //array of 3 ints
To find the length of an array use its .length property
int numGrades = grade.length; //note: not .length()!!

Searching Algorithms
 Search for a target (key) in the search space
 Search space examples are:
 All students in the class
 All numbers in a given list
 One of the two possible outcomes
 Target is found (success)
 Target is not found (failure)

Searching Algorithms
Index: 0 1 2 3 4
Value:
20 40 10 30 60
Target = 30 (success or failure?)
Target = 45 (success or failure?)
Search strategy?
List Size = N = 5
Min index = 0
Max index = 4 (N - 1)

Sequential Search
 Search in a sequential order
 Termination condition
 Target is found (success)
 List of elements is exhausted (failure)

Sequential Search
Index: 0 1 2 3 4
Value:
20 40 10 30 60
Target = 30
Step 1: Compare 30 with value at index 0
Step 4: Compare 30 with value at index 3 (success)

Sequential Search
Index: 0 1 2 3 4
Value:
20 40 10 30 60
Target = 45
Failure

Sequential Search Algorithm
Given: A list of N elements, and the target
1. index  0
2. Repeat steps 3 to 5
3. Compare target with list[index]
4. if target = list[index] then
return index // success
else if index >= N - 1
return -1 // failure
5. index  index + 1

Binary Search
 Search through a sorted list of items
 Sorted list is a pre-condition for Binary Search!
 Repeatedly divides the search space (list) into
two
 Divide-and-conquer approach

Binary Search: An Example (Key Î List)
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Target (Key) = 30
First iteration: whole list (search space), compare with mid value
Low Index (LI) = 0; High Index (HI) = 9
Choose element with index (0 + 9) / 2 = 4
Compare value at index 4 (45) with the key (30)
30 is less than 45, so the target must be in the lower half of the
list

Second Iteration: Lookup in the reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Low Index (LI) = 0; High Index (HI) = (4 - 1) = 3
30 is greater than 10, so the target must be in the higher
half of the (reduced) list

Third Iteration: Lookup in the further reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Low Index (LI) = 1 + 1 = 2; High Index (HI) = 3

Fourth Iteration: Lookup in the further reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Key is found at index 3

Binary Search: An Example (Key Ï List)
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Target (Key) = 40
First iteration: Lookup in the whole list (search space)
Low Index (LI) = 0; High Index (HI) = 9
40 is less than 45, so the target must be in the lower half of
the list

Second Iteration: Lookup in the reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Low Index (LI) = 0; High Index (HI) = (4 - 1) = 3

Third Iteration: Lookup in the further reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80

Fourth Iteration: Lookup in the further reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80

Fifth Iteration: Lookup in the further reduced search space
Index:
0 1 2 3 4 5 6 7 8 9
Value: 5 10 18 30 45 50 60 65 70 80
Since LI > HI, Key does not exist in the list
Stop; Key is not found

Binary Search Algorithm: Informal
 Middle  (LI + HI) / 2
 One of the three possibilities
 Key is equal to List[Middle]
o success and stop
 Key is less than List[Middle]
o Key should be in the left half of List, or it does not exist
 Key is greater than List[Middle]
o Key should be in the right half of List, or it does not exist
 Termination Condition
 List[Middle] is equal to Key (success) OR LI > HI
(Failure)

Binary Search Algorithm
 Input: Key, List
 Initialisation: LI  0, HI  SizeOf(List) – 1
 Repeat steps 1 and 2 until LI > HI
1. Mid  (LI + HI) / 2
2. If List[Mid] = Key then
Return Mid // success
Else If Key < List[Mid] then
HI  Mid – 1
Else
LI  Mid + 1
Return -1 // failure

Search Algorithms:Time Complexity
 Time complexity of Sequential Search algorithm:
 Best-case : O(1) comparison
o target is found immediately at the first location
 Worst-case: O(n) comparisons
o Target is not found
 Average-case: O(n) comparisons
o Target is found somewhere in the middle
 Time complexity of Binary Search algorithm:
O(log(n))  This is worst-case

Outlook
Next week, we’ll discuss basic sorting algorithms

Data Structures- Part3 arrays and searching algorithms

More Related Content

What's hot

Viewers also liked

Similar to Data Structures- Part3 arrays and searching algorithms

Recently uploaded

Data Structures- Part3 arrays and searching algorithms