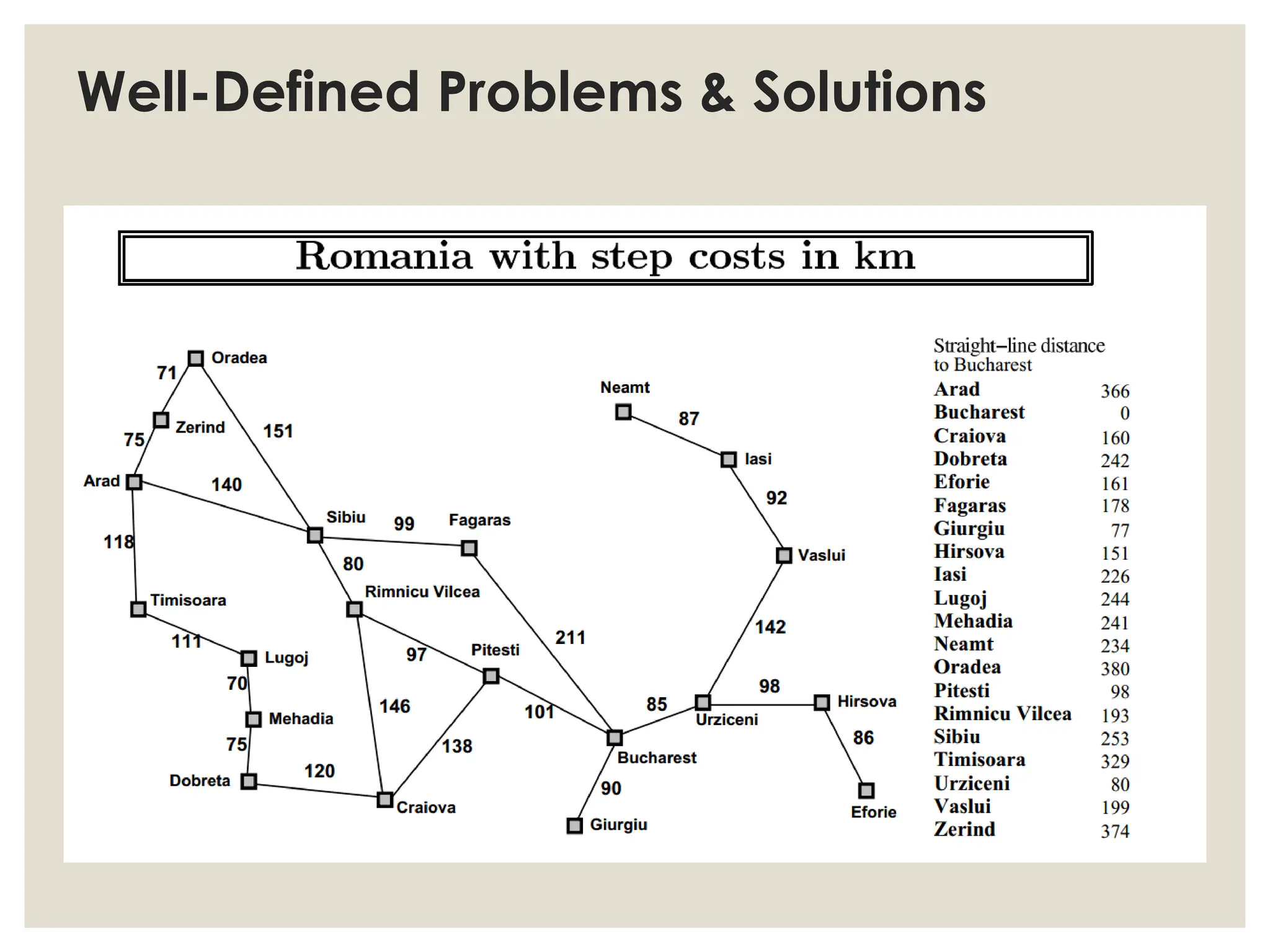
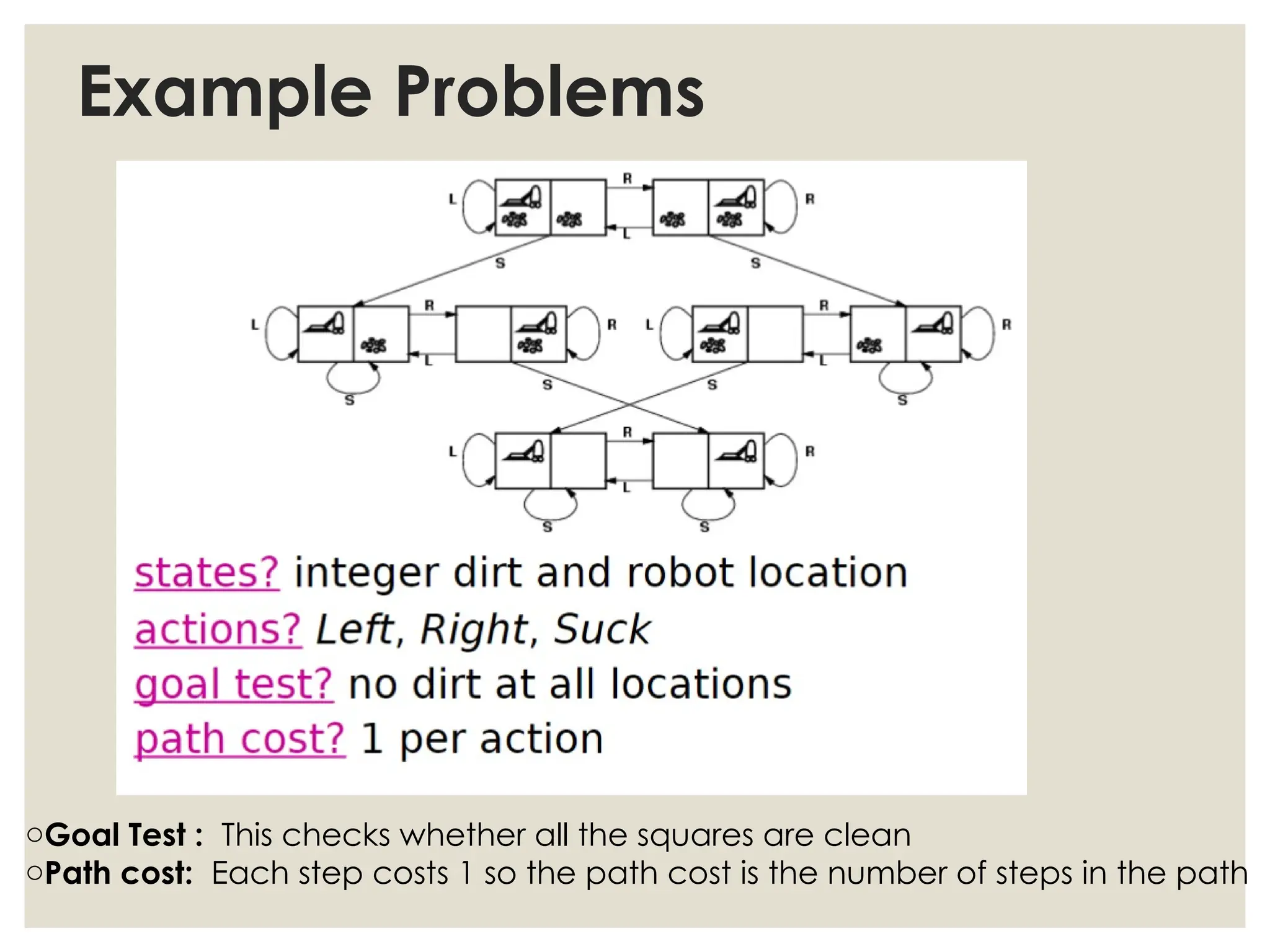
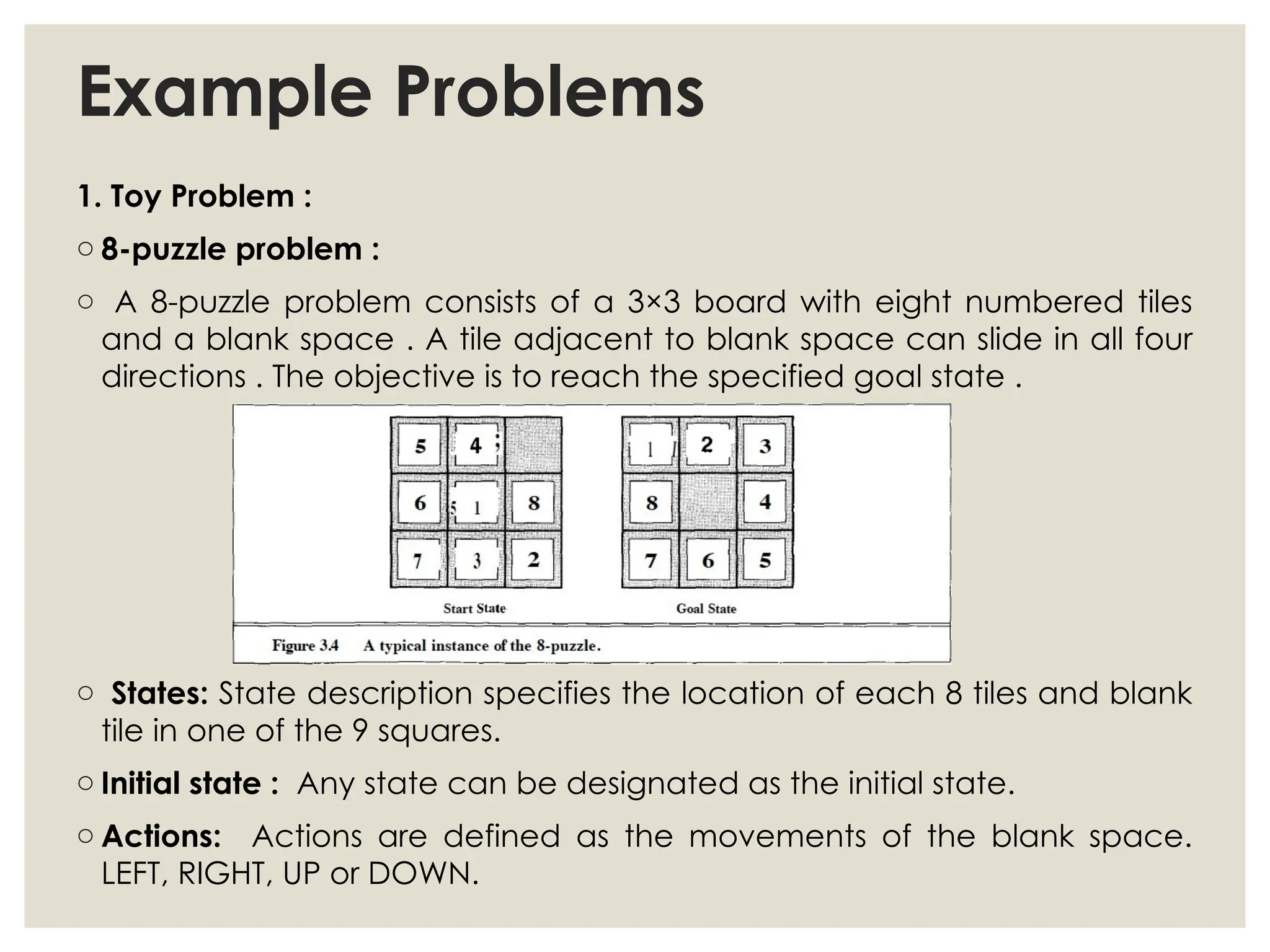
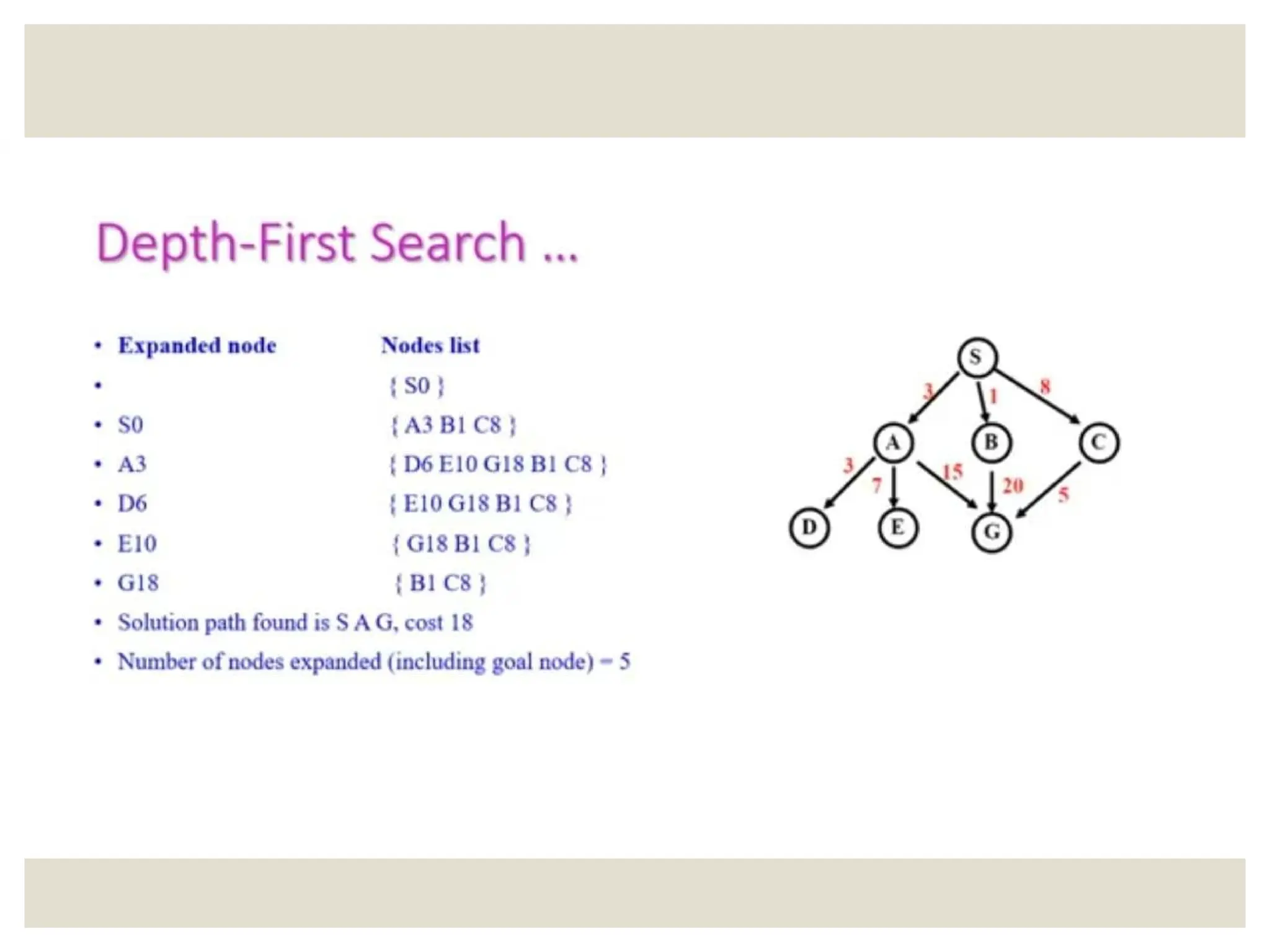
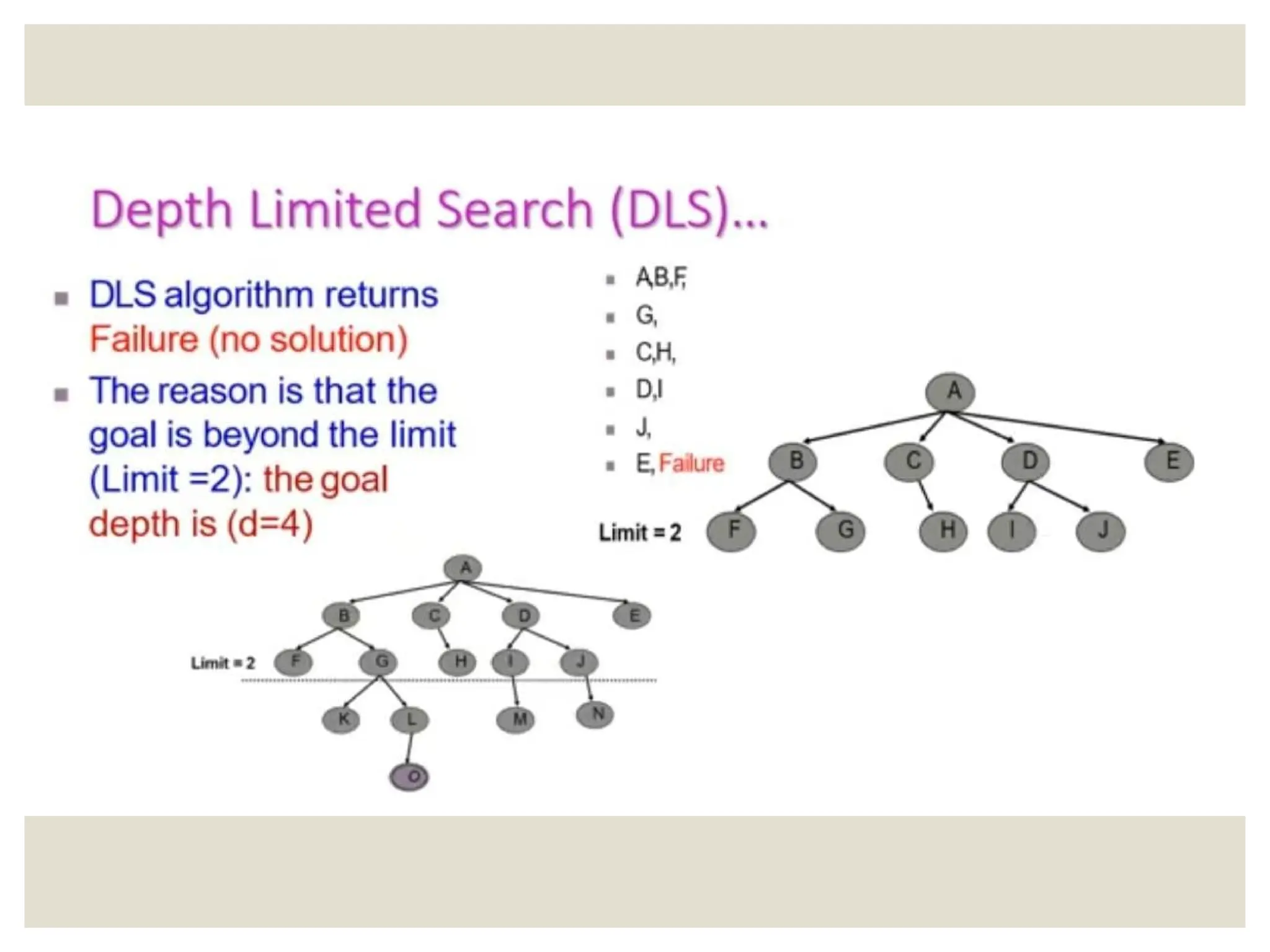
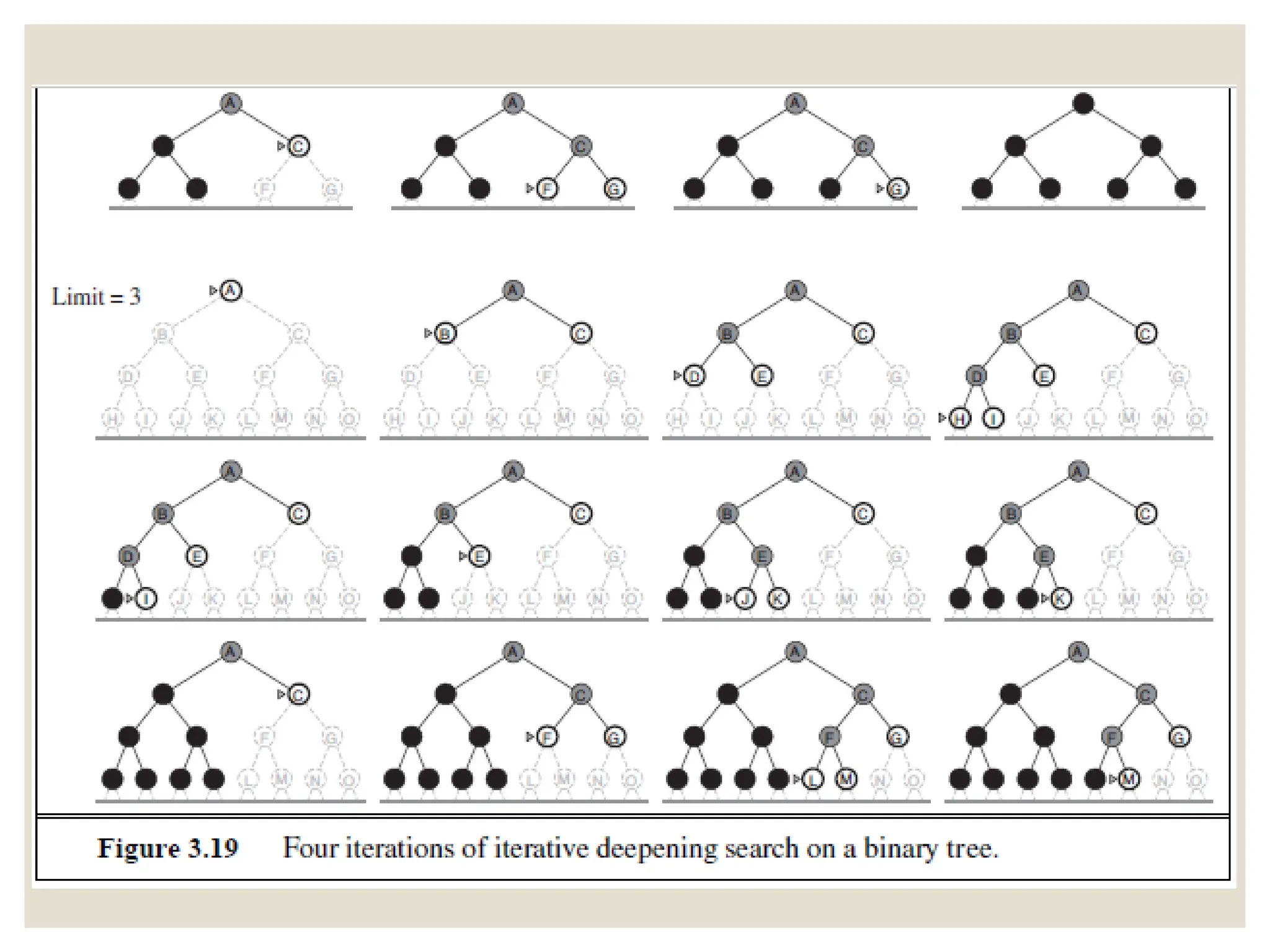
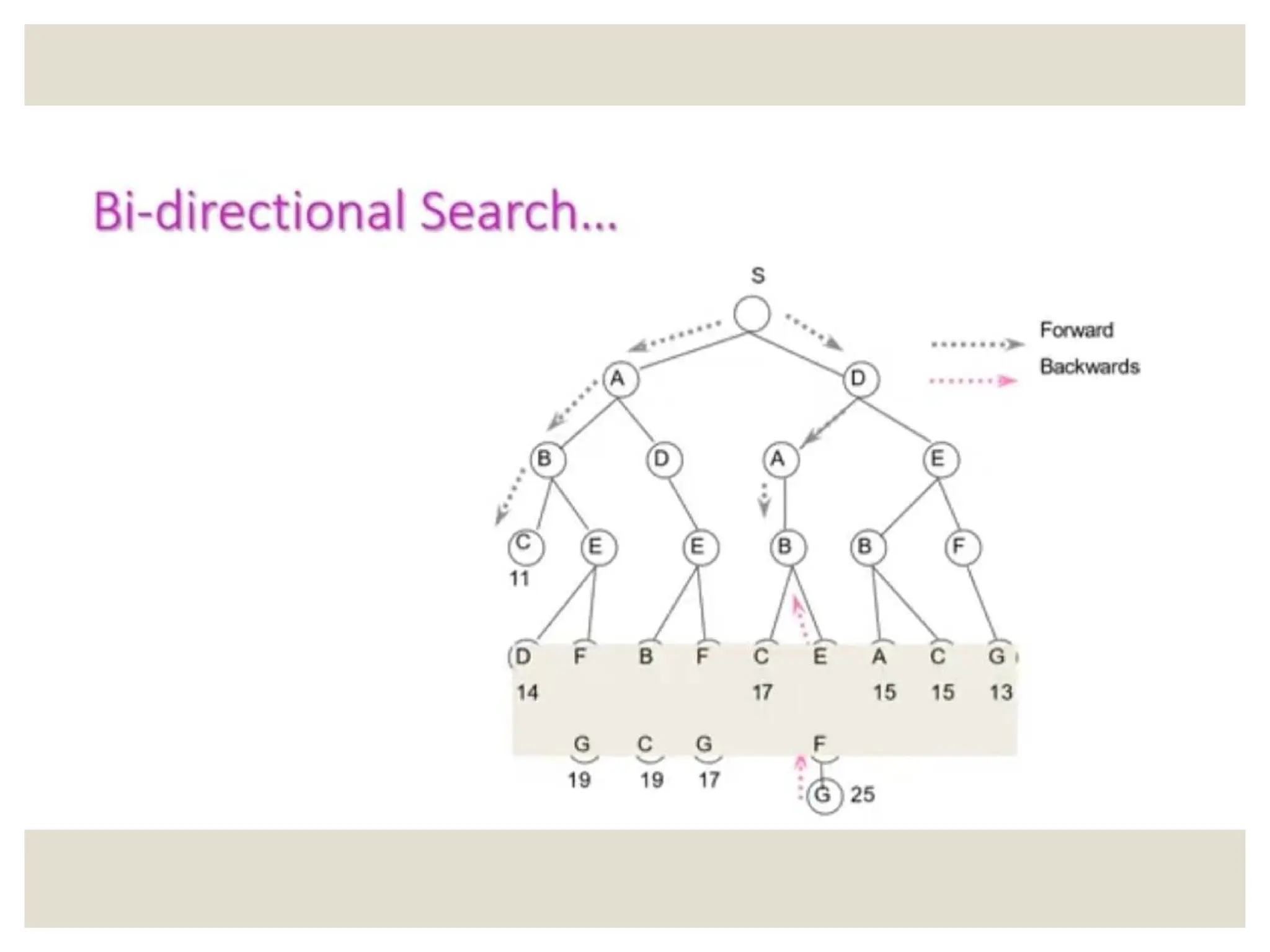
The document discusses problem-solving agents in artificial intelligence, detailing their processes which include goal formulation, problem formulation, and search algorithms to find action sequences leading to desired states. It defines well-defined problems with key components such as initial state, actions, transition models, goal tests, and path costs, and provides examples like the 8-puzzle and 8-queens problems. It also outlines performance metrics for algorithms such as completeness, optimality, time complexity, and space complexity.