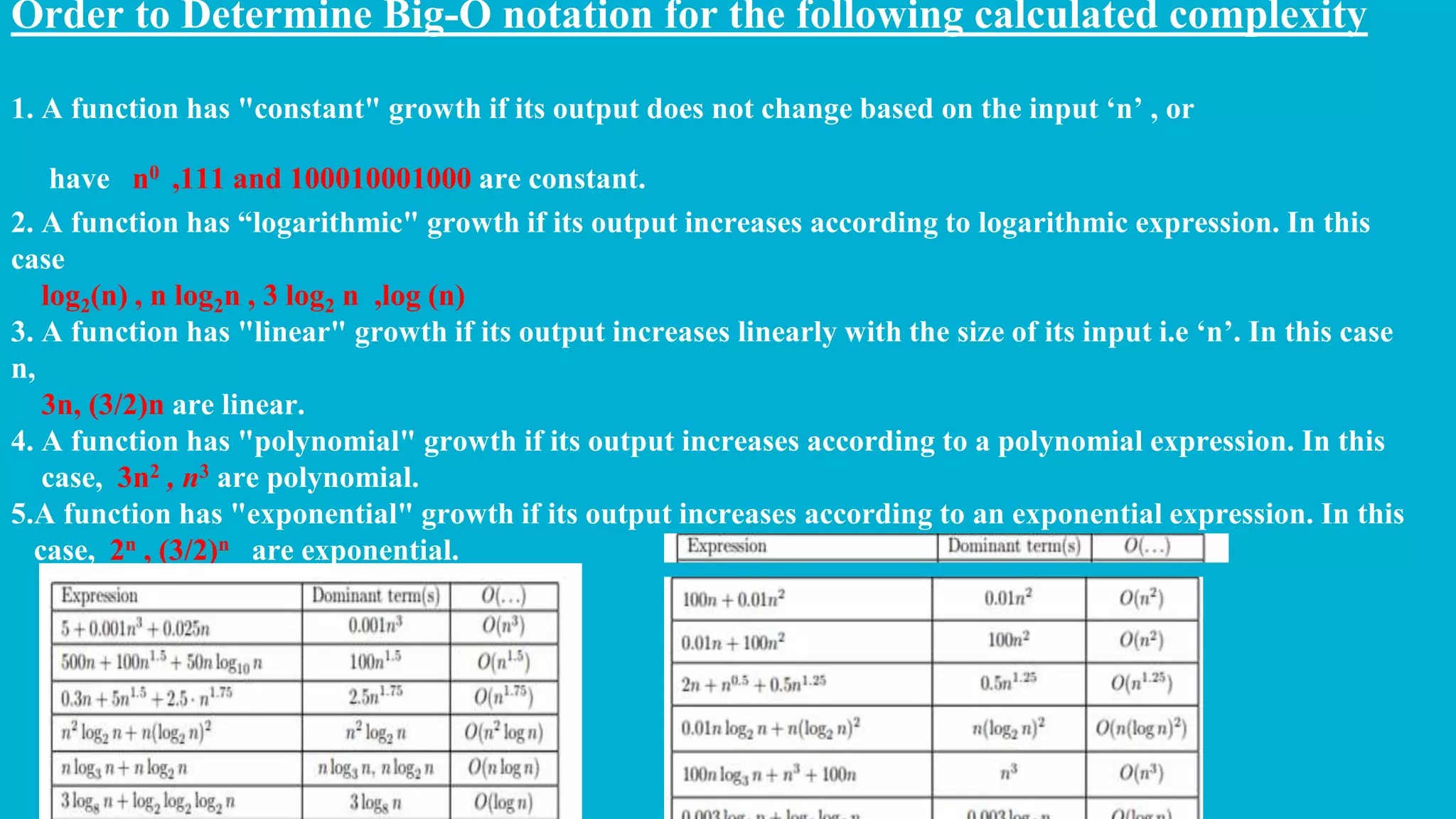
The document discusses algorithmic efficiency, highlighting the performance factors such as time and space required for algorithms, as well as external factors like input size and computer speed. It introduces big O notation to analyze growth rates of algorithms and outlines guidelines for computing complexity, including the identification of best, worst, and average cases. Different growth types are categorized, including constant, logarithmic, linear, polynomial, and exponential growths.