Downloaded 37 times
Uploaded byAndres Mendez-Vazquez
Preparation Data Structures 03 abstract data_types
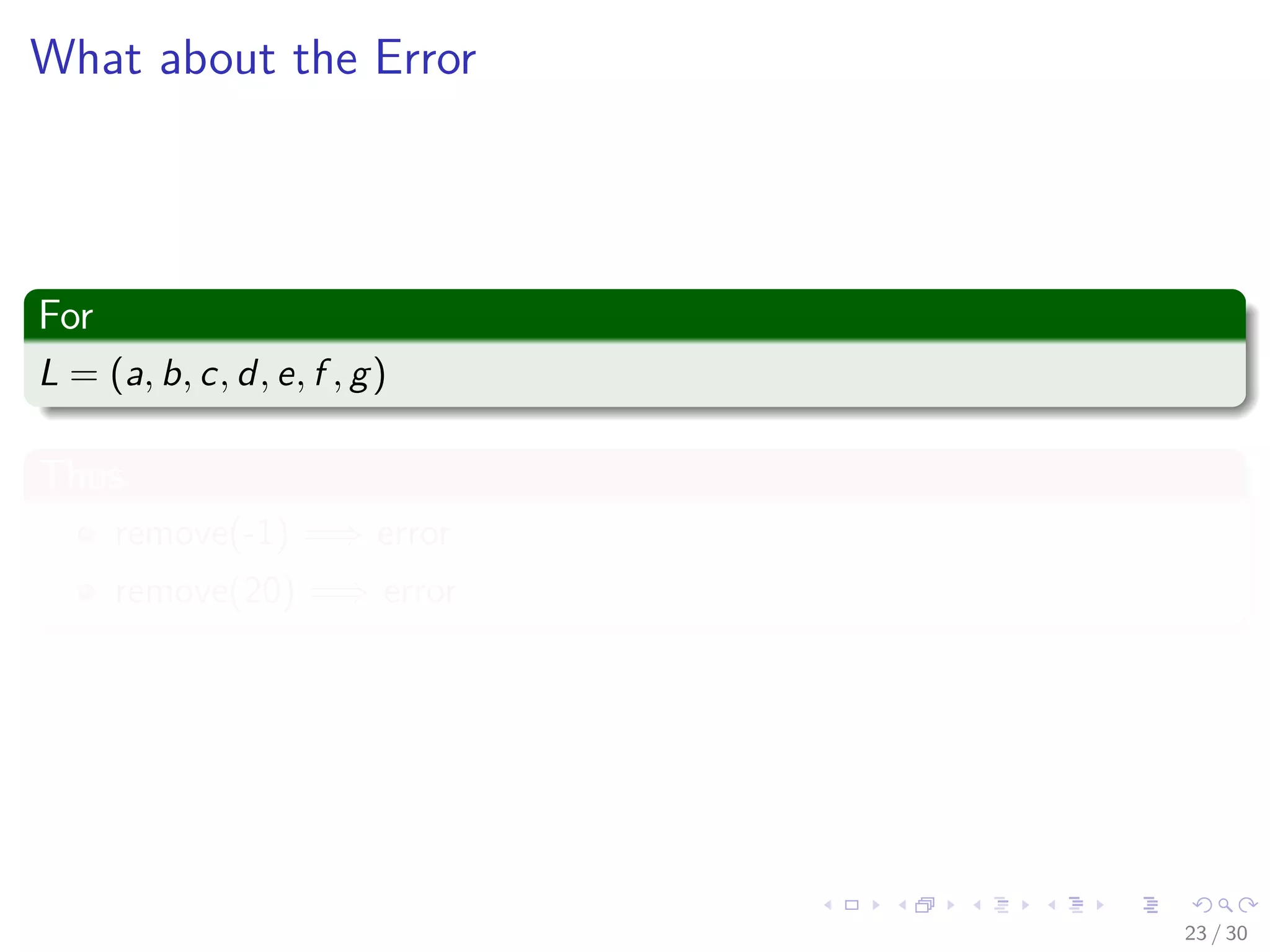
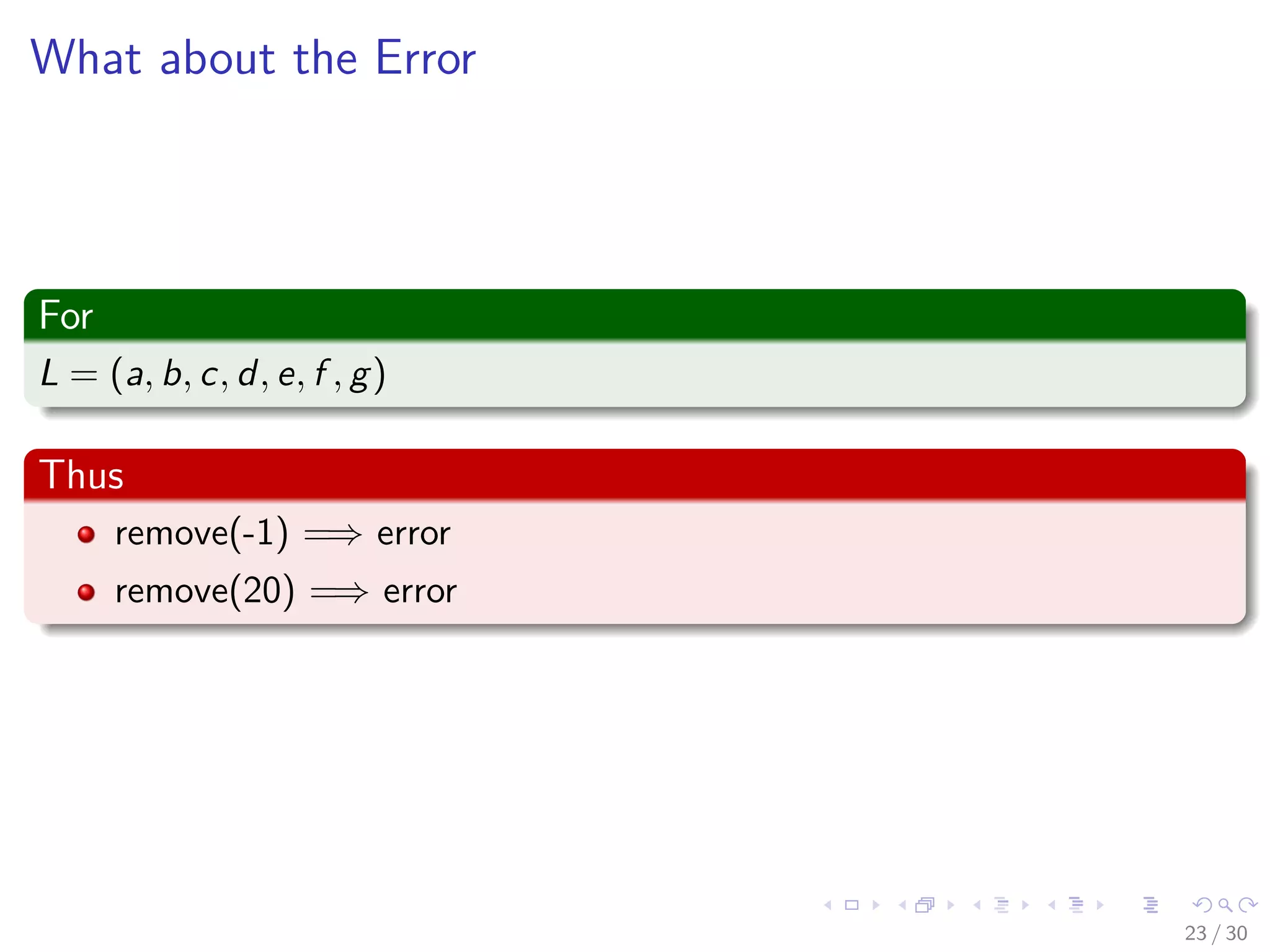
This document discusses data structures and abstract data types (ADTs). It begins by defining a data structure as a collection of data elements along with relationships between them. An ADT is defined as a specification of values and operations on those values, independent of any programming language. Linear lists are provided as an example ADT, with definitions, properties, and common operations like get and indexOf discussed. The document aims to introduce basic concepts around data structures and ADTs.
More Related Content
Similar to Preparation Data Structures 03 abstract data_types
Preparation Data Structures 03 abstract data_types
- 1. Data Structures Abstract DataTypes Andres Mendez-Vazquez May 6, 2015 1 / 30
- 2. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 2 / 30
- 3. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 3 / 30
- 4. Images/cinvestav- What is adata structure? Intuition A data object is a set or collection of instances!!! Examples integer = {0, +1, -1, +2, -2, +3, -3, ...} daysOfWeek = {S,M,T,W,Th,F,Sa} 4 / 30
- 5. Images/cinvestav- What is adata structure? Intuition A data object is a set or collection of instances!!! Examples integer = {0, +1, -1, +2, -2, +3, -3, ...} daysOfWeek = {S,M,T,W,Th,F,Sa} 4 / 30
- 6. Images/cinvestav- What is adata structure? Intuition A data object is a set or collection of instances!!! Examples integer = {0, +1, -1, +2, -2, +3, -3, ...} daysOfWeek = {S,M,T,W,Th,F,Sa} 4 / 30
- 7. Images/cinvestav- Those instance maybe related!!! Something quite basic Instances may or may not be related. Example myDataObject = {apple, chair, 2, 5.2, red, green, Jack} Thus Data Structure ≈ Data object + relationships that exist among instances and elements that comprise an instance. 5 / 30
- 8. Images/cinvestav- Those instance maybe related!!! Something quite basic Instances may or may not be related. Example myDataObject = {apple, chair, 2, 5.2, red, green, Jack} Thus Data Structure ≈ Data object + relationships that exist among instances and elements that comprise an instance. 5 / 30
- 9. Images/cinvestav- Those instance maybe related!!! Something quite basic Instances may or may not be related. Example myDataObject = {apple, chair, 2, 5.2, red, green, Jack} Thus Data Structure ≈ Data object + relationships that exist among instances and elements that comprise an instance. 5 / 30
- 10. Images/cinvestav- Examples Among instances ofintegers 369 < 370 280 + 4 = 284 Thus The relationships are usually specified by specifying operations on one or more instances. Examples add, subtract, predecessor, multiply 6 / 30
- 11. Images/cinvestav- Examples Among instances ofintegers 369 < 370 280 + 4 = 284 Thus The relationships are usually specified by specifying operations on one or more instances. Examples add, subtract, predecessor, multiply 6 / 30
- 12. Images/cinvestav- Examples Among instances ofintegers 369 < 370 280 + 4 = 284 Thus The relationships are usually specified by specifying operations on one or more instances. Examples add, subtract, predecessor, multiply 6 / 30
- 13. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 7 / 30
- 14. Images/cinvestav- Abstract Data Type DataType A data type such as int or double is a group of values and operations on those values that is defined within a specific programming language. Abstract Data Type An Abstract Data Type, or ADT, is a specification for a group of values and the operations on those values that is defined conceptually and independently of any programming language. Thus A data structure is an implementation of an ADT within a programming language. 8 / 30
- 15. Images/cinvestav- Abstract Data Type DataType A data type such as int or double is a group of values and operations on those values that is defined within a specific programming language. Abstract Data Type An Abstract Data Type, or ADT, is a specification for a group of values and the operations on those values that is defined conceptually and independently of any programming language. Thus A data structure is an implementation of an ADT within a programming language. 8 / 30
- 16. Images/cinvestav- Abstract Data Type DataType A data type such as int or double is a group of values and operations on those values that is defined within a specific programming language. Abstract Data Type An Abstract Data Type, or ADT, is a specification for a group of values and the operations on those values that is defined conceptually and independently of any programming language. Thus A data structure is an implementation of an ADT within a programming language. 8 / 30
- 17. Images/cinvestav- Using Abstract DataTypes Something Notable An abstract data type is defined indirectly, only by the operations that may be performed on it and by mathematical constraints on the effects (and possibly cost) of those operations. Using Abstract Data Types 1 An abstract object may be operated upon by the operations which define its abstract type. 2 An abstract object may be passed as a parameter to a procedure. 3 An abstract object may be assigned to a variable. 9 / 30
- 18. Images/cinvestav- Using Abstract DataTypes Something Notable An abstract data type is defined indirectly, only by the operations that may be performed on it and by mathematical constraints on the effects (and possibly cost) of those operations. Using Abstract Data Types 1 An abstract object may be operated upon by the operations which define its abstract type. 2 An abstract object may be passed as a parameter to a procedure. 3 An abstract object may be assigned to a variable. 9 / 30
- 19. Images/cinvestav- Using Abstract DataTypes Something Notable An abstract data type is defined indirectly, only by the operations that may be performed on it and by mathematical constraints on the effects (and possibly cost) of those operations. Using Abstract Data Types 1 An abstract object may be operated upon by the operations which define its abstract type. 2 An abstract object may be passed as a parameter to a procedure. 3 An abstract object may be assigned to a variable. 9 / 30
- 20. Images/cinvestav- Using Abstract DataTypes Something Notable An abstract data type is defined indirectly, only by the operations that may be performed on it and by mathematical constraints on the effects (and possibly cost) of those operations. Using Abstract Data Types 1 An abstract object may be operated upon by the operations which define its abstract type. 2 An abstract object may be passed as a parameter to a procedure. 3 An abstract object may be assigned to a variable. 9 / 30
- 21. Images/cinvestav- Using Abstract DataTypes Something Notable An abstract data type is defined indirectly, only by the operations that may be performed on it and by mathematical constraints on the effects (and possibly cost) of those operations. Using Abstract Data Types 1 An abstract object may be operated upon by the operations which define its abstract type. 2 An abstract object may be passed as a parameter to a procedure. 3 An abstract object may be assigned to a variable. 9 / 30
- 22. Images/cinvestav- For More We havethe following “PROGRAMMING WITH ABSTRACT DATA TYPES” by Barbara Liskov and Stephen Zilles 10 / 30
- 23. Images/cinvestav- Abstract Data Types:An Example We will start with An example using Lists. Actually in Java An interface in the Java programming language is an abstract type that is used to specify an interface (in the generic sense of the term) that classes must implement. 11 / 30
- 24. Images/cinvestav- Abstract Data Types:An Example We will start with An example using Lists. Actually in Java An interface in the Java programming language is an abstract type that is used to specify an interface (in the generic sense of the term) that classes must implement. 11 / 30
- 25. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 12 / 30
- 26. Images/cinvestav- Linear (or Ordered)Lists Definition A linear list is a data structure that holds a sequential list of elements. Instances They have the following structure, (e0, e1, e1, ..., en−1) Properties Where ei denotes a list element n ≥ 0 is finite List size is n 13 / 30
- 27. Images/cinvestav- Linear (or Ordered)Lists Definition A linear list is a data structure that holds a sequential list of elements. Instances They have the following structure, (e0, e1, e1, ..., en−1) Properties Where ei denotes a list element n ≥ 0 is finite List size is n 13 / 30
- 28. Images/cinvestav- Linear (or Ordered)Lists Definition A linear list is a data structure that holds a sequential list of elements. Instances They have the following structure, (e0, e1, e1, ..., en−1) Properties Where ei denotes a list element n ≥ 0 is finite List size is n 13 / 30
- 29. Images/cinvestav- Linear (or Ordered)Lists Definition A linear list is a data structure that holds a sequential list of elements. Instances They have the following structure, (e0, e1, e1, ..., en−1) Properties Where ei denotes a list element n ≥ 0 is finite List size is n 13 / 30
- 30. Images/cinvestav- What are therelations inside of a Liner List? Having this L = (e0, e1, e2, ..., en−1) Relationships e0 is the zero’th (or front) element en−1 is the last element ei immediately precedes ei+1 14 / 30
- 31. Images/cinvestav- What are therelations inside of a Liner List? Having this L = (e0, e1, e2, ..., en−1) Relationships e0 is the zero’th (or front) element en−1 is the last element ei immediately precedes ei+1 14 / 30
- 32. Images/cinvestav- What are therelations inside of a Liner List? Having this L = (e0, e1, e2, ..., en−1) Relationships e0 is the zero’th (or front) element en−1 is the last element ei immediately precedes ei+1 14 / 30
- 33. Images/cinvestav- What are therelations inside of a Liner List? Having this L = (e0, e1, e2, ..., en−1) Relationships e0 is the zero’th (or front) element en−1 is the last element ei immediately precedes ei+1 14 / 30
- 34. Images/cinvestav- Examples Simple ones Students inCOP3530 = (Jack, Jill, Abe, Henry, Mary, ..., Judy) Exams in COP3530 = (exam1, exam2, exam3) Days of Week = (S, M, T, W, Th, F, Sa) Months = (Jan, Feb, Mar, Apr, ..., Nov, Dec) 15 / 30
- 35. Images/cinvestav- Examples Simple ones Students inCOP3530 = (Jack, Jill, Abe, Henry, Mary, ..., Judy) Exams in COP3530 = (exam1, exam2, exam3) Days of Week = (S, M, T, W, Th, F, Sa) Months = (Jan, Feb, Mar, Apr, ..., Nov, Dec) 15 / 30
- 36. Images/cinvestav- Examples Simple ones Students inCOP3530 = (Jack, Jill, Abe, Henry, Mary, ..., Judy) Exams in COP3530 = (exam1, exam2, exam3) Days of Week = (S, M, T, W, Th, F, Sa) Months = (Jan, Feb, Mar, Apr, ..., Nov, Dec) 15 / 30
- 37. Images/cinvestav- Examples Simple ones Students inCOP3530 = (Jack, Jill, Abe, Henry, Mary, ..., Judy) Exams in COP3530 = (exam1, exam2, exam3) Days of Week = (S, M, T, W, Th, F, Sa) Months = (Jan, Feb, Mar, Apr, ..., Nov, Dec) 15 / 30
- 38. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 16 / 30
- 39. Images/cinvestav- Which operations mustbe supported? We need the size of a linear list Hey, we need to know how many elements the linear list has. Determine list size for L = (a, b, c, d, e) So, we need to have a operation that returns the size size(L)=5 17 / 30
- 40. Images/cinvestav- Which operations mustbe supported? We need the size of a linear list Hey, we need to know how many elements the linear list has. Determine list size for L = (a, b, c, d, e) So, we need to have a operation that returns the size size(L)=5 17 / 30
- 41. Images/cinvestav- Which operations mustbe supported? We need the size of a linear list Hey, we need to know how many elements the linear list has. Determine list size for L = (a, b, c, d, e) So, we need to have a operation that returns the size size(L)=5 17 / 30
- 42. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 43. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 44. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 45. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 46. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 47. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 48. Images/cinvestav- Linear List Operations:get(theIndex) Get operations Get element with given index. For example L = (a, b, c, d, e) Thus get(0) = a get(2) = c get(4) = e get(-1) = error get(9) = error 18 / 30
- 49. Images/cinvestav- Linear List Operations:indexOf(theElement) IndexOf operations Determine the index of an element. Example L = (a, b, d, b, a) Thus indexOf(d) = 2 indexOf(a) = 0 indexOf(z) = -1 19 / 30
- 50. Images/cinvestav- Linear List Operations:indexOf(theElement) IndexOf operations Determine the index of an element. Example L = (a, b, d, b, a) Thus indexOf(d) = 2 indexOf(a) = 0 indexOf(z) = -1 19 / 30
- 51. Images/cinvestav- Linear List Operations:indexOf(theElement) IndexOf operations Determine the index of an element. Example L = (a, b, d, b, a) Thus indexOf(d) = 2 indexOf(a) = 0 indexOf(z) = -1 19 / 30
- 52. Images/cinvestav- Linear List Operations:indexOf(theElement) IndexOf operations Determine the index of an element. Example L = (a, b, d, b, a) Thus indexOf(d) = 2 indexOf(a) = 0 indexOf(z) = -1 19 / 30
- 53. Images/cinvestav- Linear List Operations:indexOf(theElement) IndexOf operations Determine the index of an element. Example L = (a, b, d, b, a) Thus indexOf(d) = 2 indexOf(a) = 0 indexOf(z) = -1 19 / 30
- 54. Images/cinvestav- Linear List Operations:add(theIndex, theElement) Definition Add an element so that the new element has a specified index. If we have L = (a, b, c, d, e, f , g) Thus add(0,h) =⇒ L = (h, a, b, c, d, e, f , g) Thus, index of a, b, c, d, e, f , g increases by 1. 20 / 30
- 55. Images/cinvestav- Linear List Operations:add(theIndex, theElement) Definition Add an element so that the new element has a specified index. If we have L = (a, b, c, d, e, f , g) Thus add(0,h) =⇒ L = (h, a, b, c, d, e, f , g) Thus, index of a, b, c, d, e, f , g increases by 1. 20 / 30
- 56. Images/cinvestav- Linear List Operations:add(theIndex, theElement) Definition Add an element so that the new element has a specified index. If we have L = (a, b, c, d, e, f , g) Thus add(0,h) =⇒ L = (h, a, b, c, d, e, f , g) Thus, index of a, b, c, d, e, f , g increases by 1. 20 / 30
- 57. Images/cinvestav- Example add(2,h) using theoriginal L =⇒ L = (a, b, h, c, d, e, f , g) index of c, d, e, f , g increases by 1 What about out of the bound add(10,h) =⇒ error add(-6,h) =⇒ error 21 / 30
- 58. Images/cinvestav- Example add(2,h) using theoriginal L =⇒ L = (a, b, h, c, d, e, f , g) index of c, d, e, f , g increases by 1 What about out of the bound add(10,h) =⇒ error add(-6,h) =⇒ error 21 / 30
- 59. Images/cinvestav- Example add(2,h) using theoriginal L =⇒ L = (a, b, h, c, d, e, f , g) index of c, d, e, f , g increases by 1 What about out of the bound add(10,h) =⇒ error add(-6,h) =⇒ error 21 / 30
- 60. Images/cinvestav- Linear List Operations:remove(theIndex) Definition Remove and return element with given index. For example L = (a, b, c, d, e, f , g) Example Remove(2) returns c and L becomes (a, b, d, e, f , g) Index of d, e, f , g decreases by 1 22 / 30
- 61. Images/cinvestav- Linear List Operations:remove(theIndex) Definition Remove and return element with given index. For example L = (a, b, c, d, e, f , g) Example Remove(2) returns c and L becomes (a, b, d, e, f , g) Index of d, e, f , g decreases by 1 22 / 30
- 62. Images/cinvestav- Linear List Operations:remove(theIndex) Definition Remove and return element with given index. For example L = (a, b, c, d, e, f , g) Example Remove(2) returns c and L becomes (a, b, d, e, f , g) Index of d, e, f , g decreases by 1 22 / 30
- 63. Images/cinvestav- What about theError For L = (a, b, c, d, e, f , g) Thus remove(-1) =⇒ error remove(20) =⇒ error 23 / 30
- 64. Images/cinvestav- What about theError For L = (a, b, c, d, e, f , g) Thus remove(-1) =⇒ error remove(20) =⇒ error 23 / 30
- 65. Images/cinvestav- The Final AbstractData Type for Linear List Linear List AbstractDataType LinearList { instances ordered finite collections of zero or more elements operations isEmpty(): return true iff the list is empty, false otherwise size(): return the list size (i.e., number of elements in the list) get(index): return the element with “index” index indexOf(x): return the index of the first occurrence of x in the list, return -1 if x is not in the list remove(index): remove and return the indexth element, elements with higher index have their index reduced by 1 add(theIndex, x): insert x as the index of th element, elements with theIndex ≥ index have their index increased by 1 output(): output the list elements from left to right } 24 / 30
- 66. Images/cinvestav- Java Interface We canimplement this idea of Abstract Data Types Using Java through the generic interface!!! An interface may include constants and abstract methods (i.e., methods for which no implementation is provided). Example for List 25 / 30
- 67. Images/cinvestav- Java Interface We canimplement this idea of Abstract Data Types Using Java through the generic interface!!! An interface may include constants and abstract methods (i.e., methods for which no implementation is provided). Example for List p u b l i c i n t e r f a c e L i n e a r L i s t <Item>{ p u b l i c boolean isEmpty ( ) ; p u b l i c i n t s i z e ( ) ; p u b l i c Item get ( i n t index ) ; p u b l i c i n t indexOf ( Item myobject ) ; p u b l i c void add ( i n t index , Item myobject ) ; p u b l i c Item remove ( i n t index ) ; p u b l i c S t r i n g t o S t r i n g ( ) ; } 25 / 30
- 68. Images/cinvestav- Implementing the JavaInterface Using a calss to implement the interface c l a s s SimpleArrayList <Item> implements L i n e a r L i s t <Item>{ // code f o r a l l methods must be provided } 26 / 30
- 69. Images/cinvestav- Outline 1 Introduction Basic Ideas AbstractData Types 2 Linear List: An Example of ADT Basic Definition Operations 3 Generic Java Interface Abstract Classes Vs Interfaces 27 / 30
- 70. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 71. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 72. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 73. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 74. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 75. Images/cinvestav- Abstract Classes VsInterfaces However, we have another way to implement ADT Abstract Classes Abstract Classes An abstract class is a special kind of class that cannot be instantiated. It is a contract that is used to define hierarchies for all subclasses. Interface An interface is not a class. An interface has no implementation. It only has the definition of the methods without the body. 28 / 30
- 76. Images/cinvestav- Important We have A Javaclass may implement as many interfaces as it wants but can extend at most one class. This is why Once you have chosen your design you can enforce the structure using Abstract Classes!!! 29 / 30
- 77. Images/cinvestav- Important We have A Javaclass may implement as many interfaces as it wants but can extend at most one class. This is why Once you have chosen your design you can enforce the structure using Abstract Classes!!! 29 / 30
- 78. Images/cinvestav- Example of AbstractClass Code p u b l i c a b s t r a c t c l a s s L i n e a r L i s t <Item>{ p u b l i c boolean isEmpty ( ) ; p u b l i c i n t s i z e ( ) ; p u b l i c Item get ( i n t index ) ; p u b l i c i n t indexOf ( Item myobject ) ; p u b l i c void add ( i n t index , Item myobject ) ; p u b l i c Item remove ( i n t index ) ; p u b l i c S t r i n g t o S t r i n g ( ) ; } 30 / 30