Algo>Abstract data type

2
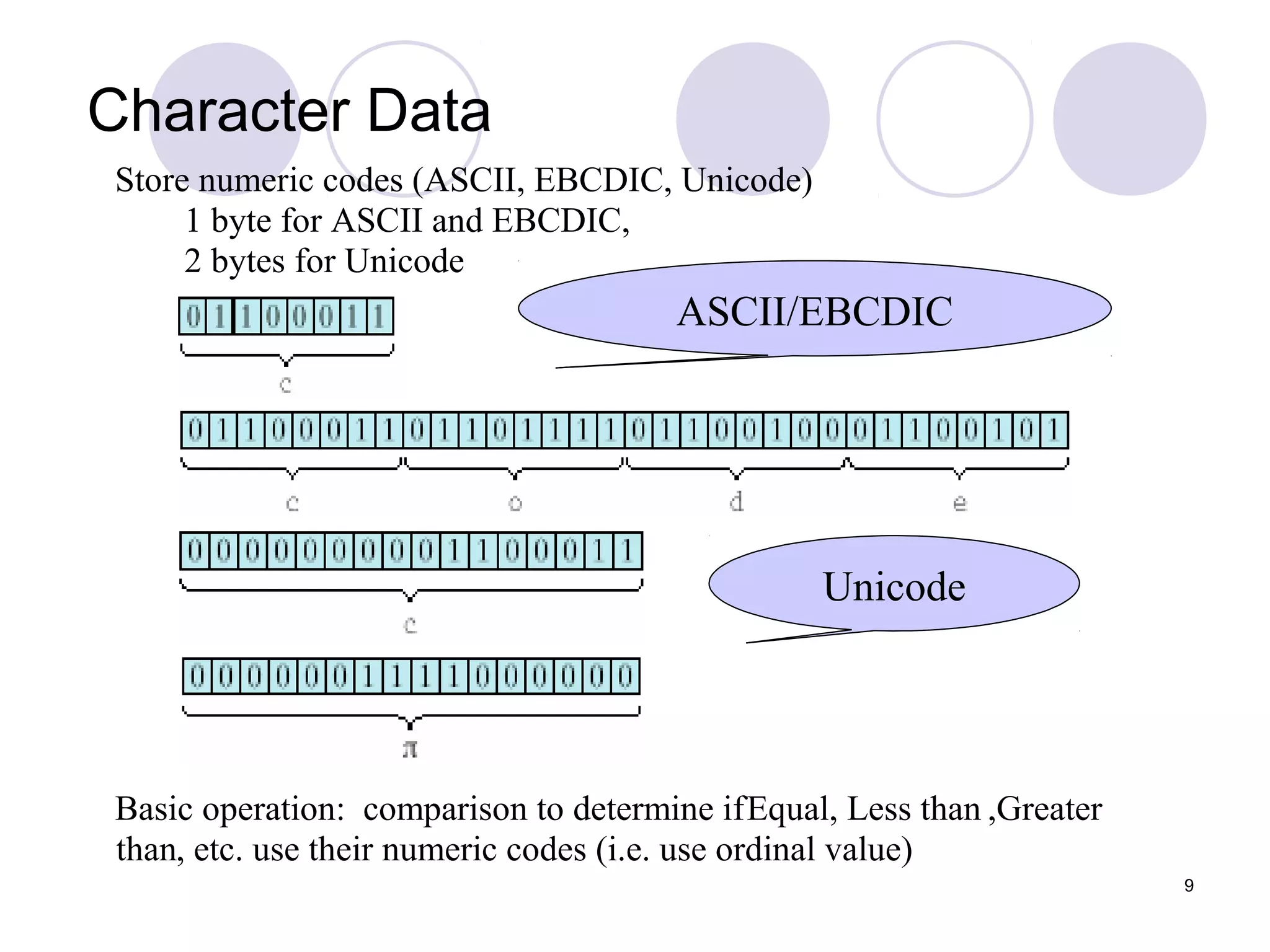
Abstract Data Types
Abstract Data Type (ADT): a definition for
a data type solely in terms of a set of
values and a set of operations on that data
type.
Each ADT operation is defined by its
inputs and outputs.
ENCAPSULATION: Hide Implementation
details

3
Def.
e.g. whole numbers (integers) and arithmetic operators for addition,
subtraction, multiplication and division.
e.g. Flight reservation
Basic operations: find empty seat, reserve a seat,
cancel a seat assignment
Why "abstract?"
Data, operations, and relations are studied
independent of implementation.
What not how is the focus.
a collection of related data items
together with
an associated set of operations
Abstract Data Types

4
Def. Consists of
storage structures (data structures)
to store the data items
and
algorithms for the basic operations.
The storage structures/data structures used in implementations are
provided in a language (primitive or built-in) or are built from the
language constructs (user-defined).
In either case, successful software design uses data abstraction:
Separating the definition of a data type from its implementation.
Abstract Data Types

5
Data Structure
A data structure is the physical implementation of an
ADT.
Each operation associated with the ADT is implemented by one
or more subroutines in the implementation.
Data structure usually refers to an organization of data
in main memory.
File structure is an organization for data on peripheral
storage, such as a disk drive.

6
Data Type
ADT:
Type
Operations
Data Items:
Logical Form
Data Items:
Physical Form
Data Structure:
Storage Space
Subroutines

7
Simple Data Types
Memory:
2-state devices ↔ bits 0 and 1
Organized into bytes (8 bits) and
words (machine dependent — e.g., 2 bytes).
Each byte (or word) has an address making it possible to store and retrieve
contents of any given memory location.
Therefore:
the most basic form of data: sequences of bits
simple data types (values are atomic — can't be subdivided) are ADTs.
Implementations have:
» Storage structures: memory locations
» Algorithms: system hardware/software to do basic operations.

8
Boolean data
Data values: {false, true}
In C/C++: false = 0, true = 1 (or nonzero)
Operations: and &&
or ||
not !
x !x
0 1
1 0
&& 0 1
0 0 0
1 0 1
| | 0 1
0 0 1
1 1 1

9
Character Data
Store numeric codes (ASCII, EBCDIC, Unicode)
1 byte for ASCII and EBCDIC,
2 bytes for Unicode
Basic operation: comparison to determine ifEqual, Less than ,Greater
than, etc. use their numeric codes (i.e. use ordinal value)
ASCII/EBCDIC
Unicode

10
Integer Data
Non-negative (unsigned) integer:
Store its base-two representation in a fixed number w of bits
(e.g., w = 16 or w = 32)
88 = 00000000010110002
Signed integer:
Store in a fixed number w of bits using one of the following representations:

11
Sign-magnitude representation
Save one bit (usually most significant) for sign
(0 = +, 1 = – )
Use base-two representation in the other bits.
88 → _0000000010110000
↑
sign bit
Cumbersome for arithmetic computations
–88 → _000000001011000
↓
1

12
Two's complement representation
For negative n (–n):
(1) Find w-bit base-2 representation of n
(2) Complement each bit.
(3) Add 1
Example: –88
1. 88 as a 16-bit base-two number 0000000001011000
Same as
sign mag.For nonnegative n:
Use ordinary base-two representation with leading (sign) bit 0
2. Complement this bit string
3. Add 1
1111111110100111
1111111110101000
(Flip all bits from rightmost 0 to the end)

Algo>Abstract data type

More Related Content

What's hot

Viewers also liked

Similar to Algo>Abstract data type

More from Ain-ul-Moiz Khawaja

Recently uploaded

Algo>Abstract data type