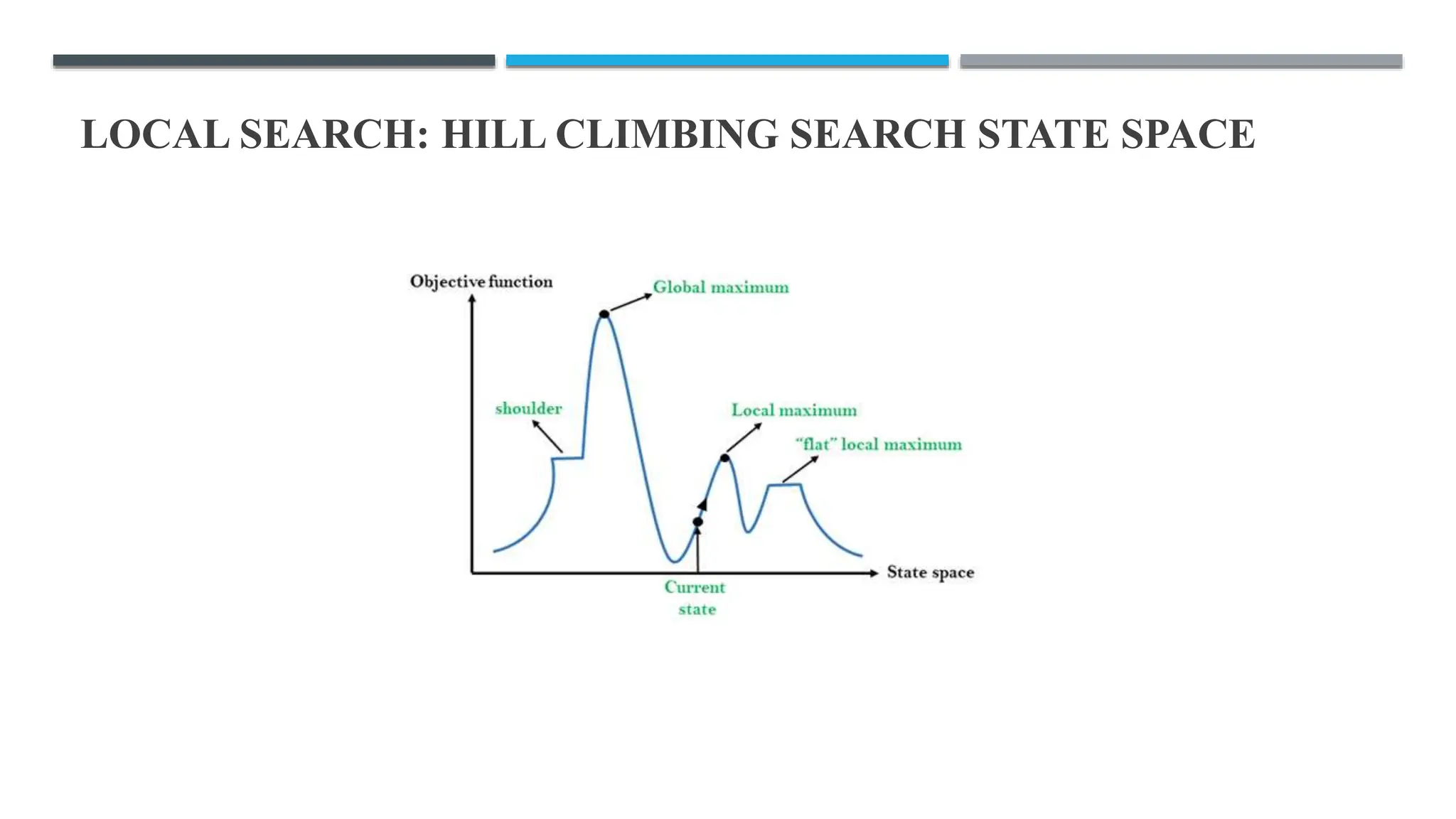
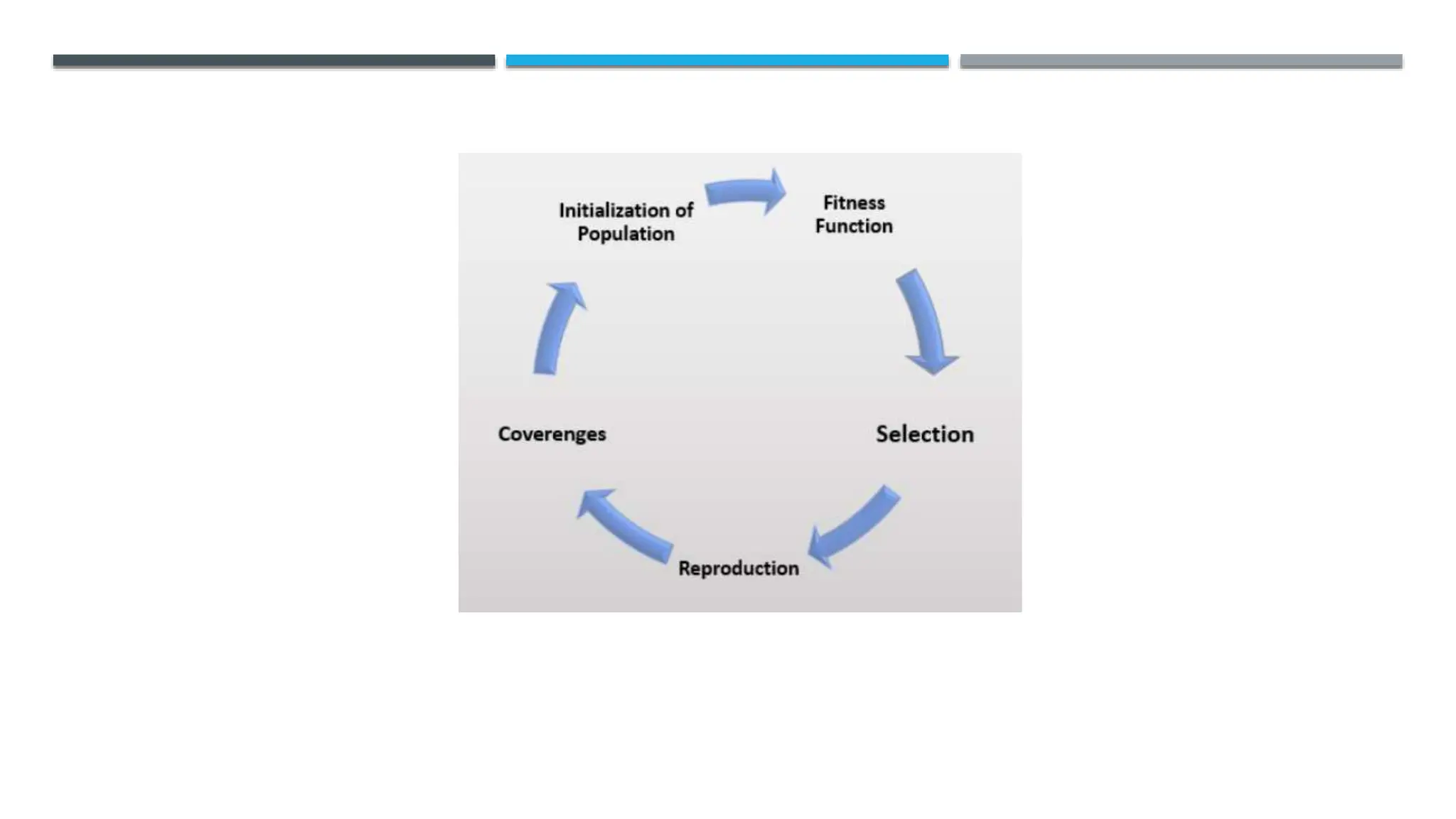
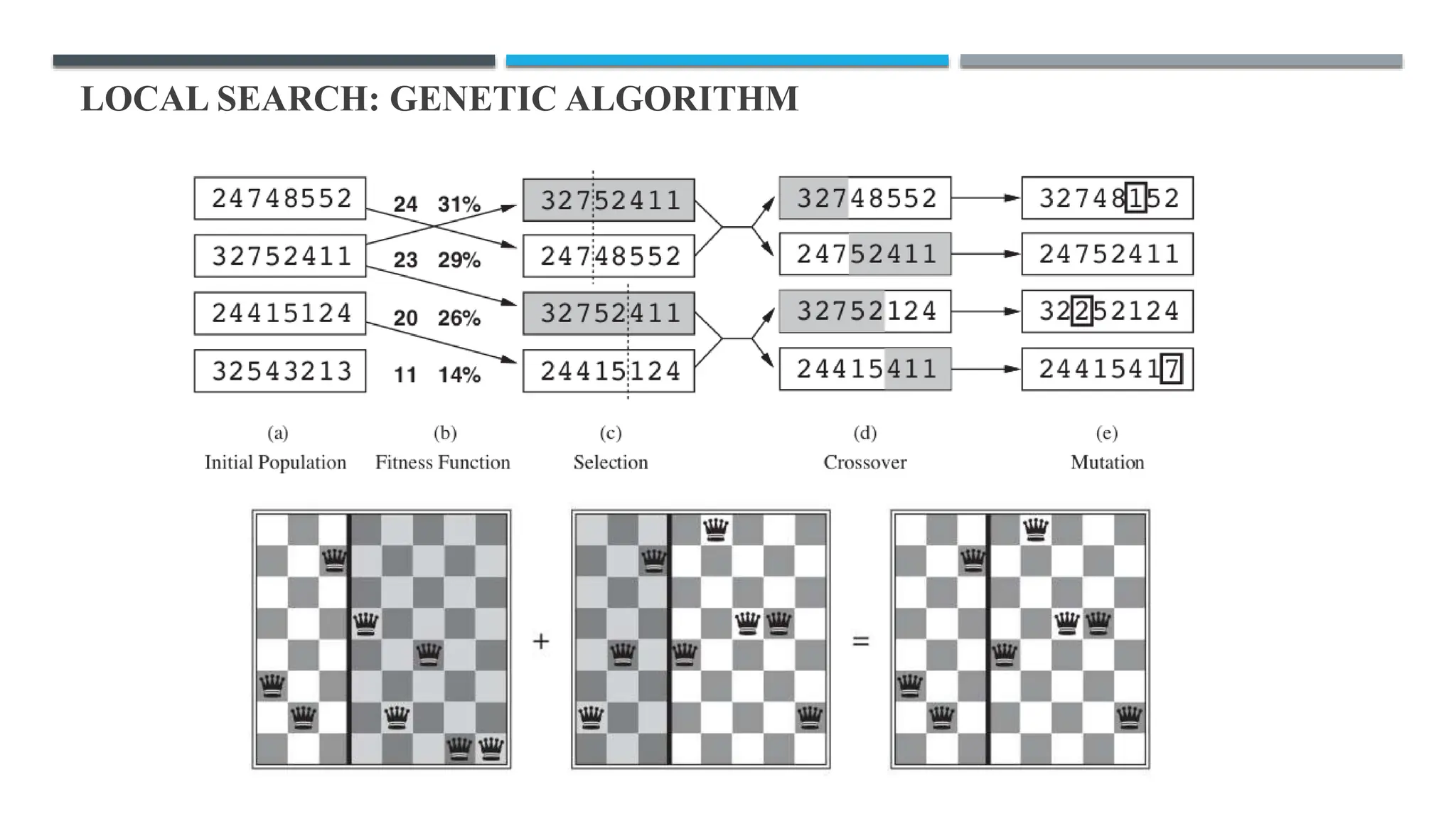
The document discusses local search algorithms, emphasizing their efficiency in exploring state spaces without maintaining paths, which is suitable for optimization problems. It details various methods such as hill climbing and genetic algorithms, describing their mechanics, advantages, and potential issues like local maxima. Additionally, it highlights the importance of strategies like simulated annealing and beam search for navigating complex search spaces.