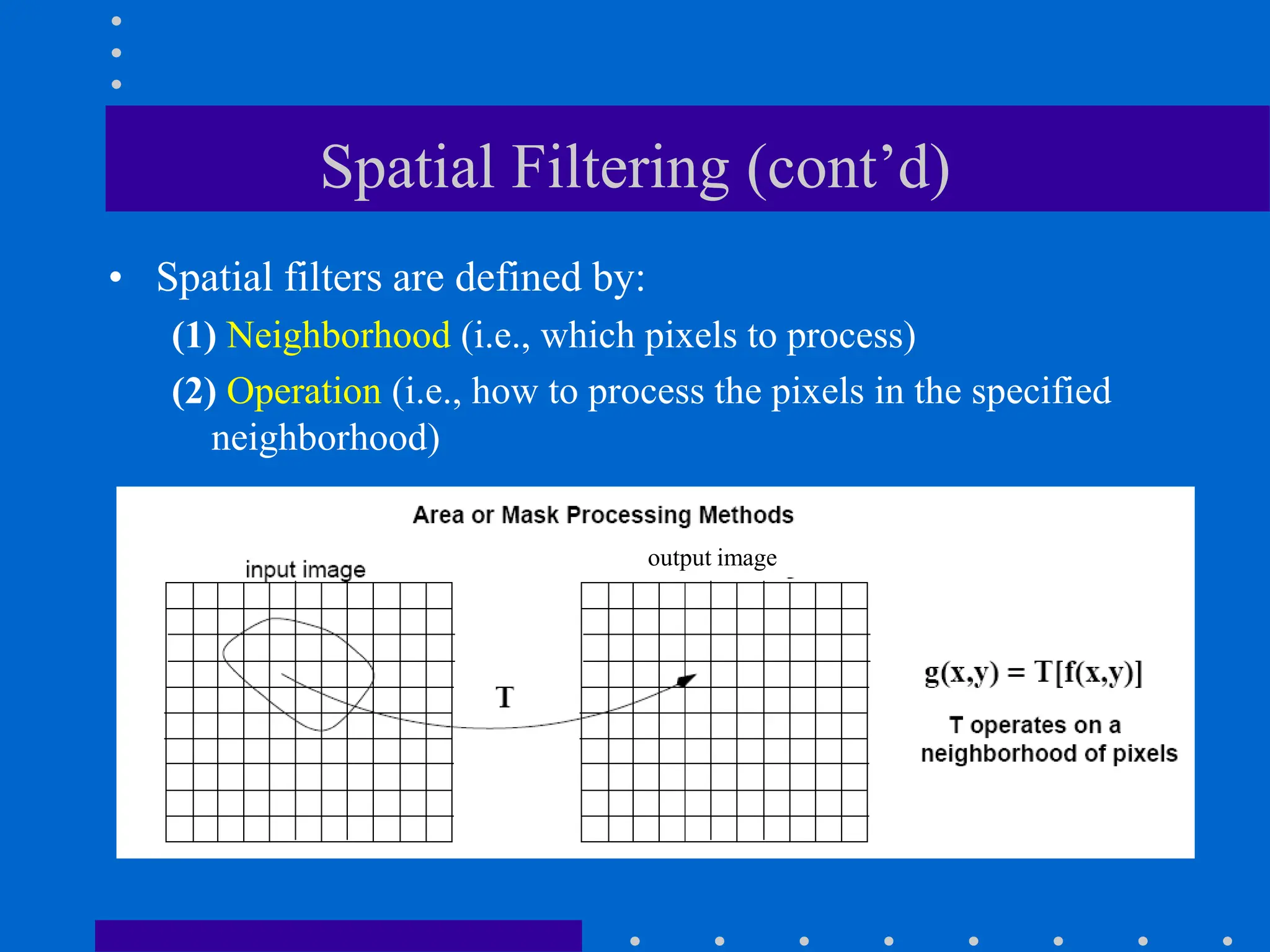
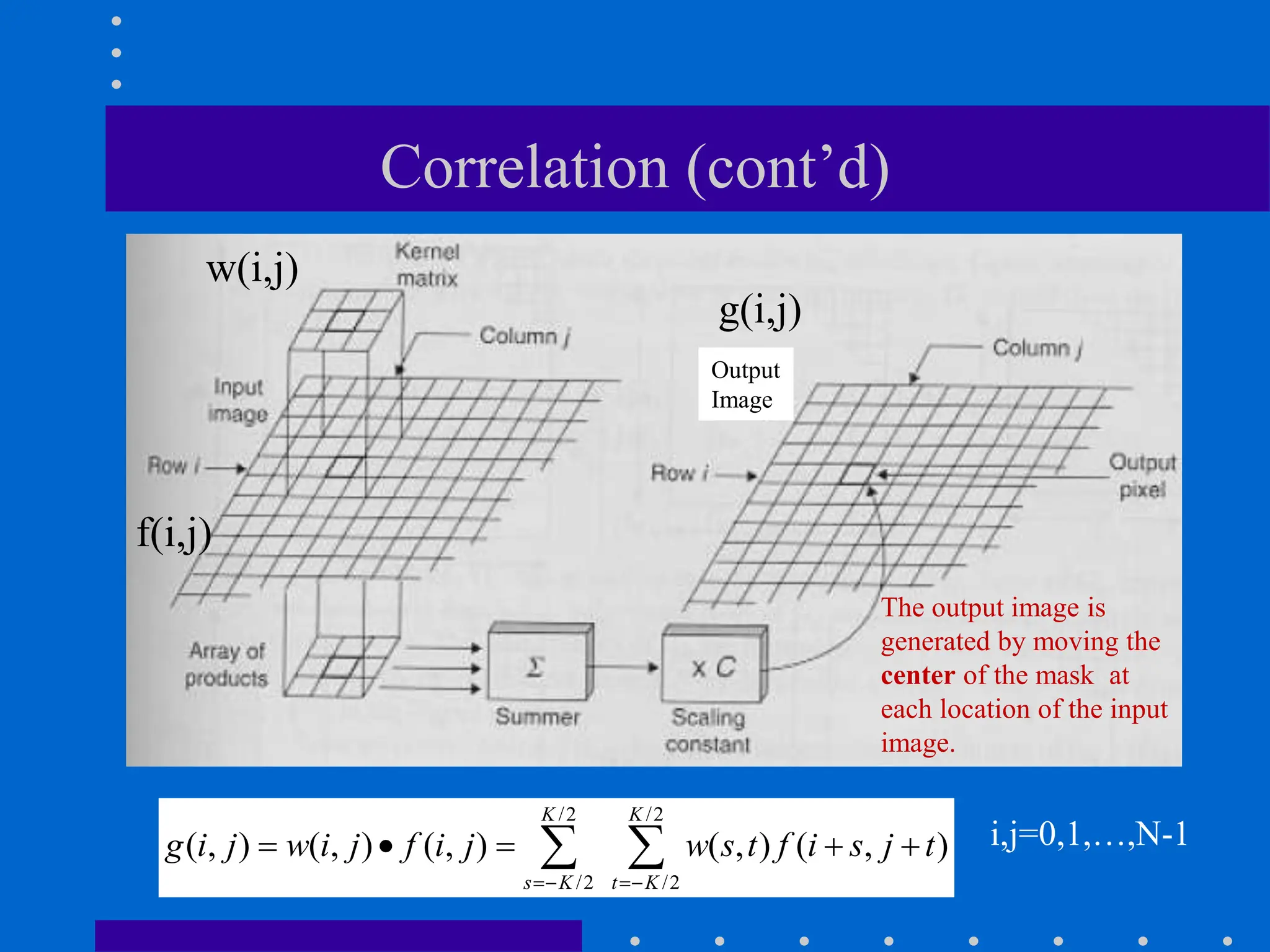
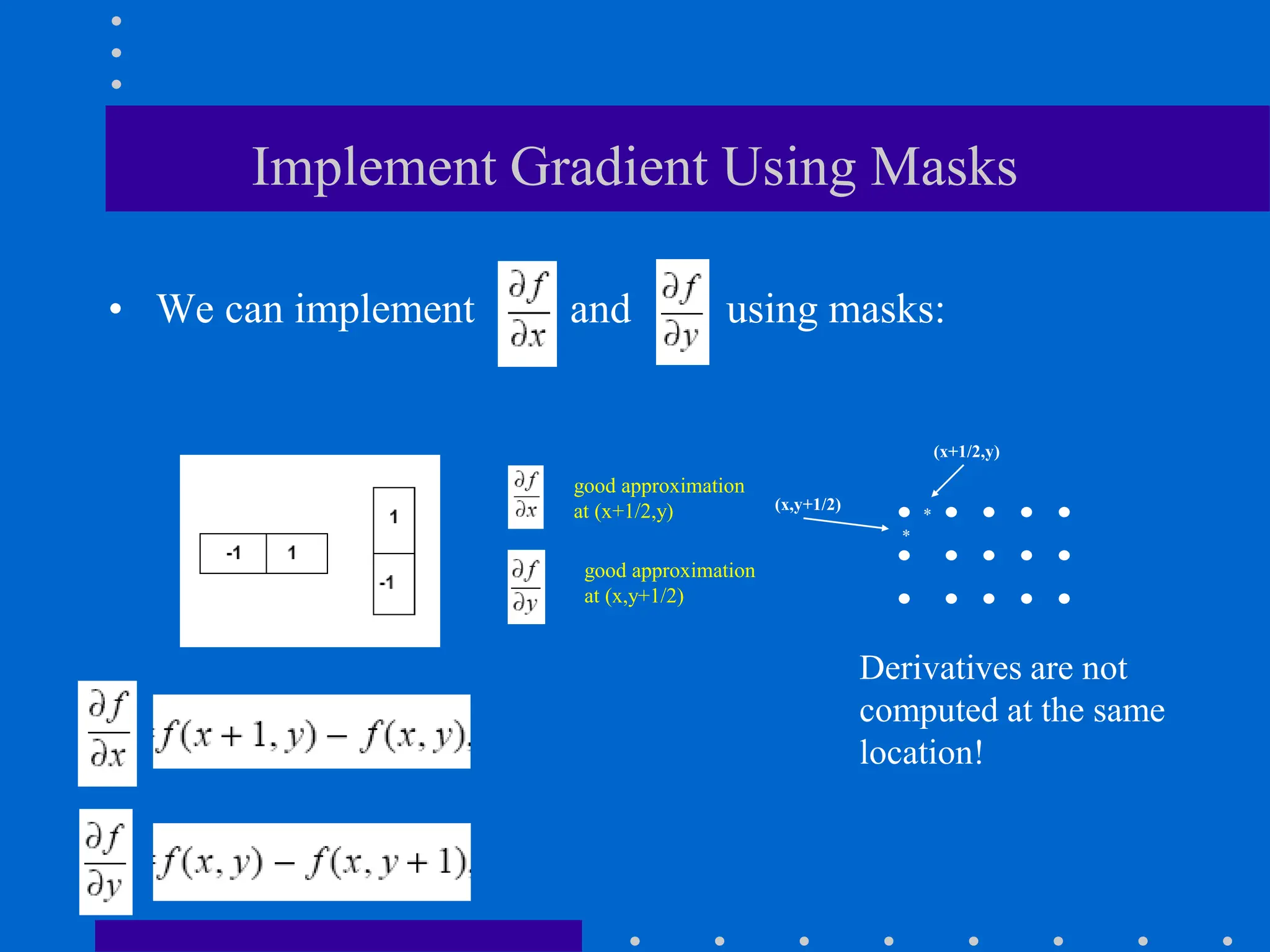
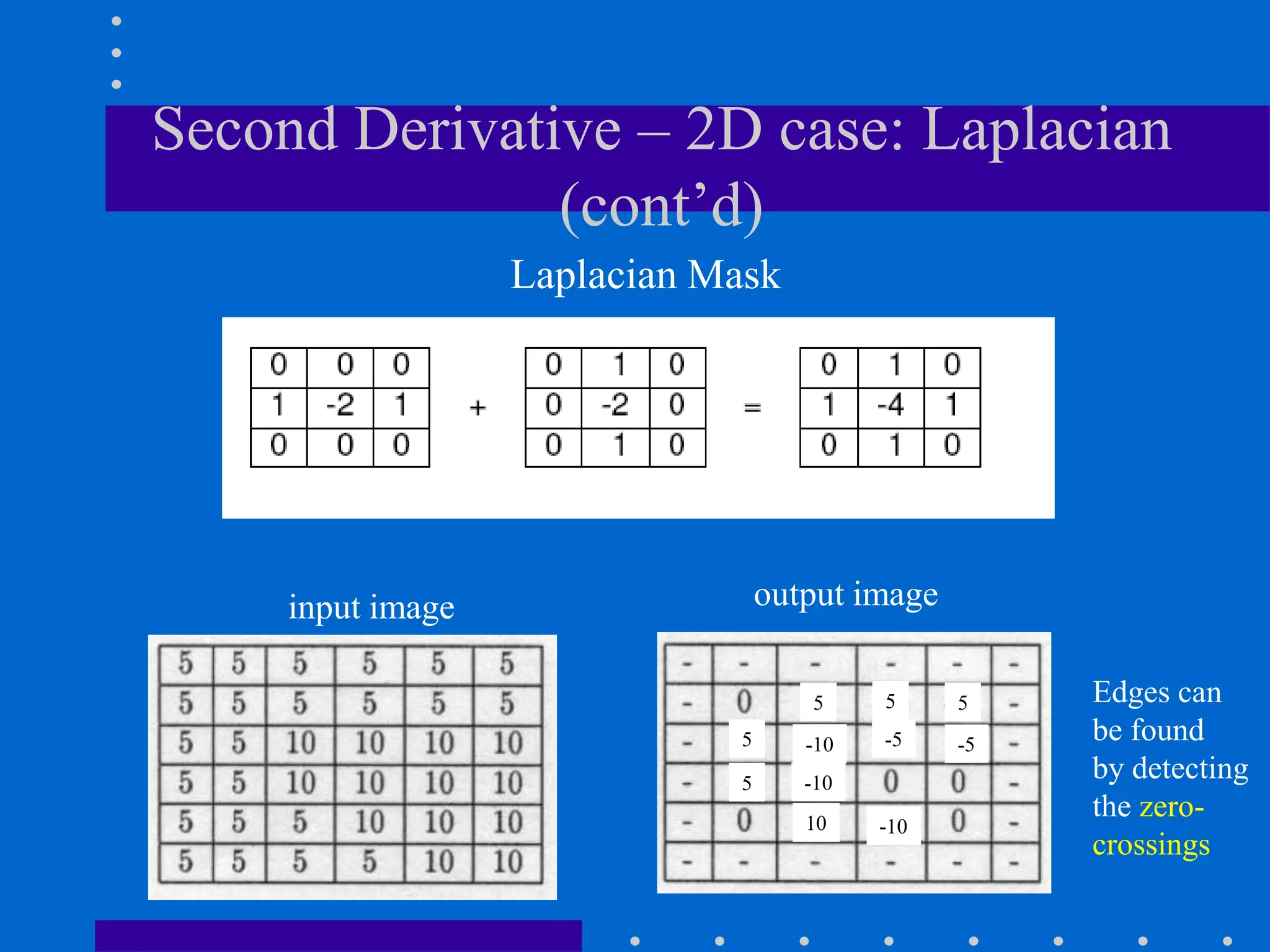
This document discusses various spatial filtering methods used in image processing. Spatial filters are defined by their neighborhood, which is usually a square window, and their operation, which processes pixels in the neighborhood. Linear filters include correlation and convolution, where the output is a linear combination of input pixels. Common filters are smoothing (low-pass) filters like averaging and Gaussian, which reduce noise and detail, and sharpening (high-pass) filters like unsharp masking and derivatives, which enhance details like edges. Derivatives like the gradient and Laplacian are used to detect edges.




































![Example: visualize partial derivatives
f
x
f
y
• Image derivatives can be visualized as an image
by mapping the values to [0, 255]](https://image.slidesharecdn.com/spatialfiltering-240417131309-7fc5270c/75/Spatial-Filtering-in-intro-image-processingr-40-2048.jpg)


![Example: Visualize Gradient Magnitude
f
y
f
x
Gradient Magnitude
(isotropic, i.e., detects
edges in all directions)
• The gradient magnitude can be visualized
as an image by mapping the values to [0, 255]](https://image.slidesharecdn.com/spatialfiltering-240417131309-7fc5270c/75/Spatial-Filtering-in-intro-image-processingr-44-2048.jpg)






![Visualize the results of the Laplacian
(cont’d)
no normalization,
negative values
clipped to zero
blurred image
scaled to [0, 255]
Example:](https://image.slidesharecdn.com/spatialfiltering-240417131309-7fc5270c/75/Spatial-Filtering-in-intro-image-processingr-52-2048.jpg)