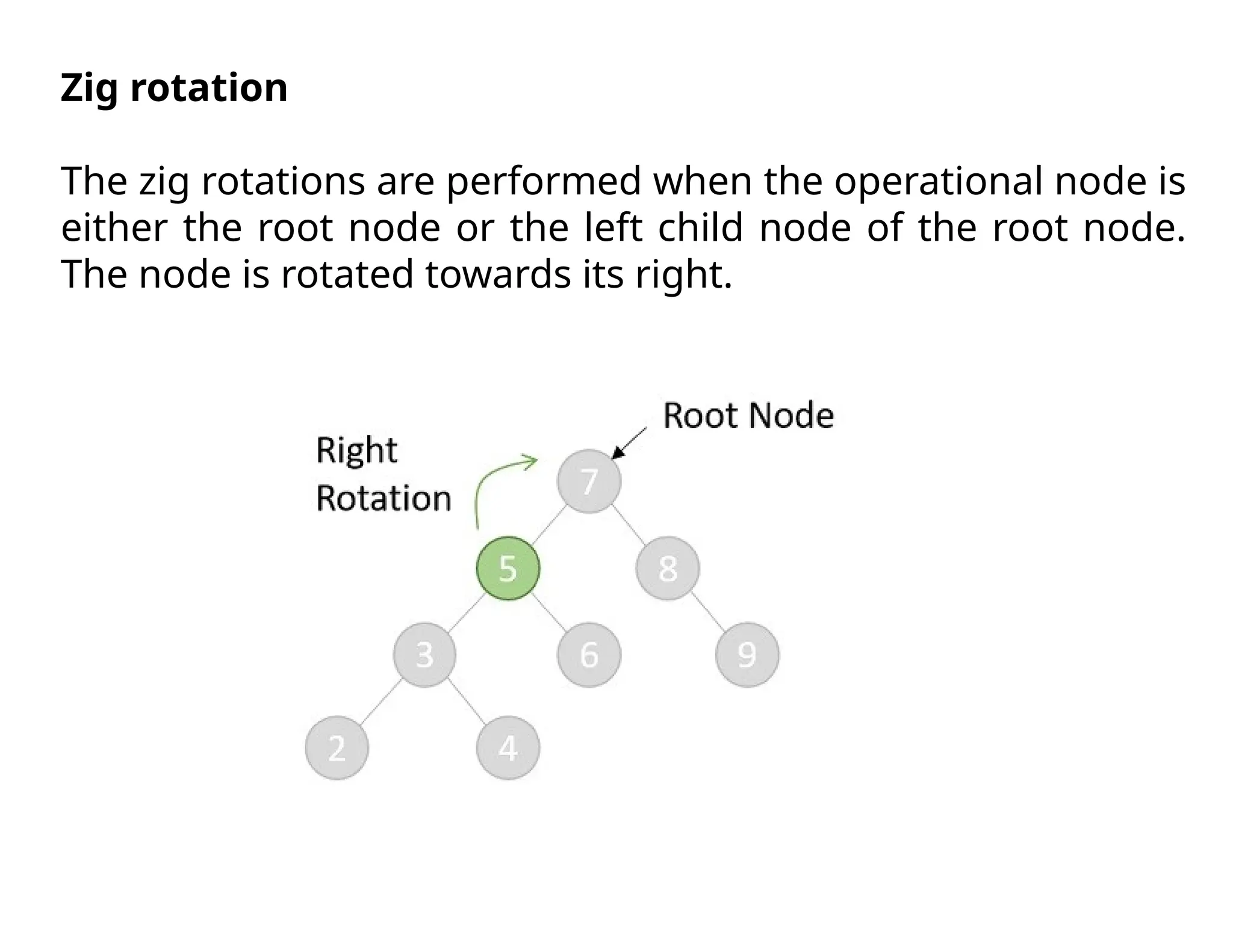
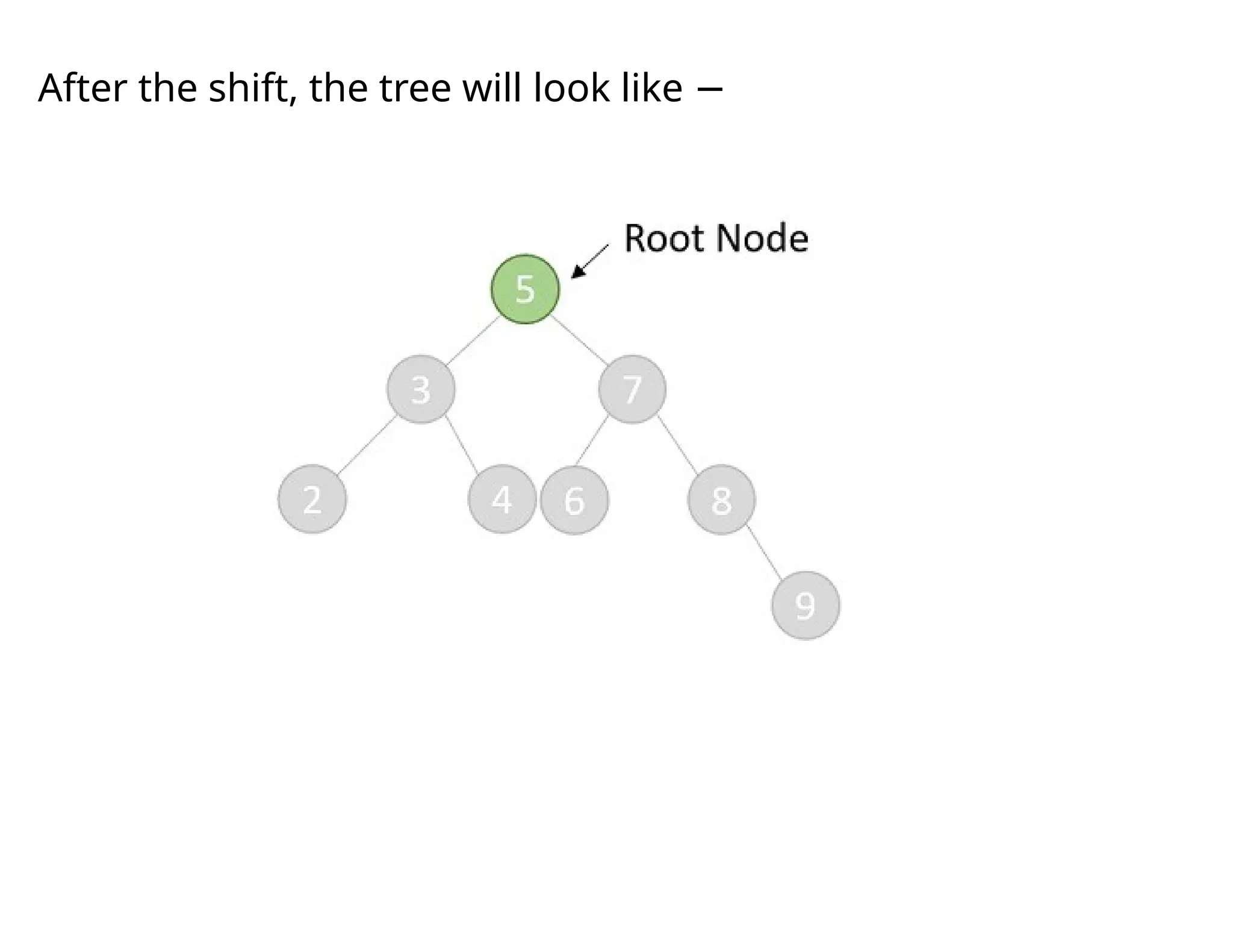
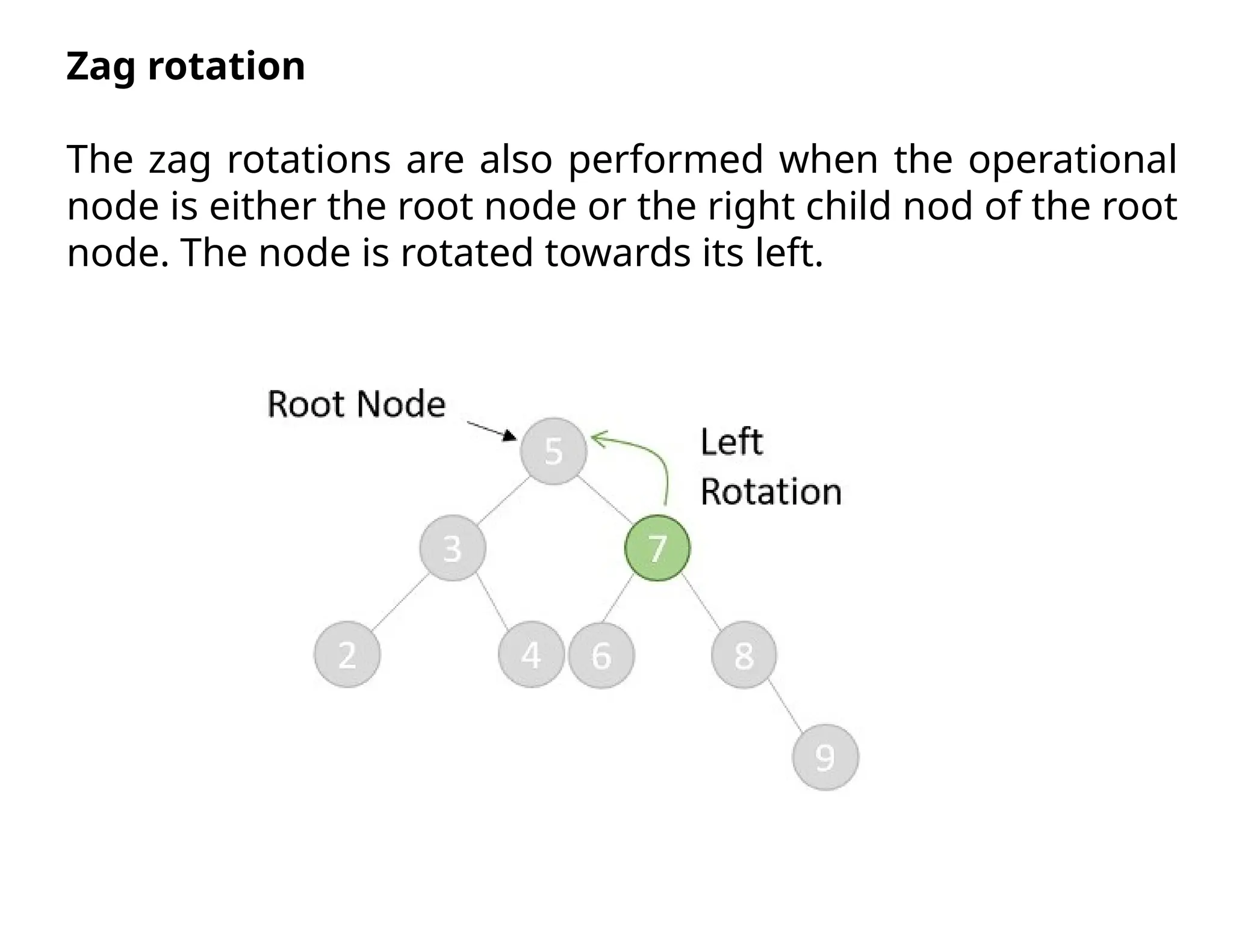
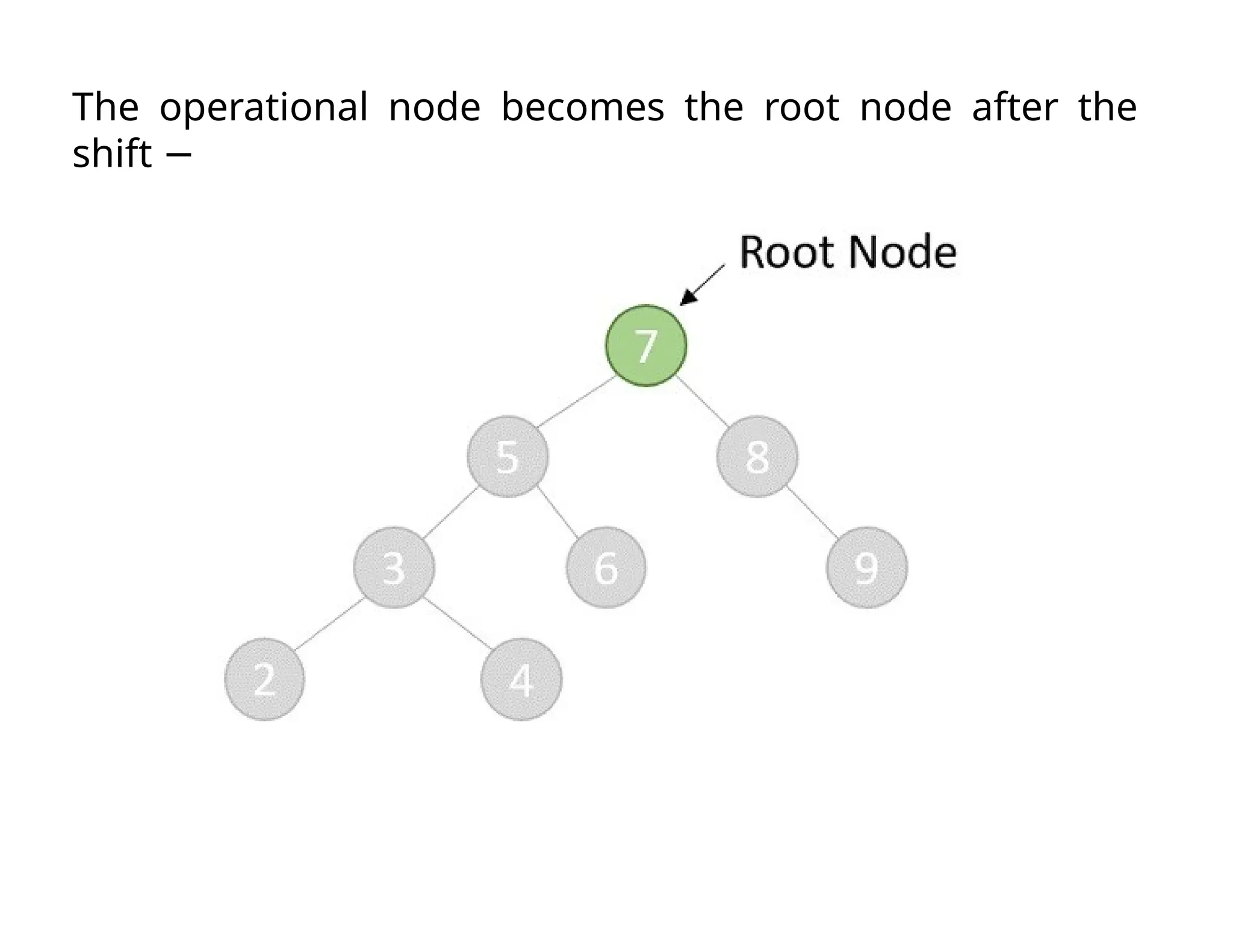
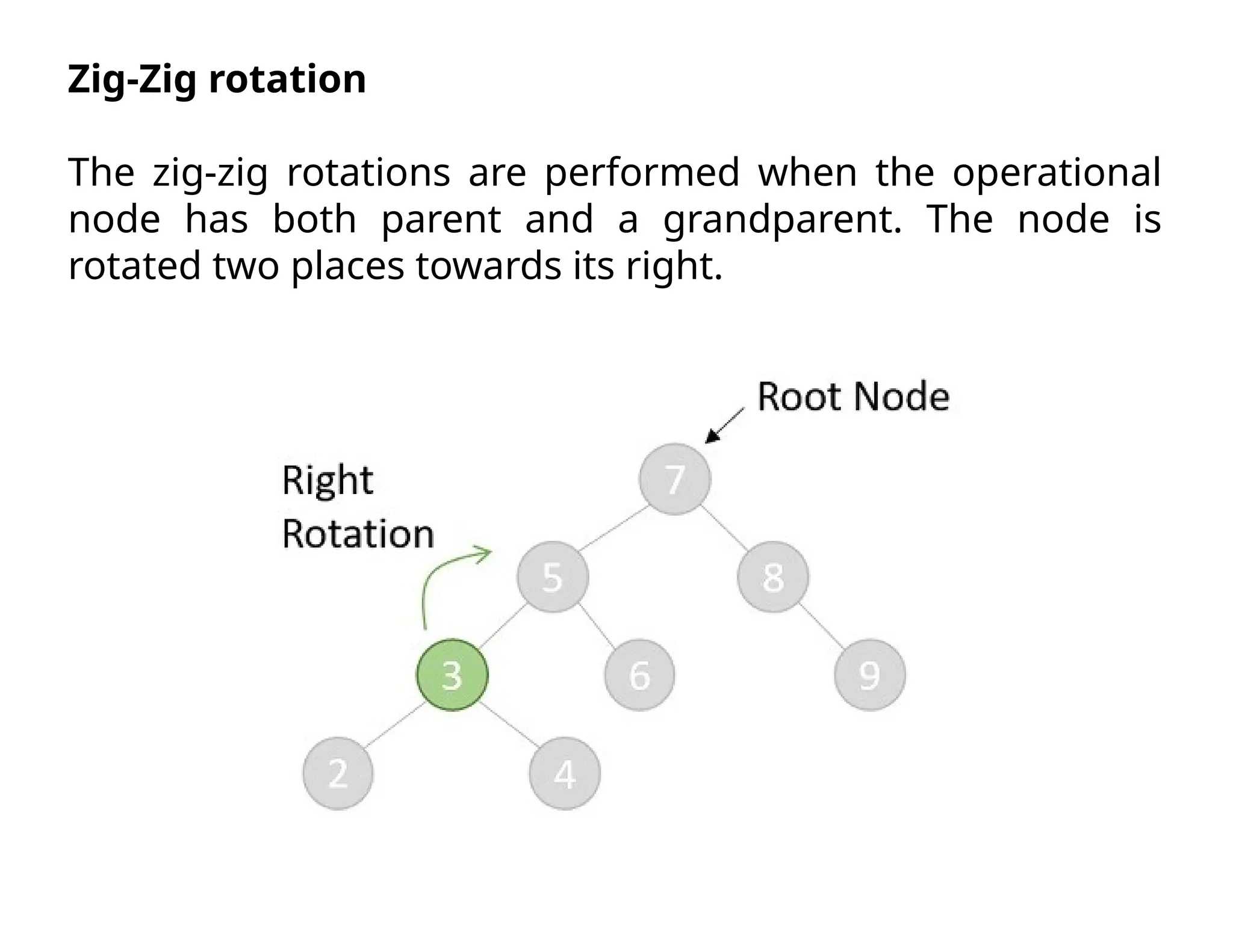
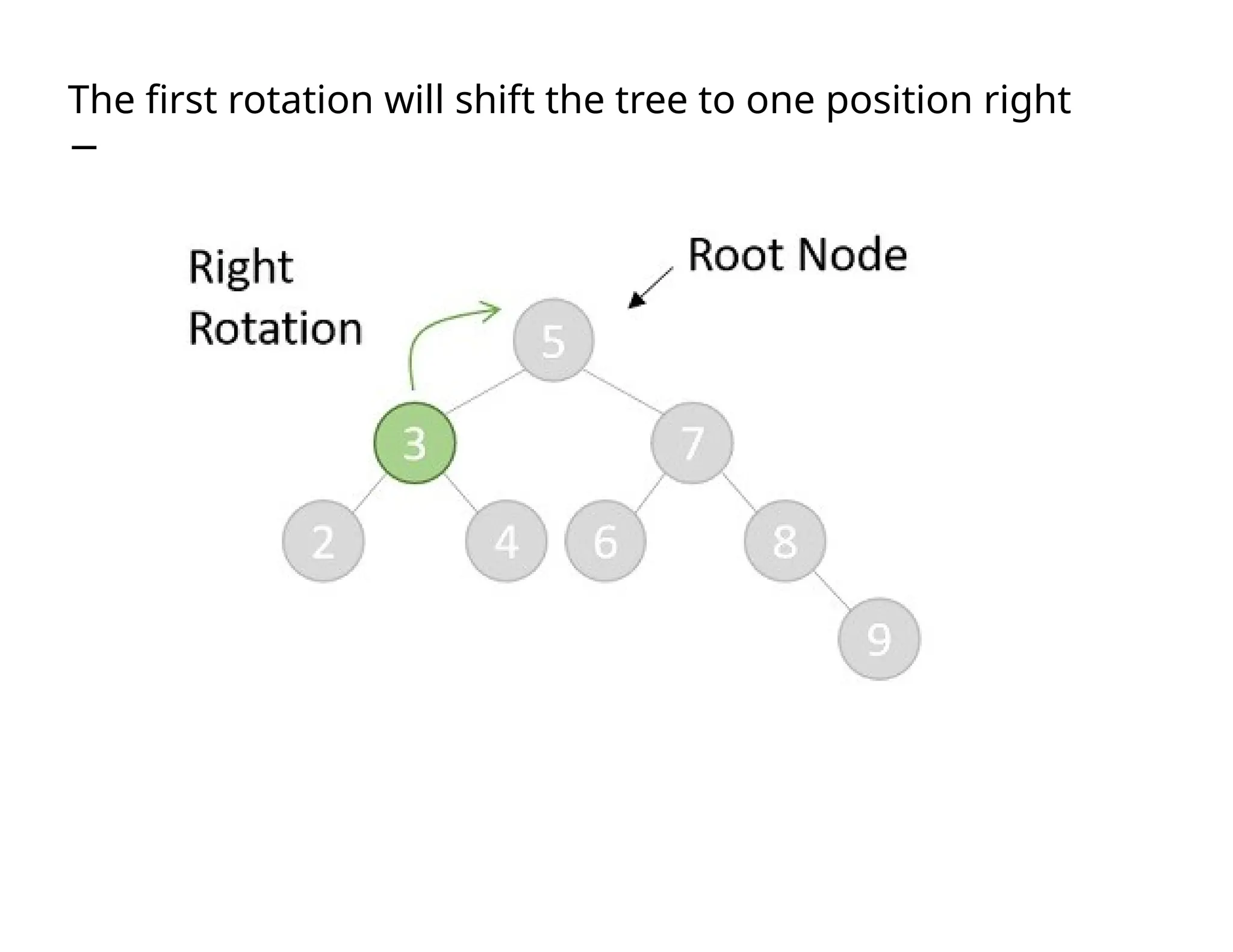
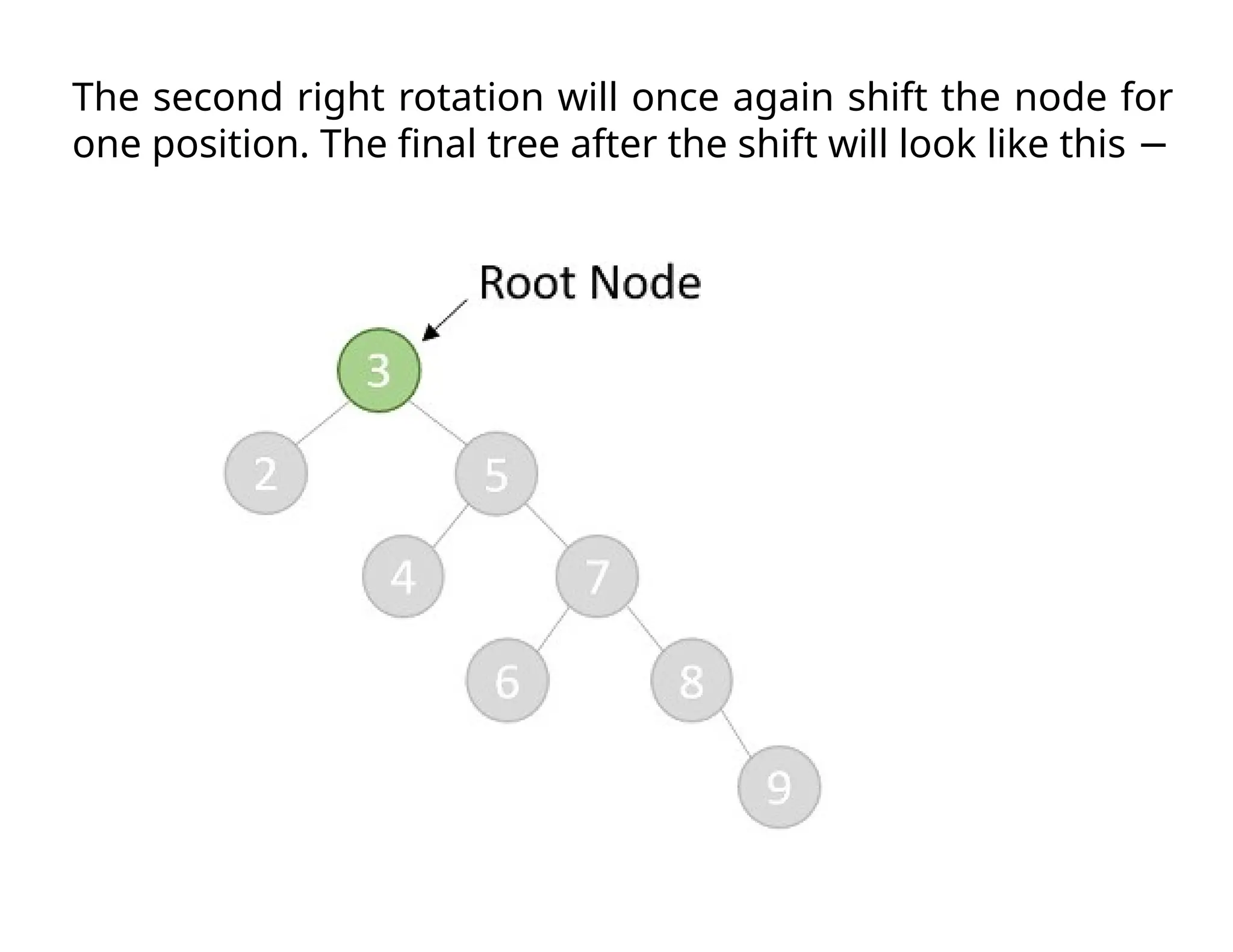
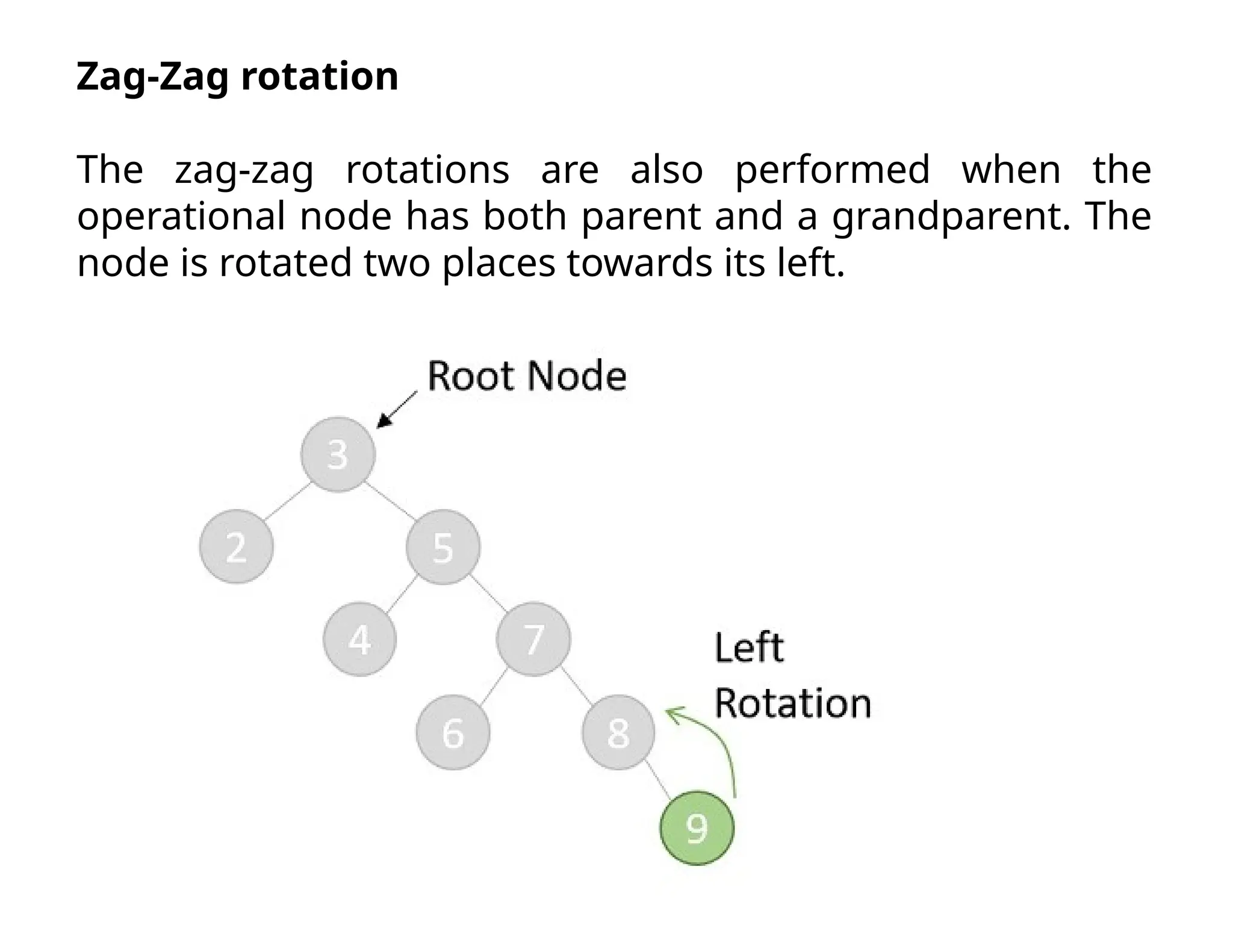
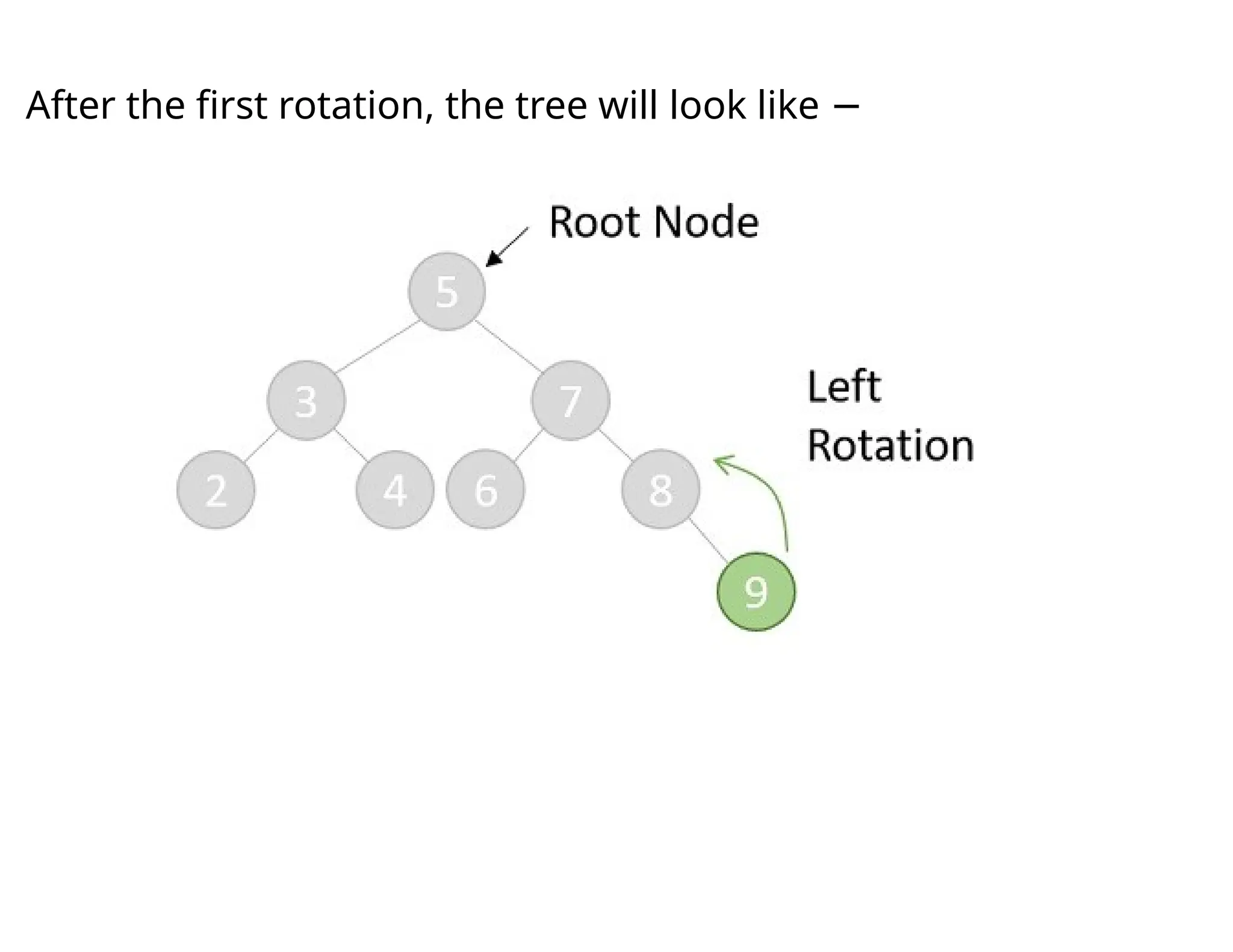
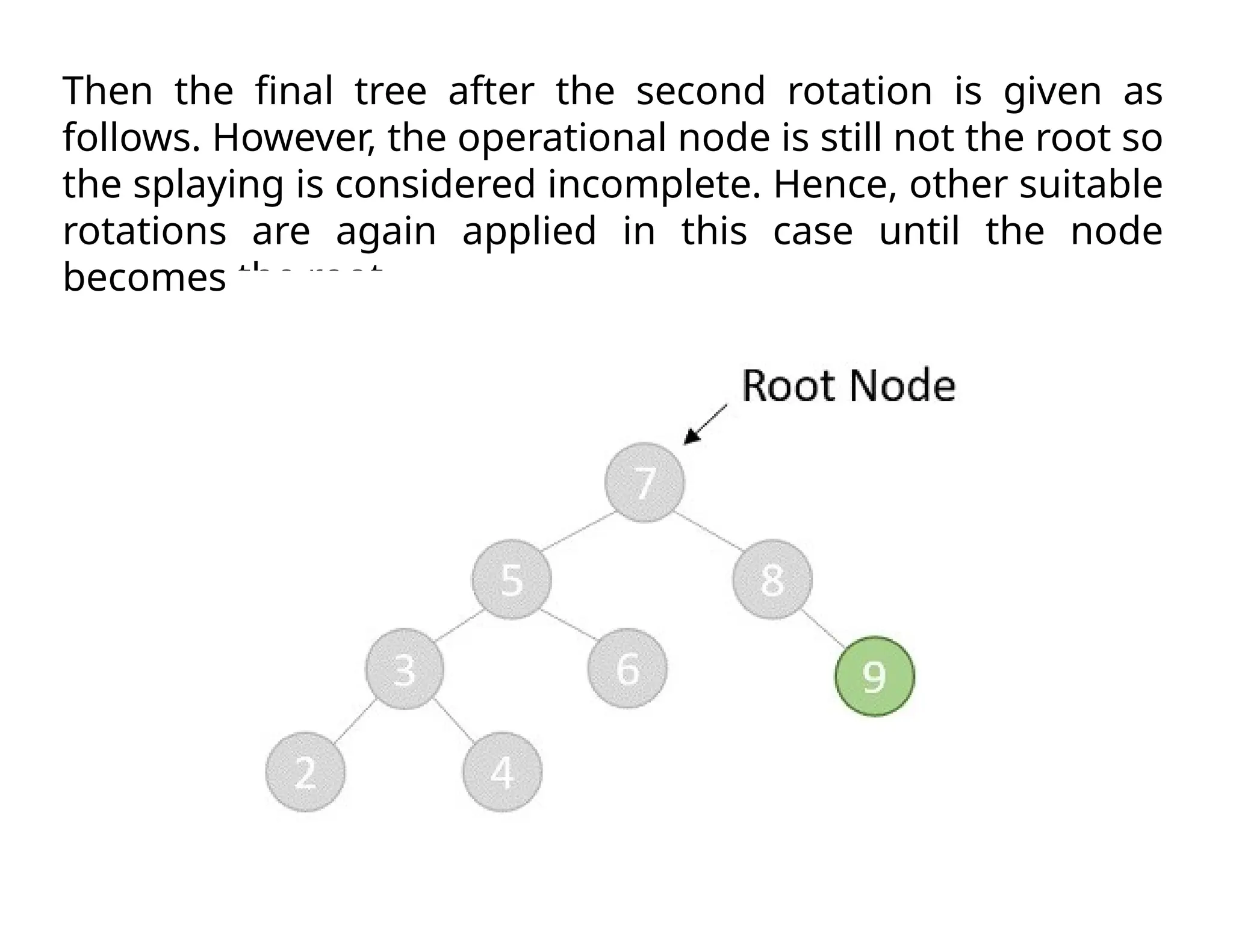
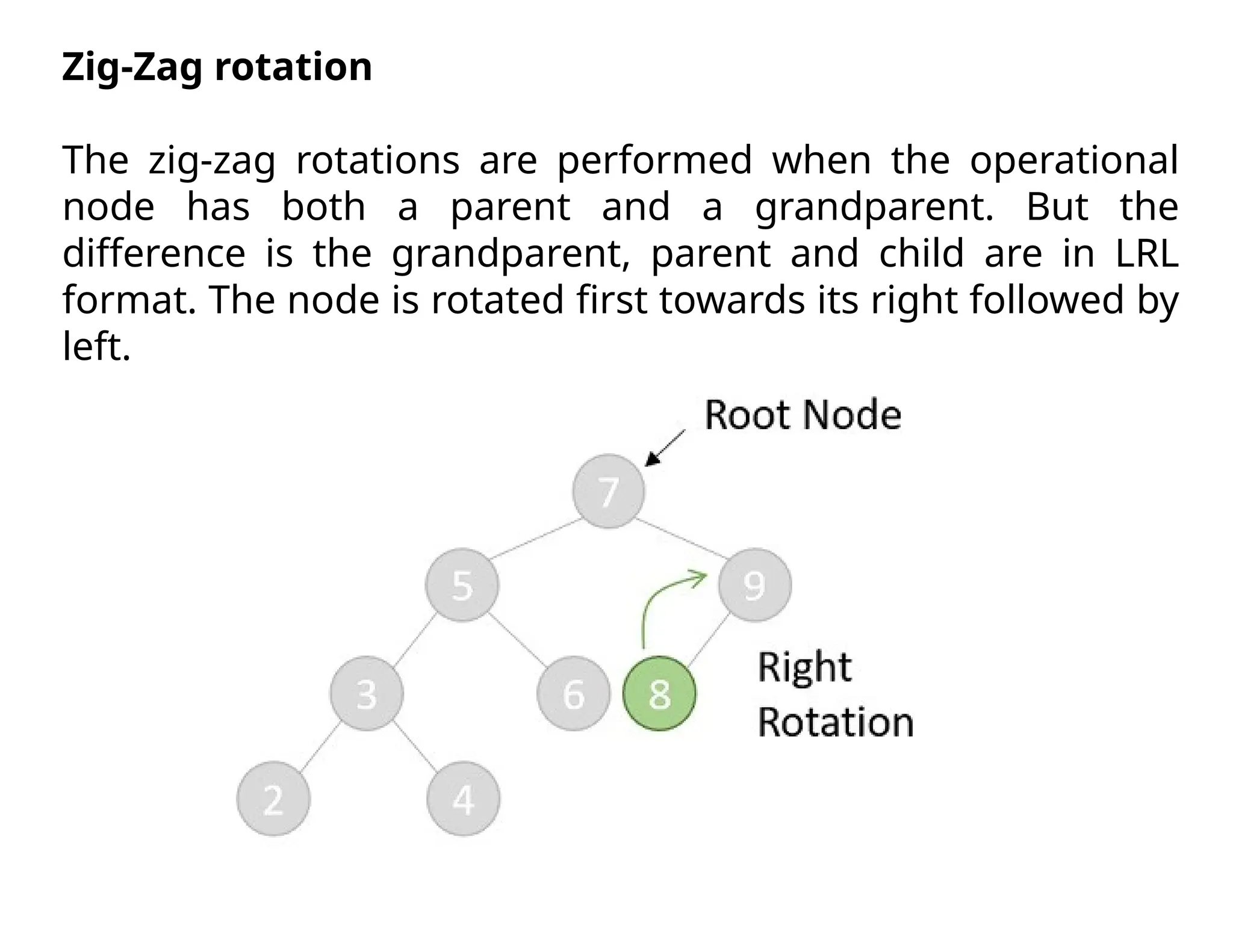
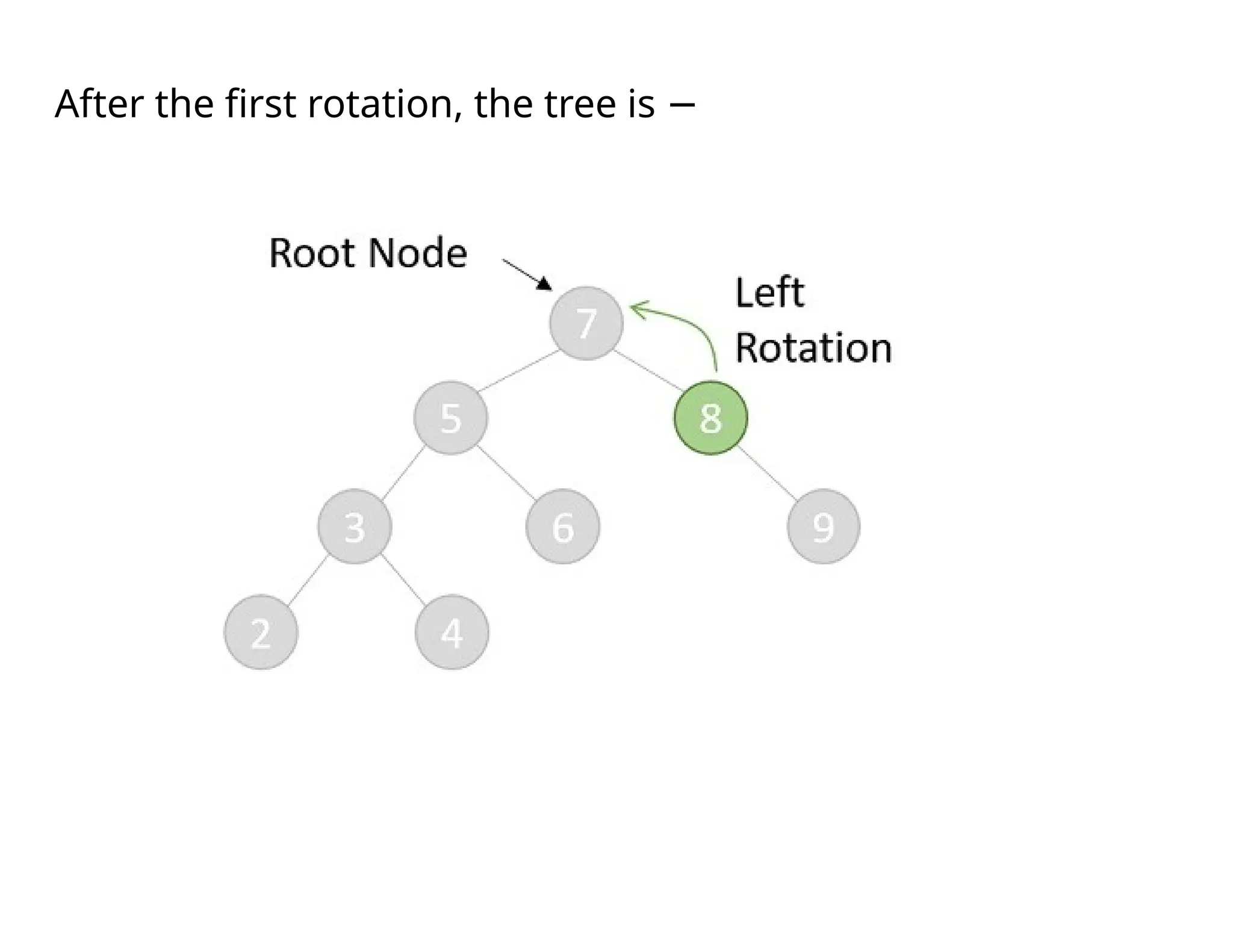
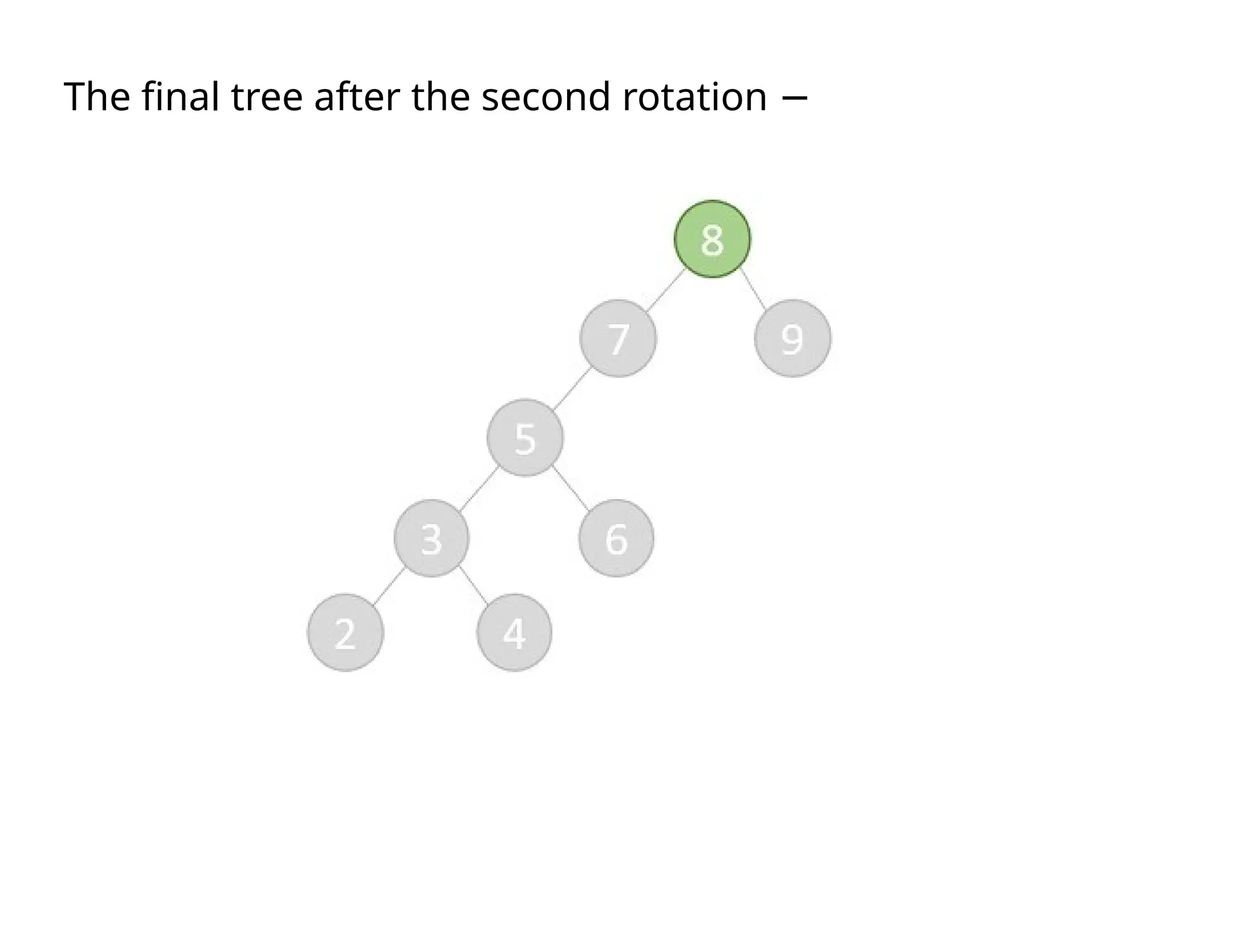
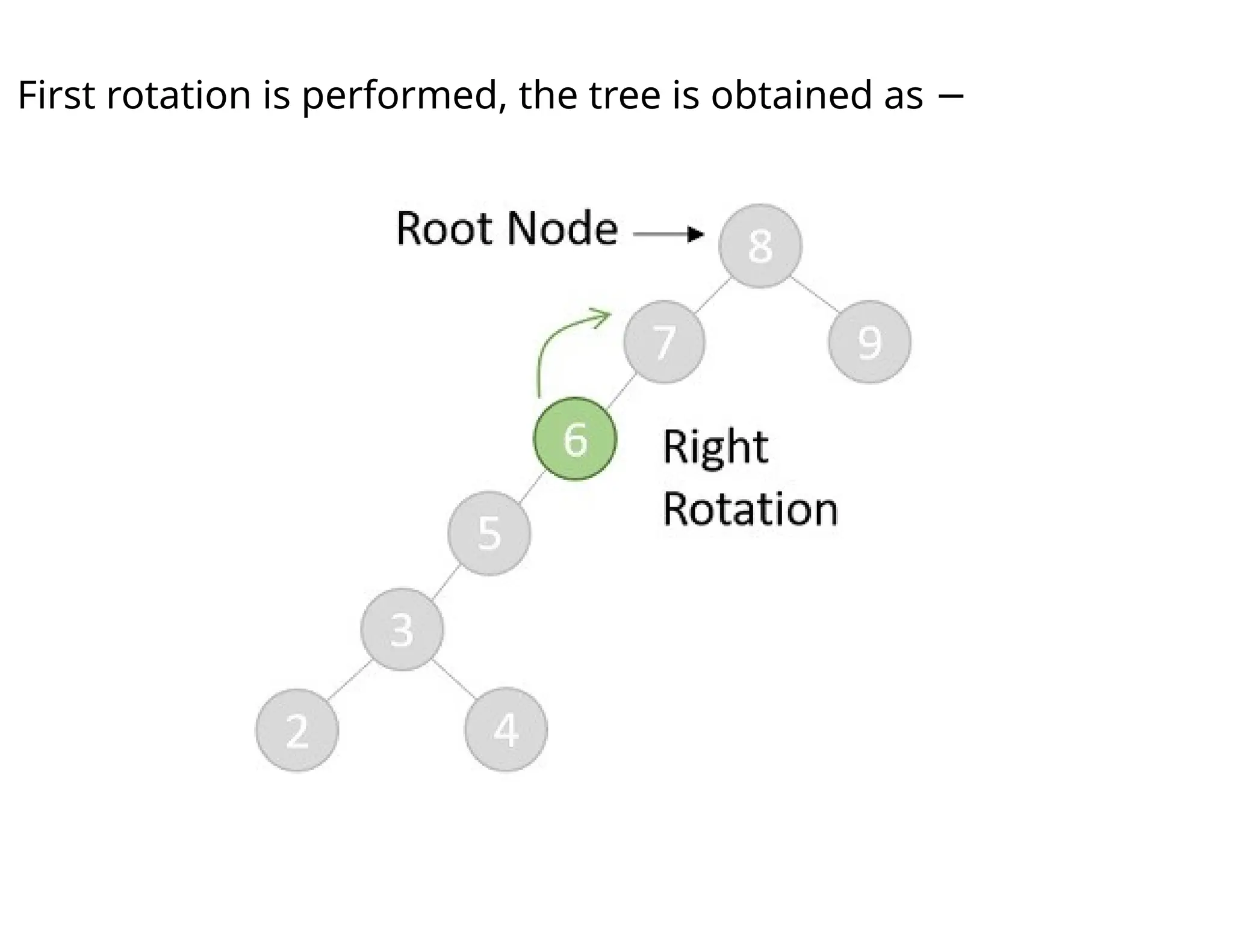
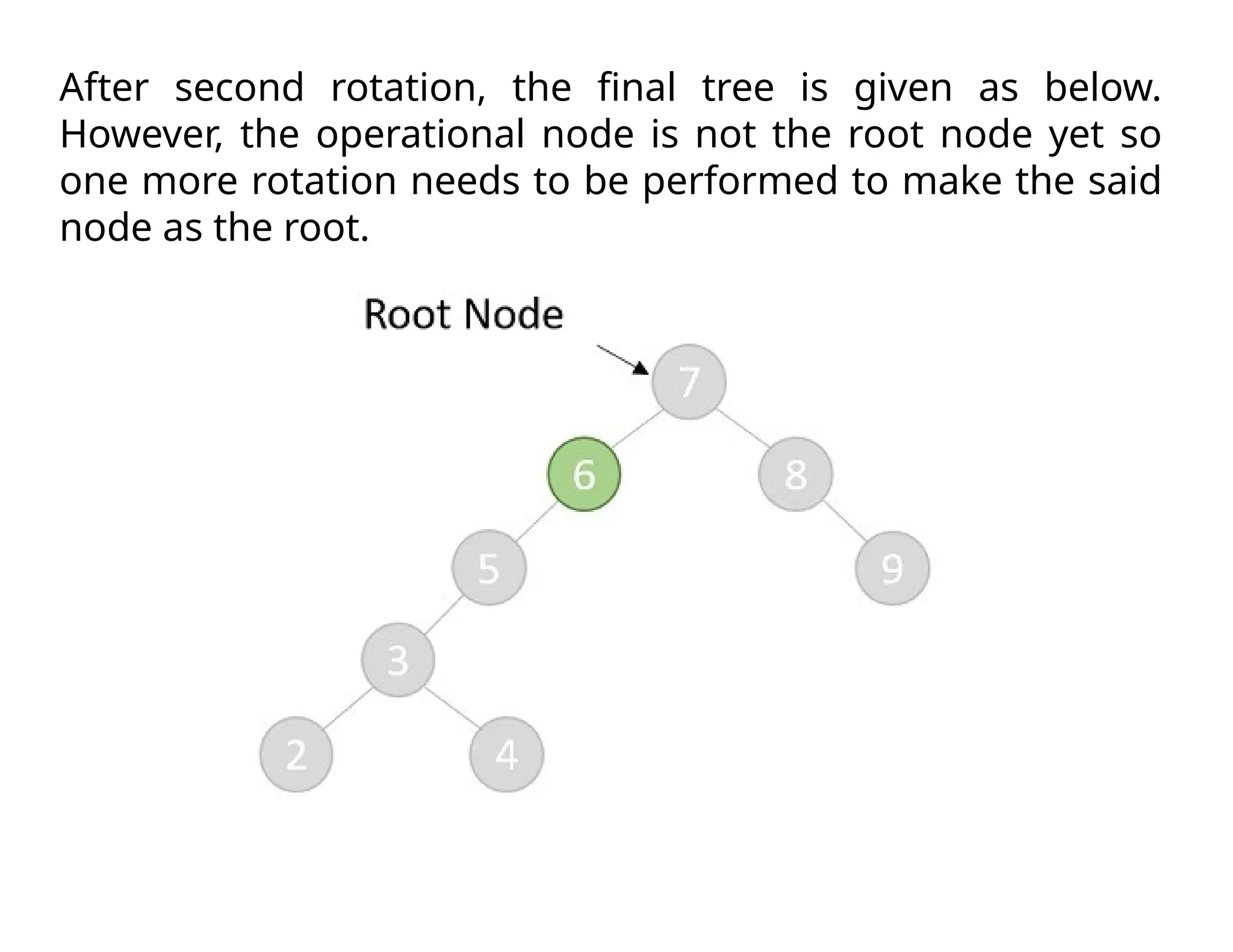
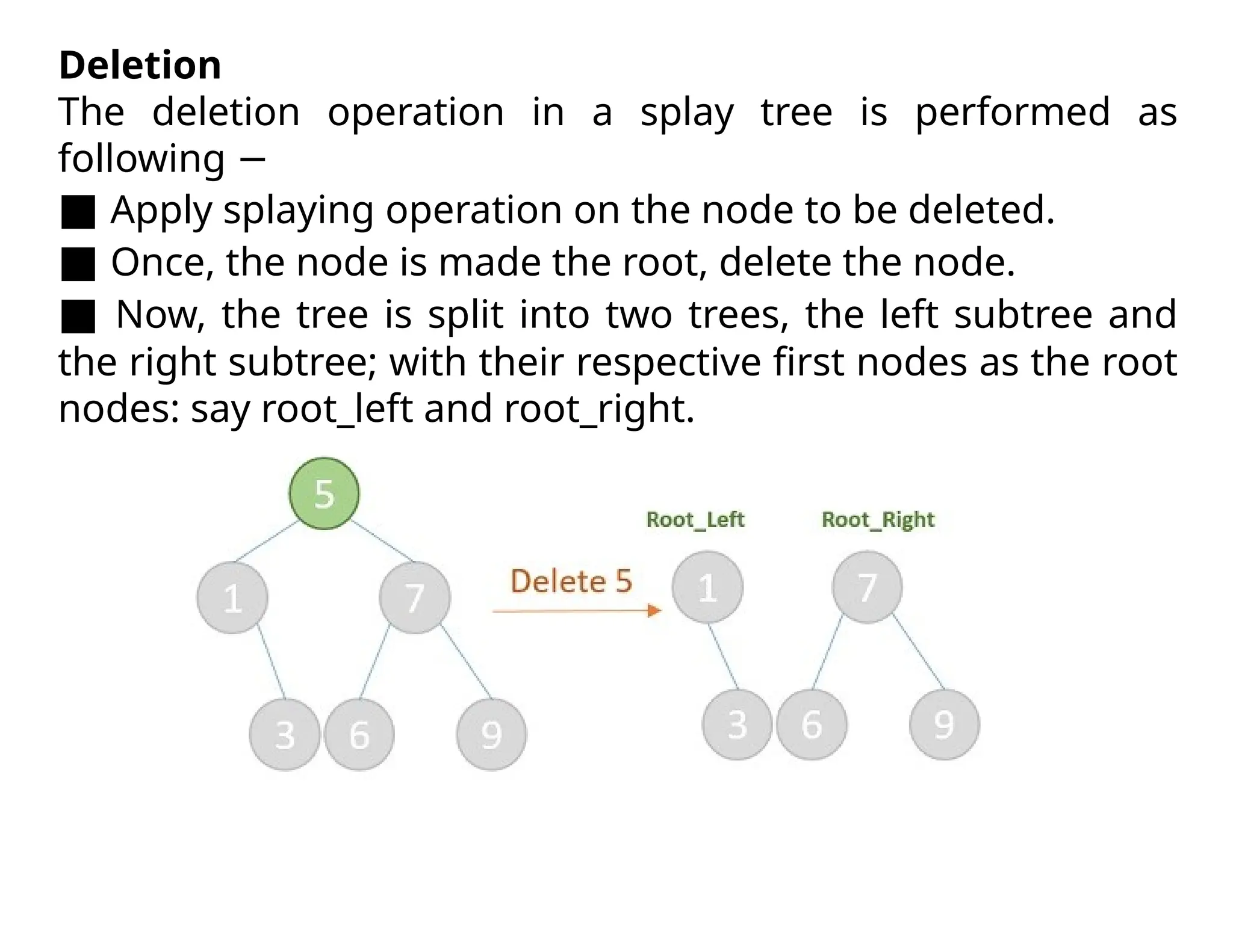
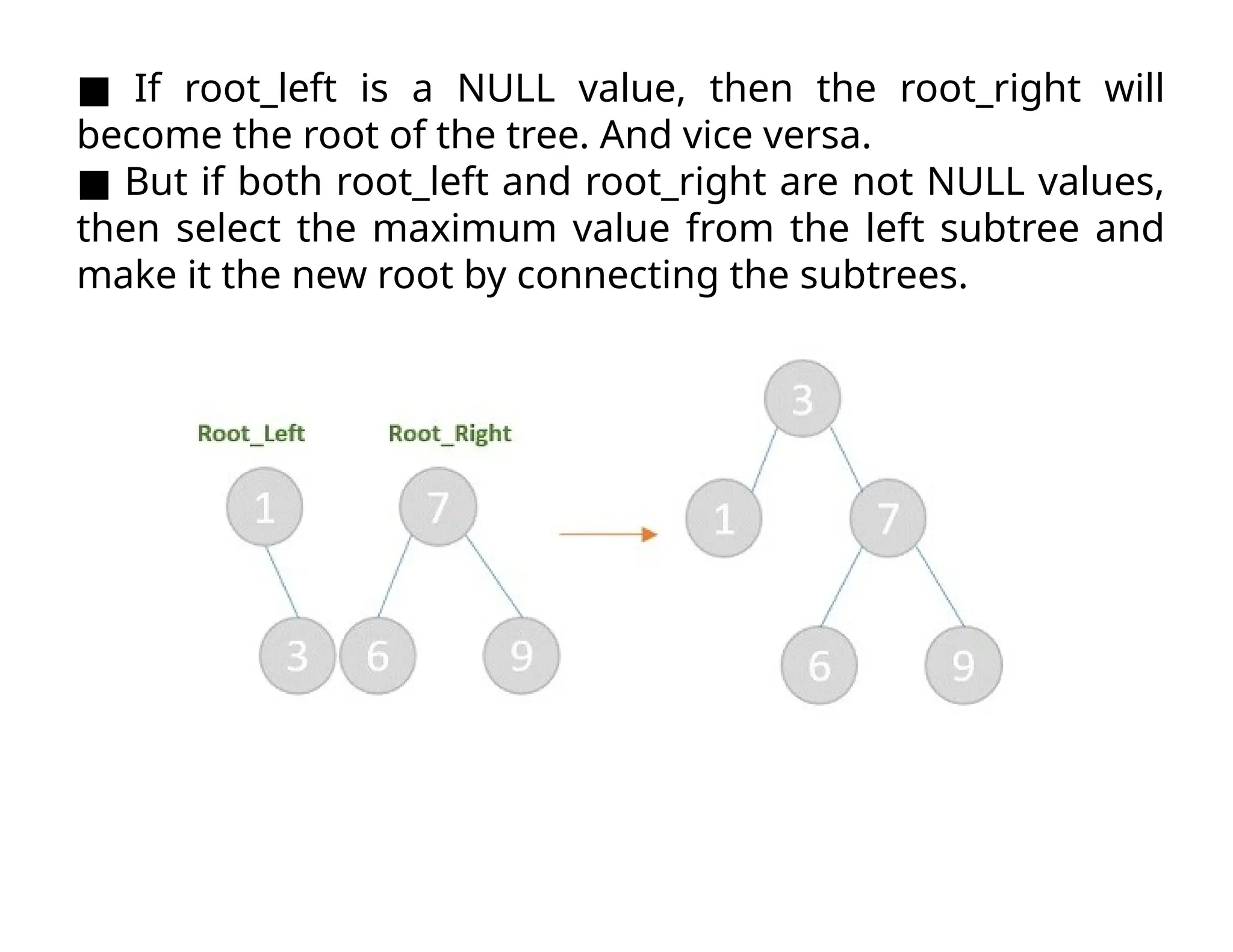
Splay trees are modified binary search trees that support operations like insertion, deletion, and searching, followed by a process called splaying to bring accessed nodes to the root. Splaying can be executed through six rotation types: zig, zag, zig-zig, zag-zag, zig-zag, and zag-zig. Each operation in a splay tree mirrors the corresponding operation in a regular binary search tree, with the added step of performing splaying afterward.