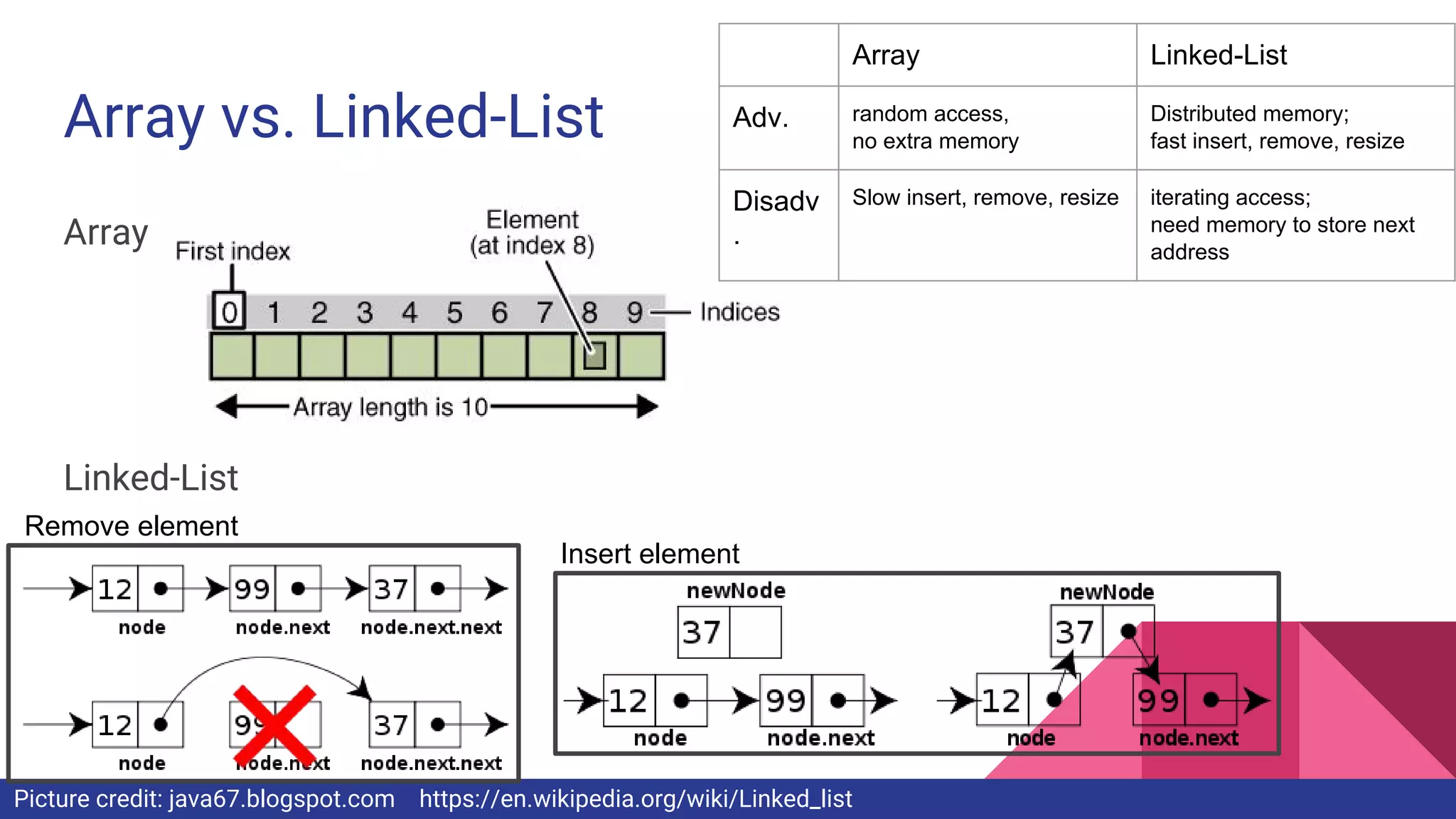
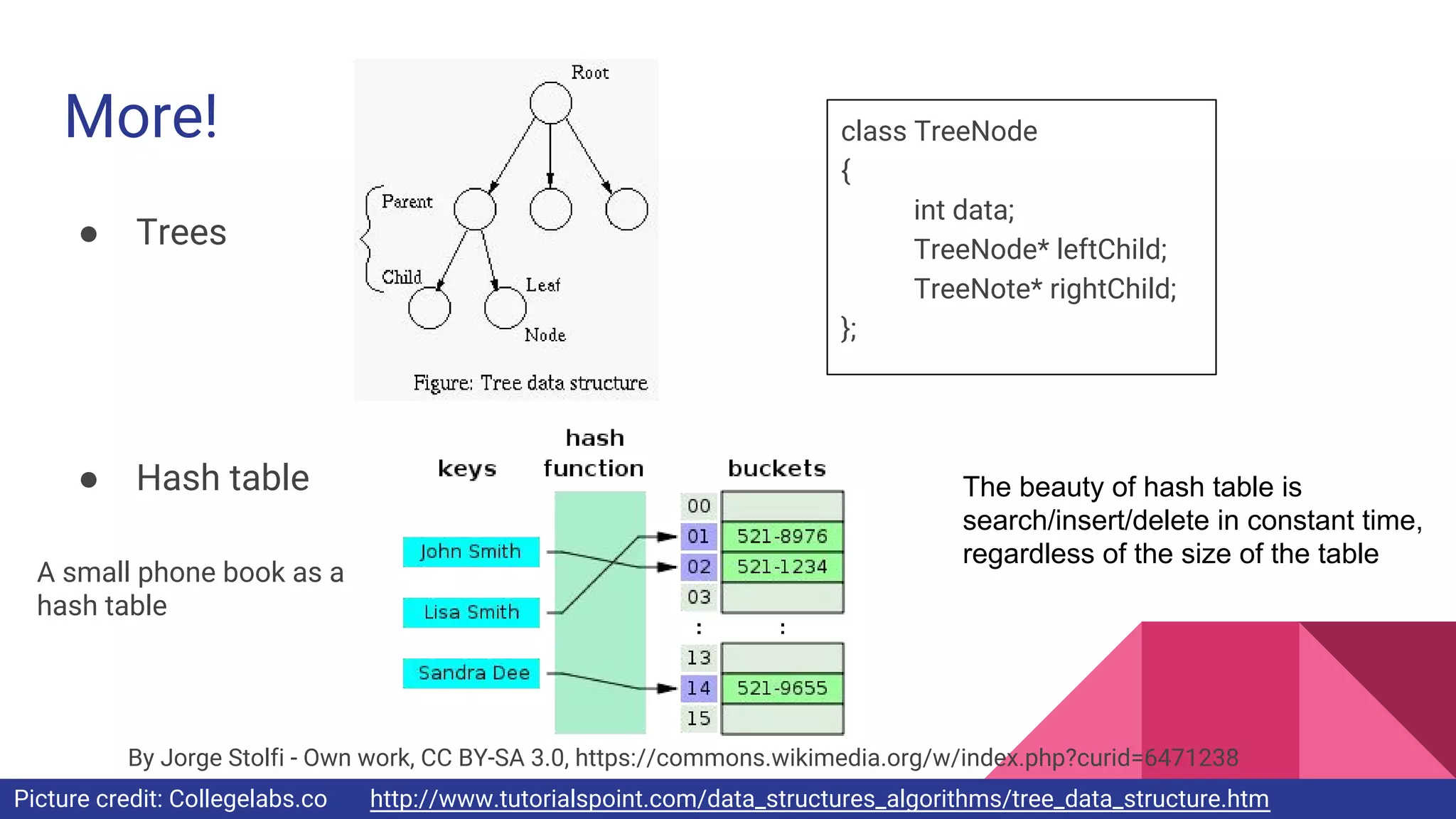
Stanford Splash Spring 2016 Basic Programming lecture introduces Yu-Sheng Chen, the instructor. Chen provides an overview of basic programming concepts like control flows, functions, and data structures. The lecture also solves sample coding problems like calculating trailing zeros in a factorial and validating parentheses to demonstrate these concepts. Complexity analysis is discussed to evaluate algorithm efficiency based on operation counts.