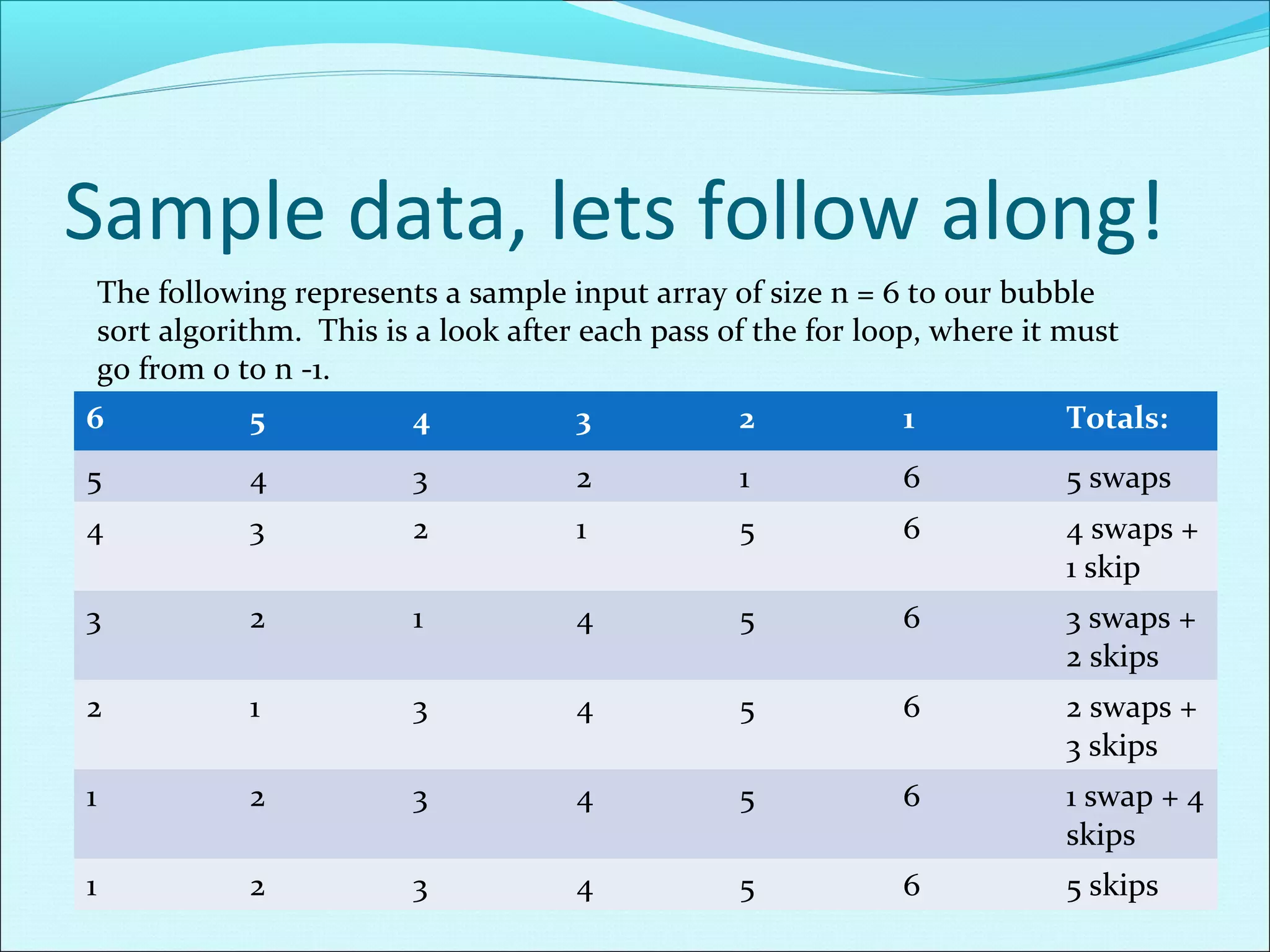
This document discusses time and space complexity analysis of algorithms. It analyzes the time complexity of bubble sort, which is O(n^2) as each pass through the array requires n-1 comparisons and there are n passes needed. Space complexity is typically a secondary concern to time complexity. Time complexity analysis allows comparison of algorithms to determine efficiency and whether an algorithm will complete in a reasonable time for a given input size. NP-complete problems cannot be solved in polynomial time but can be verified in polynomial time.



![Algorithm Analysis Time!
void bubblesort(int []array, int len){
boolean unchanged = false;
while(unchanged == false) {
unchanged = true;
for(int i = 0; i < len -1; i++)
if(a[i] > a[i+1]){
swap (a[i], a[i+1])
unchanged = false;
}
}
}](https://image.slidesharecdn.com/timeandspacecomplexity-140222083539-phpapp02/75/Time-andspacecomplexity-4-2048.jpg)