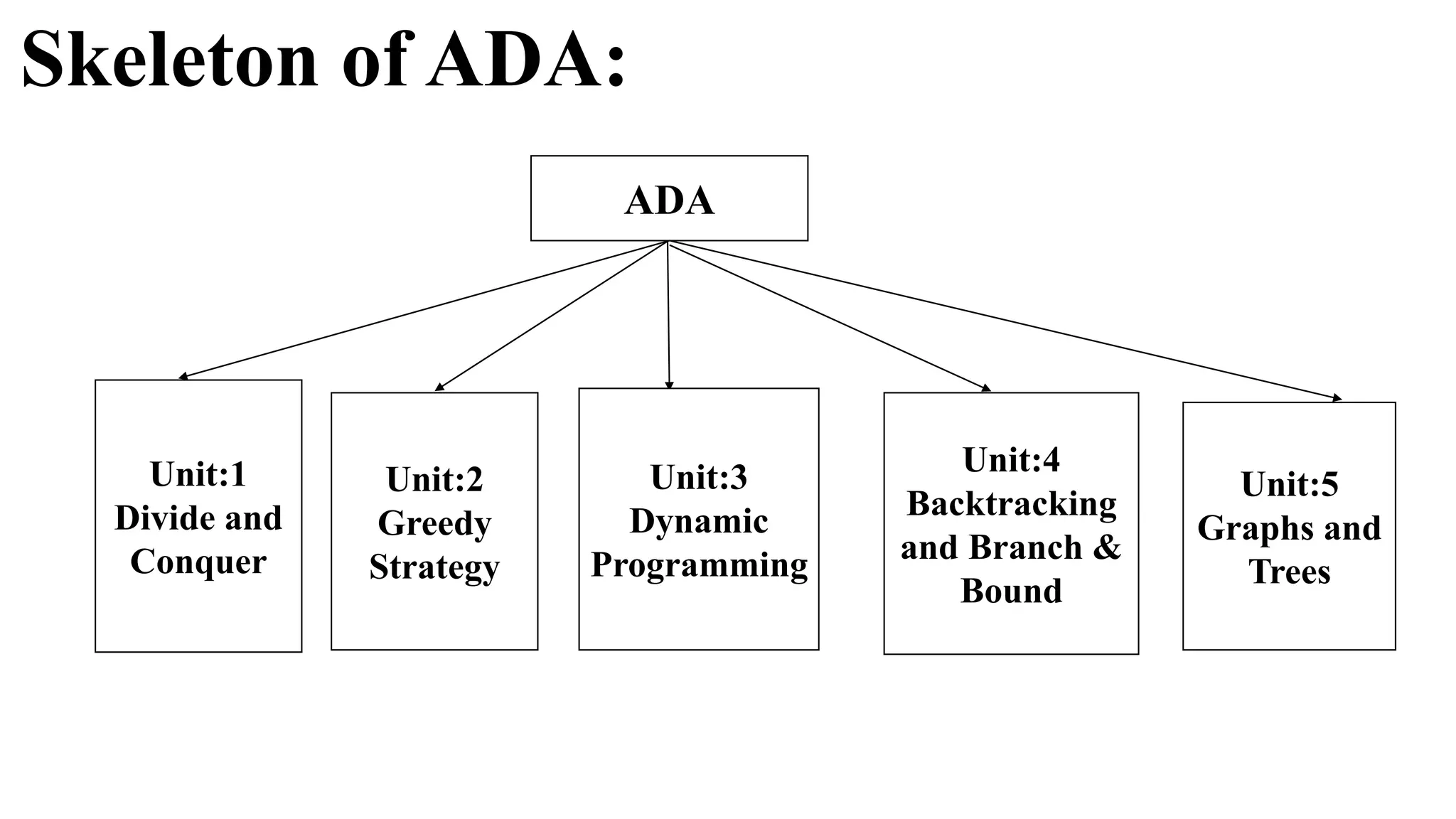
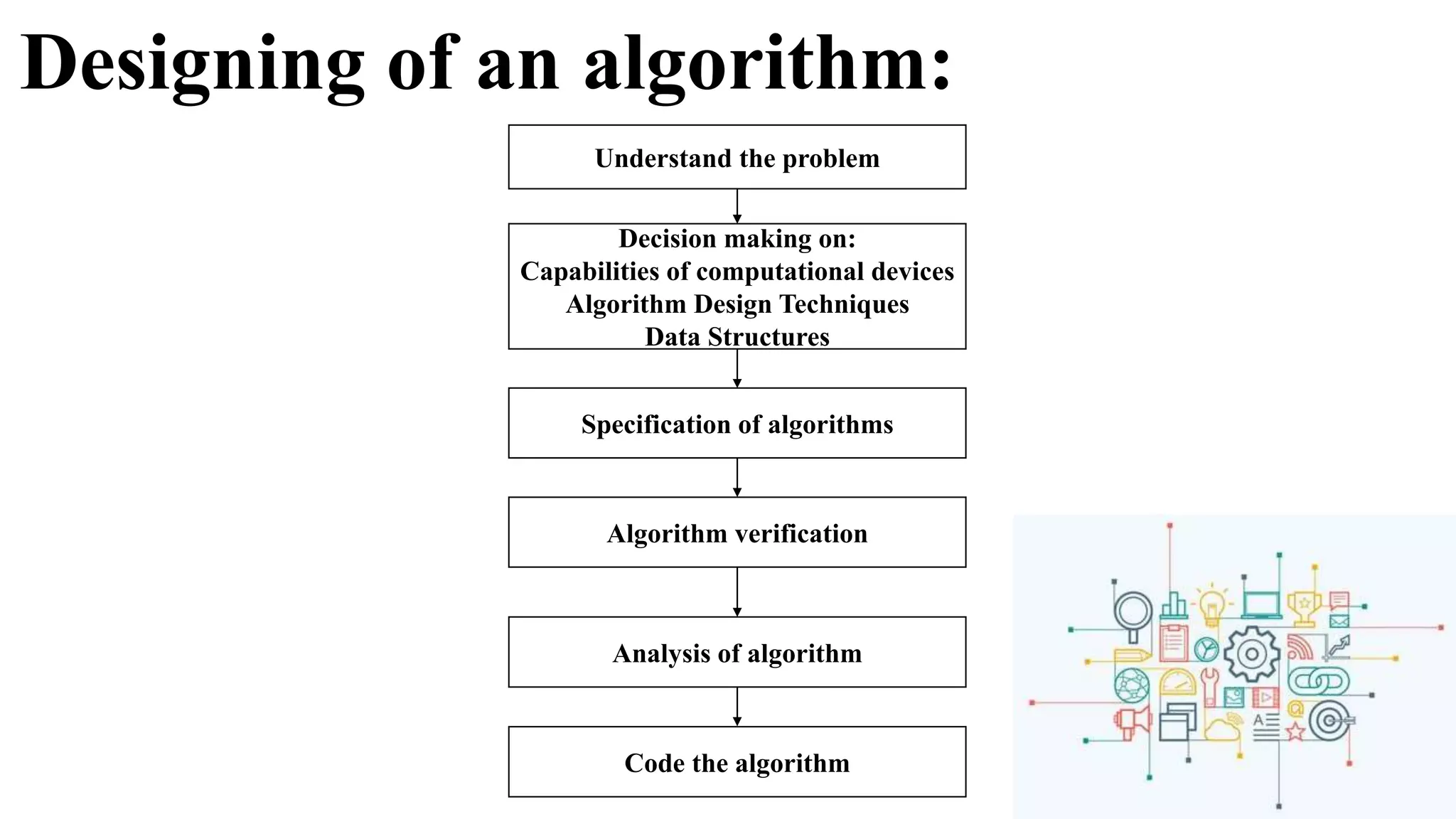
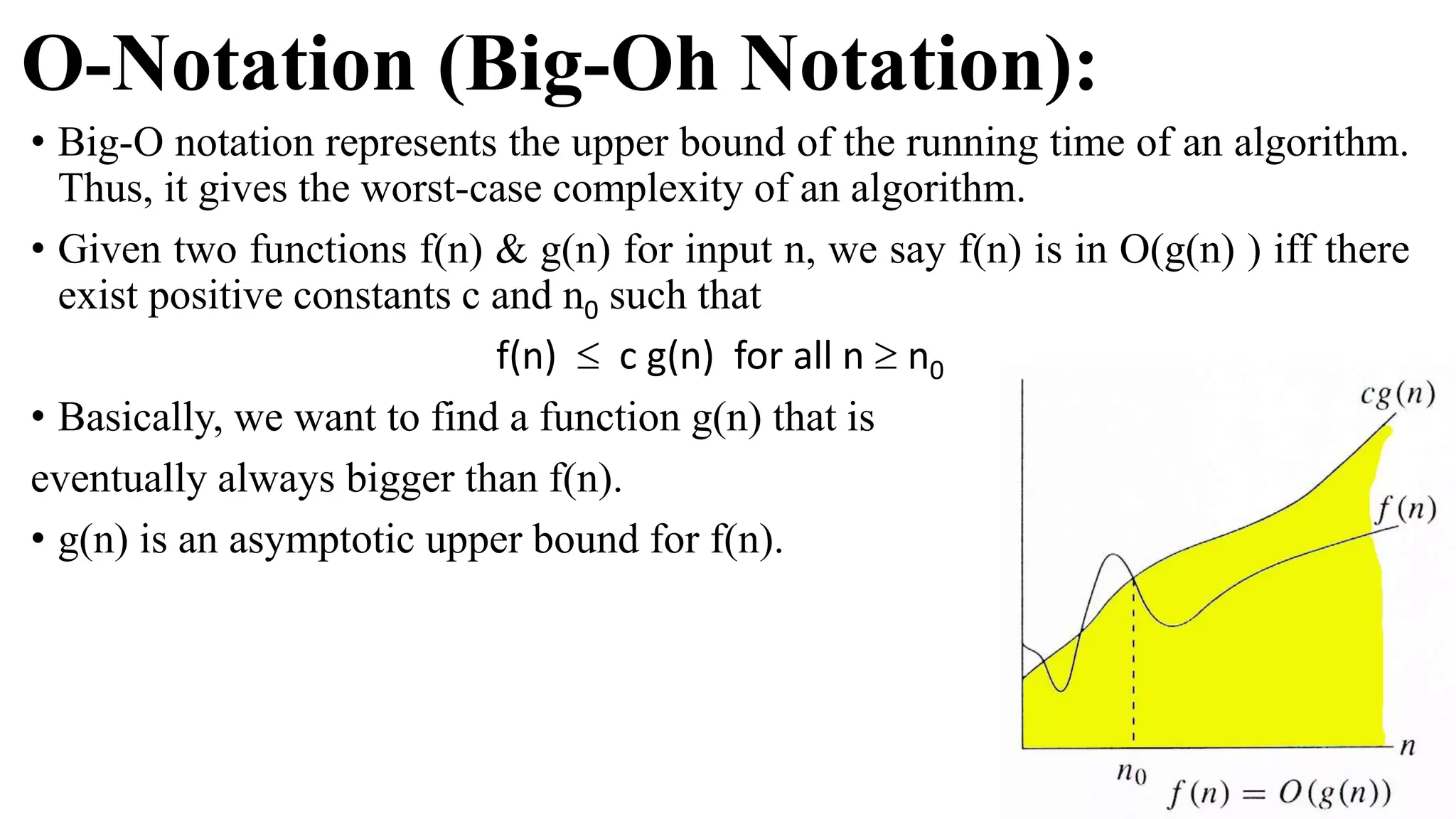
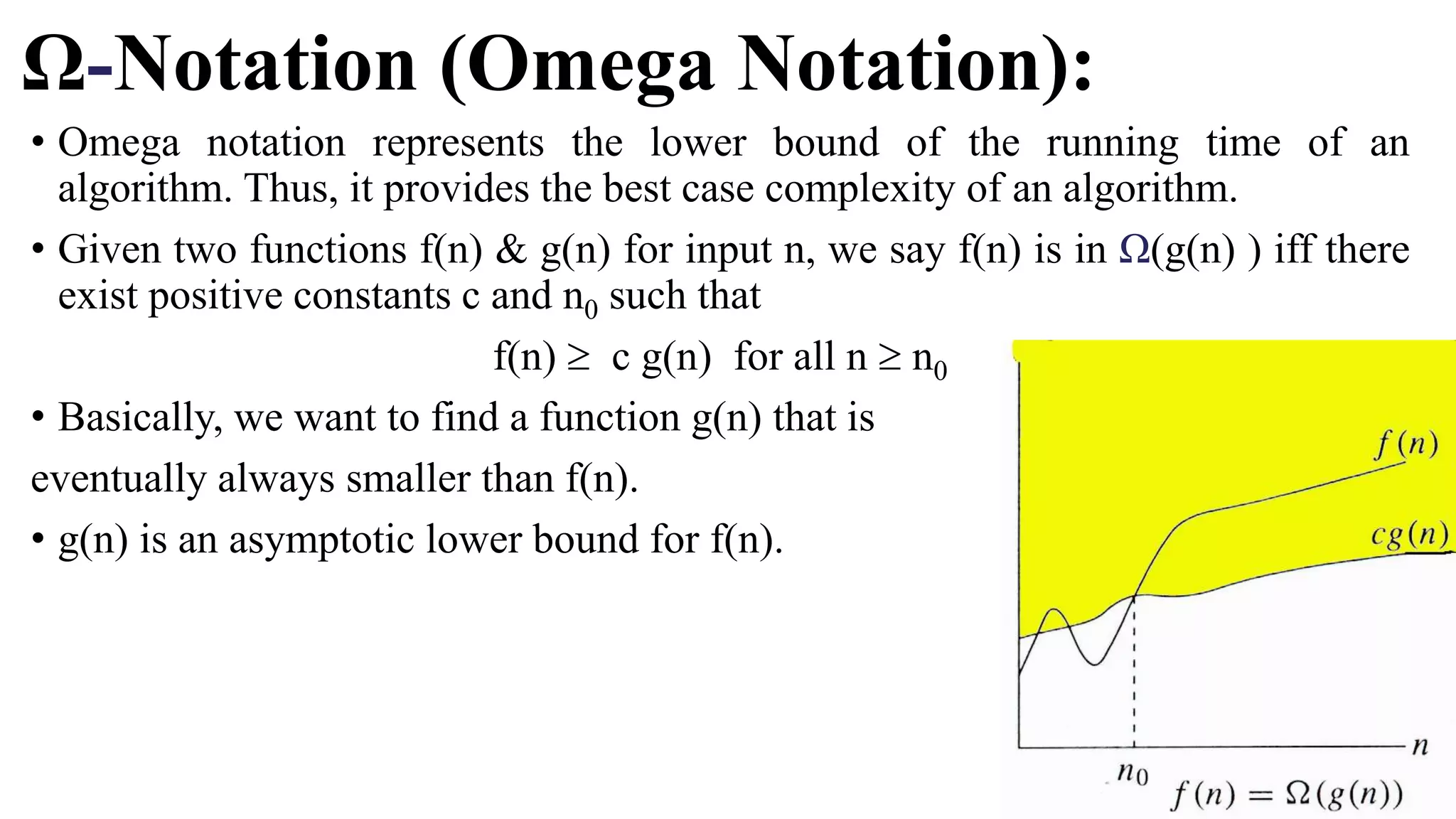
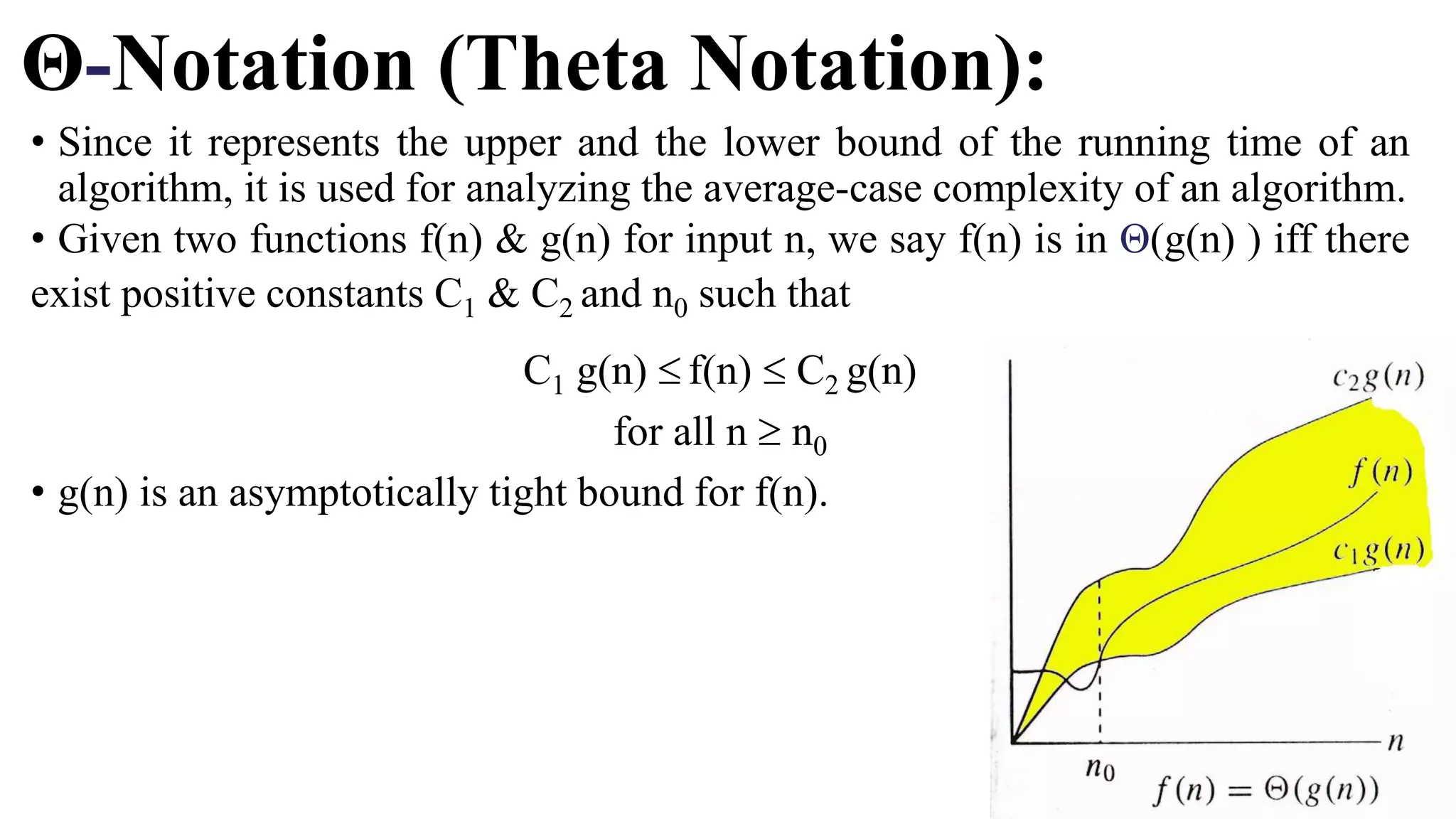
The document is an introduction to the analysis and design of algorithms, detailing key terminologies, objectives, and strategies for efficient algorithm design. It covers topics like asymptotic notations, algorithm efficiency, and various design techniques including divide and conquer, greedy strategies, and dynamic programming. By the end of the course, students should be able to analyze algorithm complexity and implement fundamental algorithms in programming contexts.