This document summarizes a lecture on algorithms and graph traversal techniques. It discusses:
1) Breadth-first search (BFS) and depth-first search (DFS) algorithms for traversing graphs. BFS uses a queue while DFS uses a stack.
2) Applications of BFS and DFS, including finding connected components, minimum spanning trees, and bi-connected components.
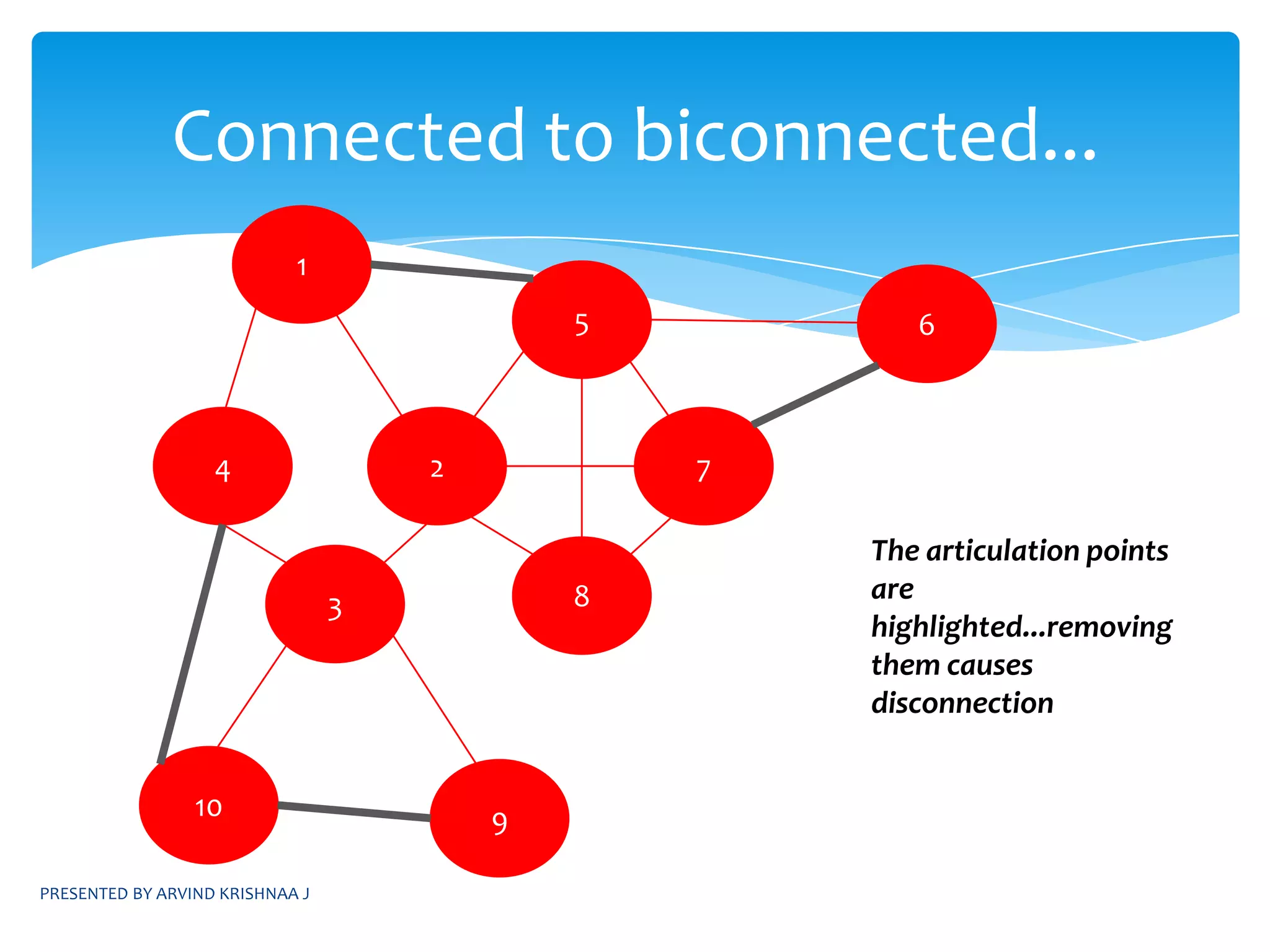
3) Identifying articulation points to determine biconnected components in a graph.
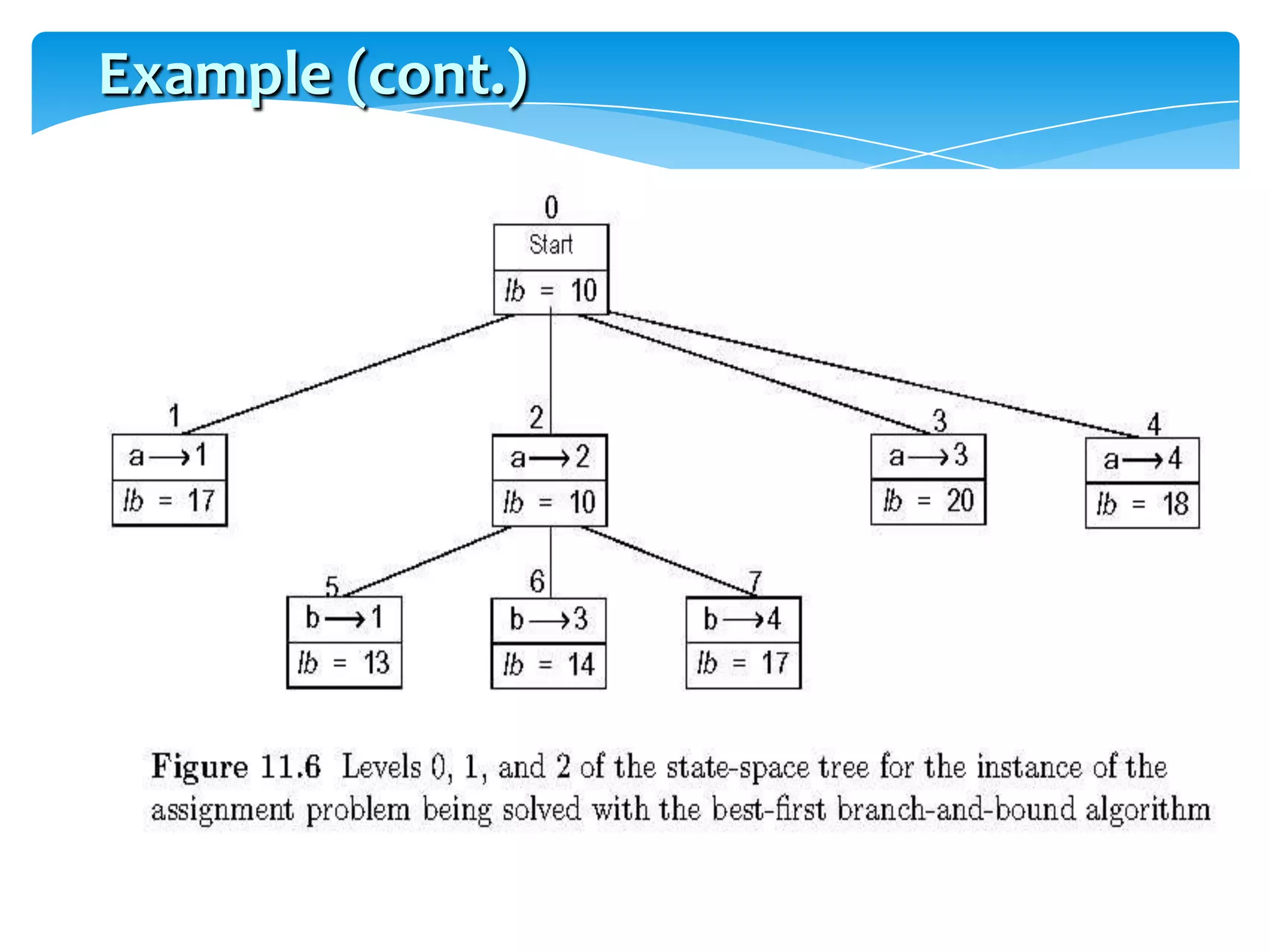
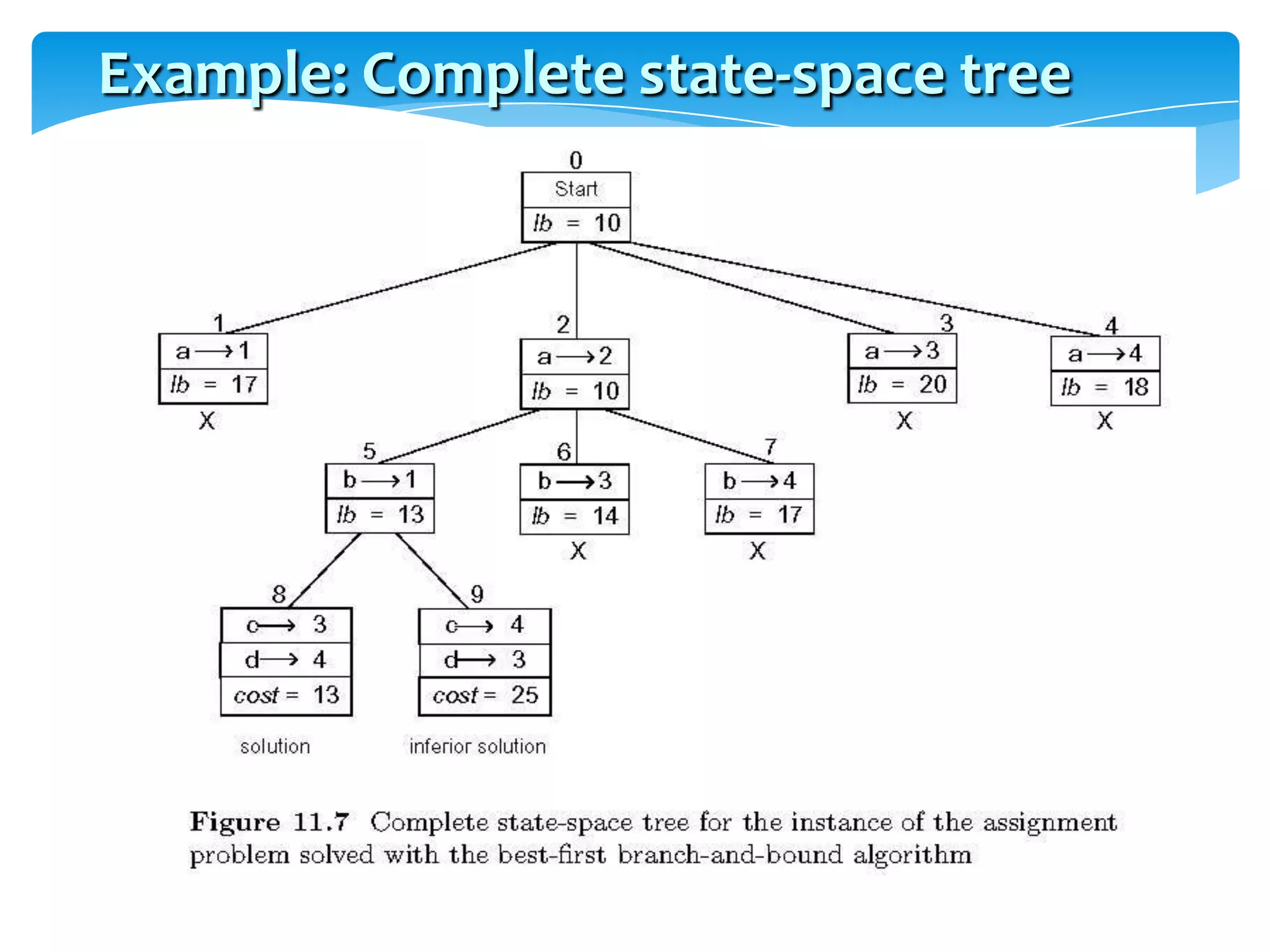
4) The 0/1 knapsack problem and approaches for solving it using greedy algorithms, backtracking, and branch and bound search.










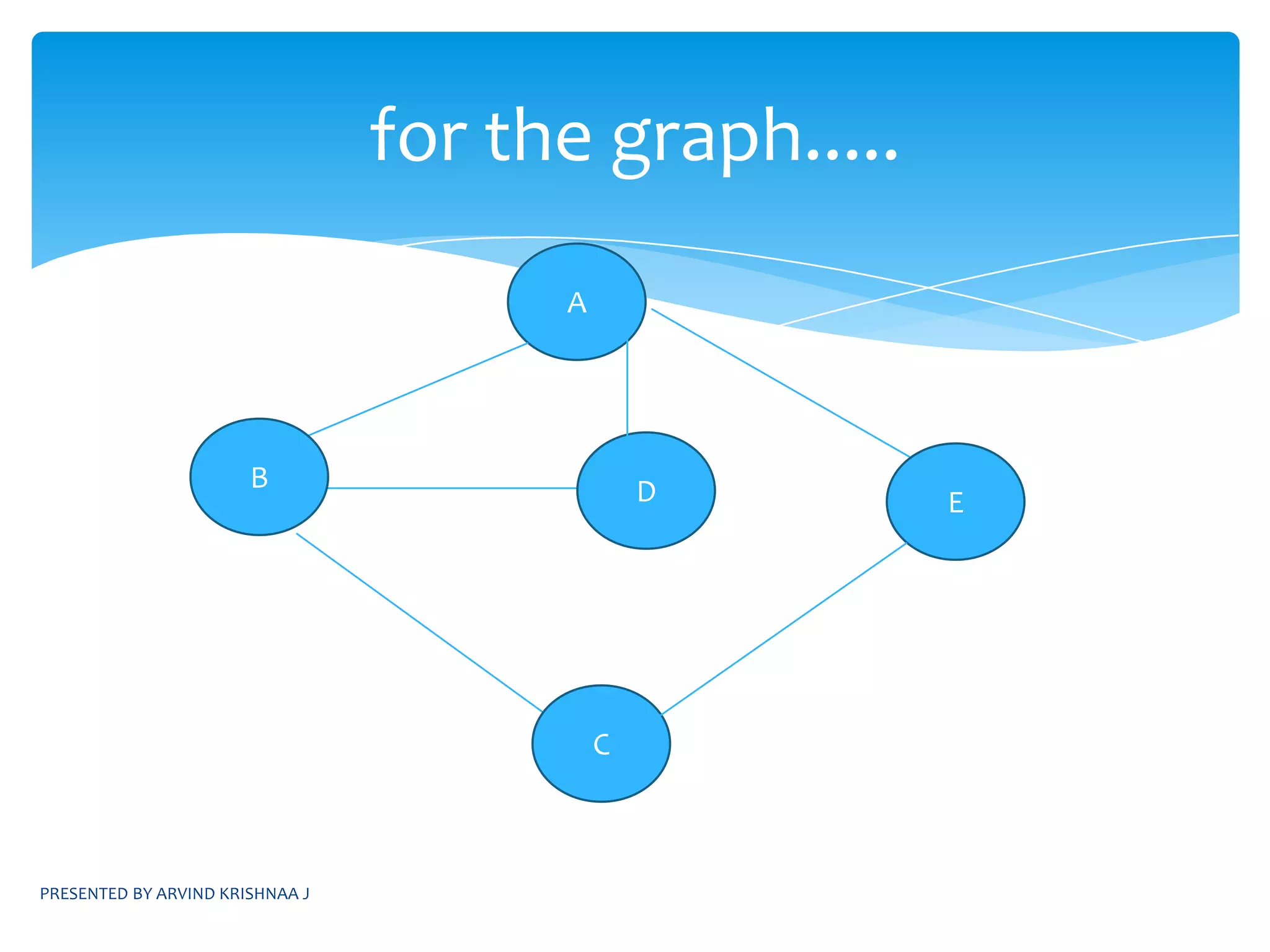
![PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR BFSvoid BFS(int v){//v being a starting vertexint u=v;Queue q[SIZE];visited[v]=1;do{for all vertices w adjacent to to u{ if(visited[w]==0)//w is unvisited {q.AddQ(w);visited[w]=1; }}if(Q.Empty()) return;q.Delete(u);}while(1);}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-12-2048.jpg)

![PRESENTED BY ARVIND KRISHNAA JPERFORMING THE BREADTH FIRST TRAVERSALvoid BFT(graph G,int n){int i;boolean visited[SIZE];for(i=1;i<=n;i++)visited[i]=0;for(i=1;i<=n;i++)if(!visited[i]) BFS[i};}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-14-2048.jpg)
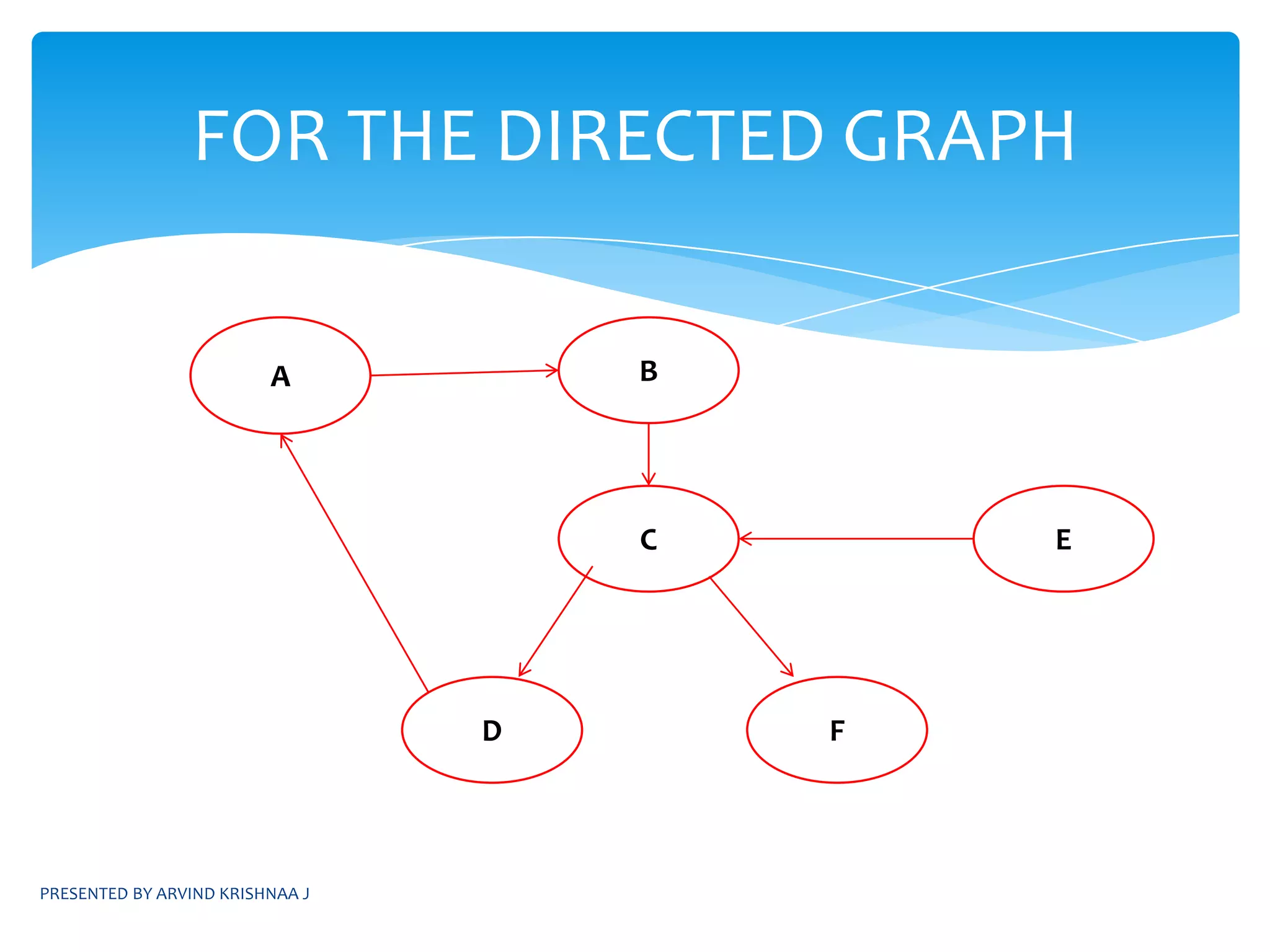
![PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR DFSvoid DFS(int v){visited[v]=1;for each vertex w adjacent to v { if(!visited[w]) DFS[w];}}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-16-2048.jpg)
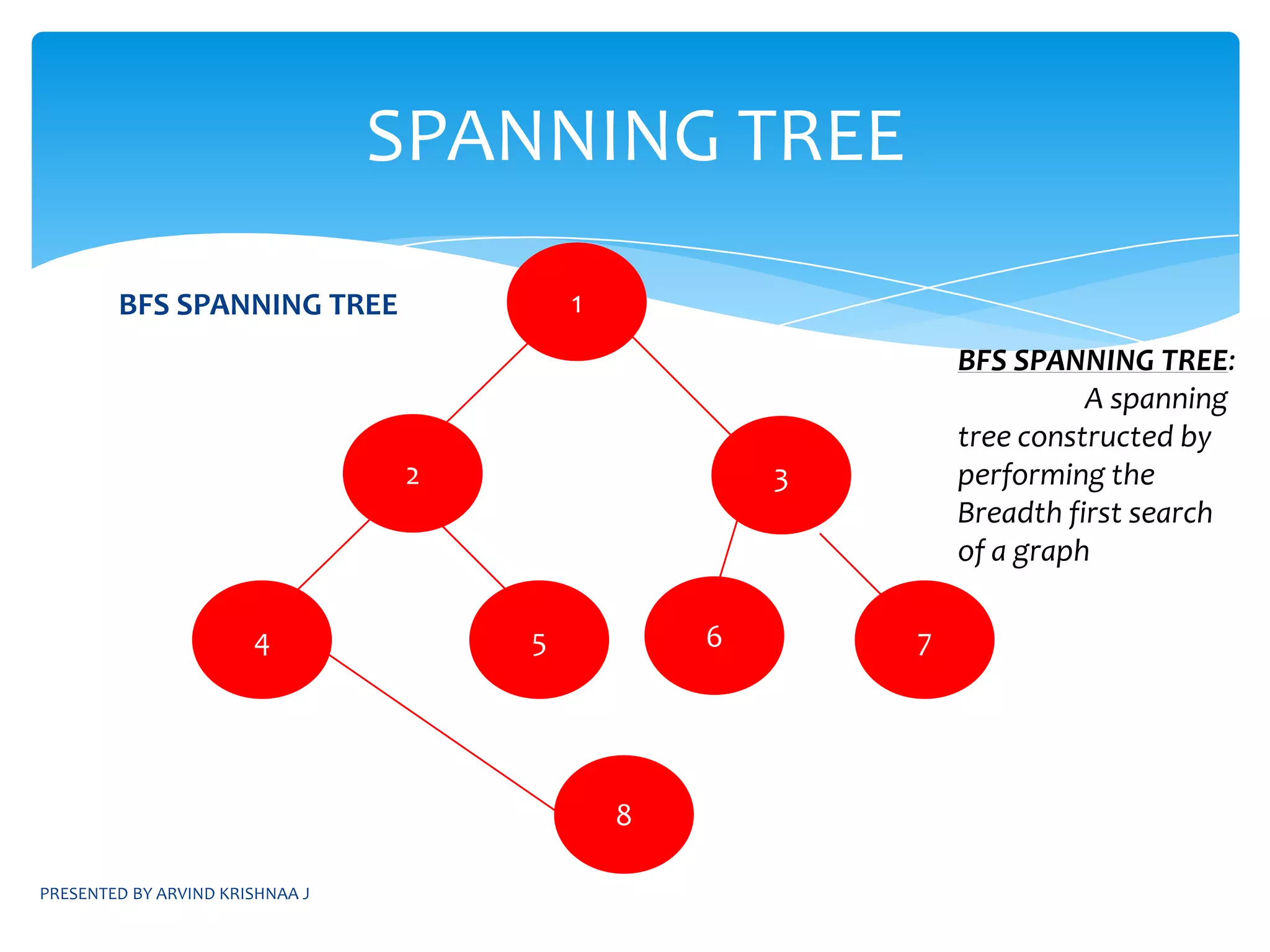
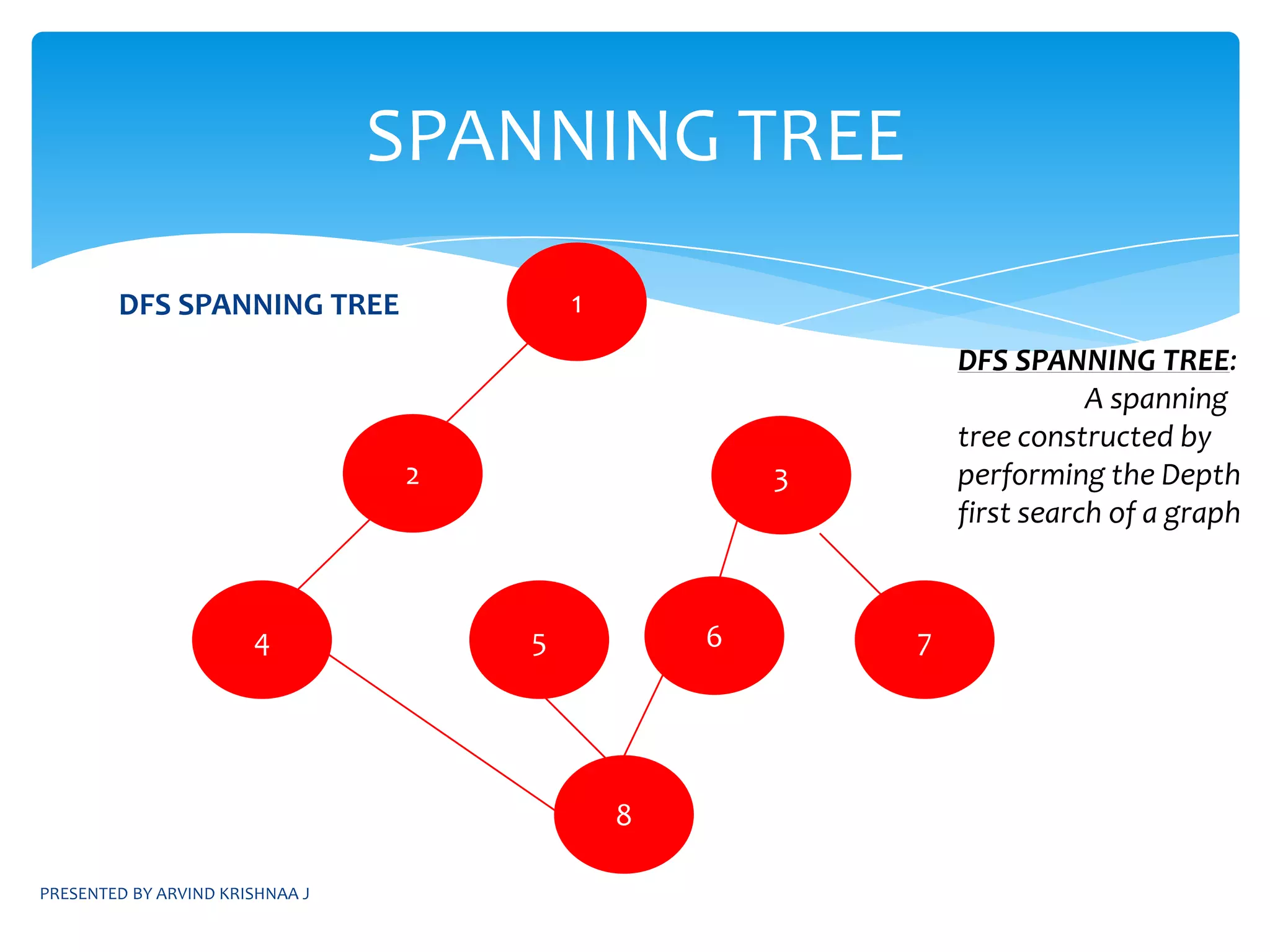

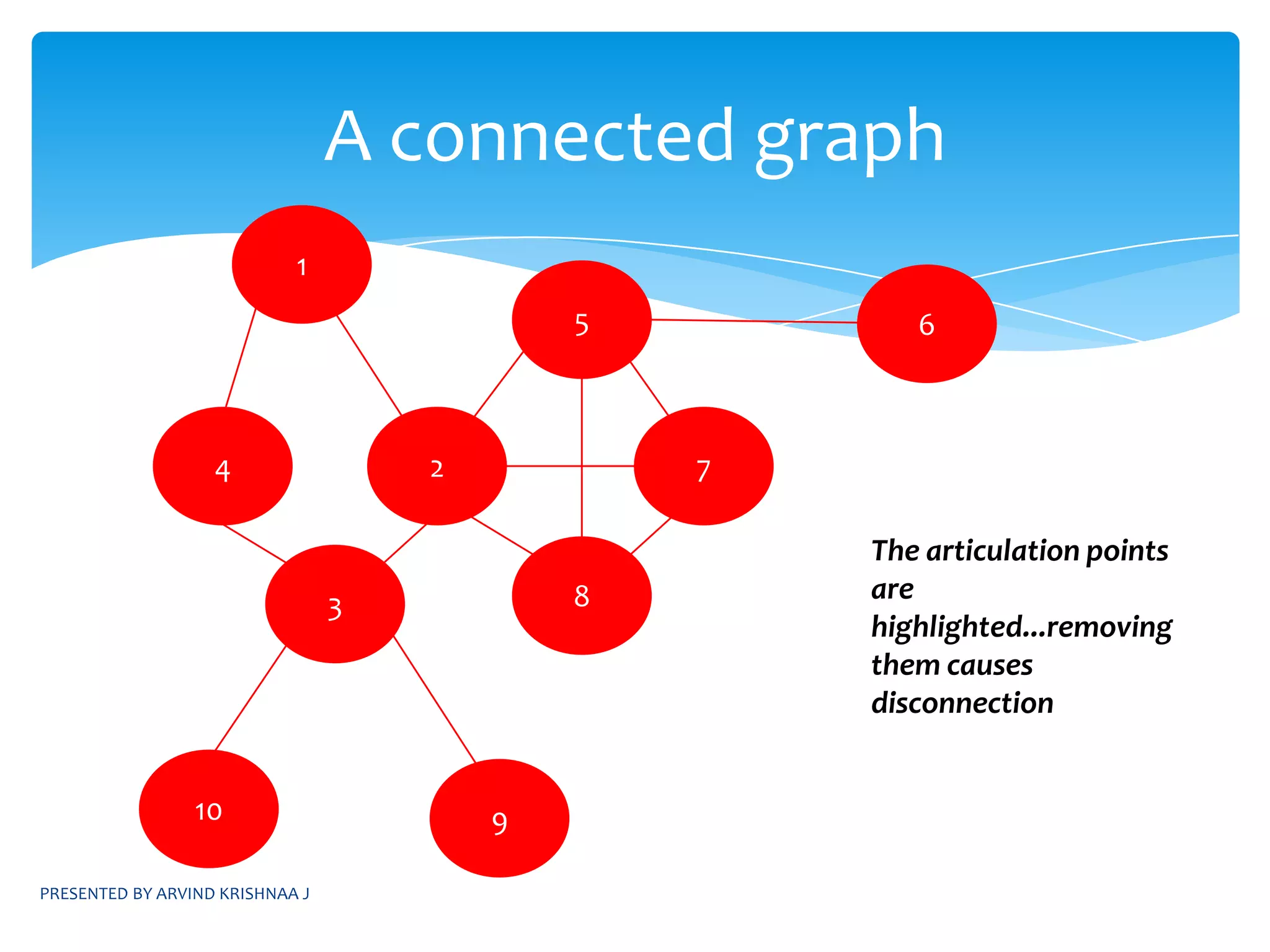





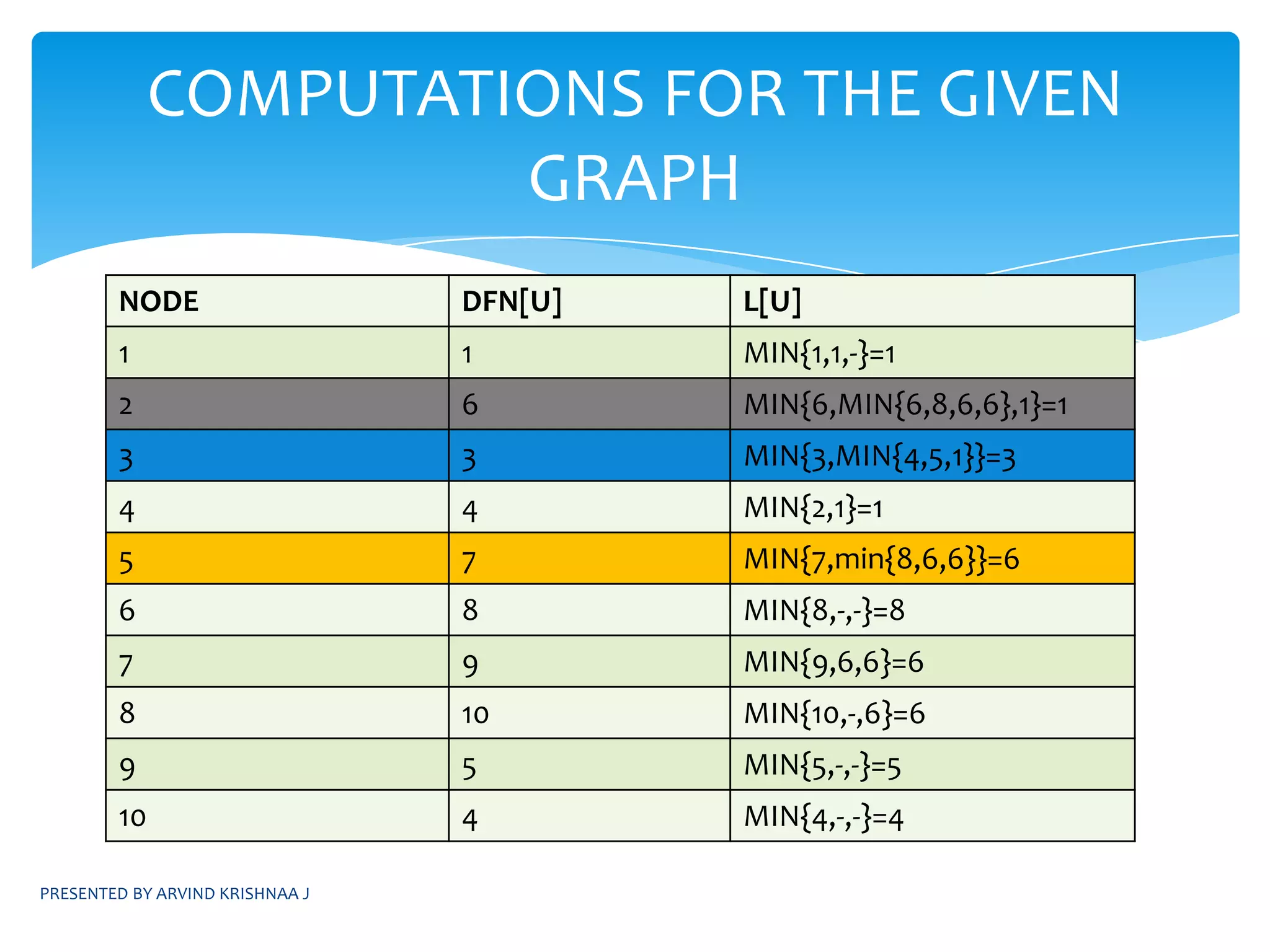



![SIMPLE ALGORITHM:Construct a DFS spanning tree for the given graphHave parameters dfn[u],L[u]Do a preorder traversal of the spanning tree and compute dfn[u] for each node as the ith node that is visitedCompute the value of L[u] asPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTSL[u]=min{ dfn[u],min{L[w]|w is a child of u}, min{ dfn[w] | (u,w) is a back edge}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-31-2048.jpg)
![SIMPLE ALGORITHM:Nodes which satisfy L[w]≥dfn[u], w being the children of u are identified as articulation pointsSPECIAL CASE OF ROOT NODENote: The root node is always listed as an articulation pointif root node has exactly one childthen exclude the root node from AP listelseroot node is also an articulation pointPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTS contd...](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-32-2048.jpg)
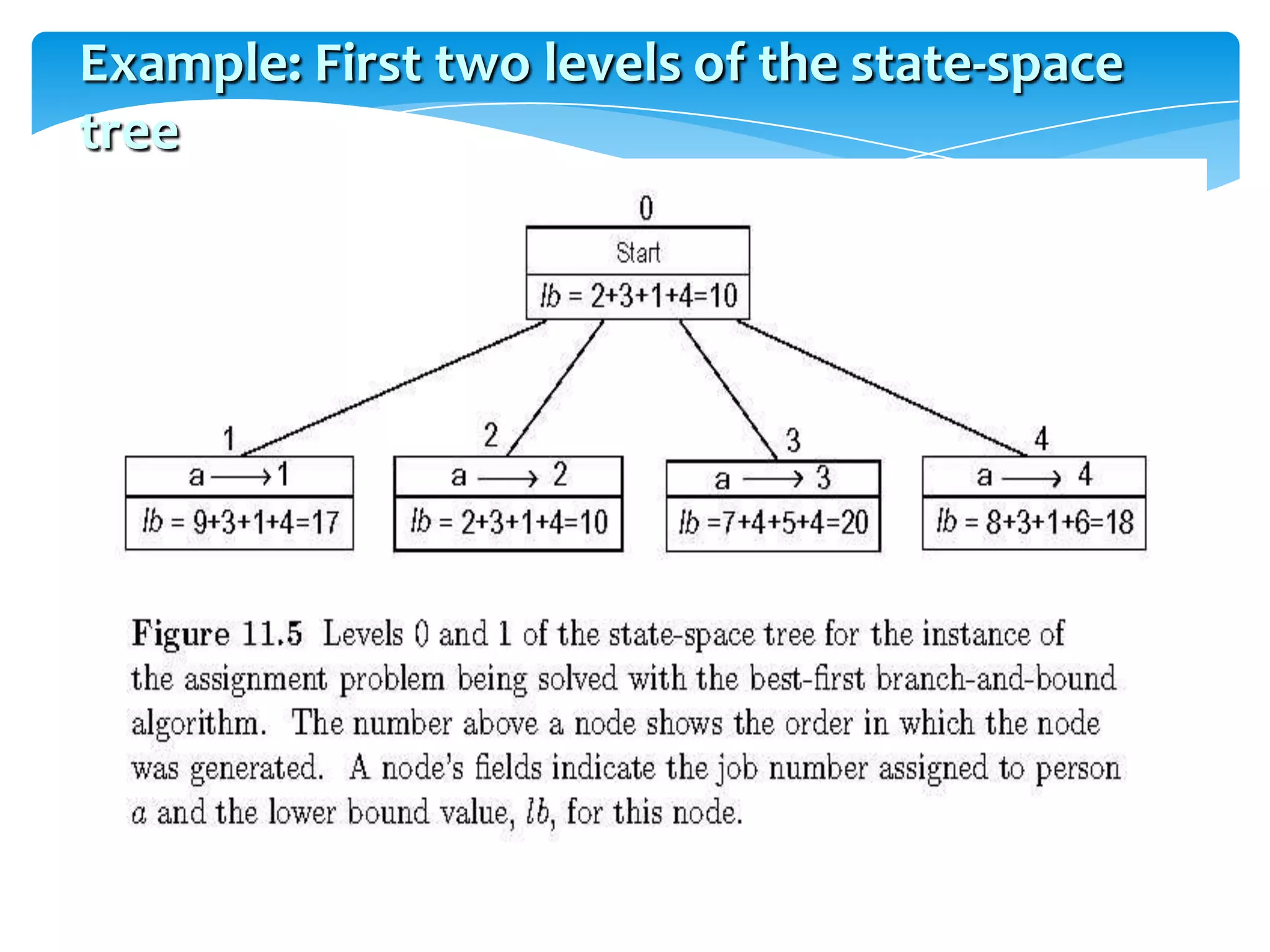








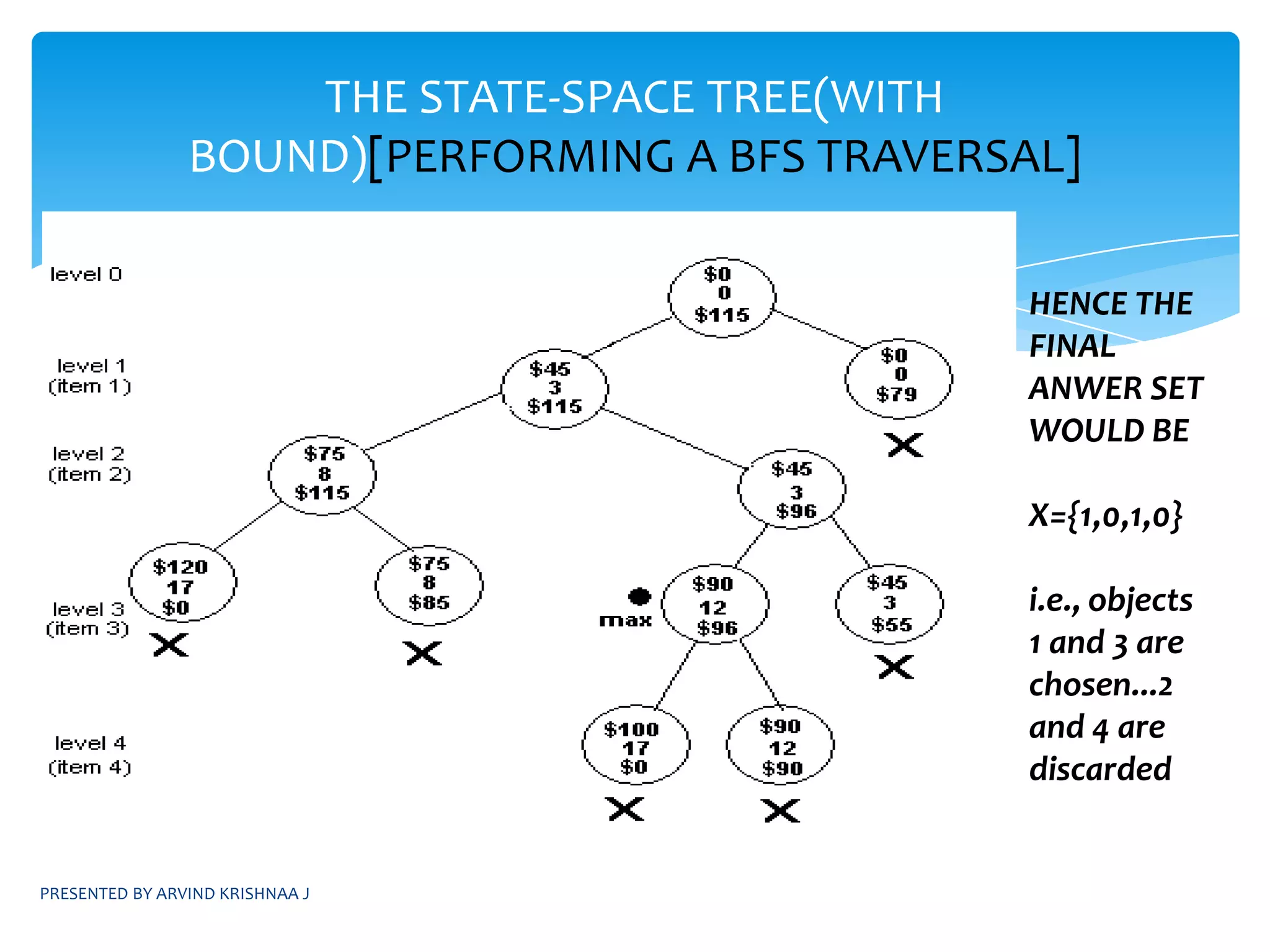










![PRESENTED BY ARVIND KRISHNAA JTHE STATE-SPACE TREE(WITH BOUND)[PERFORMING A BFS TRAVERSAL]HENCE THE FINAL ANWER SET WOULD BEX={1,0,1,0}i.e., objects 1 and 3 are chosen...2 and 4 are discarded](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/75/Design-and-Analysis-of-Algorithms-56-2048.jpg)








