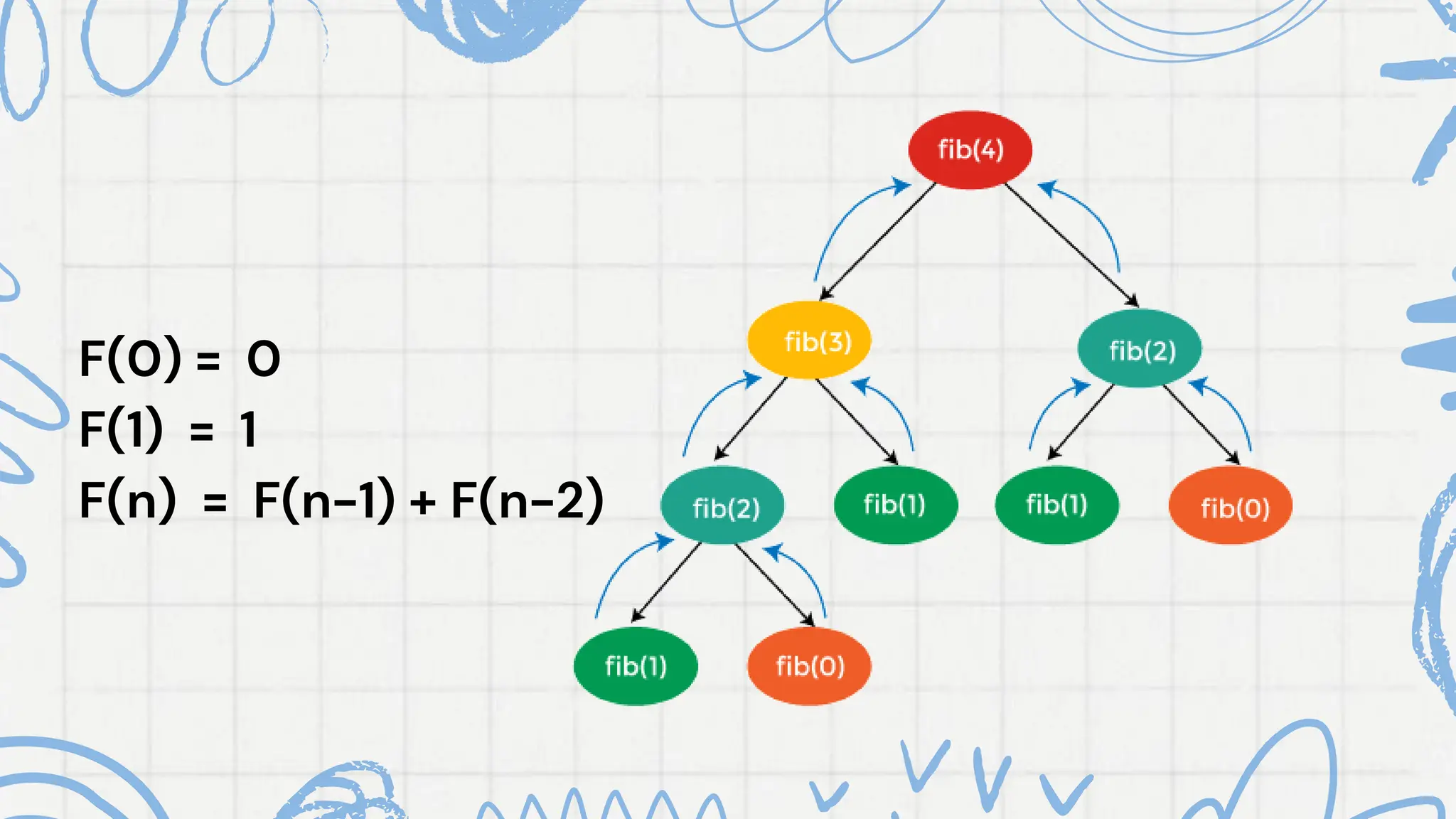
Dynamic Programming Algorithm CSI-504.pdf

Dynamic Programming Algorithm CSI-504.pdf

• 1.
  Dynamic Programming Algorithm Presented by602, 629, 630, 646
• 2.
  What is Dynamic Programming(DP) Algorithm Dynamic Programming (DP) is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems.
• 3.
  How does DP works •Identify Subproblems: Divide the main problem into smaller, independent subproblems. • Store Solutions: Solve each subproblem and store the solution in a table or array. • Build Up Solutions: Use the stored solutions to build up the solution to the main problem. • Avoid Redundancy: By storing solutions, DP ensures that each subproblem is solved only once, reducing computation time.
• 4.
  Example of DynamicProgramming (DP) Example 1: Consider the problem of finding the Fibonacci sequence: Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Brute Force Approach: To find the nth Fibonacci number using a brute force approach, you would simply add the (n-1)th and (n-2)th Fibonacci numbers. This would work, but it would be inefficient for large values of n, as it would require calculating all the previous Fibonacci numbers.
• 5.
  F(0) = 0 F(1)= 1 F(n) = F(n-1) + F(n-2)
• 6.
  Fibonacci Series usingDynamic Programming Subproblems: F(0), F(1), F(2), F(3), … Store Solutions: Create a table to store the values of F(n) as they are calculated. Build Up Solutions: For F(n), look up F(n-1) and F(n-2) in the table and add them. Avoid Redundancy: The table ensures that each subproblem (e.g., F(2)) is solved only once. By using DP, we can efficiently calculate the Fibonacci sequence without having to recompute subproblems.
• 7.
  Approaches of Dynamic Programming (DP) Dynamicprogramming can be achieved using two approaches: 01. Top-Down Approach 02. Bottom-Down Approach
• 8.
  Top-Down Approach In thetop-down approach, also known as memoization, we start with the final solution and recursively break it down into smaller subproblems. To avoid redundant calculations, we store the results of solved subproblems in a memoization table. Let’s breakdown Top down approach: • Starts with the final solution and recursively breaks it down into smaller subproblems. • Stores the solutions to subproblems in a table to avoid redundant calculations. • Suitable when the number of subproblems is large and many of them are reused.
• 9.
  Bottom-Down Approach In thebottom-up approach, also known as tabulation, we start with the smallest subproblems and gradually build up to the final solution. We store the results of solved subproblems in a table to avoid redundant calculations. Let’s breakdown Bottom-up approach: • Starts with the smallest subproblems and gradually builds up to the final solution. • Fills a table with solutions to subproblems in a bottom-up manner. • Suitable when the number of subproblems is small and the optimal solution can be directly computed from the solutions to smaller subproblems.
• 10.
  Applications: Dynamic programming hasa wide range of applications, including: • Optimization: Knapsack problem, shortest path problem, maximum subarray problem • Computer Science: Longest common subsequence, edit distance, string matching • Operations Research: Inventory management, scheduling, resource allocation
• 11.
  Thank you very much!