julia-Latest Programming language

OVERVIEW













INTRODUCTION
FEATURES
DATA TYPES
MATHEMATICAL OPERATORS
COMPLEX AND RATIONAL NUMBERS’
STRINGS
FUNCTIONS
CONTROL FLOW
JULIA STANDARD Library
SIMPLE PLOTING
ADVANTAGES
CONCLUSION

INTRODUCTION


Julia is a high-level, highperformance dynamic programming
language for technical computing,
with syntax that is familiar to users
of other technical computing
environments. It provides a
sophisticated compiler, distributed
parallel execution, numerical
accuracy, and an extensive
mathematical function library.

Appeared in 2012
Designed by Jeff Bezanson, Stefan Karpinski, Viral B.
Shah, Alan Edelman (MIT Group Leader)
OS

Linux, FreeBSD, Windows

Stable
release
Typing
discipline
Influenced
by

0.1.2 (March 7, 2013))

License
Usual
filename
extensions

MIT License
.jl

Dynamic with optional type annotations
and type inference
MATLAB, Scheme, Lisp, C Python Perl
Ruby

FEATURES





High-Performance JIT Compiler
Designed for Parallelism & Cloud
Computing
Free, Open Source & Library-Friendly

DATATYPES
Integers and Floating-Point
Numbers
Integer Types
Int8— signed 8-bit integers ranging
from -2^7 to 2^7 - 1.
Uint8 — unsigned 8-bit integers
ranging from 0 to 2^8 - 1.
Int16 — signed 16-bit integers ranging
from -2^15 to 2^15 - 1.
ranging from 0 to 2^16 - 1

from -2^31 to 2^31 - 1.
from -2^63 to 2^63 - 1.

Int128 - signed 128-bit integers ranging
from -2^127 to 2^127 - 1.
Uint128 - unsigned 128-bit integers

Bool- either true or false, which
correspond numerically to 1 and 0.
Char- a 32-bit numeric type
representing a Unicode character.
Floating-point types:
Float32- IEEE 754 32-bit floating-point
numbers.
 Float64-IEEE 754 64-bit floating-point
numbers.


Arbitrary Precision
Arithmetic




allow computations with
arbitrary precision integers and
floating point numbers
The BigInt and BigFloat types
are available in Julia for
arbitrary precision integer and
floating point numbers
respectively.

Numeric Literal Coefficients






make common numeric formulas and
expressions clearer
writing polynomial expressions much
cleaner.
makes writing exponential functions
more elegant.

Syntax Conflicts




The hexadecimal integer literal
expression 0xff could be
interpreted as the numeric literal
0 multiplied by the variable xff.
The floating-point literal
expression 1e10 could be
interpreted as the numeric literal
1 multiplied by the variable e10,
and similarly with the equivalent
E form.

MATHEMATICAL
OPERATORS



Arithmetic Operators
Bitwise Operators
 Arithmetic

operators

• +x-unary plus is the identity operation.
• x-unary minus maps values to their
additive inverses.
• x + y-binary plus performs addition.
• x – y-binary minus performs subtraction.
• x * y- times performs multiplication.
• x / y-divide performs division.

Bitwise Operators
• ~x
•x&y
•x|y
• x $ y• x >> y
• x >> y• x << y

bitwise not.
bitwise and.
bitwise or.
bitwise xor.
logical shift right.
arithmetic shift right.
logical/arithmetic shift
left.

NUMERIC COMPARISON
 Comparison

Operators

• ==equality.
• != inequality.
• <less than.
• <=less than or equal to.
• >greater than.
• >=greater than or equal to.

MATHEMATICALFUNCTIONS
o

o

Julia provides a comprehensive
collection of mathematical
functions and operators
All the standard trignometric
functions are inluded

Some examples
• sqrt(x)— the square root of x.
• cbrt(x)— the cube root of x.
• pow(x,y)—x raised to the
exponent y.
• exp(x)— the natural exponential
function at x.
• log(x)— the natural logarithm of
x.

Complex Numbers


We can perform all the standard
arithmetic operations with complex
numbers:
julia> (1 + 2im)*(2 - 3im)
8 + 1im



Standard functions to manipulate
complex values are provided:
julia> real(1 + 2im)
1
Julia> imag(1 + 2im)
2

julia> conj(1 + 2im)
1 - 2im

Rational Numbers




Julia has a rational number type to
represent exact ratios of integers.
Rationals are constructed using
the // operator:
If the numerator and denominator of
a rational have common factors,
they are reduced to lowest terms
such that the denominator is nonnegative:
Julia> 6//9
2//3
julia> 5//-15
-1//3

STRINGS

•

Strings are finite sequences of
characters. Julia supports the full
range of unicode characters:
Characters
A Char value represents a single
character: it is just a 32-bit integer
with a special literal representation
and appropriate arithmetic
behaviors, whose numeric value is
interpreted as a Unicode code point

Interpolation





To reduce the need for these
verbose calls to strcat, Julia
allows interpolation into string
literals using $, as in Perl:
julia> "$greet, $whom.n"
"Hello, world.n"

STRING FUNCTIONS
 strchr

function:
Julia> strchr("xylophone", ’x’)
1
 repeat:
julia> repeat(".:Z:.", 10)
".:Z:..:Z:..:Z:..:Z:..:Z:..:Z:..:Z:..:Z:..
:Z:..:Z:.“
 •endof(str) gives the maximal
(byte) index that can be used to
index into str.

• i = start(str) gives the first valid index at
which a character can be found in str
(typically 1).
• c, j = next(str,i) returns next character at or
after the index i and the next valid character
index
following that. With start and endof, can be
used to iterate through the characters in str.
• ind2chr(str,i) gives the number of
characters in str up to and including any at
index i
• chr2ind(str,j) gives the index at which the
jth character in str occurs.

FUNCTIONS




In Julia, a function is an object
that maps a tuple of argument
values to a return value
syntax for defining functions in
Julia is:
function f(x,y)
x+y
end

CONTROL FLOW
• Compound Expressions: begin
and (;).
• Conditional Evaluation: if-elseifelse and ?: (ternary operator).
• Short-Circuit Evaluation: &&, ||
and chained comparisons.
• Repeated Evaluation: Loops:
while and for.

Julia Standard Library
There are 65 pacages in Julia
some of them are:
1. ArgPars-Package for parsing
command-line arguments to
Julia programs.
2. Calculus-Calculus functions
in Julia
3.Calendar-Calendar time
package for Julia
4. Color-Basic color
manipulation utilities

5.Graph-Working with graphs in
Julia
6. HTTP-HTTP library (server,
client, parser) for the Julia
language
7. Languages-A package for
working with human language
8.Sound-Reading and writing from
WAV files (should probably be
named WAV)
9. Winston-2D plotting for Julia

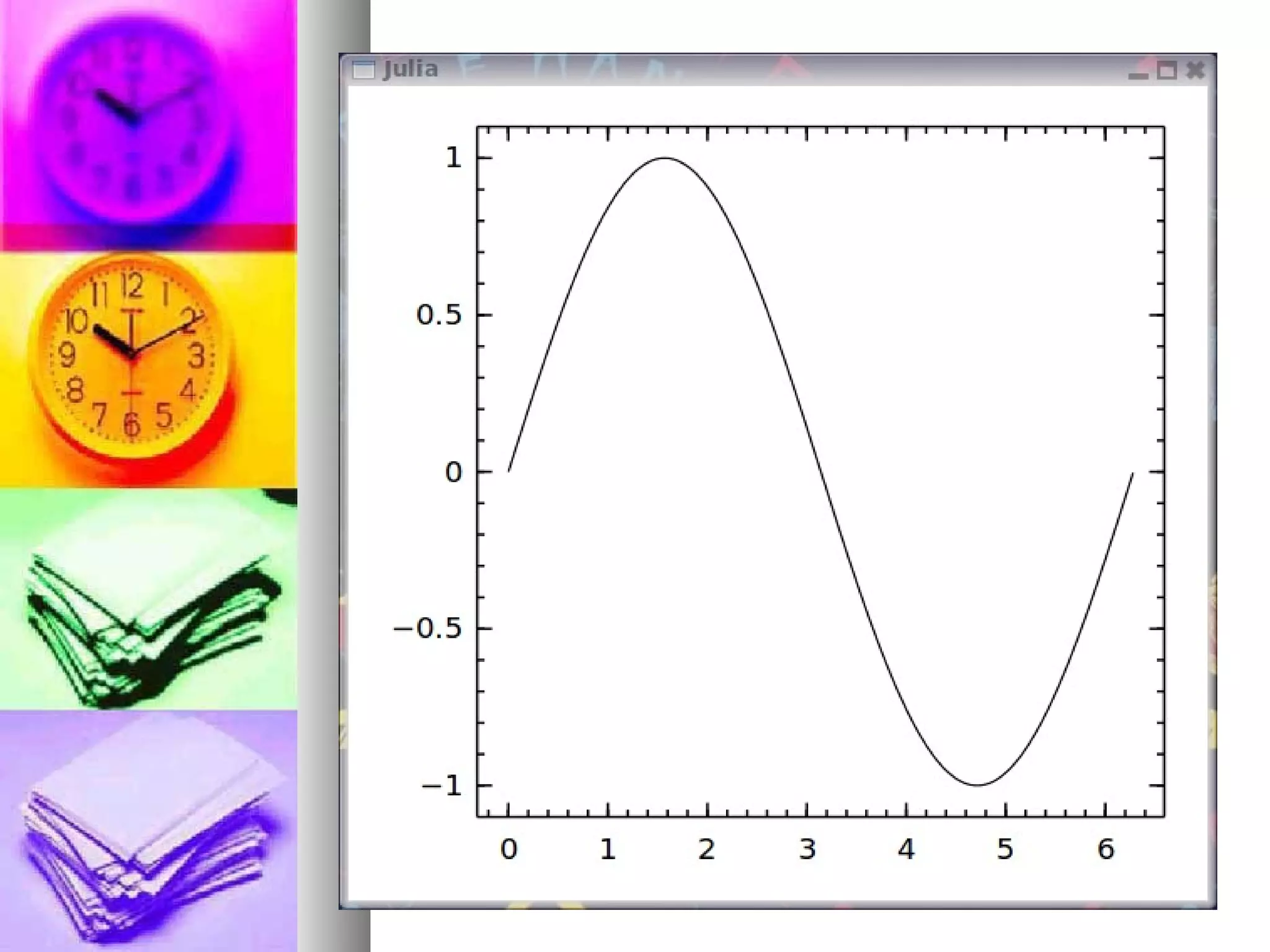
Simple Ploting
To plot sin(x) between 0 and 2π,
you can go like this
julia> xVector=[0:0.01:2*pi];
julia> yVector=0.0*xVector;
julia> for n=1:length(xVector):
yVector[n] = sin(xVector[n]);
end
julia> plot(xVector, yVector)

Advantages of JULIA

• Free and open source (MIT
licensed)
• User-defined types are as fast
and compact as built-ins
• Designed for parallelism and
distributed computation
• Elegant and extensible
conversions and promotions for
numeric and other types
• Call C functions directly

CONCLUSION
Julia is a is a flexible dynamic
language, appropriate for scientific and
numerical computing
Julia features optional typing, multiple
dispatch, and good performance,
achieved using type inference and justintime (JIT) compilation.
Julia combines the features of many
other Programing languages like
C,Matlab,java etc.
Which is useful for scientific
computing.It is a User friendly and easly
Understandable Programming Language

REFERENCES
"The Julia Language" (official website).
O'Reilly Strata. Retrieved 7 February
2013.
 Krill, Paul. "New Julia language seeks to
be the C for scientists " InfoWorld.
Retrieved 7 February 2013.
 "Julia: A Fast Dynamic Language for
Technical Computing" (PDF). 2012.
 "Why We Created Julia"(World Wide Web
log). Feb 2012. Retrieved 7 February
2013.
 "The Julia Studio" (official website).
 Julia Language Documentation Release
development


julia-Latest Programming language

julia-Latest Programming language

More Related Content

What's hot

Similar to julia-Latest Programming language

Recently uploaded

julia-Latest Programming language