Downloaded 540 times
![Kruskal AlgorithmKRUSKAL(V,E,W)A ← ΦFor each vertex vЄG[v]Do MAKESET[v]sort E into nondecreasing order of weight wDo if FINDSET [u]≠FINDSET[v]A ← A U {(U,V)}UNION(U,V)Return (A)](https://image.slidesharecdn.com/kruskalalgorithm-100607232435-phpapp01/75/Kruskal-Algorithm-1-2048.jpg)


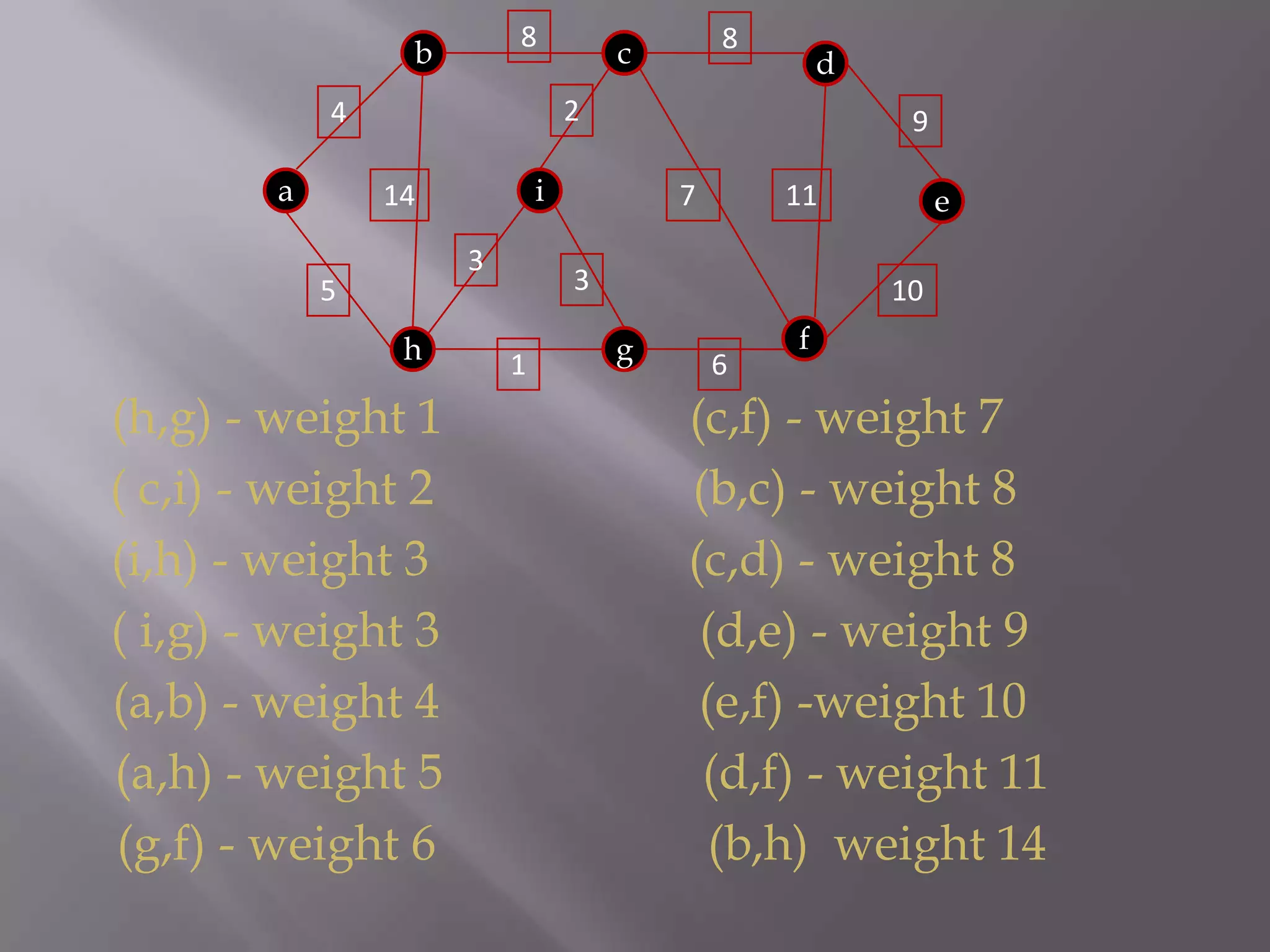

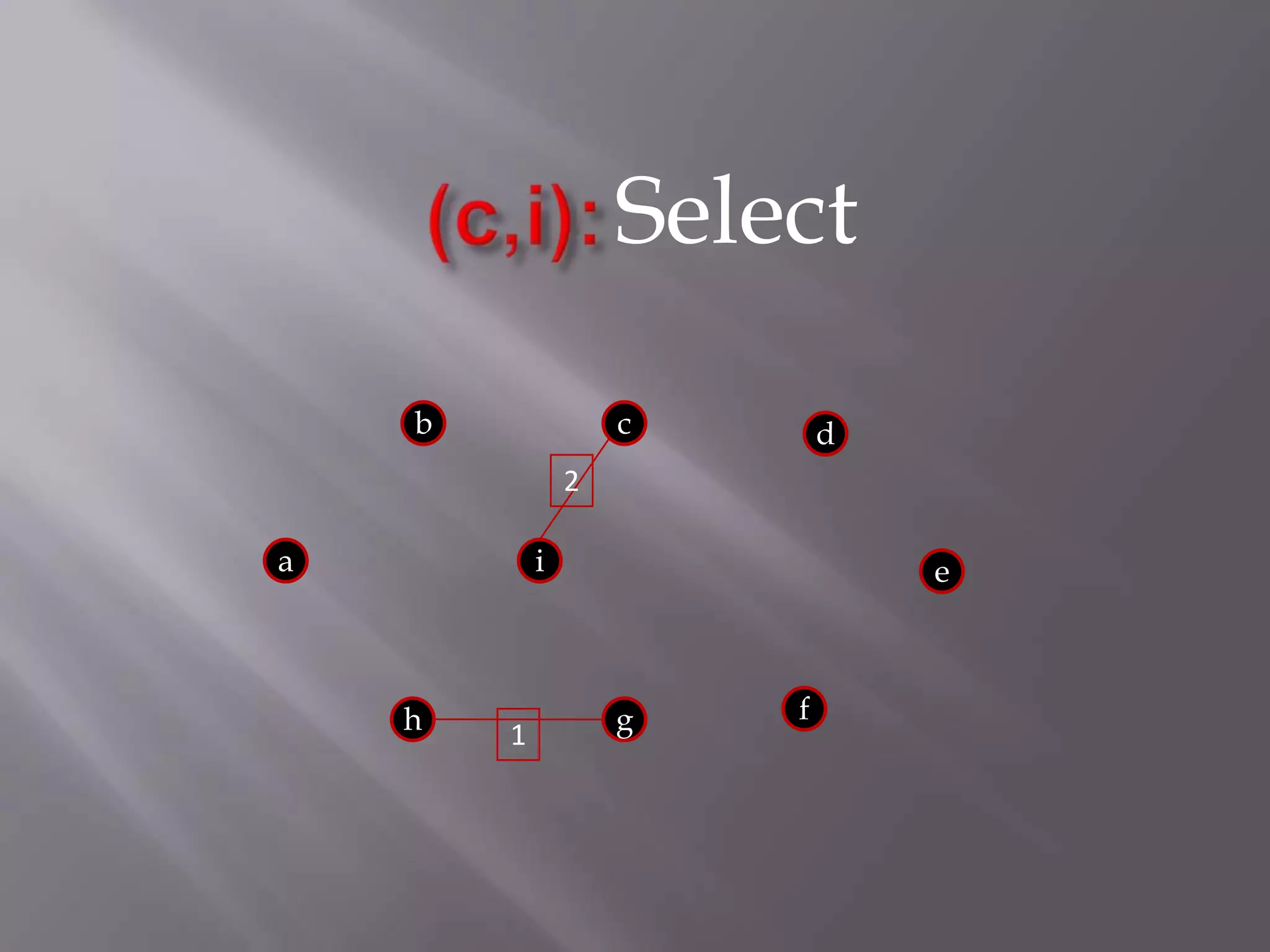
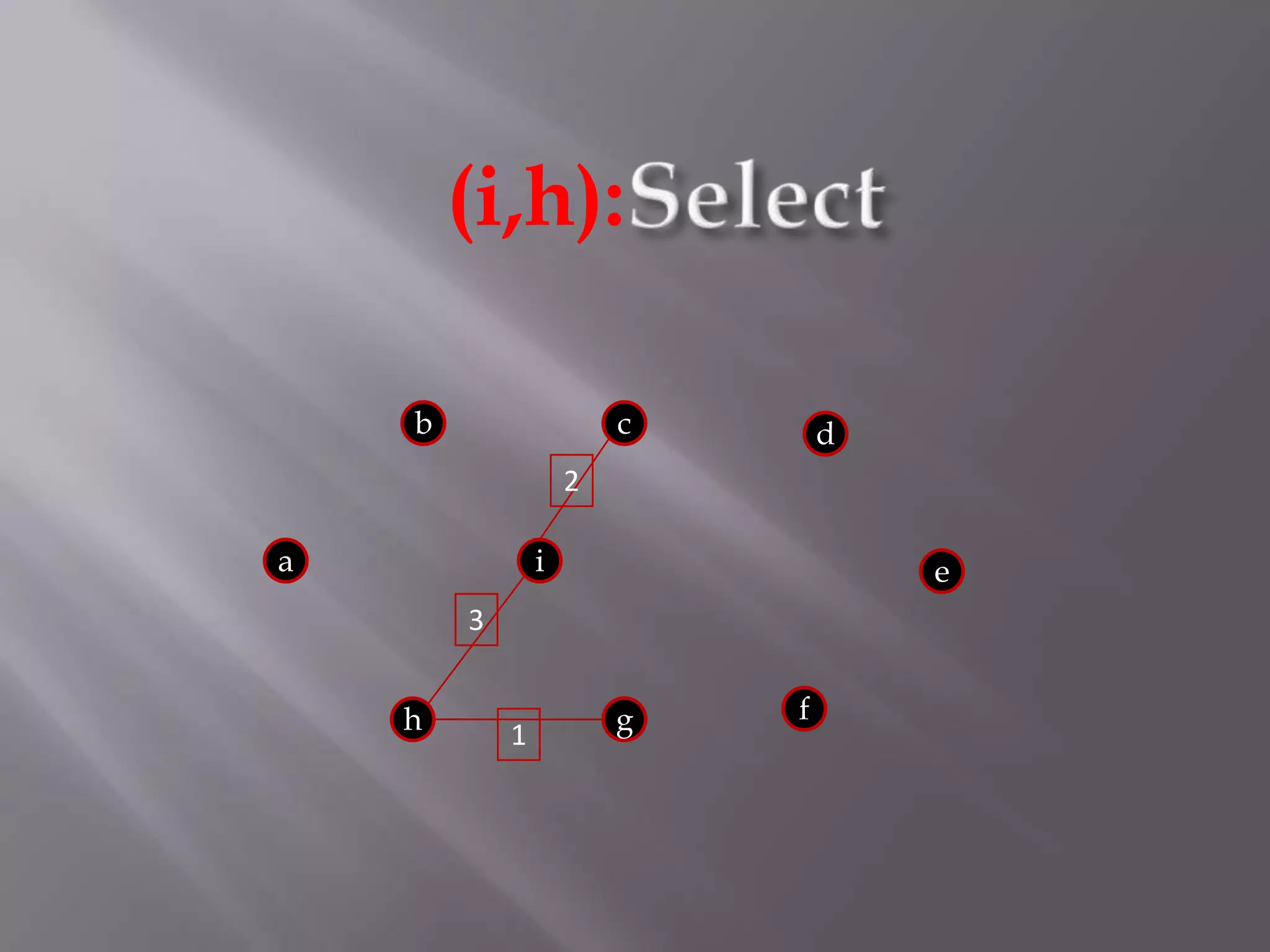

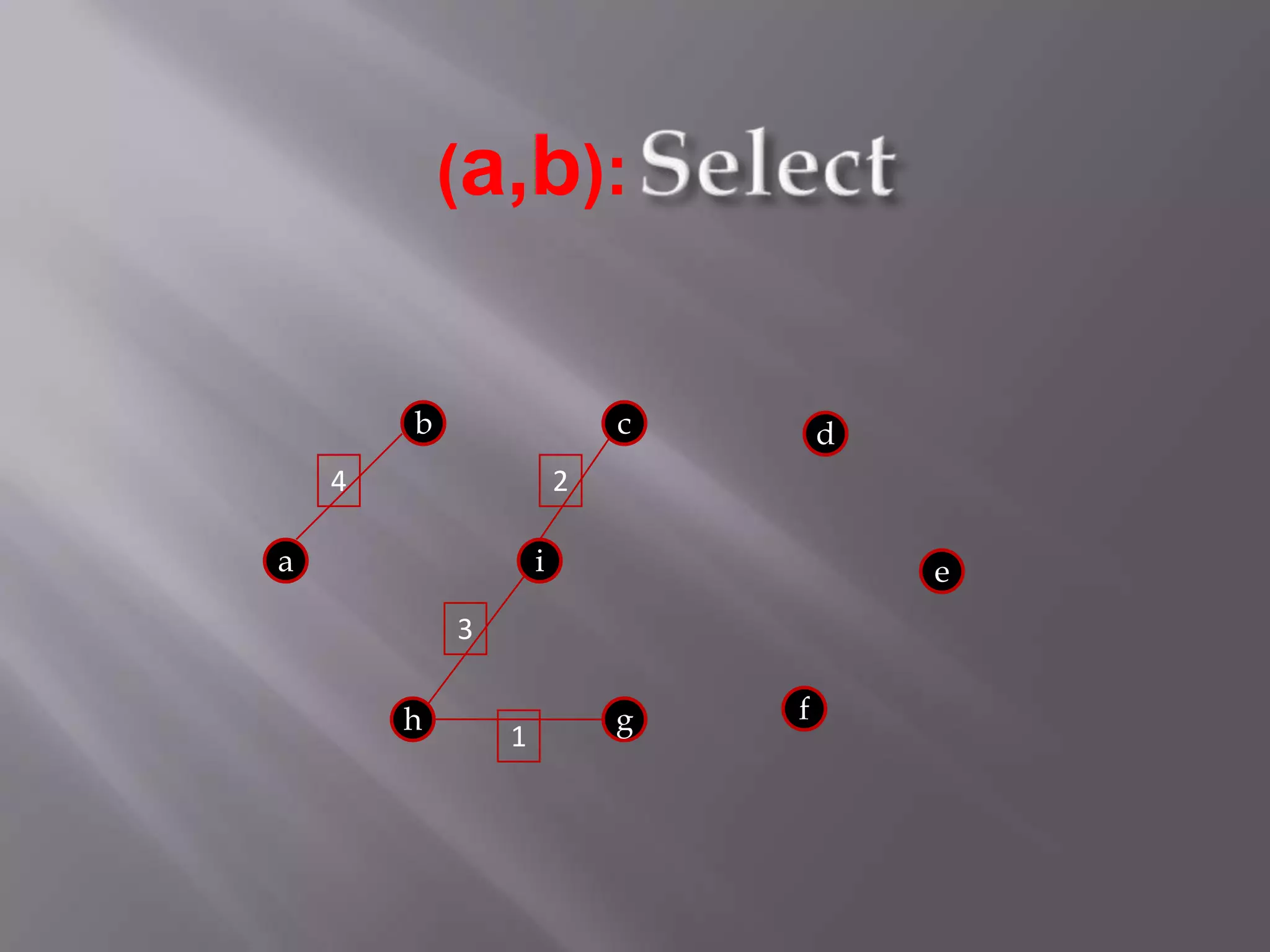
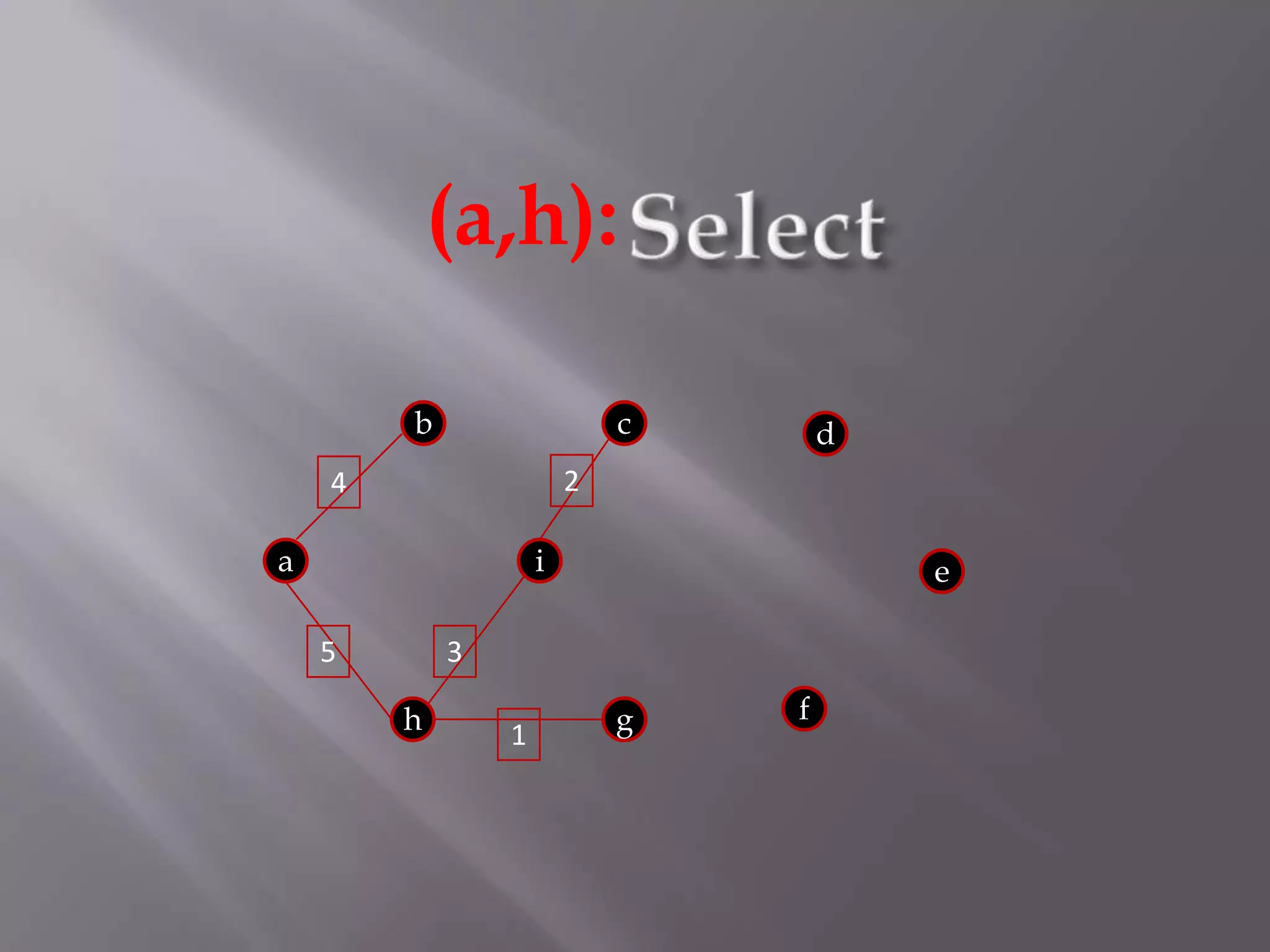
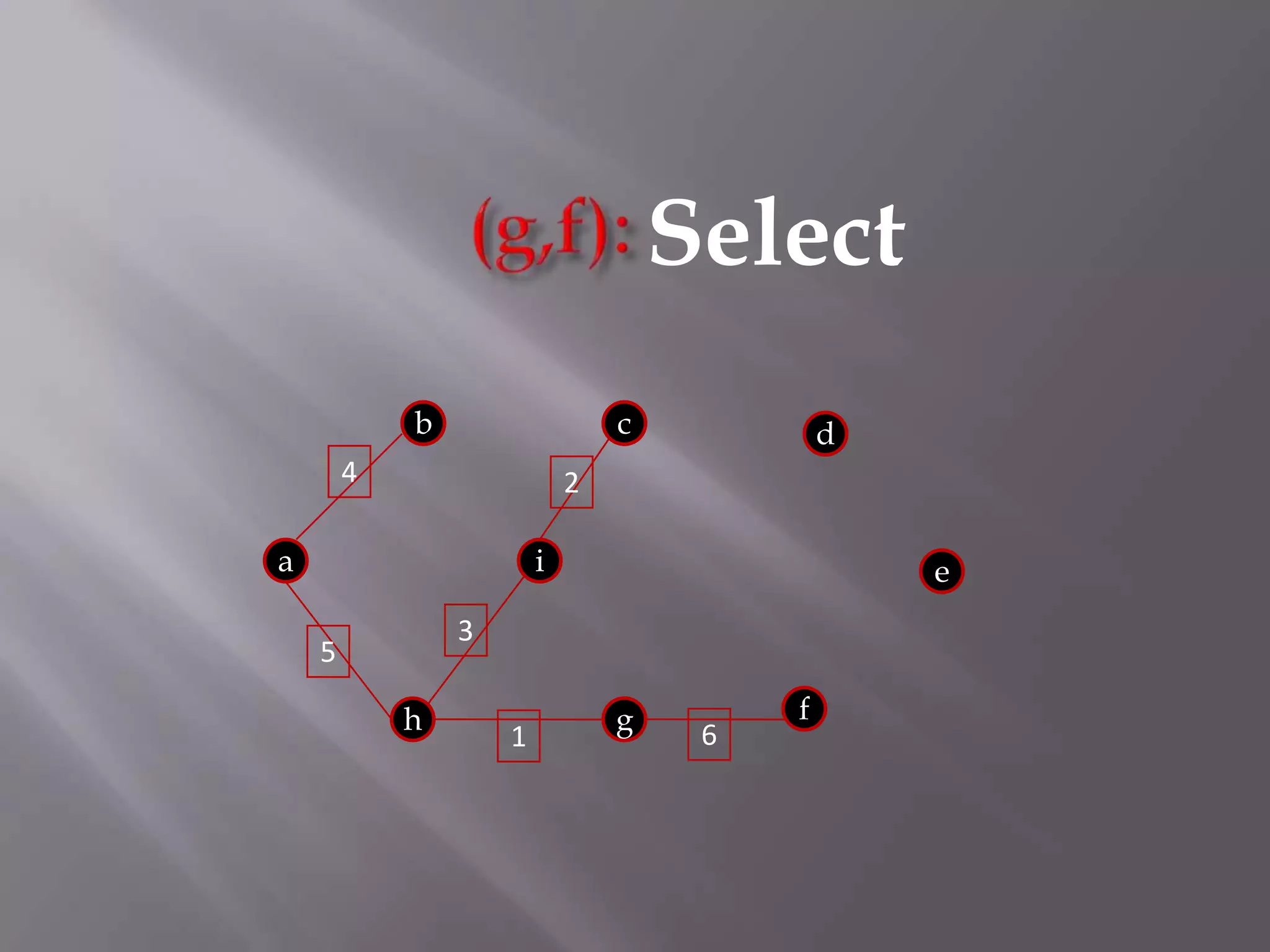
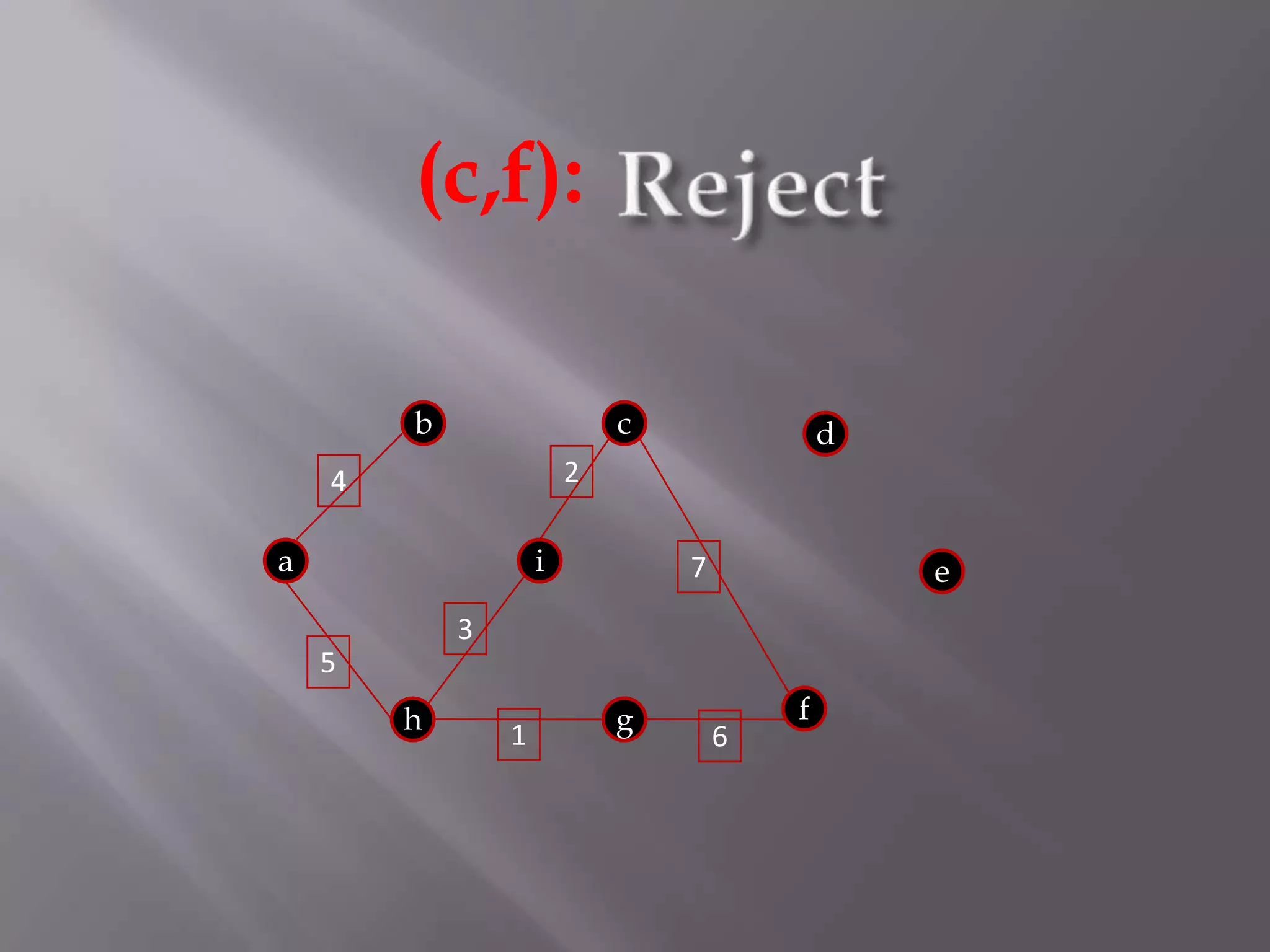
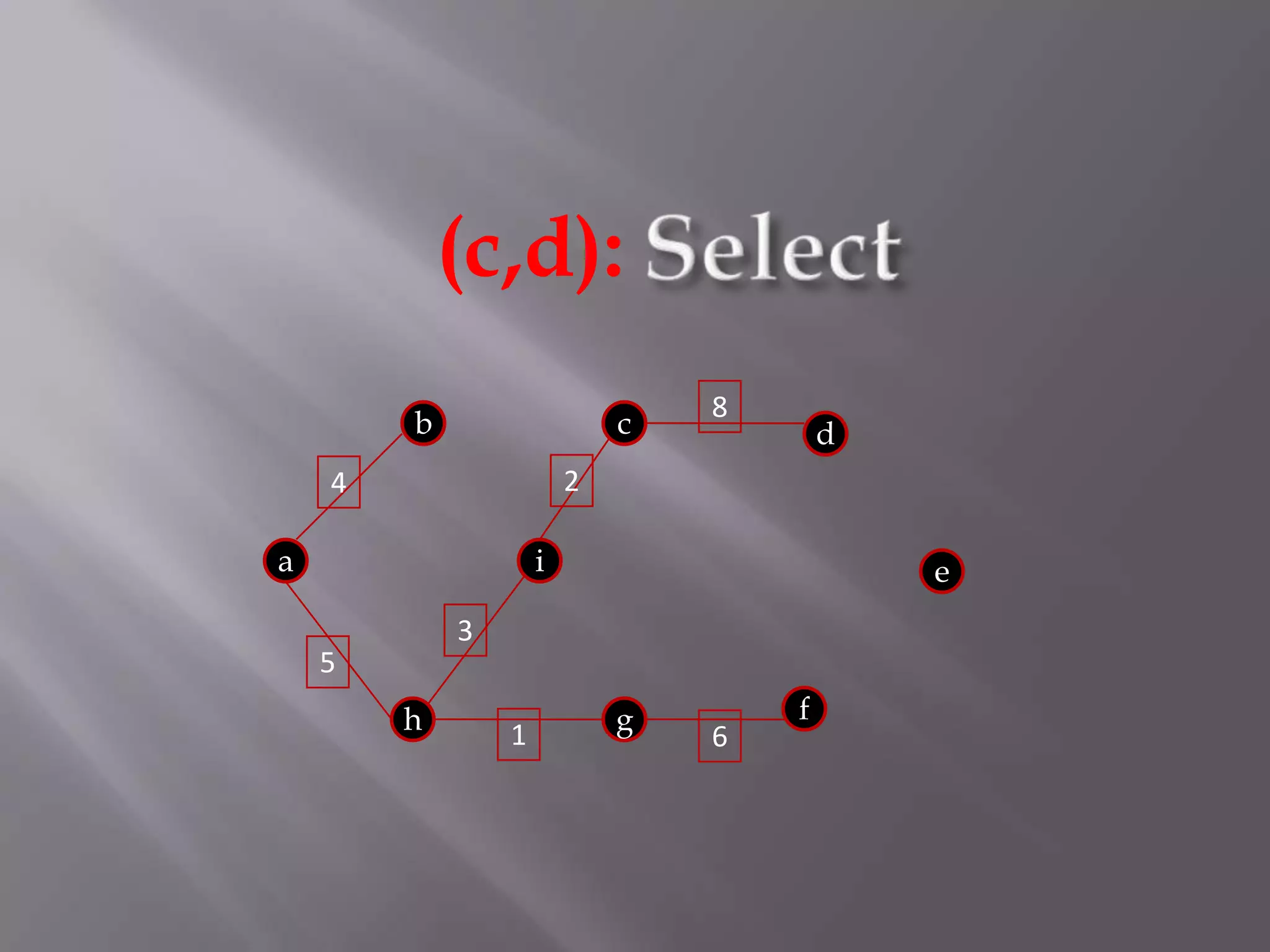
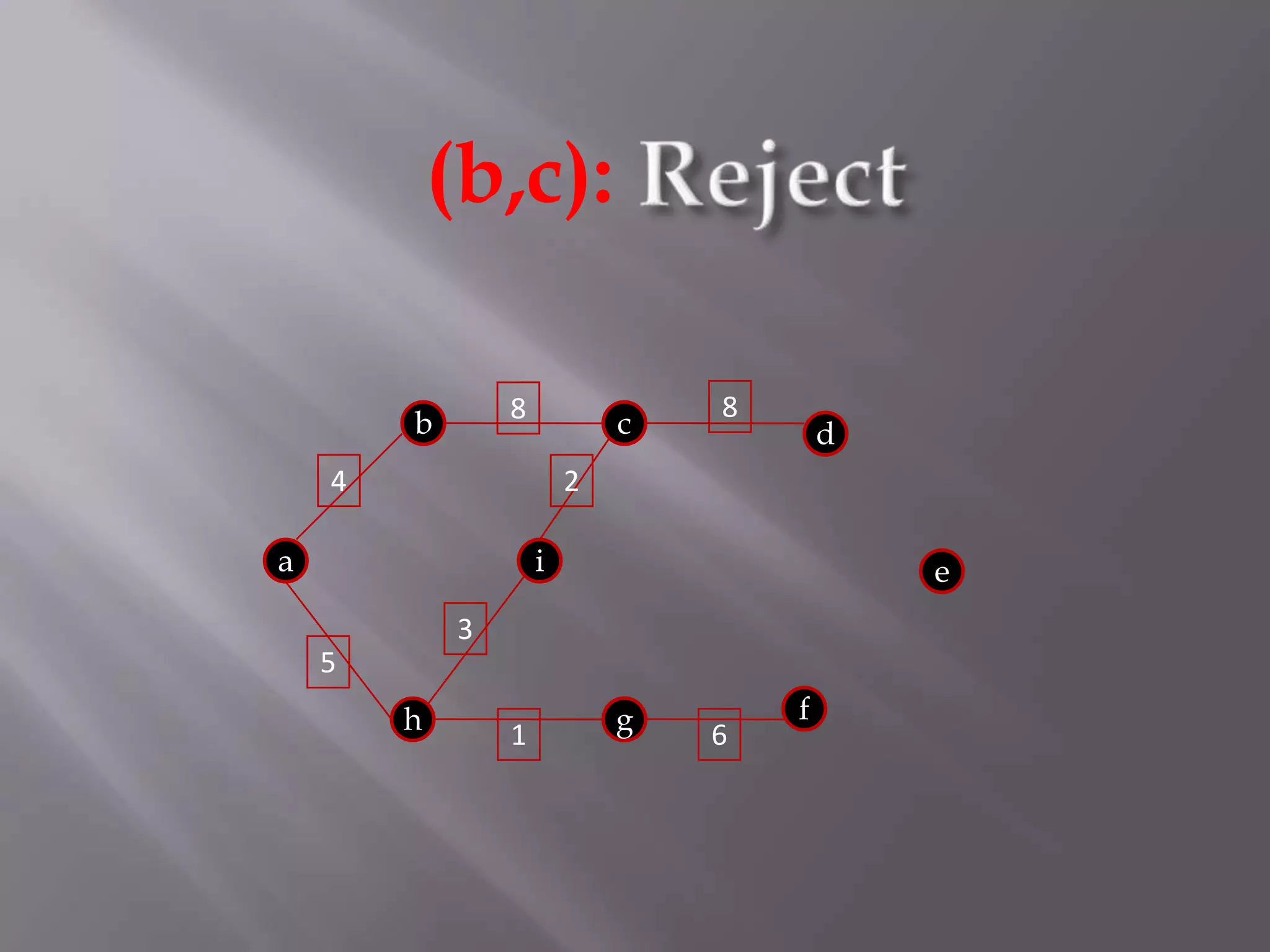
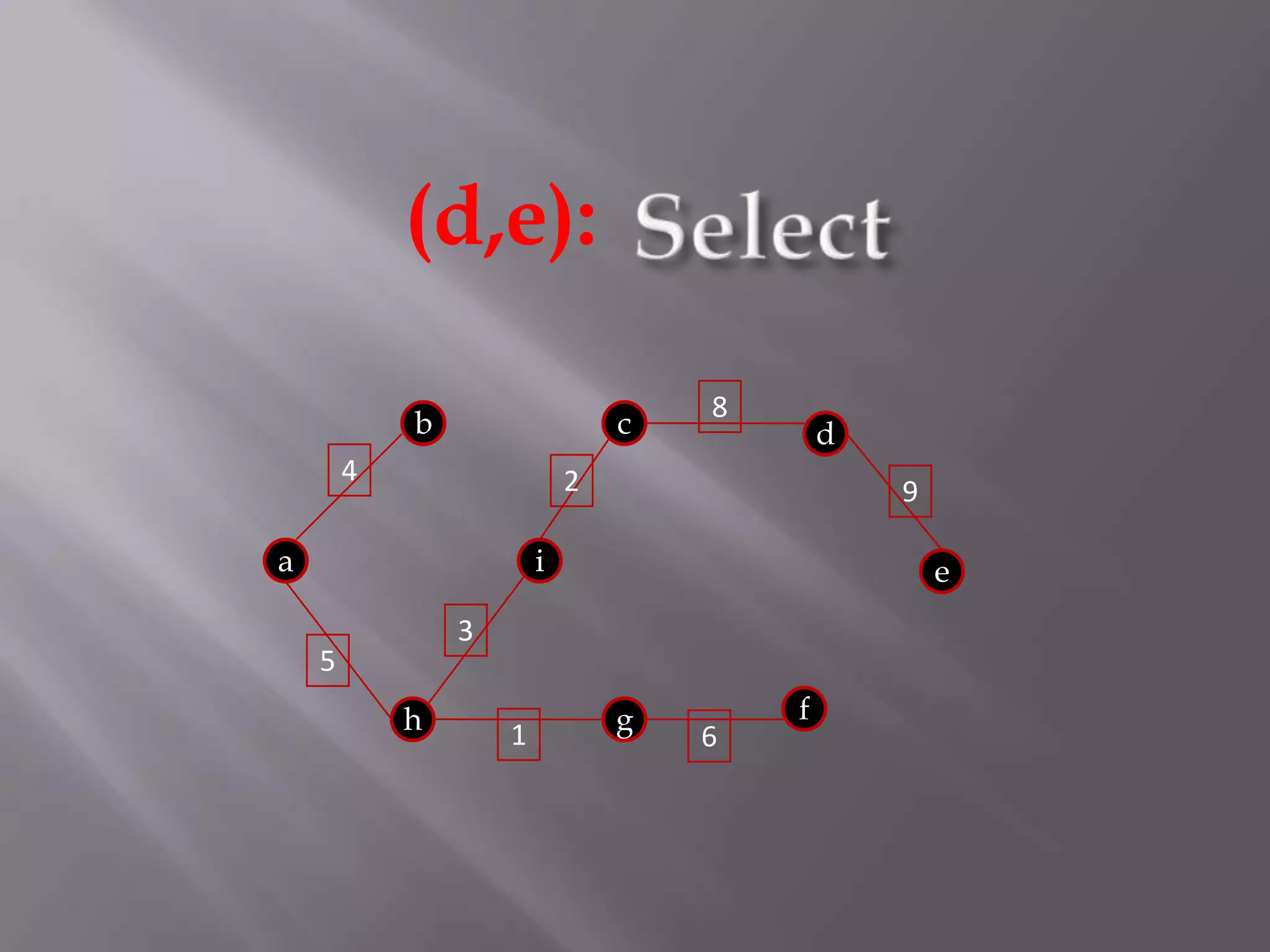
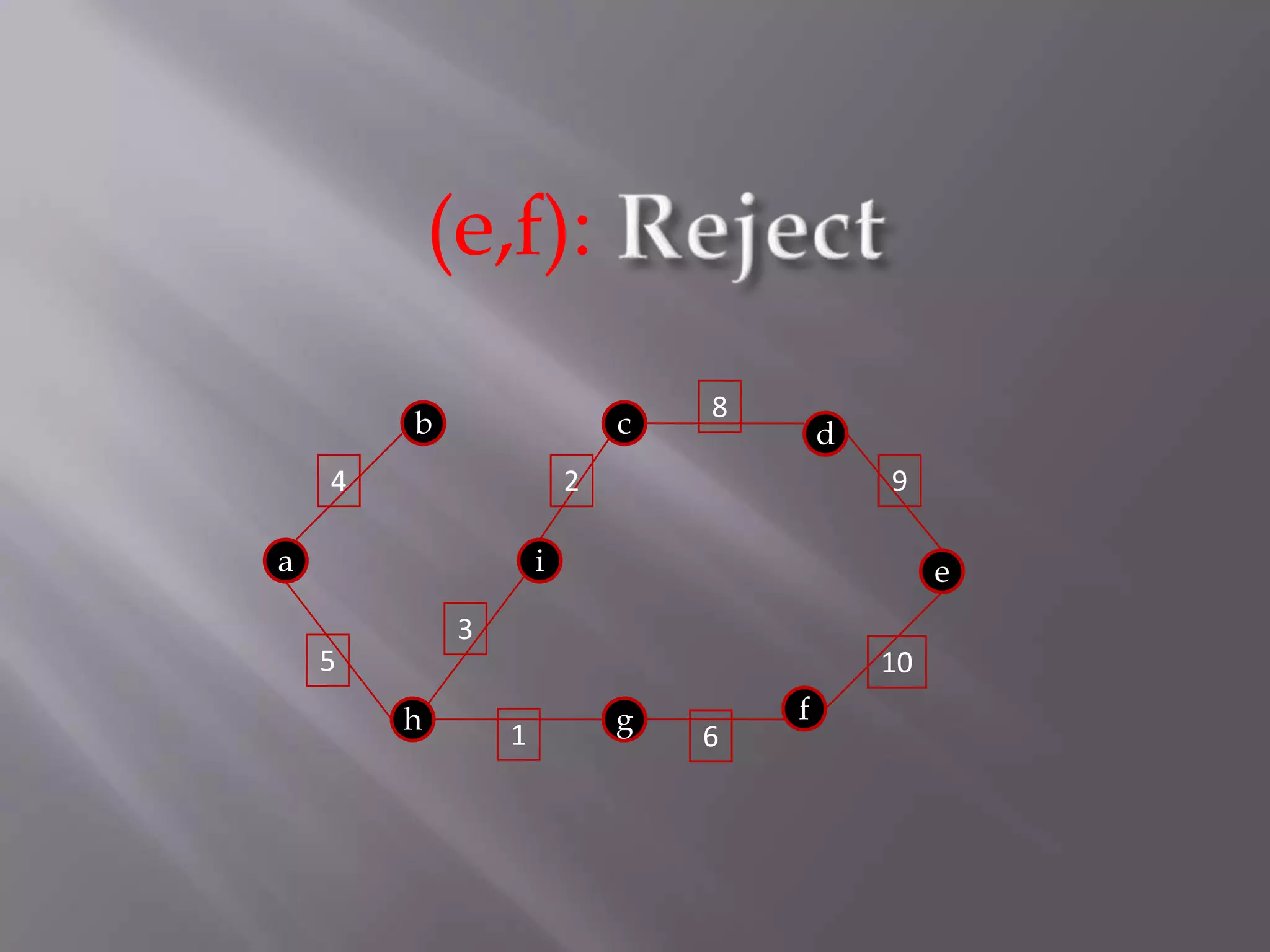
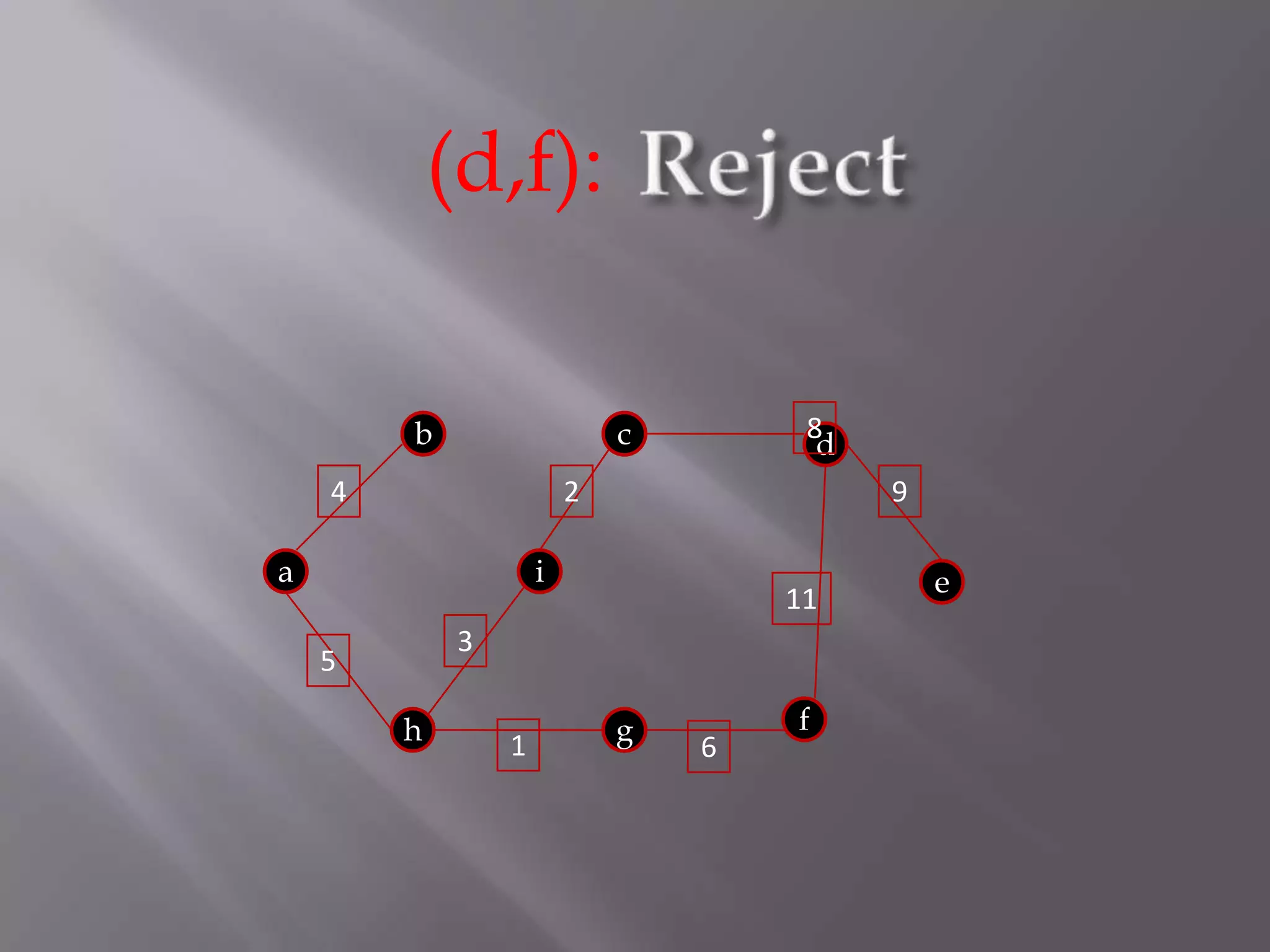
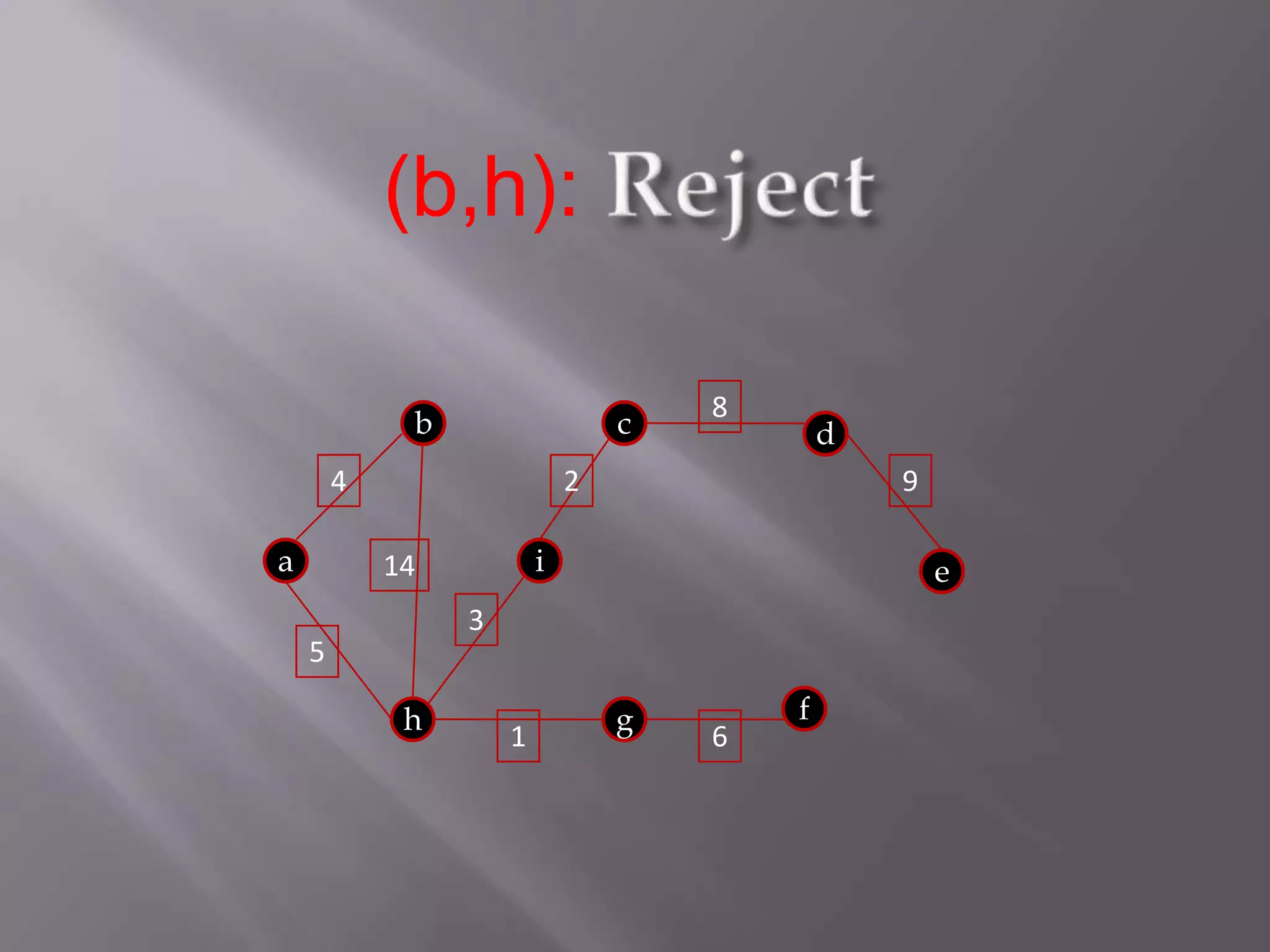


The Kruskal algorithm is used to find the minimum spanning tree (MST) of a connected undirected weighted graph. It works by sorting the edges in non-decreasing order of their weight, and then selecting edges one by one if they do not form a cycle with the previously selected edges. The algorithm is applied on the given graph, sorting its edges by weight and sequentially selecting edges that do not form cycles. This results in a MST with total weight of 38.
![Kruskal AlgorithmKRUSKAL(V,E,W)A ← ΦFor each vertex vЄG[v]Do MAKESET[v]sort E into nondecreasing order of weight wDo if FINDSET [u]≠FINDSET[v]A ← A U {(U,V)}UNION(U,V)Return (A)](https://image.slidesharecdn.com/kruskalalgorithm-100607232435-phpapp01/75/Kruskal-Algorithm-1-2048.jpg)

















