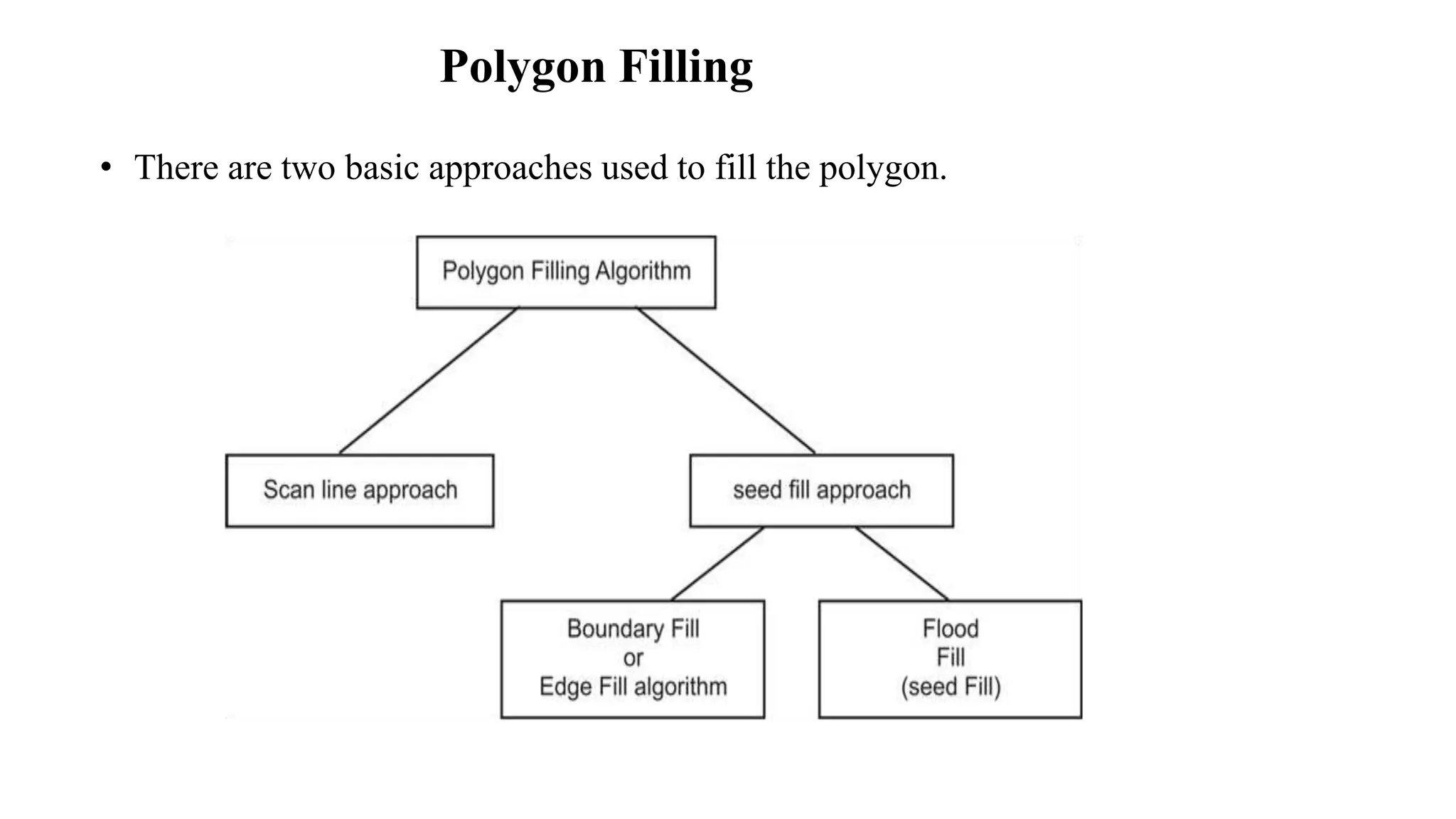
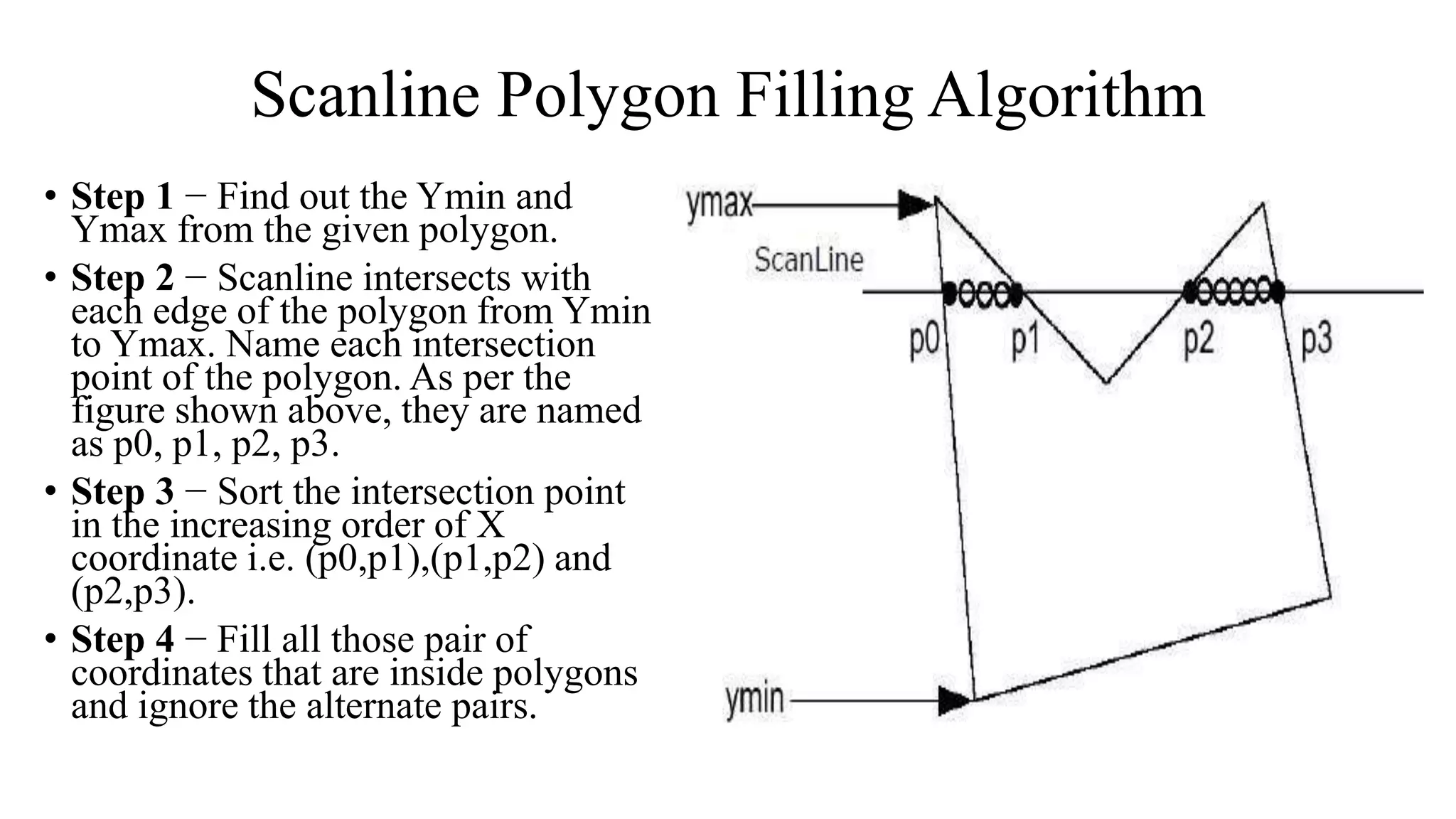
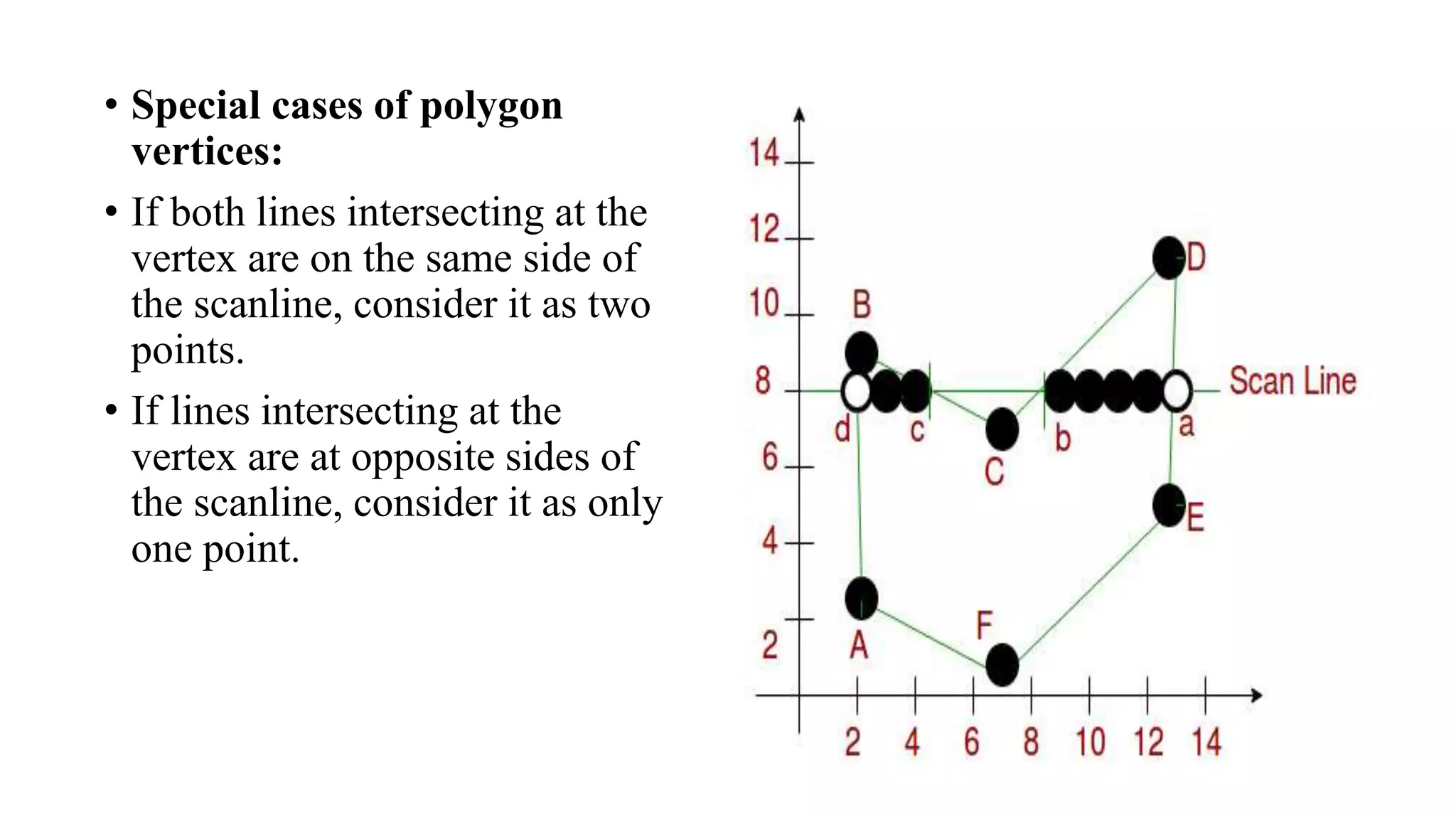
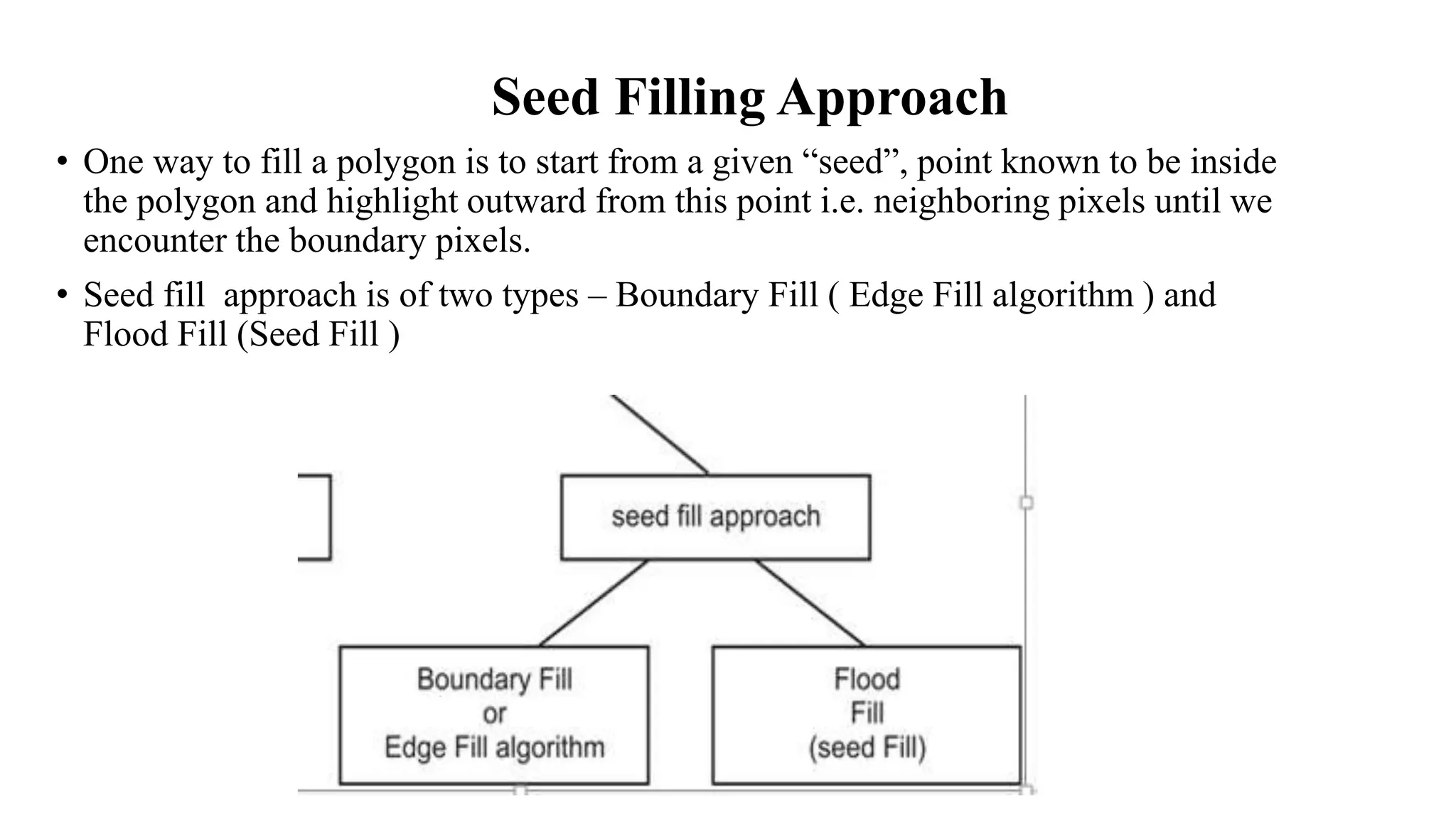
The document outlines algorithms for filling polygons, focusing on methods such as the even-odd method, scanline filling, and seed filling approaches like boundary and flood fill algorithms. It describes the process of determining interior pixels and highlights the differences between 4-connected and 8-connected methods for filling. The document also includes considerations for polygon edge cases and poses questions related to these algorithms.