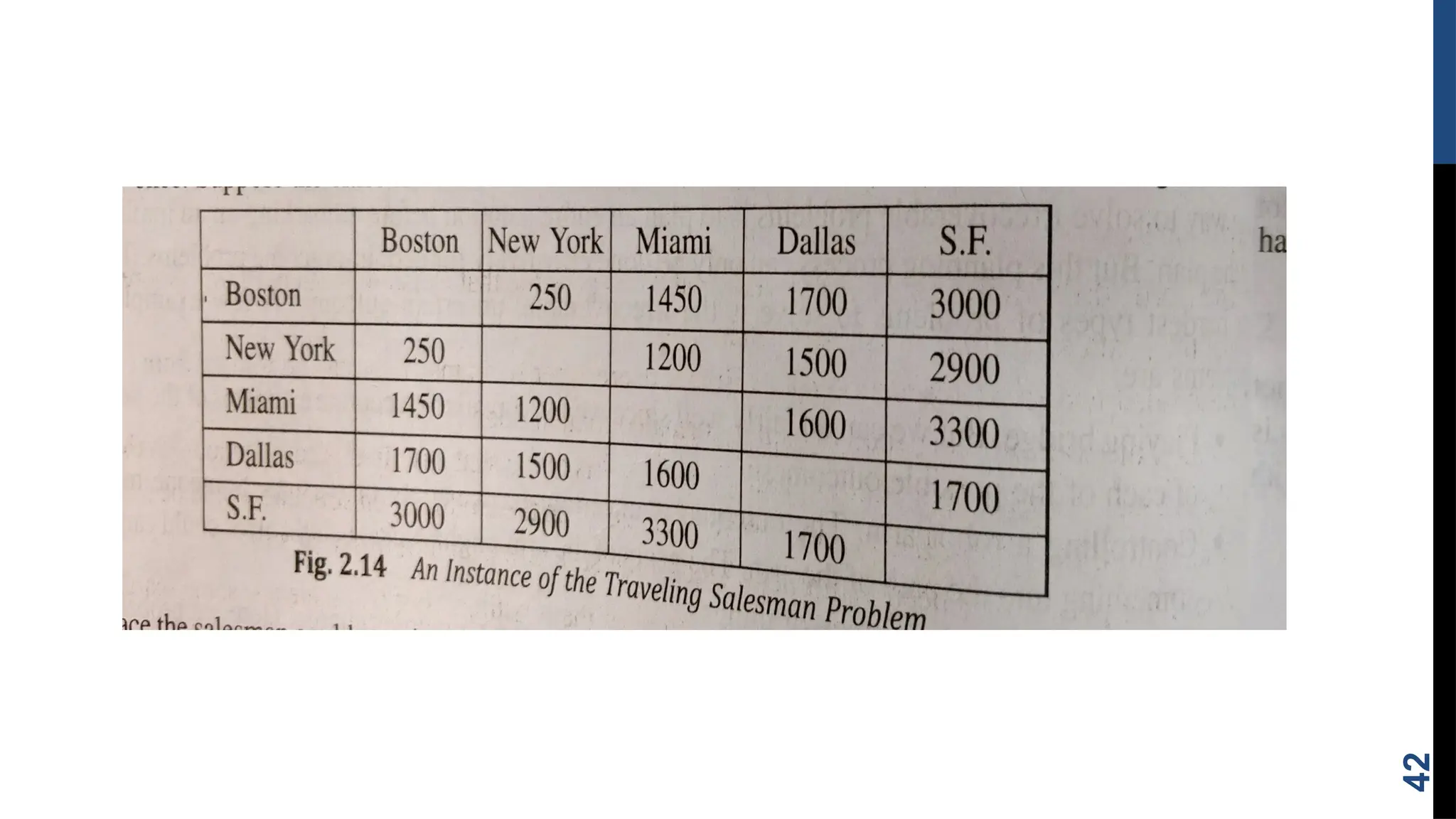
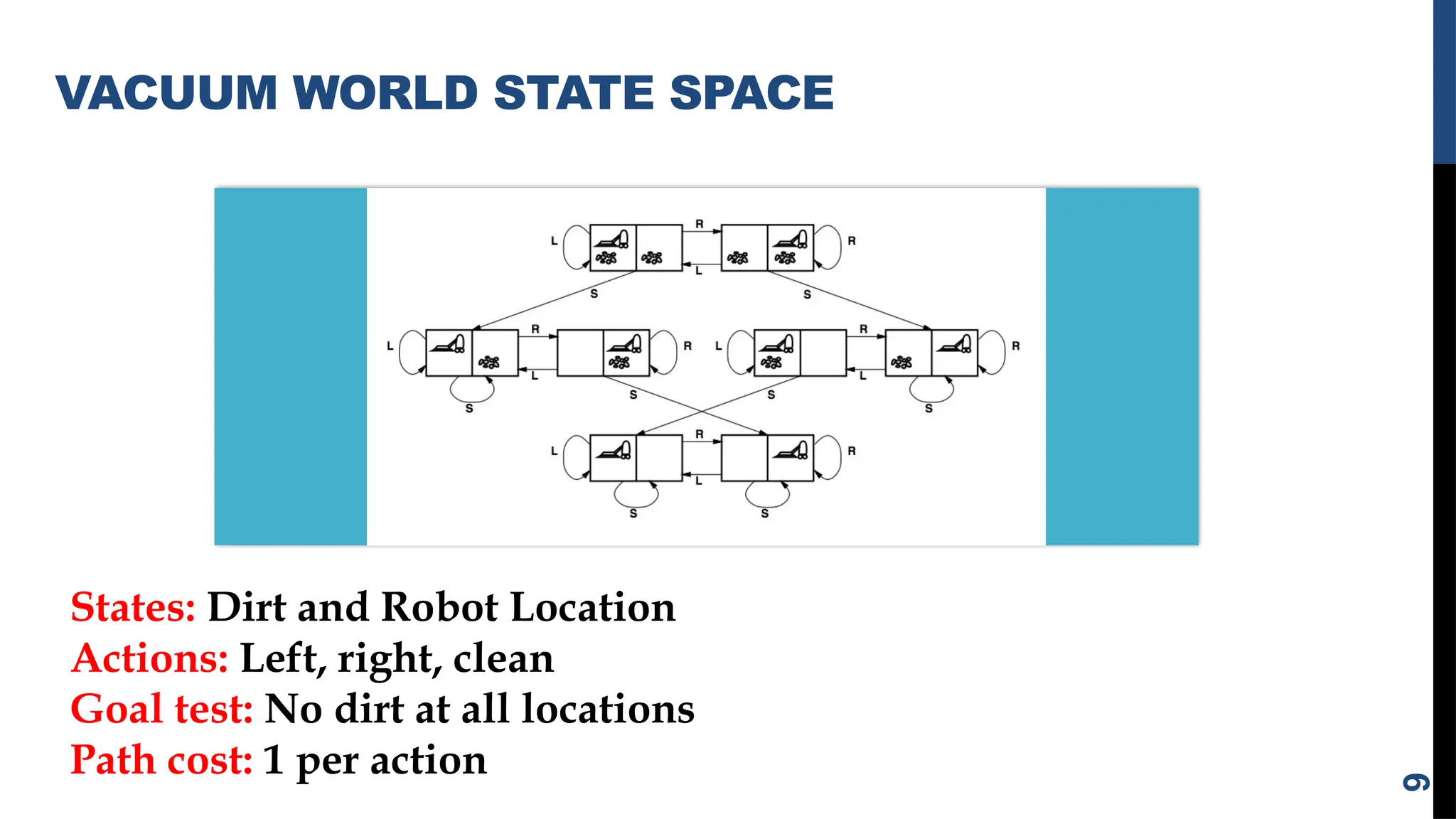
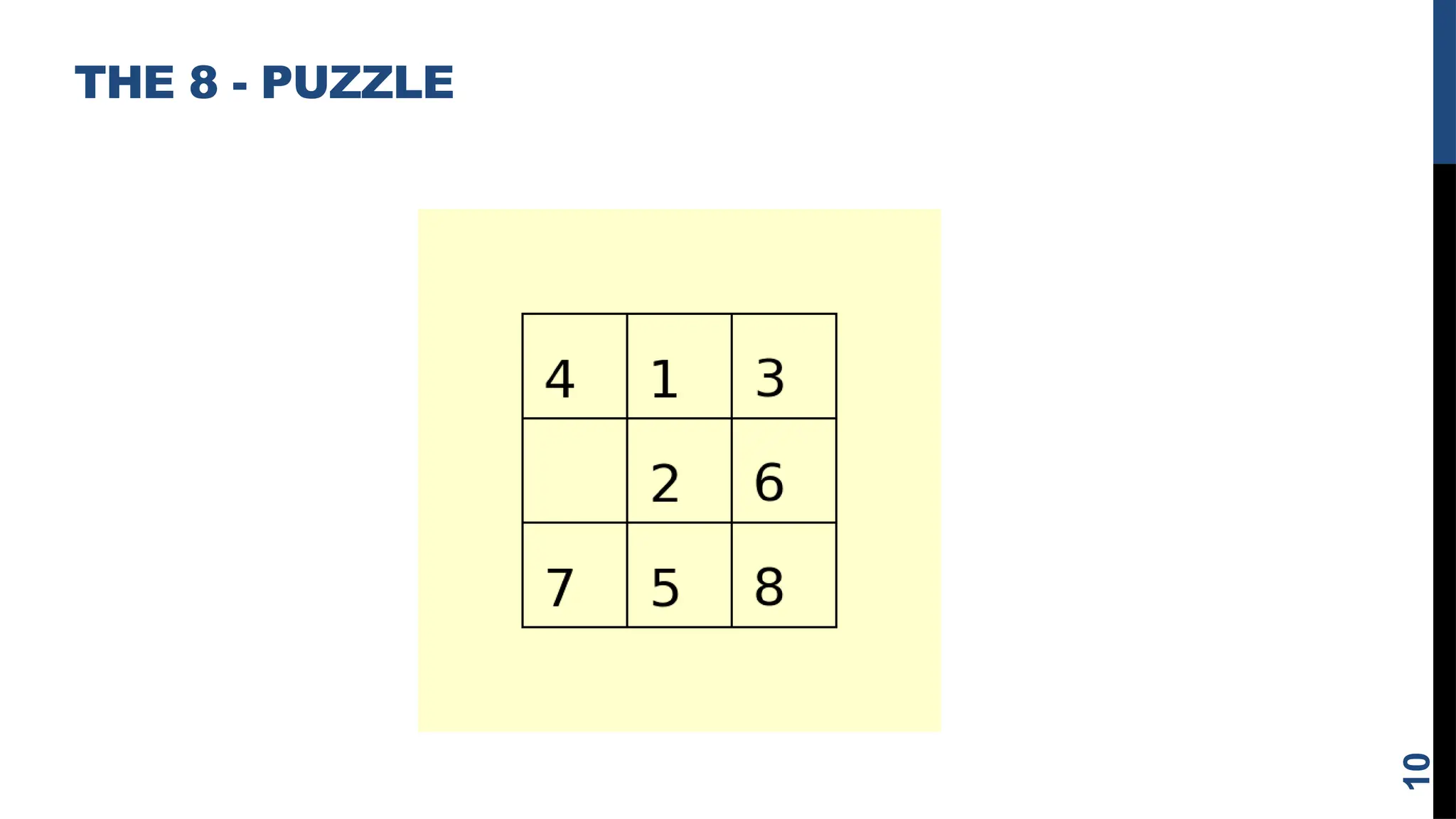
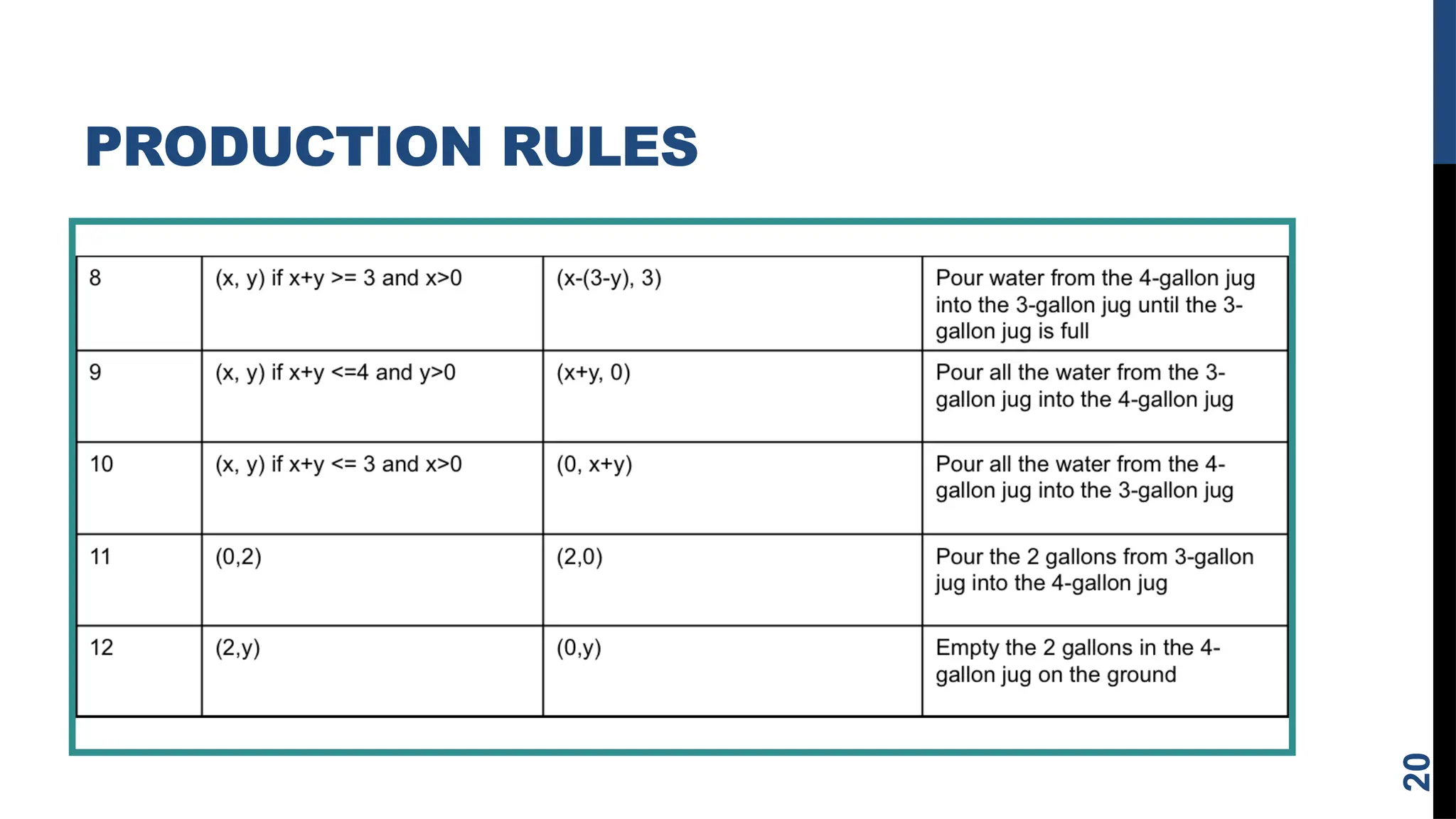
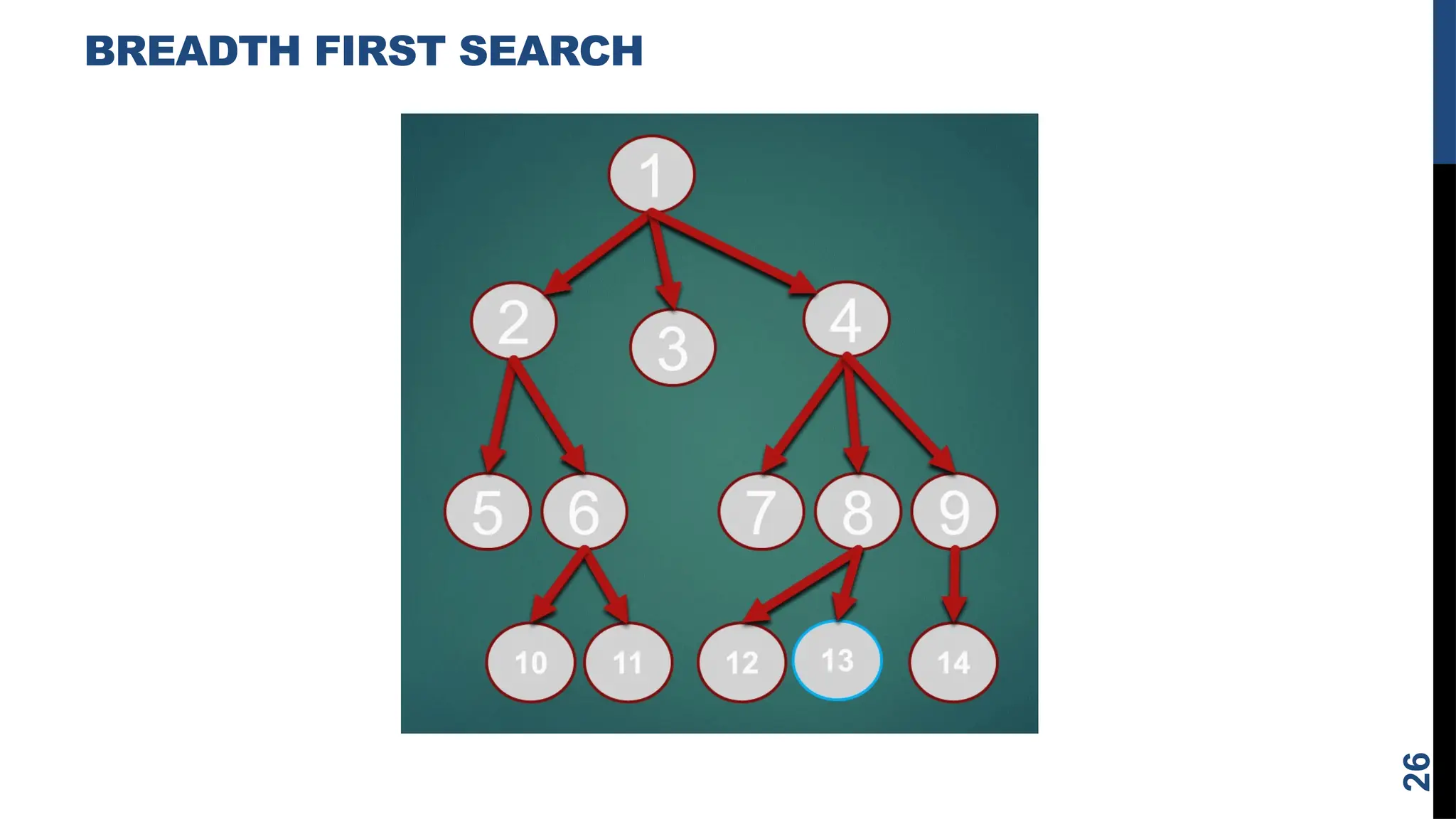
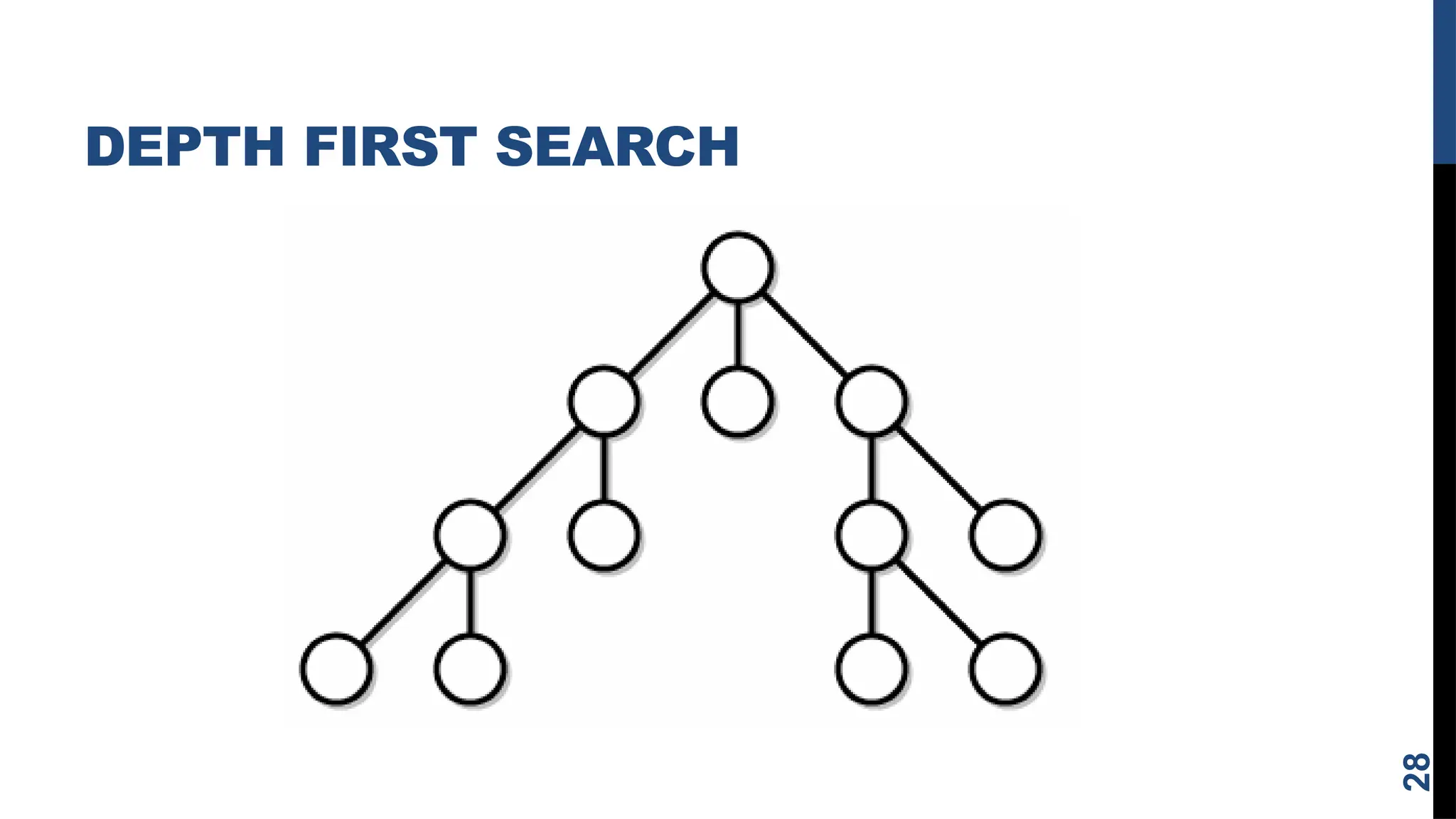
The document outlines the concept of problem solving as a state space search, discussing various techniques such as breadth-first search, depth-first search, and heuristic search. It emphasizes the importance of problem formulation, characteristics, and the role of knowledge in solving problems across different scenarios like chess, the water jug problem, and the 8-puzzle. Additionally, it describes production systems and their characteristics, highlighting the distinctions between different types of production systems, their applications, and the implications for search program design.






























![BLOCKS WORLD PROBLEM
NON DECOMPOSABLE
36
Following operators
are available:
CLEAR(x) [ block x
has nothing on it]->
ON(x, Table)
CLEAR(x) and
CLEAR(y) -> ON(x,y)
[ put x on y]
C
A B
A
B
C
Start: ON(C,A)
Goal:
ON(B,C) and
ON(A,B)
ON(B,C)
ON(B,C) and ON(A,B)
ON(B,C)
ON(A,B)
CLEAR(A) ON(A,B)
CLEAR(A) ON(A,B)](https://image.slidesharecdn.com/unit-ich2-240916041004-2c219e98/75/problem-space-and-problem-definition-in-ai-36-2048.jpg)