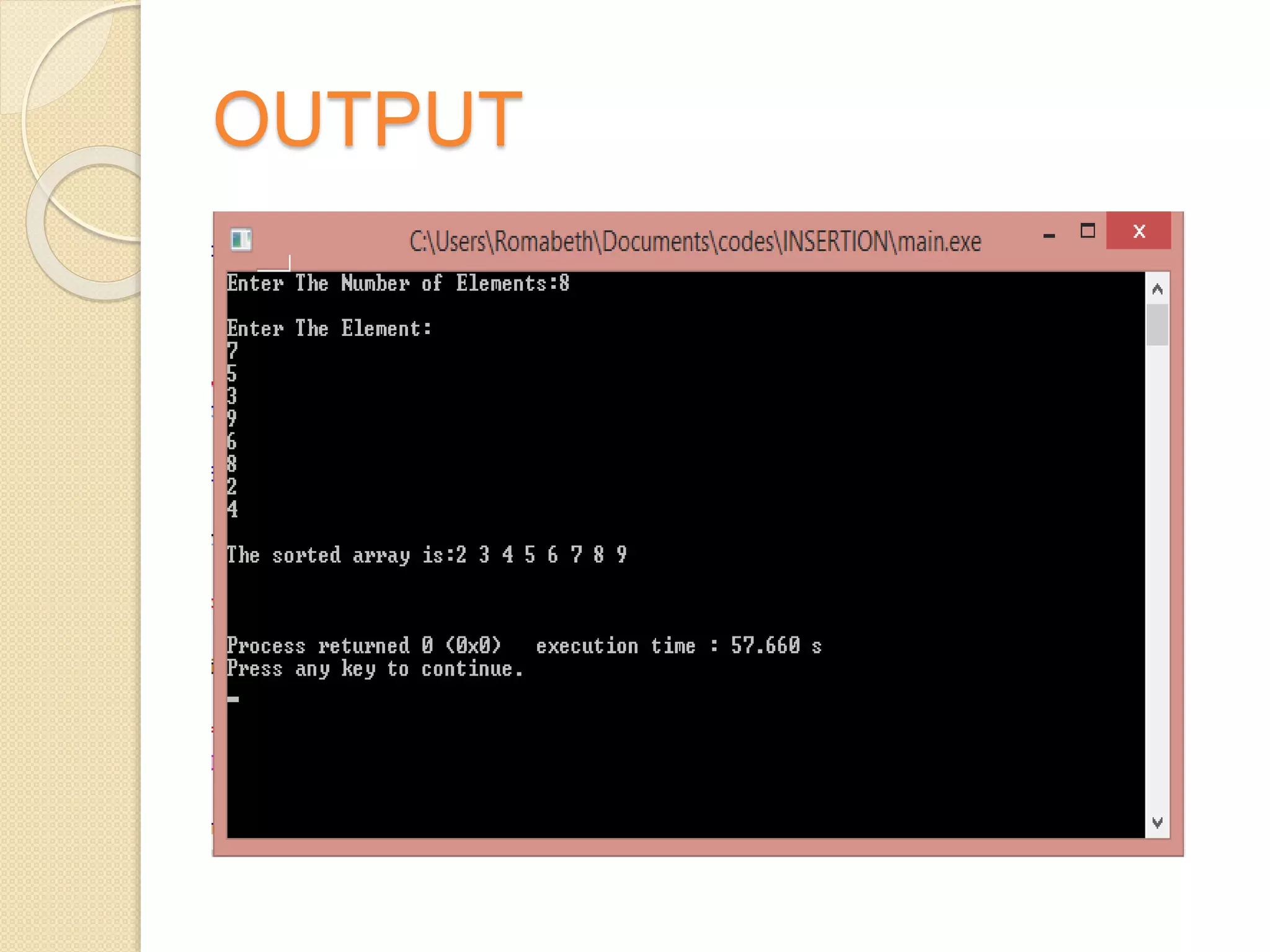
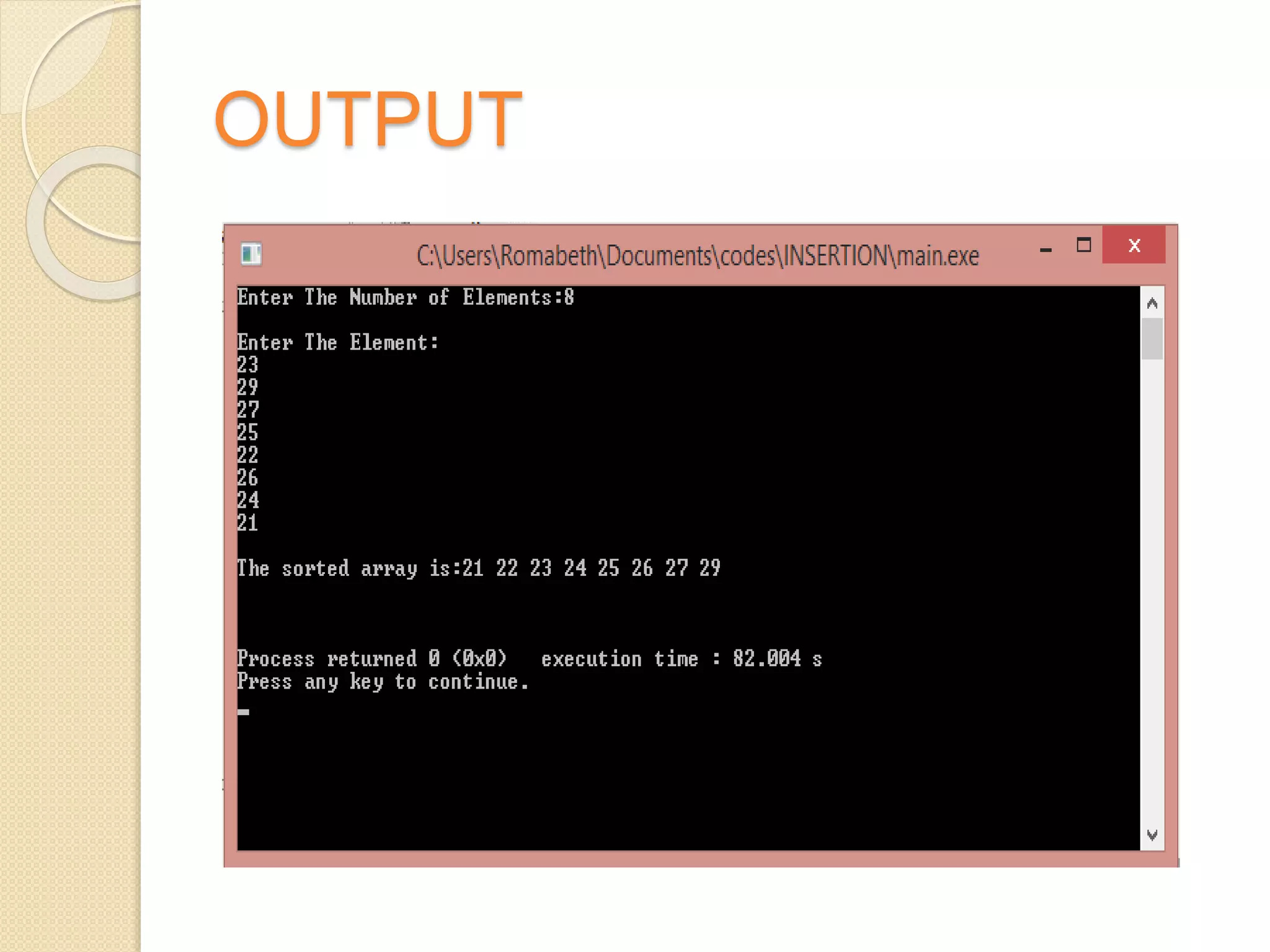
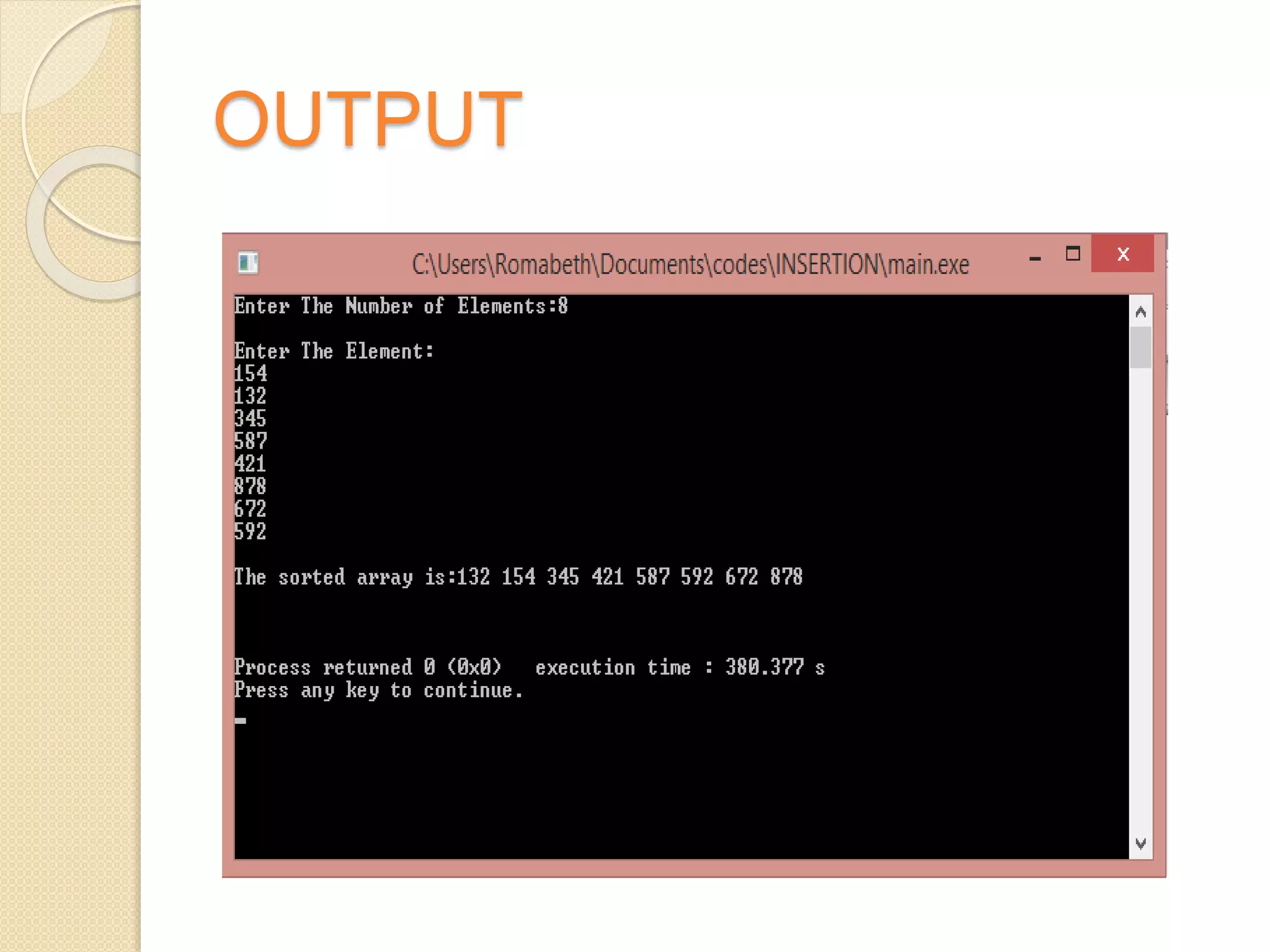
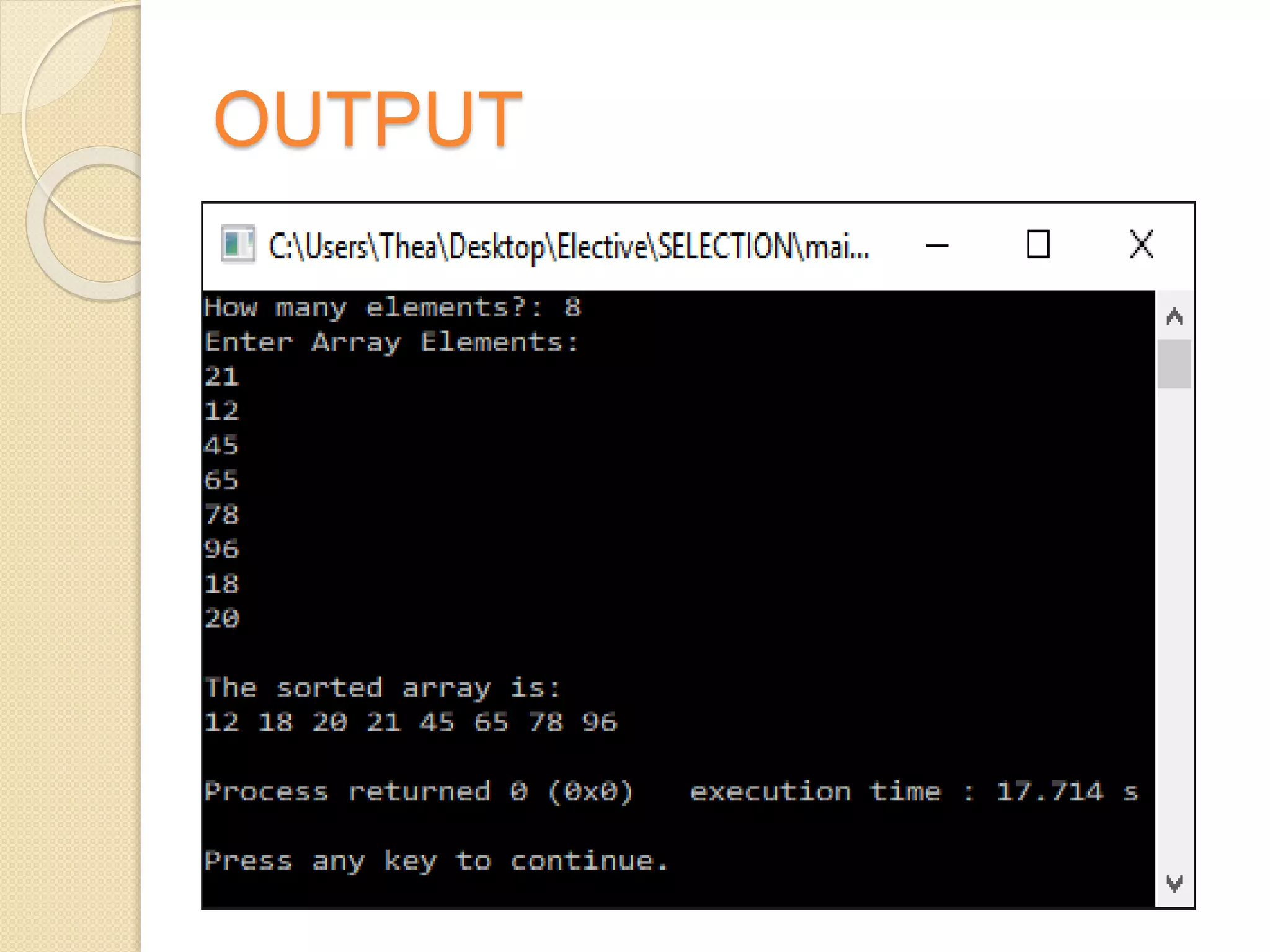
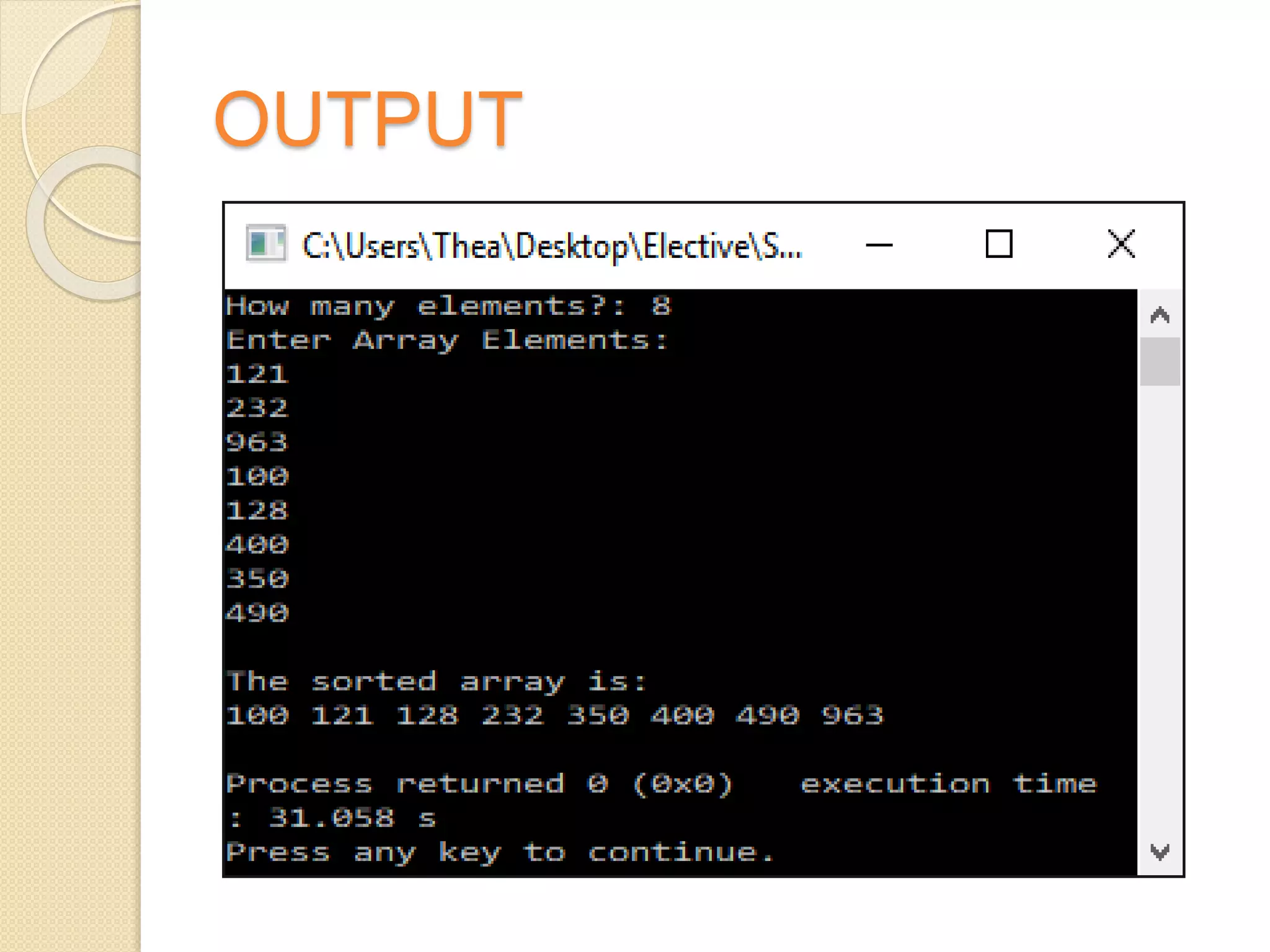
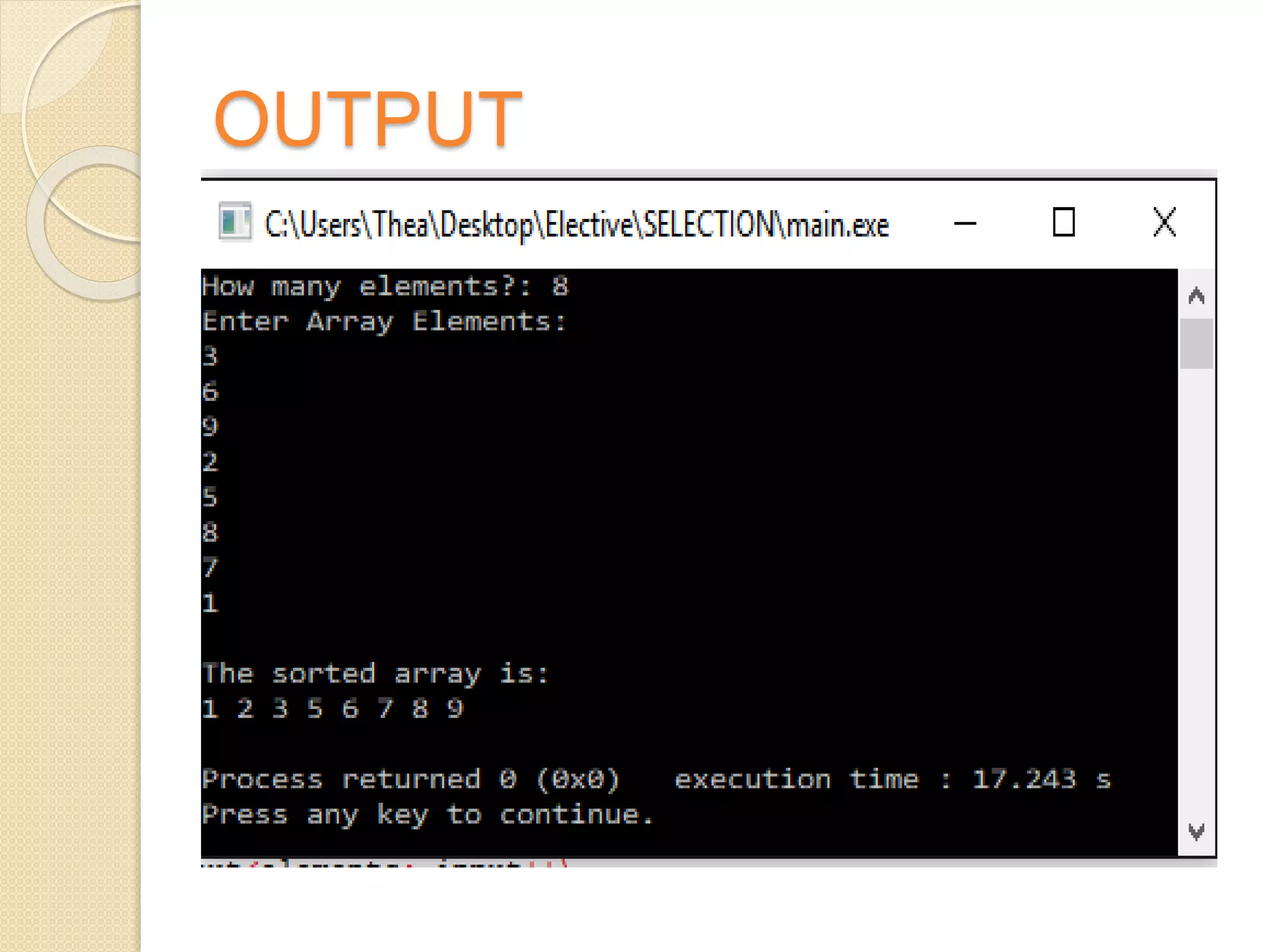
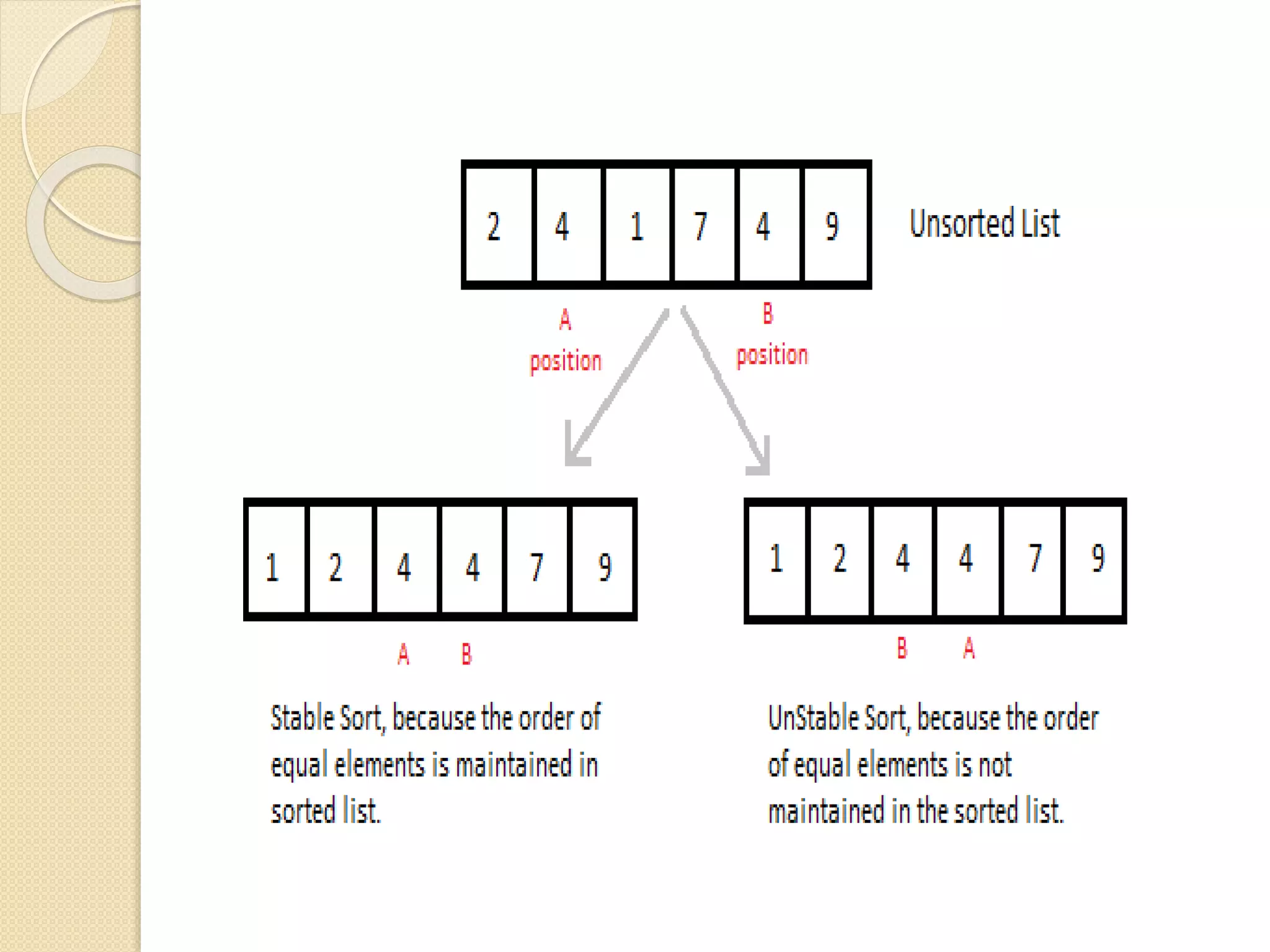
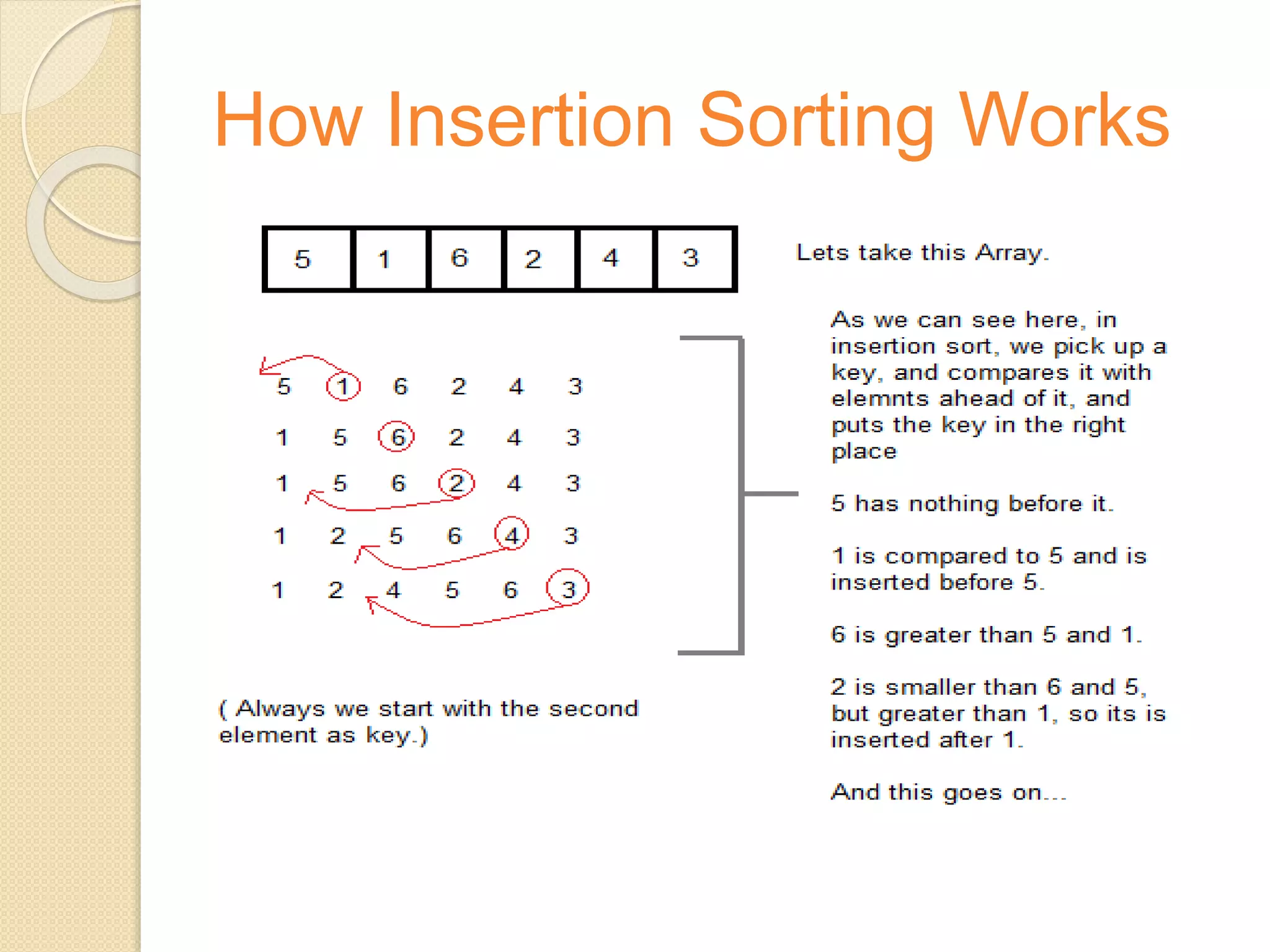
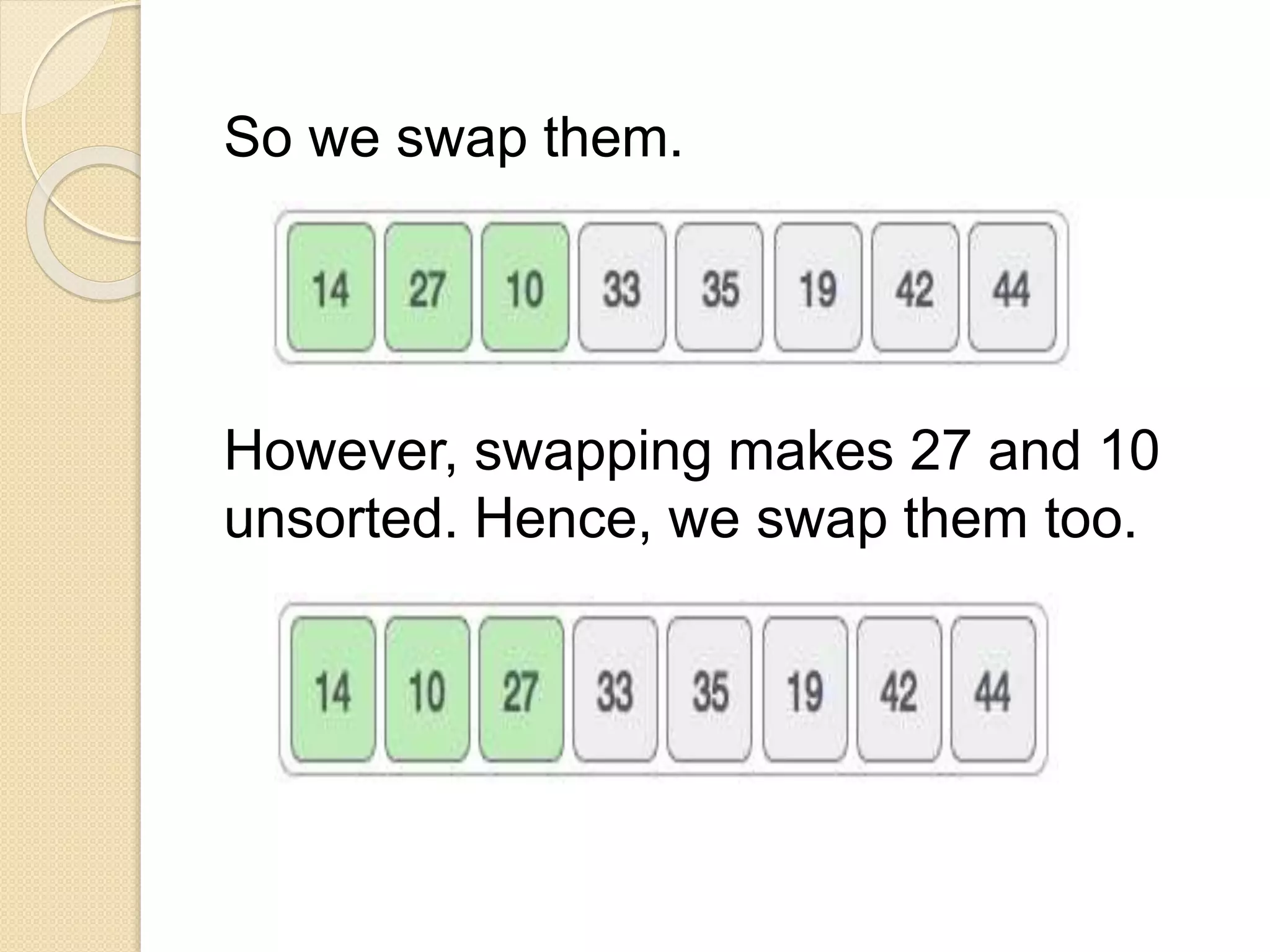
This document discusses two sorting algorithms: selection sort and insertion sort. Selection sort works by finding the smallest element in the unsorted array and swapping it into the sorted position. This continues until the array is fully sorted. Insertion sort shifts elements in the sorted portion of the array to make room to insert new elements in sorted order. It is more efficient than selection sort for smaller datasets or datasets that are already partially sorted. Pseudocode and examples are provided to illustrate how each algorithm works.










![PROGRAM
#include<iostream>
using namespace std;
int main()
{
int elements, arr[10], input, j, temp;
cout<<“How many elements?:”;
cin>>elements;
cout<<“Enter Array Elements:n”;](https://image.slidesharecdn.com/selectionsortandinsertionsort-171214040133/75/Selection-Sort-and-Insertion-Sort-11-2048.jpg)
![for(input=0;input<elements;input++)
{
for(j=input+1;j<elements;j++)
{
if(arr[input]>arr[j];
{
temp=arr[input]
arr[input]=arr[j]
arr[j]=temp;
}
}
}
Cout<<“nThe sorted array is:n”;
For(input=0;input<elements;input++)
{
cout<<arr[input]<<“ “;
}
Cout<<“n”;
}](https://image.slidesharecdn.com/selectionsortandinsertionsort-171214040133/75/Selection-Sort-and-Insertion-Sort-12-2048.jpg)














![PROGRAM
#include<iostream>
Using namespace std;
Int main()
{
int i,j,n,temp,a[30];
cout<< “Enter the number of elements:”
cin>>n;
cout<<“Enter the elementn”;
for(i-=1;i<n;i++)
{
cin>>a[i];
}](https://image.slidesharecdn.com/selectionsortandinsertionsort-171214040133/75/Selection-Sort-and-Insertion-Sort-33-2048.jpg)
![for(i=1;i<=n-1;i++)
{
temp=a[i];
j=i-1;
while((temp<a[j])&&(j>=0))
{
a[j+1]=a[j]; //moves element forward
j=j-1;
}
a[j+1]=temp; //insert element forward
}
Cout<< “nThe sorted array is:”;
For(i=0;i<n;i++)
{
cout<< a[i]<<“ “;
}
Return 0;
}](https://image.slidesharecdn.com/selectionsortandinsertionsort-171214040133/75/Selection-Sort-and-Insertion-Sort-34-2048.jpg)