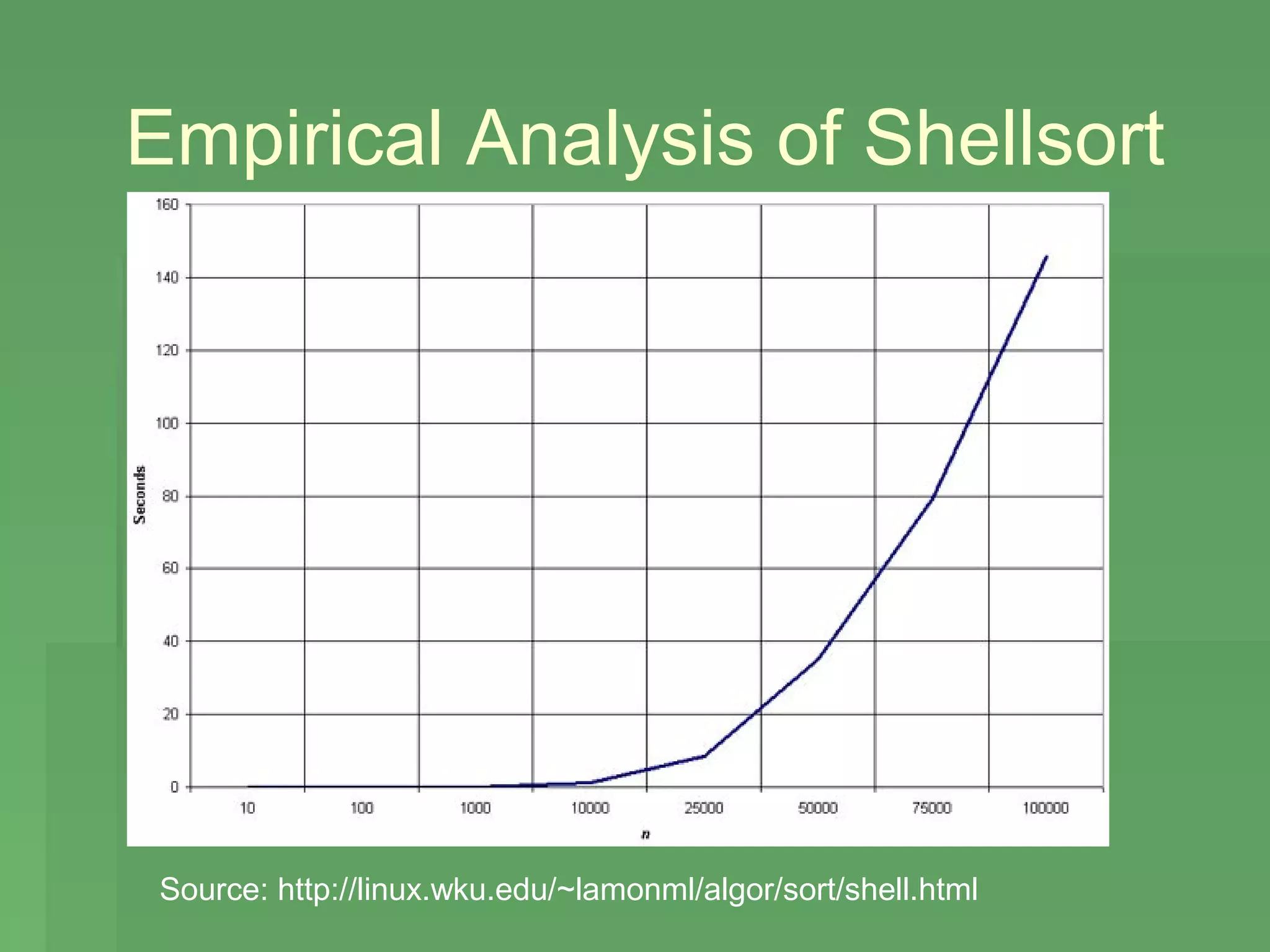
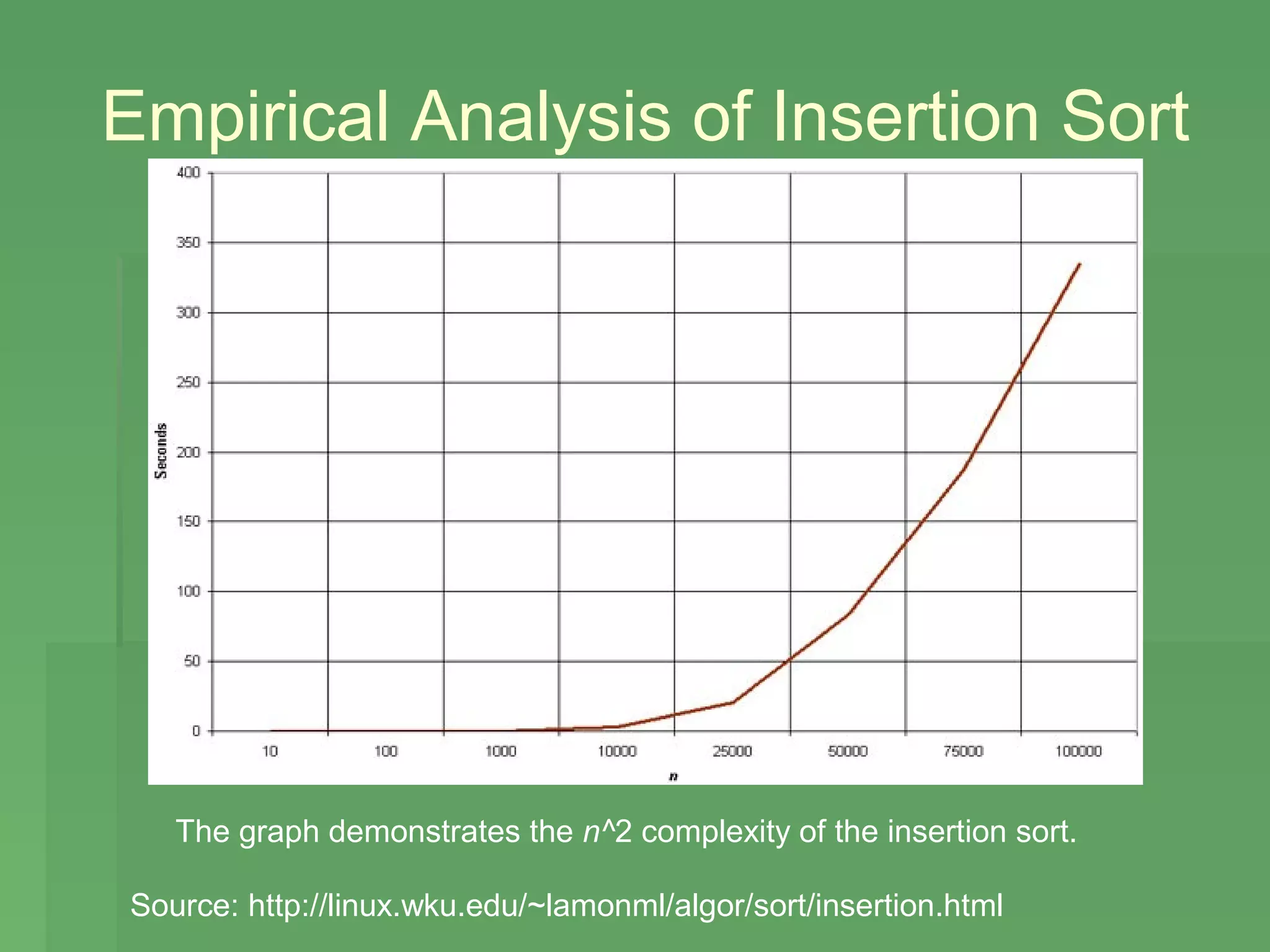
This document provides an overview and comparison of insertion sort and shellsort sorting algorithms. It describes how insertion sort works by repeatedly inserting elements into a sorted left portion of the array. Shellsort improves on insertion sort by making passes with larger increments to shift values into approximate positions before final sorting. The document discusses the time complexities of both algorithms and provides examples to illustrate how they work.





















![Shellsort
After each phase and some increment
hk, for every i, we have a[ i ] ≤ a [ i + hk ]
all elements spaced hk apart are sorted.
The file is said to be hk – sorted.](https://image.slidesharecdn.com/issort-andyle-120924110113-phpapp02/75/Sorting-Techniques-23-2048.jpg)