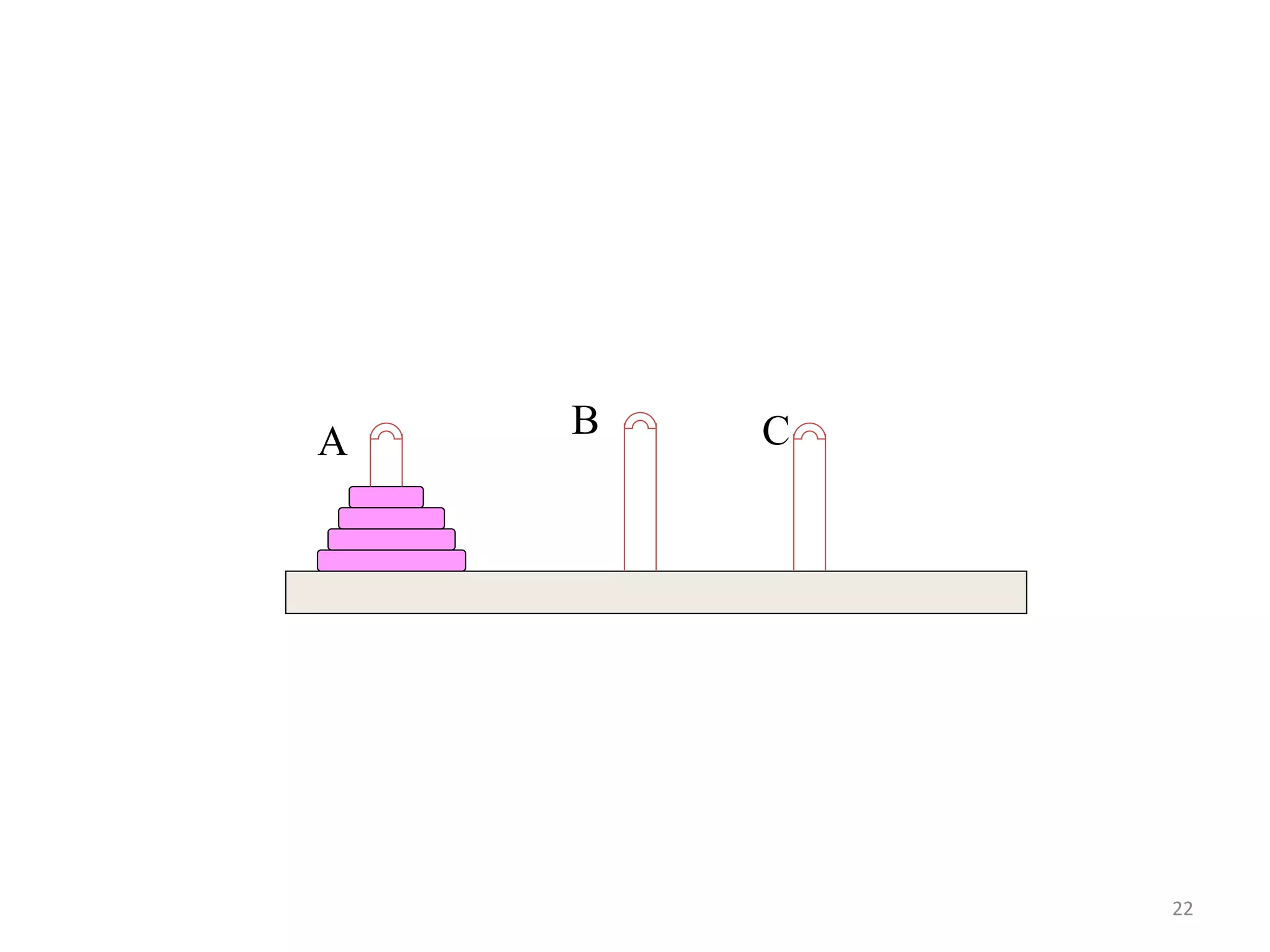
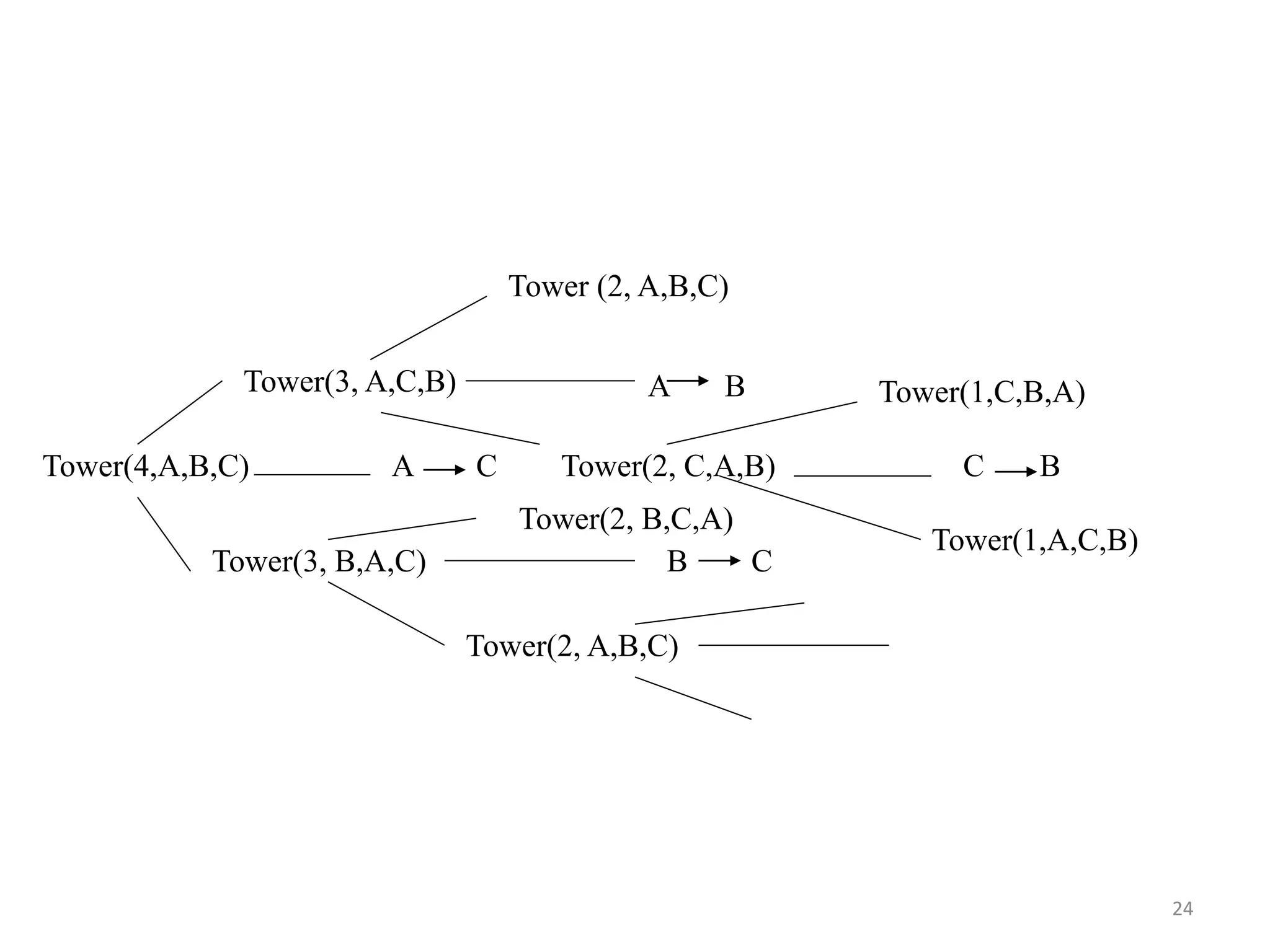
A stack is a linear data structure that follows the LIFO (last in, first out) principle. Elements can only be inserted or removed from one end, called the top. Stacks have common operations like push to add an element and pop to remove the top element. Stacks have many applications including evaluating arithmetic expressions in postfix notation, implementing recursion, and solving puzzles like Towers of Hanoi. The document discusses stack implementations using arrays and linked lists and provides examples of stack applications.


![5
Push and Pop operations on Stack
PUSH(STACK,TOP,MAXSTACK,ITEM)
1. [STACK already filled]
If TOP=MAXSTACK, then Print
OVERFLOW and Return.
2. Set TOP=TOP+1
3. Set STACK[TOP]=ITEM.
4. Return.
top
empty stack
A
top
push an element
top
push another
A
B
top
pop
A
POP(STACK,TOP,ITEM)
1. If TOP=0, then print
UNDERFLOW and Return
2. Set ITEM=STACK[TOP].
3. Set TOP=TOP-1.
4. Return.](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-5-2048.jpg)
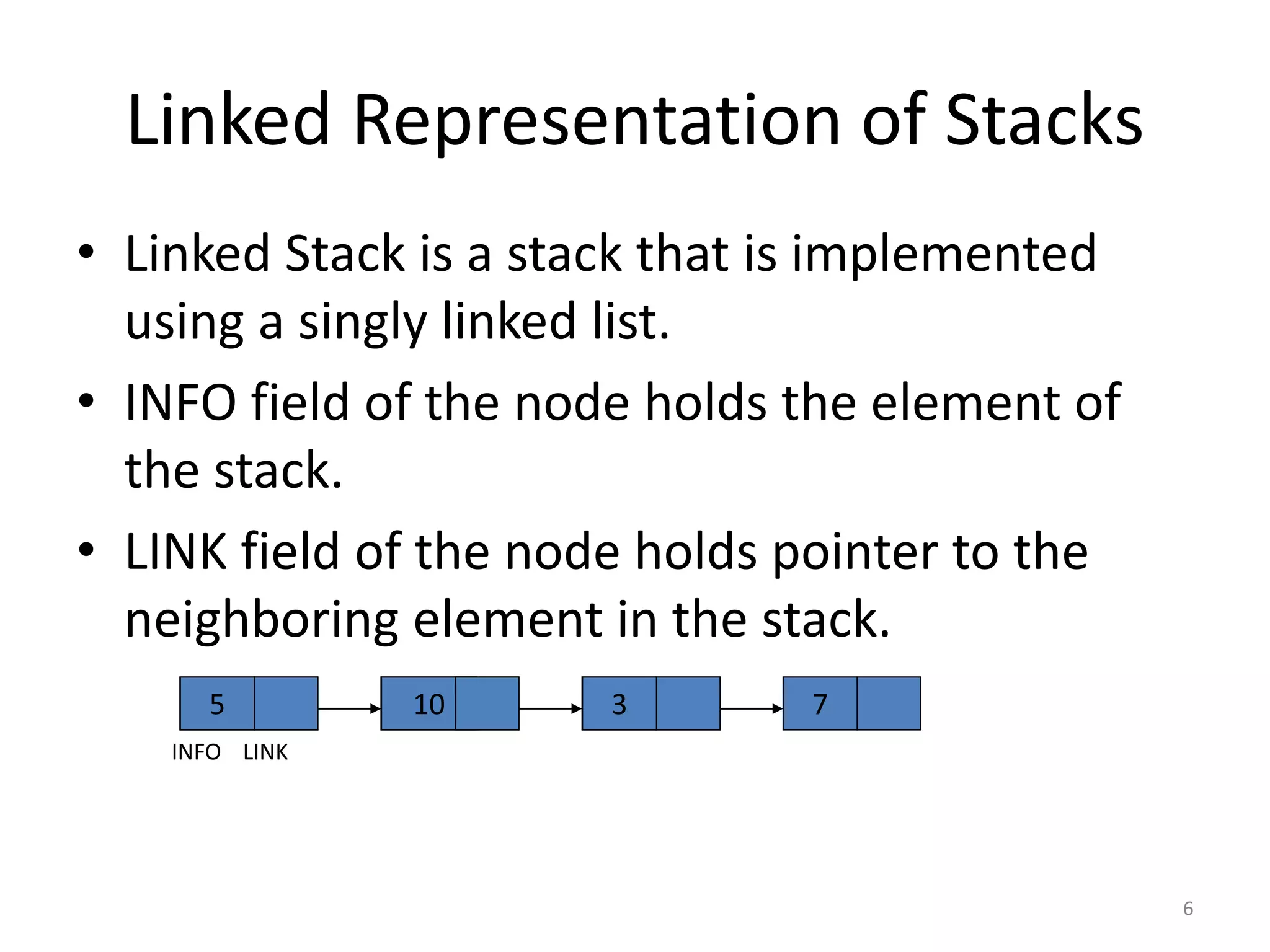
![7
PUSH operation in Linked Stack
1. If AVAIL == NULL then write OVERFLOW and
Exit
2. Set NEW = AVAIL and AVAIL=LINK[AVAIL]
3. Set INFO[NEW] = ITEM
4. Set LINK[NEW] = TOP
5. Set TOP = NEW
6. Exit
*AVAIL is the pointer to available free nodes list.](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-7-2048.jpg)
![8
POP operation in Linked Stack
1. If TOP == NULL then write UNDERFLOW and
Exit
2. Set ITEM = INFO[TOP]
3. Set TEMP = TOP and TOP = LINK[TOP]
4. Set LINK[TEMP]=AVAIL and AVAIL=TEMP
5. Exit
*TEMP is the temporary node to save the deleted node
and add it to available free nodes list.](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-8-2048.jpg)



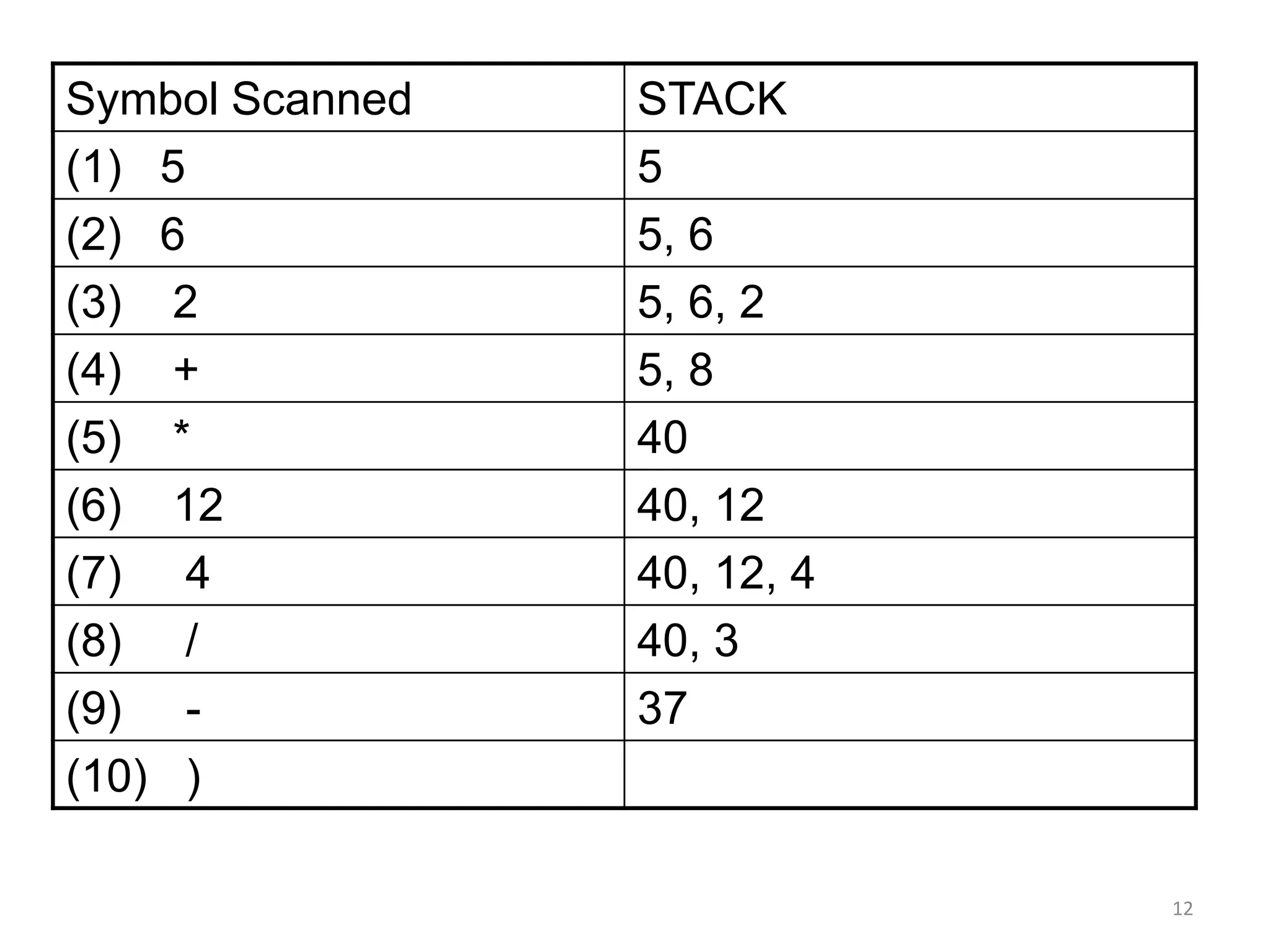

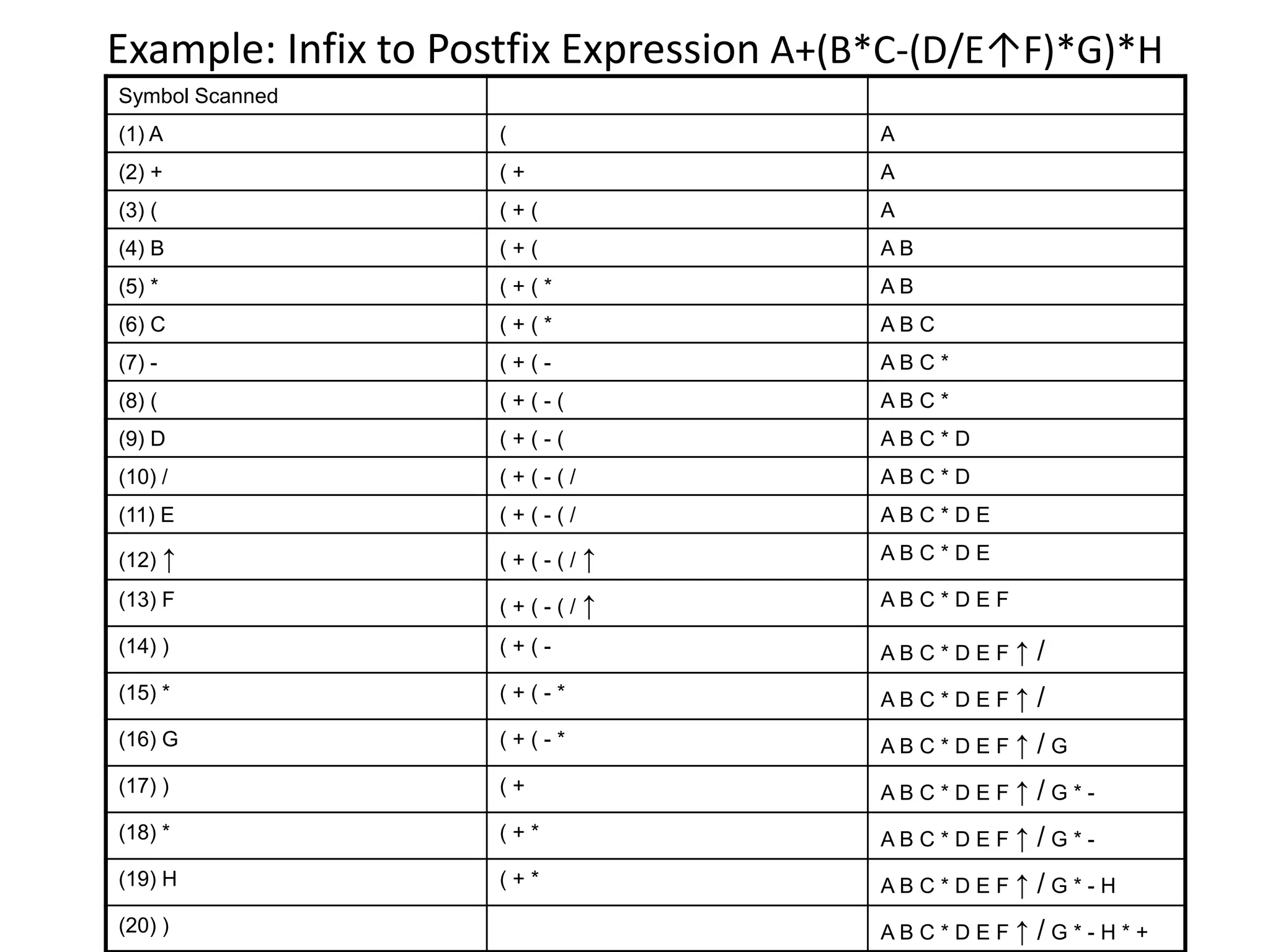


![1717
Quick Sort Algorithm
QUICK (A, N, BEG, END, LOC)
1. [Initialize] Set LEFT= BEG, RIGHT=END and LOC=BEG
2. [Scan from right to left]
a) Repeat while A[LOC]<=A[RIGHT] and LOC != RIGHT
RIGHT=RIGHT-1
[End of loop]
b) If LOC=RIGHT then : Return
c) If A[LOC]>A[RIGHT] then
i) Interchange A[LOC] and A[RIGHT]
ii) Set LOC=RIGHT
iii) Go to step 3
[End of If structure]](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-17-2048.jpg)
![18
3. [Scan from left to right]
a) Repeat while A[LEFT]<=A[LOC] and LEFT!=LOC
LEFT=LEFT+1
[End of loop]
b) If LOC=LEFT, then Return
c) If A[LEFT]>A[LOC], then
i) Interchange A[LEFT] and A[LOC]
ii) Set LOC=LEFT
iii) Goto step 2
[End of If structure]
18](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-18-2048.jpg)
![19
(QuickSort) This algorithm sorts an array A with N elements.
1. TOP=NULL.
2. If N>1 then TOP=TOP+1, LOWER[1]=1, UPPER[1]=N.
3. Repeat Steps 4 to 7 while TOP!=NULL.
4. Set BEG=LOWER[TOP], END=UPPER[TOP].
TOP=TOP-1
5. Call QUICK(A, N, BEG, END, LOC).
6. If BEG<LOC-1 then
TOP=TOP+1, LOWER[TOP]=BEG, UPPER[TOP]=LOC-1
[End of If structure]
7. If LOC+1<END then
TOP=TOP+1, LOWER[TOP]=LOC+1, UPPER[TOP]=END
[End of If Structure]
[End of Step 3 loop]
8. Exit.
19](https://image.slidesharecdn.com/3-201004091122/75/Stacks-in-DATA-STRUCTURE-19-2048.jpg)