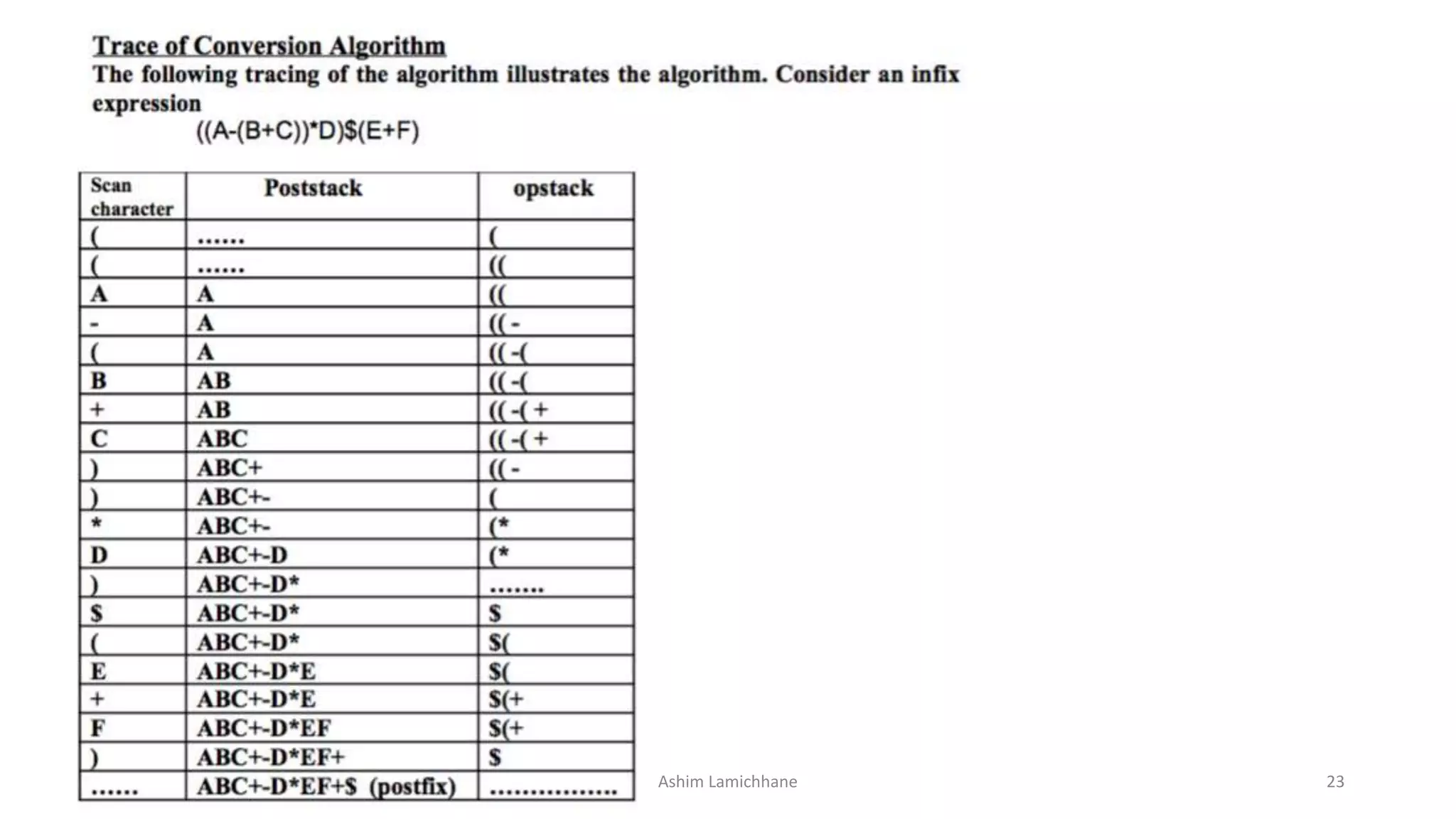
The document provides an overview of stacks as a linear data structure that follows the Last In First Out (LIFO) principle, outlining its operations such as push and pop, and emphasizing its use cases in scenarios requiring insertion or deletion at one end. It also covers various notations for expressions including infix, prefix, and postfix, along with methods for converting and evaluating these expressions. Additionally, the document touches on recursion, illustrating it through the Tower of Hanoi problem and discussing its pros and cons.















![Evaluation of Postfix Expressions
• From above we get,
2 3 * 5 4 * + 9 –
Stack
EvaluatePostfix(exp)
{
create a stack S
for i=0 to length (exp) -1
{
if (exp[i] is operand)
PUSH(exp[i])
elseif (exp[i] is operator)
op2 <- pop()
op1 <- pop()
res– Perform(exp[i],op1,op2)
PUSH(res)
}
return top of STACK
}
2
3
Ashim Lamichhane 17](https://image.slidesharecdn.com/thestack-160620061743/75/The-Stack-And-Recursion-17-2048.jpg)