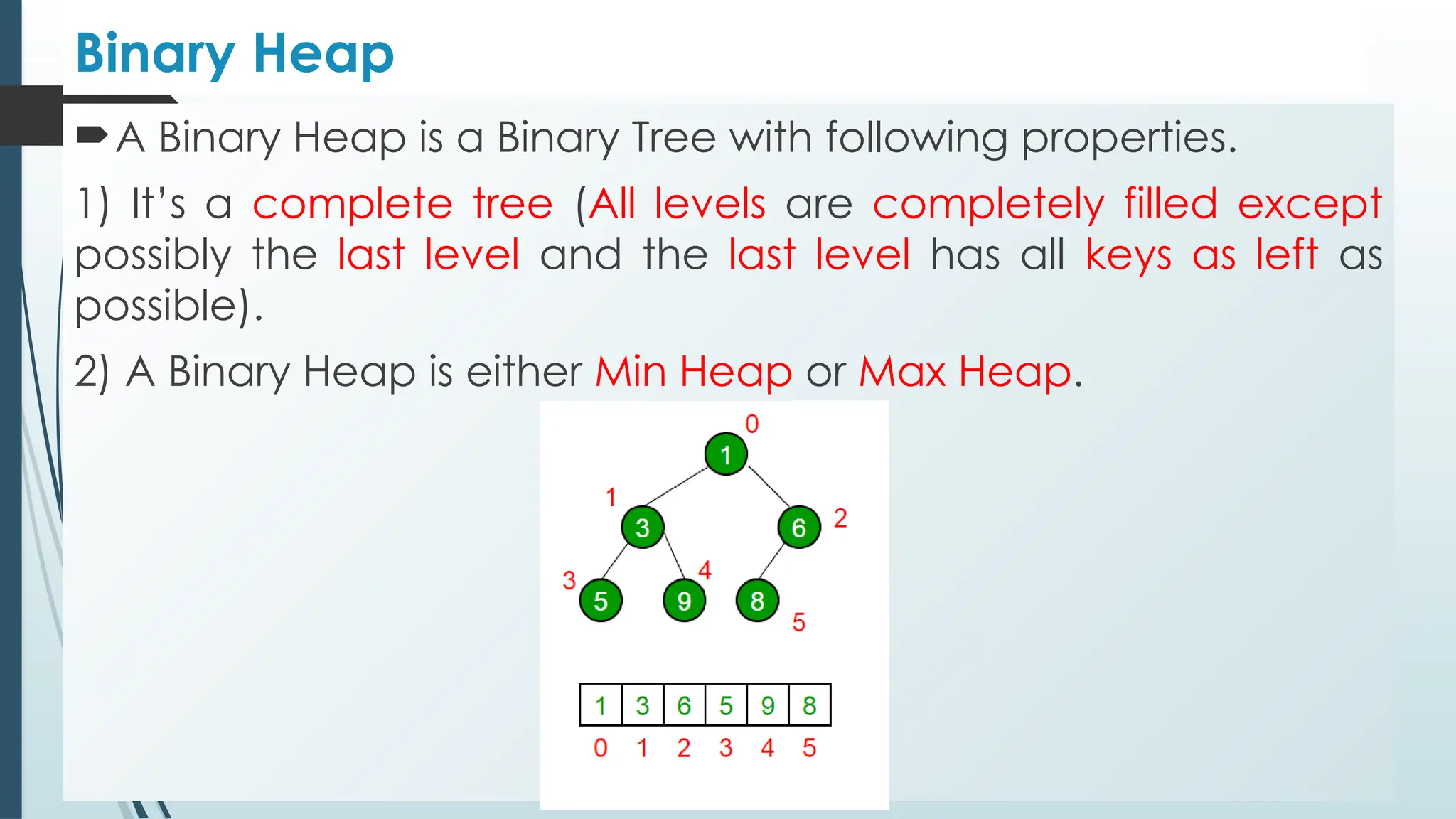
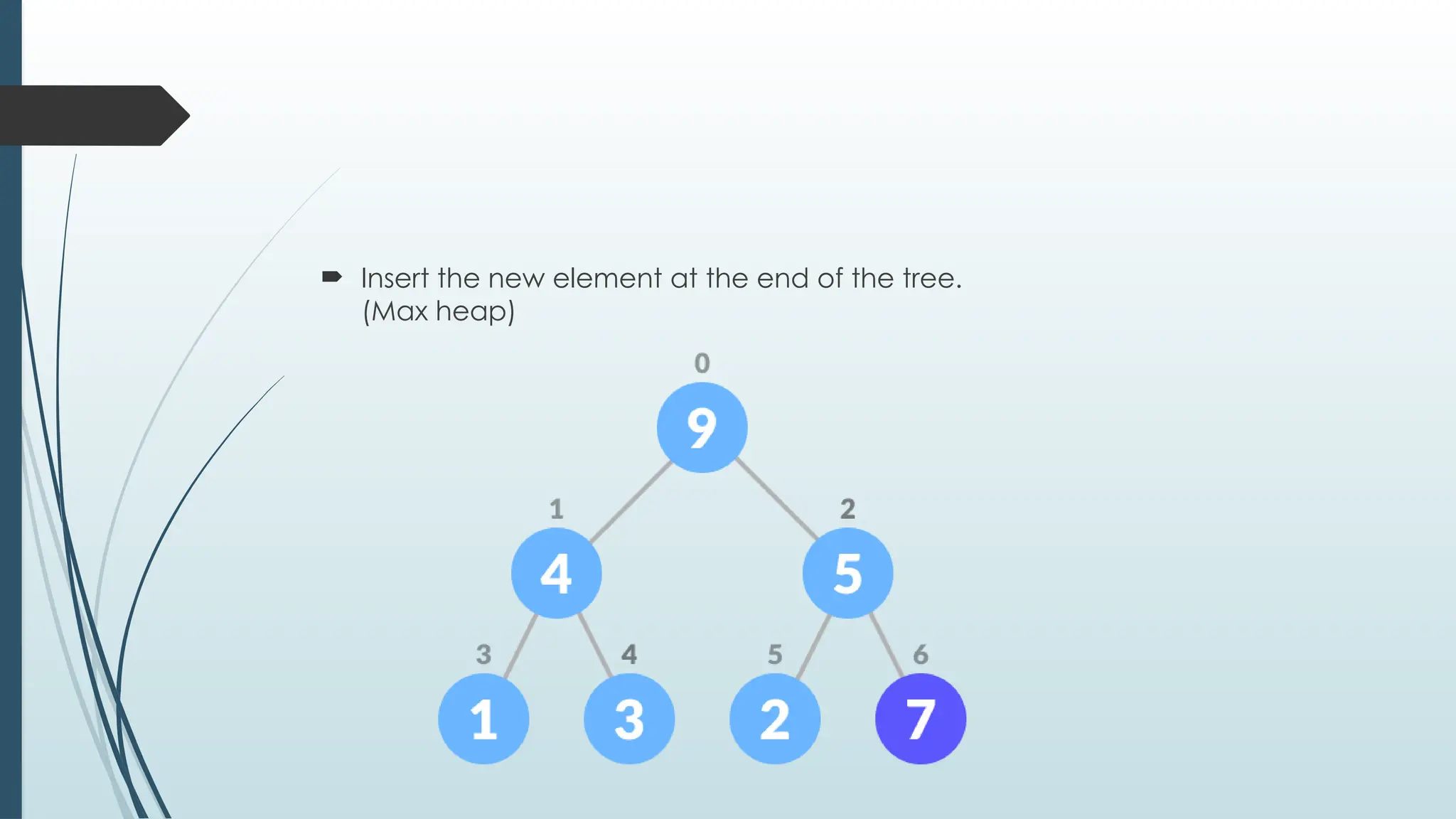
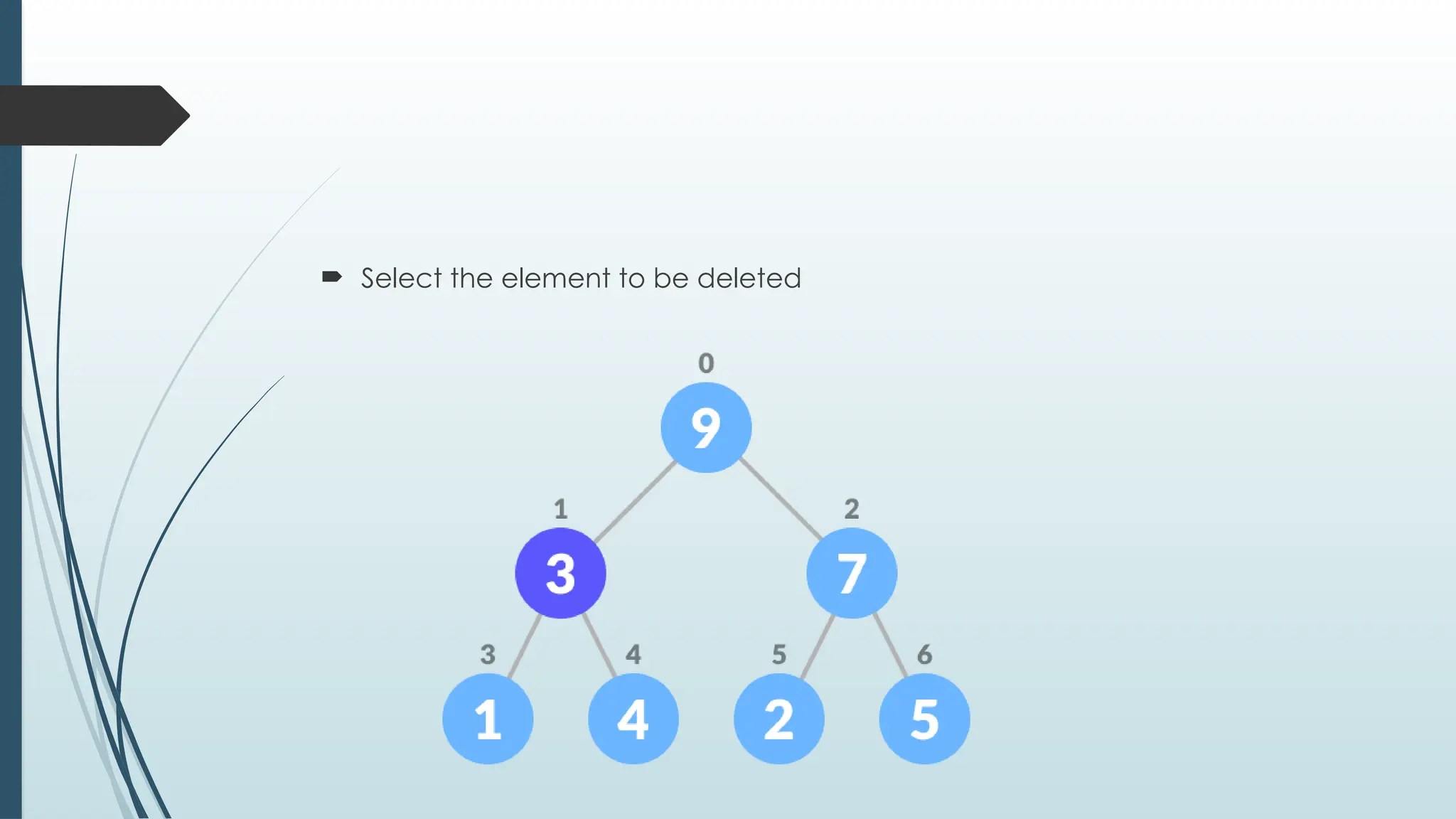
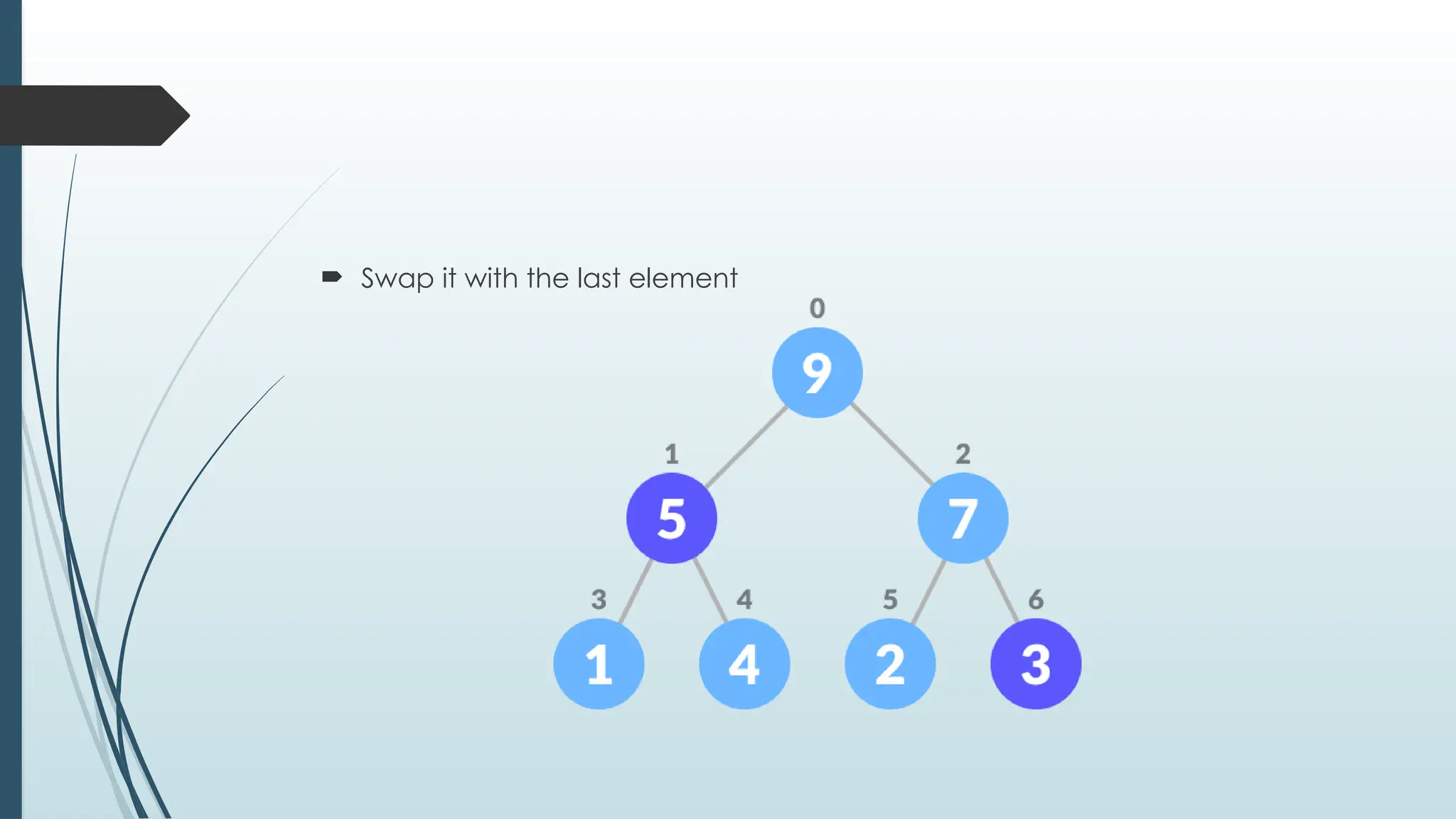
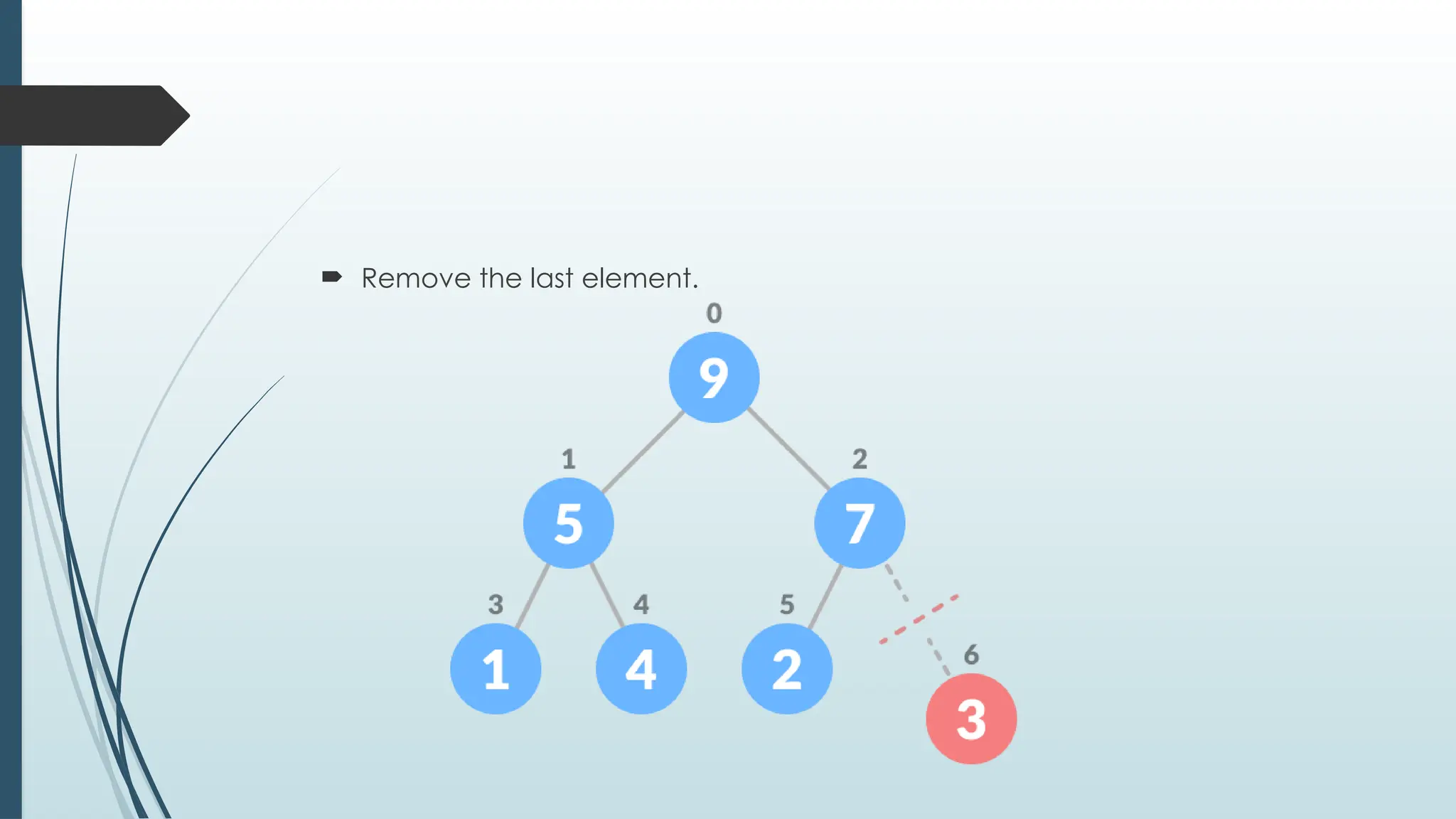
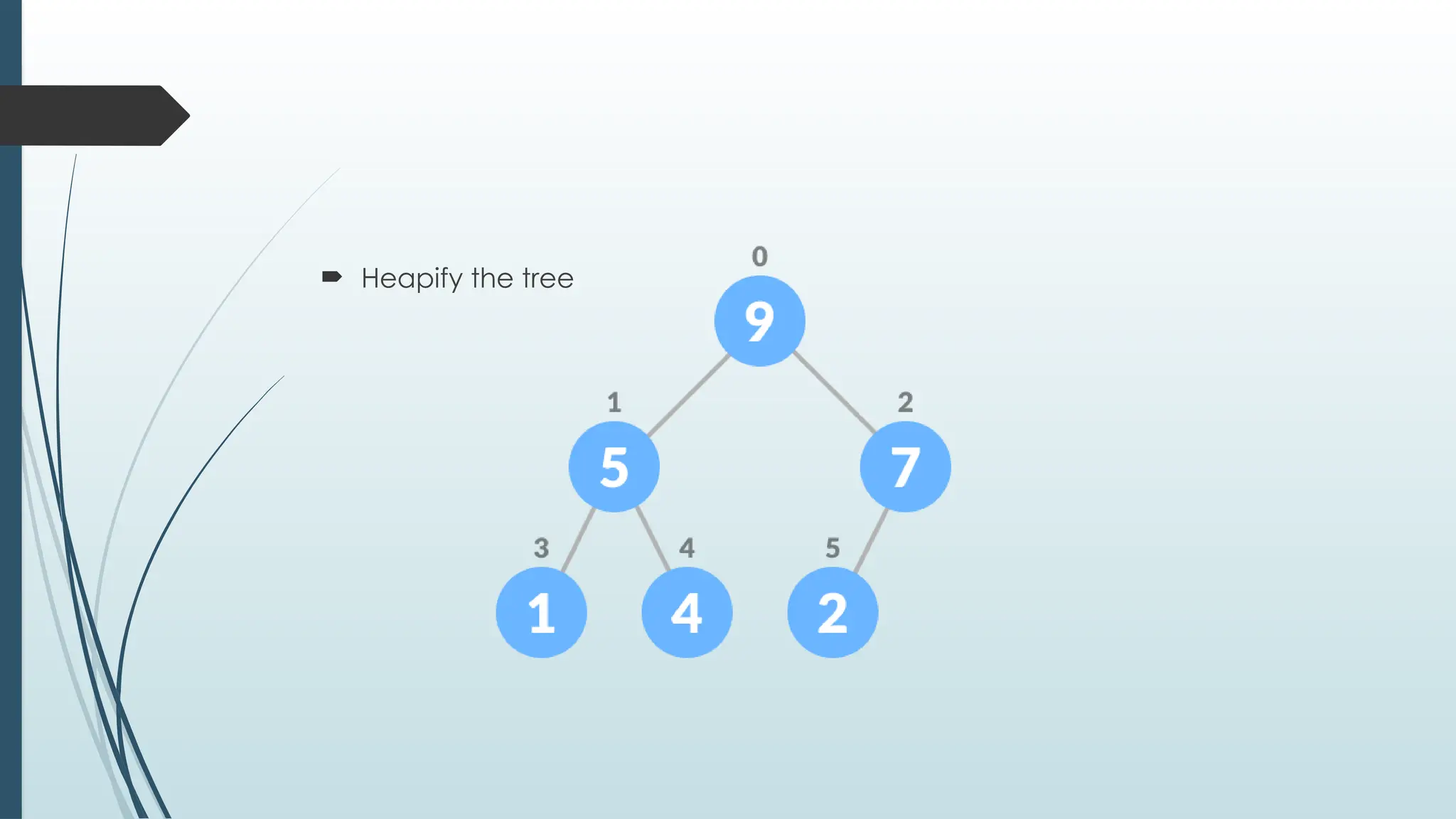
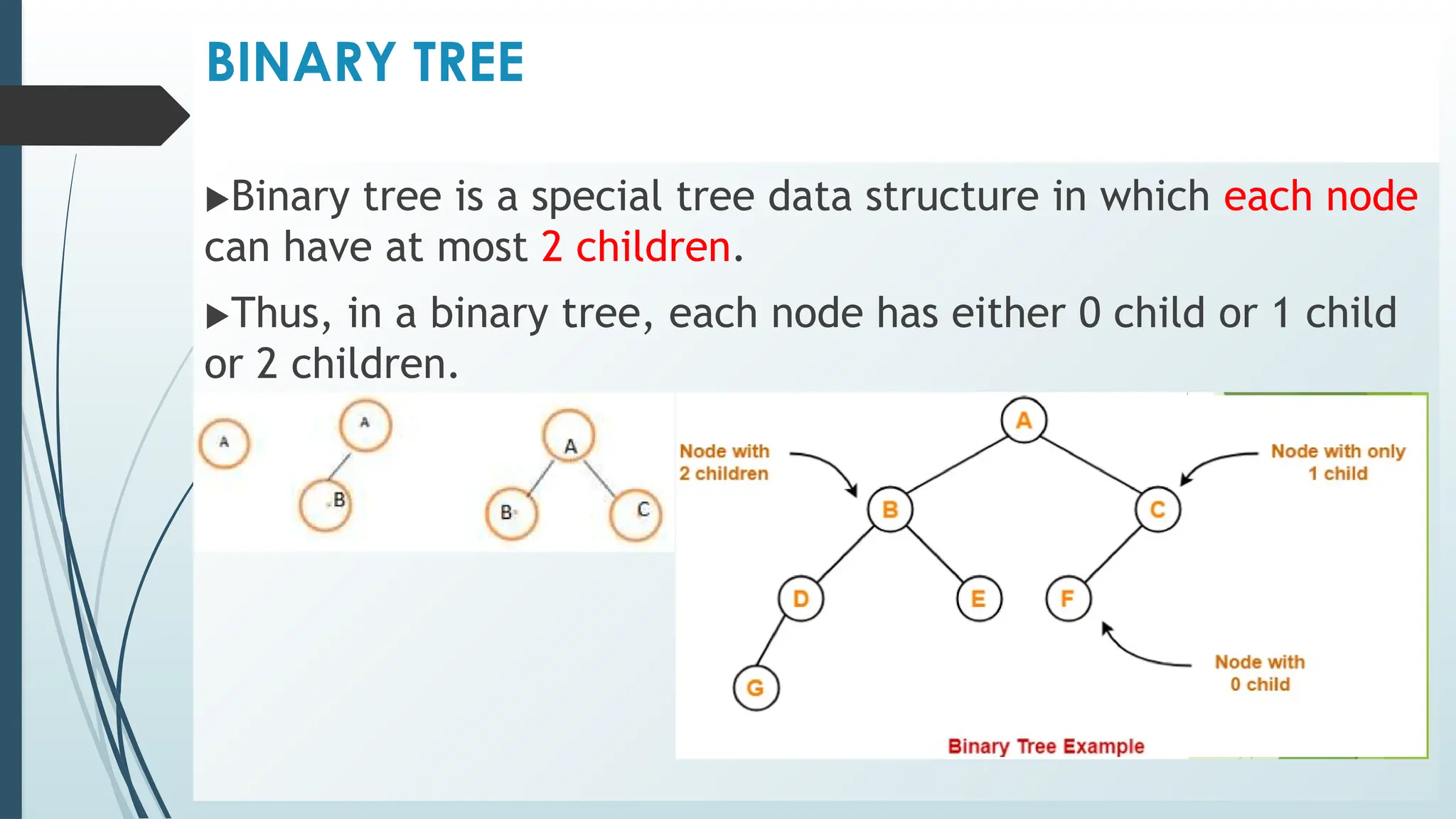
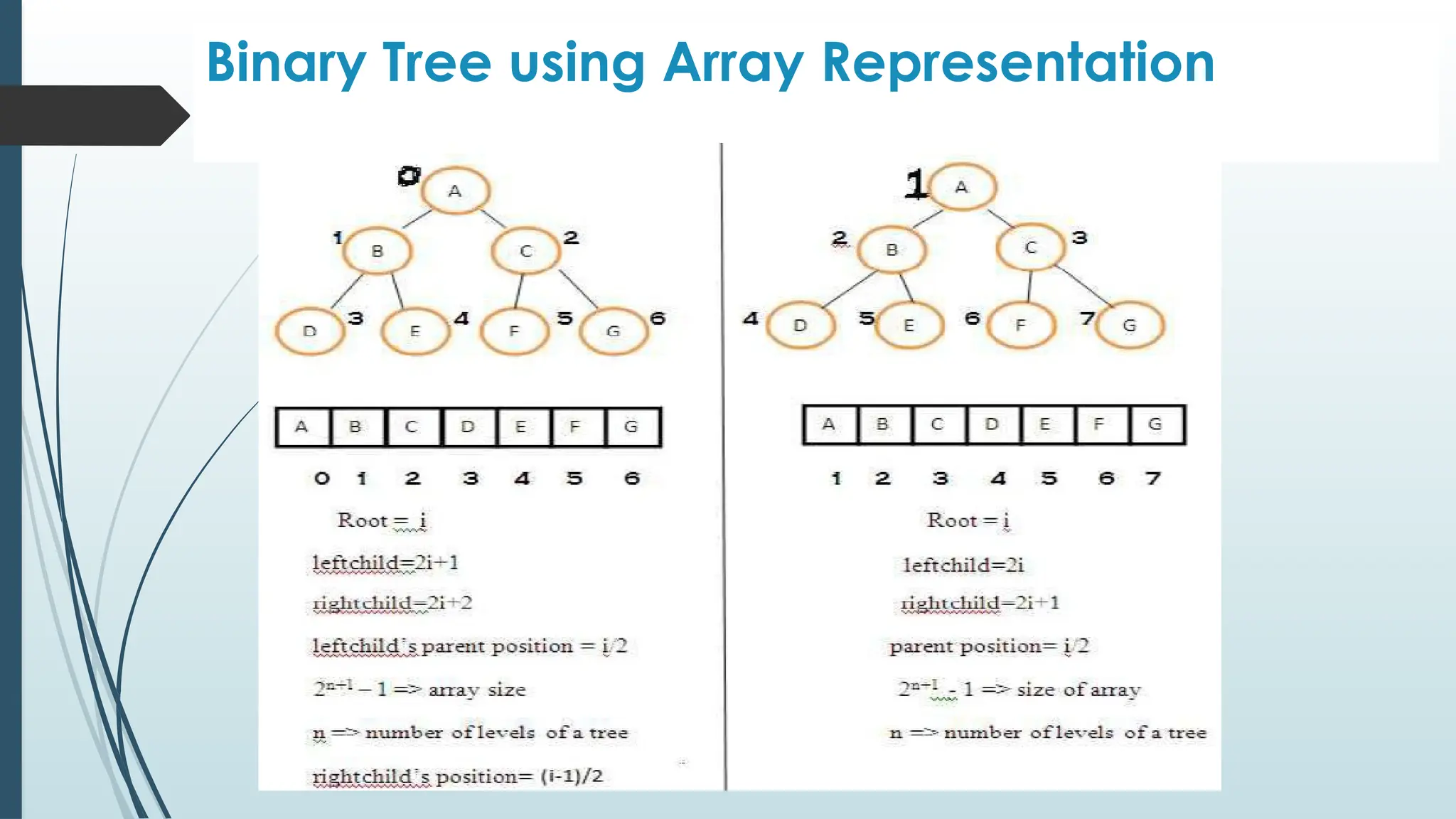
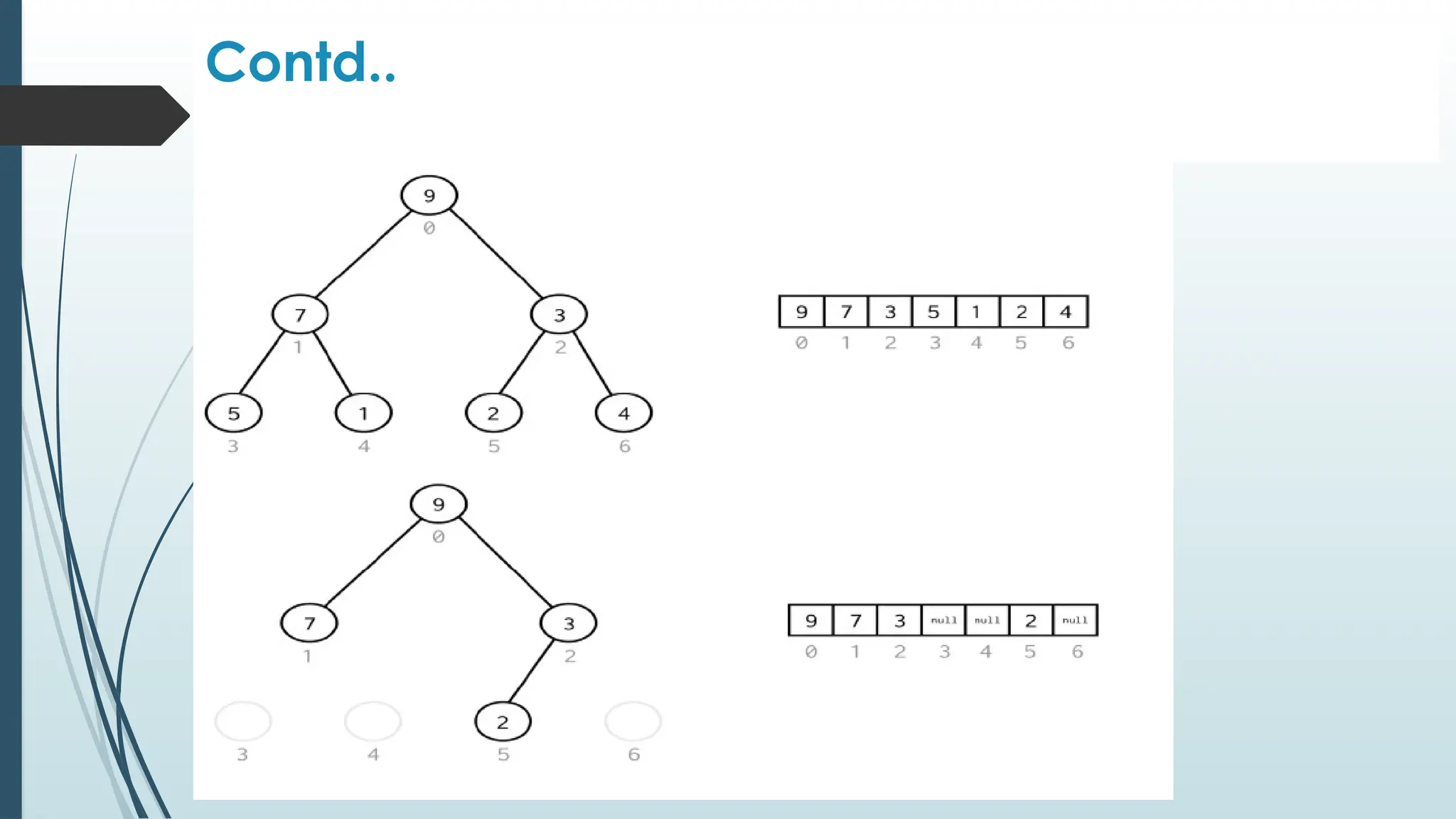
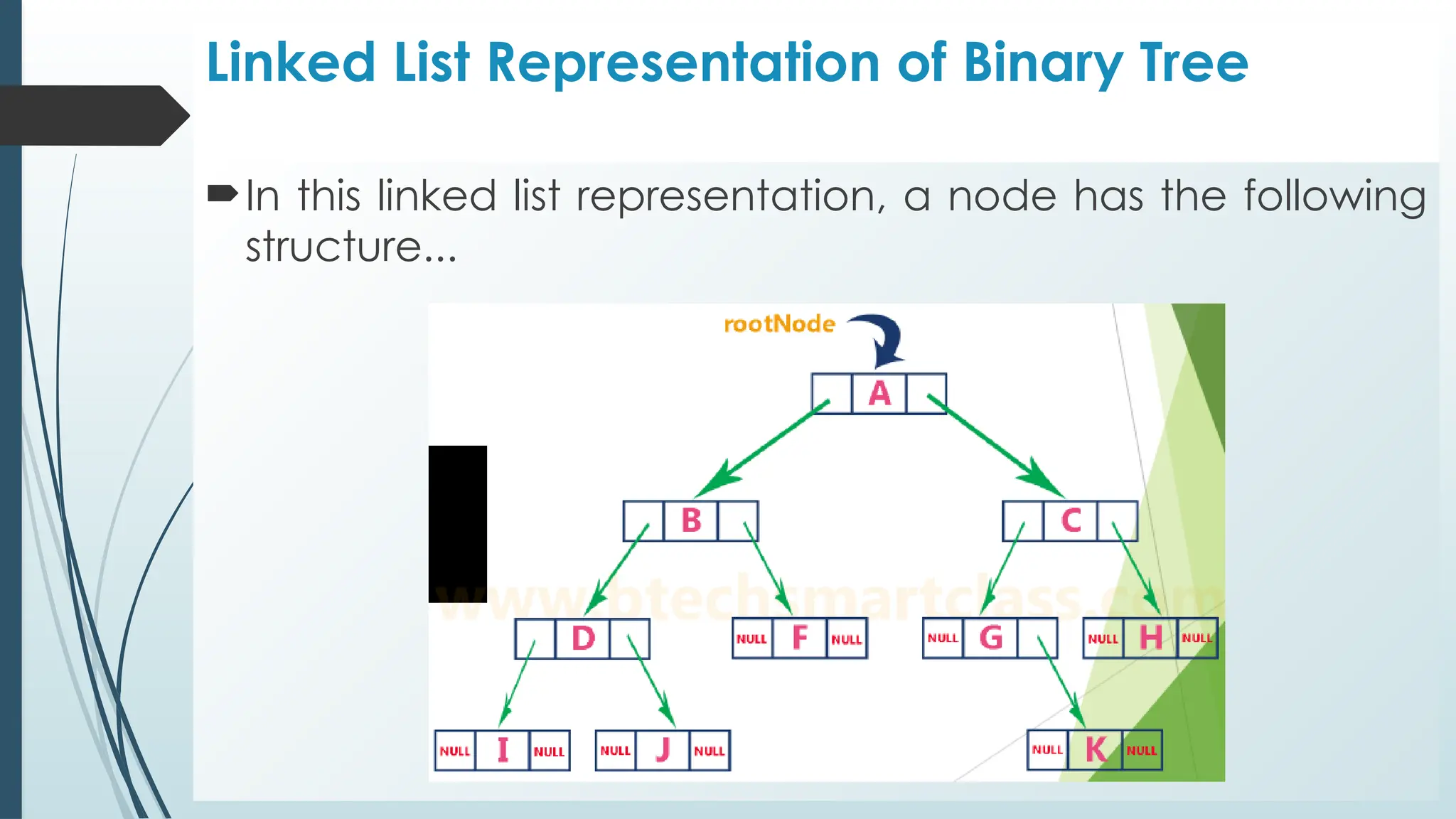
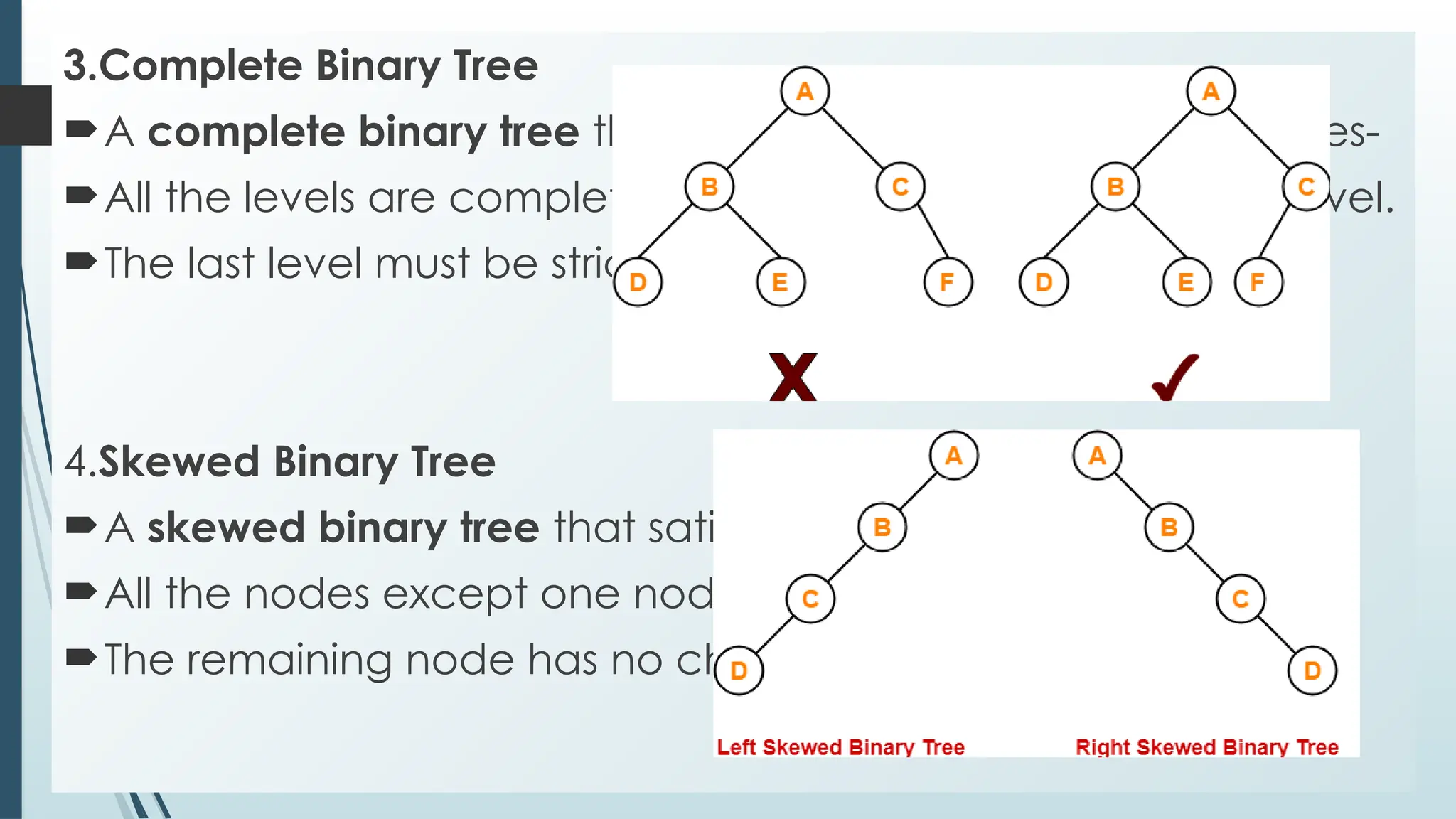
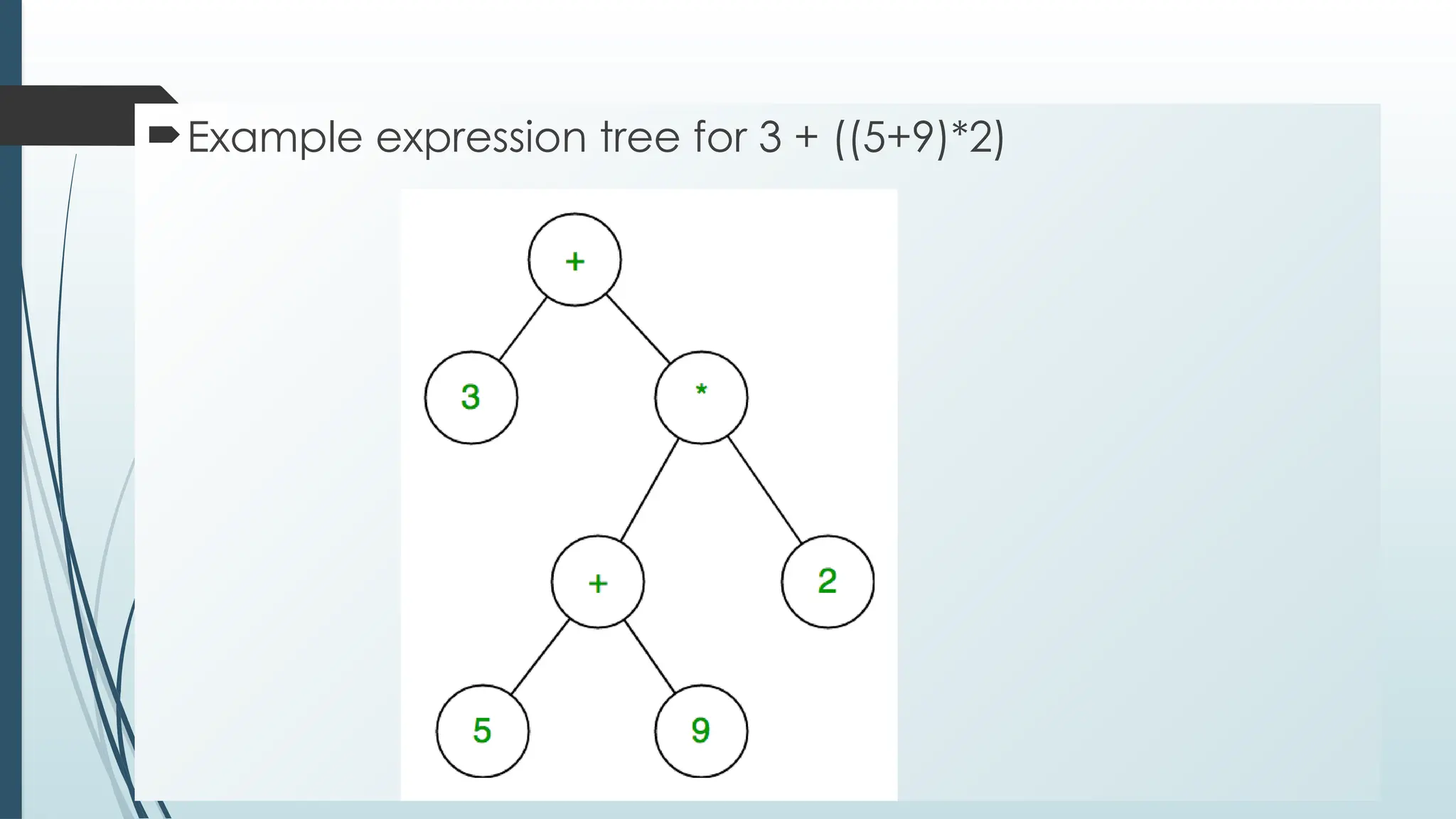
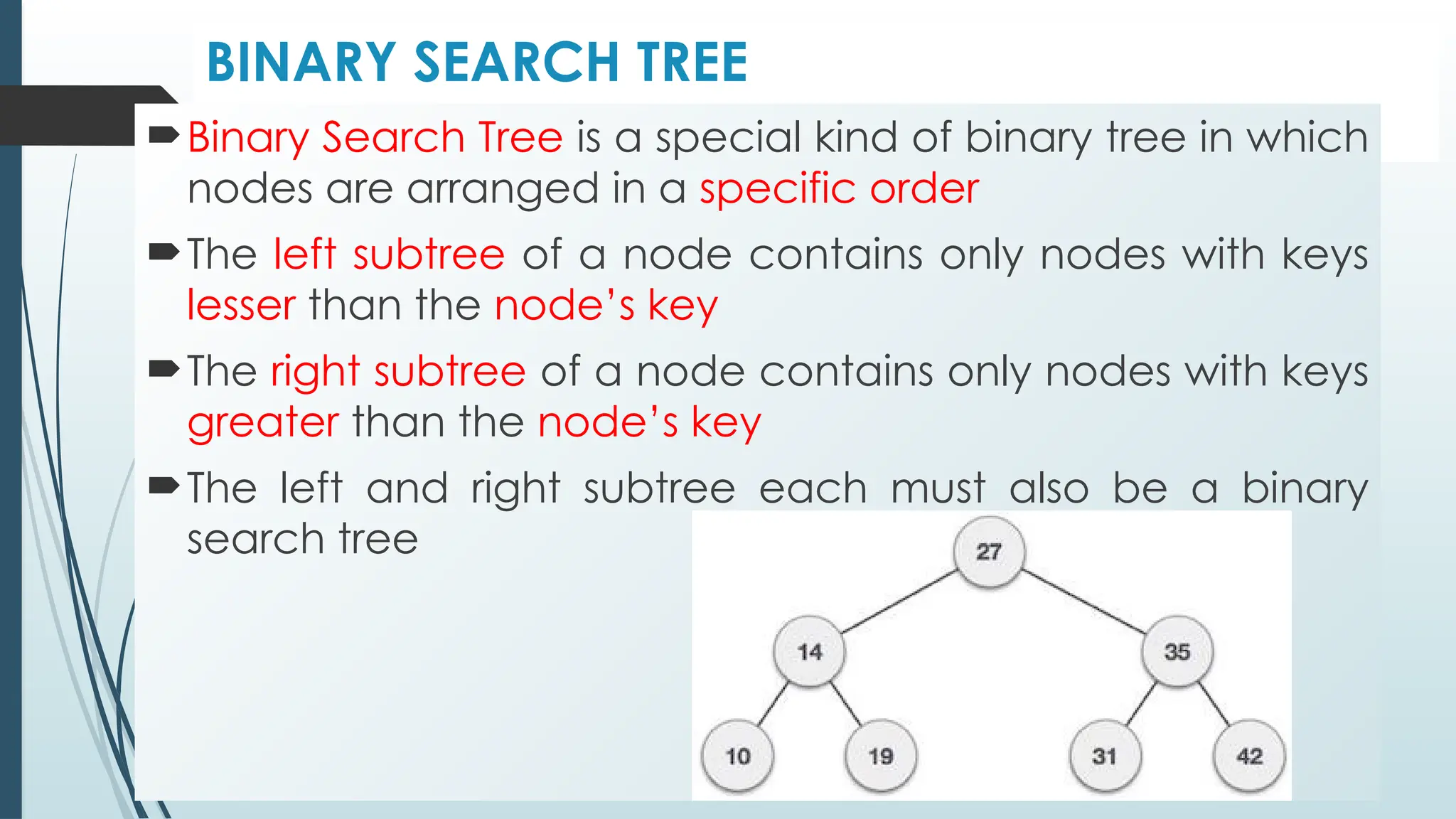
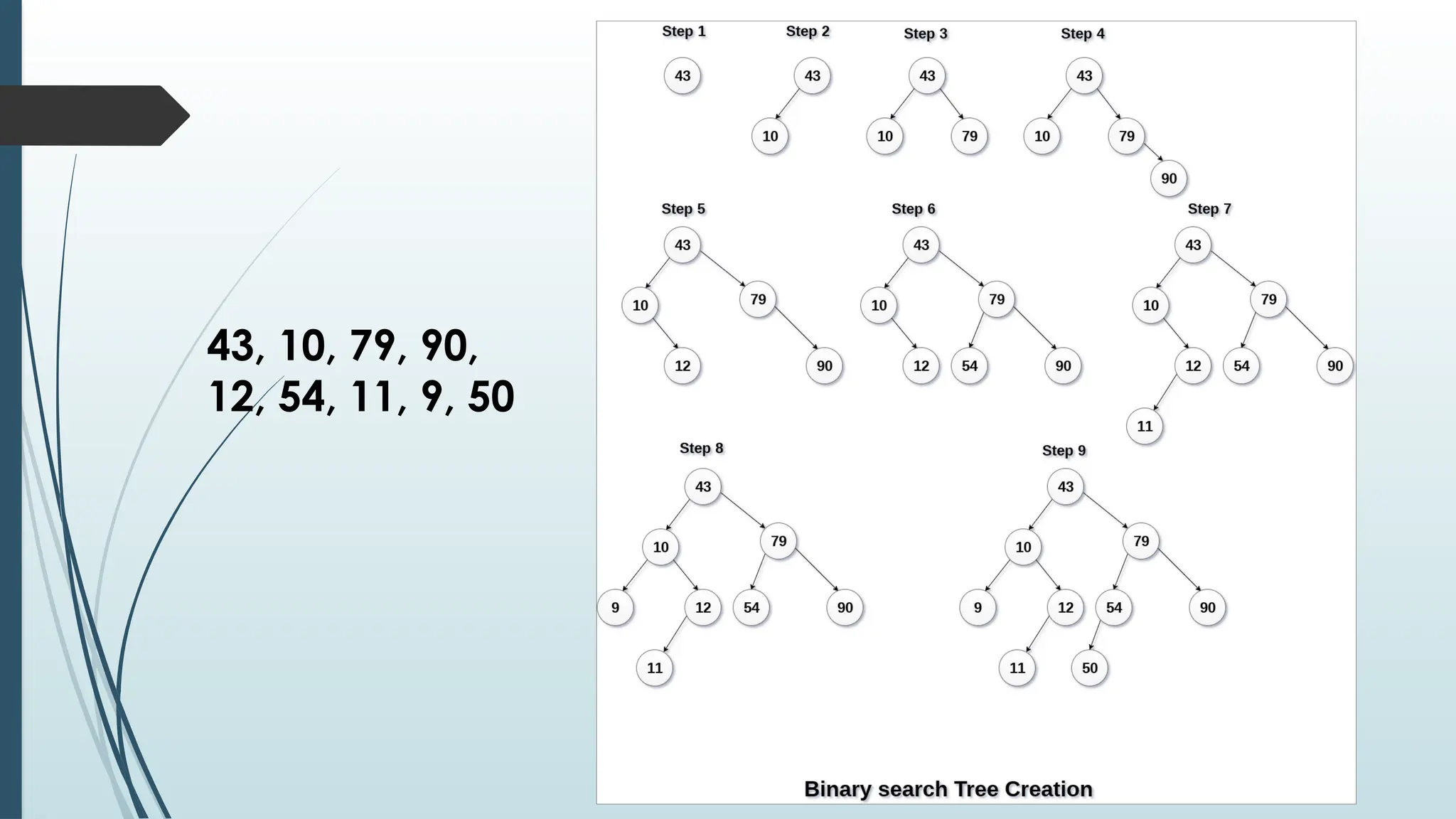
The document provides an overview of non-linear data structures, particularly trees, including their definitions, types, and operations. It explains tree terminology, binary trees, AVL trees, and various tree traversal methods, alongside their applications such as binary search trees and heaps. Key concepts such as tree balance factors and operations for insertion, deletion, and searching in binary search trees are also discussed.




















![Routine:
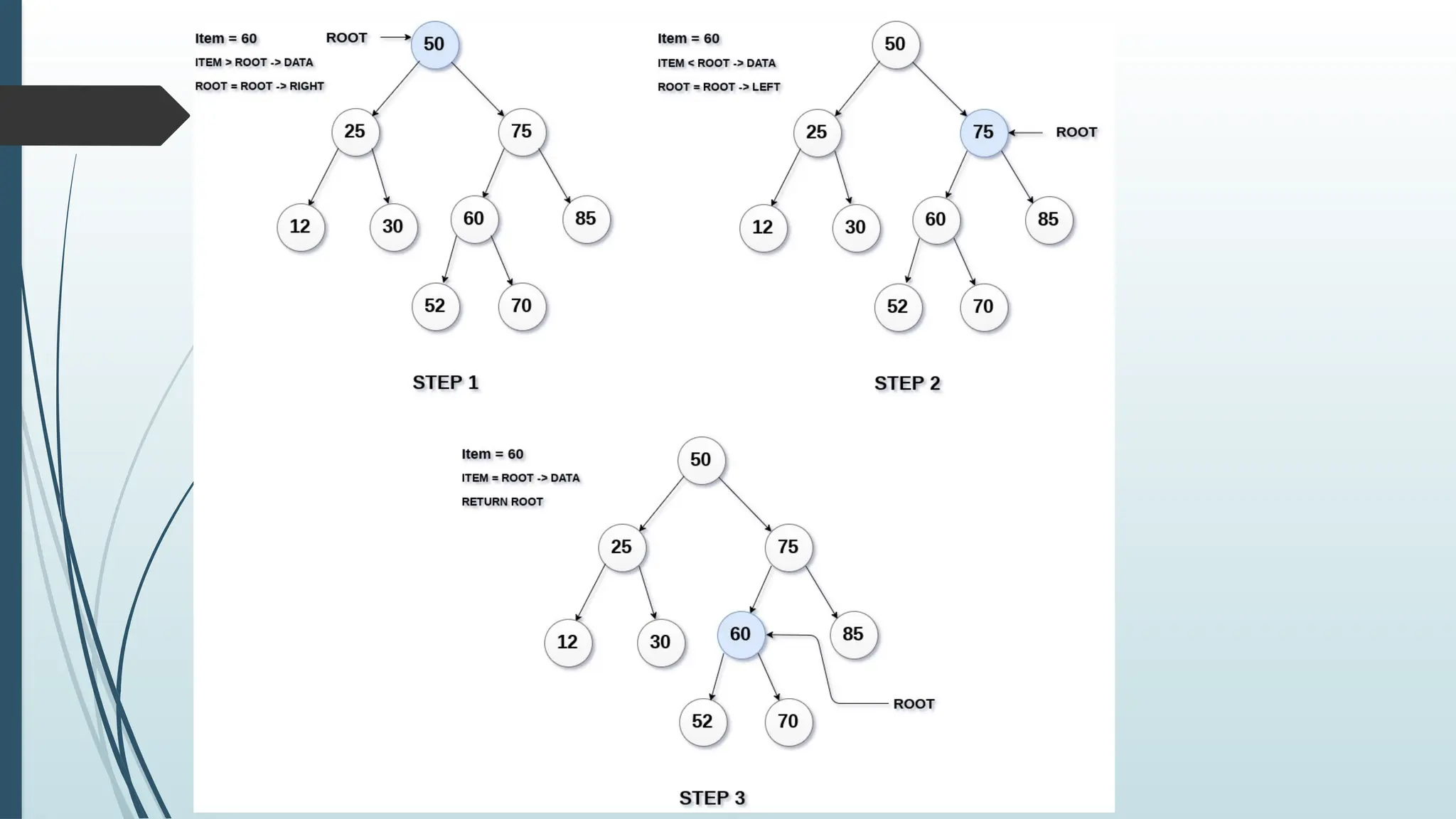
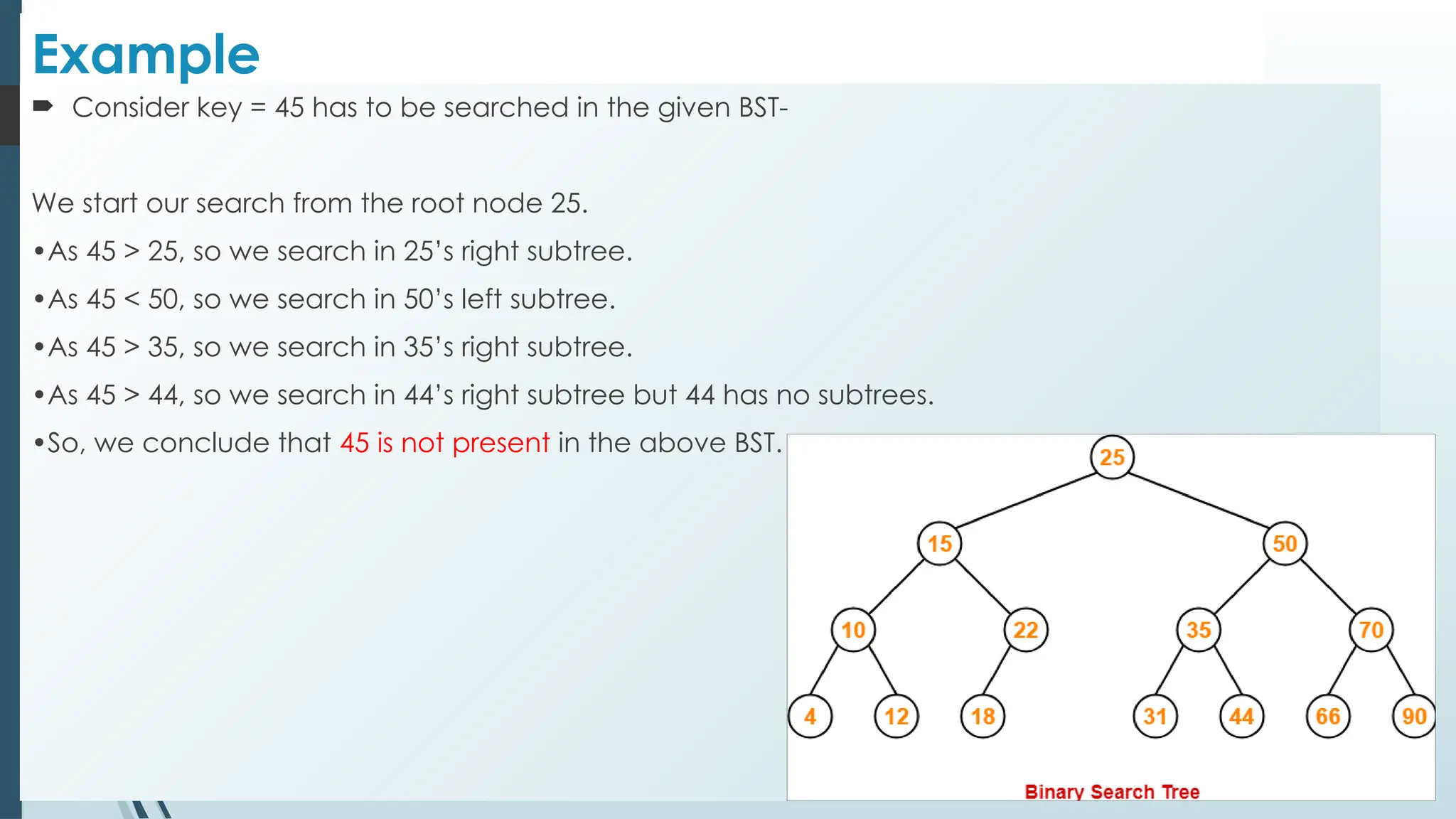
Search (ROOT, ITEM)
IF ROOT --> DATA = ITEM OR
ROOT == NULL
Return ROOT
ELSE
IF ITEM < ROOT --> DATA
Return search(ROOT --> LEFT, ITEM)
ELSE
Return search(ROOT --> RIGHT, ITEM)
[END OF IF]
[END OF IF]](https://image.slidesharecdn.com/unitiiinonlineardatastructures-trees-241126054300-1ba19308/75/UNIT-III-Non-Linear-Data-Structures-Trees-pptx-41-2048.jpg)

![Routine:
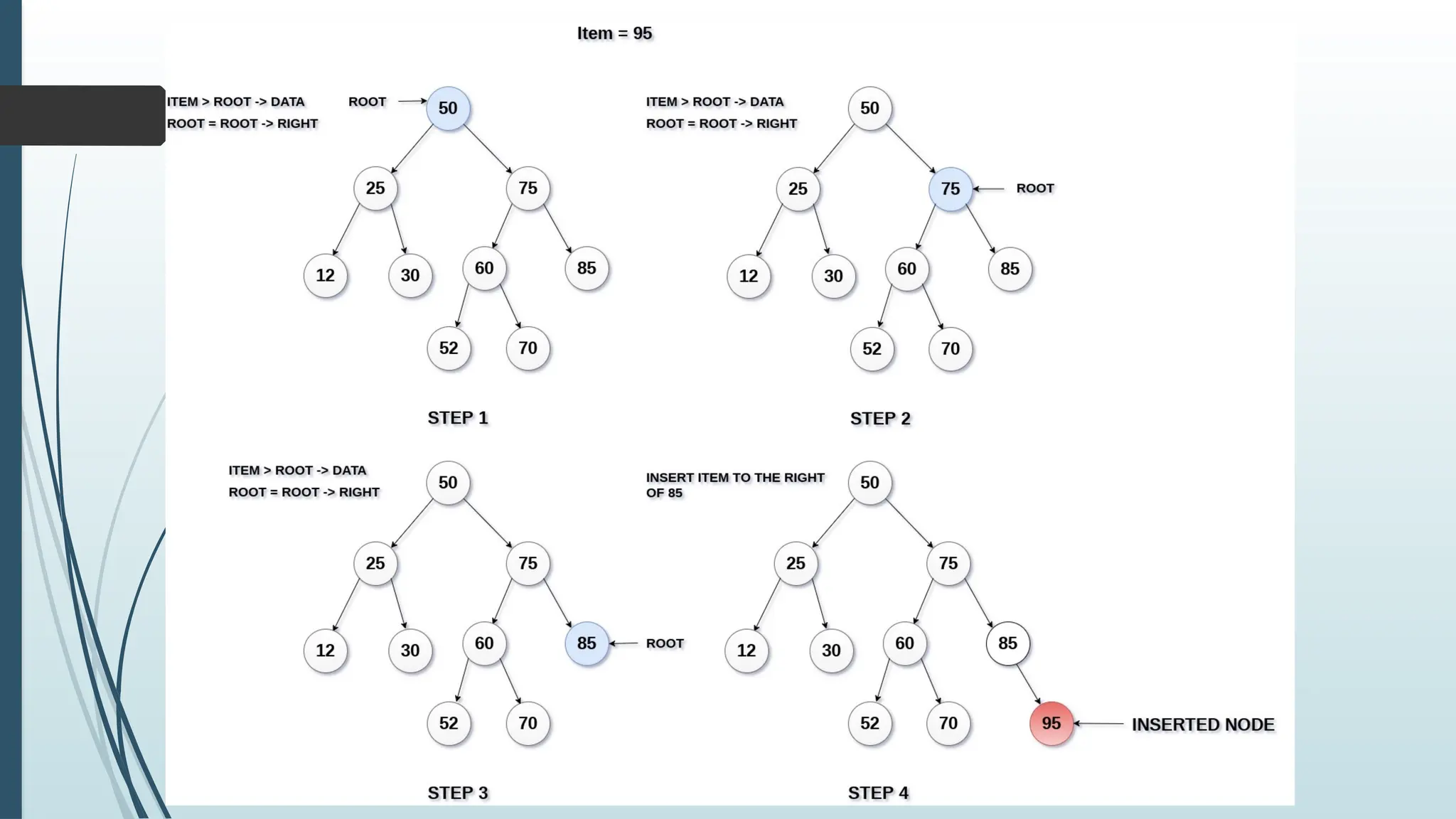
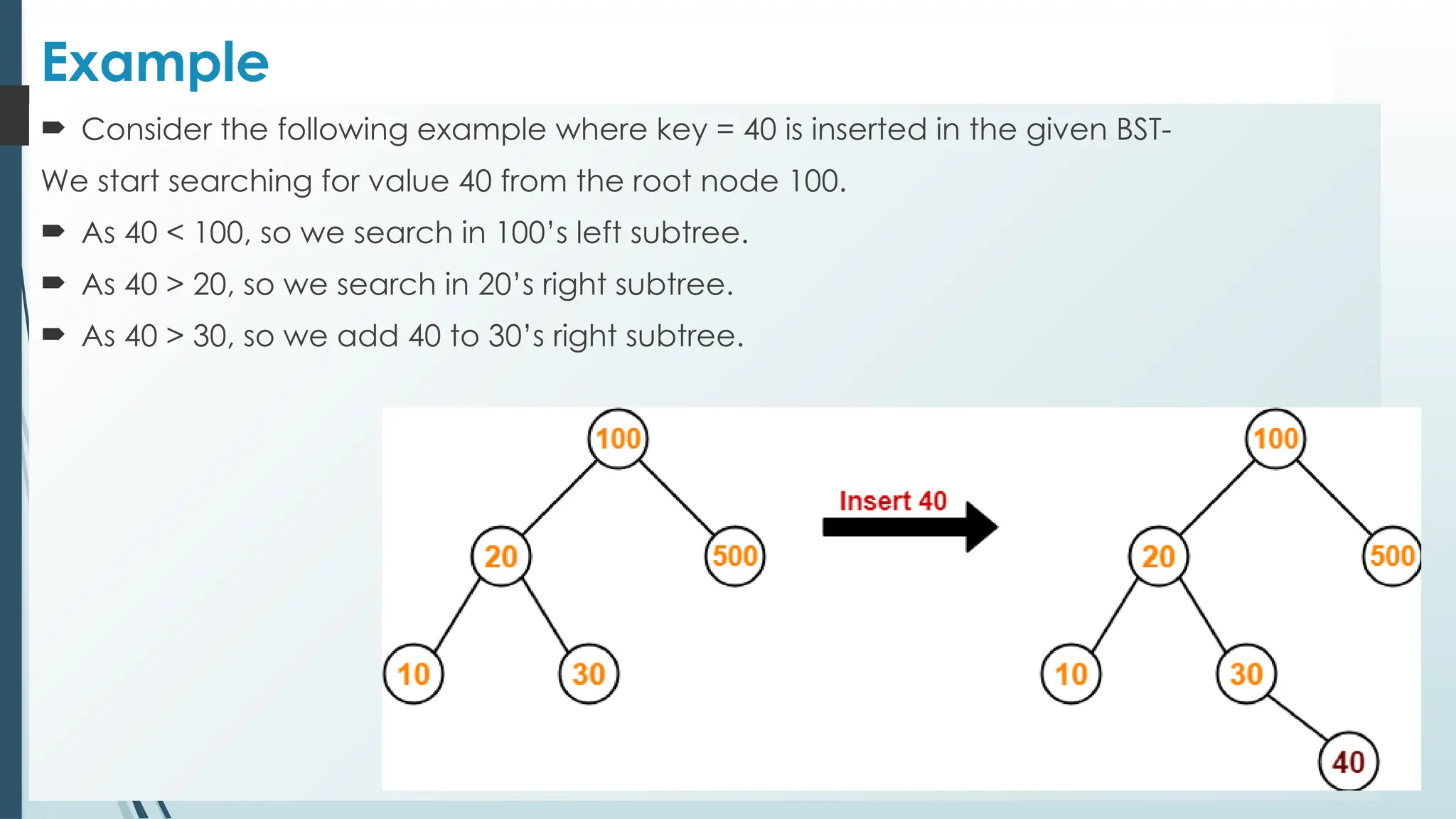
Insert(ROOT, ITEM)
IF ROOT == NULL
Allocate memory for TREE
SET ROOT --> DATA = ITEM
SET ROOT --> LEFT = ROOT --> RIGHT = NULL
ELSE
IF ITEM < ROOT --> DATA
Insert(ROOT --> LEFT, ITEM)
ELSE
Insert(ROOT --> RIGHT, ITEM)
[END OF IF]
[END OF IF]](https://image.slidesharecdn.com/unitiiinonlineardatastructures-trees-241126054300-1ba19308/75/UNIT-III-Non-Linear-Data-Structures-Trees-pptx-45-2048.jpg)














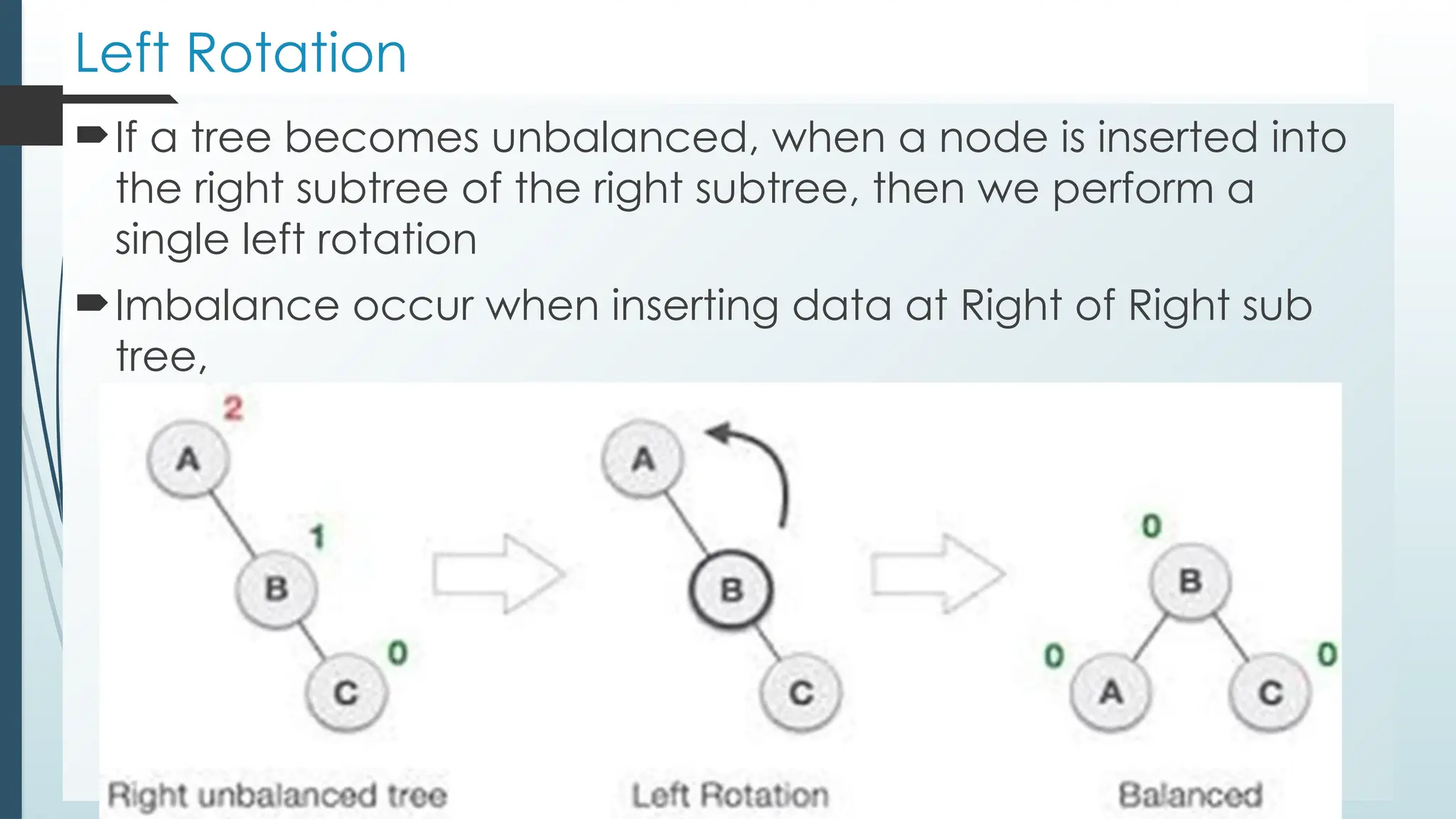
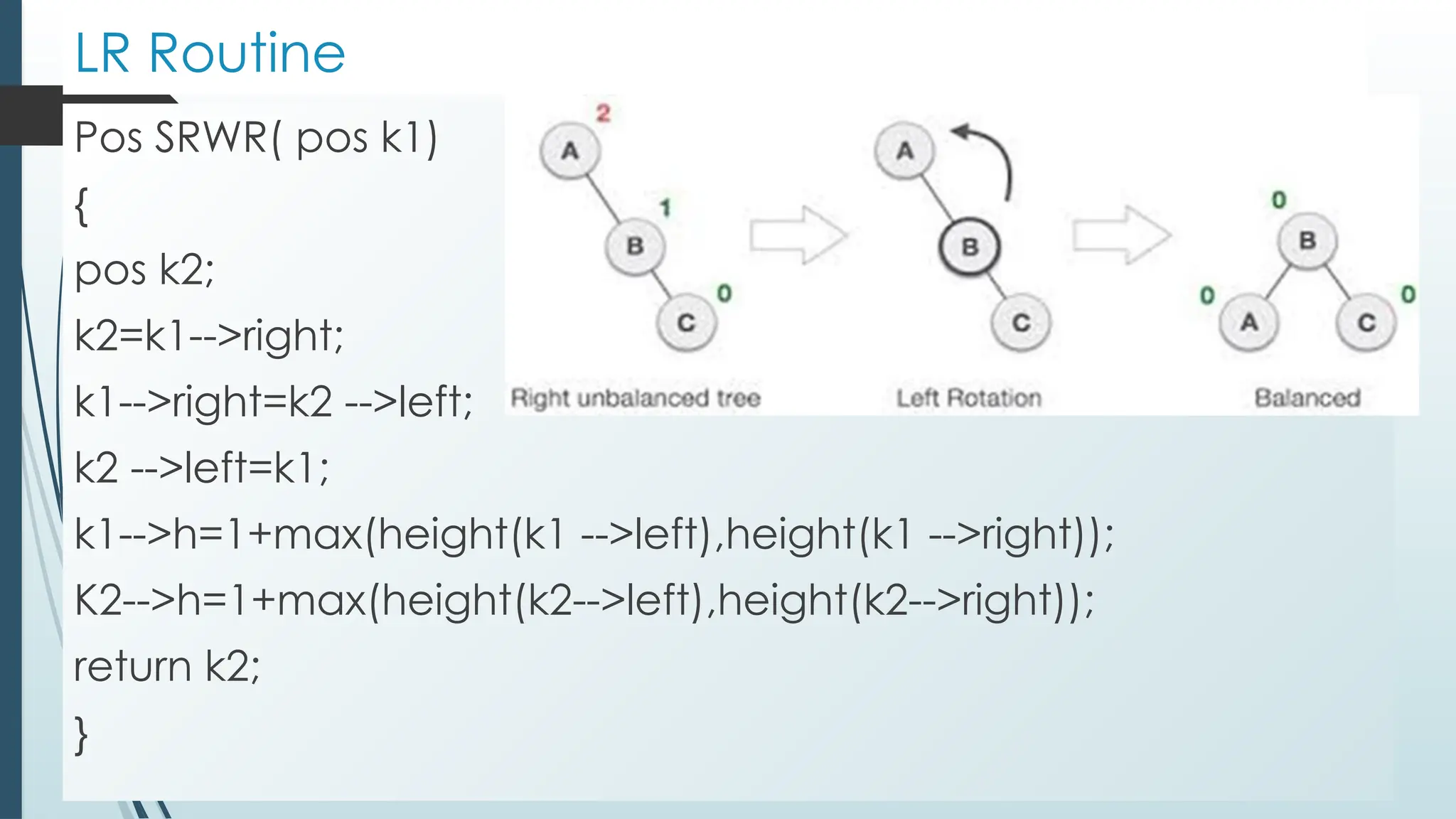
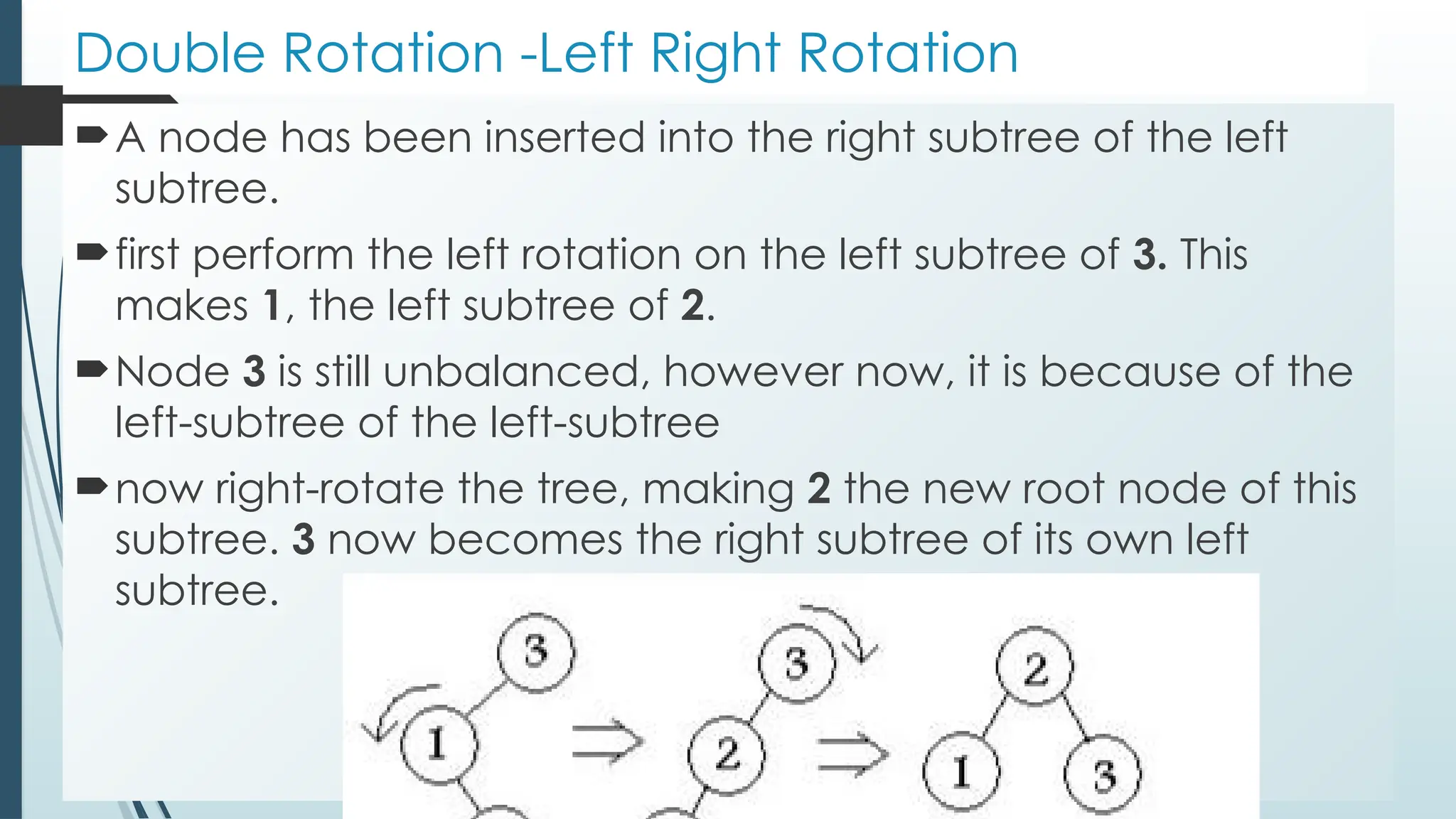


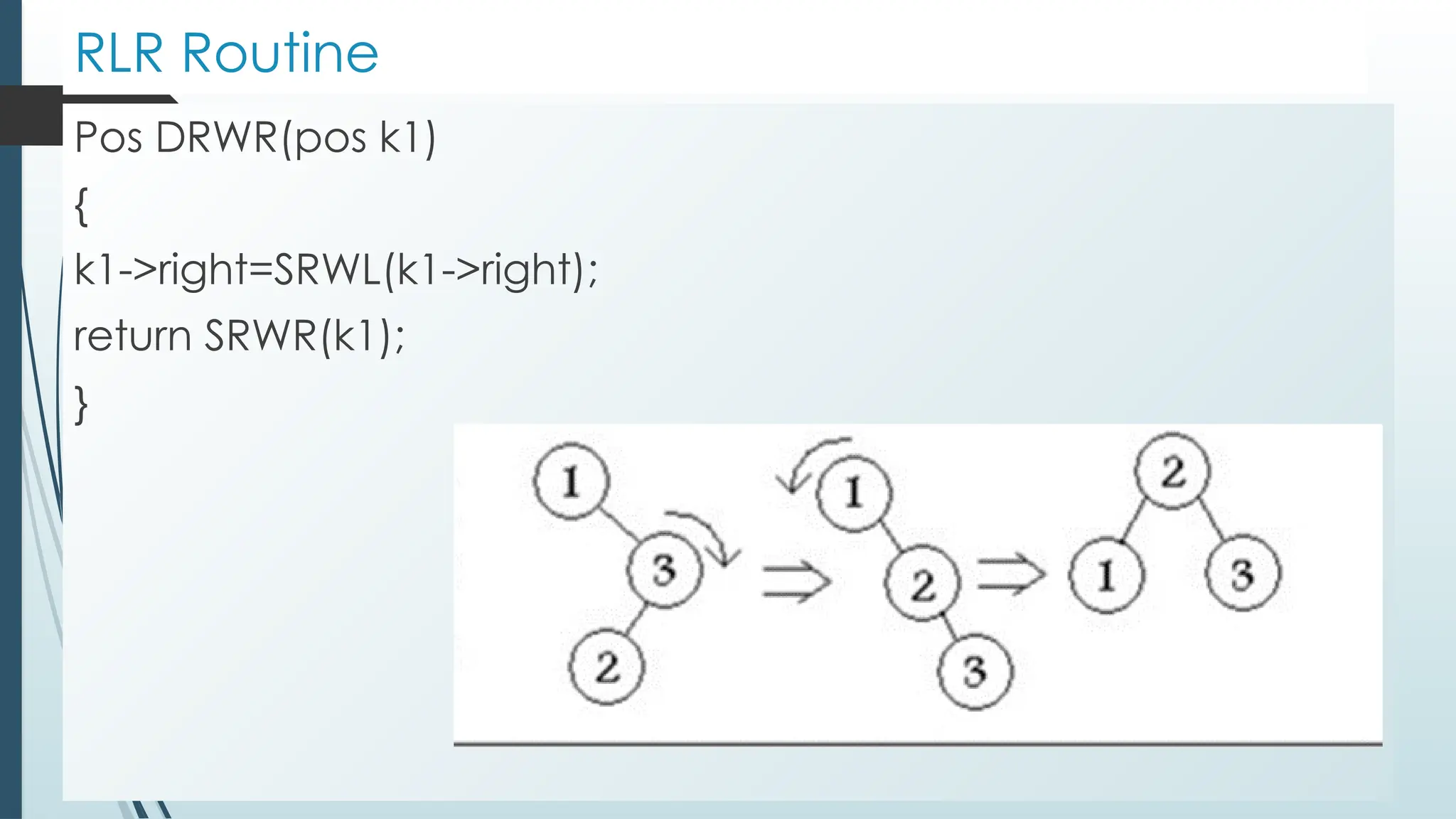






![Properties of B tree
Each node has a maximum of M children and minimum of
m/2 children
Each node should have maximum of m-1 keys
Root 2 childran
Minimum key 1 (root)
Other nodes [m/2]-1
Keys should be arranged in a defined order within the node
Key to be inserted into a fullnode, the node is splitted into two
nodes by taking the median value.
All Leaves are to be at same level.
no empty subtrees](https://image.slidesharecdn.com/unitiiinonlineardatastructures-trees-241126054300-1ba19308/75/UNIT-III-Non-Linear-Data-Structures-Trees-pptx-88-2048.jpg)