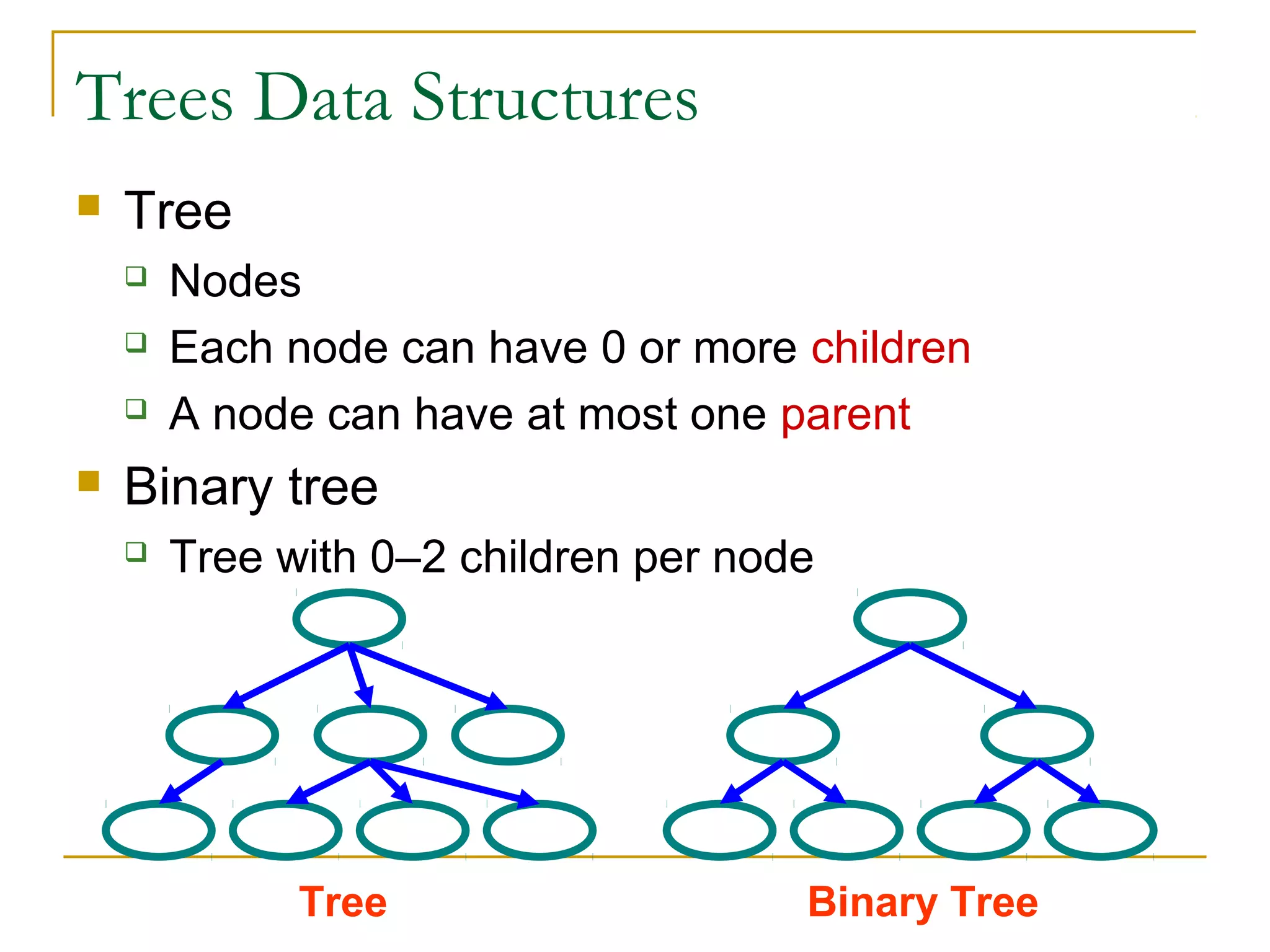
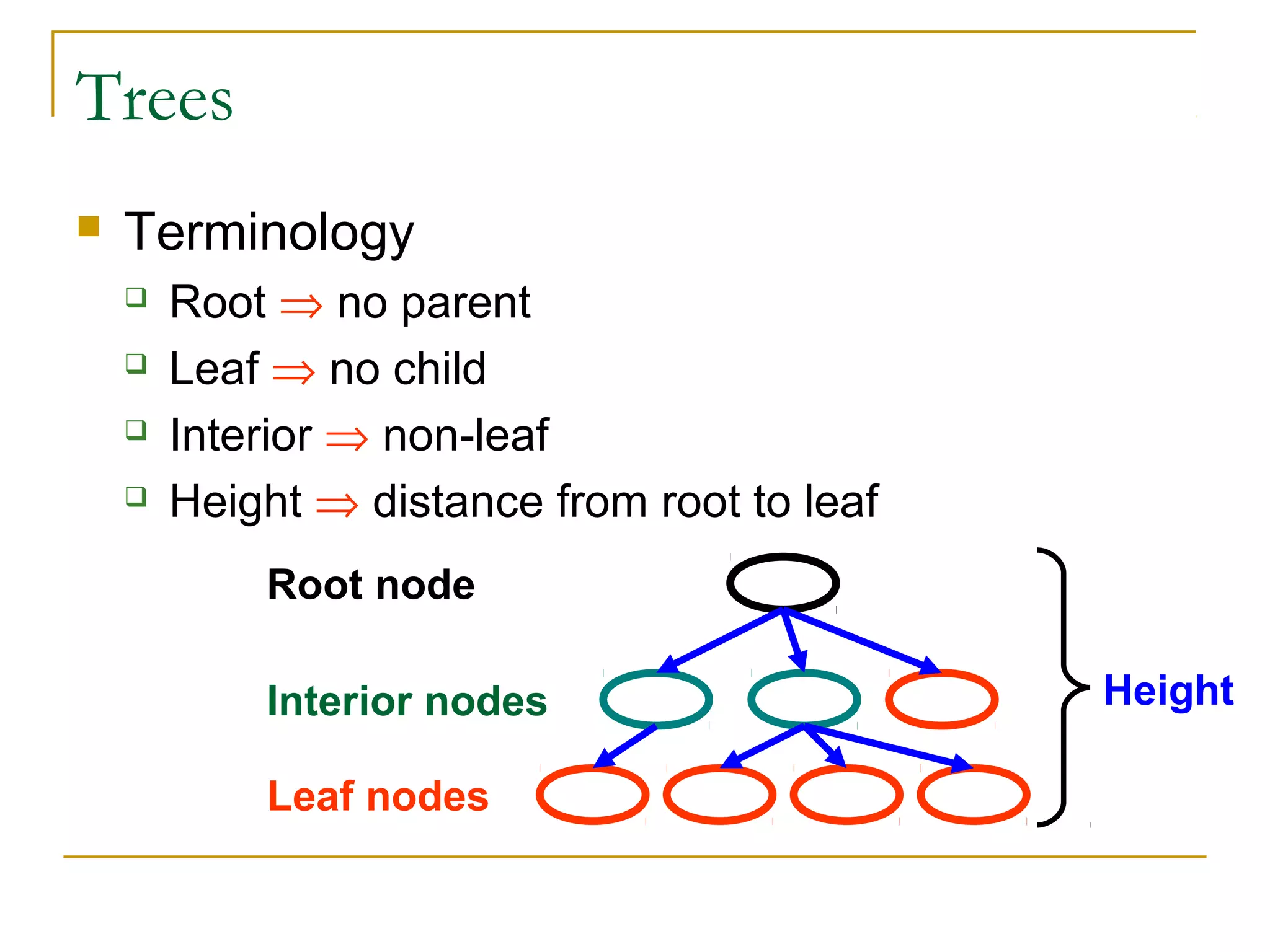
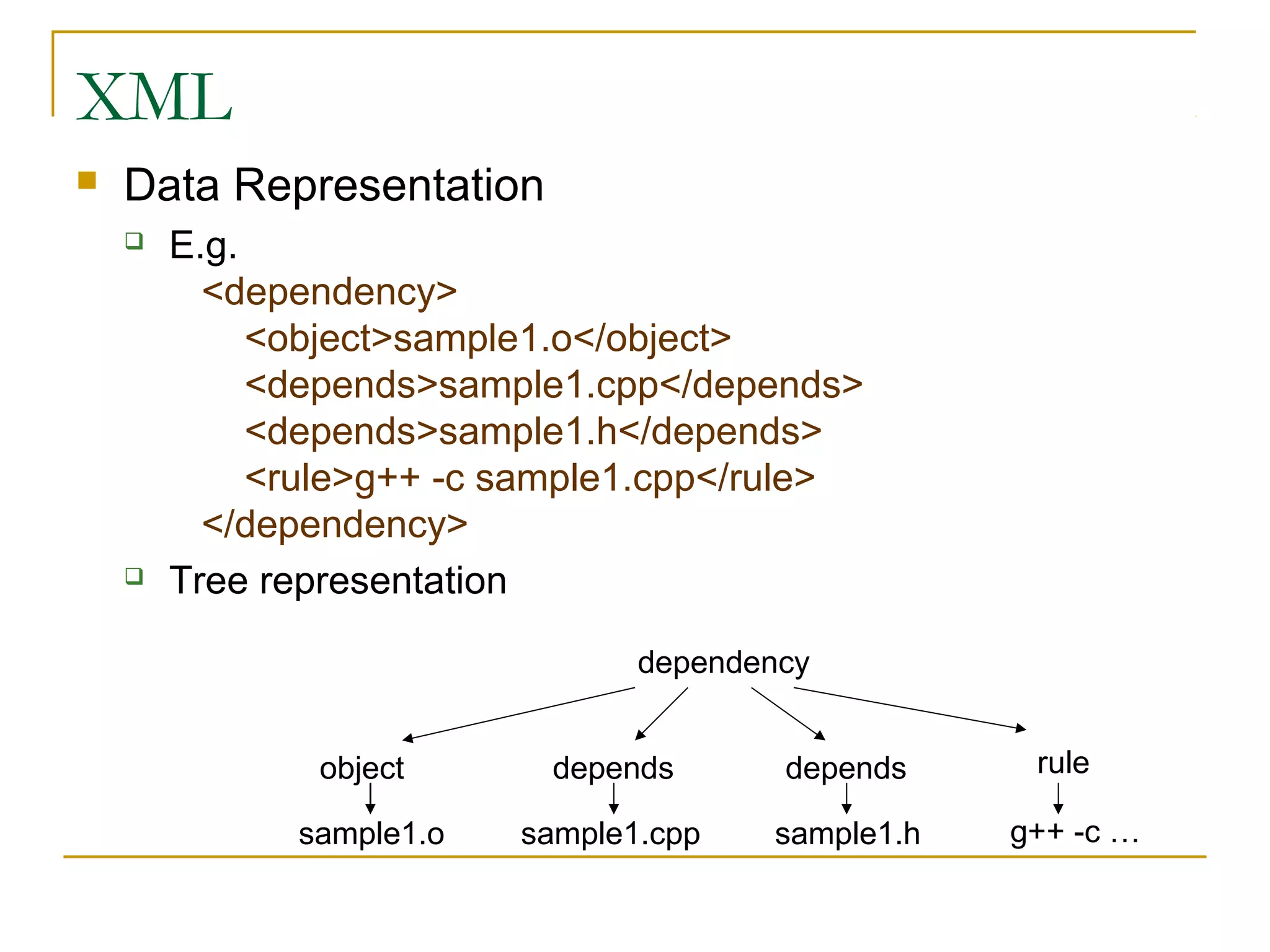
1) Tree data structures involve nodes that can have zero or more child nodes and at most one parent node. Binary trees restrict nodes to having zero, one, or two children.
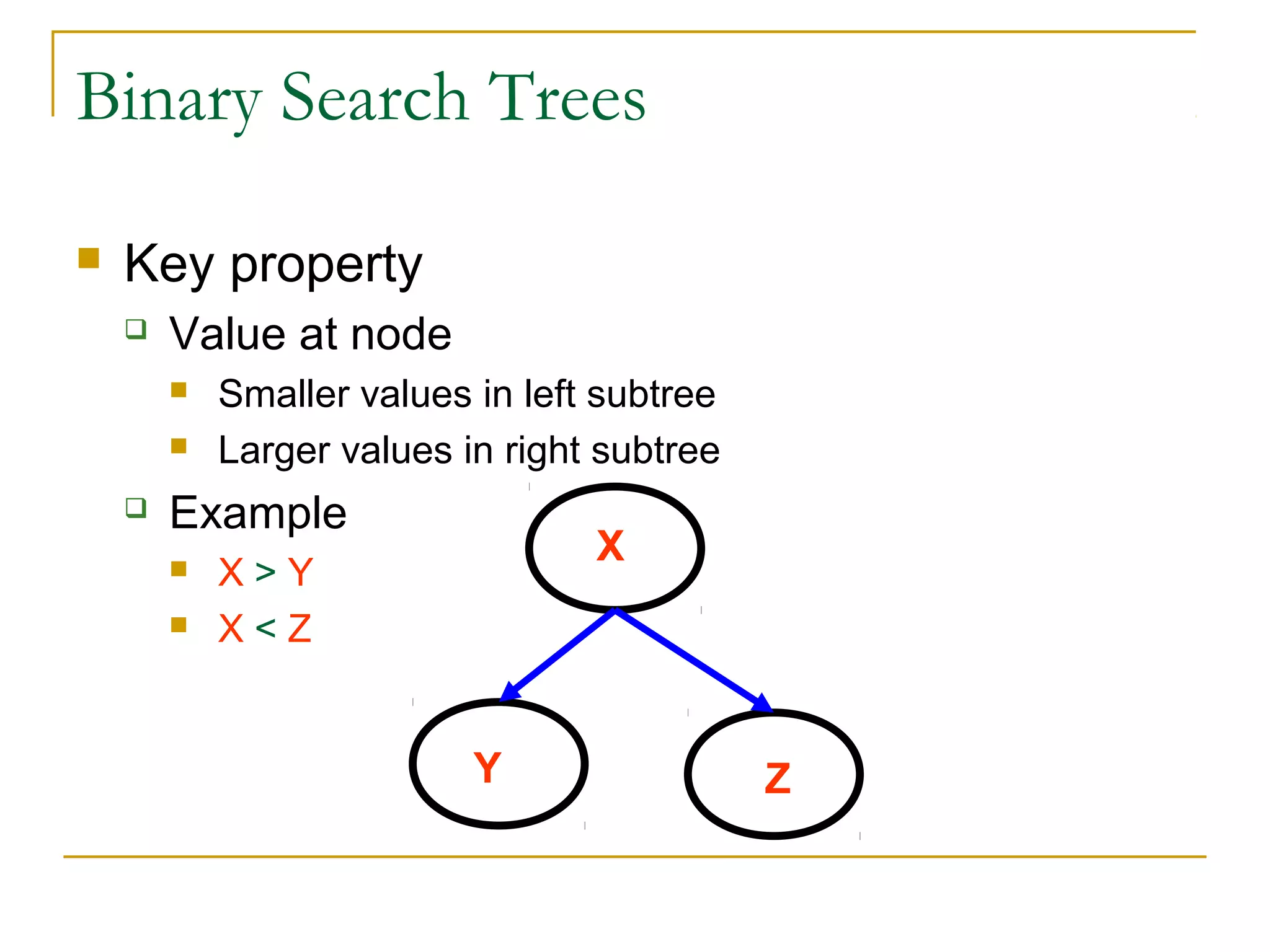
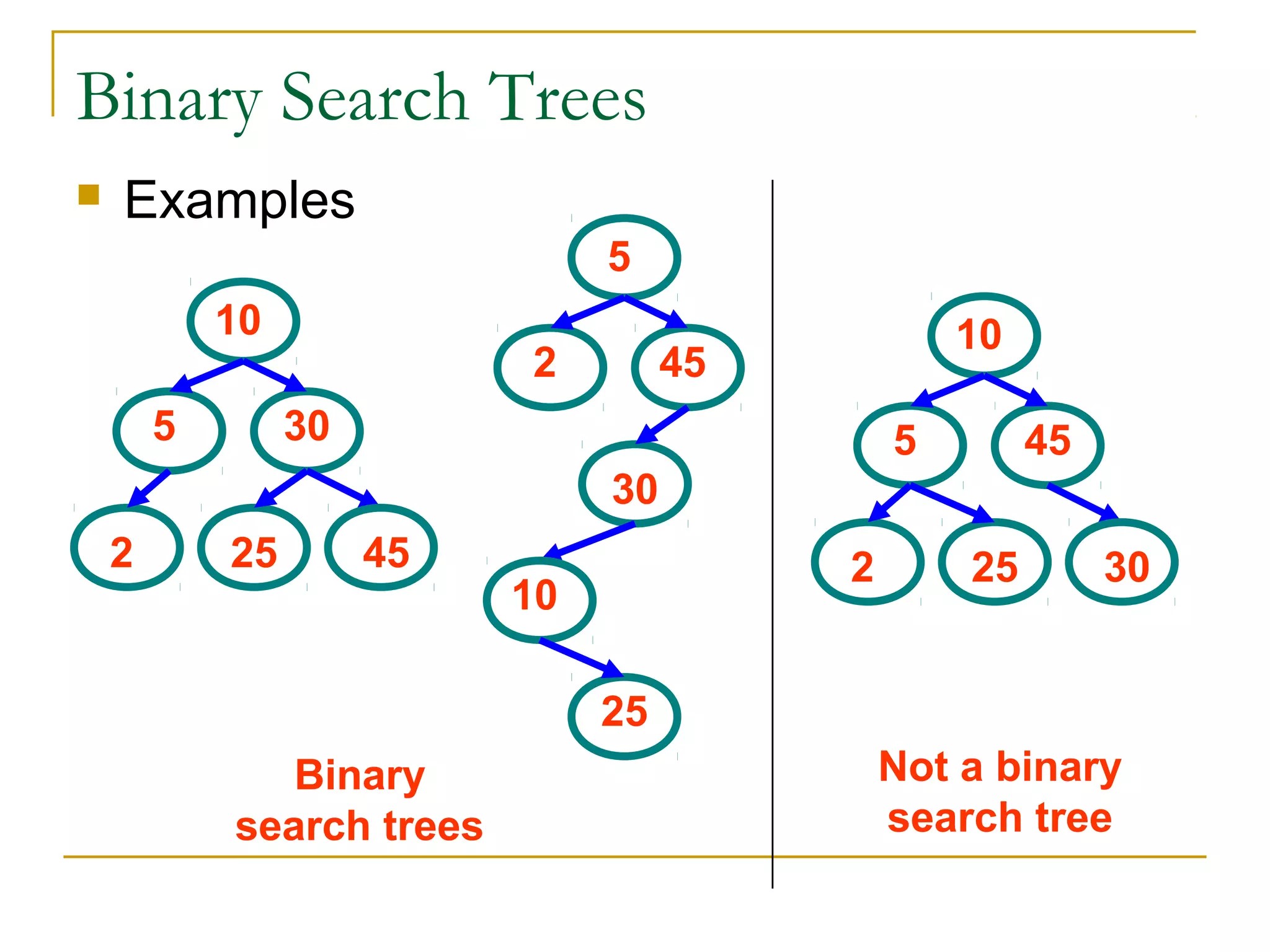
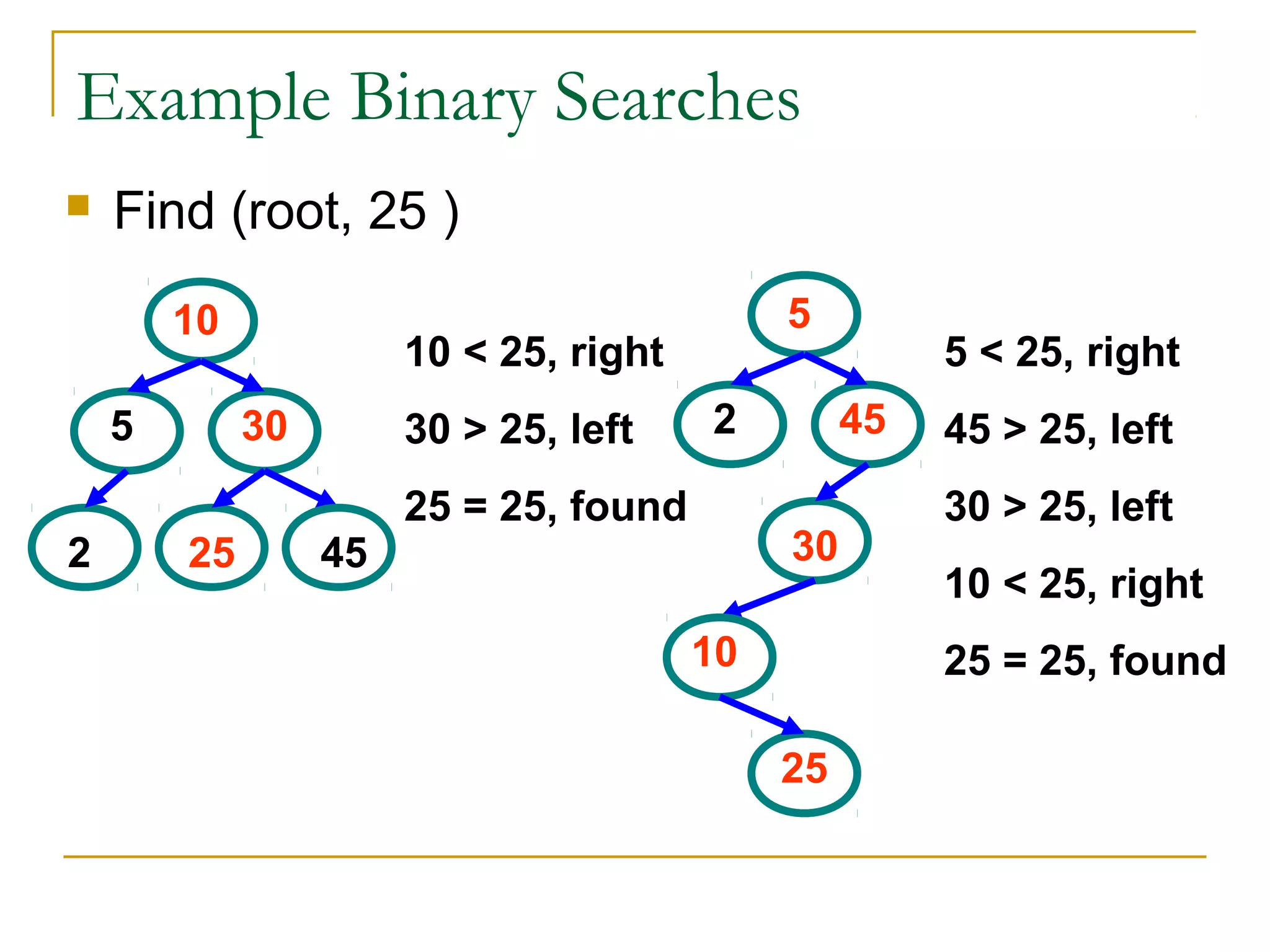
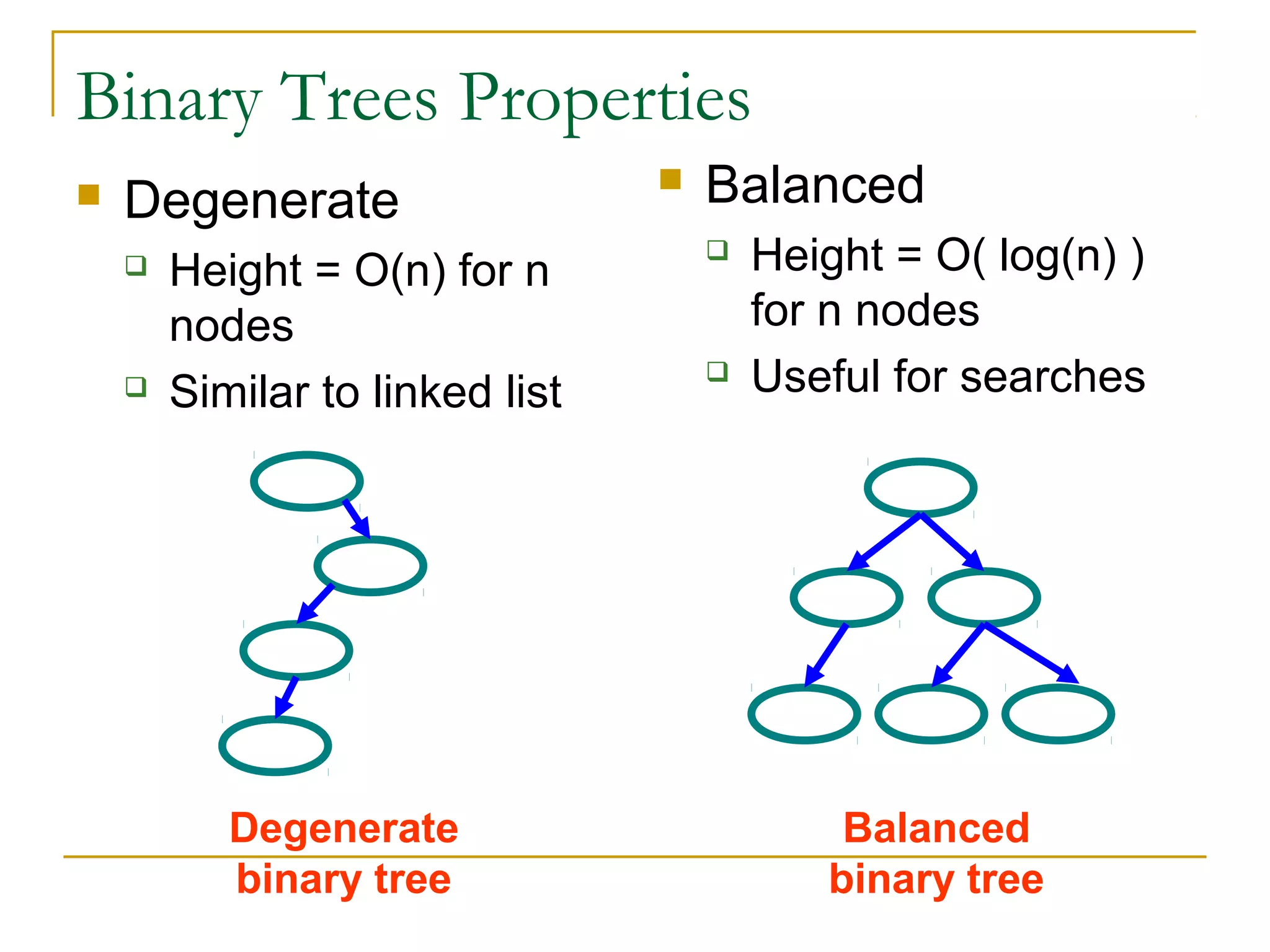
2) Binary search trees have the property that all left descendants of a node are less than the node's value and all right descendants are greater. This allows efficient searching in O(log n) time.
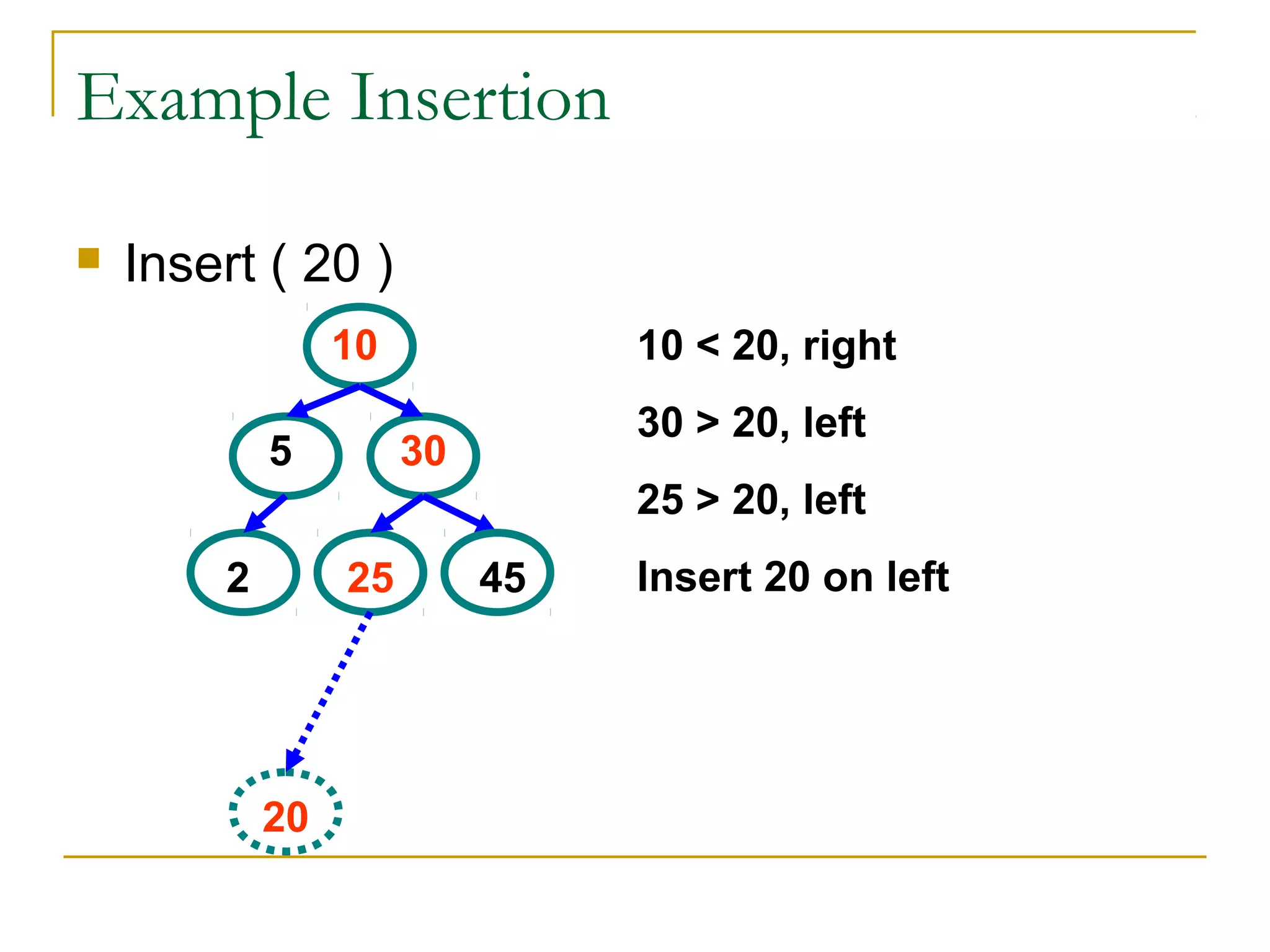
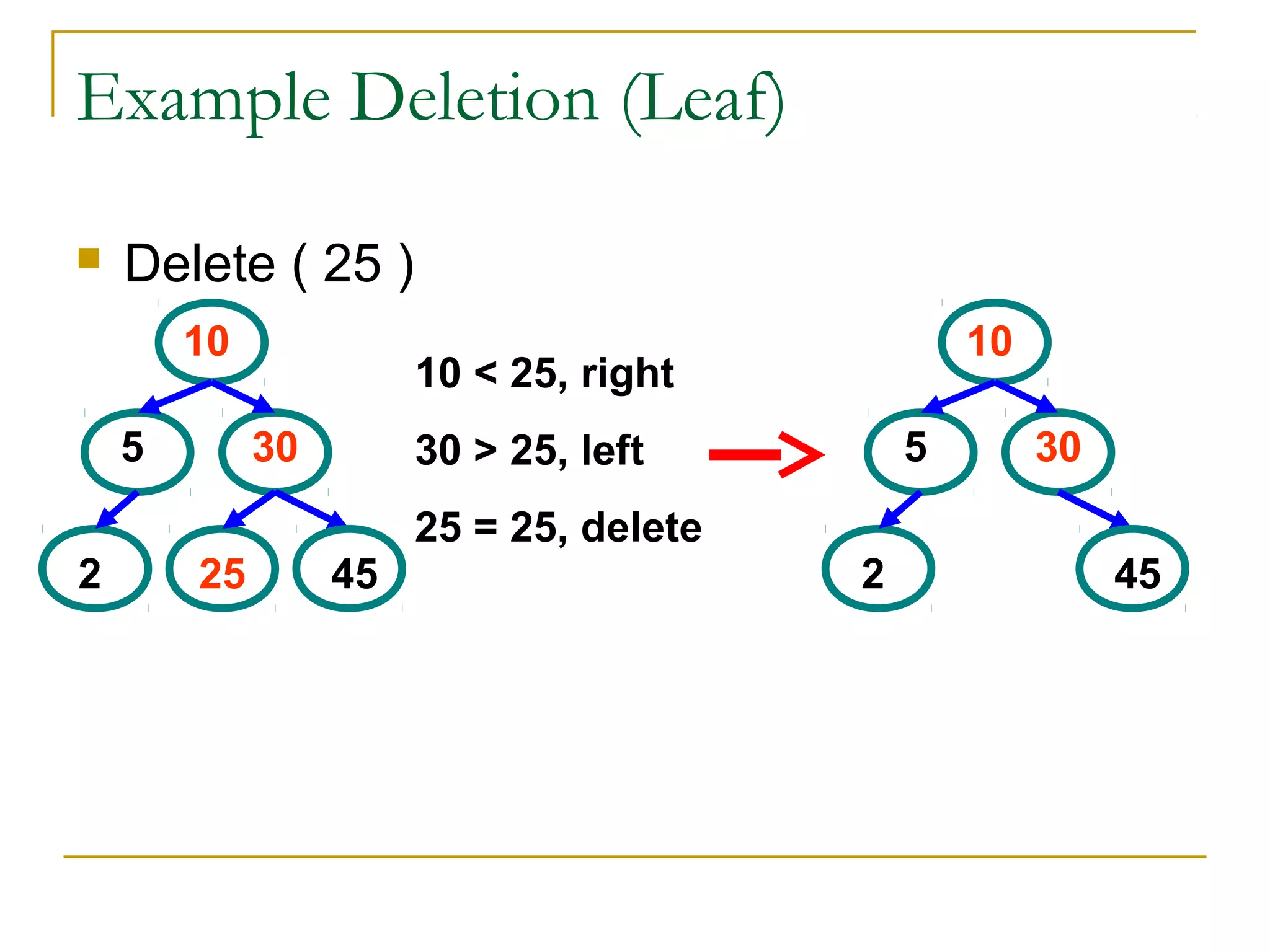
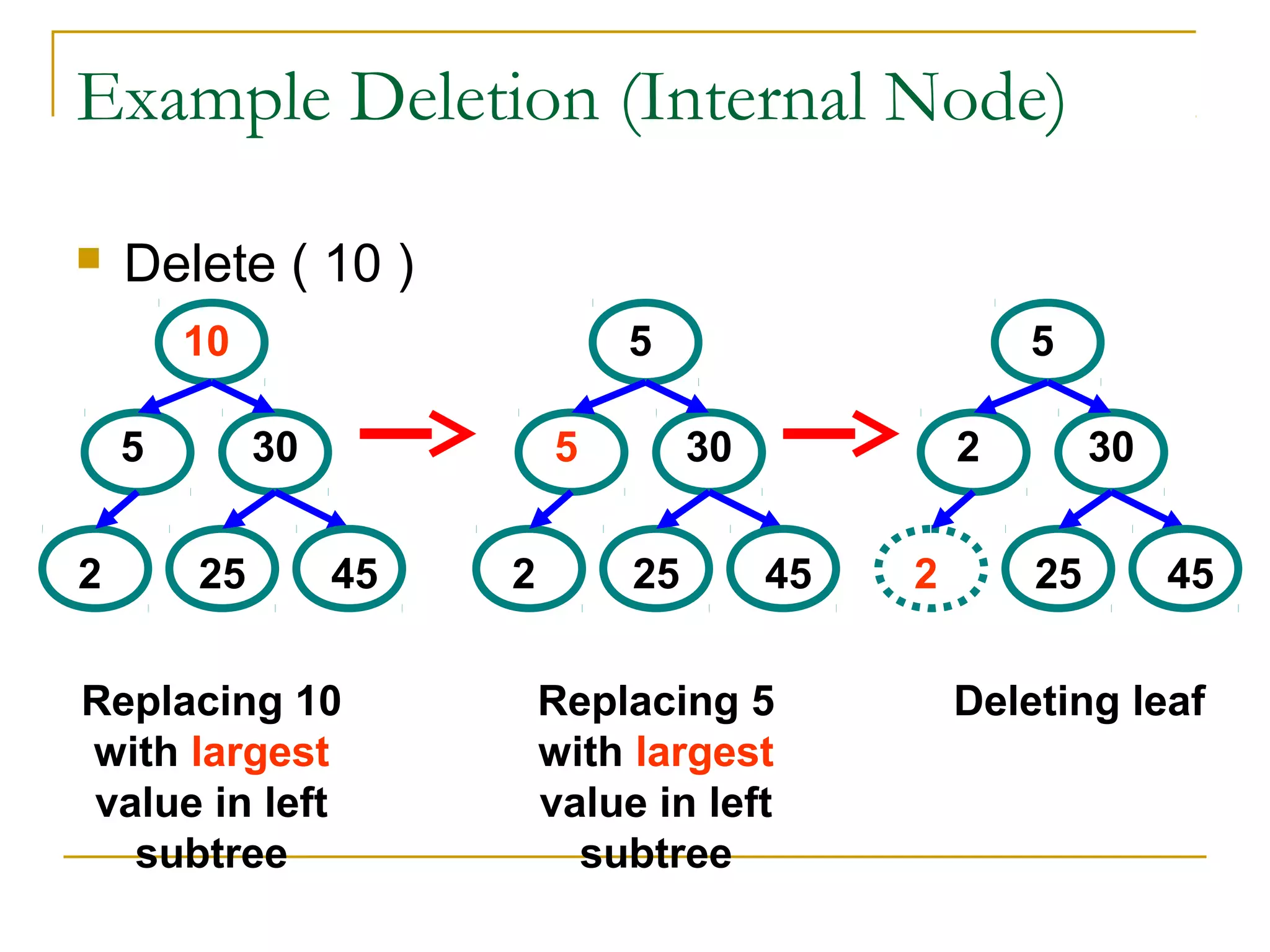
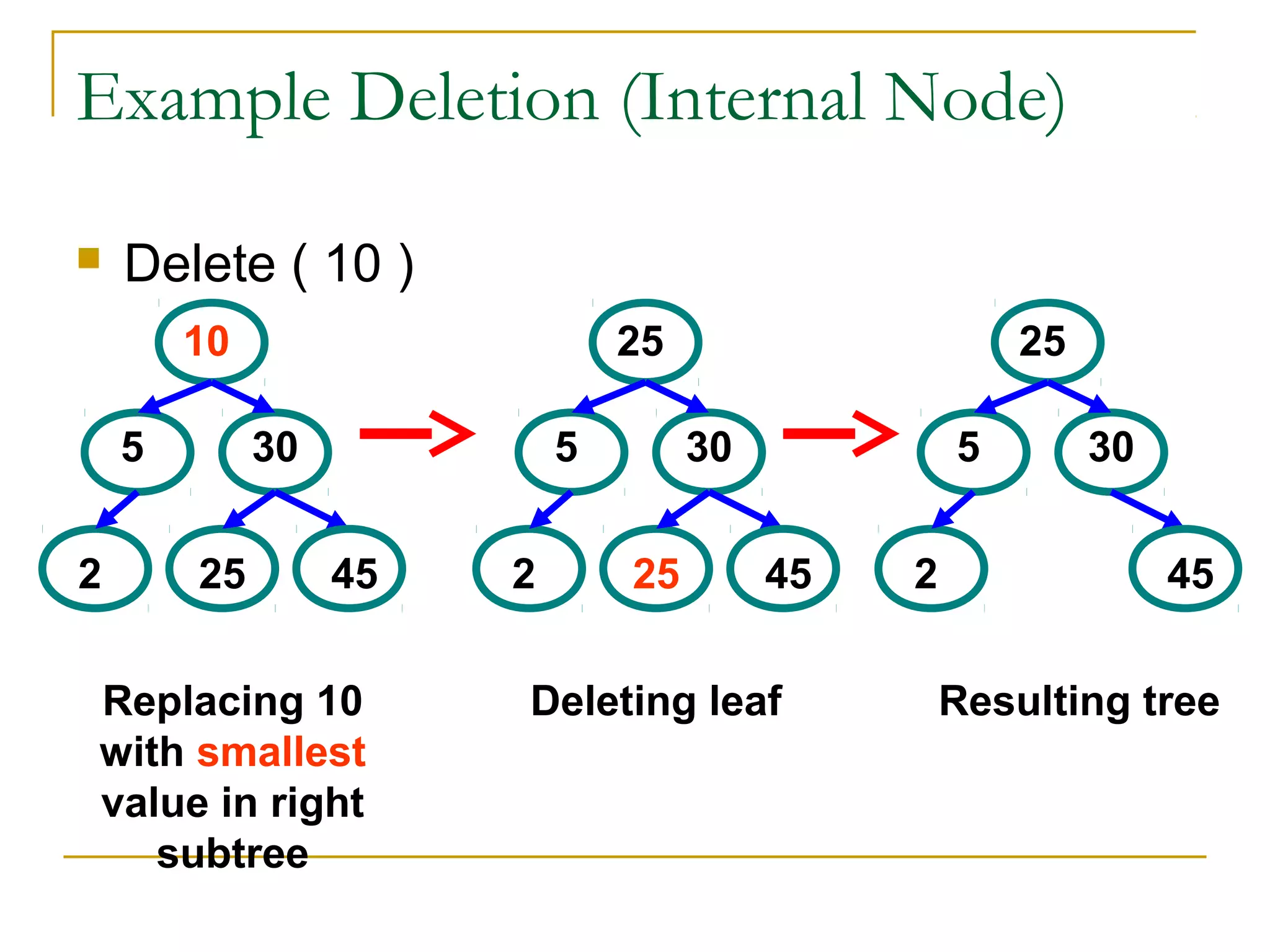
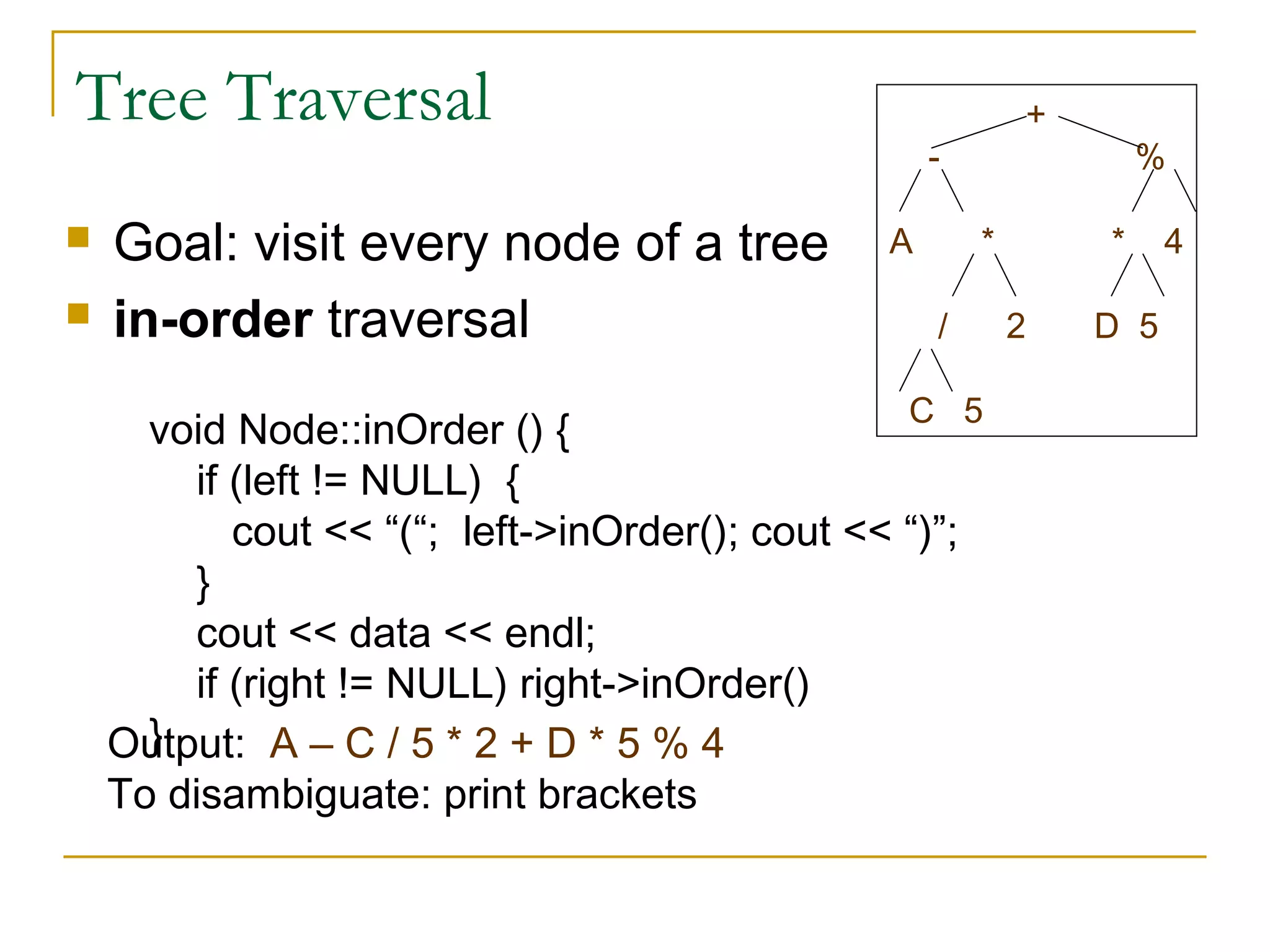
3) Common tree operations include insertion, deletion, and traversal. Balanced binary search trees use rotations to maintain balance during these operations.