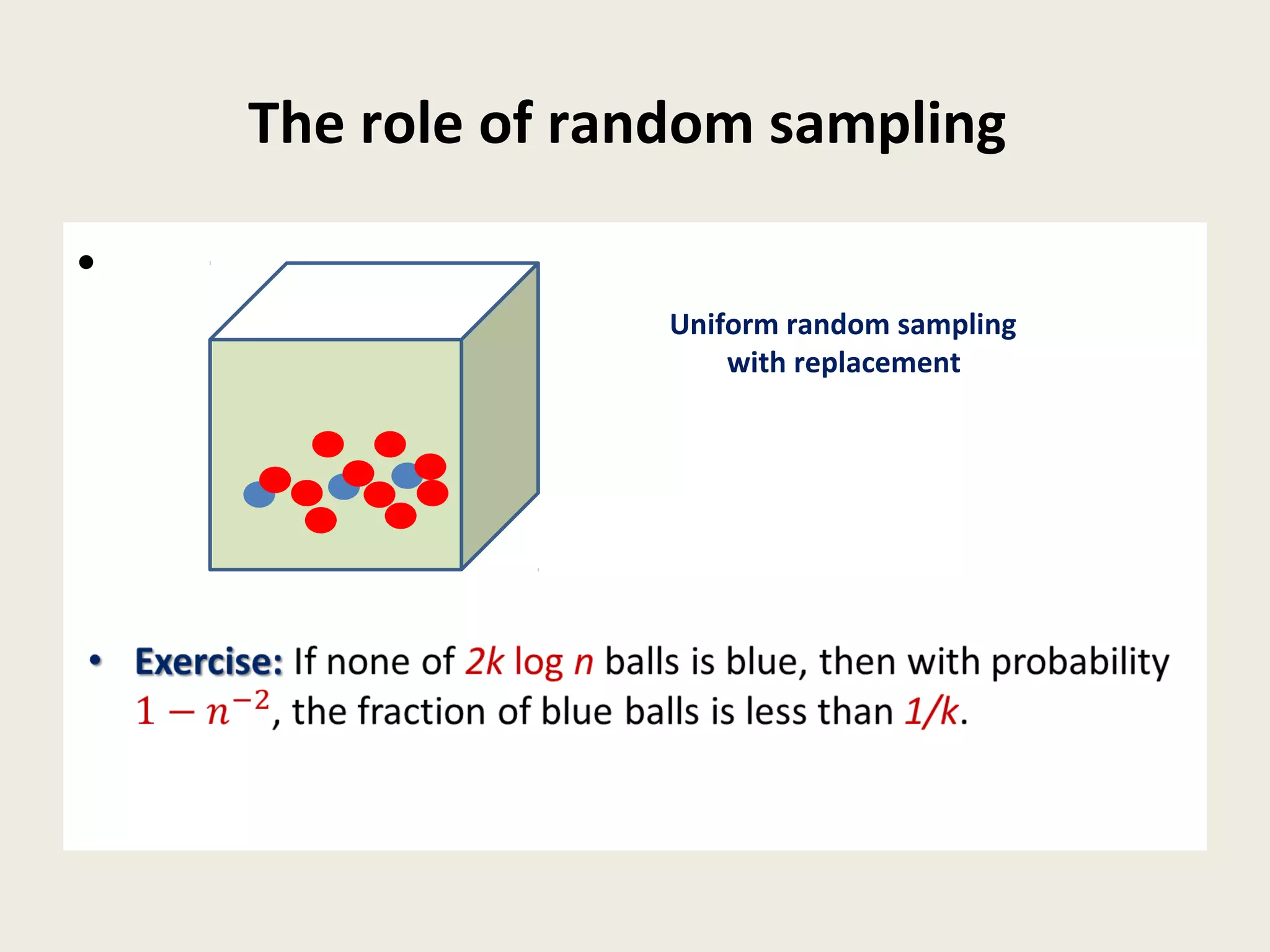
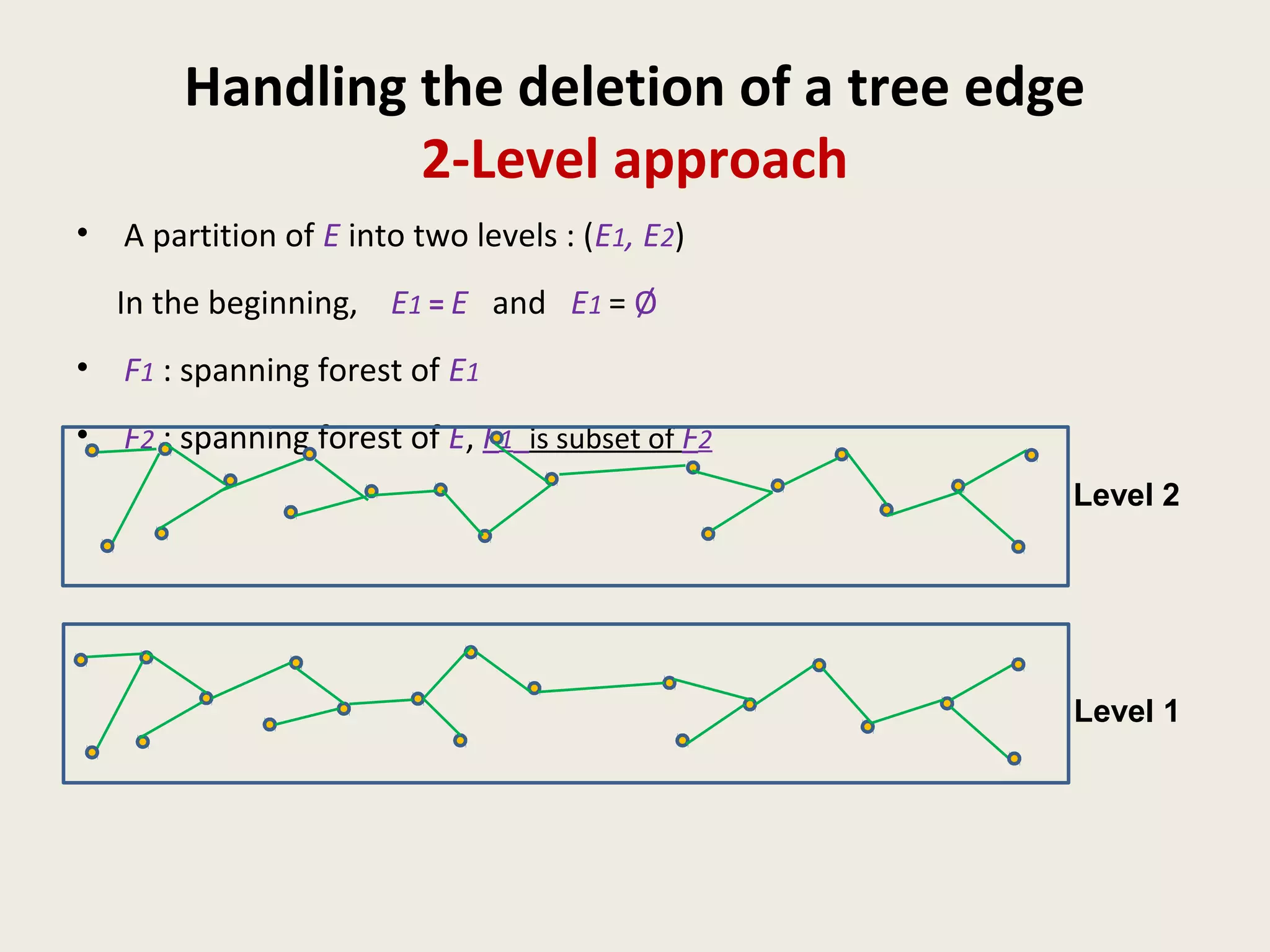
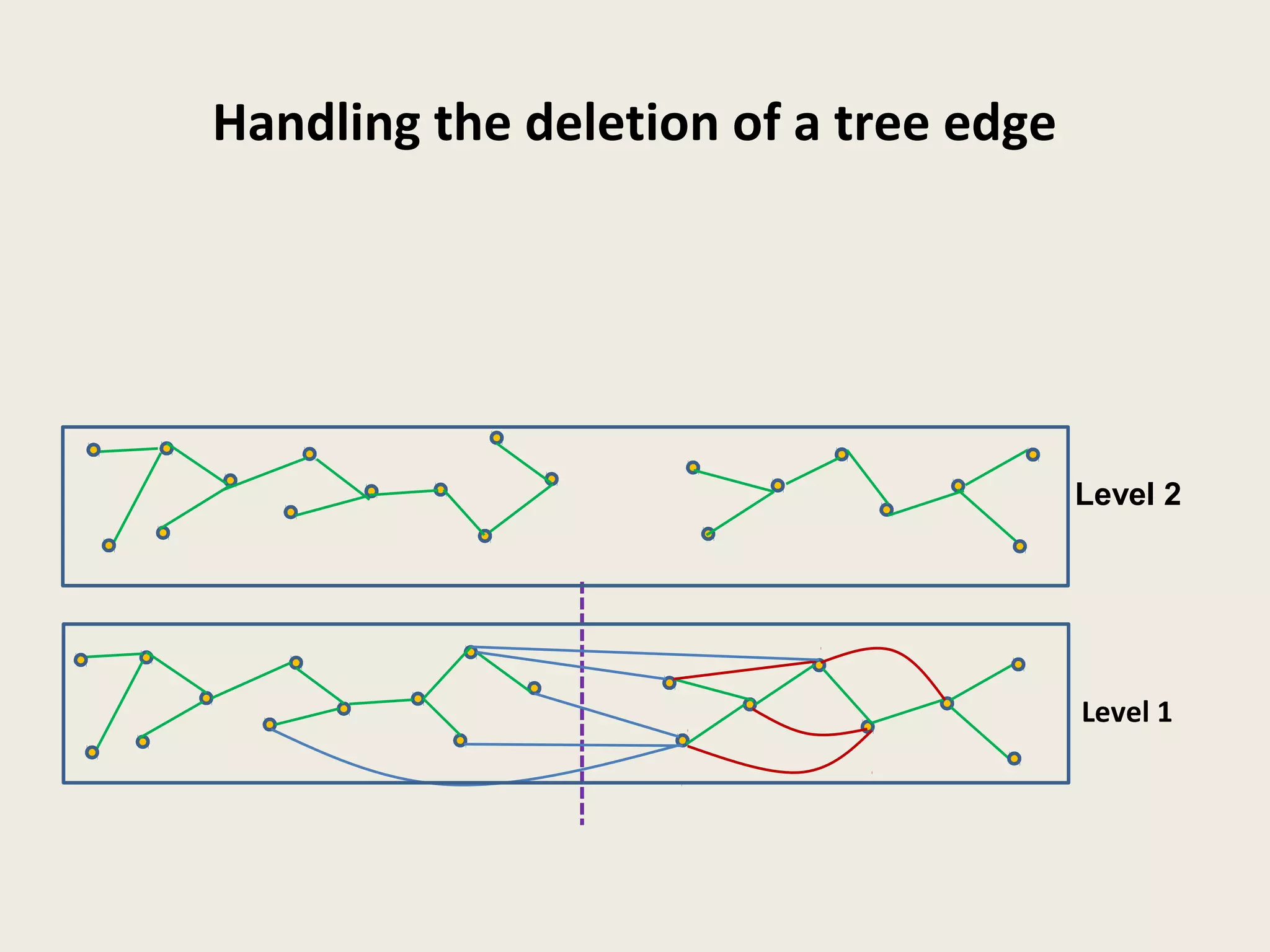
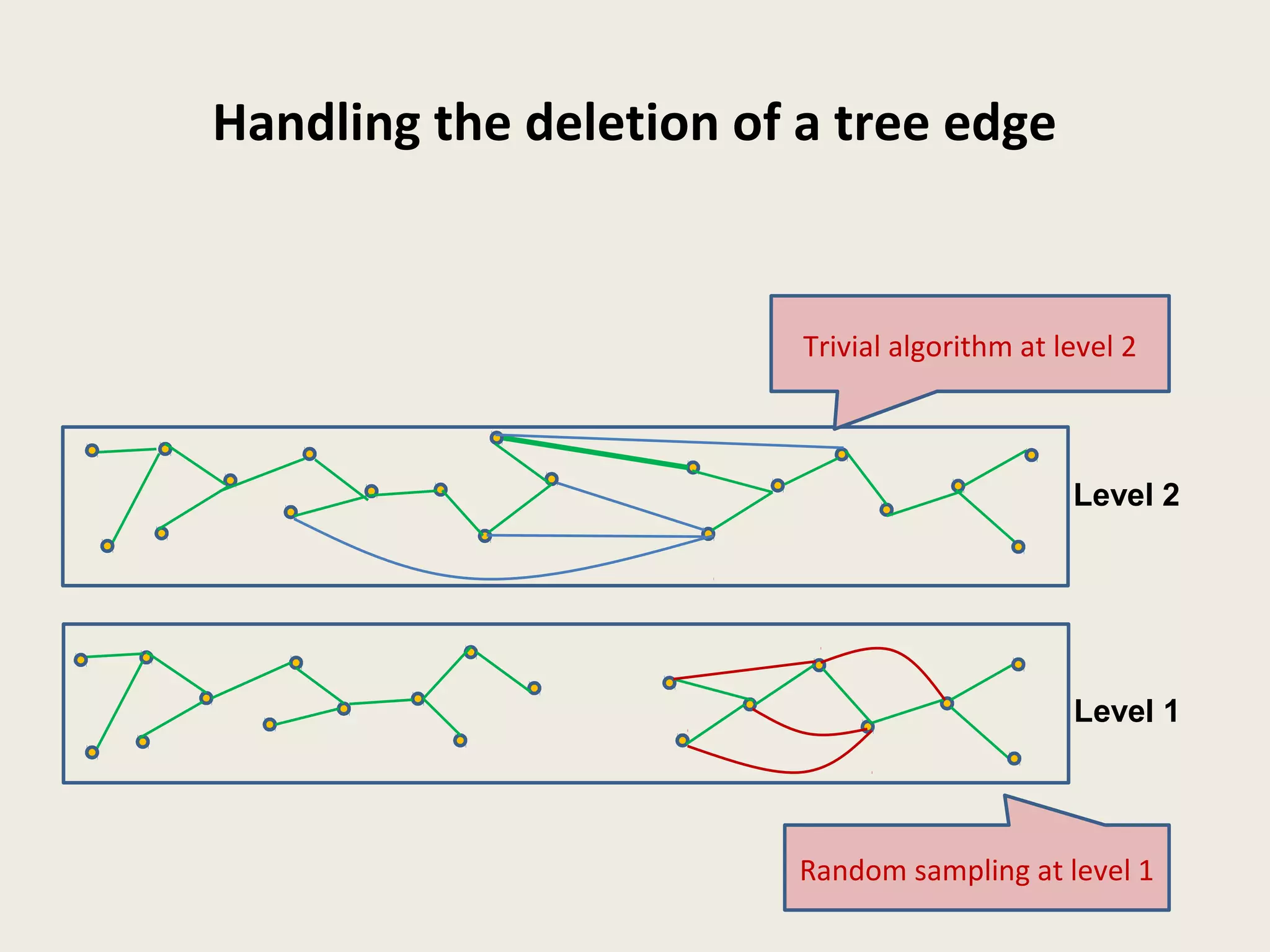
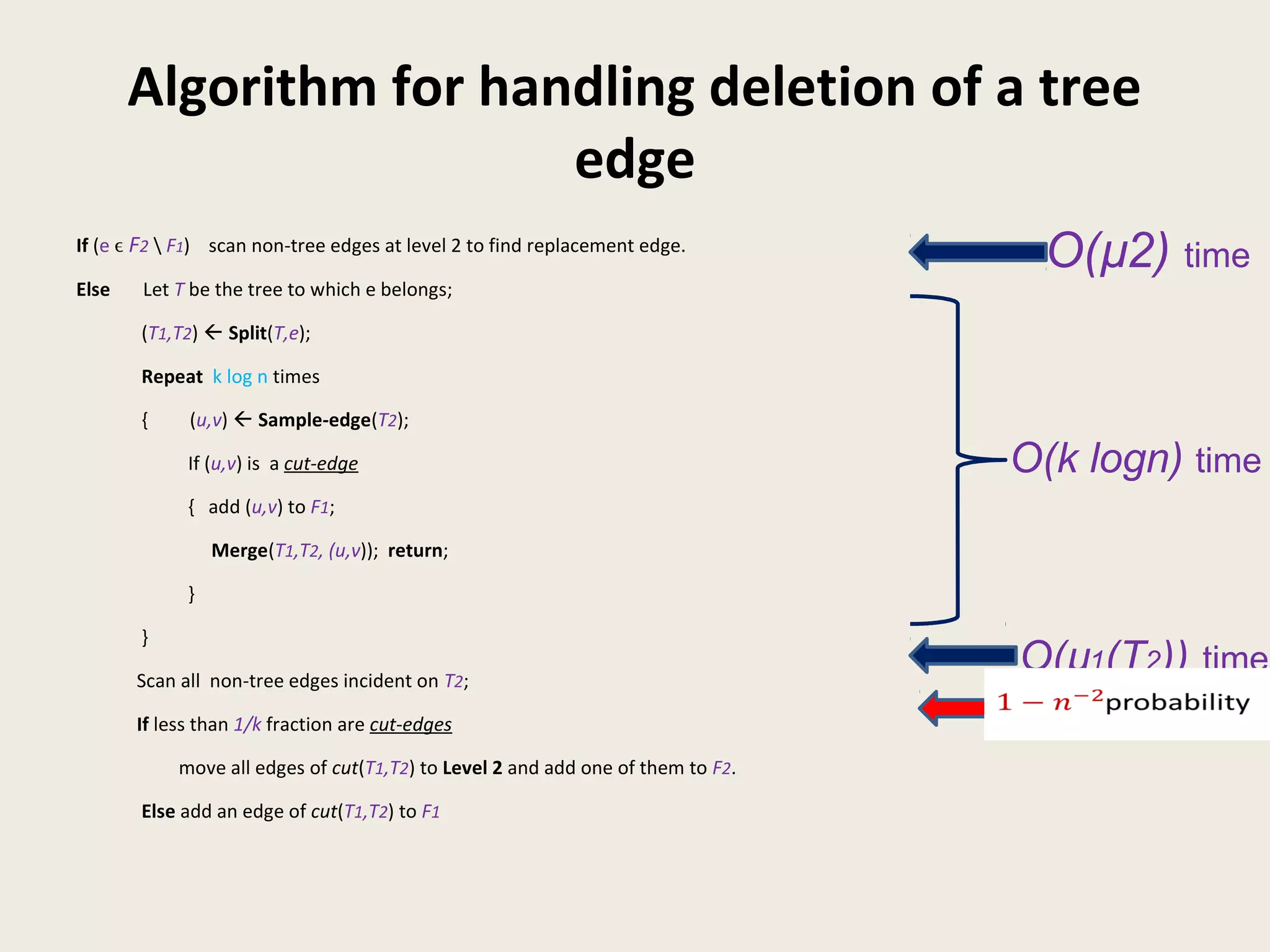
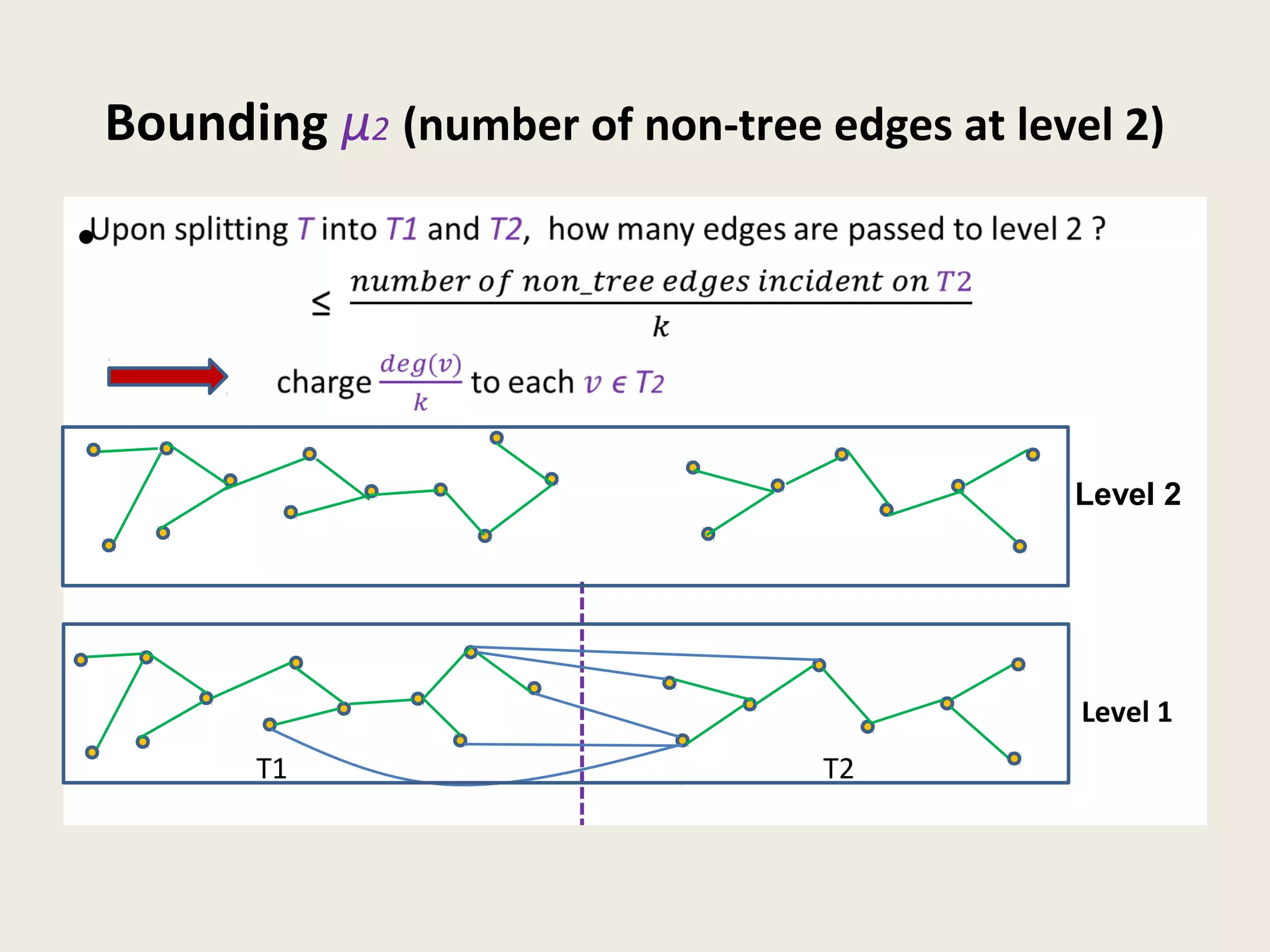
This document summarizes a talk on dynamic graph algorithms. It begins with an introduction to dynamic graph algorithms, which involve maintaining a graph structure and answering queries efficiently as the graph undergoes a sequence of edge insertions and deletions. It then discusses several examples of fully dynamic algorithms for problems like connectivity, minimum spanning trees, and graph spanners. A key data structure introduced is the Euler tour tree, which represents a dynamic tree as a one-dimensional structure to support efficient updates and queries. The document concludes by outlining a fully dynamic randomized algorithm for maintaining connectivity under edge updates with polylogarithmic update time, using a hierarchical approach with multiple levels of edge partitions and ET trees.




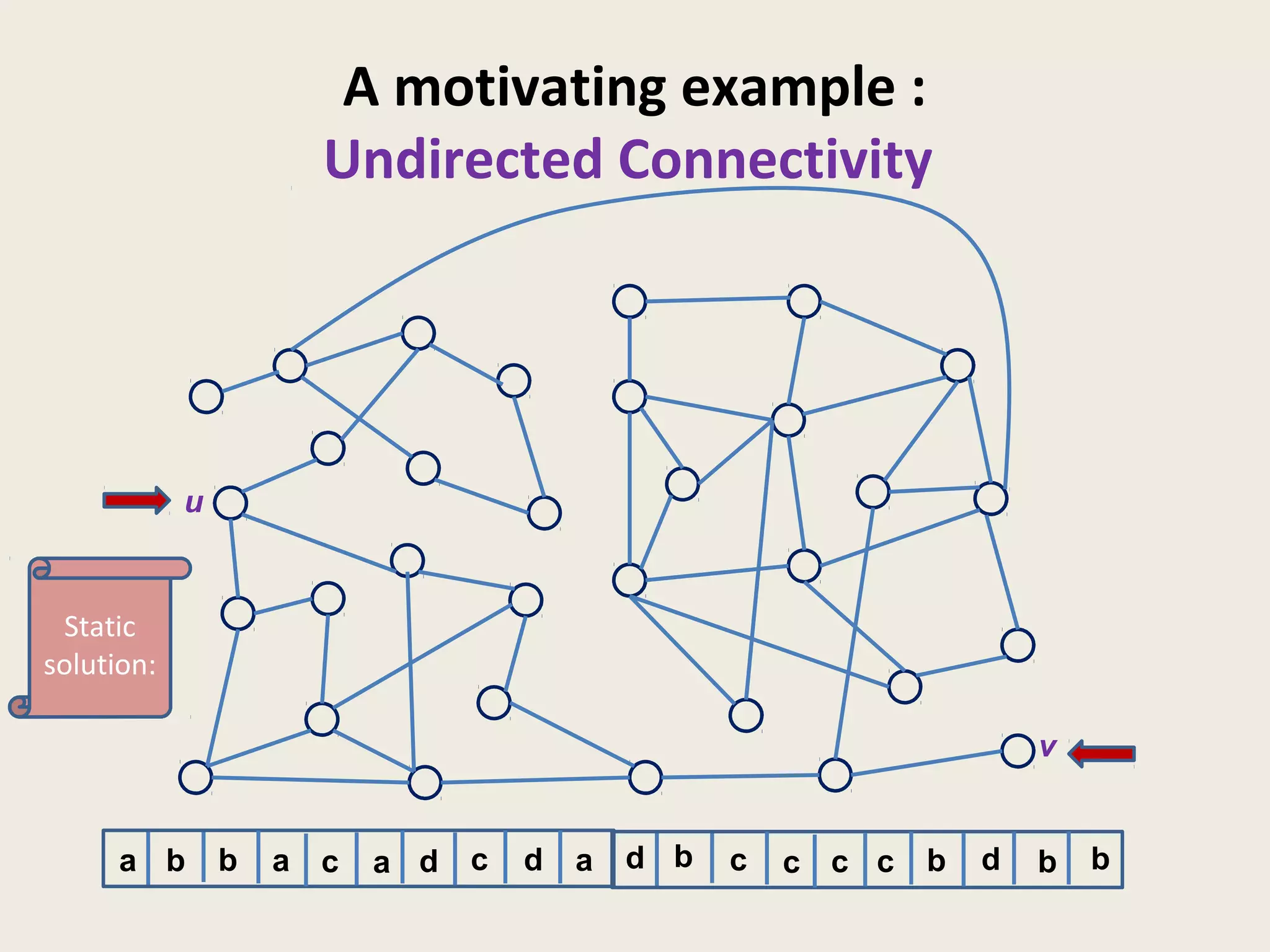
![A motivating example :
Undirected Connectivity
• Incremental Algorithm: O(log* n) update time
(Disjoint Set Union Algorithm [Tarjan 1975])
• Decremental Algorithm:
– O(n) update time [Even and Shiloach, 1981]
– O(log n) update time [Thorup 1997]](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-7-2048.jpg)
![A motivating example :
Undirected Connectivity
Fully Dynamic Algorithms:
1. O() update time [Frederickson, 1982]
2. O() update time [Eppstein, Galil, Italiano, Nissenzweig 1991]
3. O(polylog n) expected update time, O(log n) query time
[King and Henzinger 1995]
4. O(polylog n) update time, O(log n) query time
[Holm, Litchenberg, Thorup 1998]
•](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-8-2048.jpg)


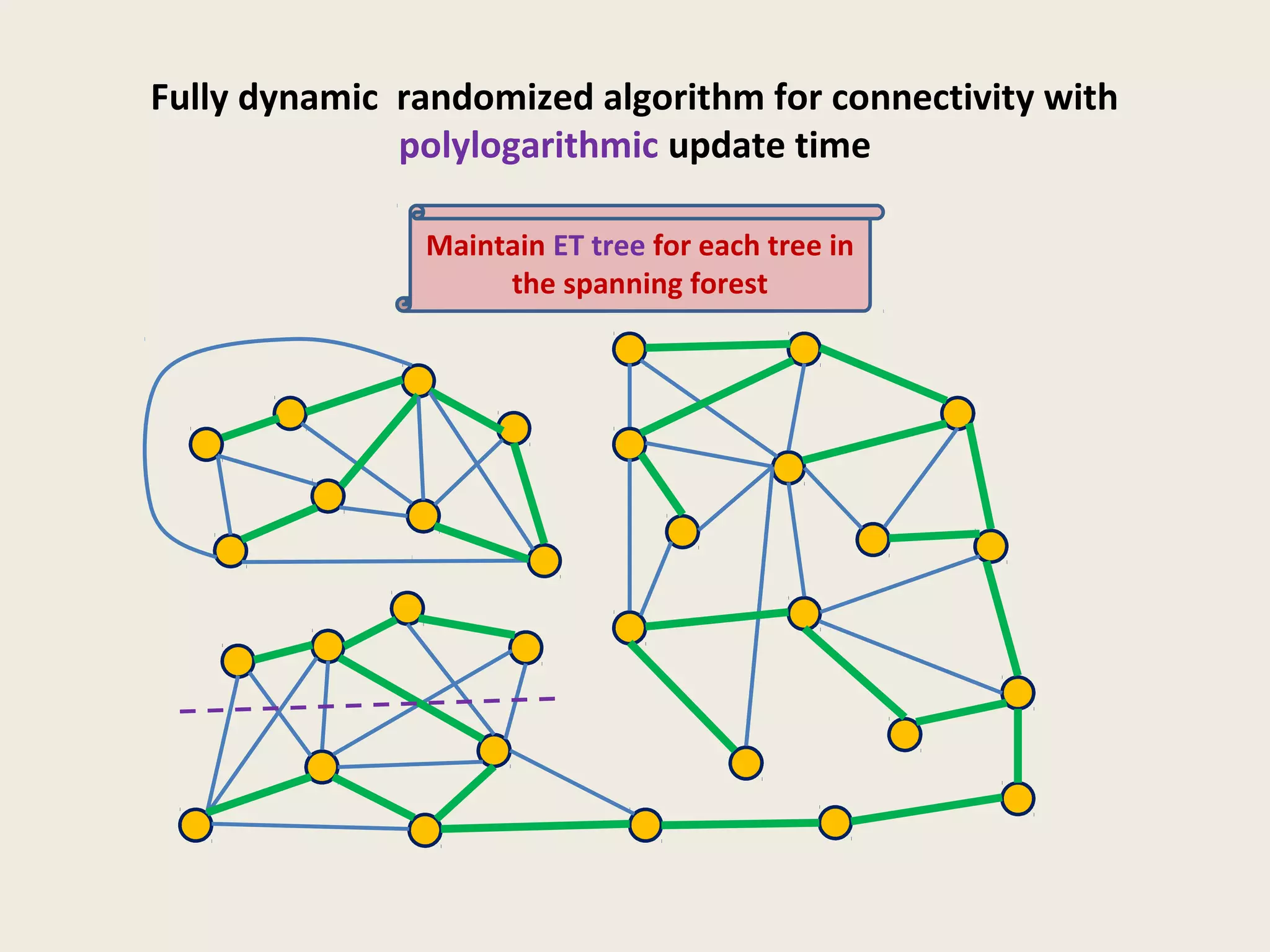
![Fully dynamic algorithms for undirected
graphs
1. Connectivity
2. 2-edge connectivity
3. Bi-connectivity
4. Bipartiteness
5. Min. spanning tree
O(polylog n) update time [Holm, Litchenberg, Thorup 1998]](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-11-2048.jpg)
![Fully dynamic algorithms for undirected
graphs
• Min-cut
– Best static algorithm: O(m polylog n) (Randomized) [Karger, 1996]
– Fully dynamic algorithm: O() update time [Thorup, 2001]
• Graph spanner
Definition:
A subgraph which is sparse and yet preserves all-pairs distances approximately.
– Best static algorithm: O(m) [Halperin, Zwick, 1996]
– Fully dynamic algorithm: O(polylog n) update time
[Baswana, Khurana, and Sarkar, 2008]
•](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-12-2048.jpg)
![Dynamic algorithms for directed graphs
Maintaining BFS tree under deletion of edges :
O(n) time per edge deletion [Even & Shiloach, 1981]
• Unbeaten till date.
• Used in many dynamic algorithms for directed graphs.
Not as good bounds as
undirected graphs](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-13-2048.jpg)
![Dynamic algorithms for directed graphs
Transitive Closure
• Incremental algorithm: O(n) update time [Italiano, 1986]
• Decremental algorithm: O(n) update time
– Randomized [Roditty and Zwick, 2002]
– Deterministic [Lacki, 2011 ]
• Fully Dynamic algorithm: O() update time [Roditty, 2003]
All-pairs Shortest paths
• Fully dynamic algorithms:
– Amortized O() update time [Demetrescu and Italiano, 2003]
– Worst case O() update time [Thorup, 2005]
•](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-14-2048.jpg)



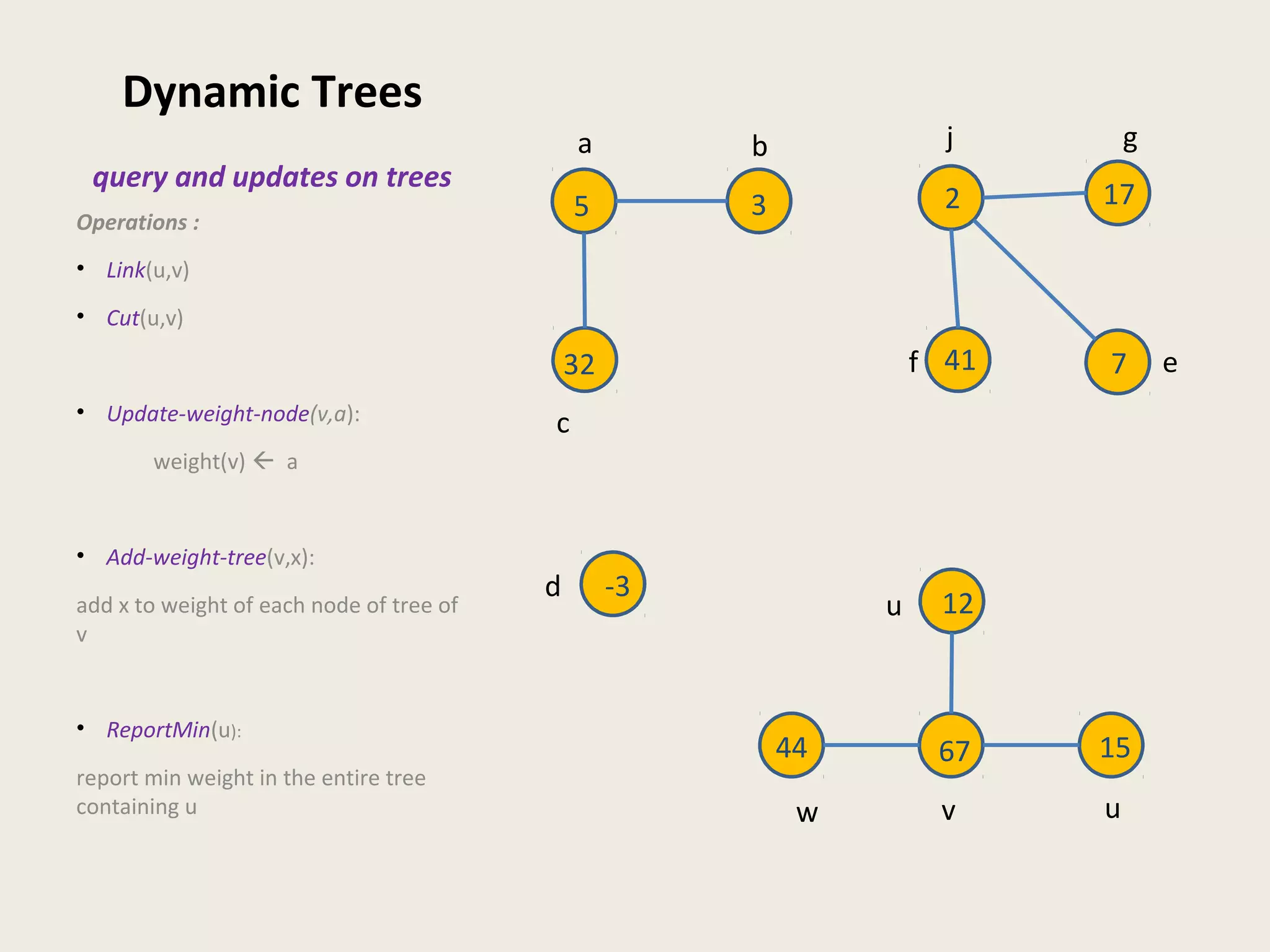
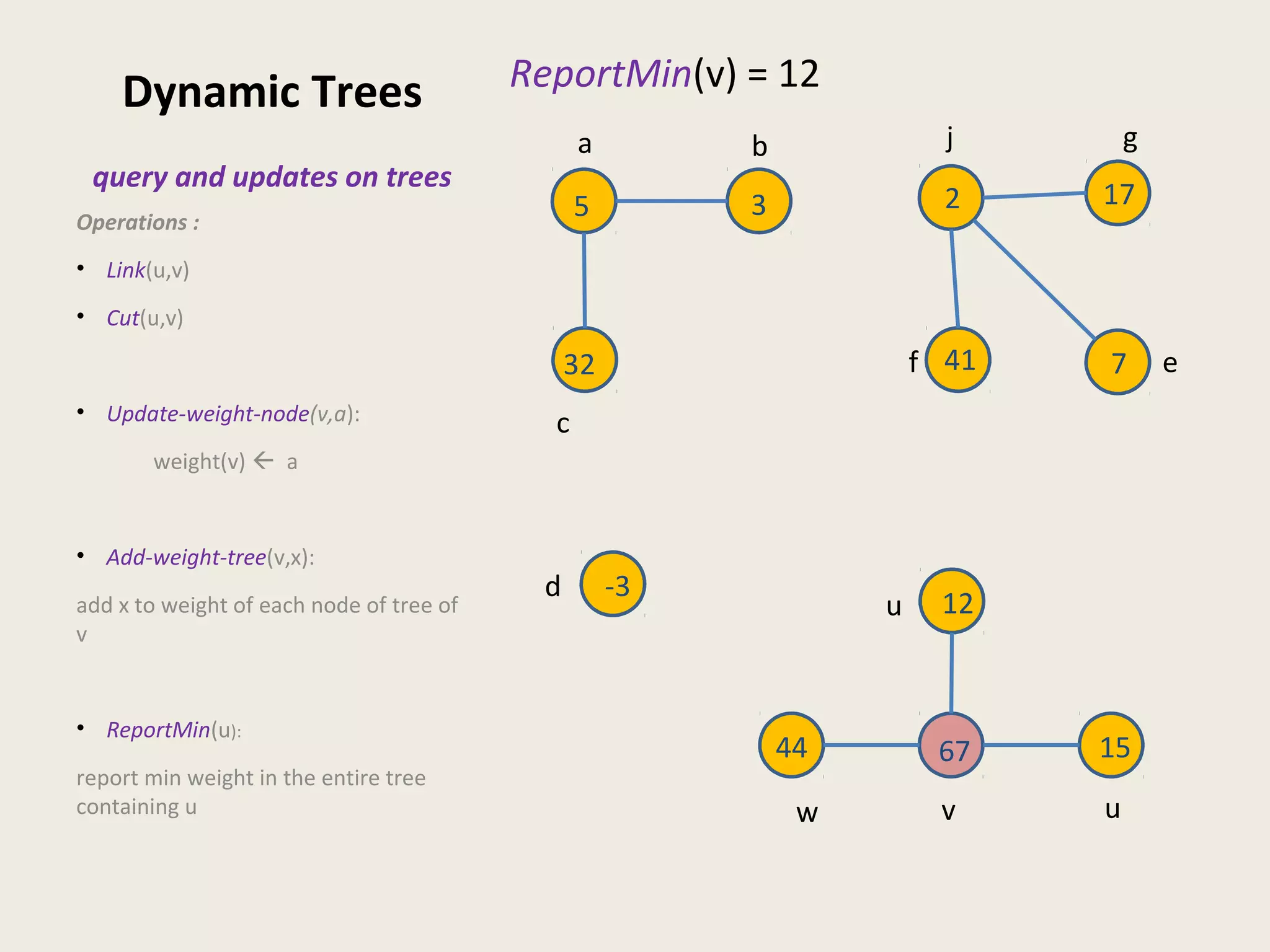
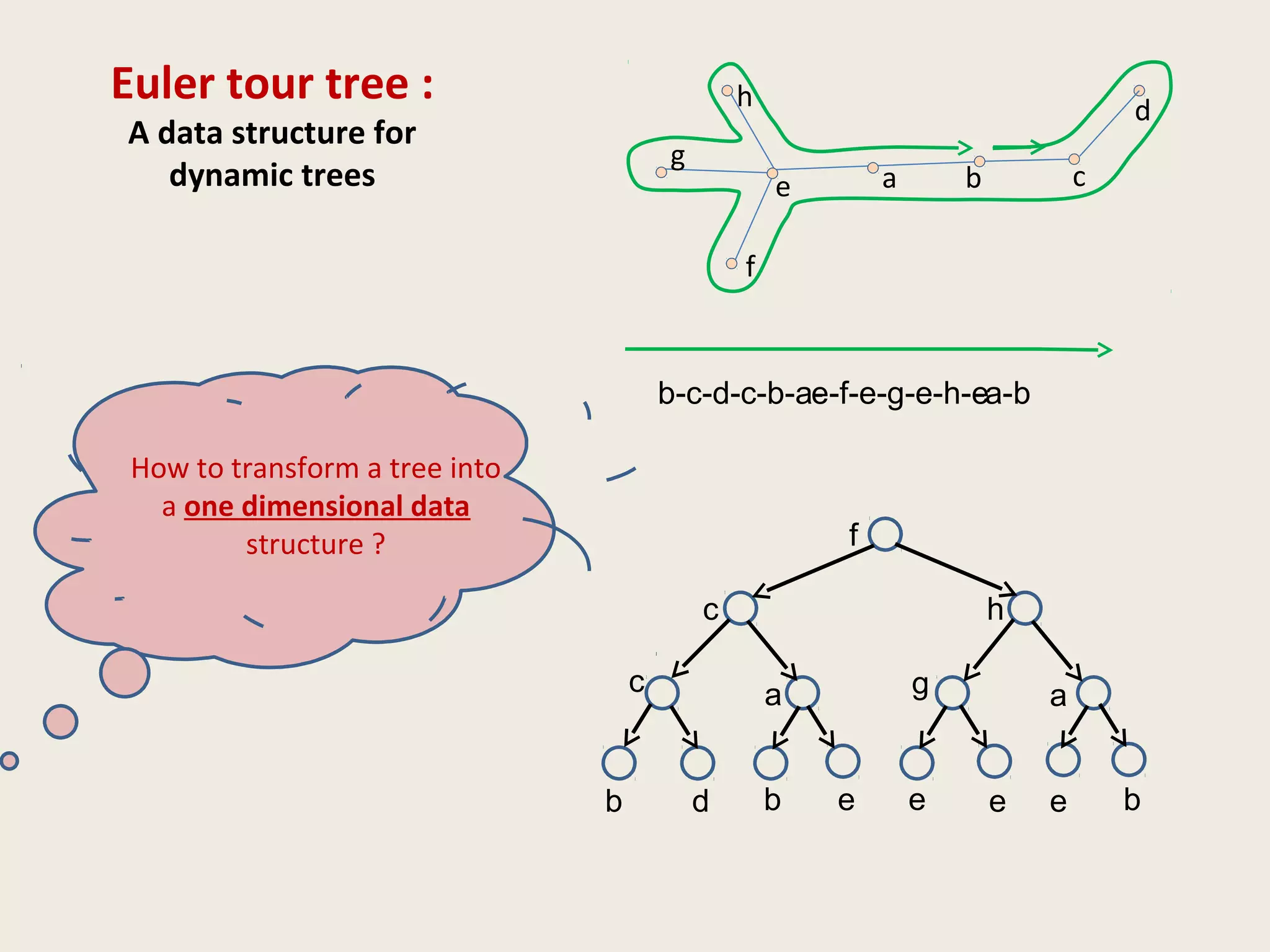
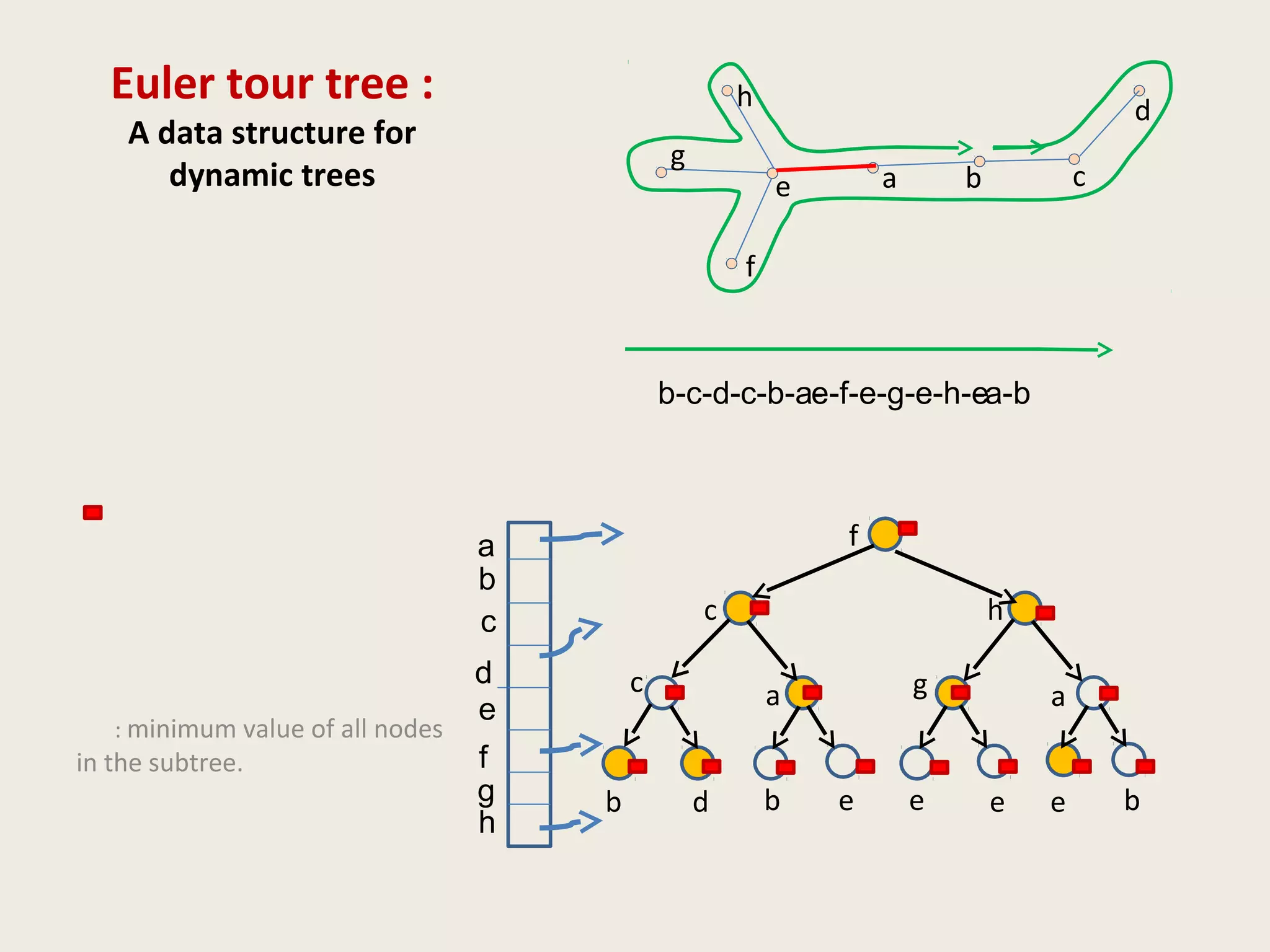
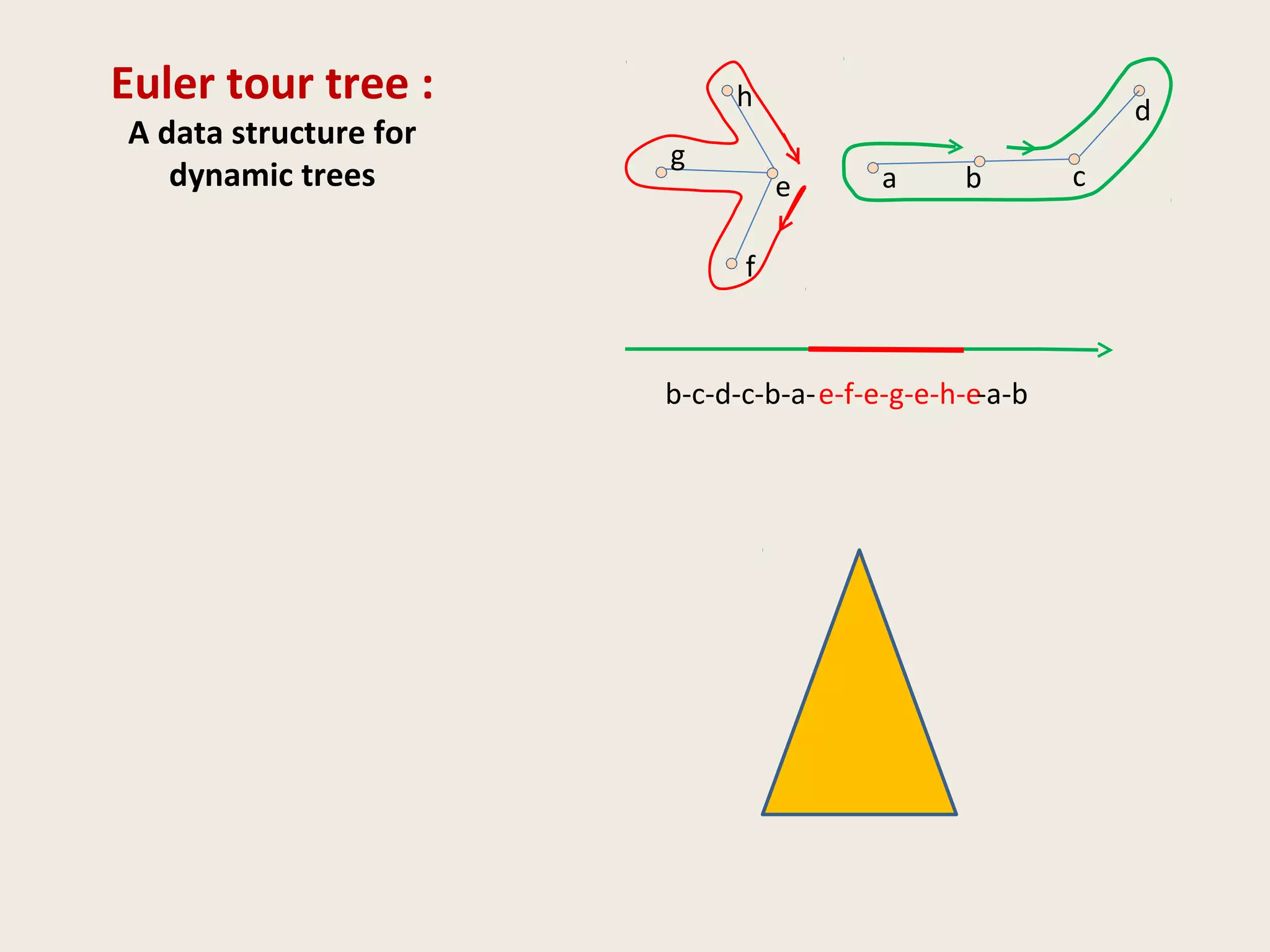
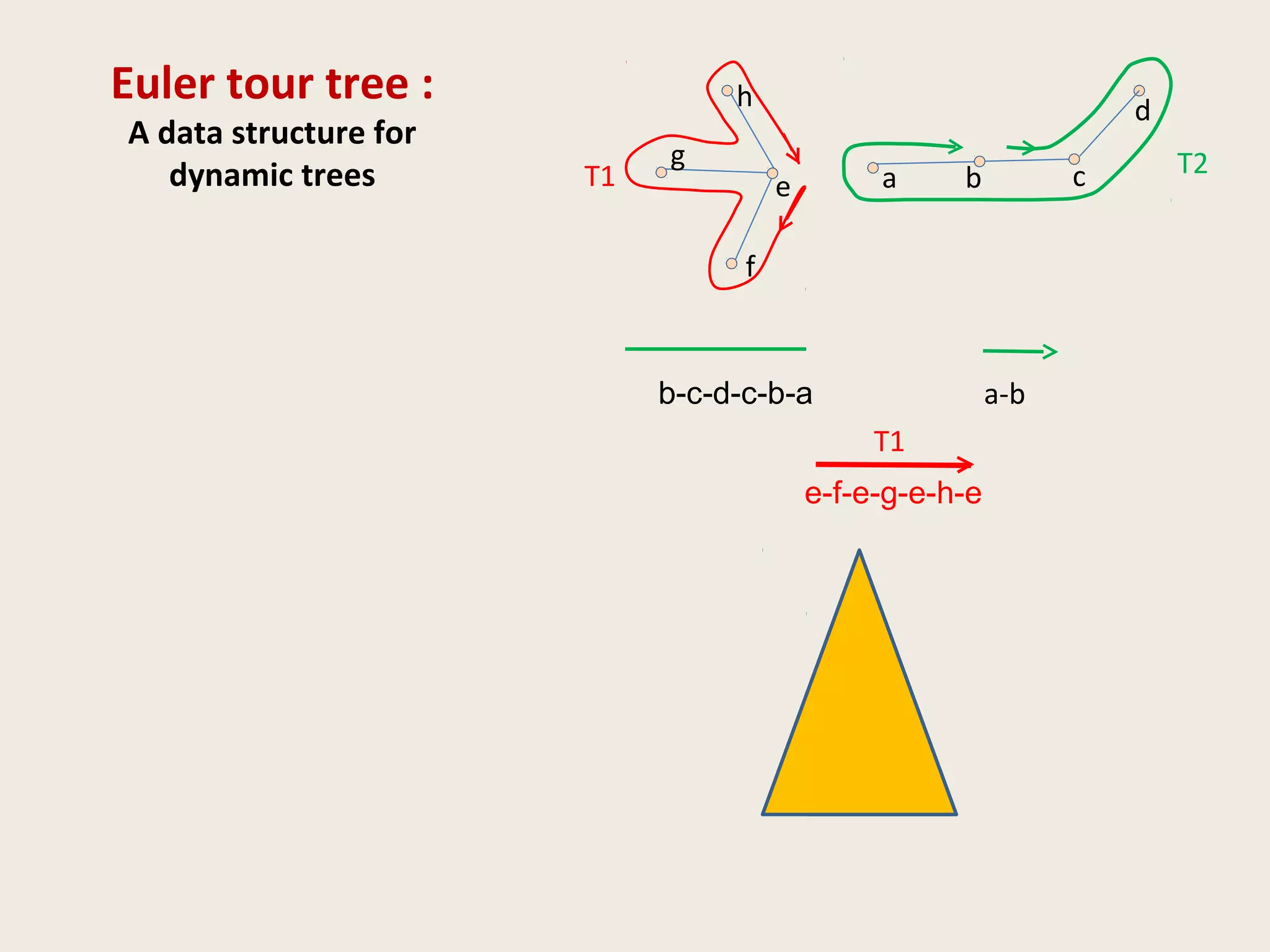
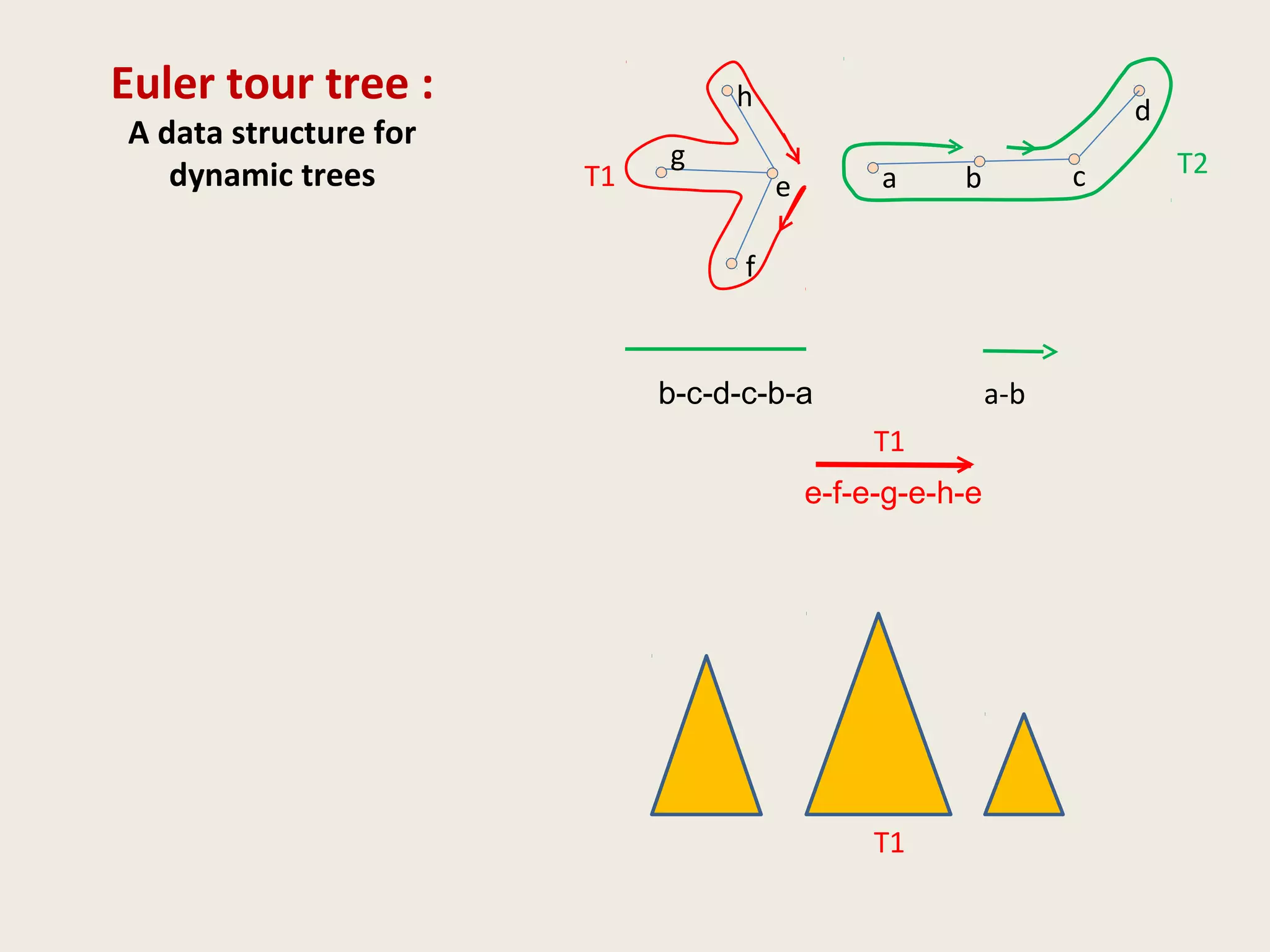
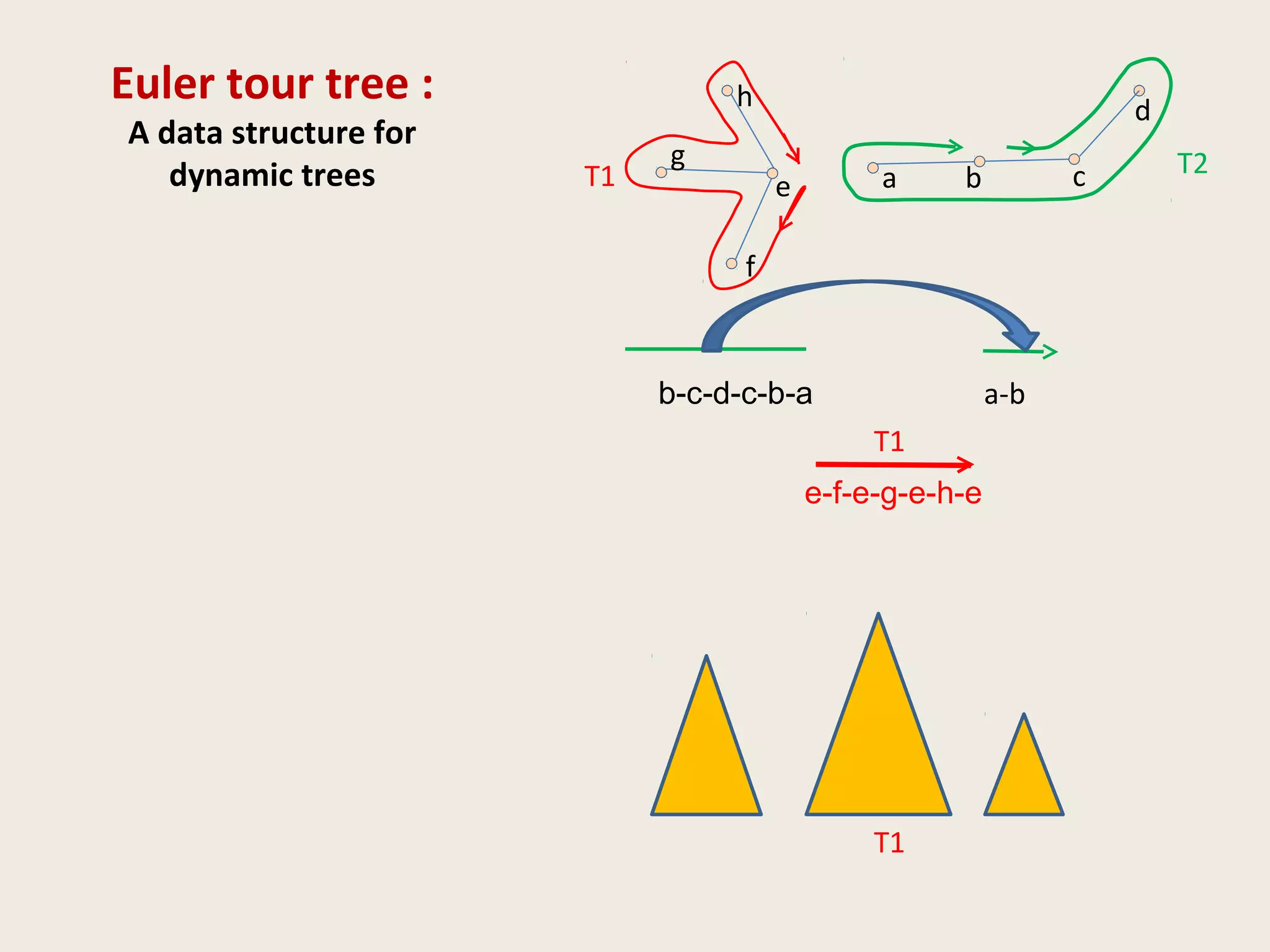
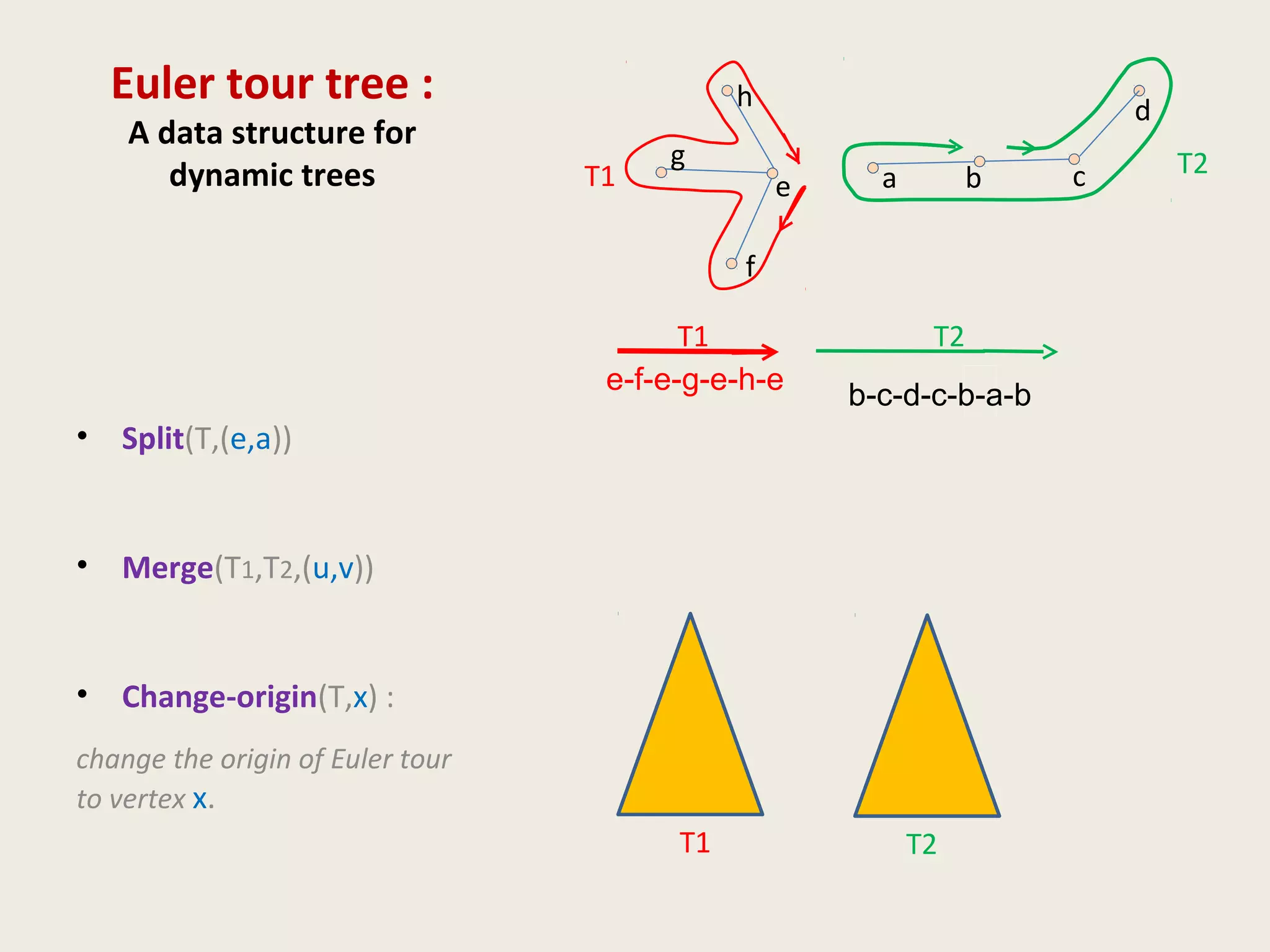
![Data Structures for Dynamic Trees
• ST Tree [Sleator & Tarjan, 1983]
Operations and queries on edges of paths
• ET tree [Henzinger and King, 1995]
Operations and queries on nodes of a tree
• Top tree [Alstrup et al., TALG 2005]
(generalization of Topology Tree [Frederickson, 1982])
Topological properties (diameter, center)](https://image.slidesharecdn.com/5-150507111504-lva1-app6891/75/5-3-dyn-algo-i-21-2048.jpg)