Downloaded 17 times
![ Suppose:
◦ The range of keys is 0..m-1
◦ Keys are distinct
The idea:
◦ Set up an array T[0..m-1] in which
T[i] = x if x T and key[x] = i
T[i] = NULL otherwise
◦ This is called a direct-address table
Operations take O(1) time!
6](https://image.slidesharecdn.com/lec-05hashing-140504015411-phpapp01/85/Advance-algorithm-hashing-lec-I-6-320.jpg)
![ Suppose:
◦ The range of keys is 0..m-1
◦ Keys are distinct
The idea:
◦ Set up an array T[0..m-1] in which
T[i] = x if x T and key[x] = i
T[i] = NULL otherwise
◦ This is called a direct-address table
Operations take O(1) time!
6](https://image.slidesharecdn.com/lec-05hashing-140504015411-phpapp01/75/Advance-algorithm-hashing-lec-I-6-2048.jpg)
Uploaded bySajid Marwat
Advance algorithm hashing lec I
The document discusses hash tables as an efficient data structure for implementing dictionary operations. It describes how hash tables work by using a hash function to map keys to array indices, allowing for fast lookup times of O(1) on average. When collisions occur where two keys map to the same index, techniques like chaining can be used to resolve them. Hash tables are preferable to direct address tables when the key universe is very large relative to the actual number of keys, as they avoid wasting large amounts of memory when most array slots would be empty.
More Related Content
Similar to Advance algorithm hashing lec I
Advance algorithm hashing lec I
- 1.
- 2. Tables Directaddress tables Hash tables Collision and collision resolution Chaining 2
- 3. Many applicationsrequire a dynamic set that supports dictionary operations. Example: a compiler maintaining a symbol table where keys correspond to identifiers Hash table is a good data structure for implementing dictionary operations Although searching can take as long as a linked list implementation i.e. O(n) in worst case. 3
- 4. With reasonableassumptions it can take O(1) time. In practice hashing performs extremely well. A hash table is a generalization of an ordinary array where direct addressing takes O(1) time. When the actual keys are NOT small relative to the total number of keys, hashing is an effective alternative. A key can be accessed using an array index, or is computed. 4
- 5. Table isan abstract storage that contains table entries Each table entry contains a unique key k. Each table entry may also contain some information, I, associated with its key. A table entry is an ordered pair (K, I) 5
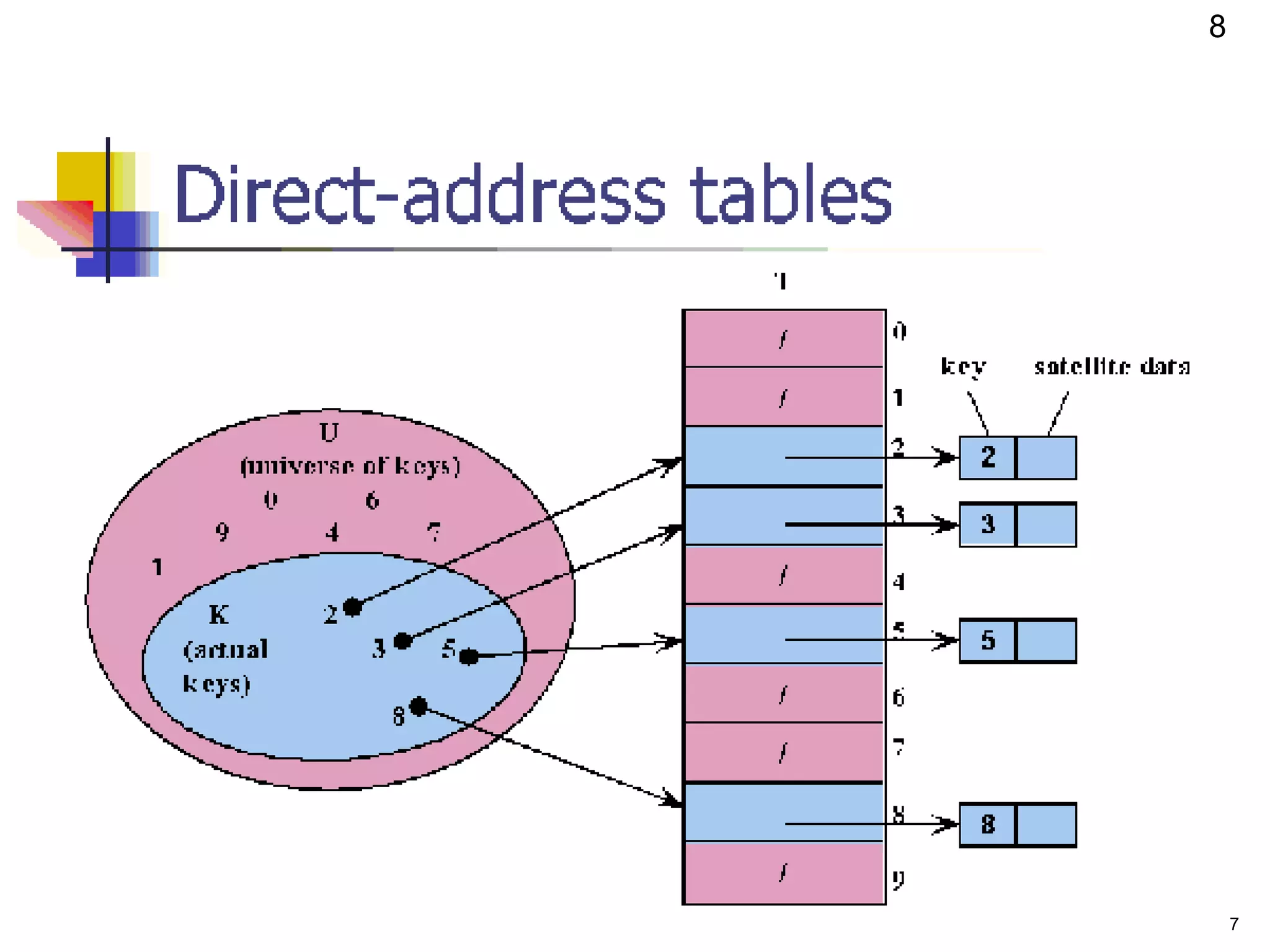
- 6. Suppose: ◦ Therange of keys is 0..m-1 ◦ Keys are distinct The idea: ◦ Set up an array T[0..m-1] in which T[i] = x if x T and key[x] = i T[i] = NULL otherwise ◦ This is called a direct-address table Operations take O(1) time! 6
- 7.
- 8. Direct Addressingis the most efficient way to access the data since. It takes only single step for any operation on direct address table. It works well when the Universe U of keys is reasonable small. 8
- 9. When the universeU is very large… Storing a table T of size U may be impractical, given the memory available on a typical computer. The set K of the keys actually stored may be so small relative to U that most of the space allocated for T would be wasted. 9
- 10. A table,50 students in a class. The key, 9 digit SSN, used to identify each student. Number of different 9 digit number=109 The fraction of actual keys needed. 50/109, 0.000005% Percent of the memory allocated for table wasted, 99.999995% 10
- 11. The tableshould be of small fixed size. Any key in the universe should be able to be mapped in the slot into table, using some mapping function 11