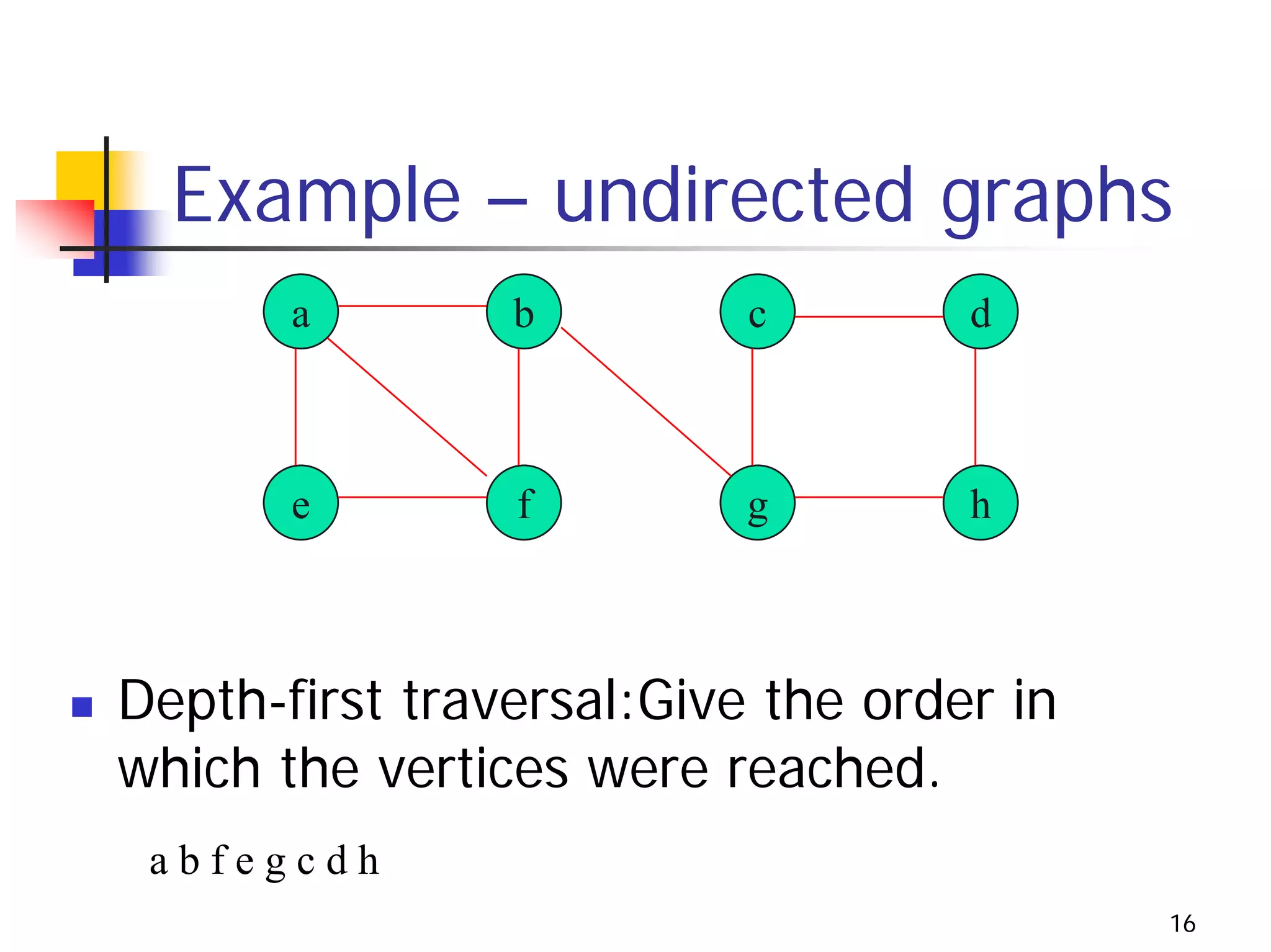
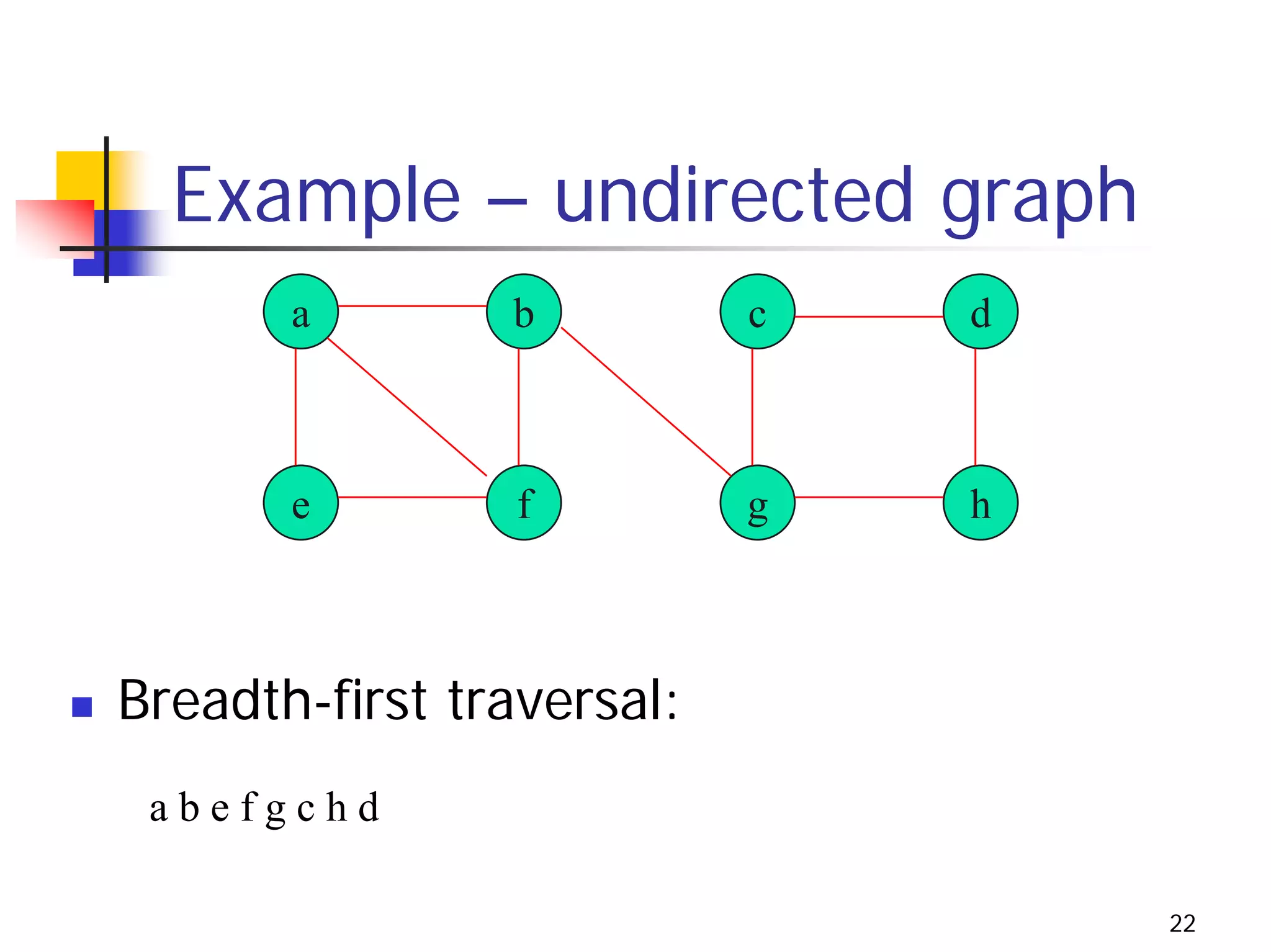
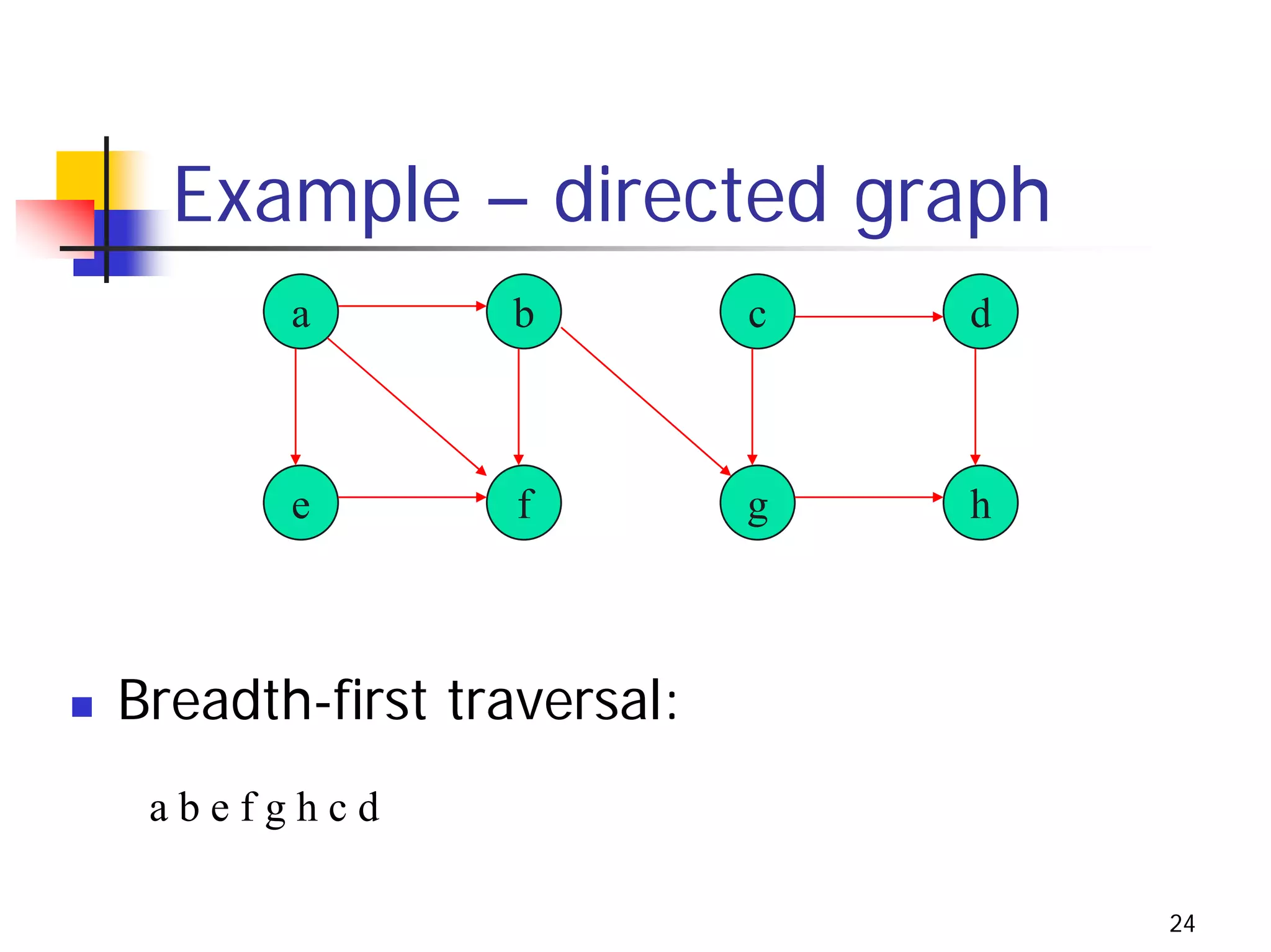
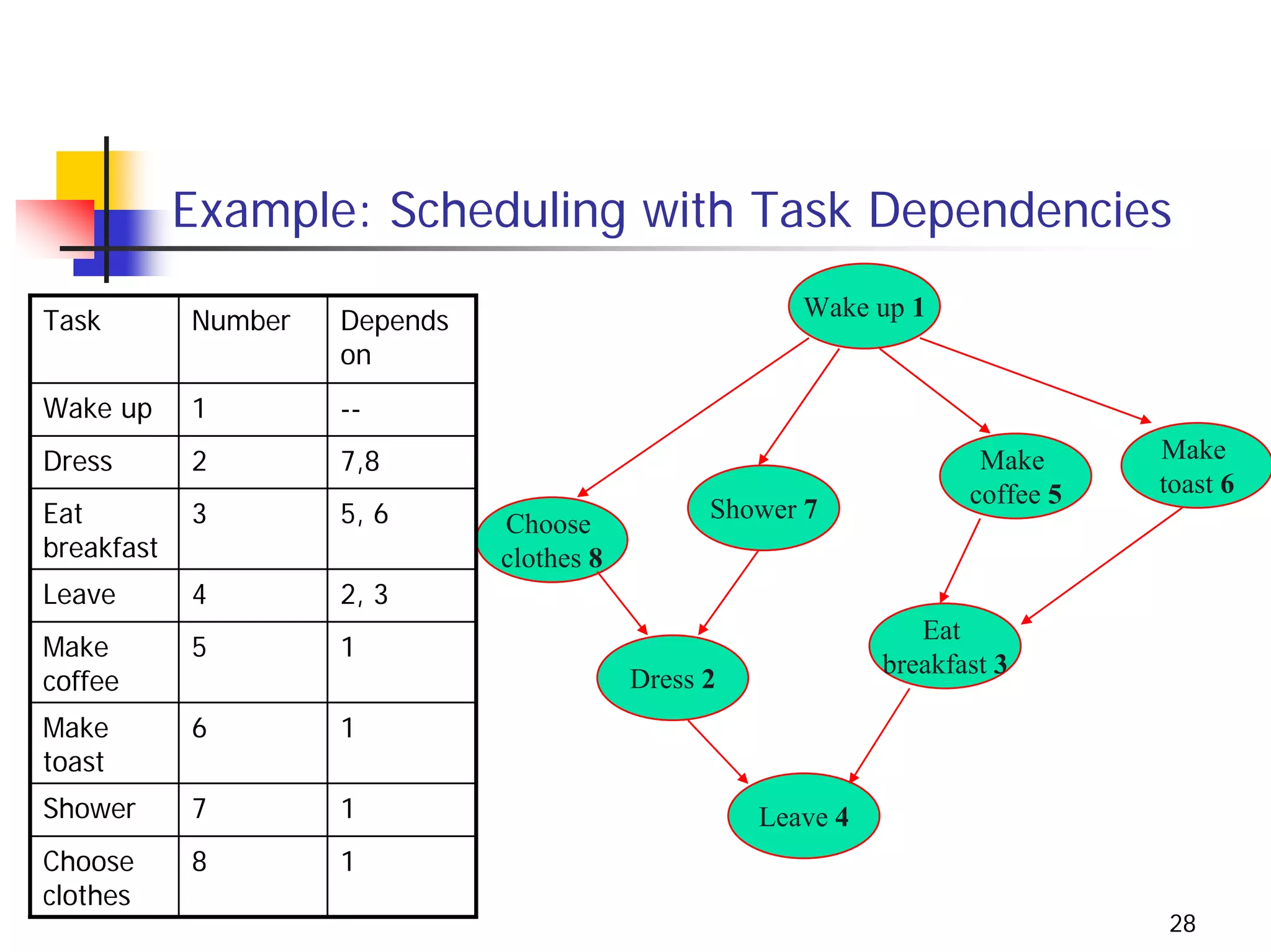
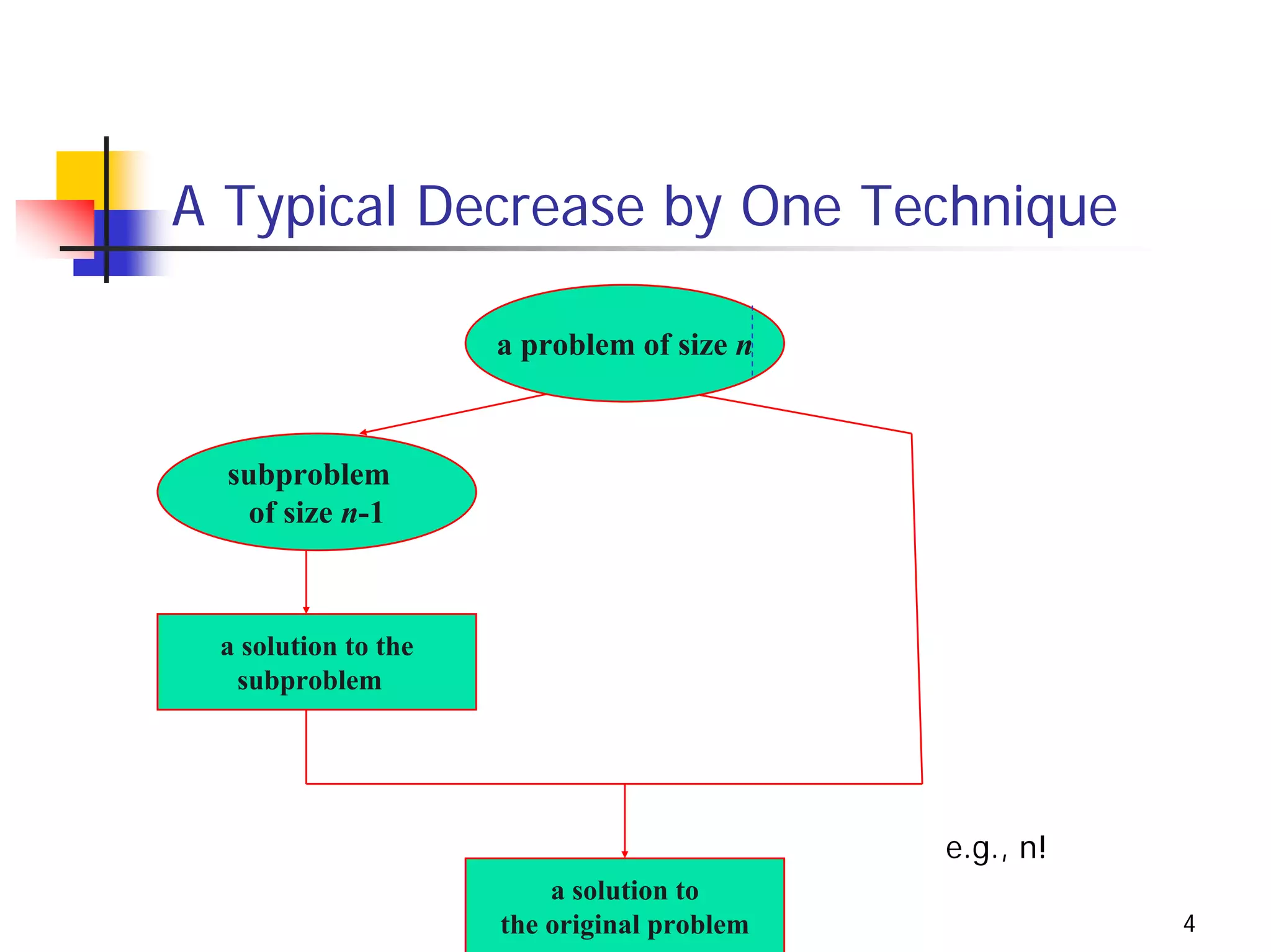
The document discusses decrease and conquer algorithms, which solve problems by recursively or iteratively reducing the size of the problem and combining solutions to the smaller subproblems, including examples like insertion sort, binary search, and graph traversal algorithms like depth-first search and breadth-first search.






![Insertion Sort: an Iterative Solution
ALGORITHM InsertionSortIter(A[0..n-1])
//An iterative implementation of insertion sort
//Input: An array A[0..n-1] of n orderable elements
//Output: Array A[0..n-1] sorted in nondecreasing order
for i 1 to n – 1 do // i: the index of the first element of the unsorted part.
key = A[i]
for j i – 1 to 0 do // j: the index of the sorted part of the array
if (key< A[j]) //compare the key with each element in the sorted part
A[j+1] A[j]
else
break
A[j +1] key //insert the key to the sorted part of the array
Efficiency?
9](https://image.slidesharecdn.com/s05cs303chap5-120411101319-phpapp02/75/Algorithm-chapter-5-9-2048.jpg)
![Insertion Sort: a Recursive Solution
ALGORITHM InsertionSortRecur(A[0..n-1], n-1)
//A recursive implementation of insertion sort
//Input: An array A[0..n-1] of n orderable elements Index of the last element
//Output: Array A[0..n-1] sorted in nondecreasing order
if n > 1
InsertionSortRecur(A[0..n-1], n-2)
Insert(A[0..n-1], n-1) //insert A[n-1] to A[0..n-2]
Index of the element/key to be inserted.
ALGORITHM Insert(A[0..m], m)
//Insert A[m] to the sorted subarray A[0..m-1] of A[0..n-1]
//Input: A subarray A[0..m] of A[0..n-1]
//Output: Array A[0..m] sorted in nondecreasing order
key = A[m]
for j m – 1 to 0 do
if (key< A[j])
A[j+1] A[j] Recurrence relation?
else
break
A[j +1] key 10](https://image.slidesharecdn.com/s05cs303chap5-120411101319-phpapp02/75/Algorithm-chapter-5-10-2048.jpg)