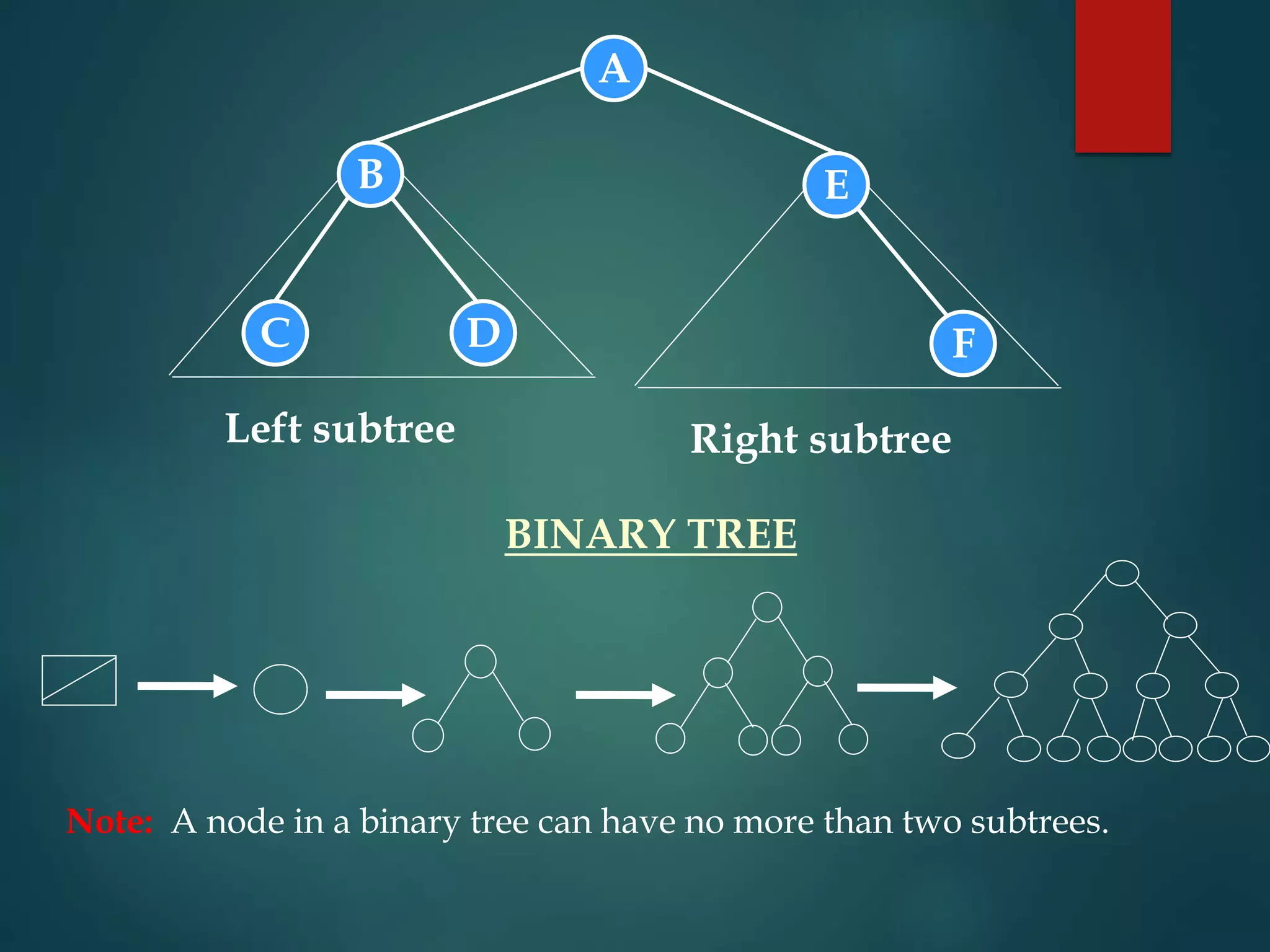
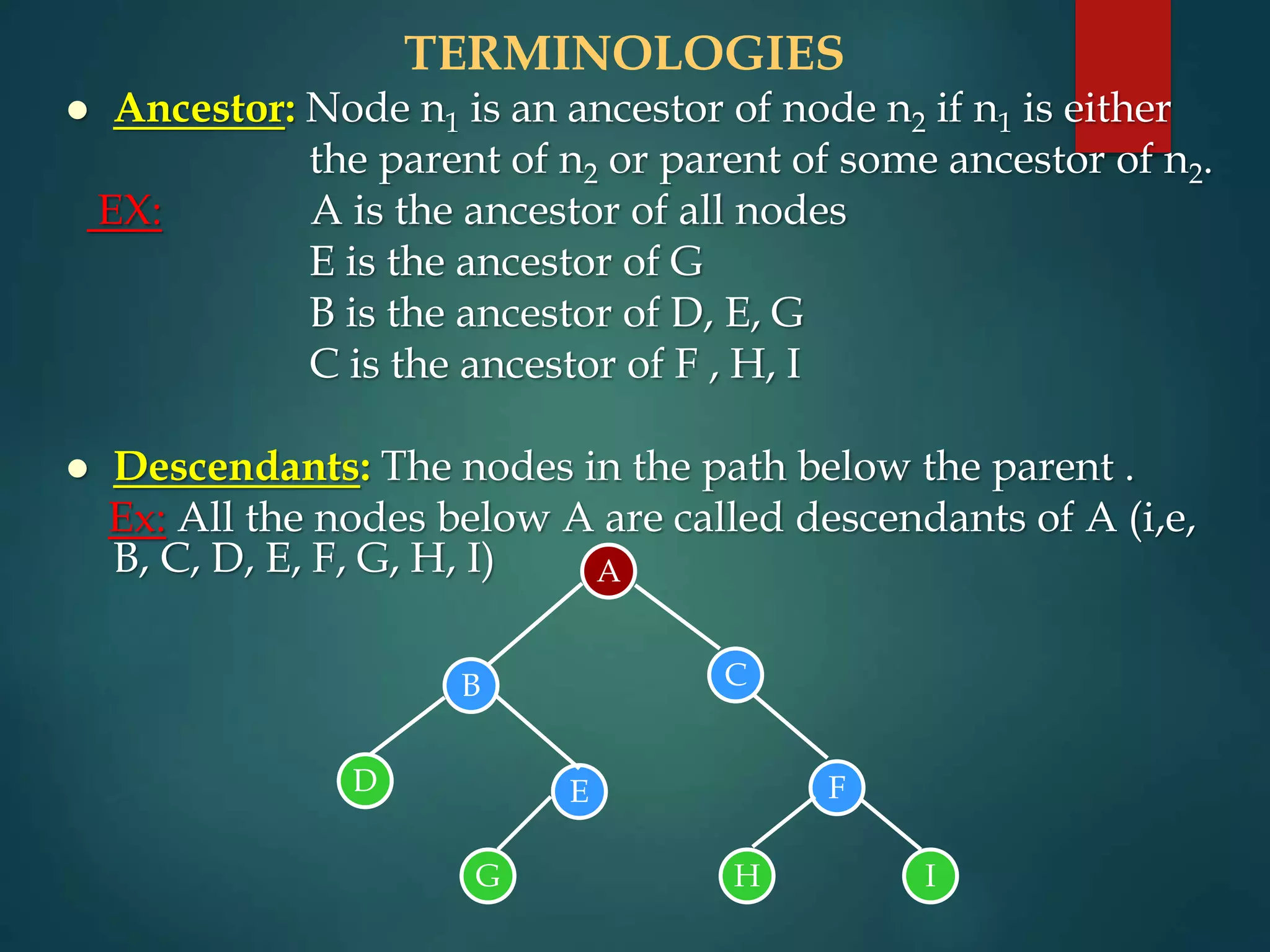
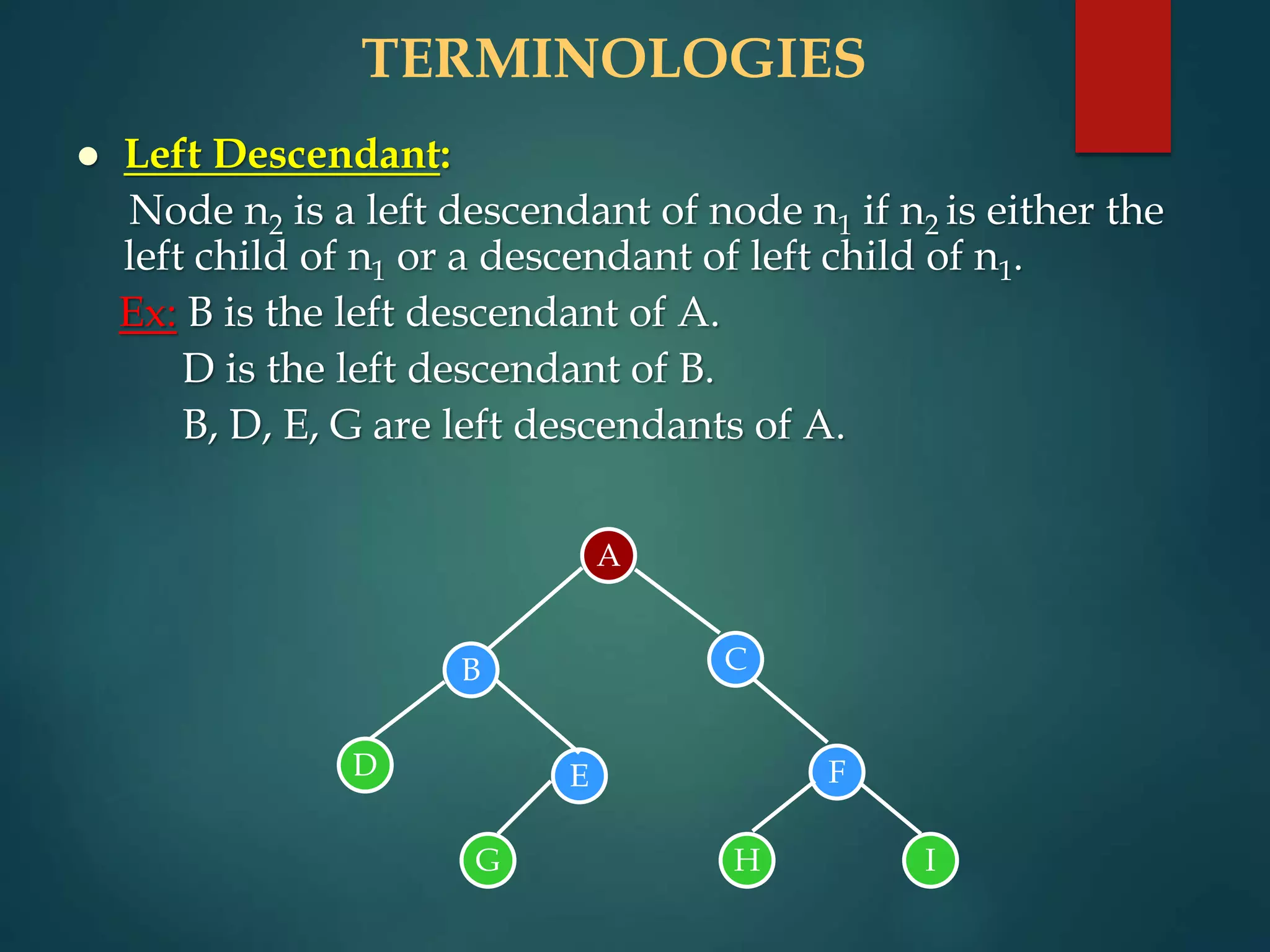
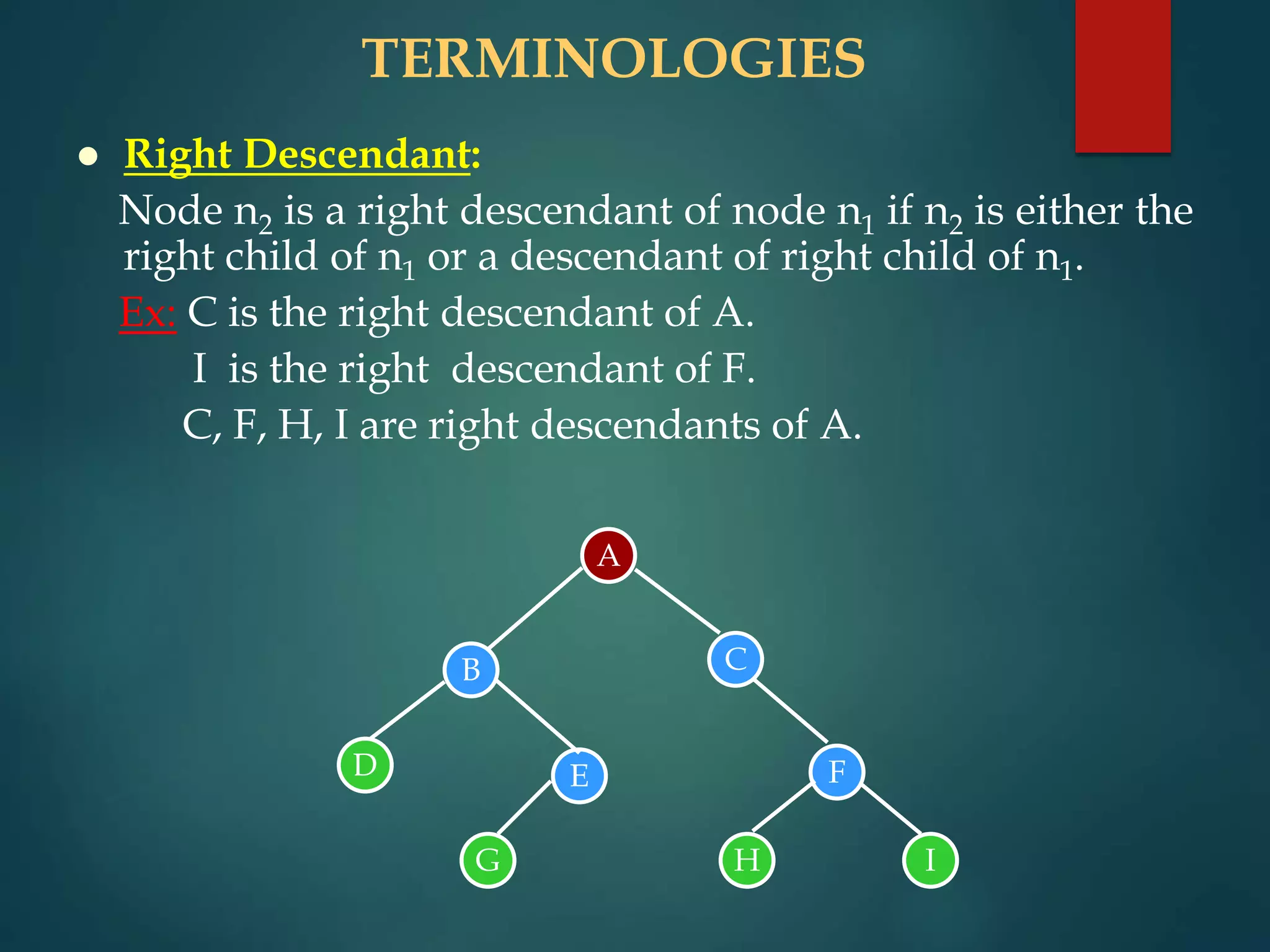
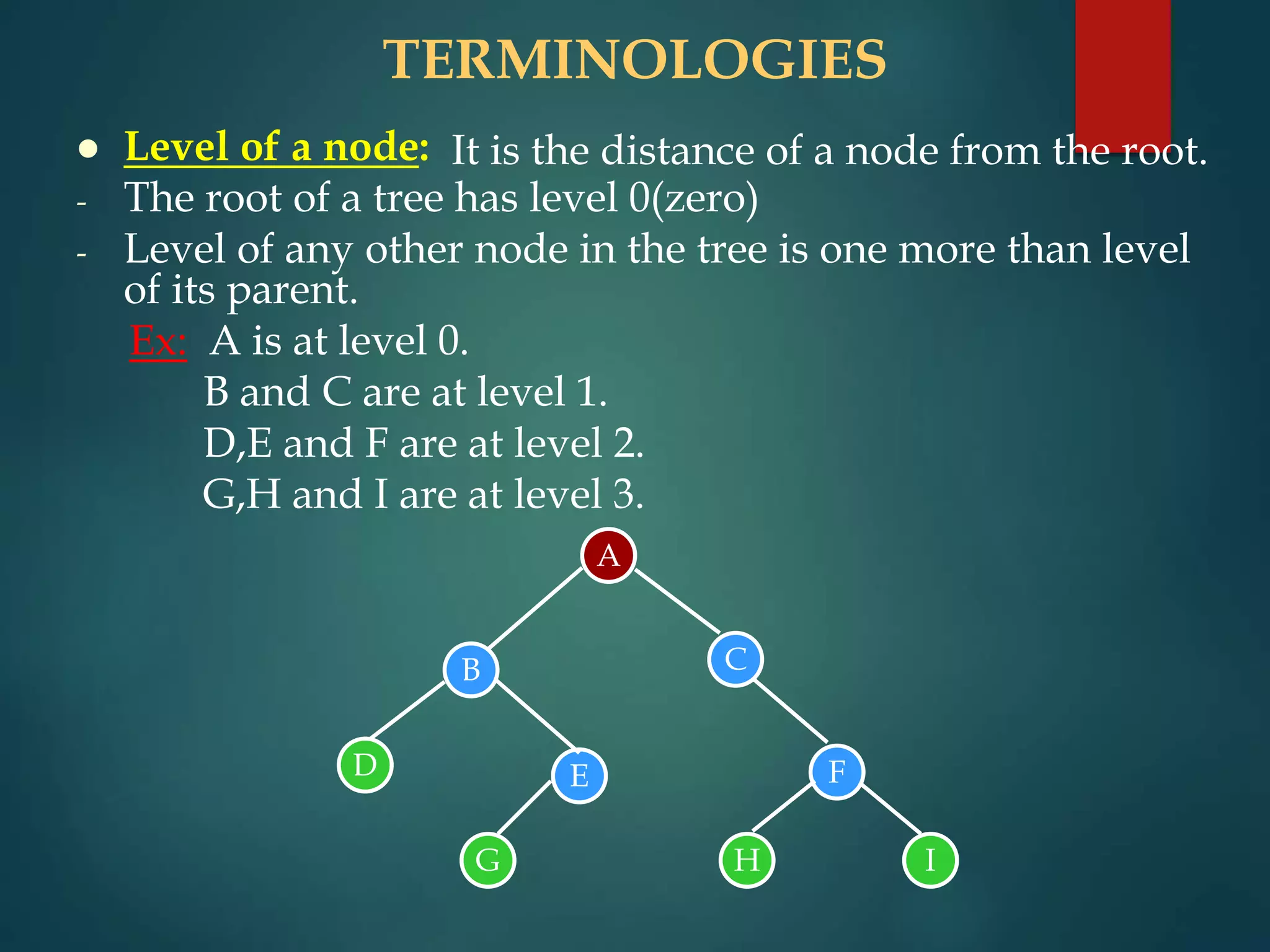
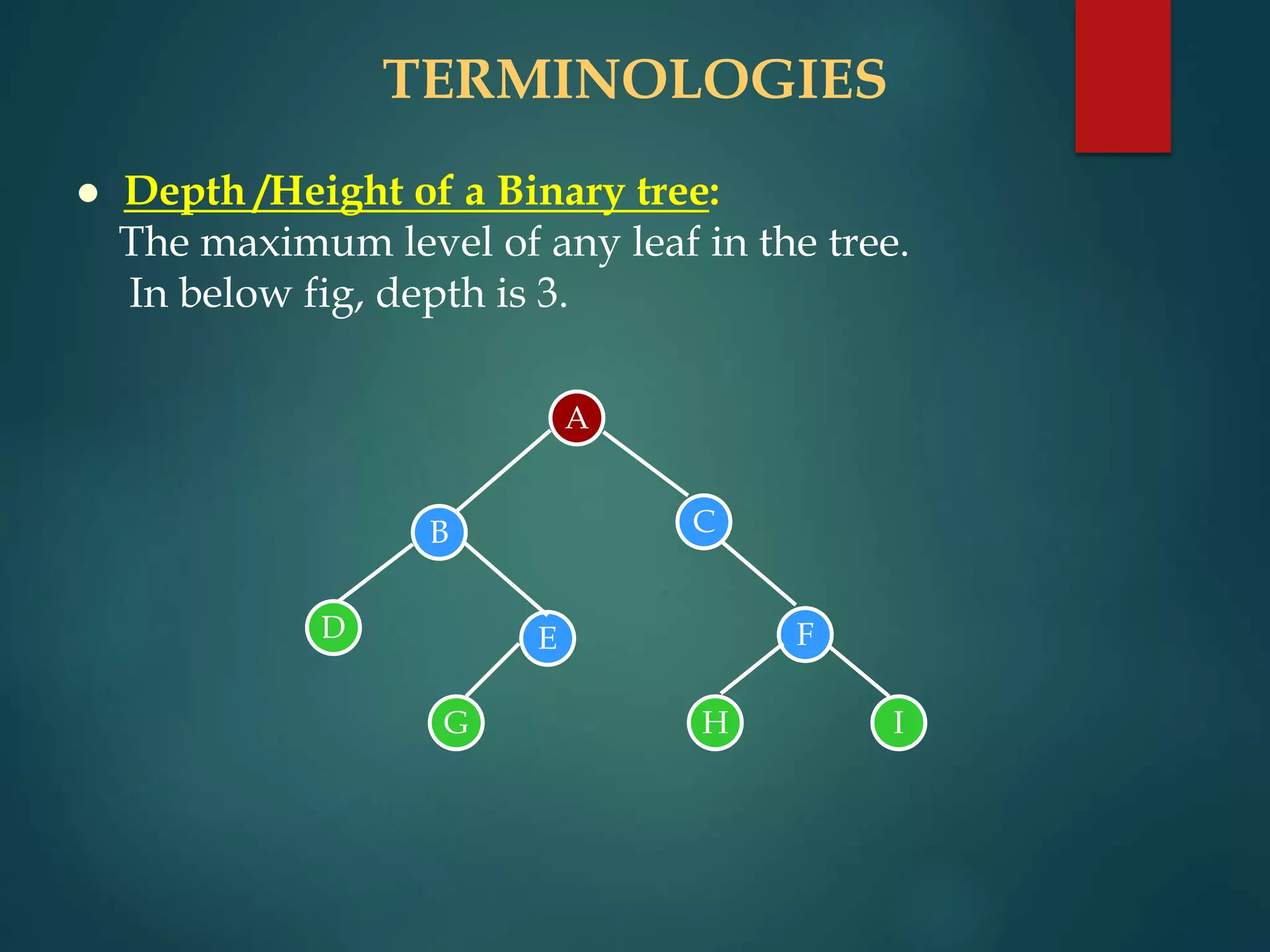
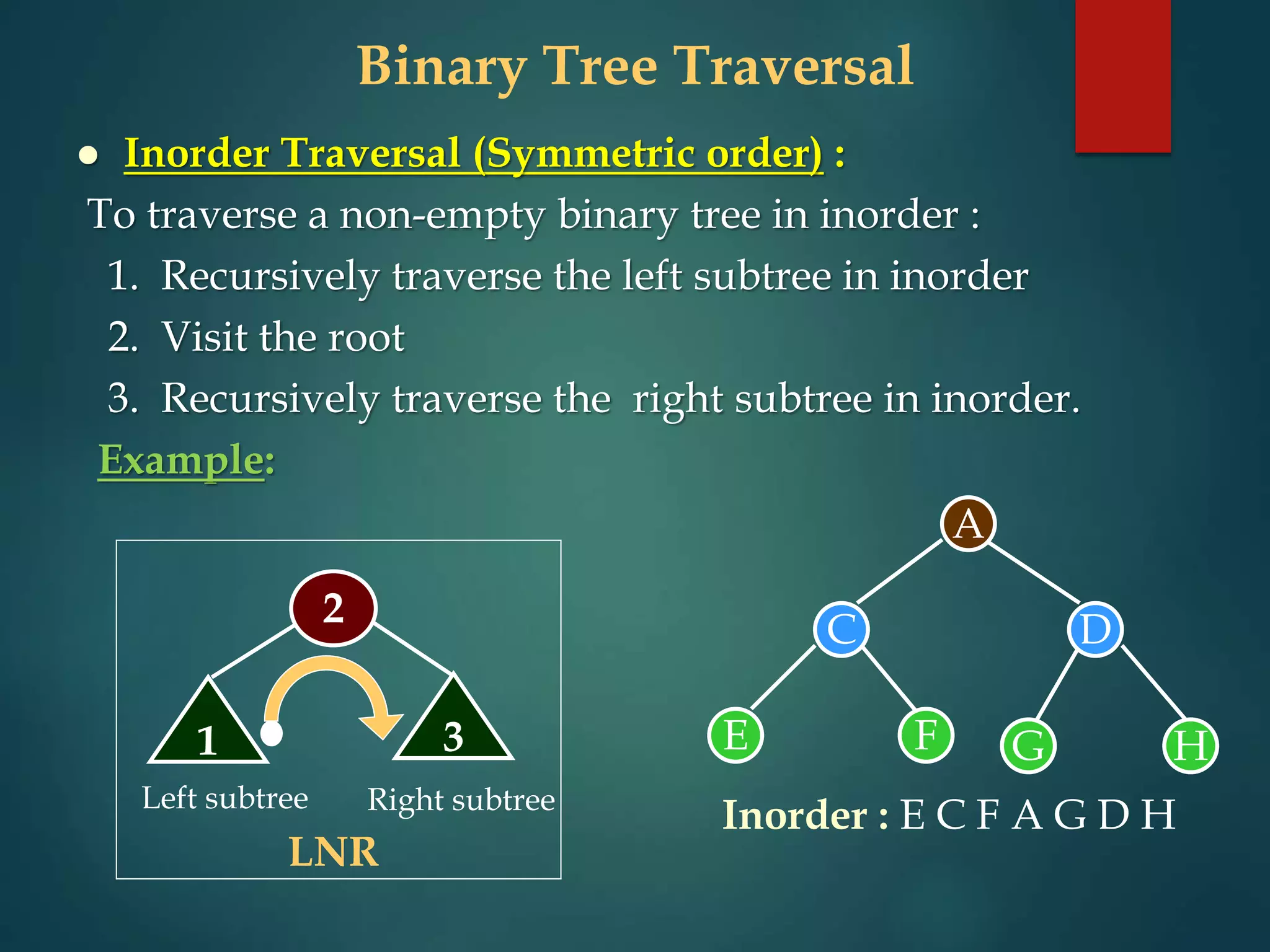
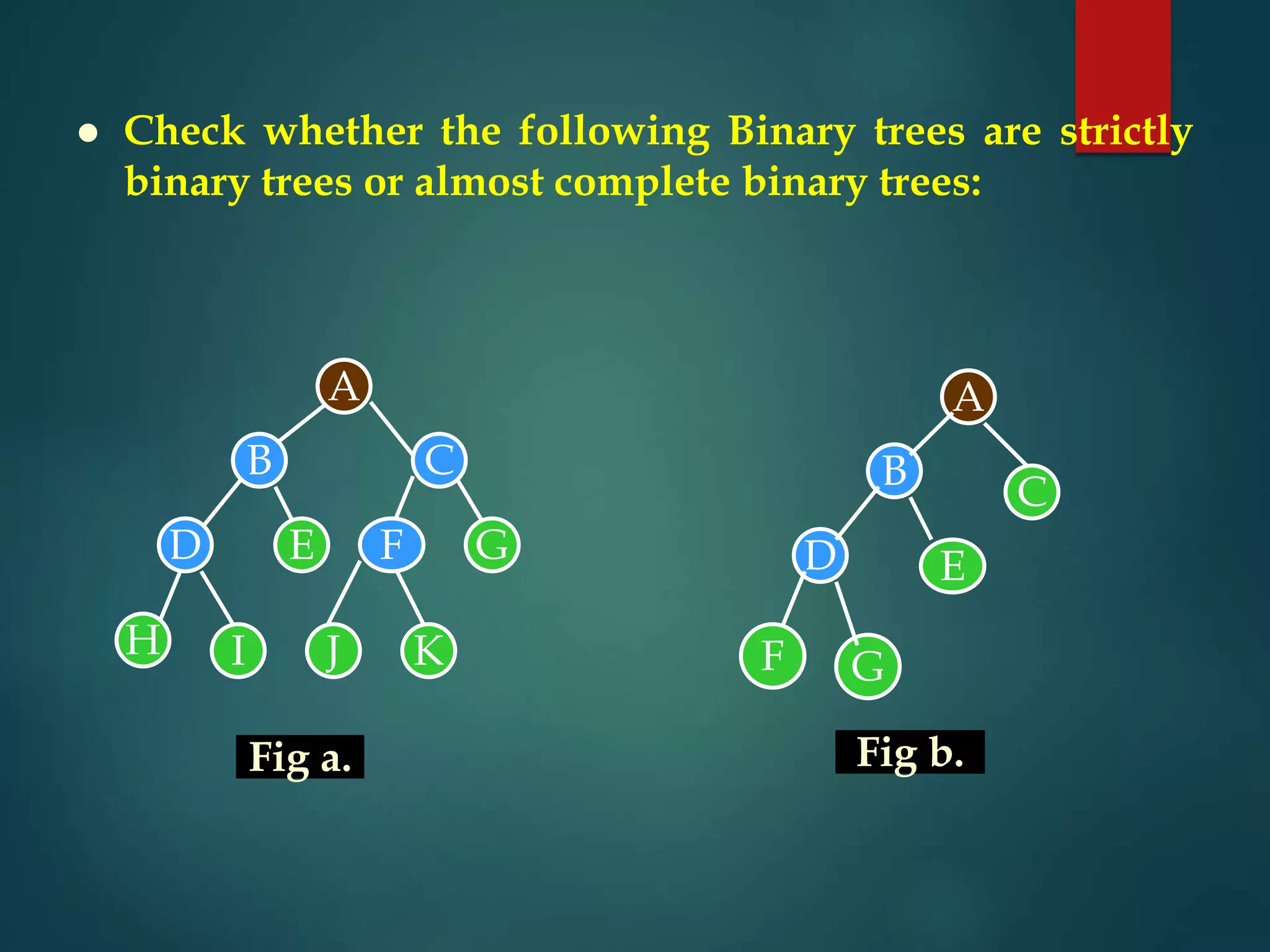
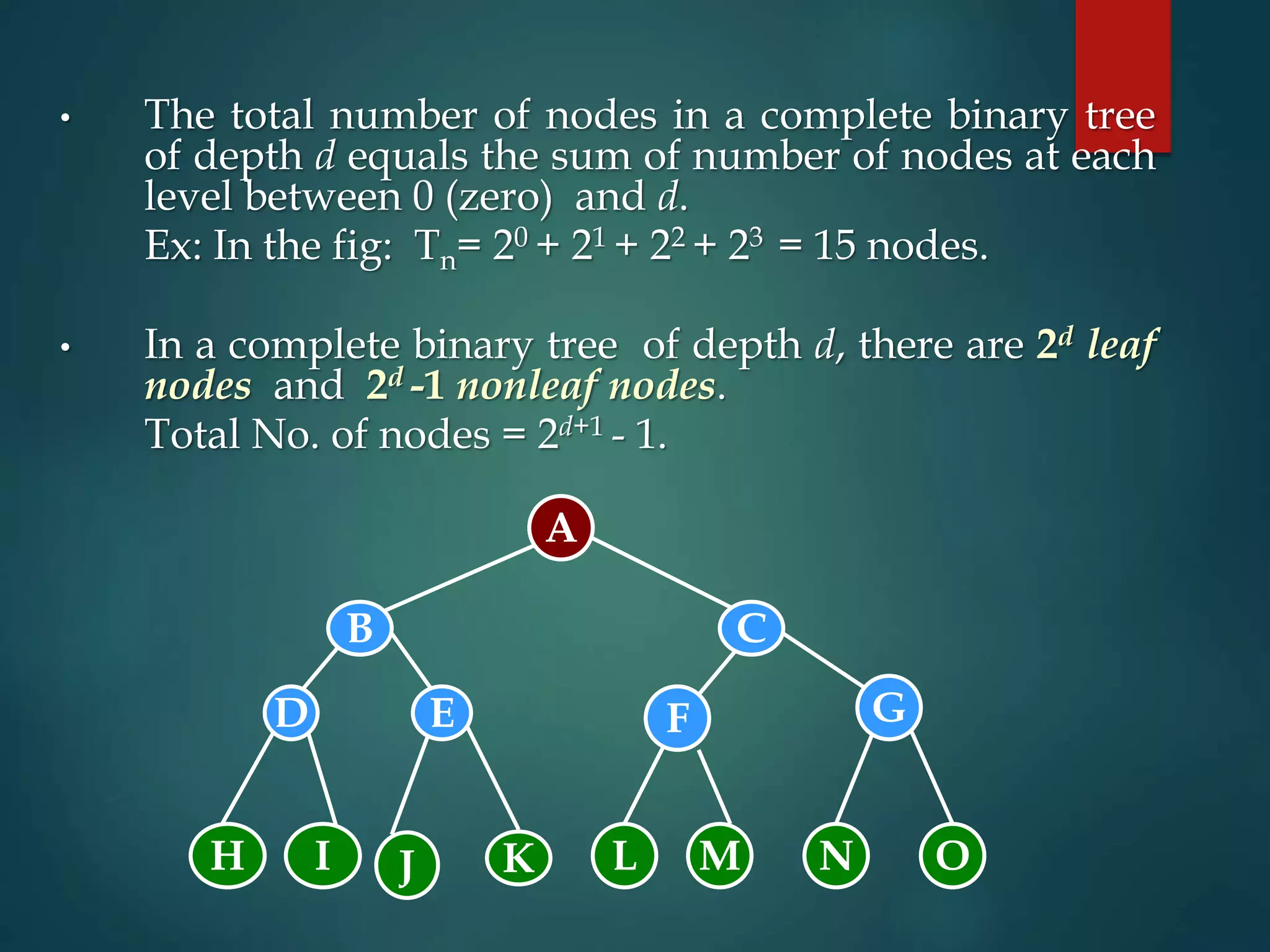
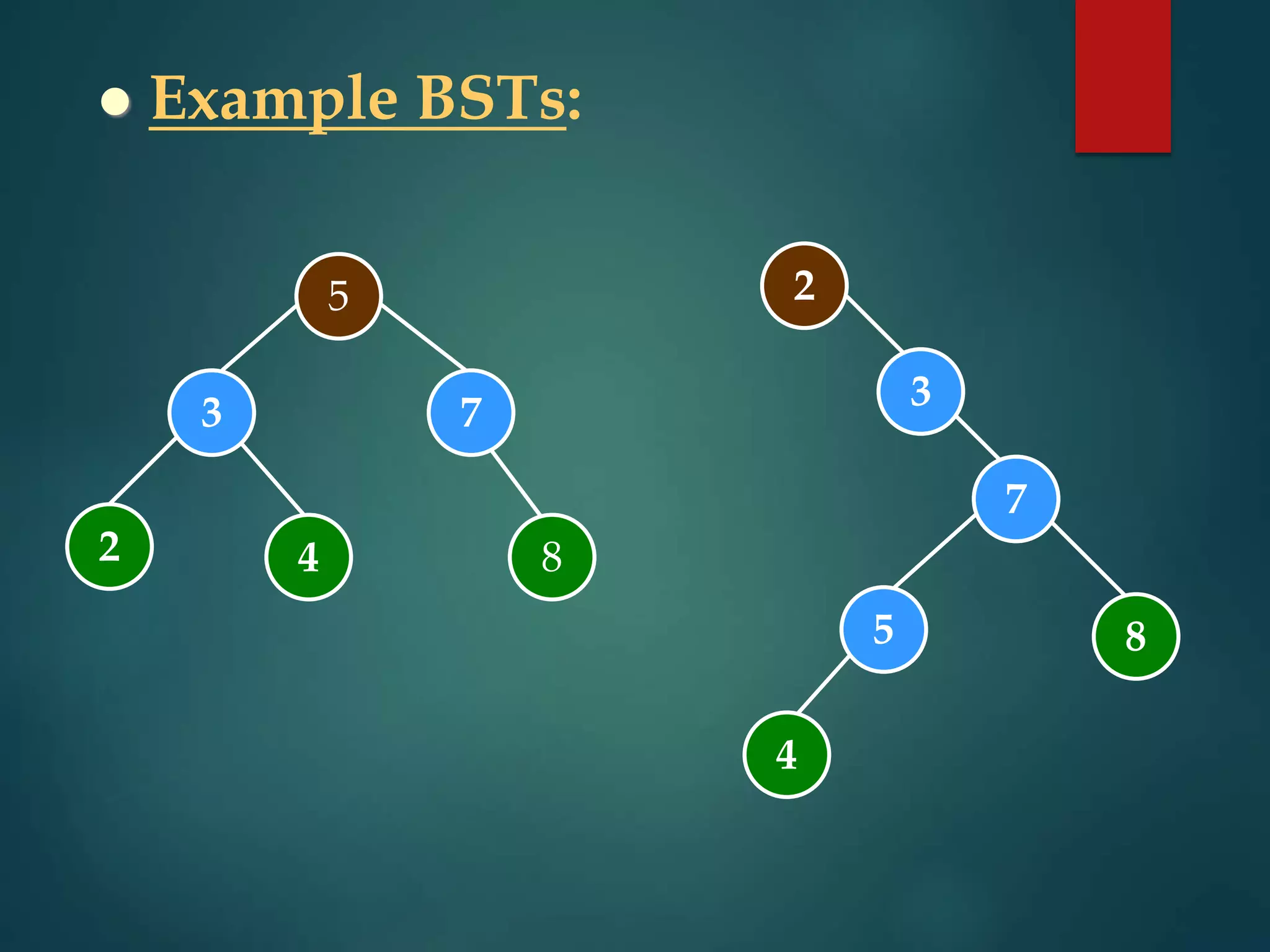
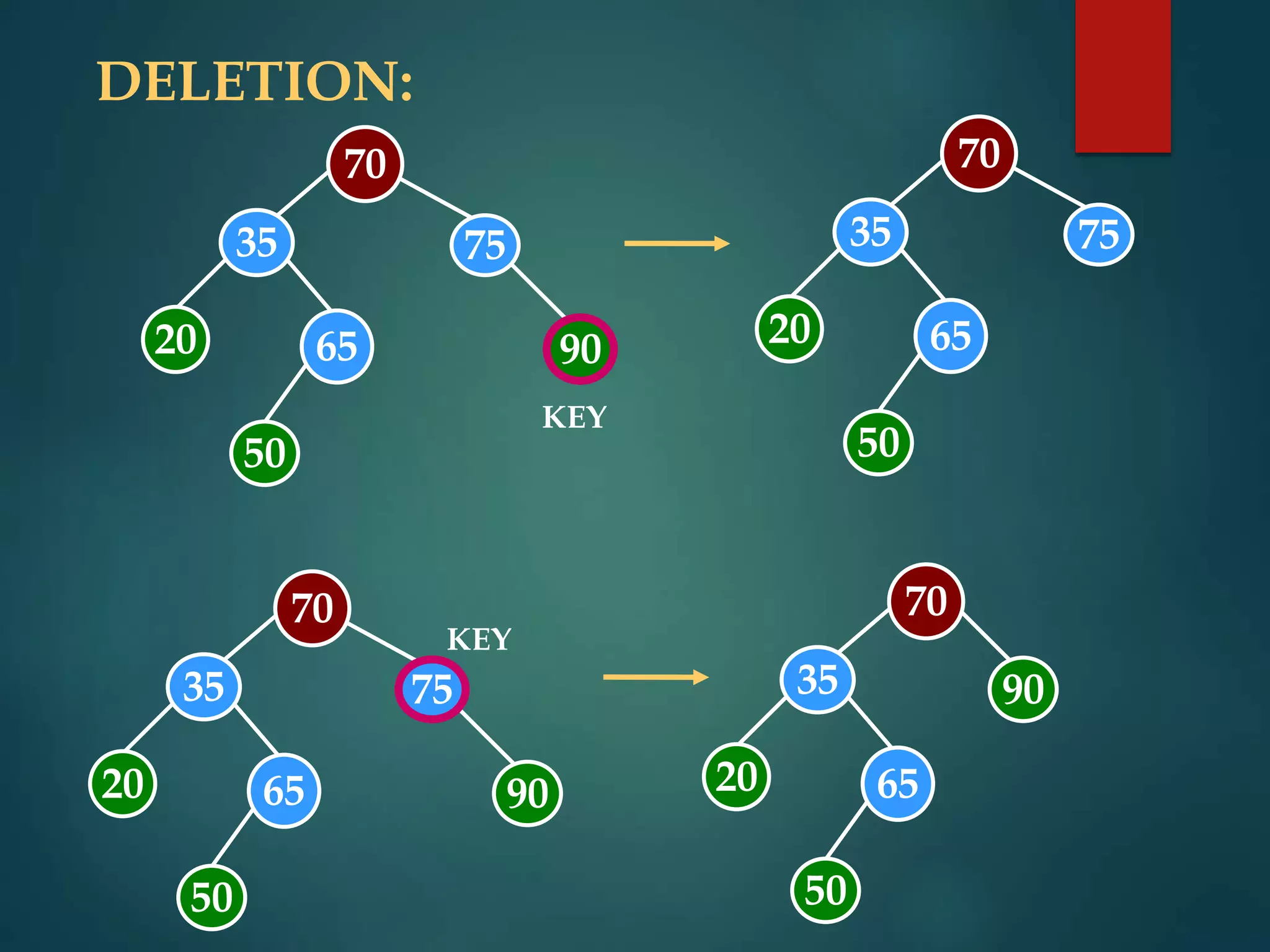
The document discusses various non-linear data structures, focusing on binary trees. It defines key terminology related to binary trees such as root, leaf nodes, ancestors, descendants, etc. It also covers different types of binary trees like strictly binary trees, complete binary trees, binary search trees. The document discusses various binary tree representations, traversals (inorder, preorder, postorder), and operations like searching, insertion, and deletion on binary search trees. It briefly introduces threaded binary trees at the end.











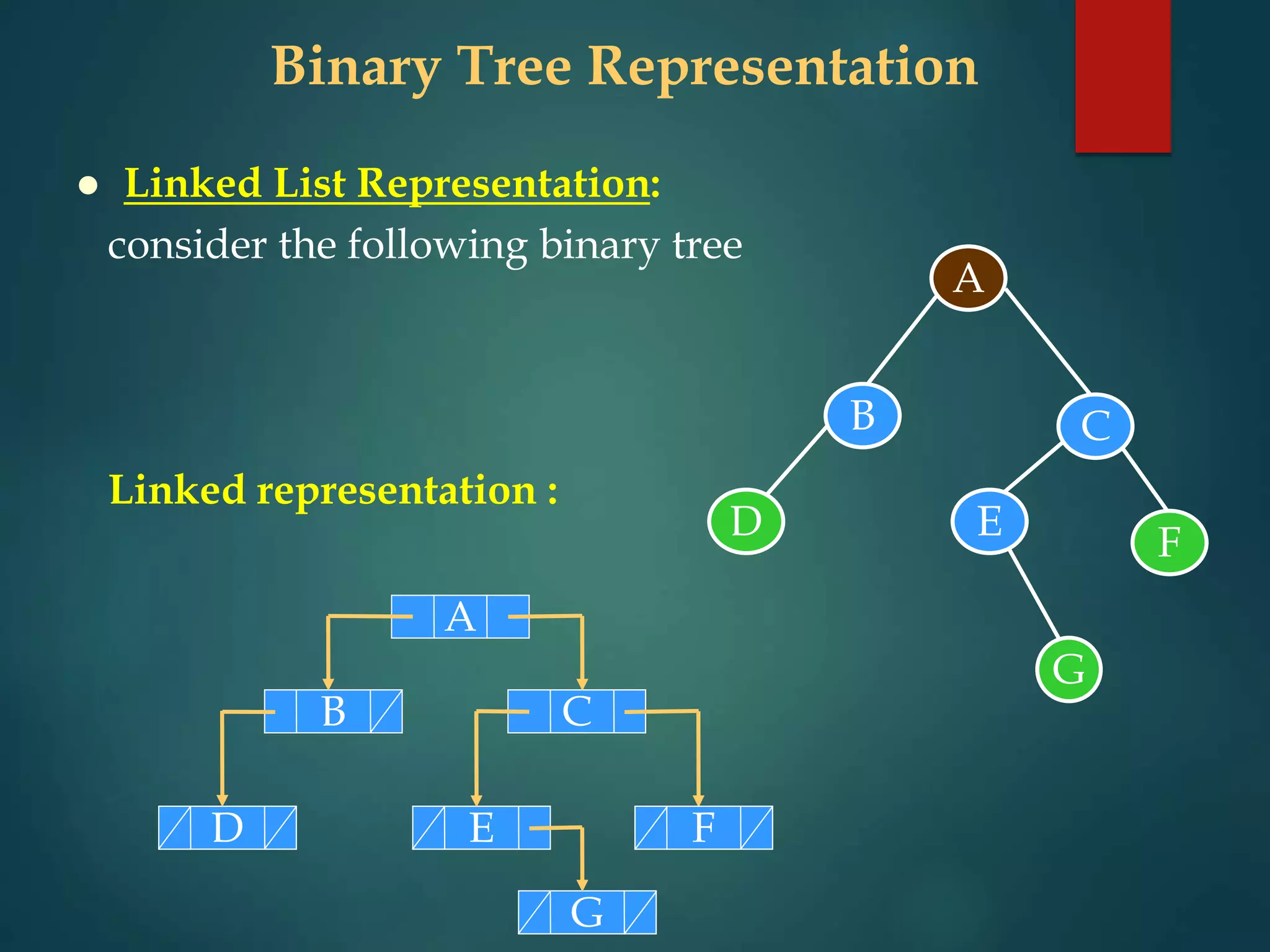
![Binary Tree Representation
Array Representation:
A
B
D
C
E F
G
A B C E
D F G
0 1 2 4
3 5 6 7 8 9 10 11 1213 15
14
A[i]
i
If the height of the binary tree is d then the array index ranges from
0 to 2d+1-1.
For the above binary tree, the array index ranges from 0 to 23+1-1
i.e., 0 to 15.
If P is the parent, then the left and right child are at the position
2P+1 and 2P+2 respectively.](https://image.slidesharecdn.com/binarytree-230427143750-99aeeb46/75/binary-tree-pptx-18-2048.jpg)
























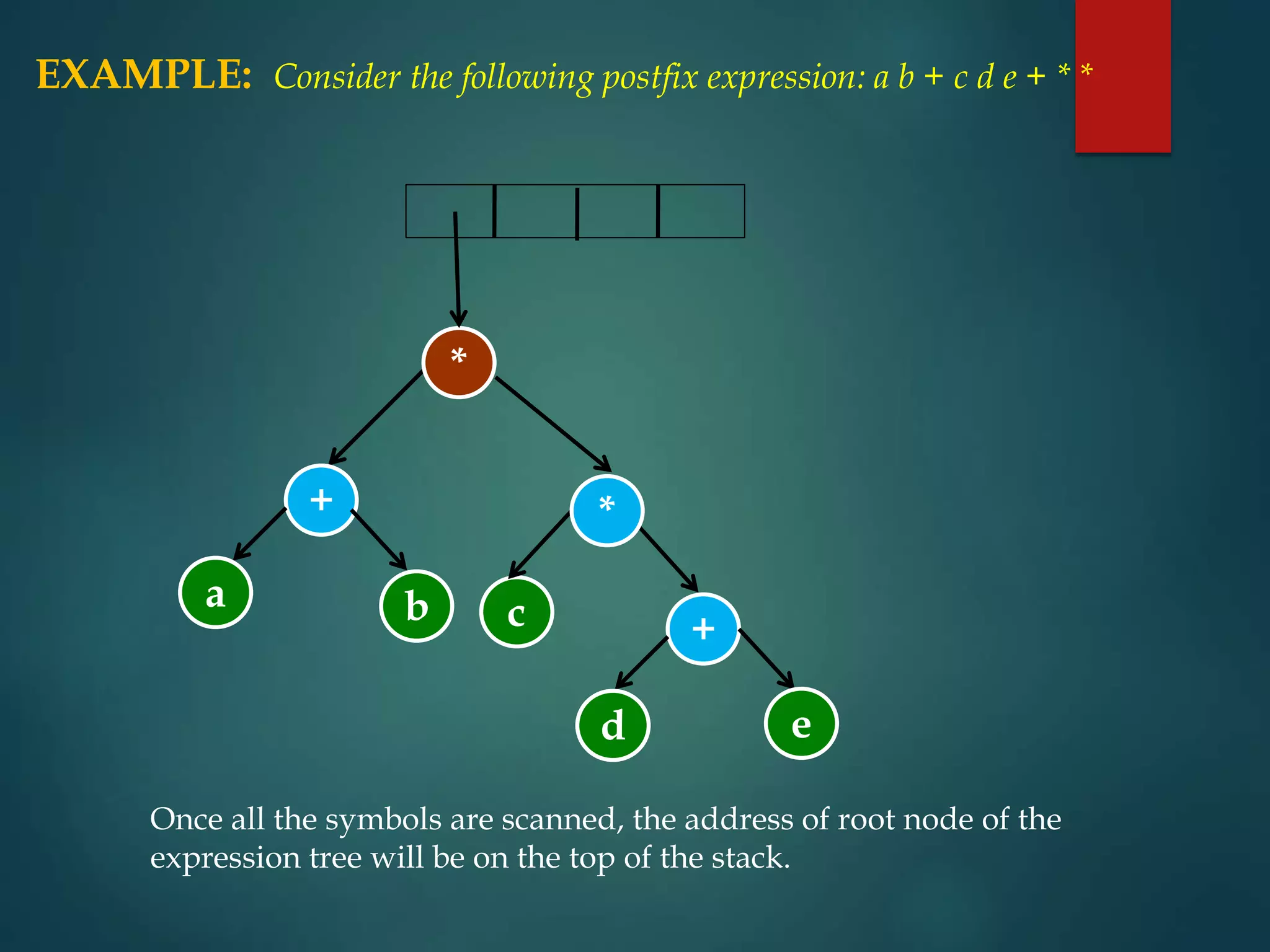





![Program 13: Develop a C program to construct an expression tree for a given postfix
expression and evaluate the expression tree.
#include<stdio.h>
#include<stdlib.h>
#include<ctype.h>
#include<math.h>
typedef struct node
{
char info;
struct node *lchild,*rchild;
}NODE;
NODE * create_tree(char postfix[])
{
NODE *newnode, *stack[20];
int i, top = -1;
char ch;
for(i=0;postfix[i]!='0‘;i++)
{
ch=postfix[i];
newnode = (NODE*)malloc(sizeof(NODE));
newnode->info = ch;
newnode->lchild = newnode->rchild = NULL;
if(isalnum(ch))
stack[++top]=newnode;
else
{
newnode->rchild = stack[top--];
newnode->lchild = stack[top--];
stack[++top]=newnode;
}
}
return(stack[top--]);
}](https://image.slidesharecdn.com/binarytree-230427143750-99aeeb46/75/binary-tree-pptx-62-2048.jpg)
![Program 13: Develop a C program to construct an expression tree for a given postfix
expression and evaluate the expression tree.
float eval(NODE *root)
{
float num;
switch(root->info)
{
case '+' : return (eval(root->lchild) + eval(root->rchild));
case '-' : return (eval(root->lchild) - eval(root->rchild));
case '*' : return (eval(root->lchild) * eval(root->rchild));
case '/' : return (eval(root->lchild) / eval(root->rchild));
case '^' : return (pow(eval(root->lchild), eval(root->rchild)));
default: if(isalpha(root->info))
{
printf("n%c = ",root->info);
scanf("%f",&num);
return(num);
}
else
return(root->info - '0');
}
}
int main()
{
char postfix[30];
float res;
NODE * root = NULL;
printf("nEnter a valid Postfix expressionn");
scanf("%s",postfix);
root = create_tree(postfix);
res = eval (root);
printf("nResult = %f",res);
return 0;
}](https://image.slidesharecdn.com/binarytree-230427143750-99aeeb46/75/binary-tree-pptx-63-2048.jpg)