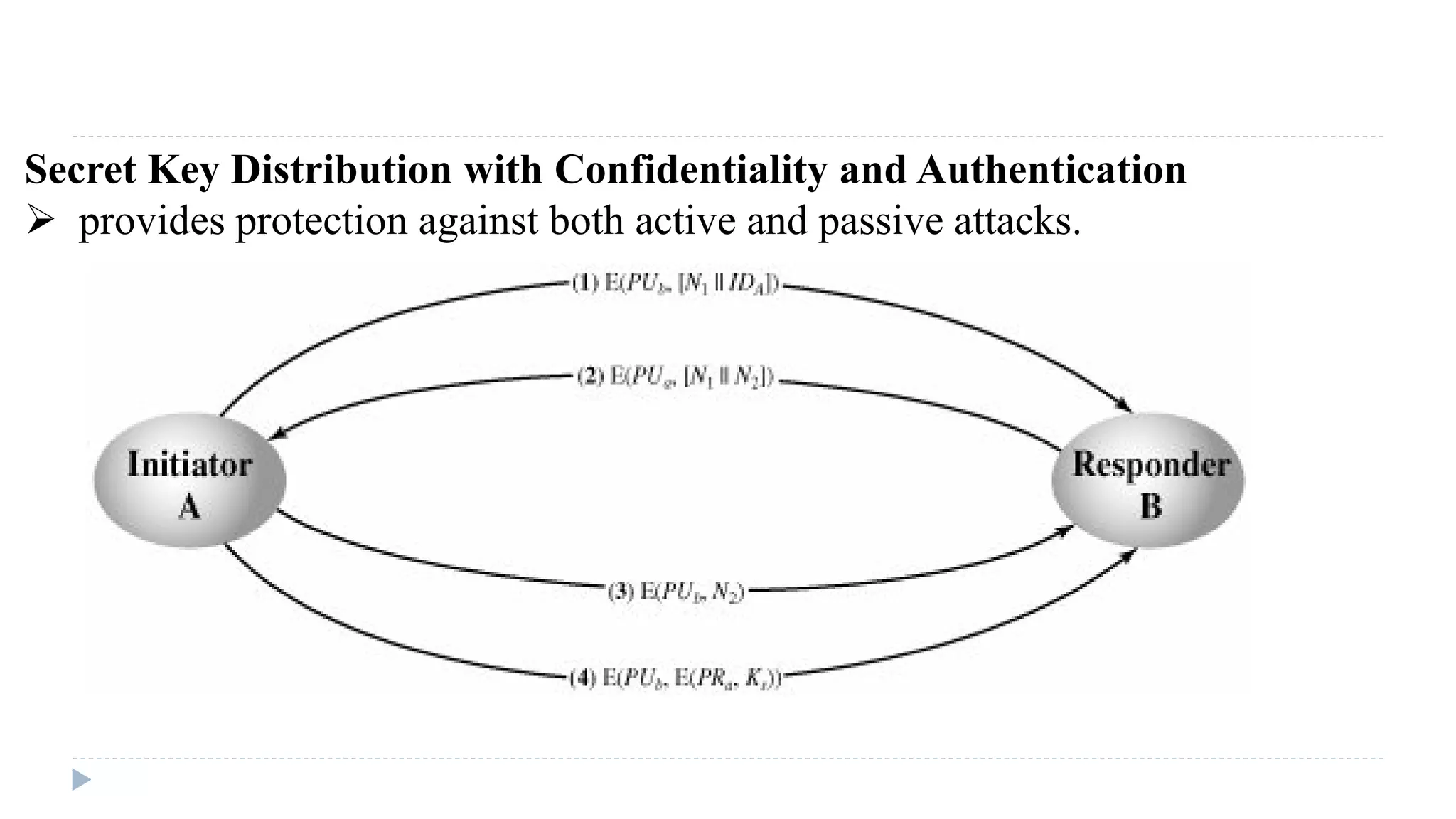
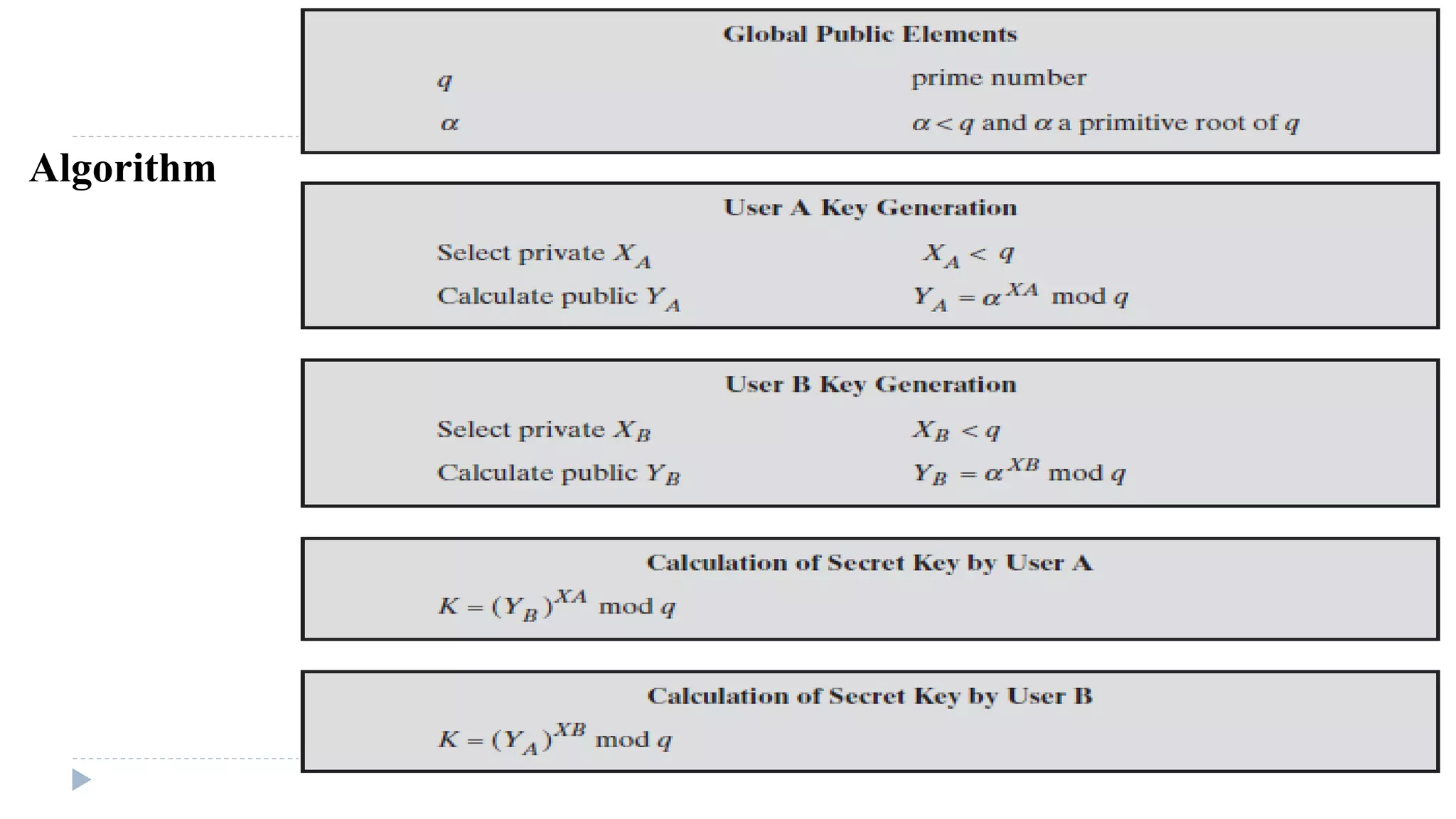
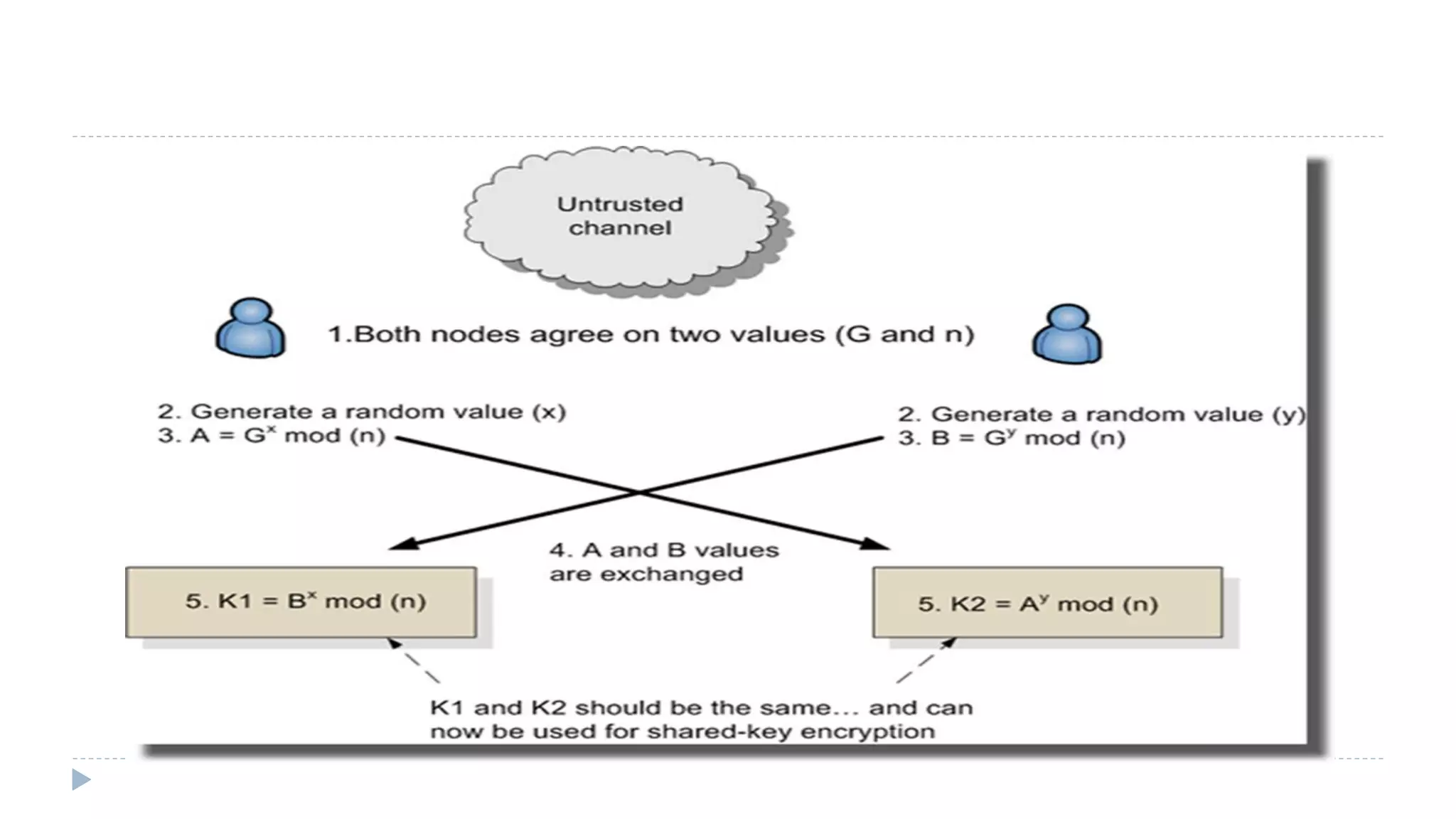
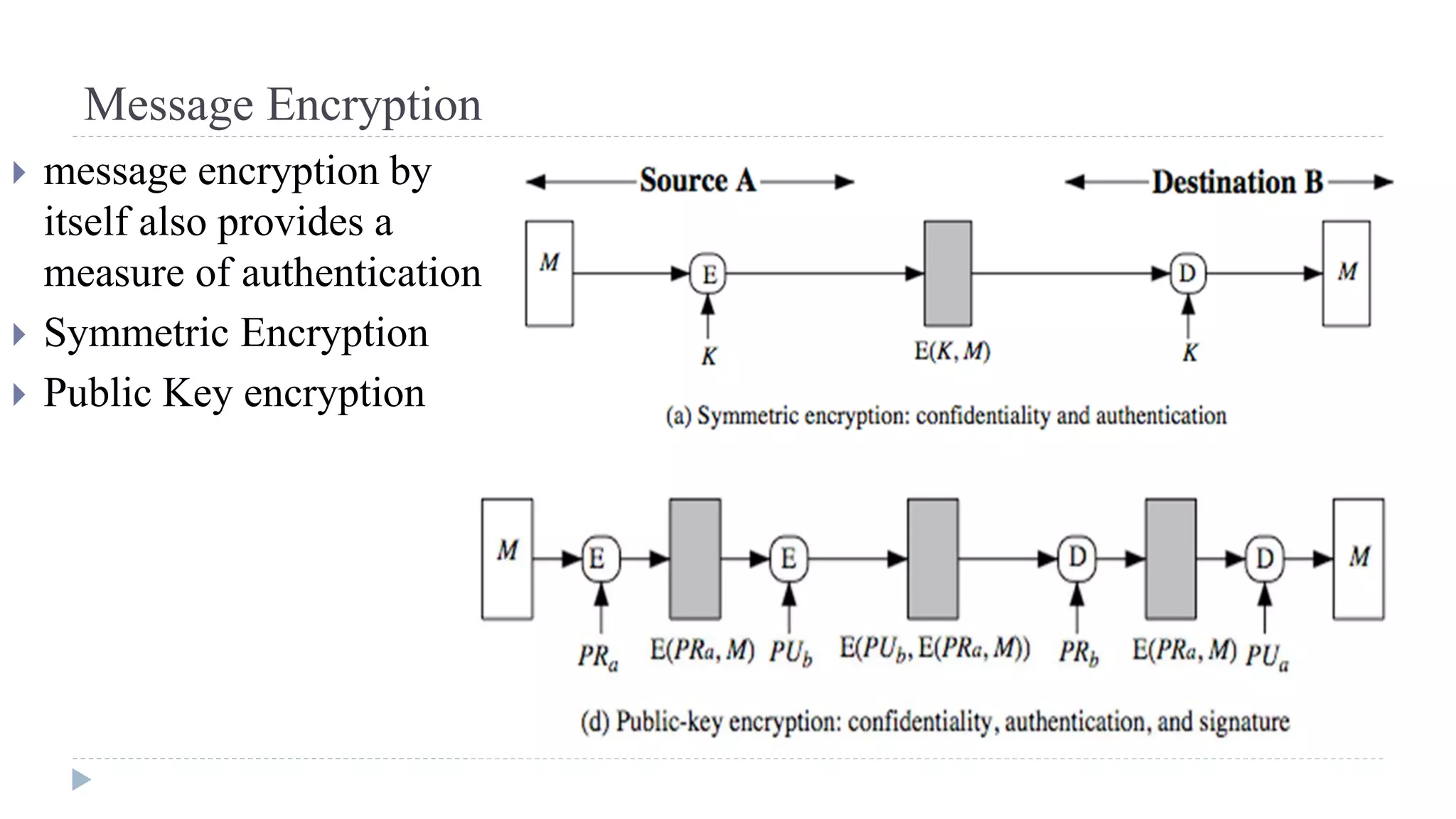
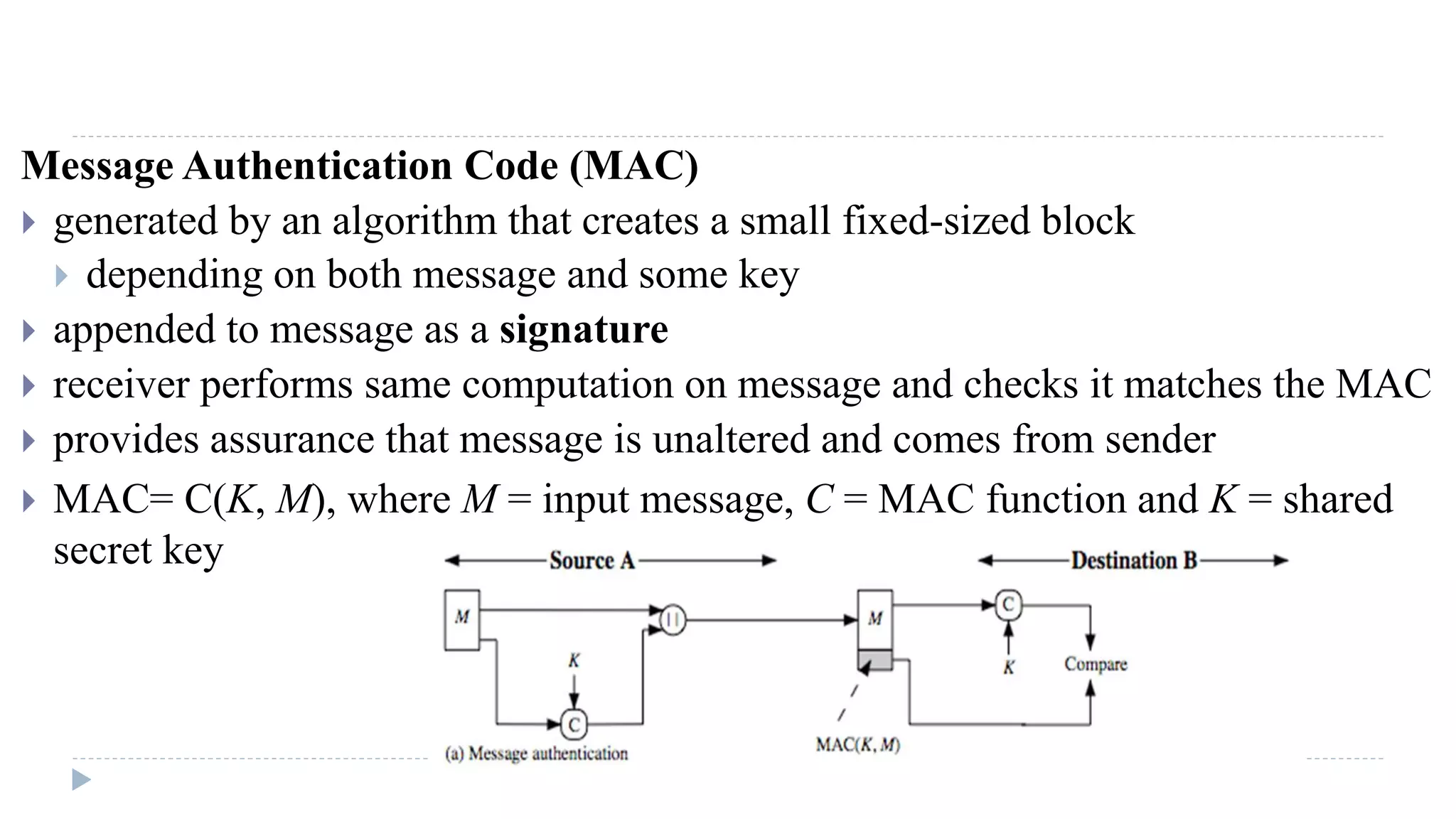
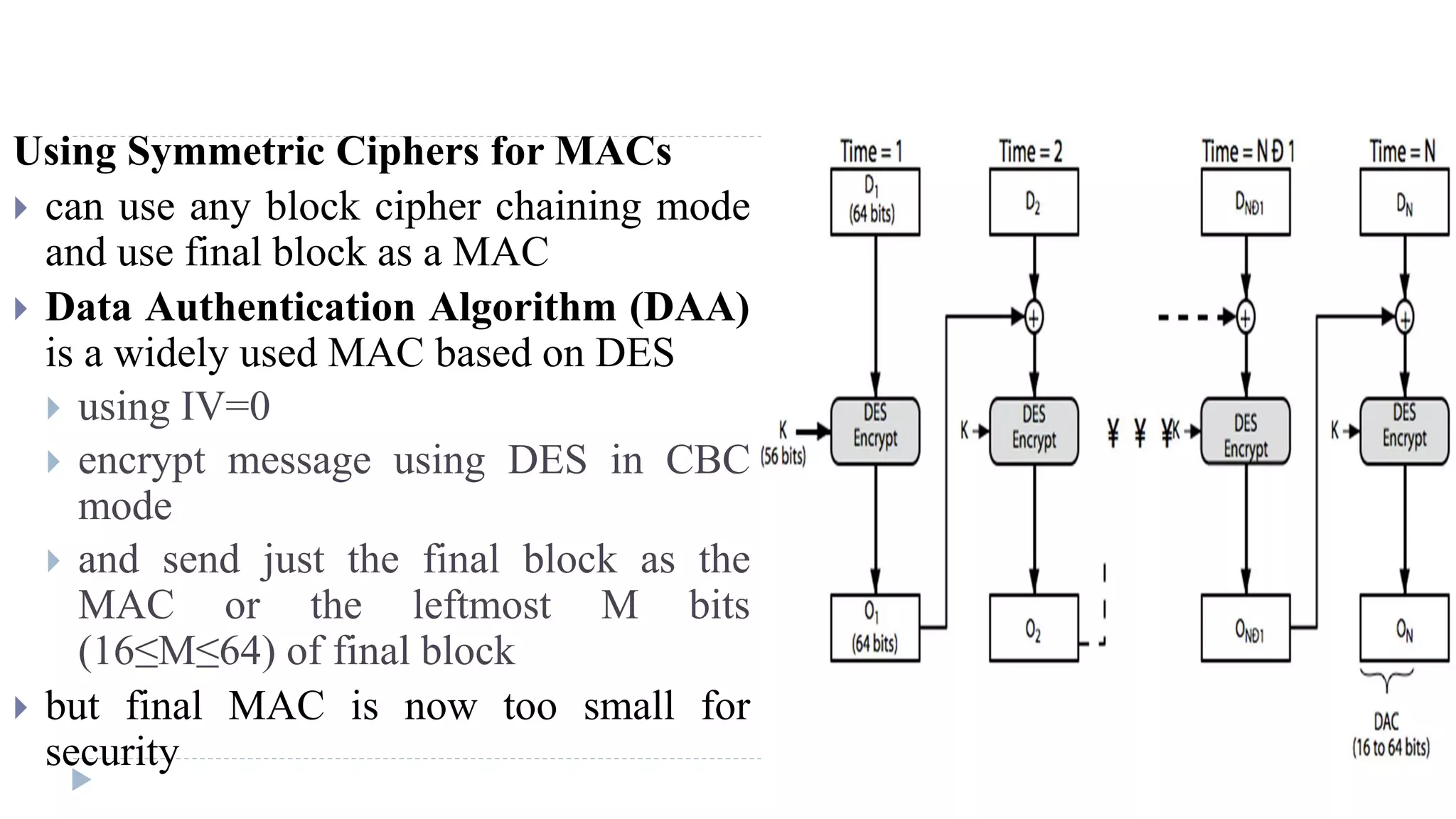
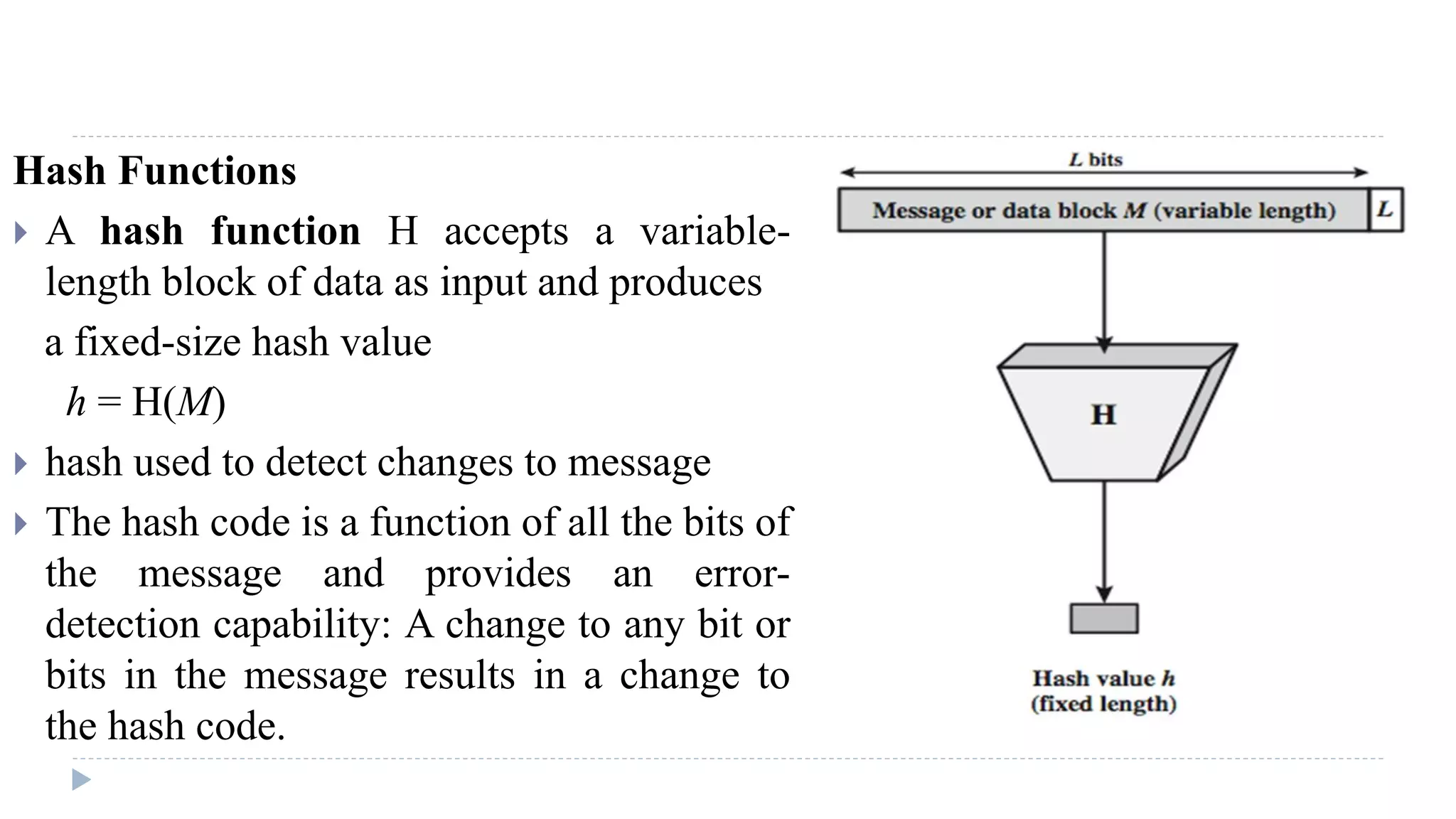
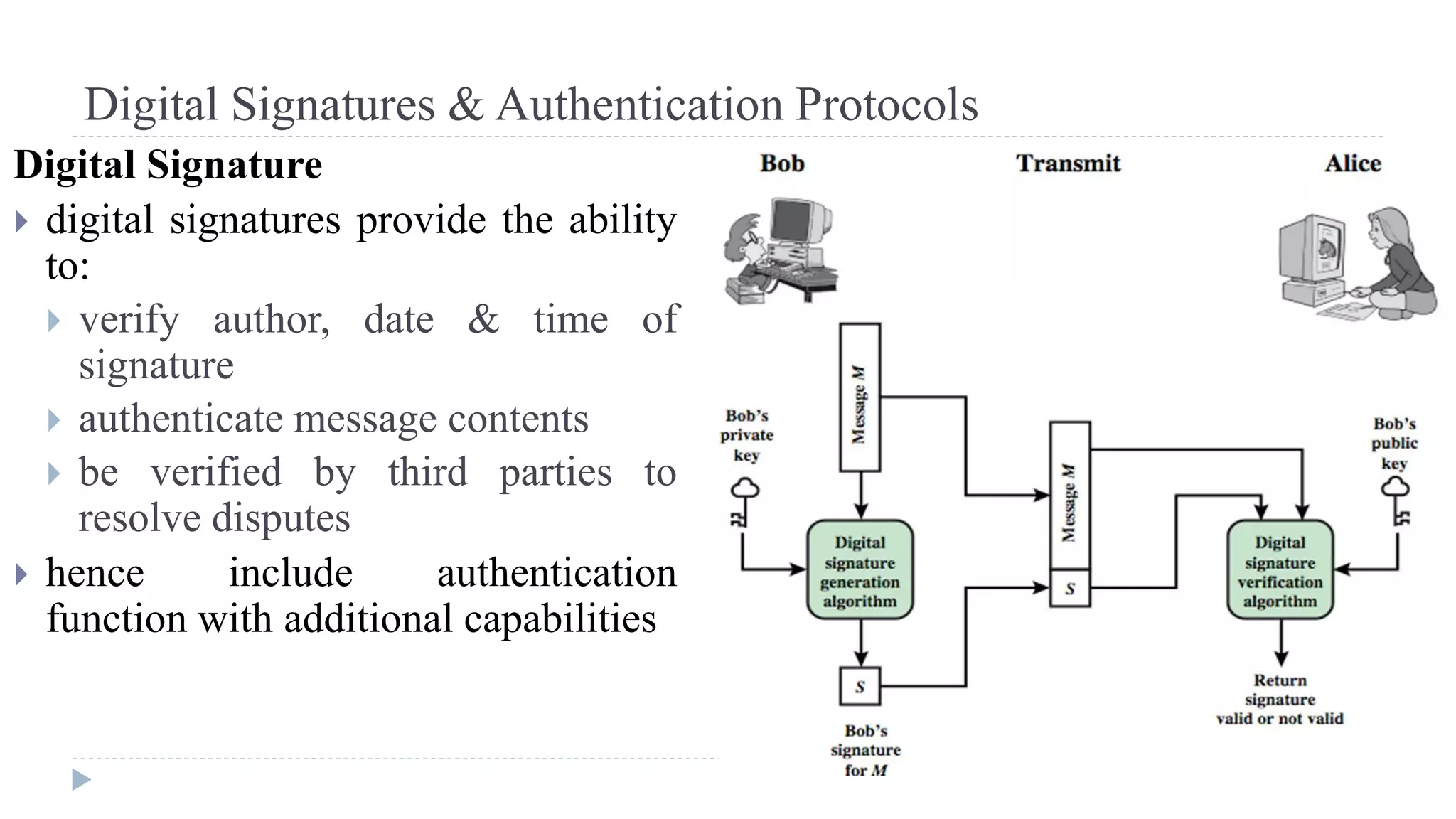
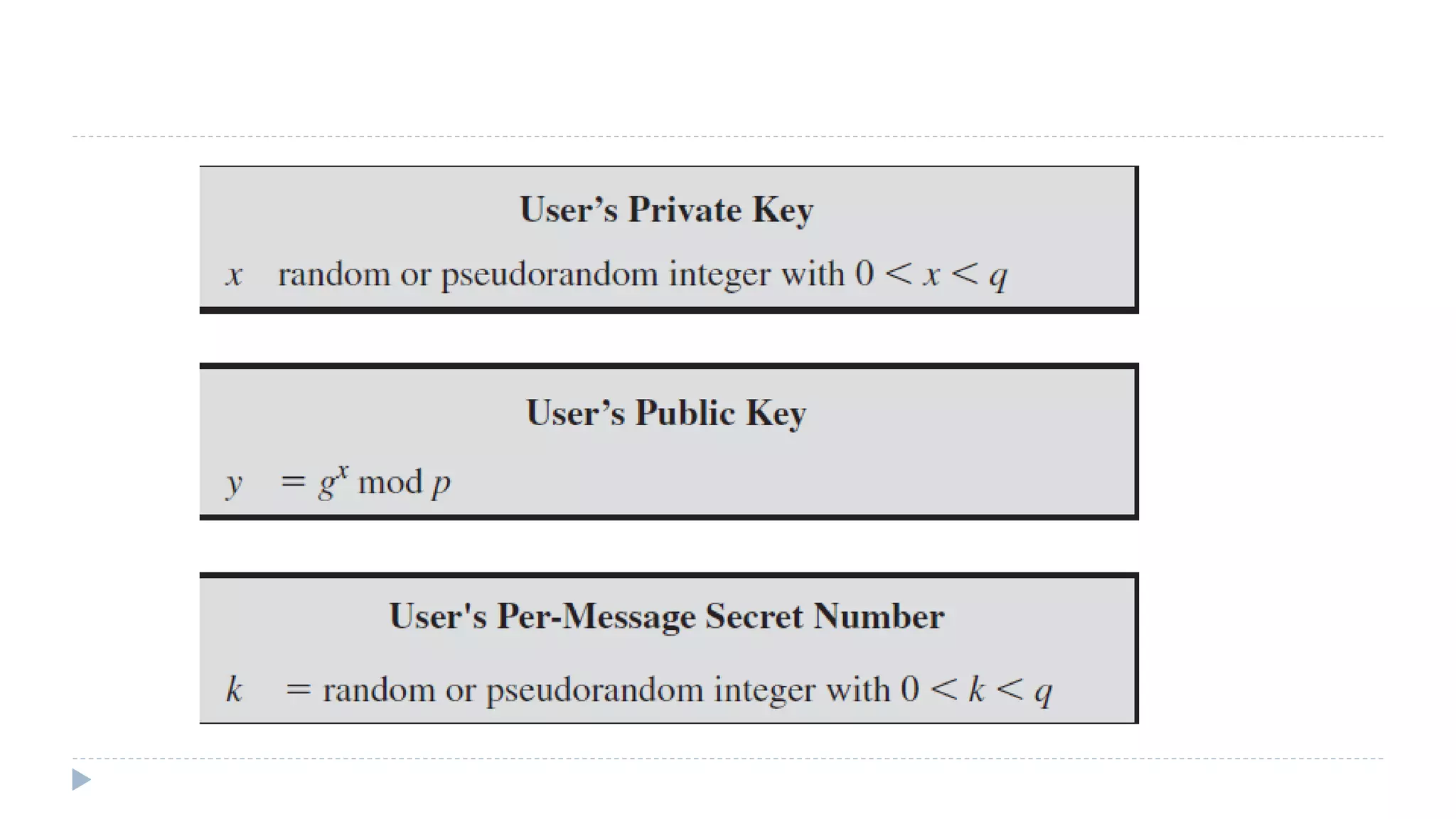
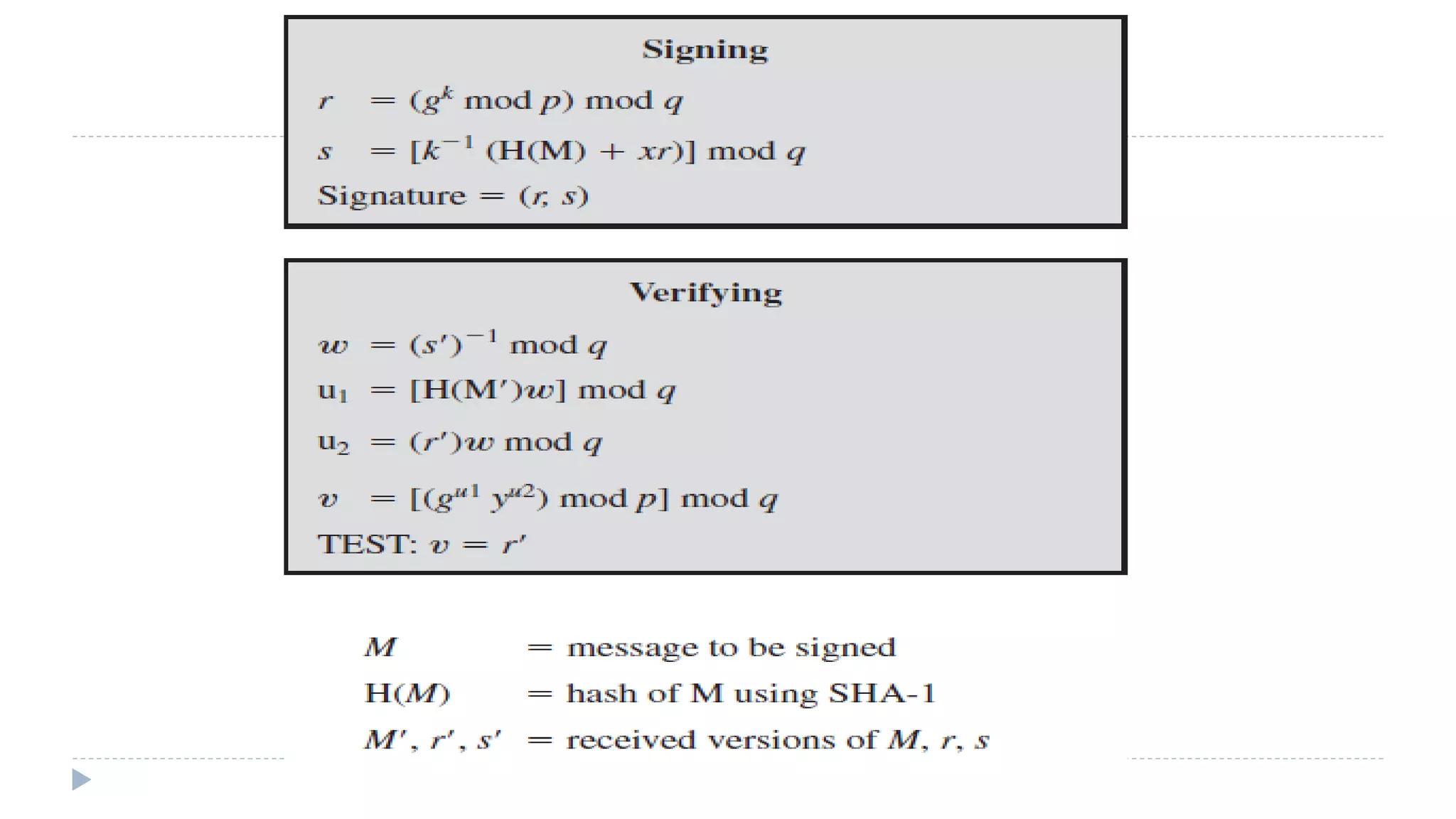
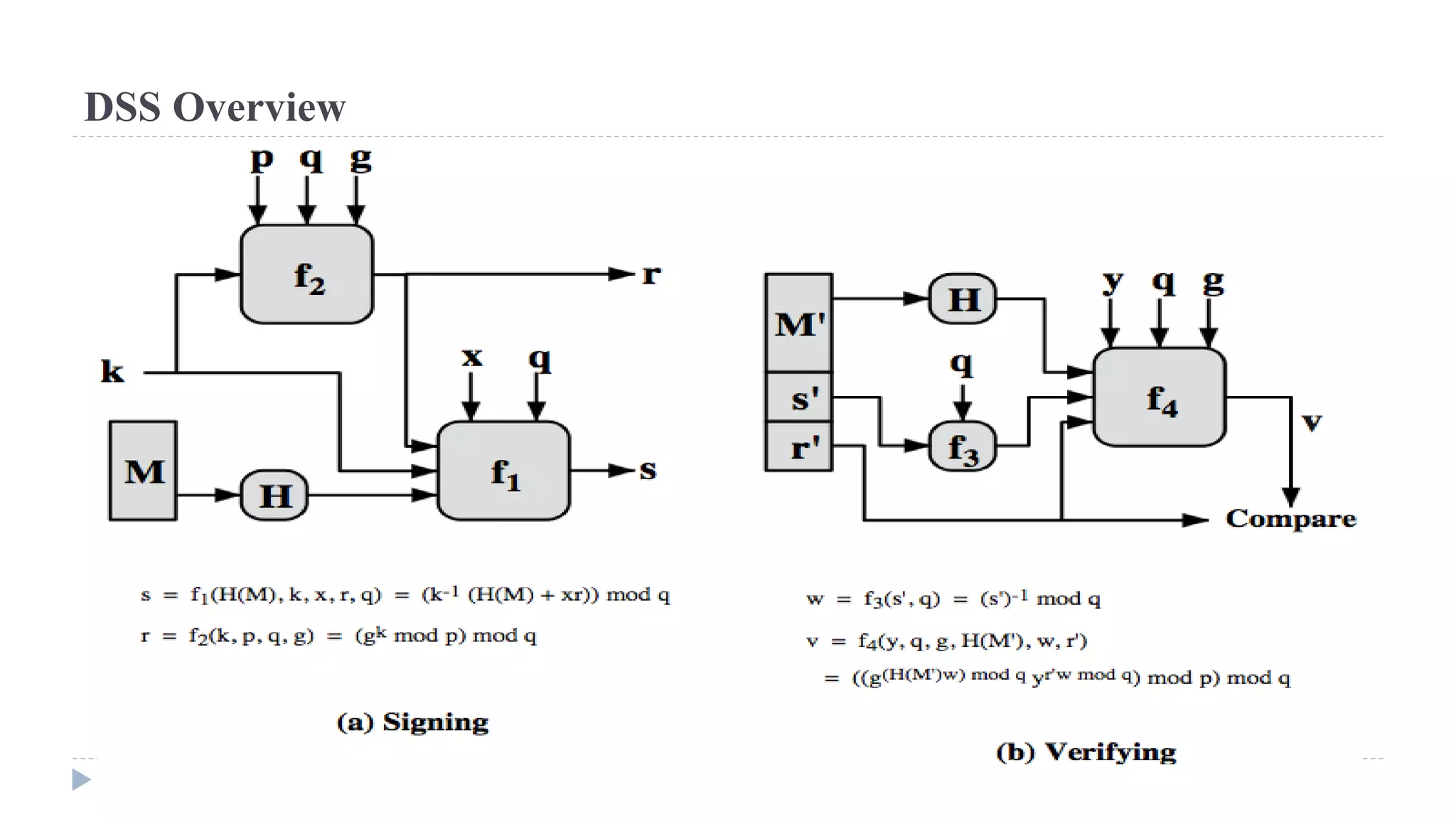
The document discusses various aspects of computer security, specifically focusing on key management and encryption methods like public-key encryption, Diffie-Hellman key exchange, and elliptic curve cryptography. It outlines protocols for securely distributing public keys and secret keys, as well as methods for message authentication, including the use of hash functions and message authentication codes (MACs). Furthermore, it examines security measures against attacks and presents various algorithms such as SHA and HMAC for maintaining integrity and authenticity in communications.






![Public-Key Certificates
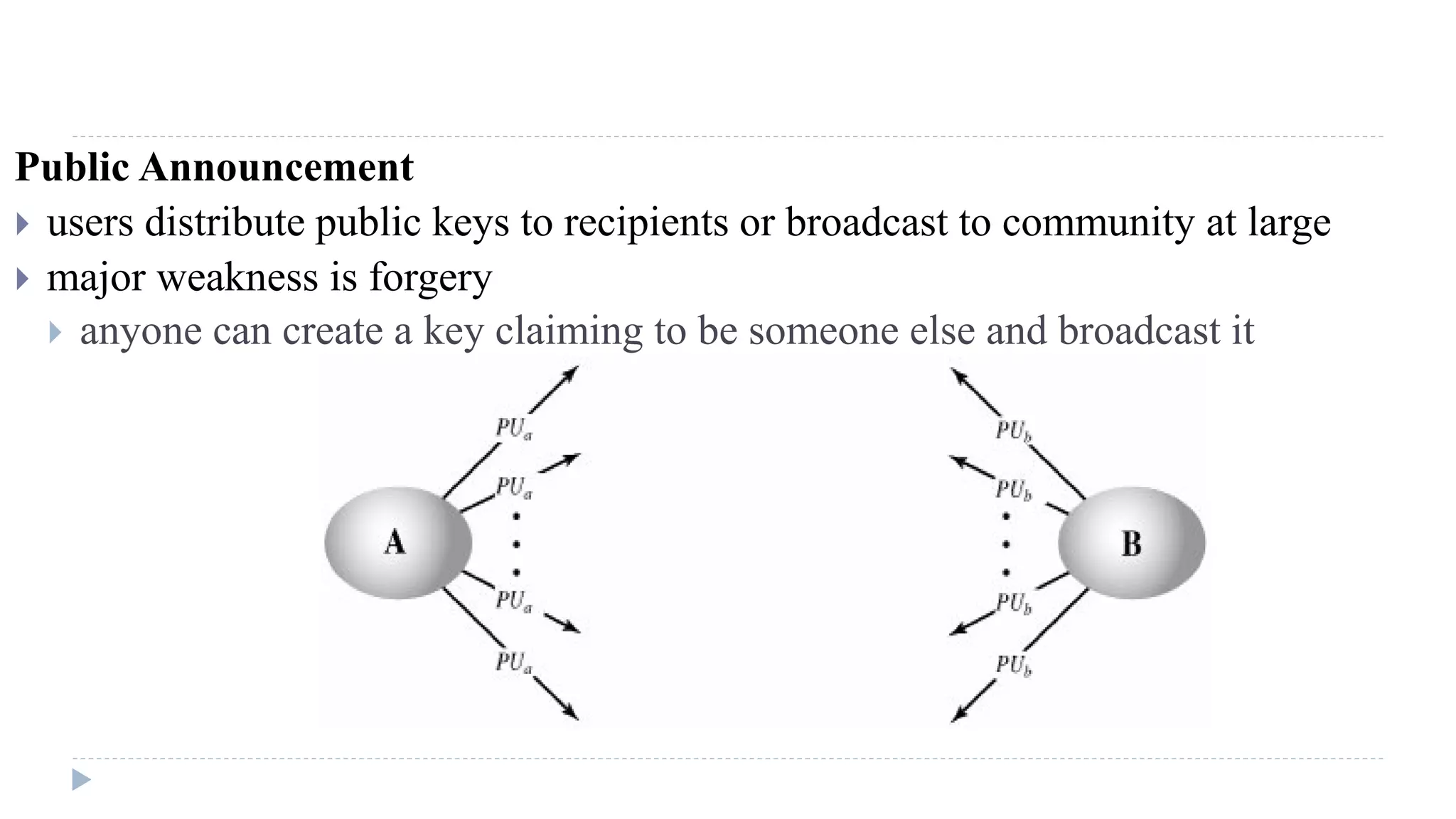
certificates allow key exchange without real-time access to public-key authority
certificate consists of a public key plus an identifier of the key owner
with all contents signed by a trusted Certificate Authority (CA)
A user can present his or her public key to the authority in a secure manner, and
obtain a certificate.
The user can then publish the certificate. Anyone needed this user's public key can
obtain the certificate and verify that it is valid by way of the attached trusted
signature.
any other participant, who reads and verifies the certificate as follows:
D(PUauth, CA) = D(PUauth, E(PRauth, [T||IDA||PUa])) = (T||IDA||PUa)](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-9-2048.jpg)









![Elliptic Curve Cryptography
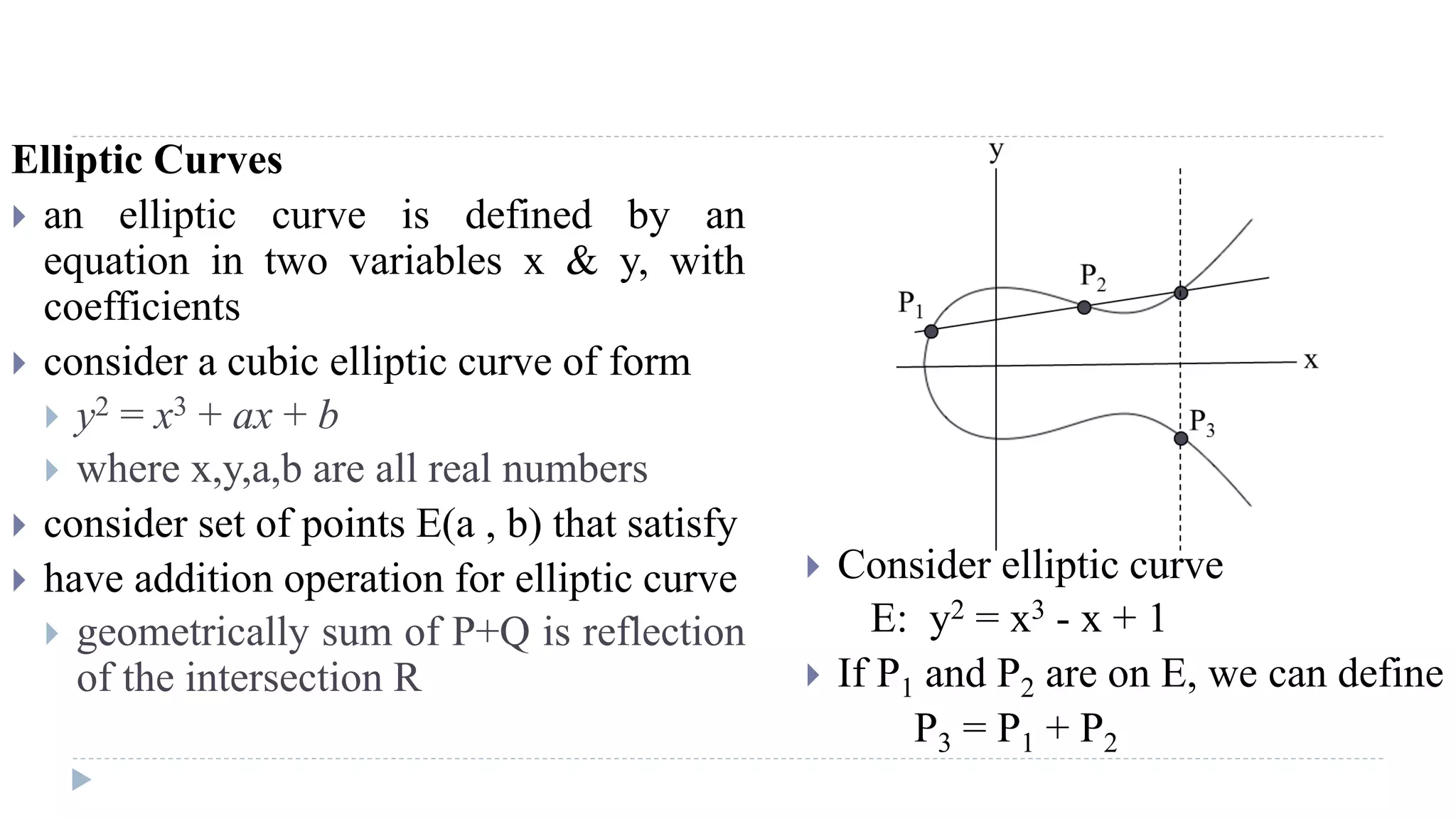
Elliptic curve cryptography [ECC] is a public-key cryptosystem
Elliptic curves are used as an extension to other current cryptosystems.
Elliptic Curve Diffie-Hellman Key Exchange
Elliptic Curve Digital Signature Algorithm
The central part of any cryptosystem involving elliptic curves is the elliptic
group.](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-25-2048.jpg)
![Generic Procedures of ECC
Both parties agree to some publicly-known data items
The elliptic curve equation
values of a and b
prime, q
The elliptic group computed from the elliptic curve equation
A base point, G, taken from the elliptic group
Similar to the generator used in current cryptosystems
Each user generates their public/private key pair
Private Key = an integer, selected from the interval [1, q-1]
Public Key = product, of private key and base point ( x*B)](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-26-2048.jpg)









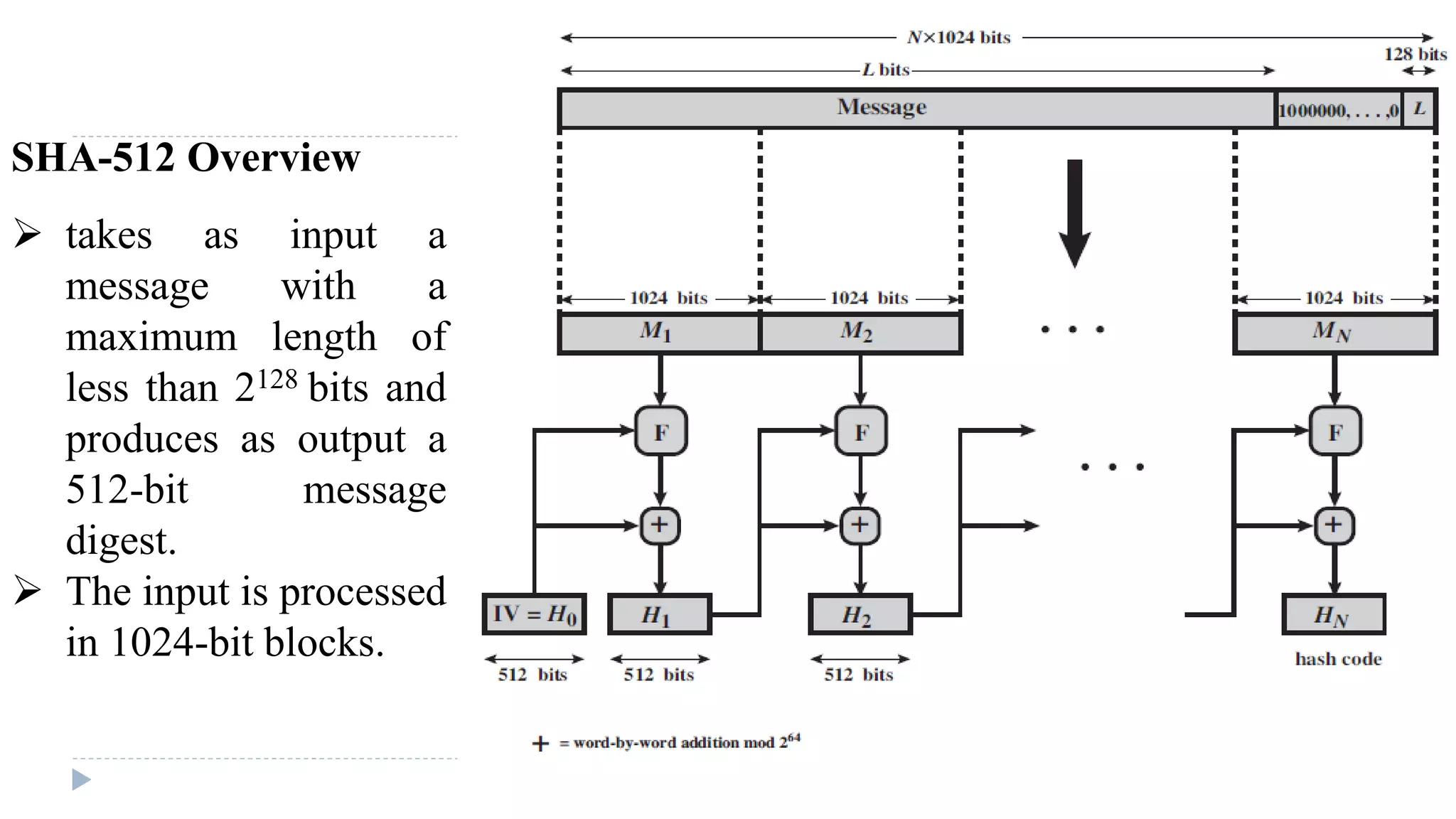

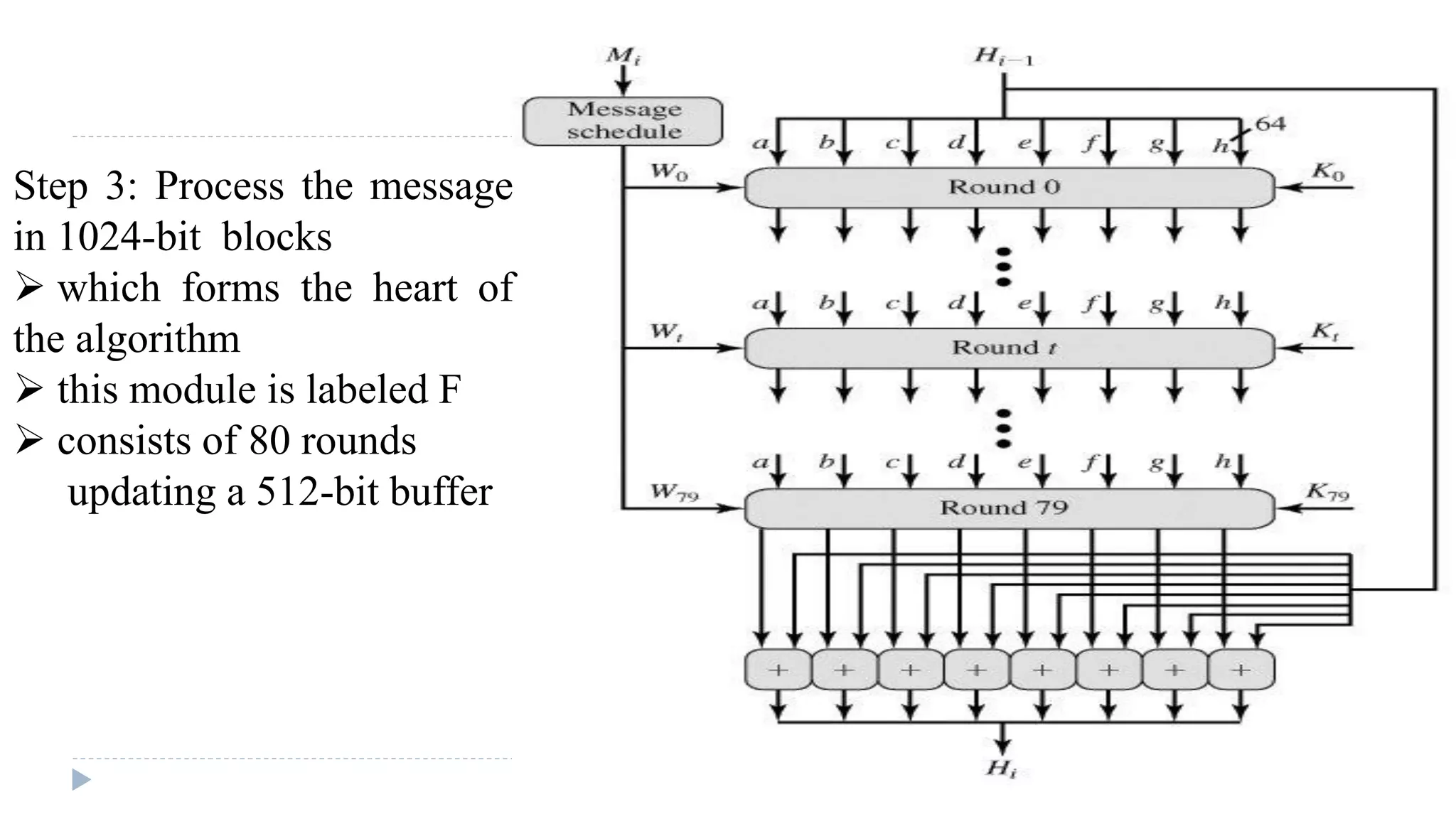

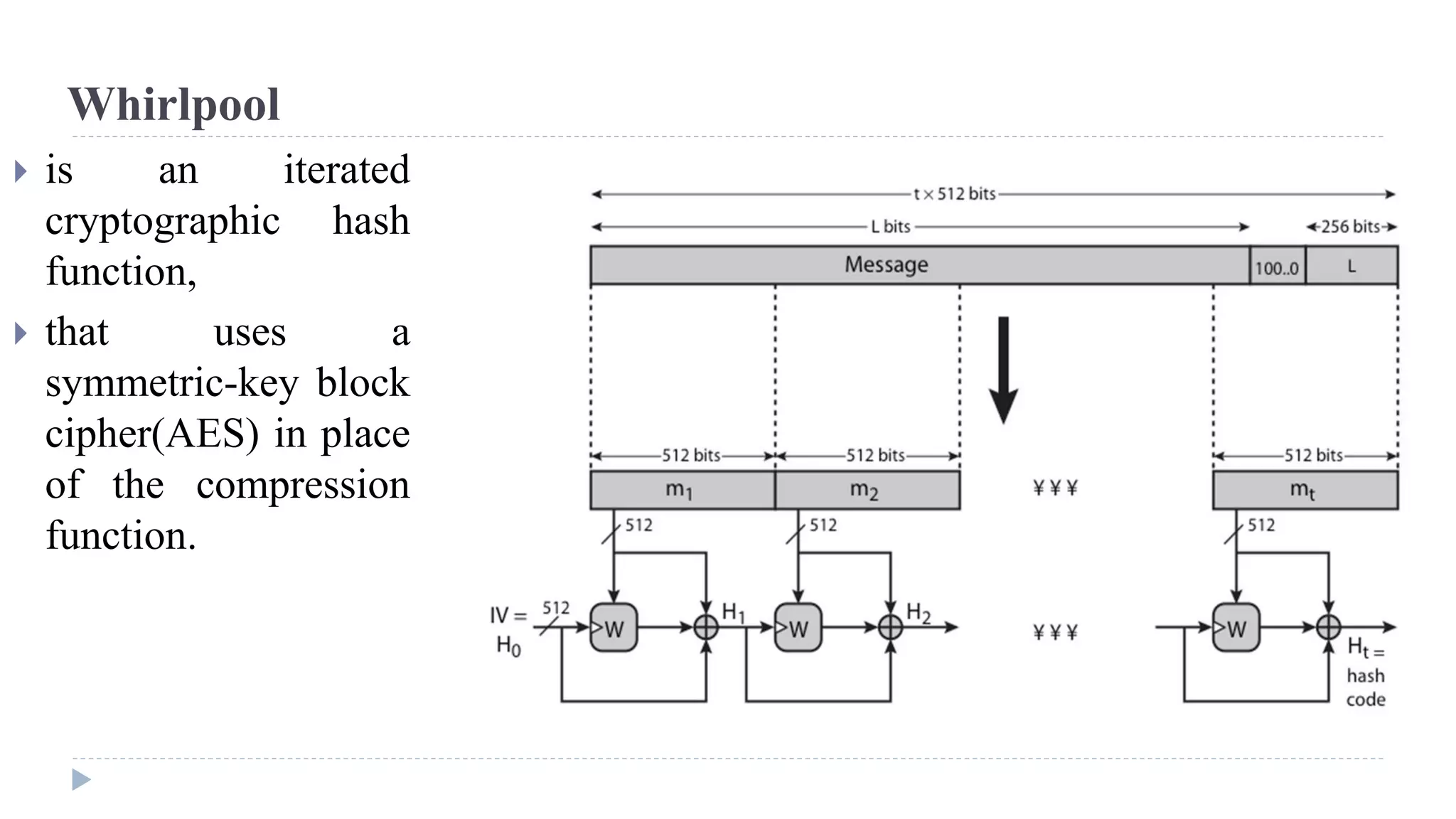

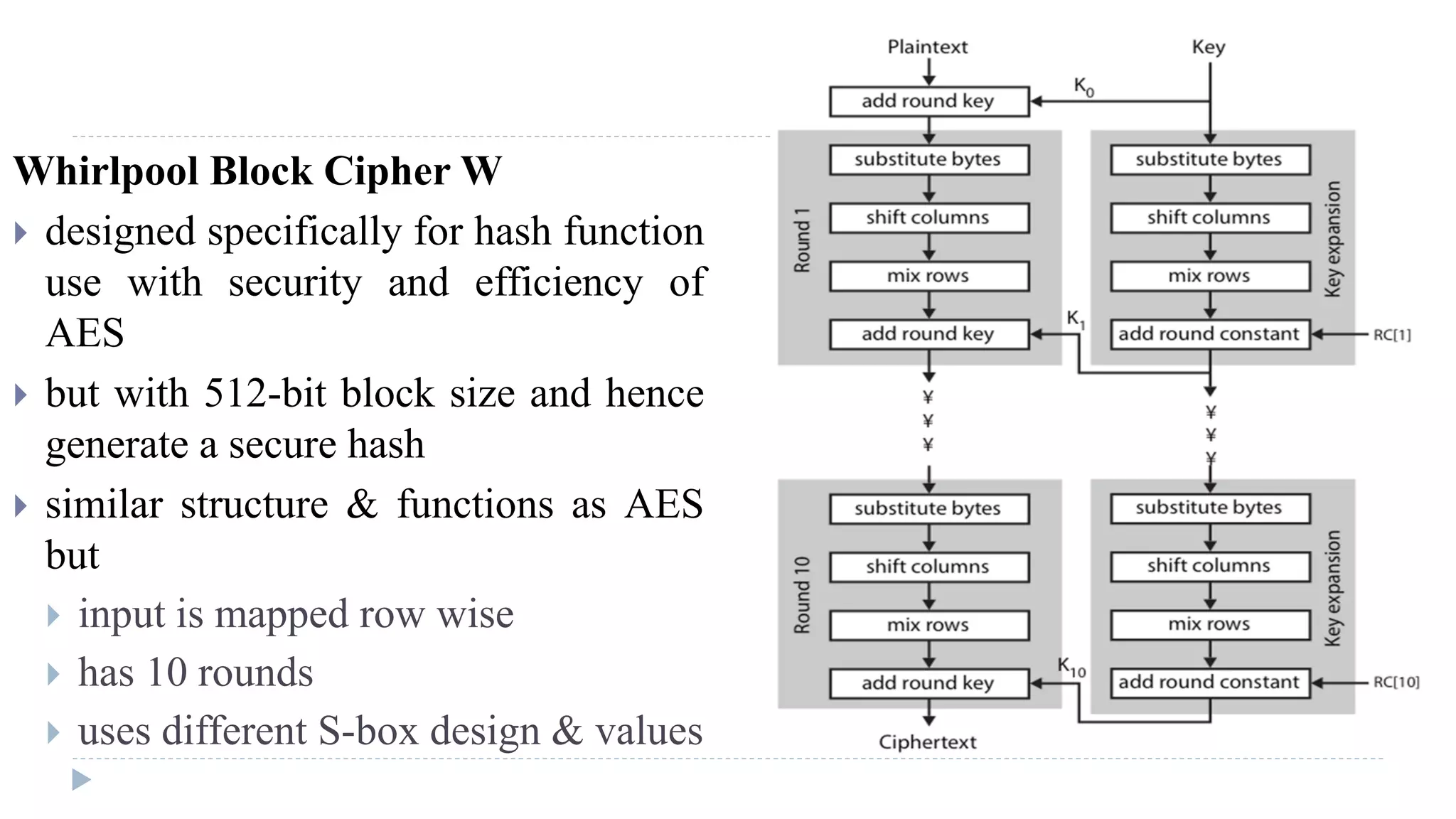



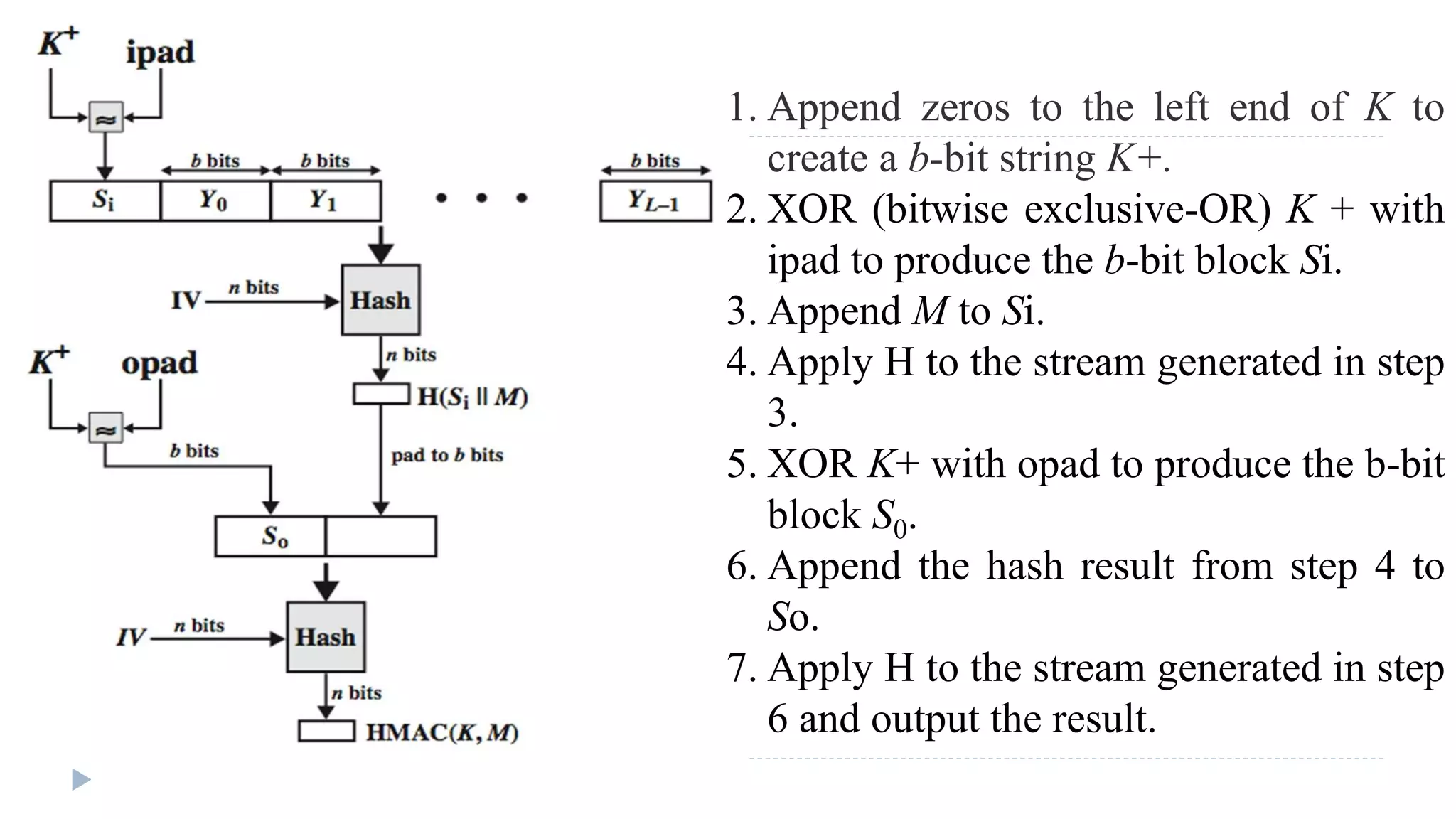
![Algorithm
b = number of bits in a block
K+ is K padded with zeros on the left so that the result is b bits in length.
ipad is a pad value of 36 hex repeated to fill block
opad is a pad value of 5C hex repeated to fill block.
M is the message input
Yi = ith block of M,
H = embedded hash function.
L = number of blocks in M.
n = length of hash code produced by embedded hash function
Then HMAC can be represented as:
HMACK = Hash[(K+ XOR opad) || Hash[(K+ XOR ipad)||M)]]](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-51-2048.jpg)











![Needham-Schroeder Protocol
used to securely distribute a new session key for
communications between A & B
key distribution protocol for session between A
and B mediated by KDC
protocol overview is:
1. A->KDC: IDA || IDB || N1
2. KDC -> A: EKa[Ks || IDB || N1 || EKb[Ks||IDA] ]
3. A -> B: EKb[Ks||IDA]
4. B -> A: EKs[N2]
5. A -> B: EKs[f(N2)]
Ka and Kb:Secret keys
Ks: session key](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-70-2048.jpg)

![Denning AS Protocol
1. A -> AS: IDA || IDB
2. AS -> A: EPRas[IDA||PUa||T] || EPRas[IDB||PUb||T]
3. A -> B: EPRas[IDA||PUa||T] || EPRas[IDB||PUb||T] || EPUb[EPRas[Ks||T]]
timestamps prevent replay but require synchronized clocks](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-72-2048.jpg)

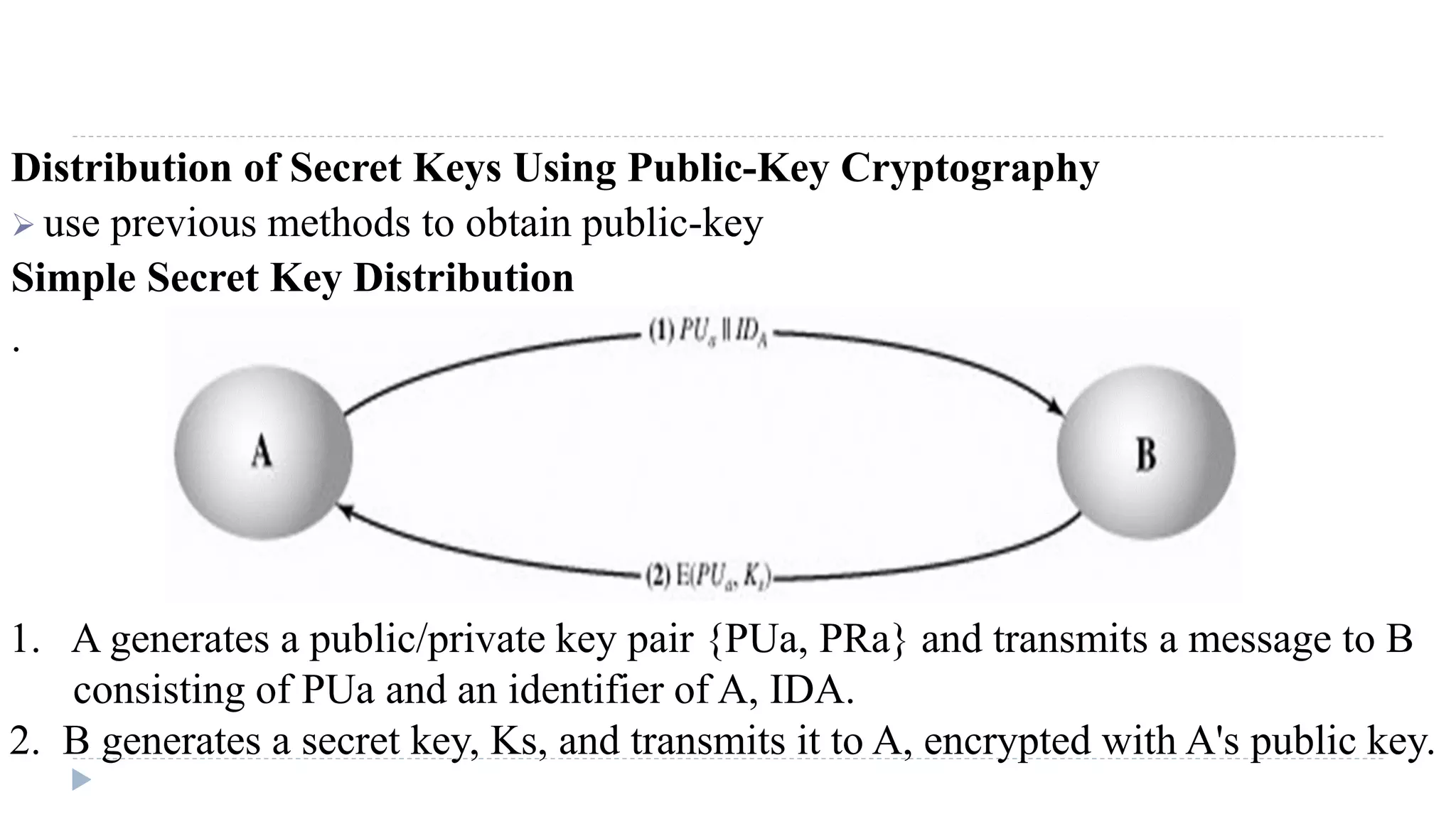
![Using Symmetric Encryption
This scheme requires the sender to issue a request to the intended recipient,
await a response that includes a session key, and only then send the message.
1. A->KDC: IDA || IDB || N1
2. KDC -> A: EKa[Ks || IDB || N1 || EKb[Ks||IDA] ]
3. A -> B: EKb[Ks||IDA] || EKs[M]](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-74-2048.jpg)
![Public-Key Approaches
have seen some public-key approaches
if confidentiality is major concern, can use:
A->B: EPUb[Ks] || EKs[M]
has encrypted session key, encrypted message
if authentication needed use a digital signature with a digital certificate:
A->B: M || EPRa[H(M)] || EPRas[T||IDA||PUa]
with message, signature, certificate](https://image.slidesharecdn.com/computersecurity-module3-150328033906-conversion-gate01/75/Computer-security-module-3-75-2048.jpg)