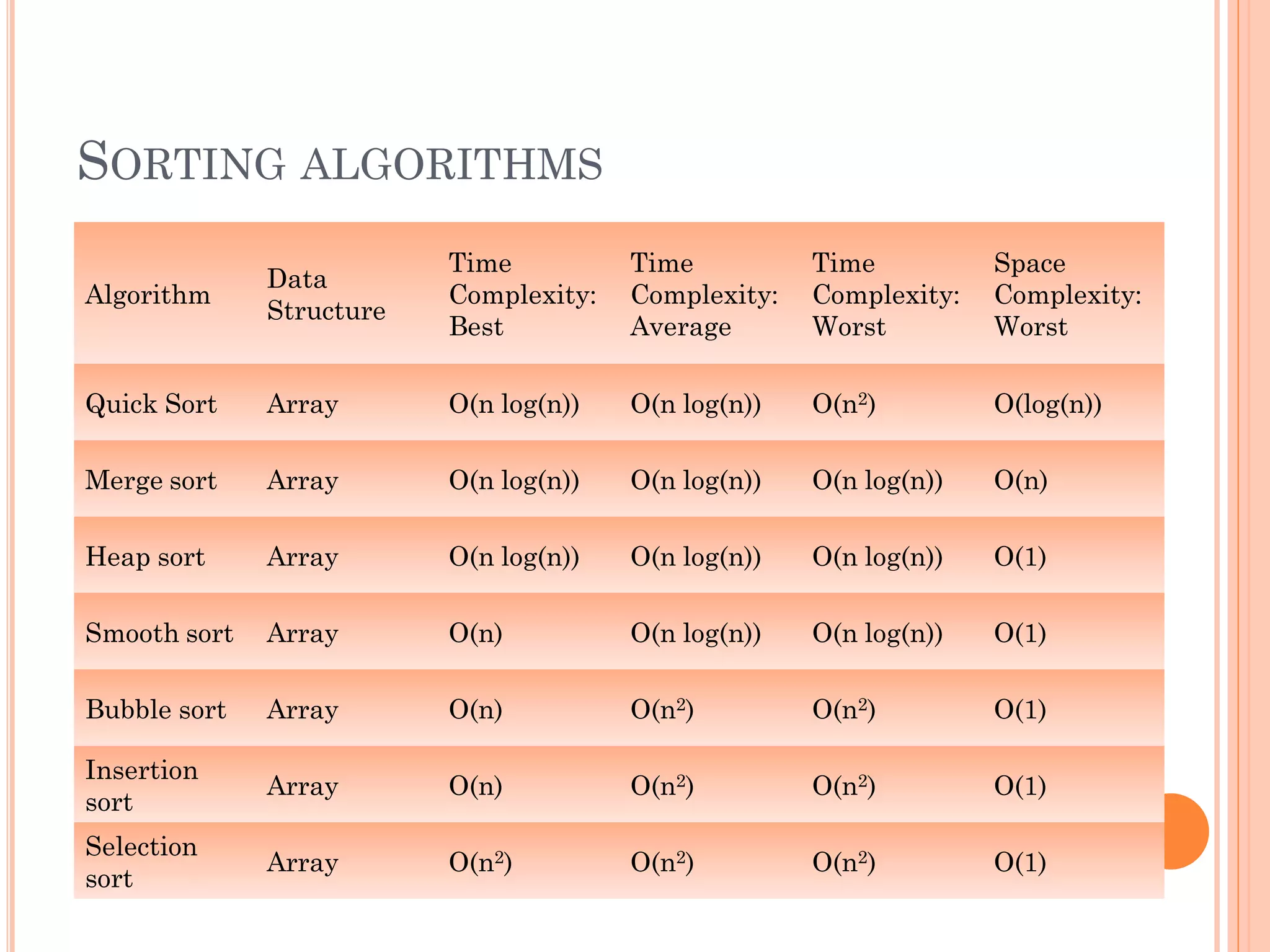
This document discusses algorithms and analysis of algorithms. It covers key concepts like time complexity, space complexity, asymptotic notations, best case, worst case and average case time complexities. Examples are provided to illustrate linear, quadratic and logarithmic time complexities. Common sorting algorithms like quicksort, mergesort, heapsort, bubblesort and insertionsort are summarized along with their time and space complexities.






![EXAMPLES
Exp(1)
int main(){
printf(“KIIT UNIVERSITY”);
}
Exp(2)
void bubble(int a[], int n){
int i,j;
for(i=0;i<n-1;i++){
for(j=0;j<n-1-i;j++)
if(a[j]>a[j+1])
swap (a[j],a[j+1])
}
}](https://image.slidesharecdn.com/algorithmandanalysis-150911063159-lva1-app6891/75/Data-Structure-Algorithm-and-analysis-7-2048.jpg)





![EXAMPLE - 3
1. int i, j, n=5, a[5]={12, 2, 51, 35, 7};
2. for(i=0;i<n-1;i++){
3. for(j=0;j<n-1-i;j++)
4. if(a[j]>a[j+1]){
5. a[j] = a[j] + a[j+1];
6. a[j+1] = a[j] - a[j+1];
7. a[j] = a[j] - a[j+1]; }
8. for(i=0 ; i<n ; i++)
9. printf(“%d”, a[i]);
T(n) = ?](https://image.slidesharecdn.com/algorithmandanalysis-150911063159-lva1-app6891/75/Data-Structure-Algorithm-and-analysis-13-2048.jpg)



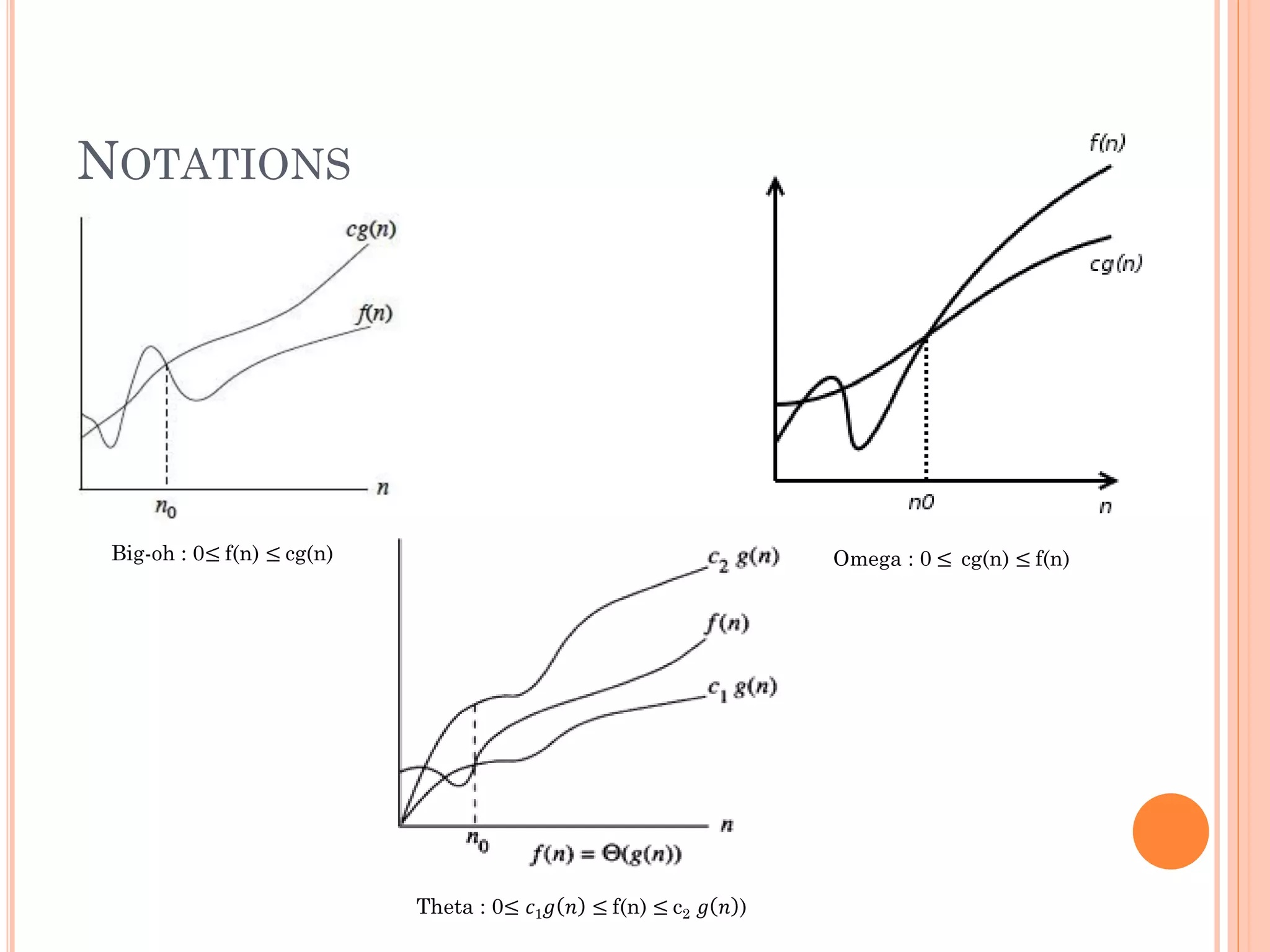
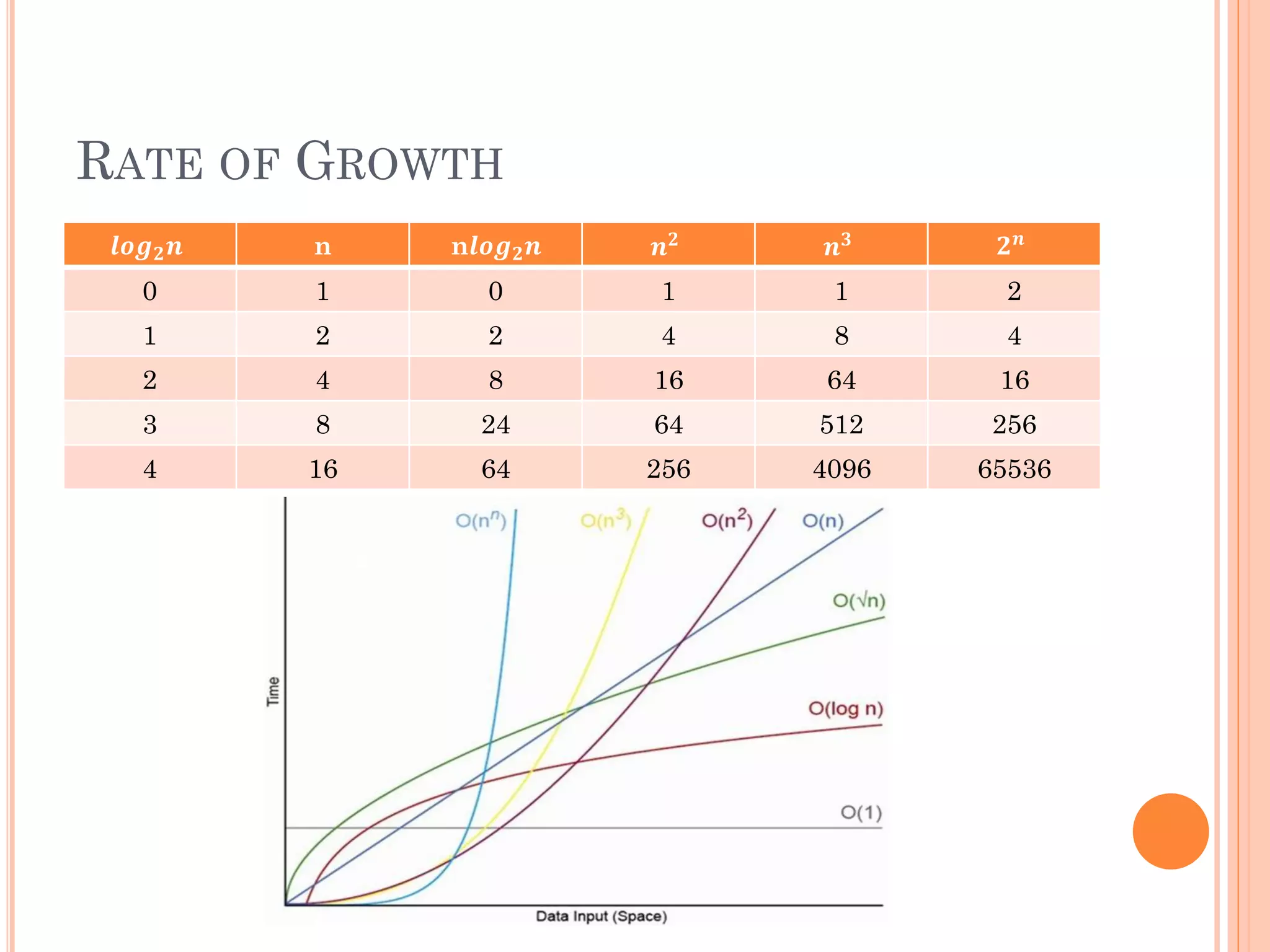
![TYPES OF TIME COMPLEXITY
Best Case Time complexity
Exp(1) – Linear search/Binary search
Linear search, key=3
a[0]==key, T(n)=O(1)
Binary search, key=24
m=(0+4)/2 = 2
a[2]==key, T(n)=O(1)
3 5 24 45 78](https://image.slidesharecdn.com/algorithmandanalysis-150911063159-lva1-app6891/75/Data-Structure-Algorithm-and-analysis-19-2048.jpg)
![TYPES OF TIME COMPLEXITY
Worst Case Time complexity
Exp(2) – Linear search/Binary search
Linear search, key=78 / 80
a[0]==key, T(n)=O(n) / O(n+1) ≈ O(n)
Binary search, key=78 / 80
m=(0+4)/2 = 2 …
a[2]!=key,…
finally T(n)=O(log2 𝑛) ….(*)
3 5 24 45 78](https://image.slidesharecdn.com/algorithmandanalysis-150911063159-lva1-app6891/75/Data-Structure-Algorithm-and-analysis-20-2048.jpg)
![TYPES OF TIME COMPLEXITY
Average Case Time complexity
Exp(3) – Linear search/Binary search
Linear search, key=24
a[0]==key, T(n)=O((n+1)/2) ≈ O(n)
There are n cases that can occur, i.e. find at the first place,
the second place, the third place and so on up to the nth
place. If found at the ith place then i comparisons are
required. Hence the average number of comparisons over
these n cases is:
average = (1+2+3.....+n)/n = (n+1)/2
where the result was used that 1+2+3 ...+n is equal to
n(n+1)/2.
Binary search, key=5
m=(0+4)/2 = 2, m=(0+1)/2=0, m=(1+1)/2=1
a[1]==key, finally T(n) ≈ O(log2 𝑛) ….(*)
3 5 24 45 78](https://image.slidesharecdn.com/algorithmandanalysis-150911063159-lva1-app6891/75/Data-Structure-Algorithm-and-analysis-21-2048.jpg)