The document discusses various sorting algorithms:
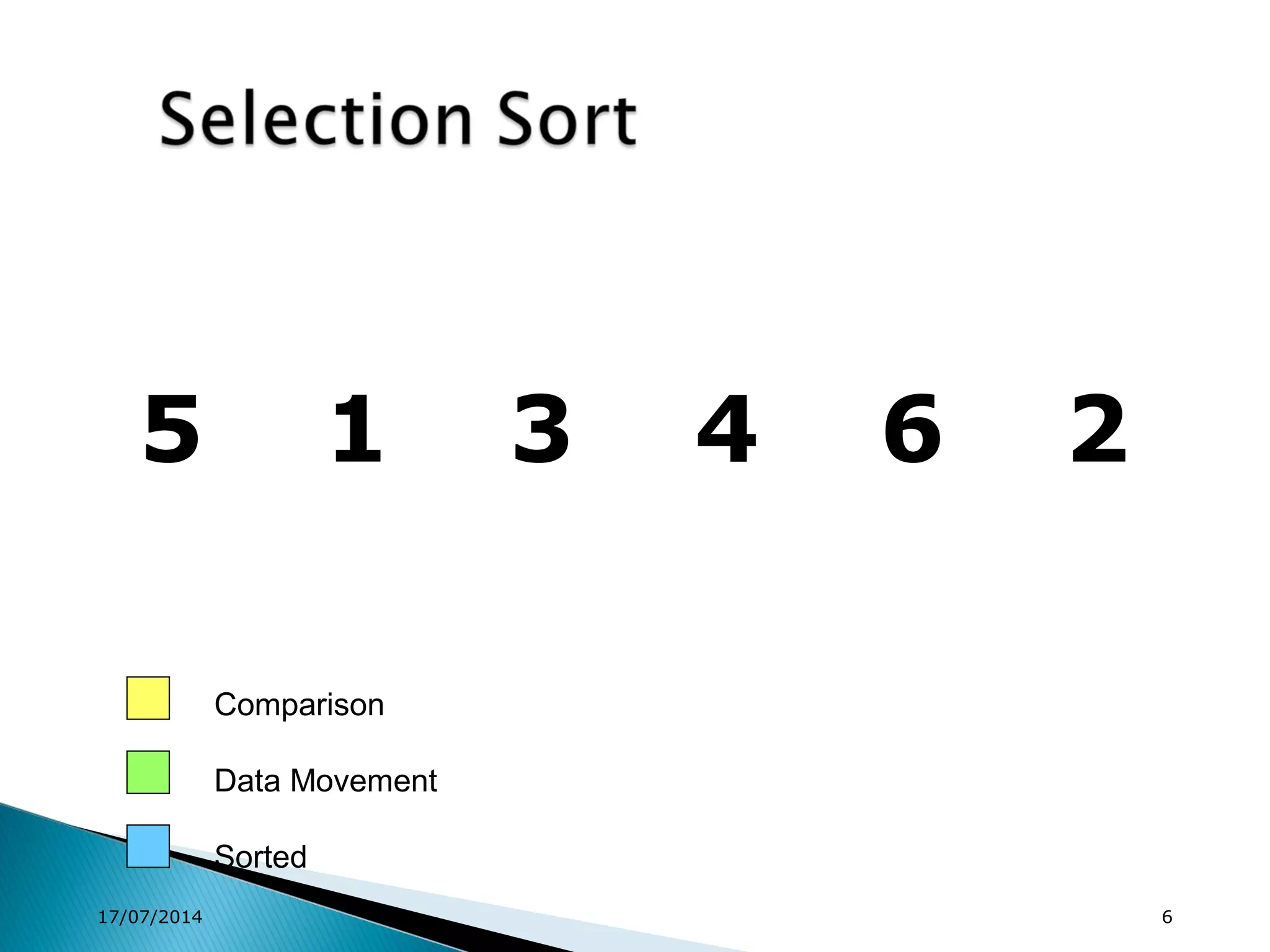
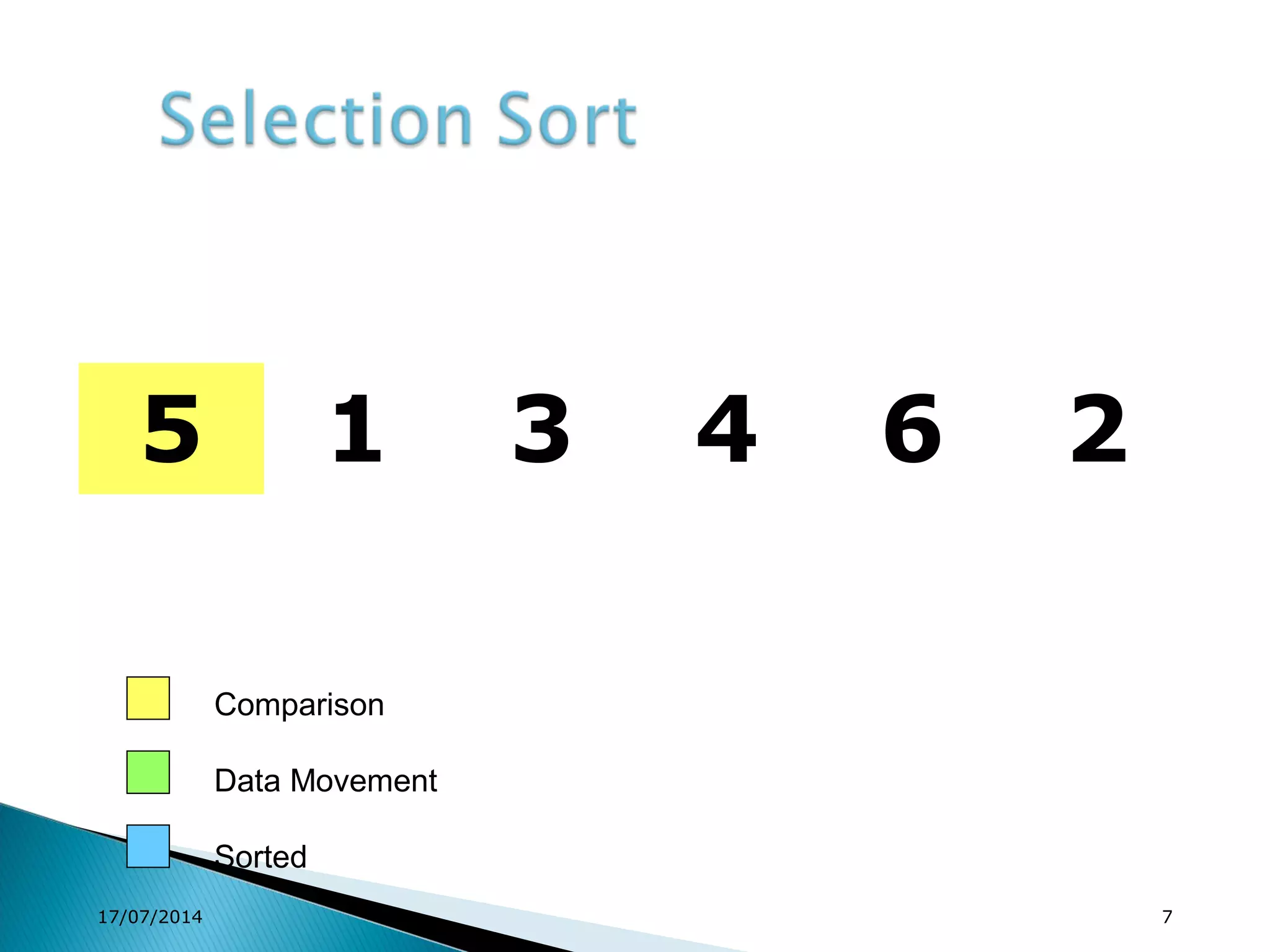
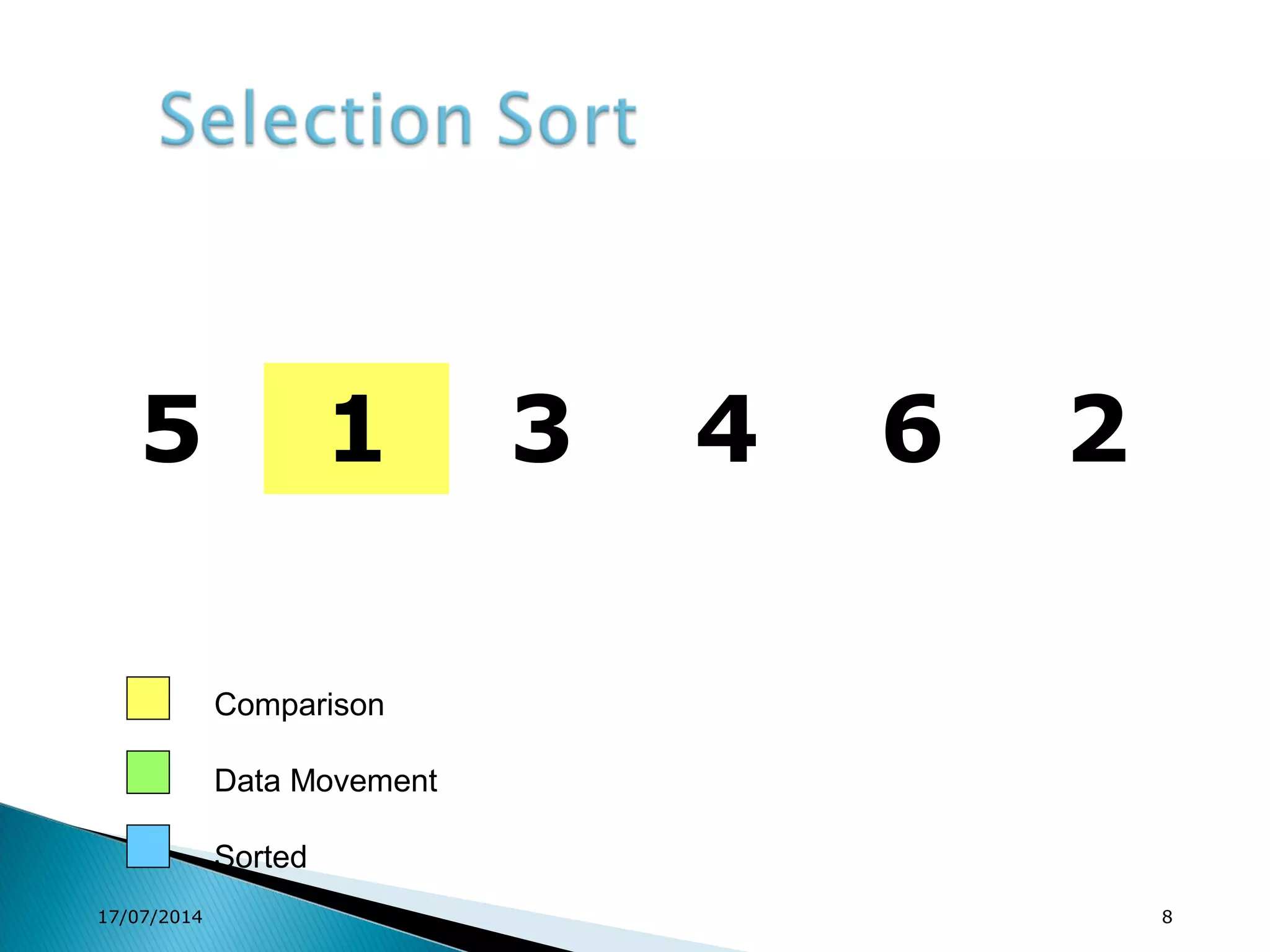
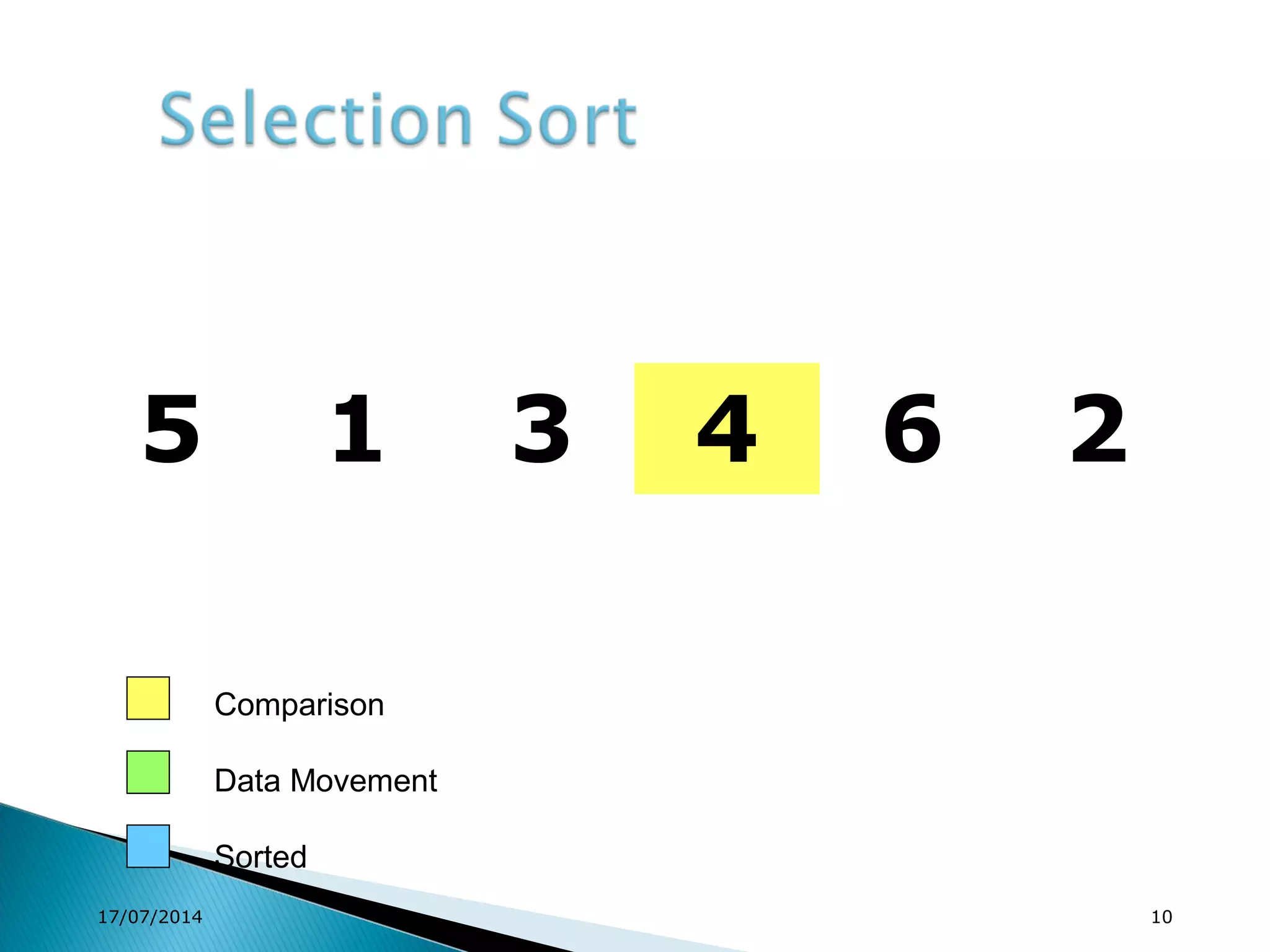
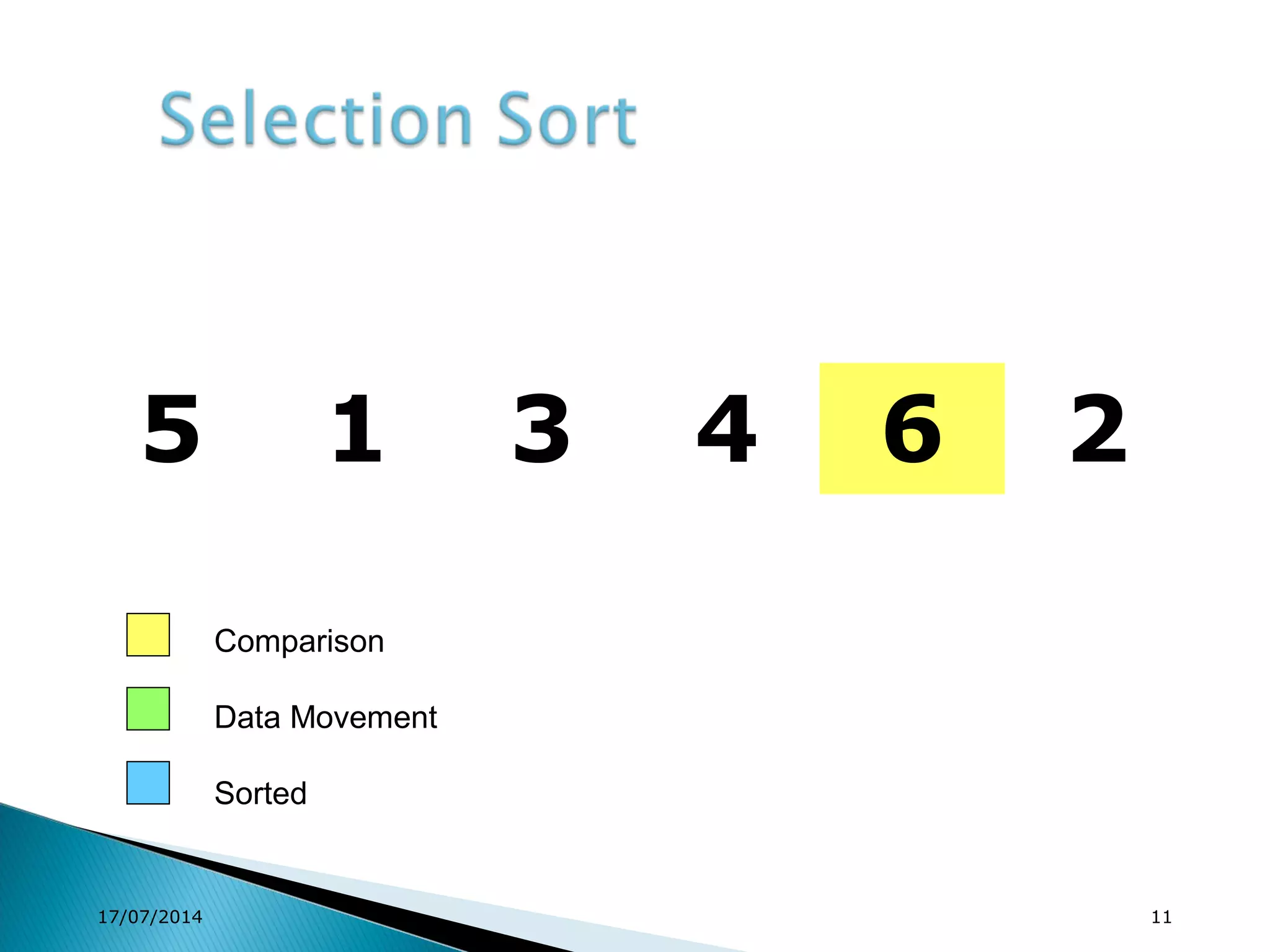
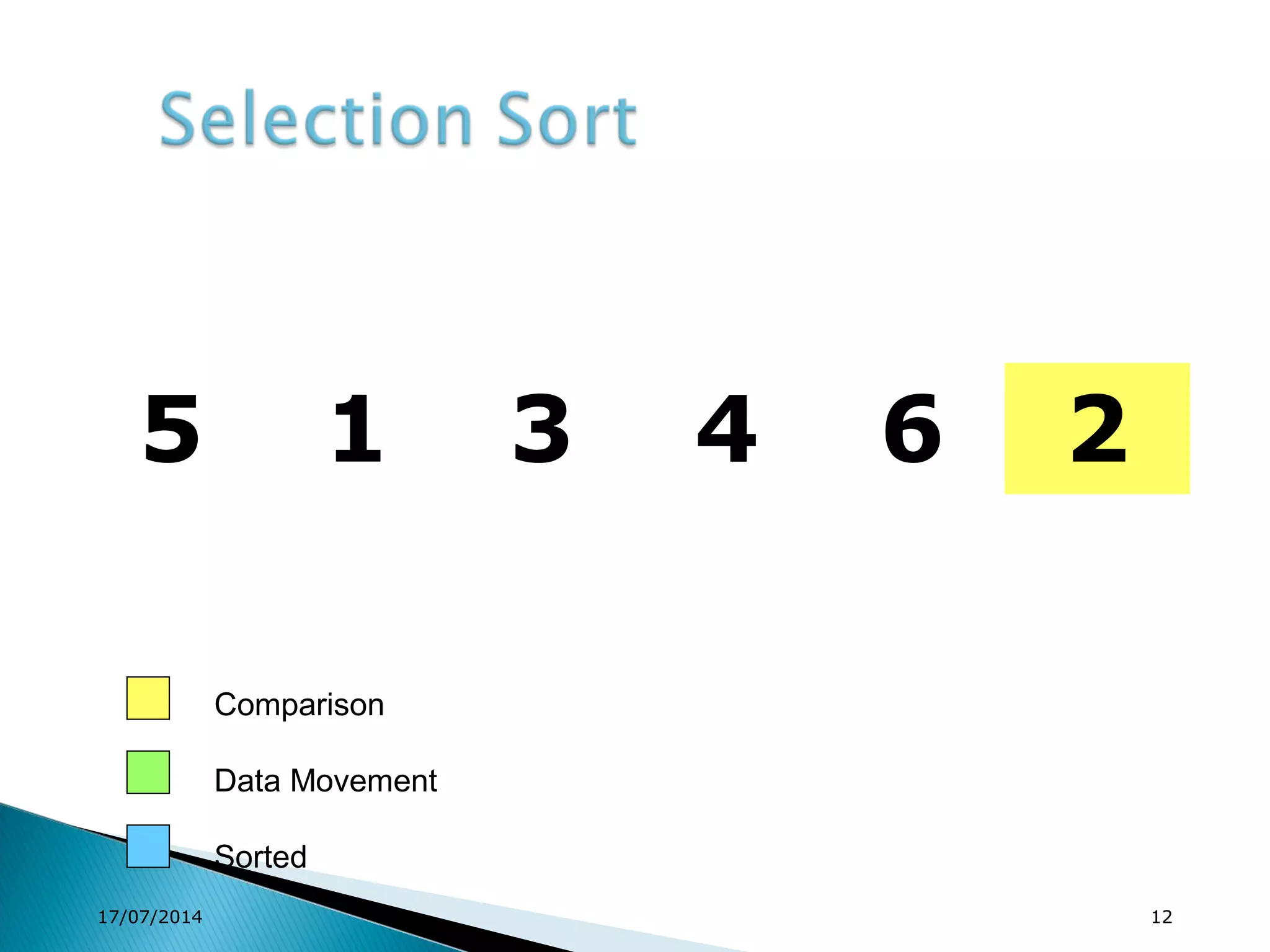
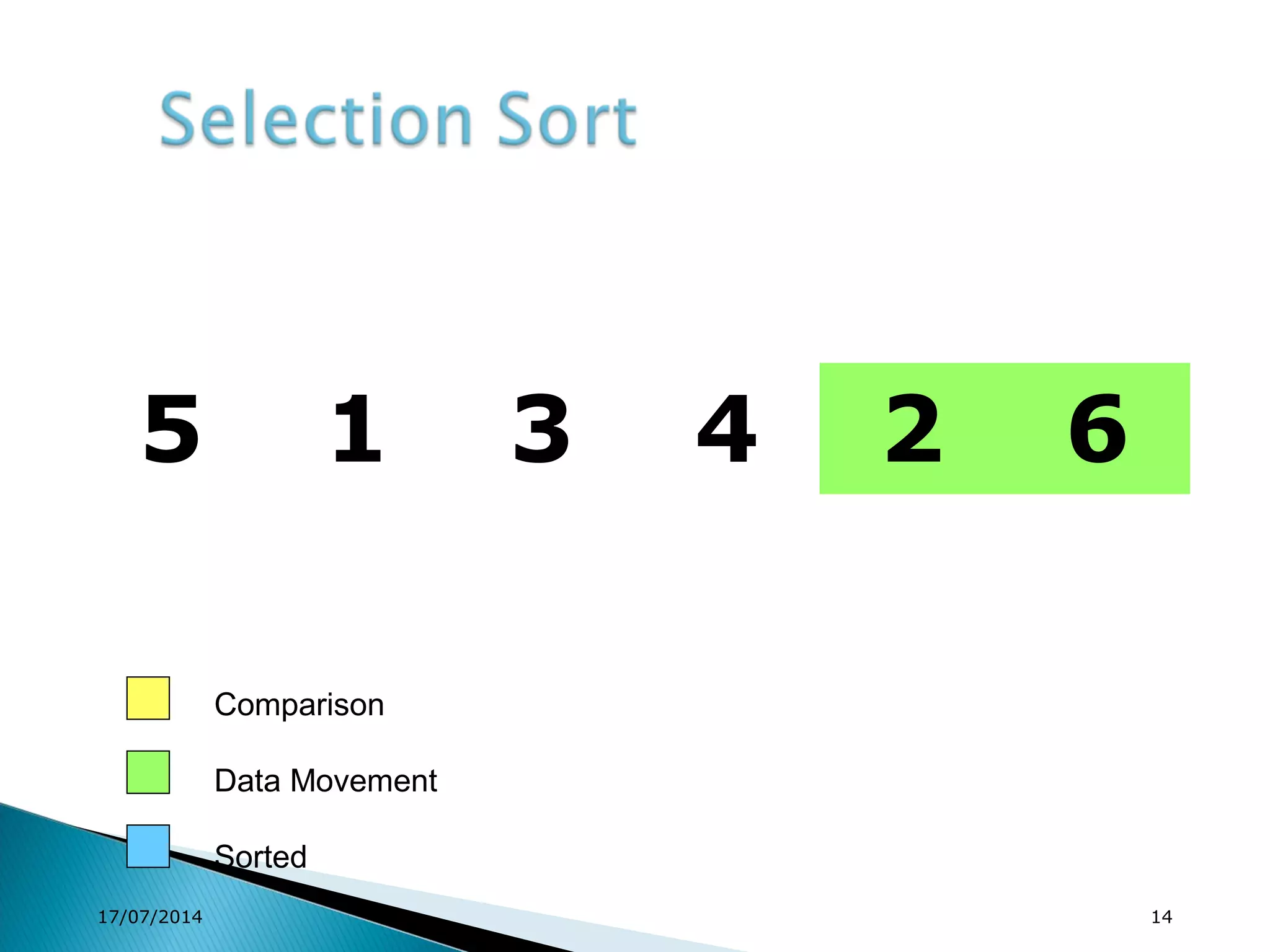
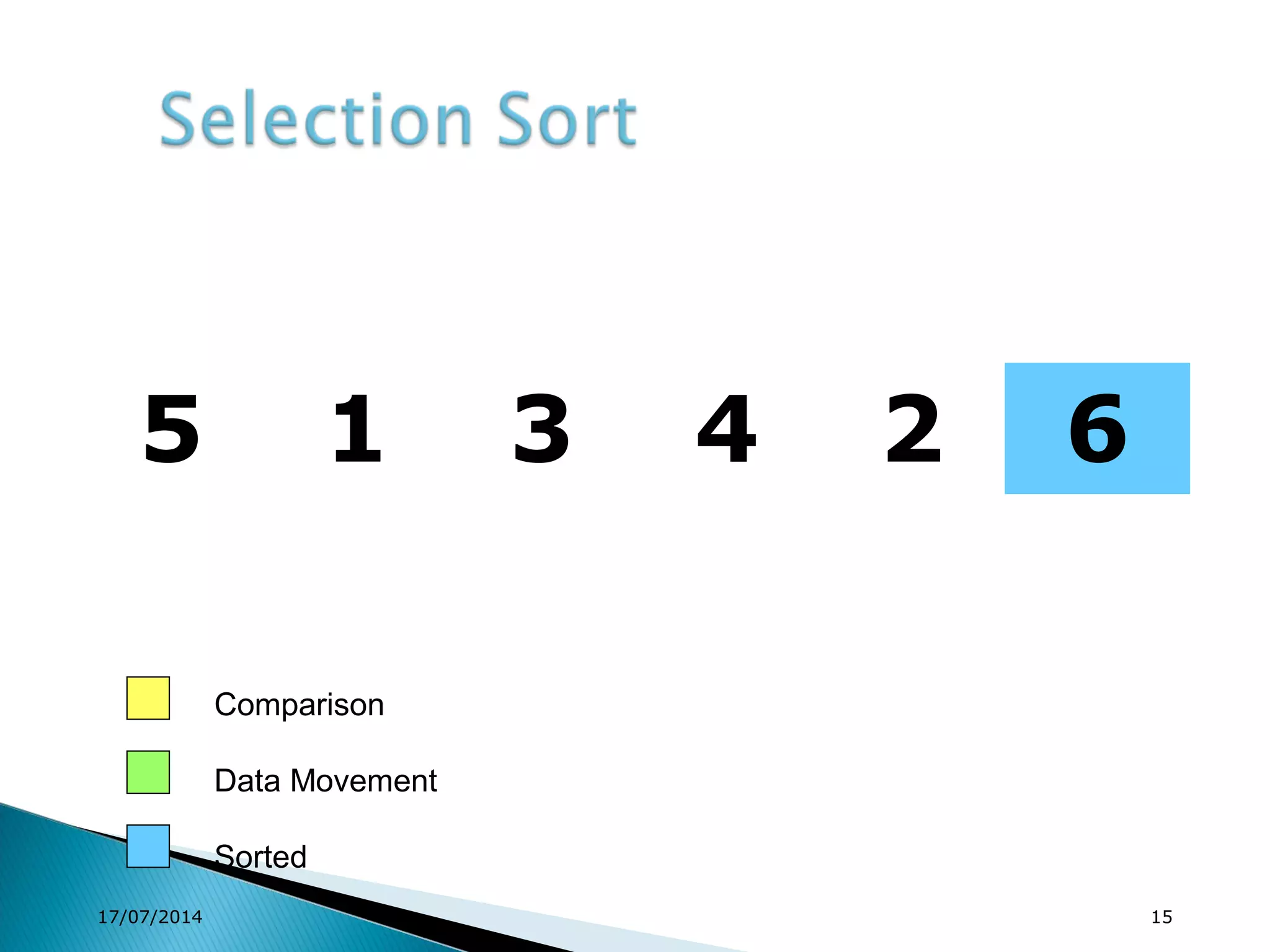
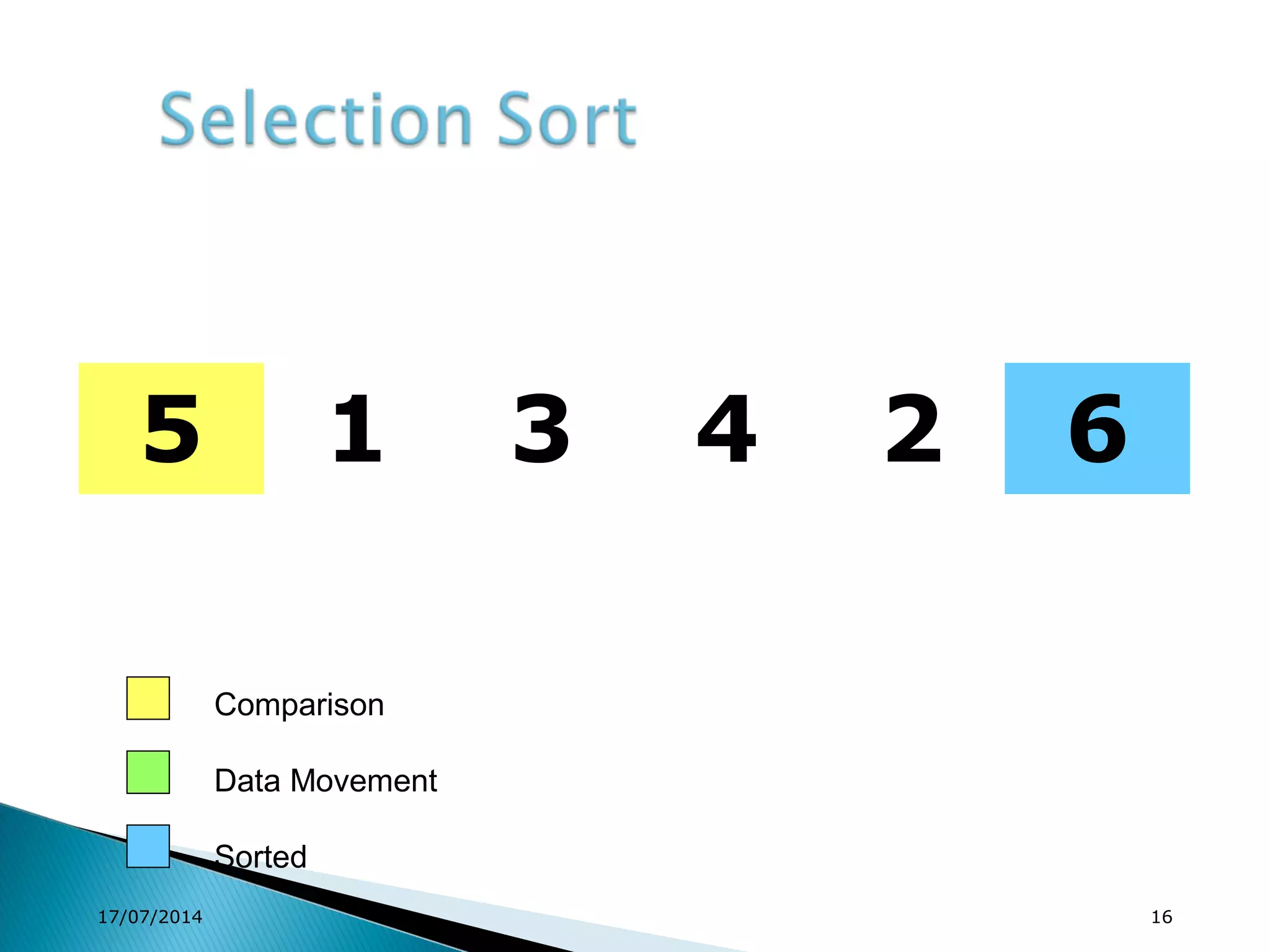
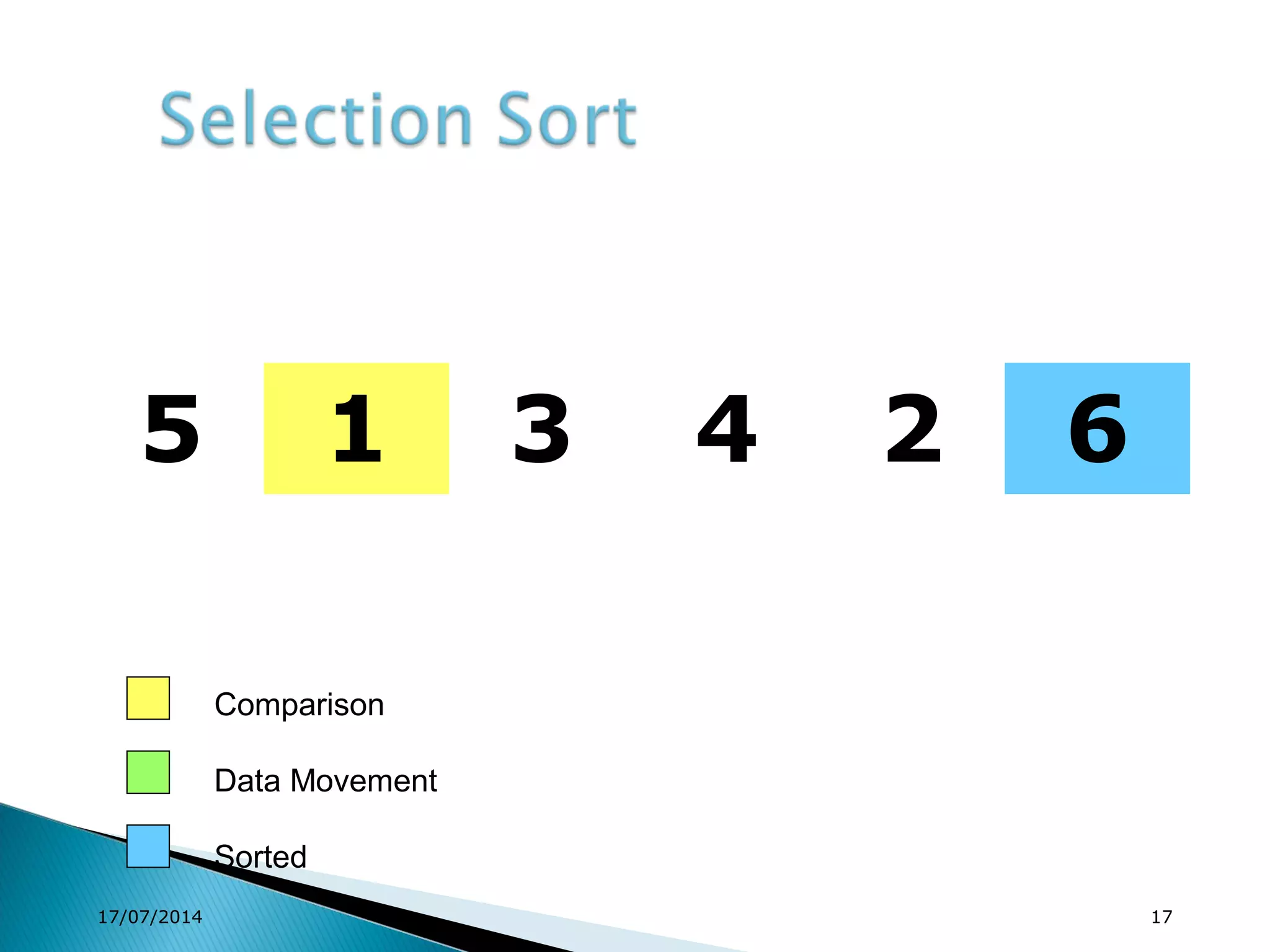
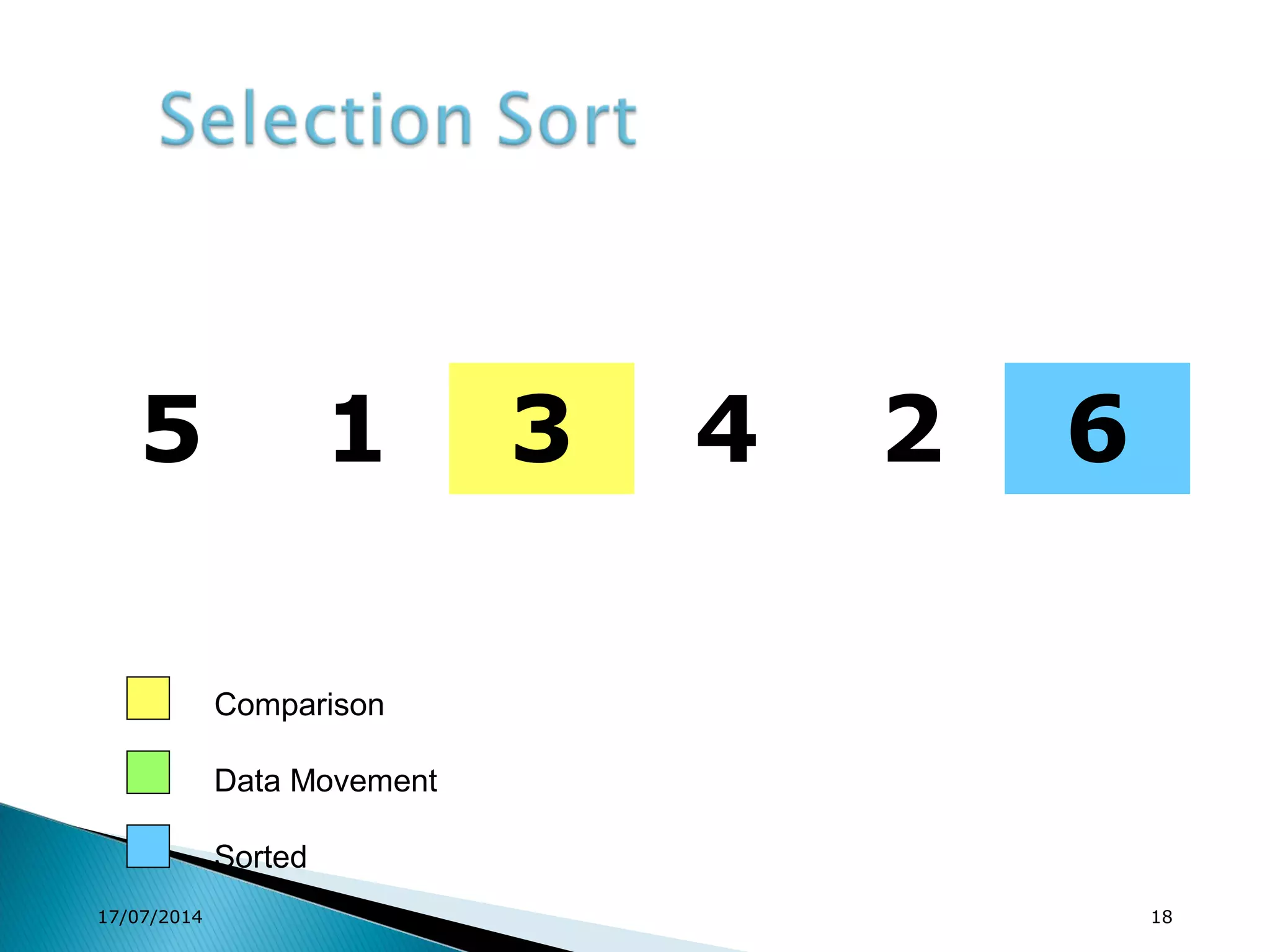
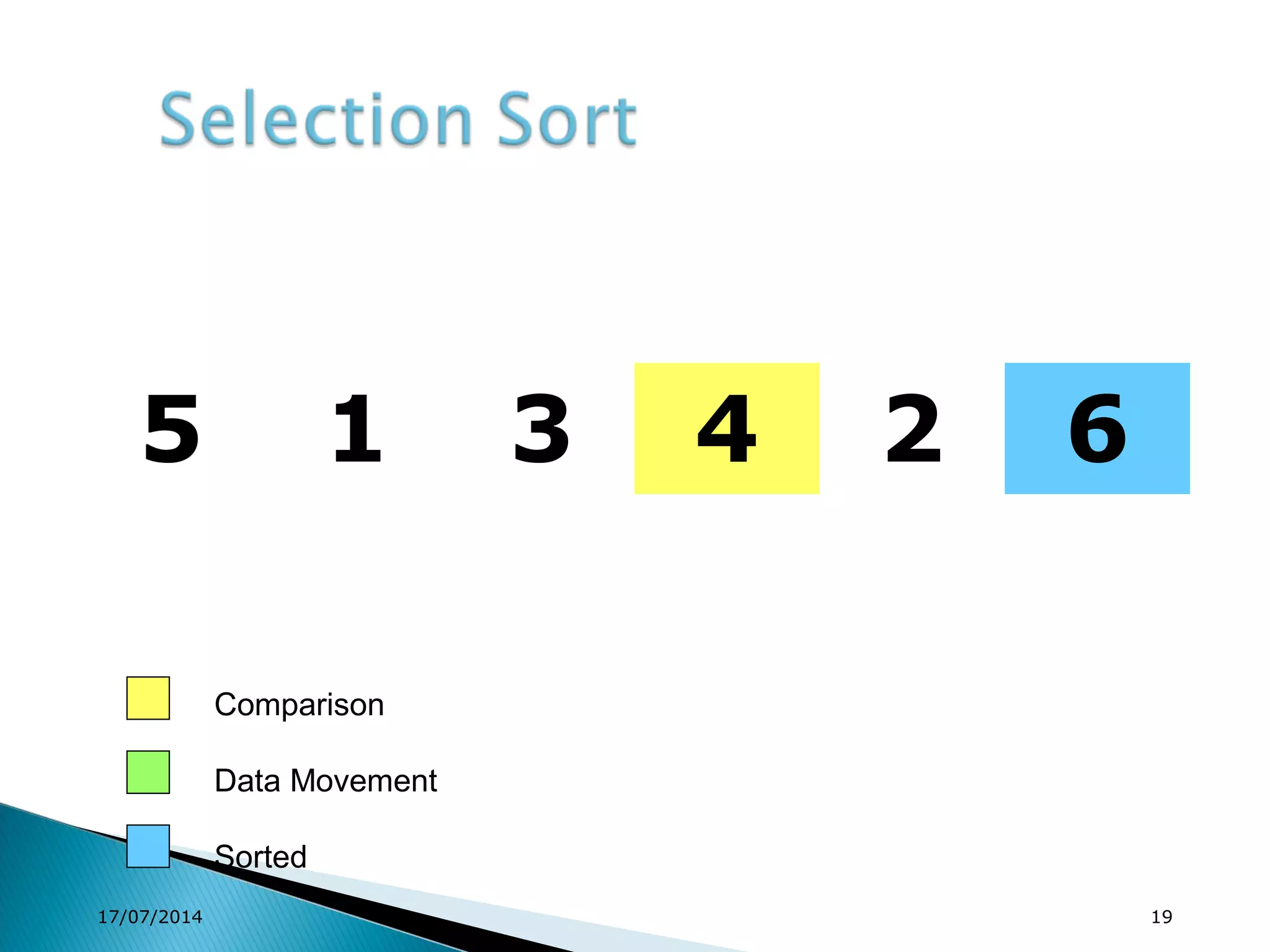
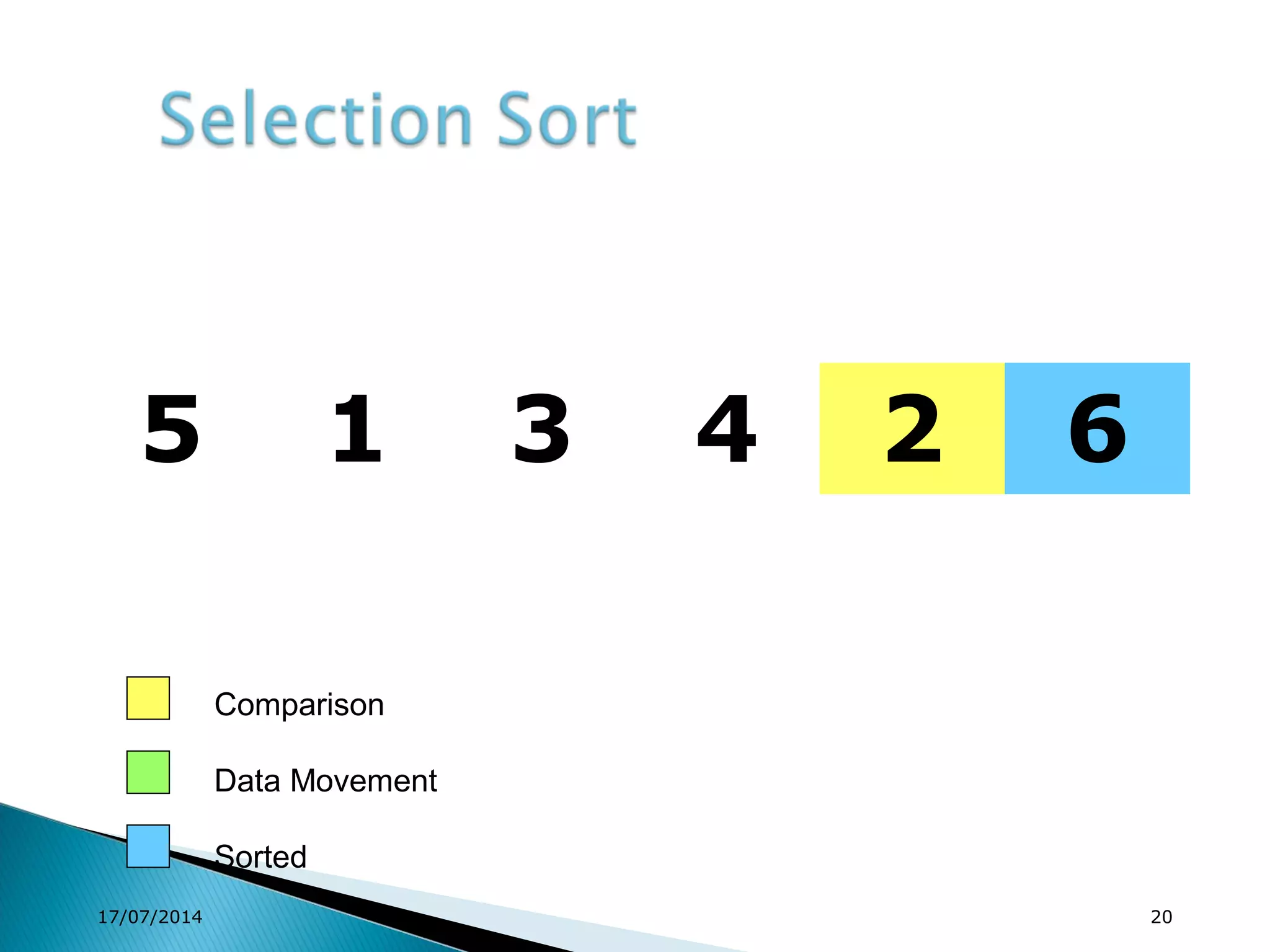
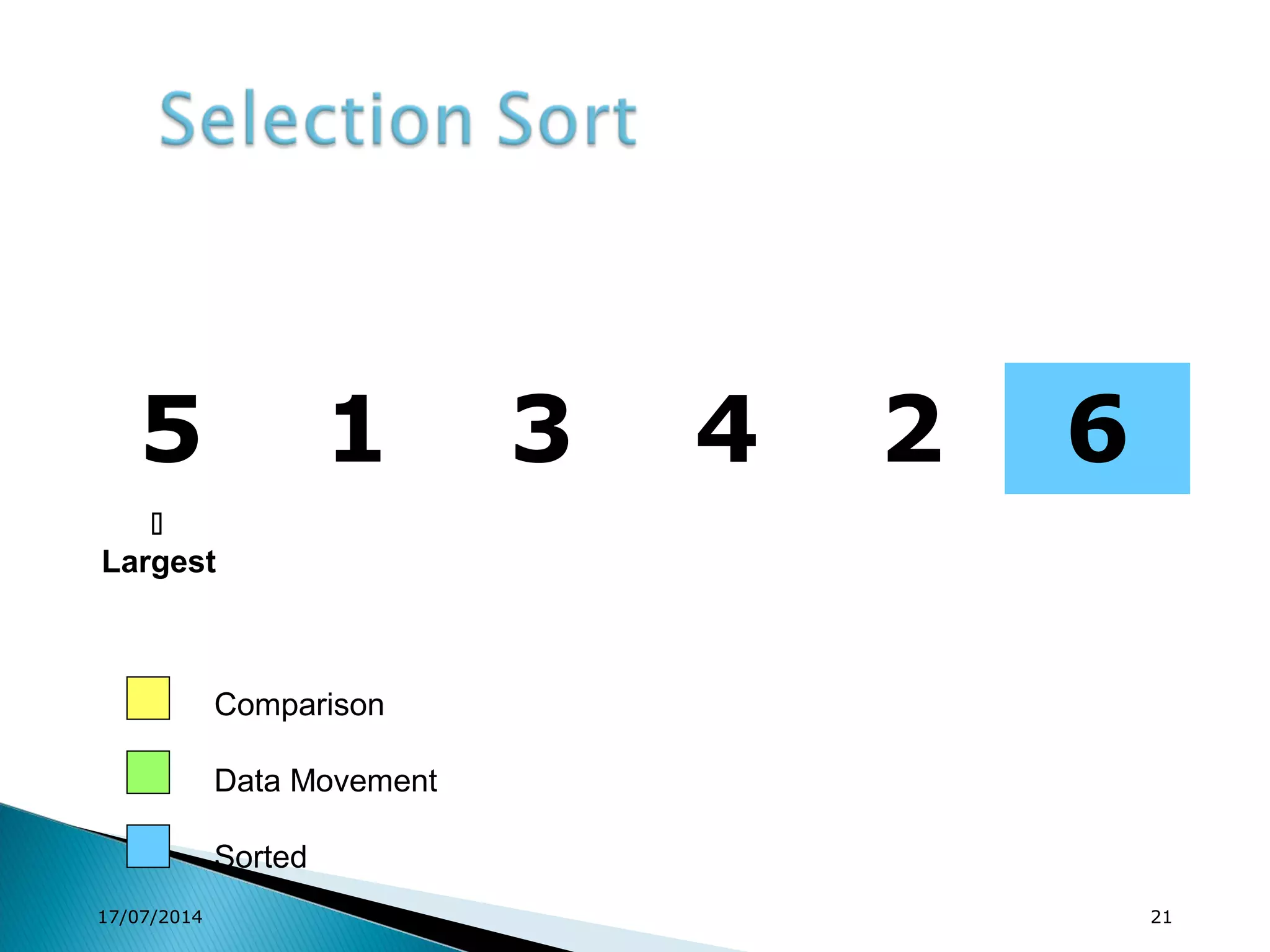
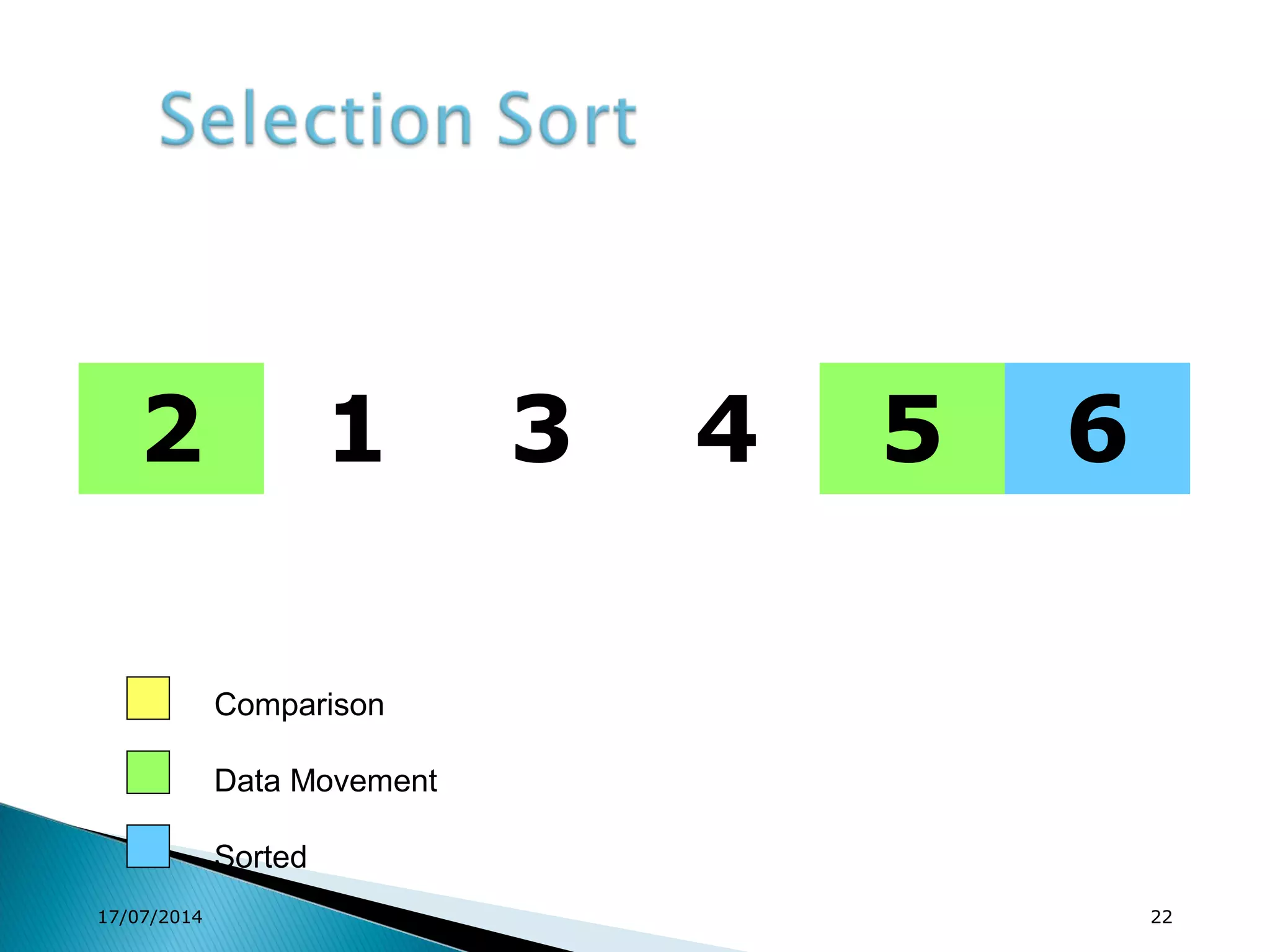
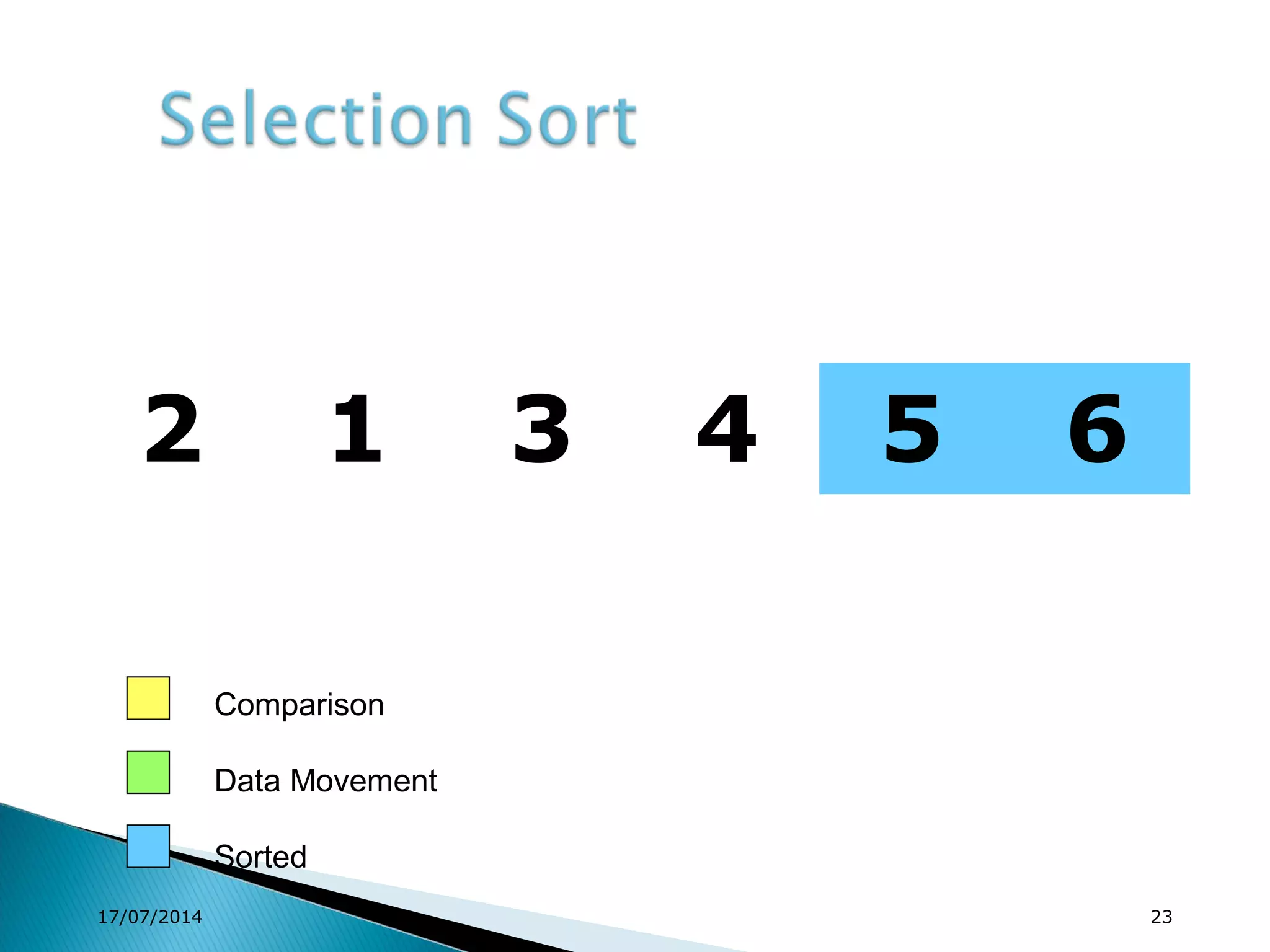
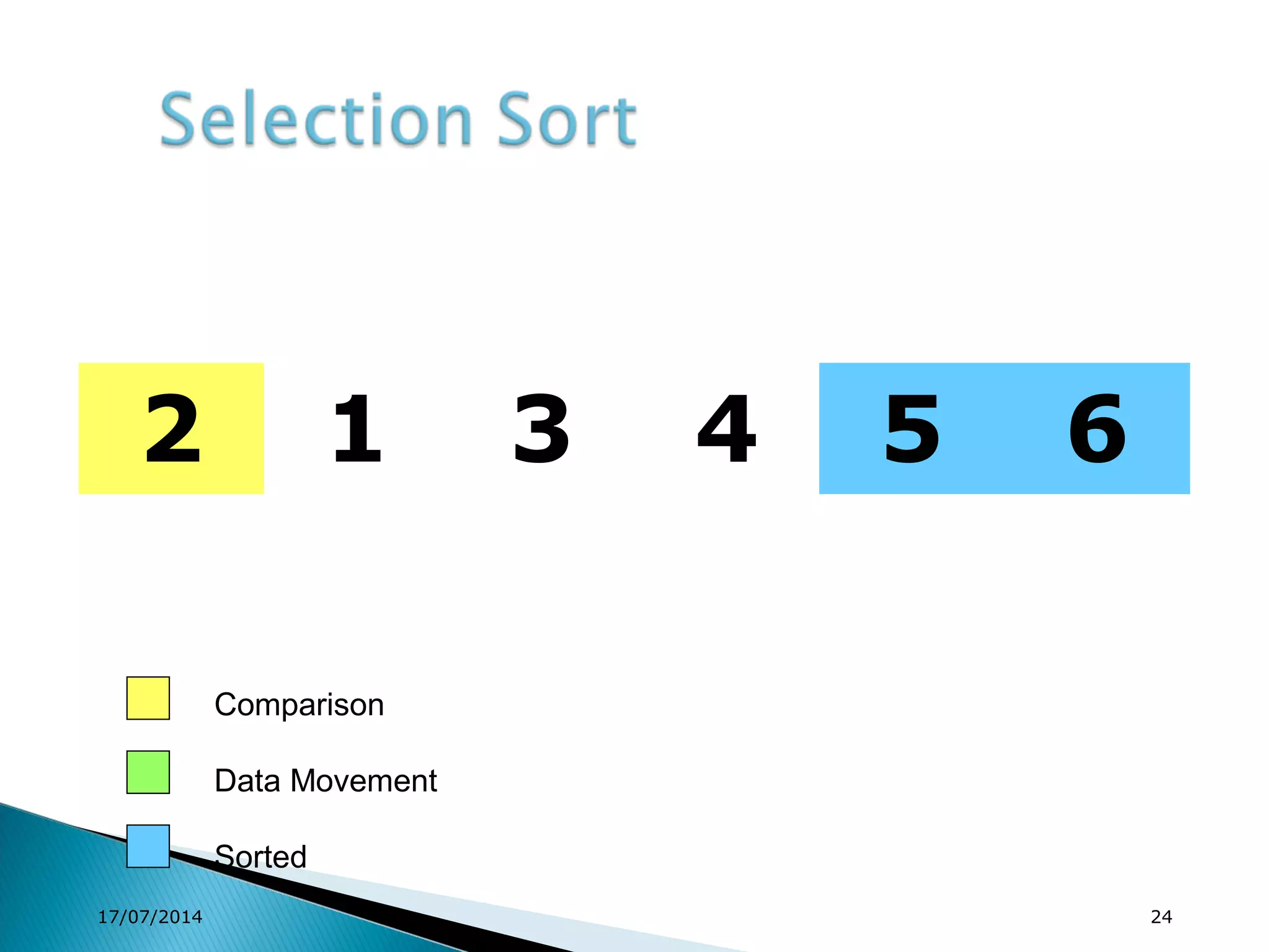
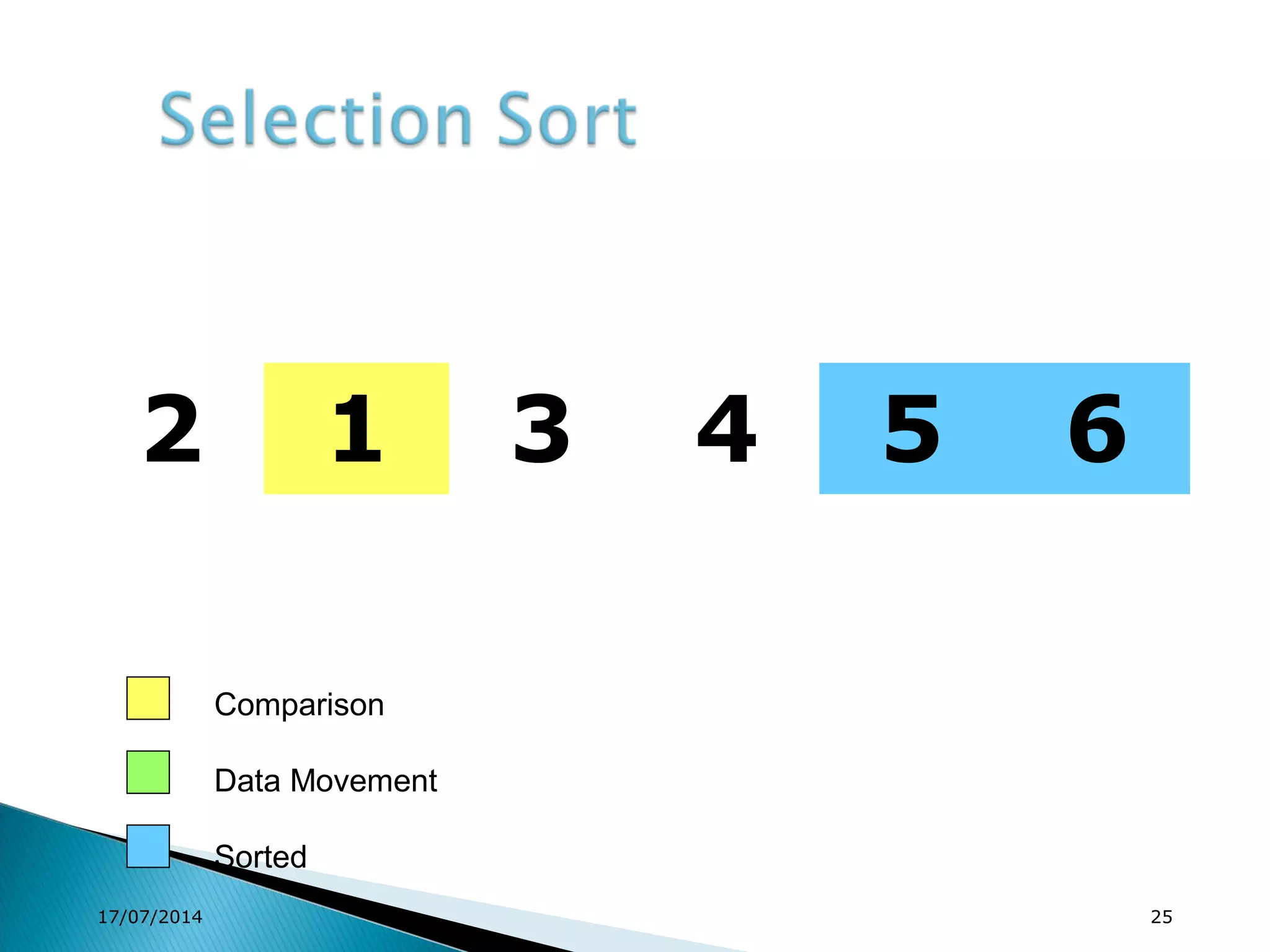
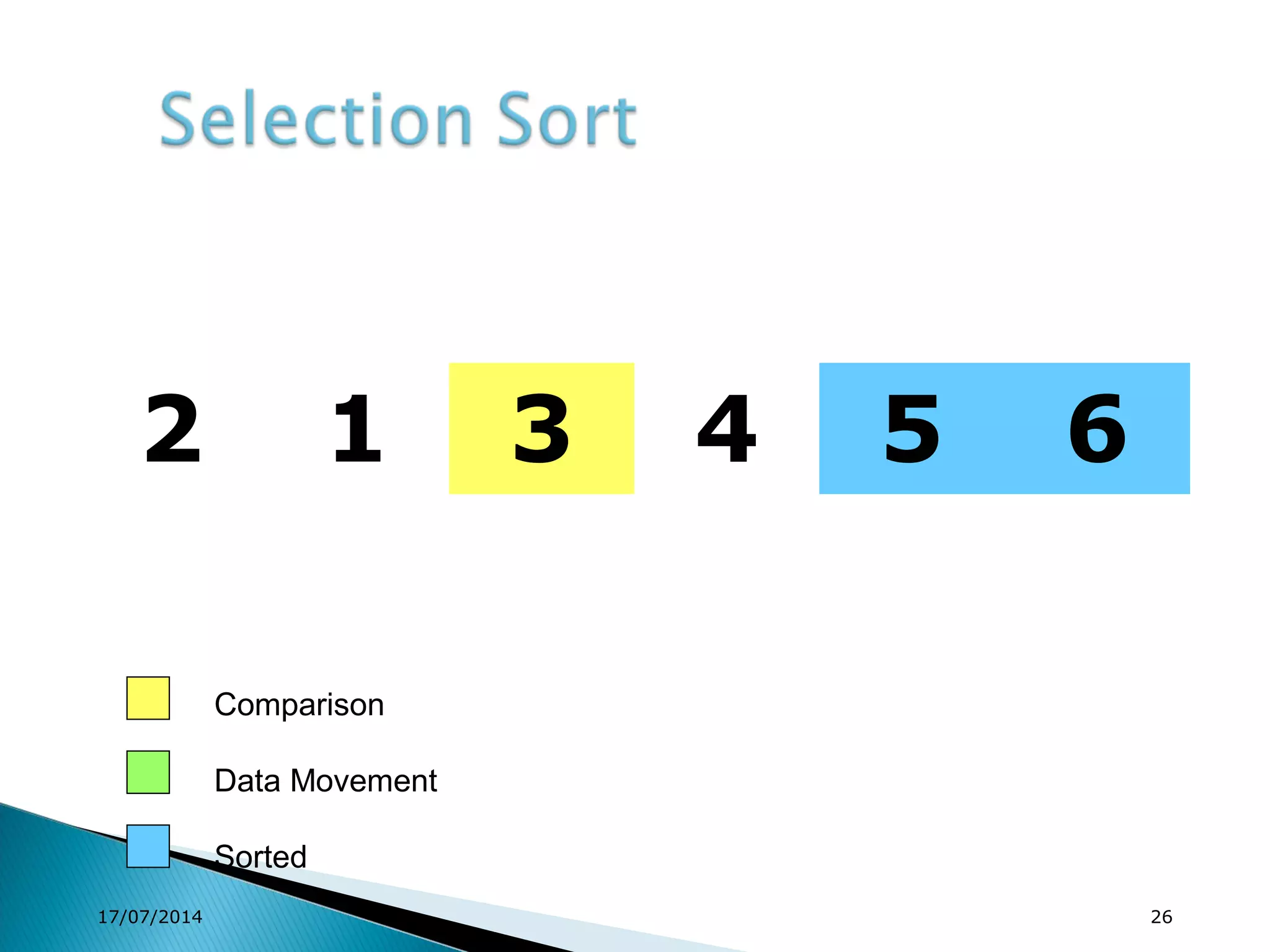
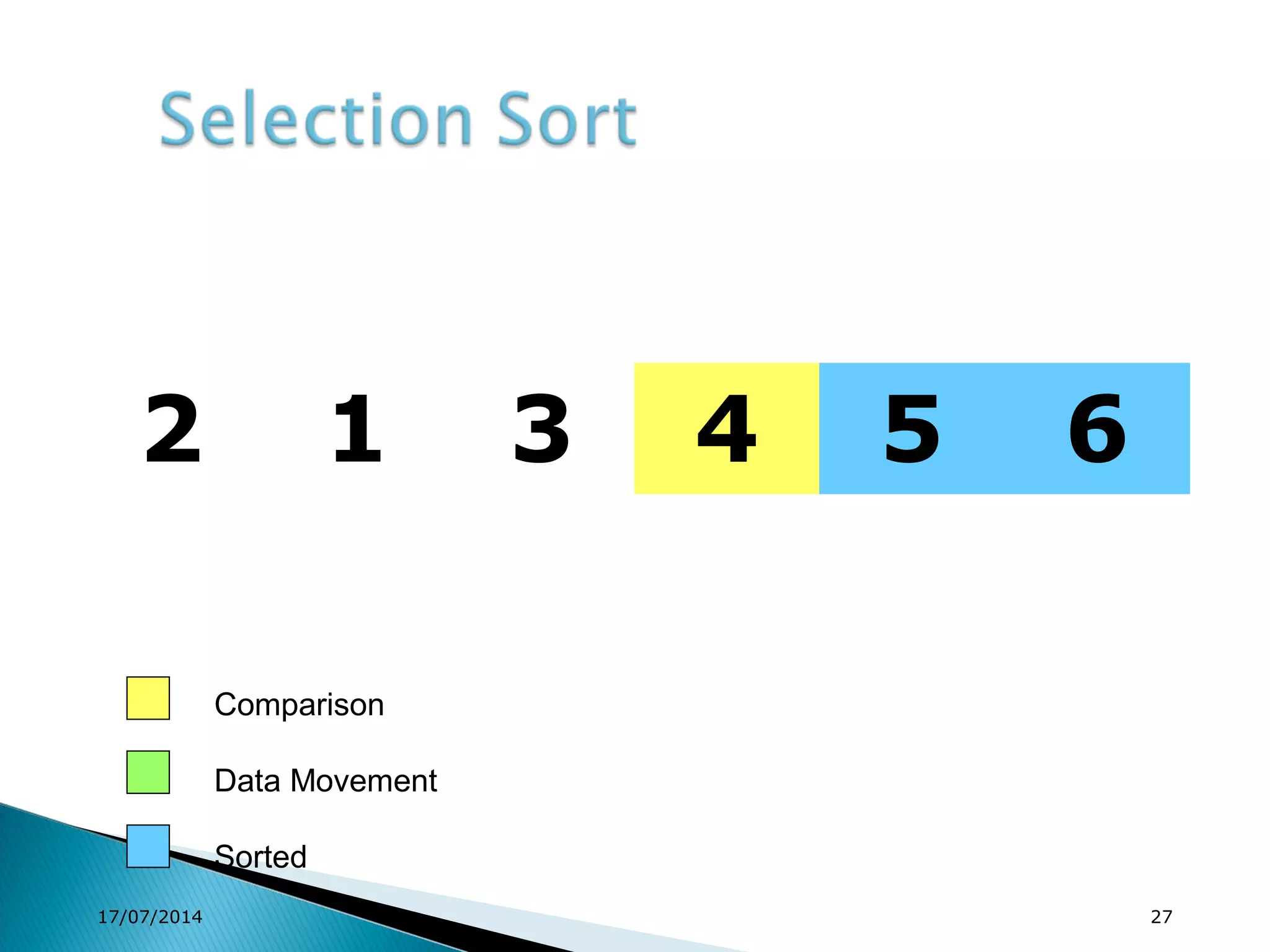
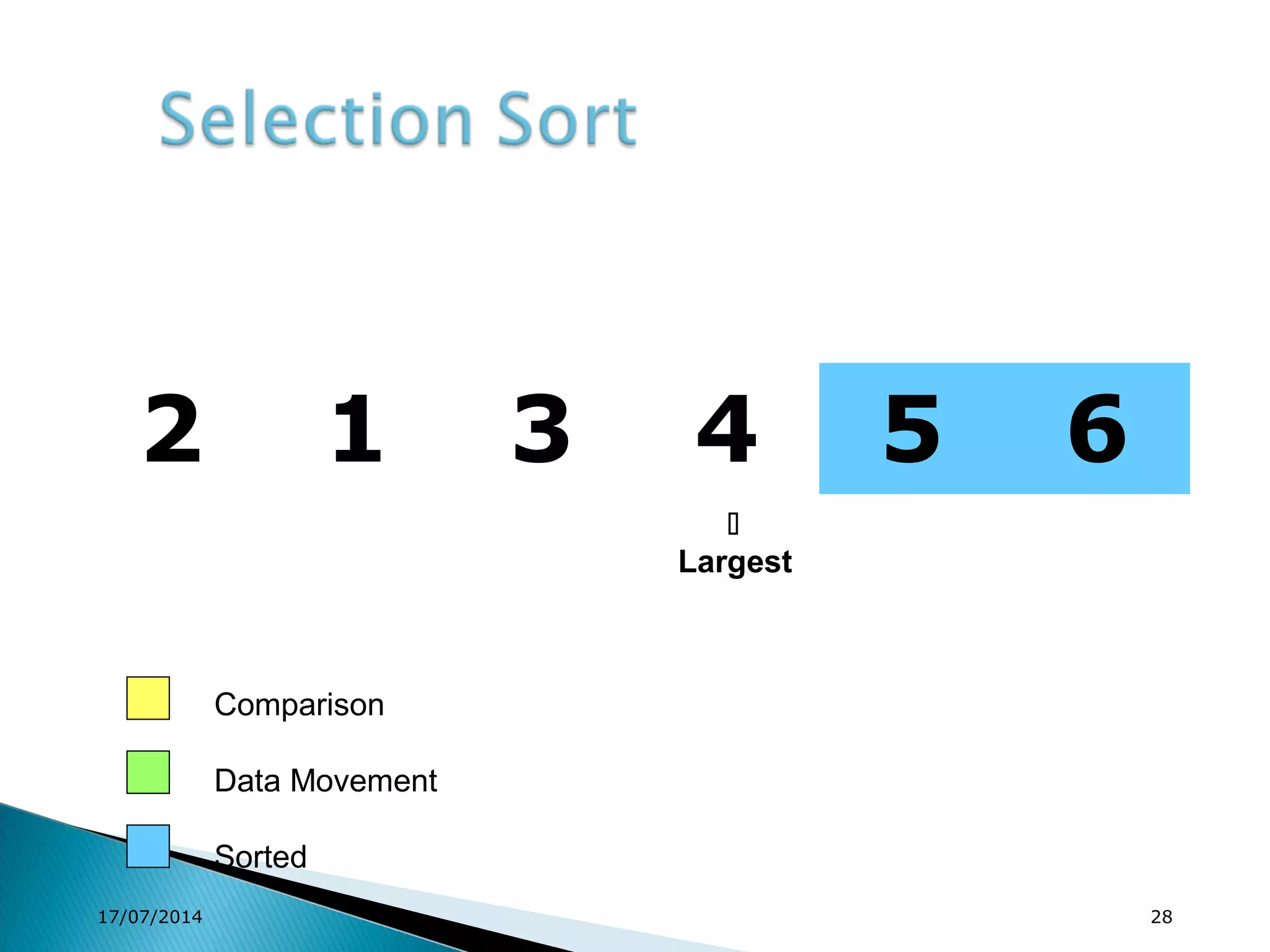
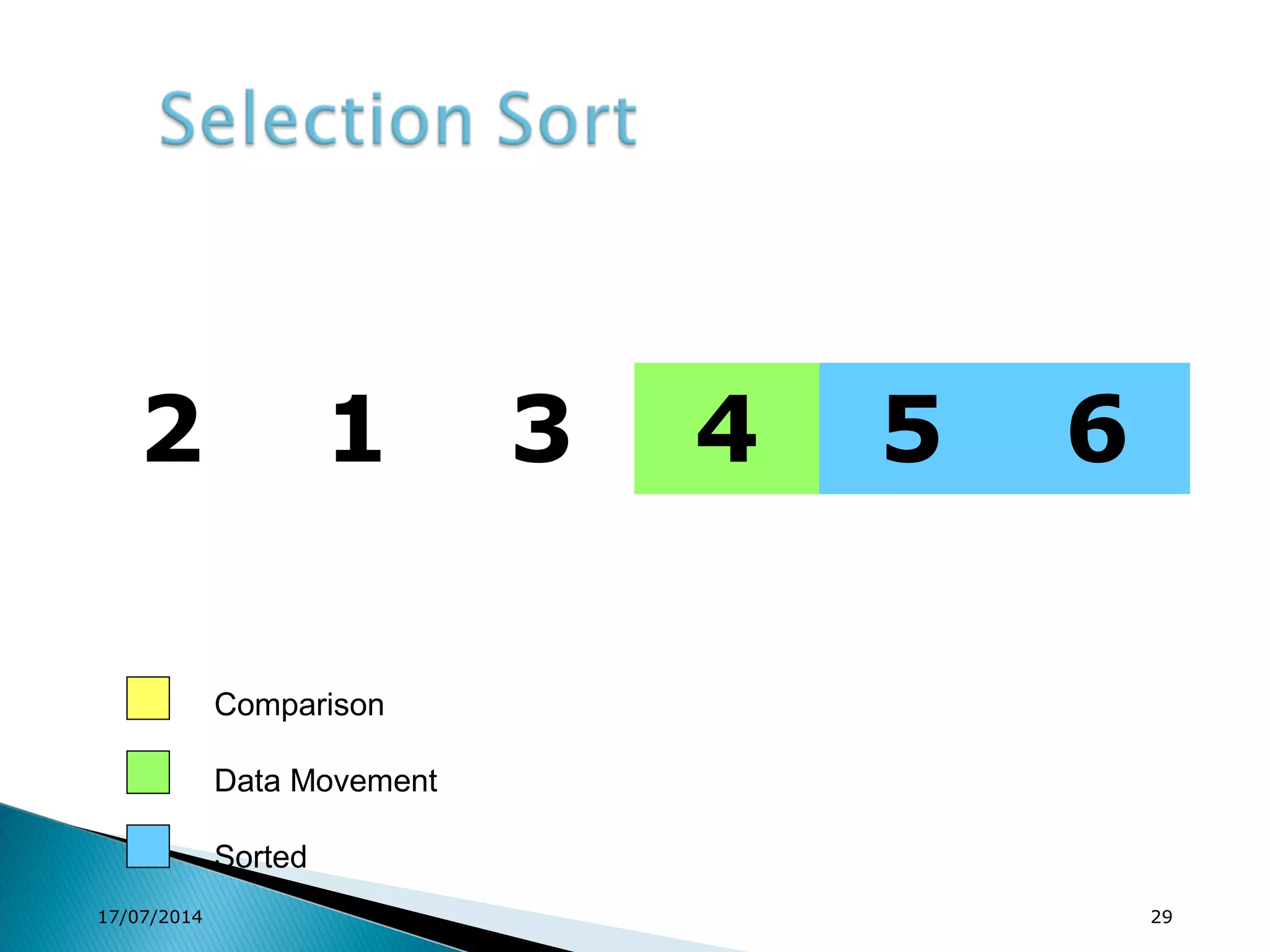
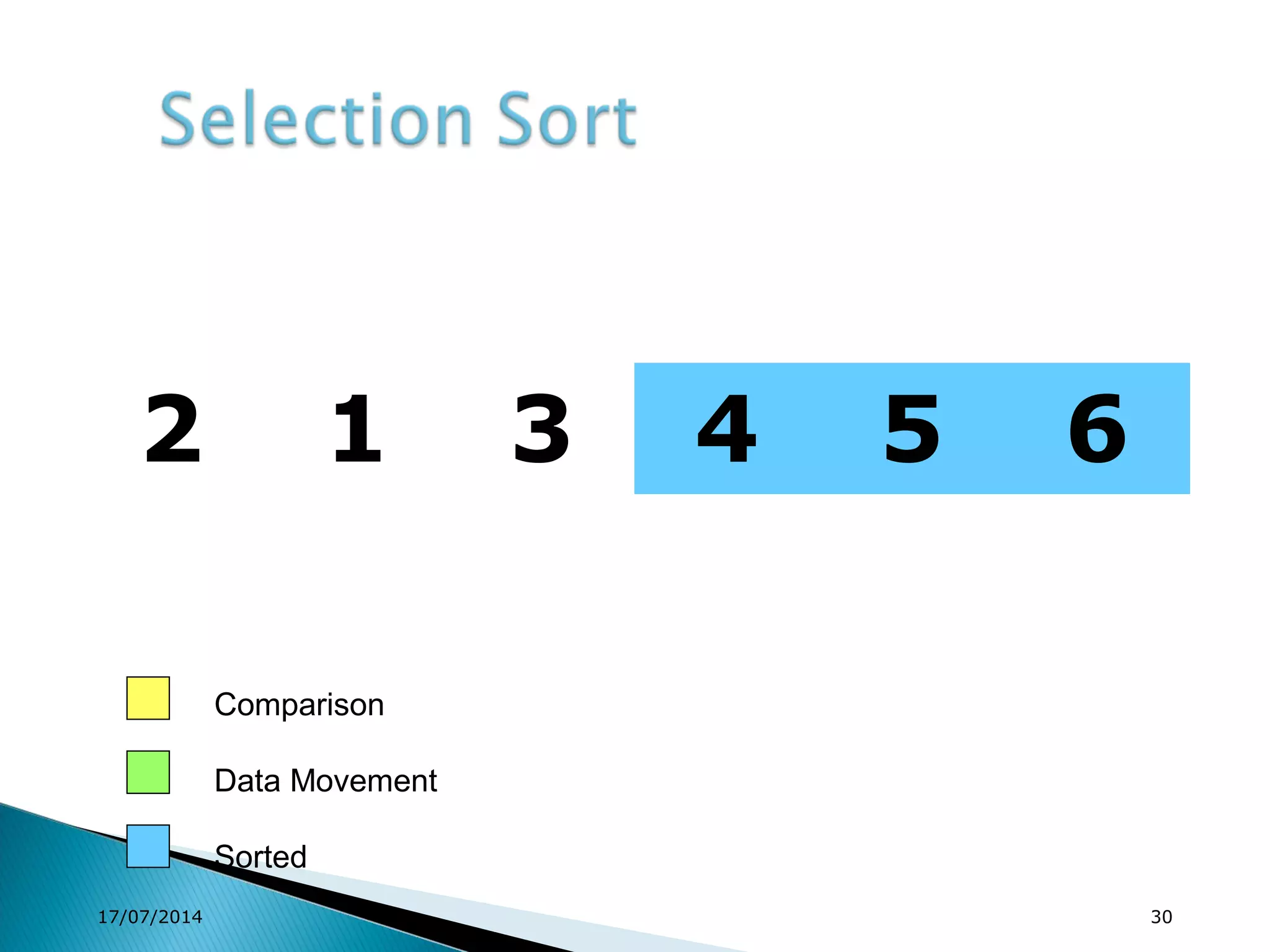
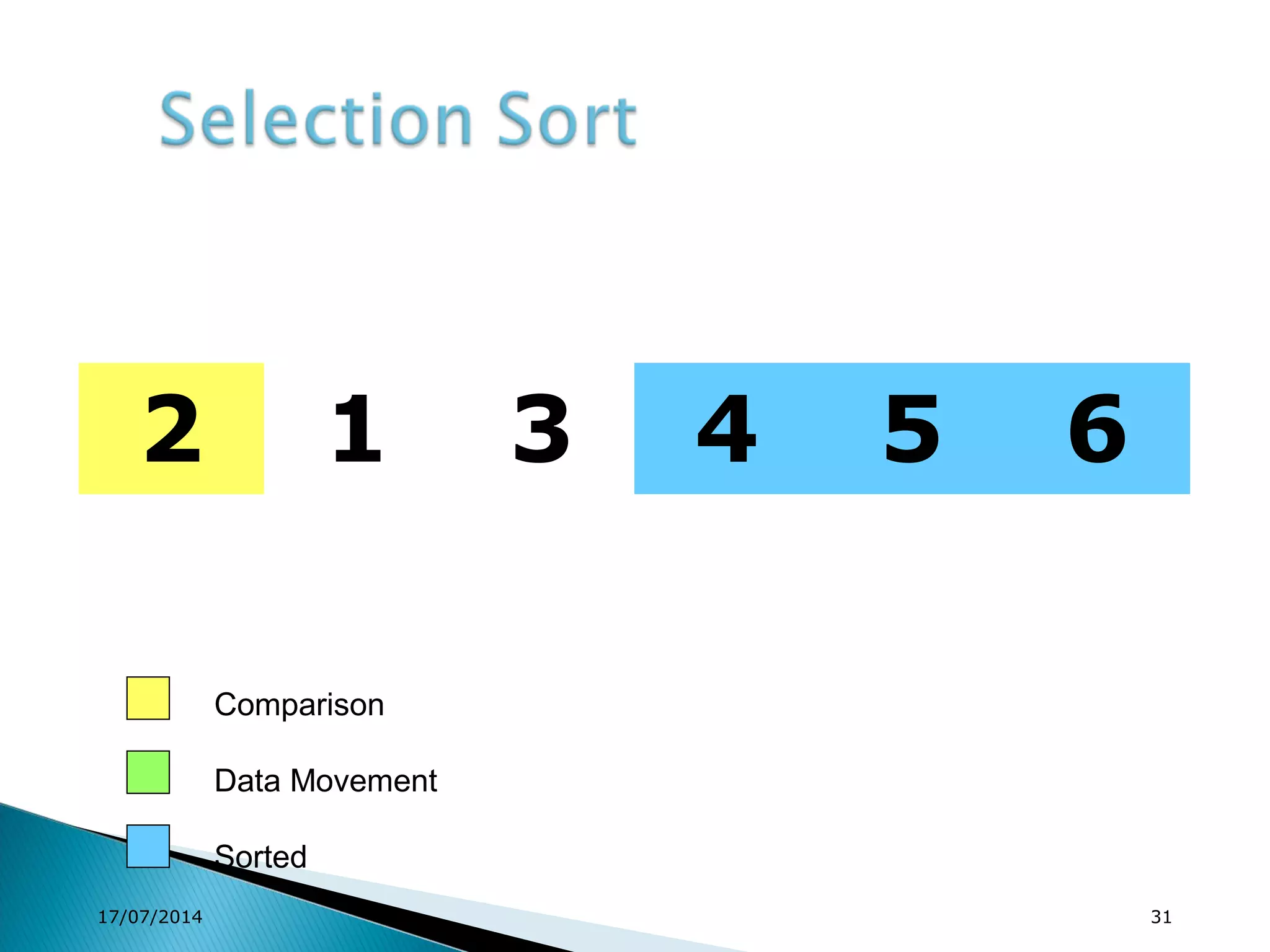
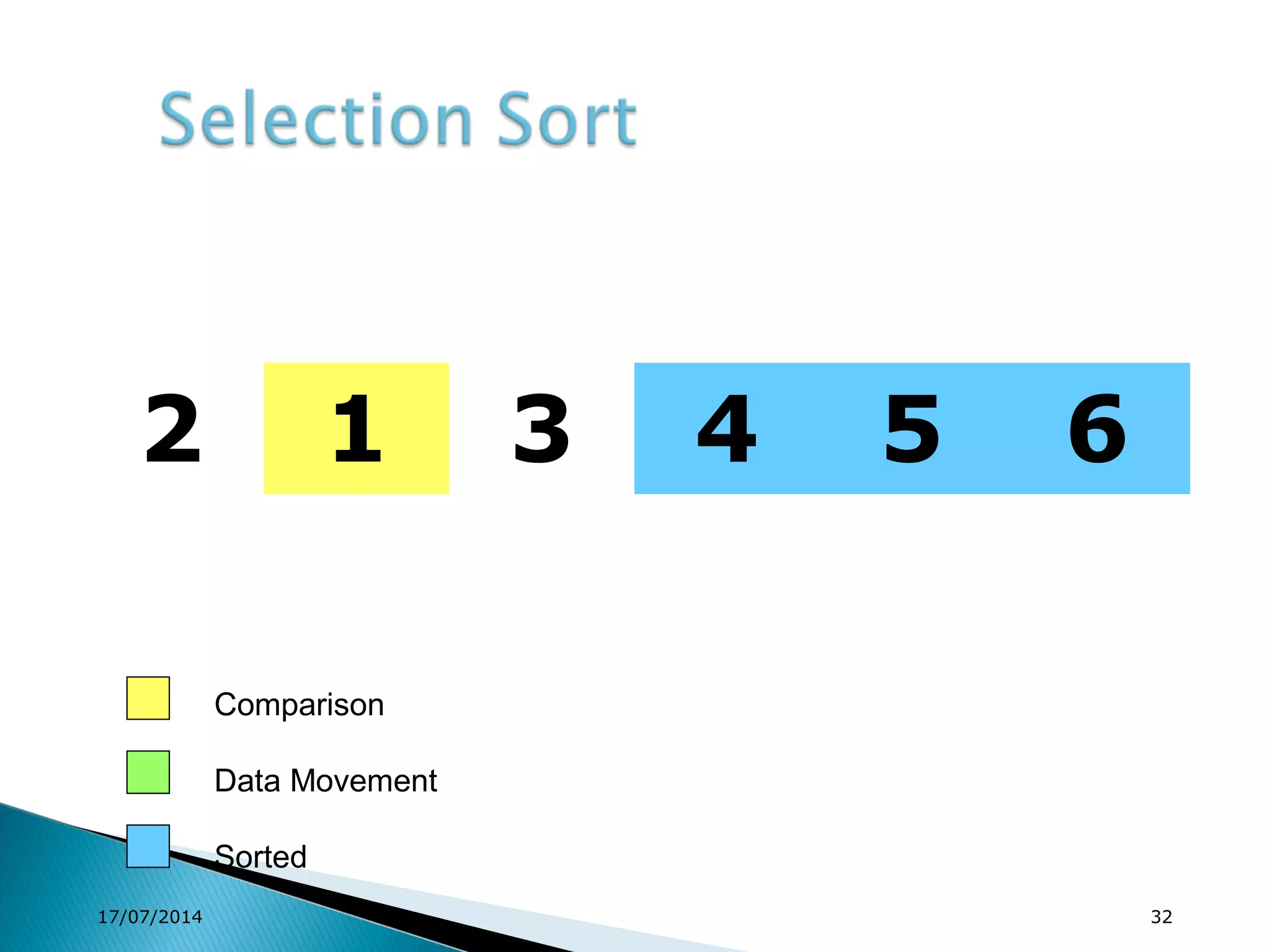
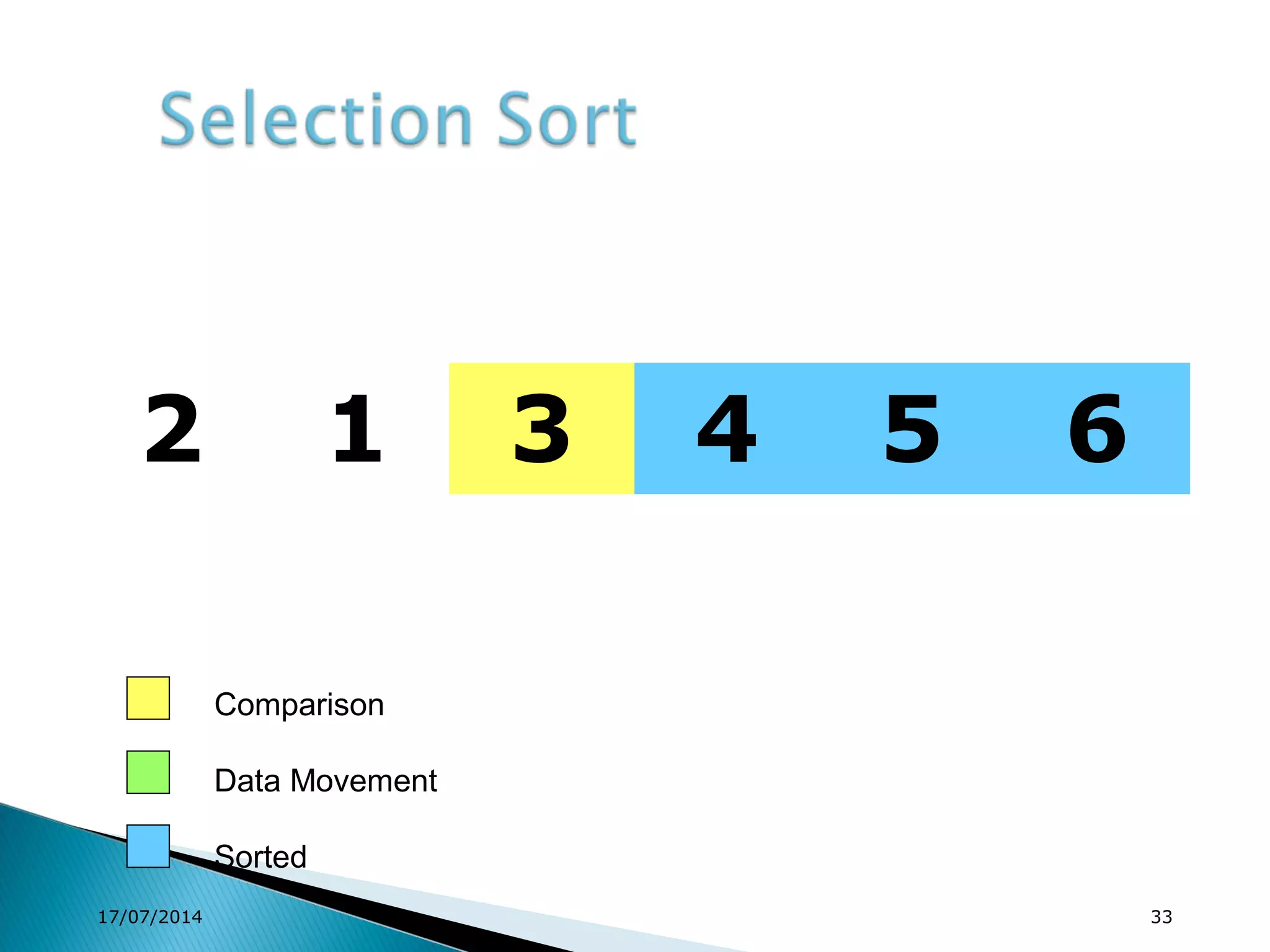
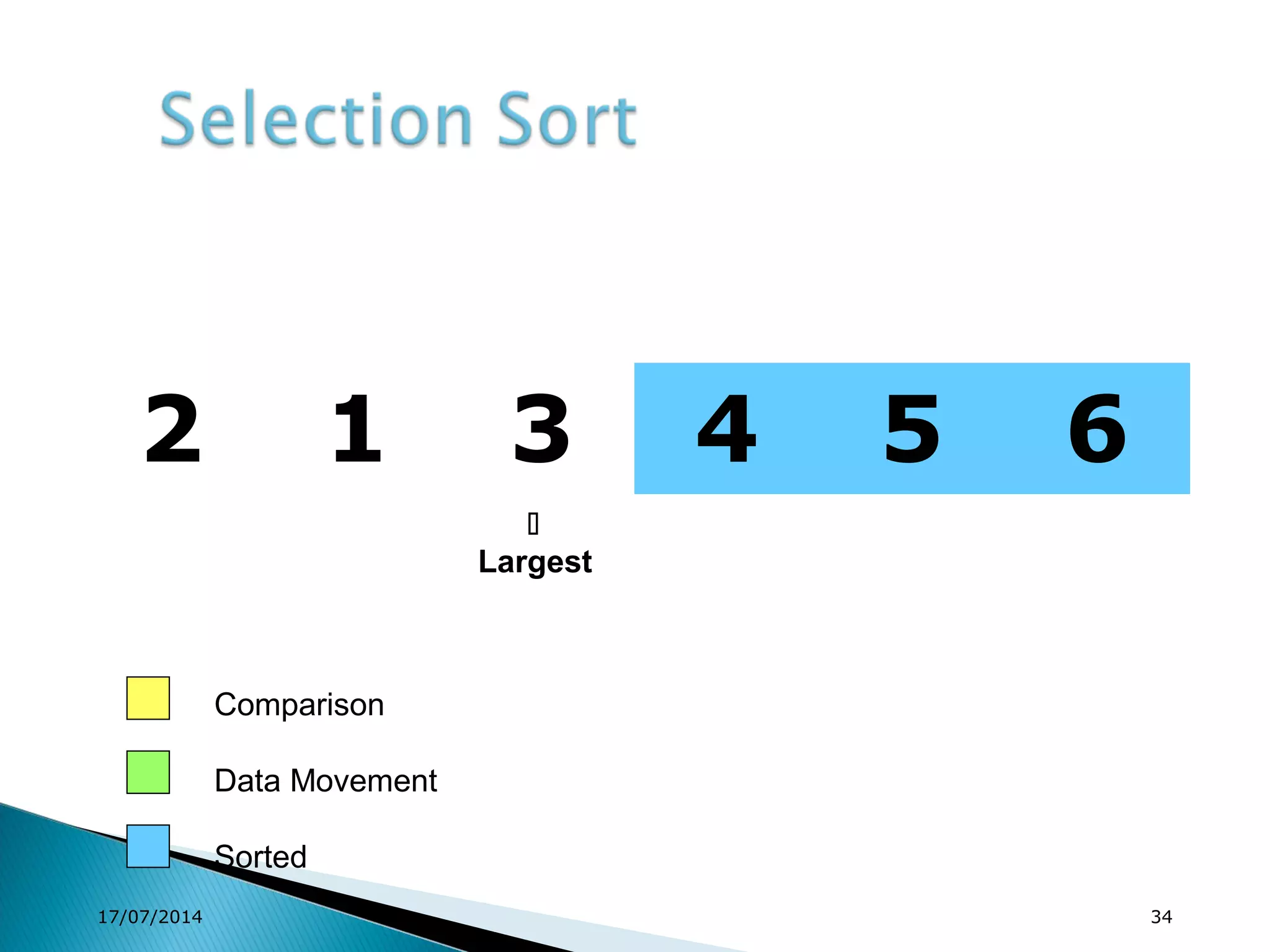
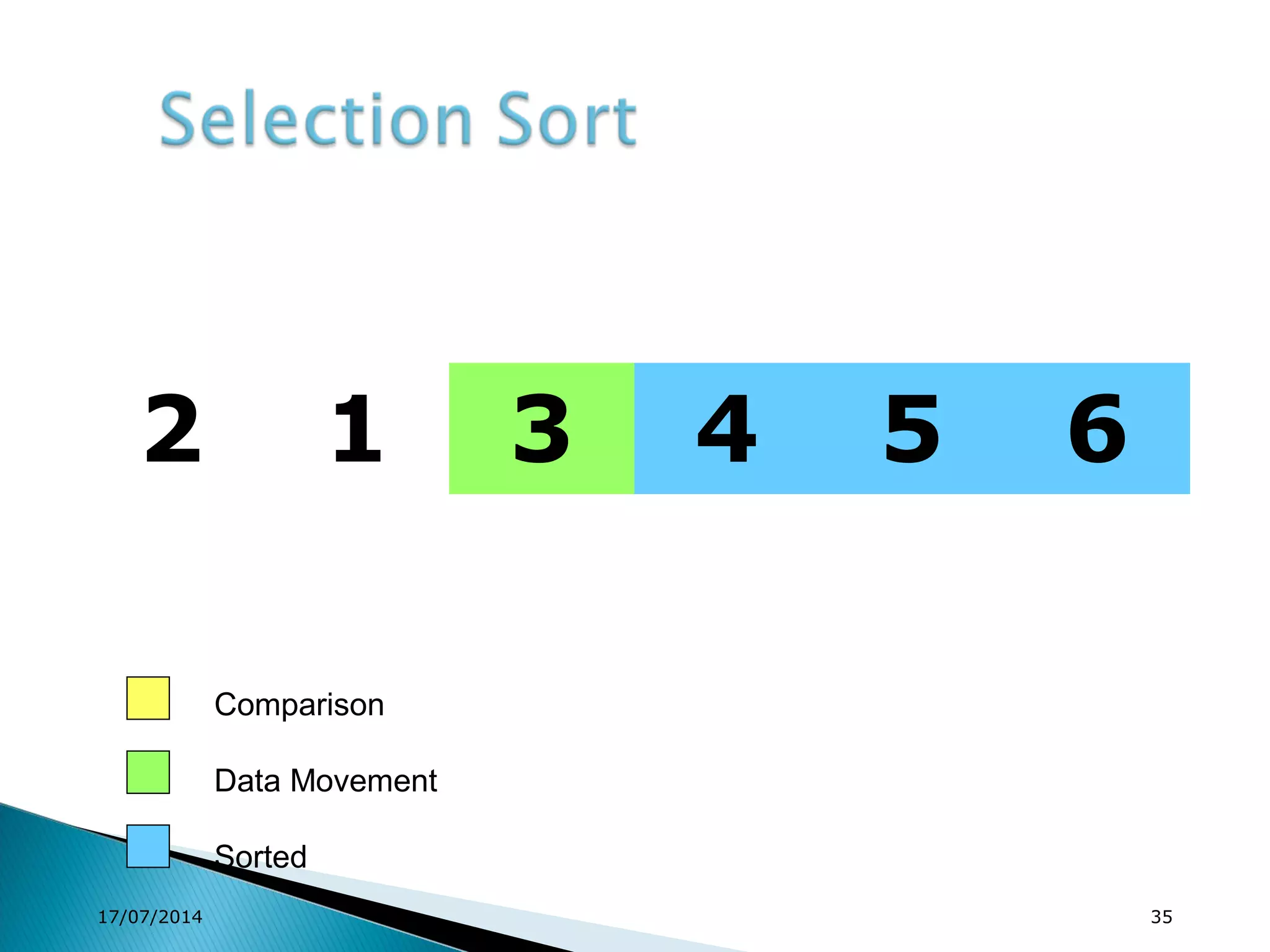
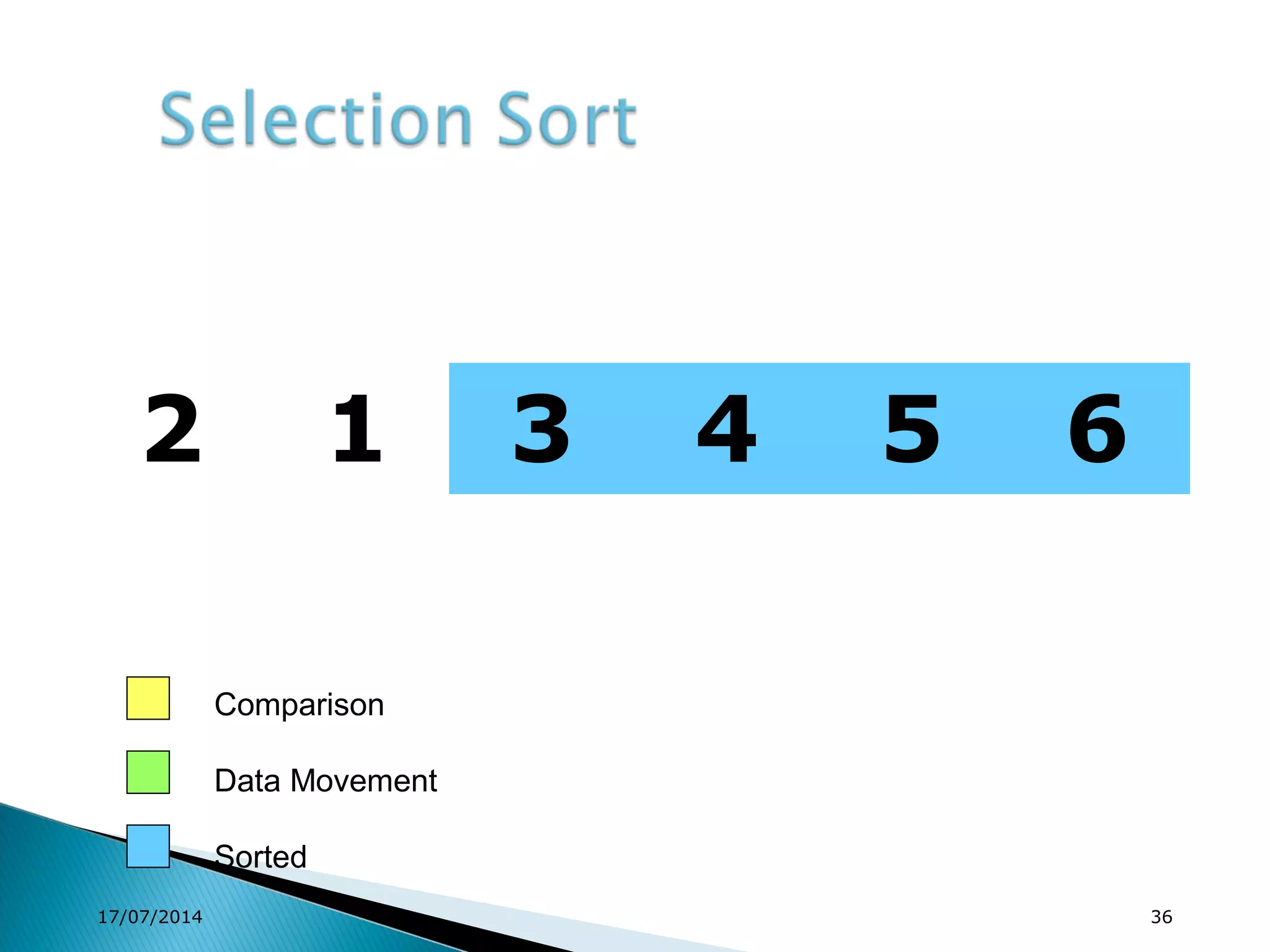
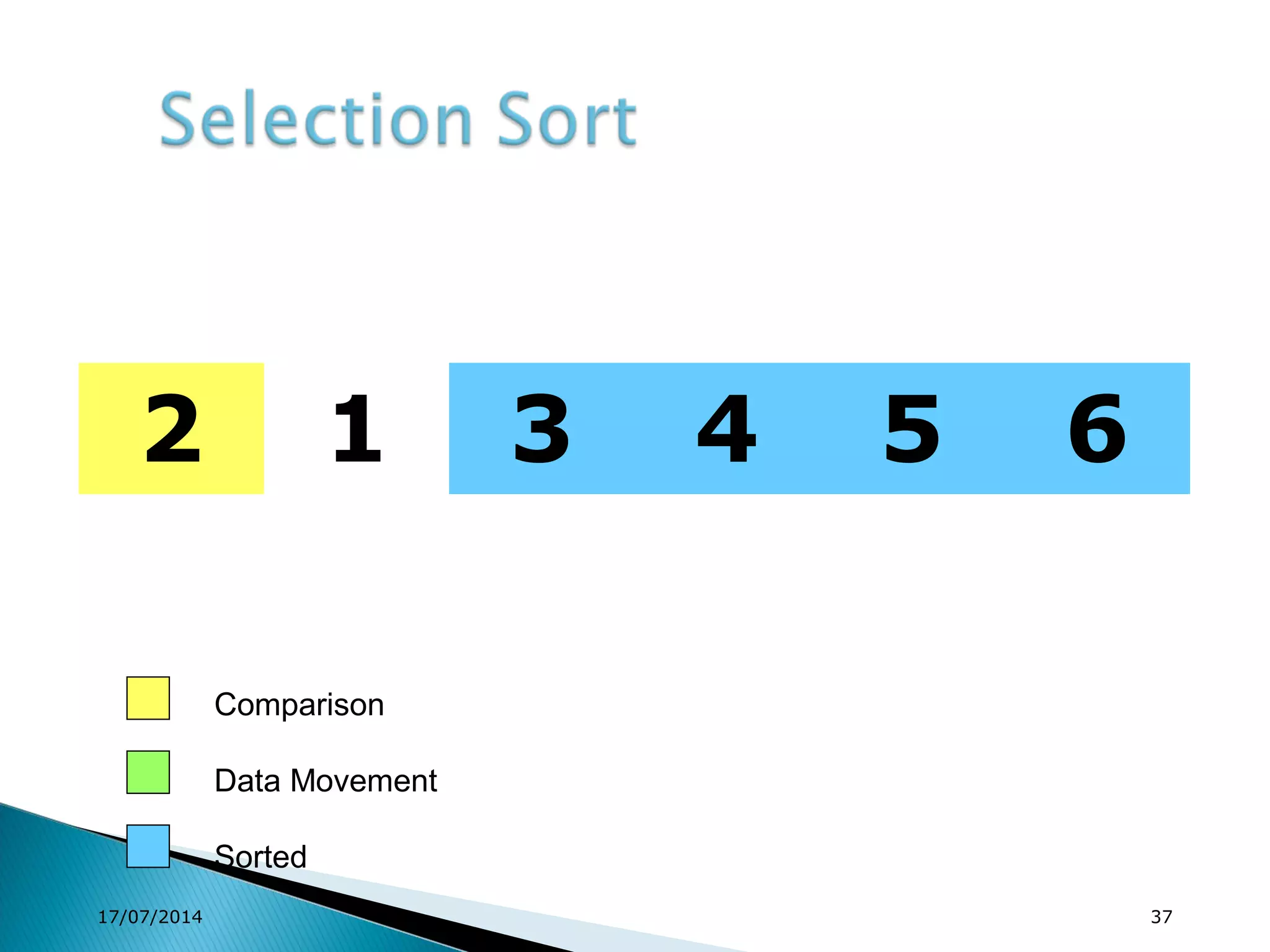
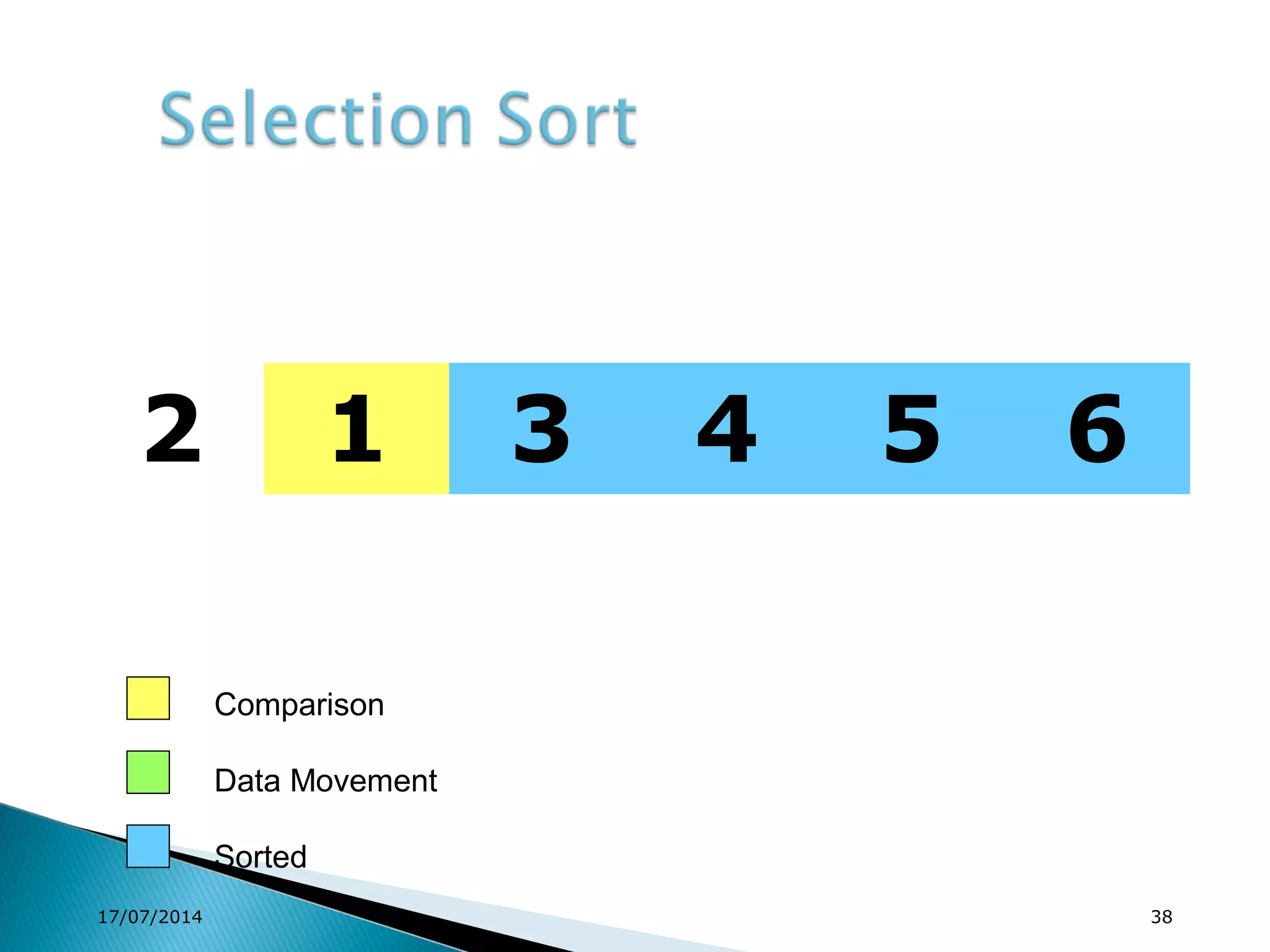
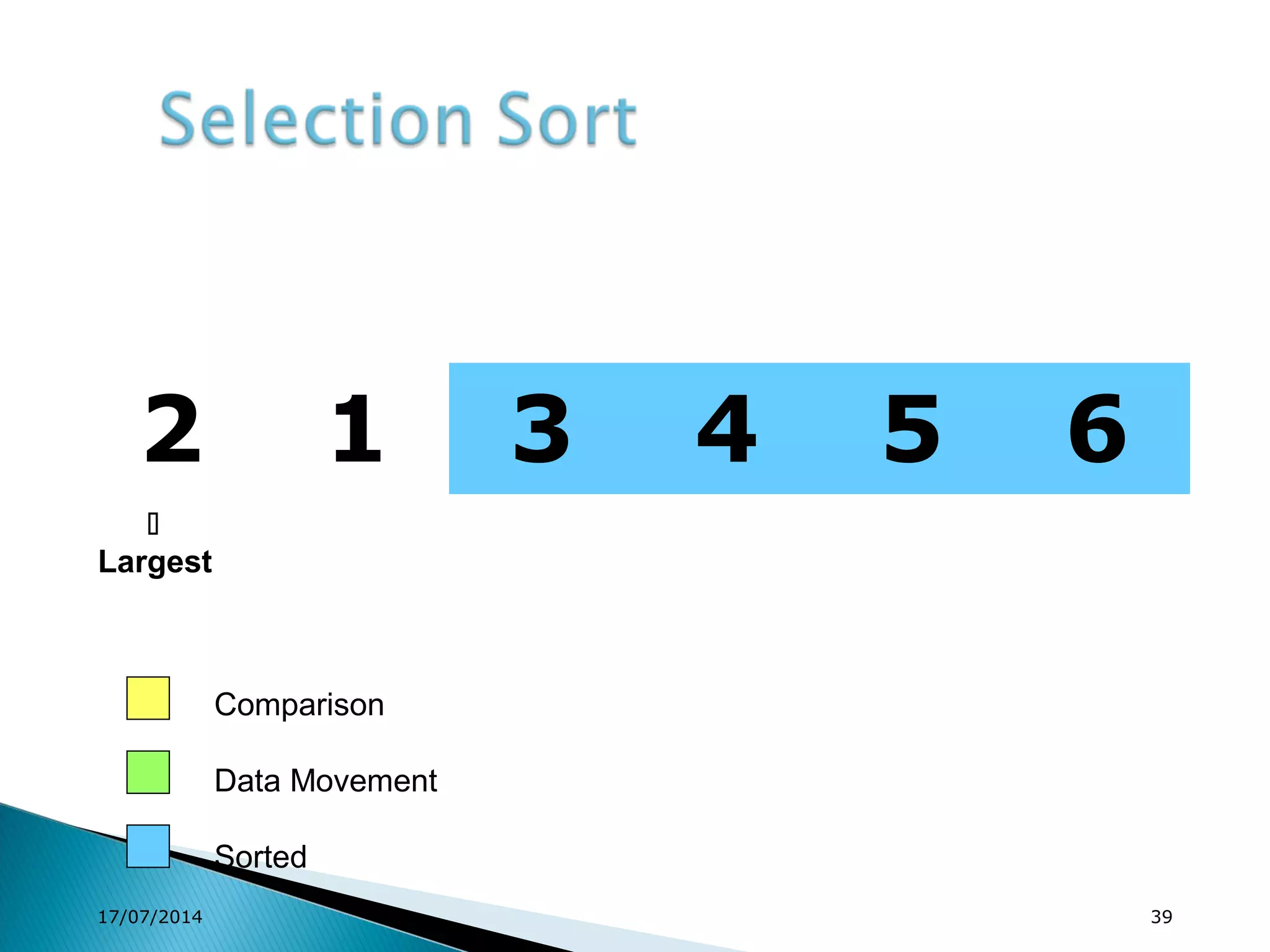
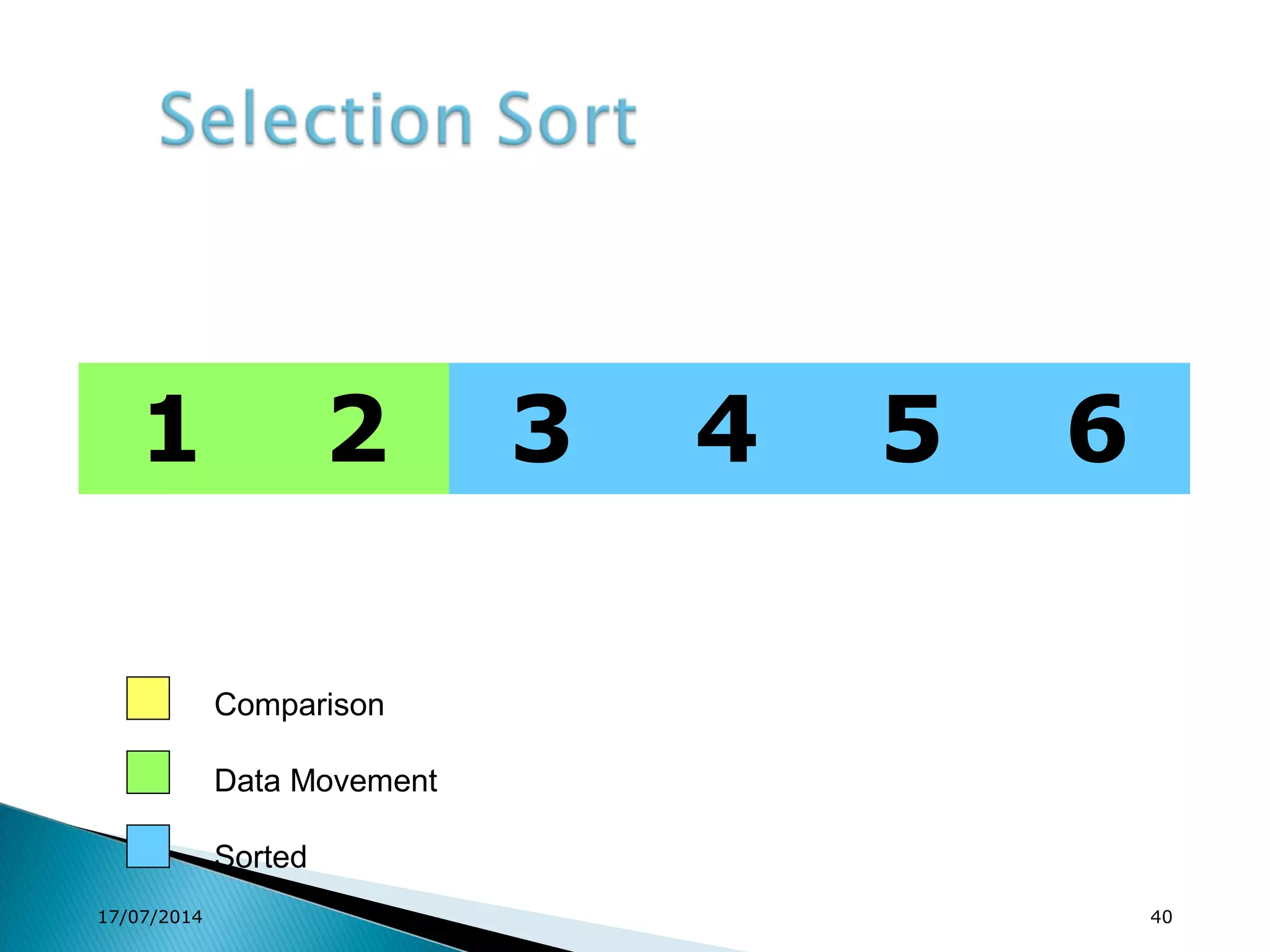
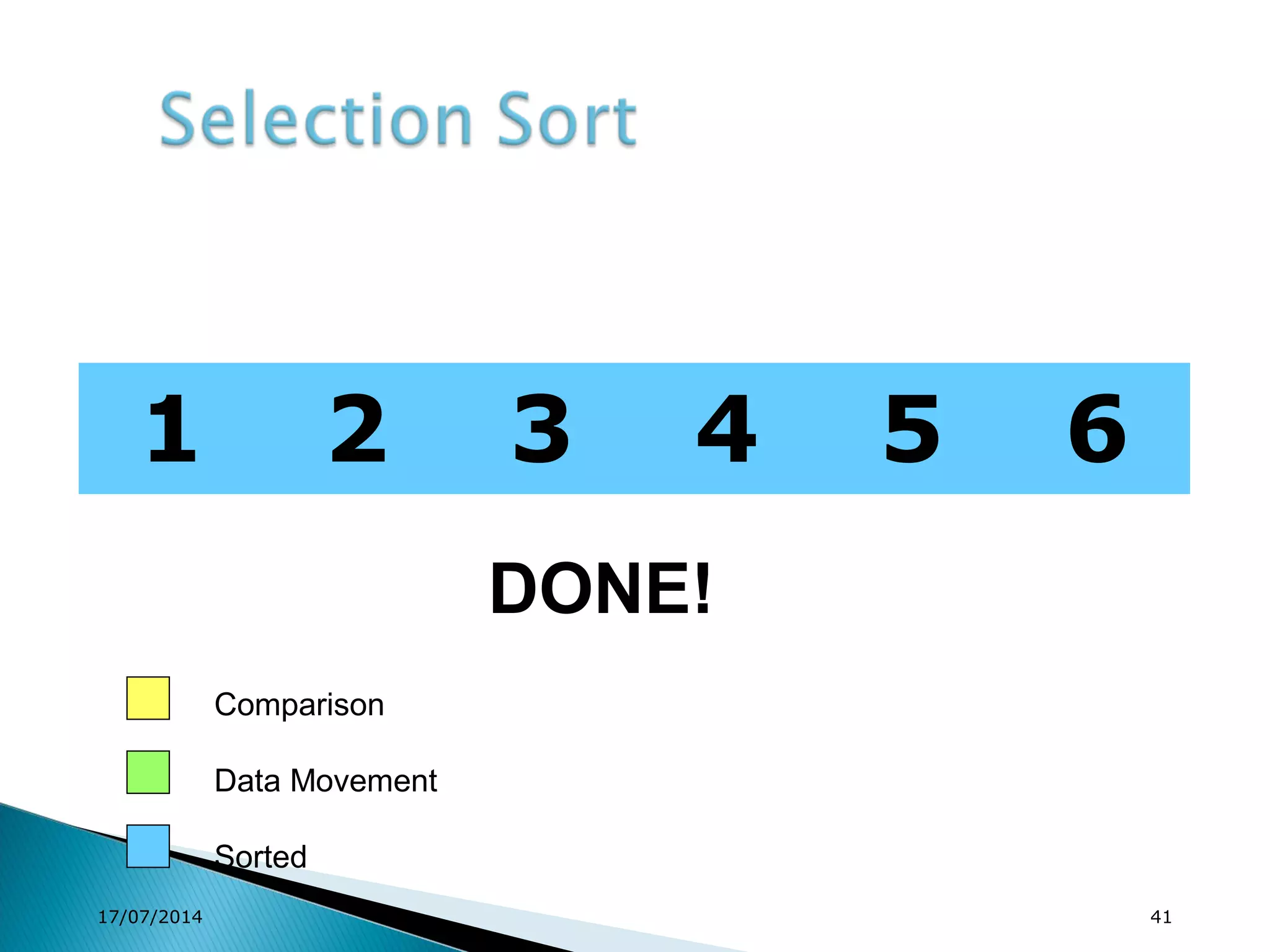
1. Brute force algorithms like selection sort and bubble sort are described. Radix sort, which sorts elements based on digit positions, is also introduced.
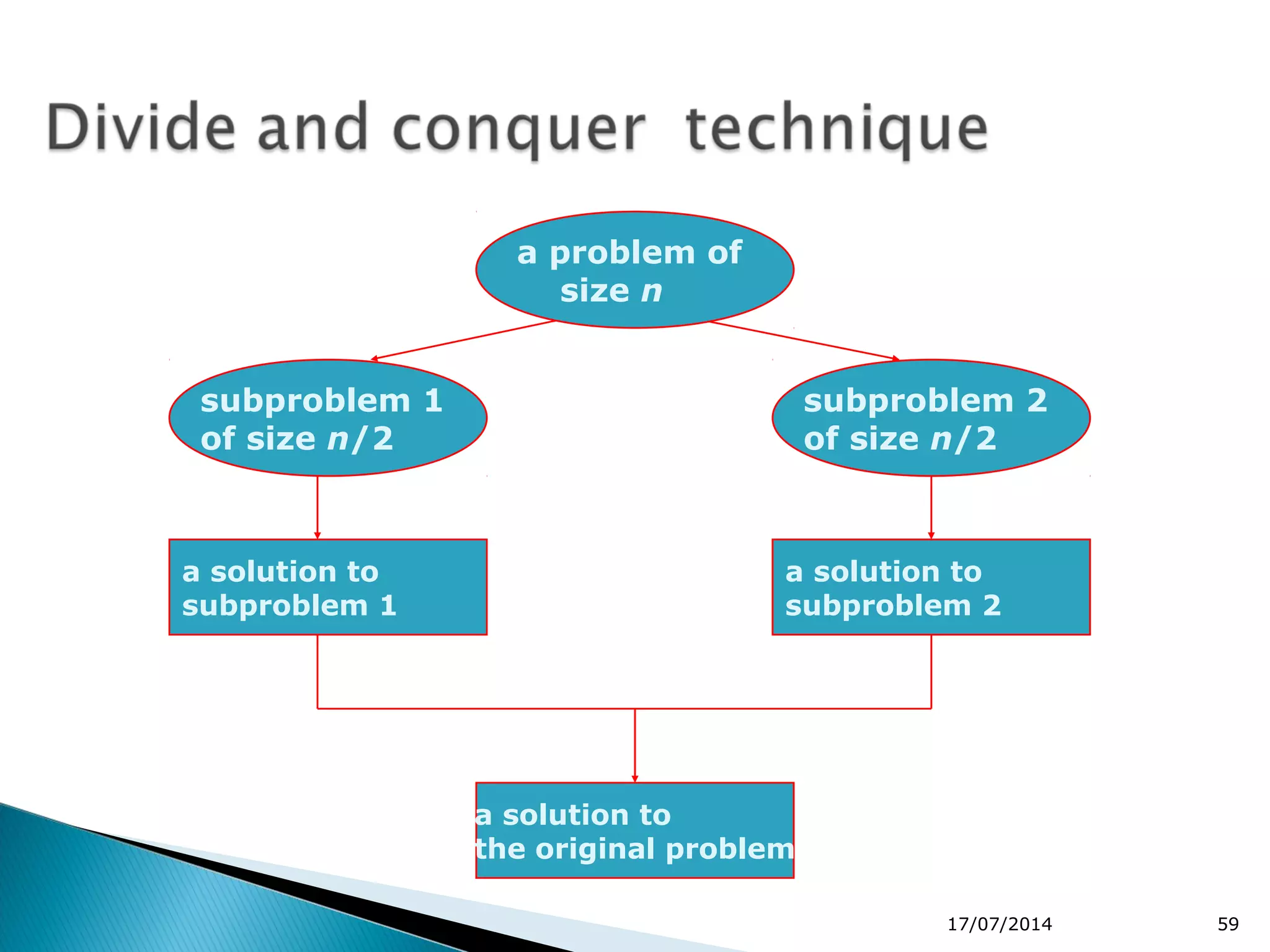
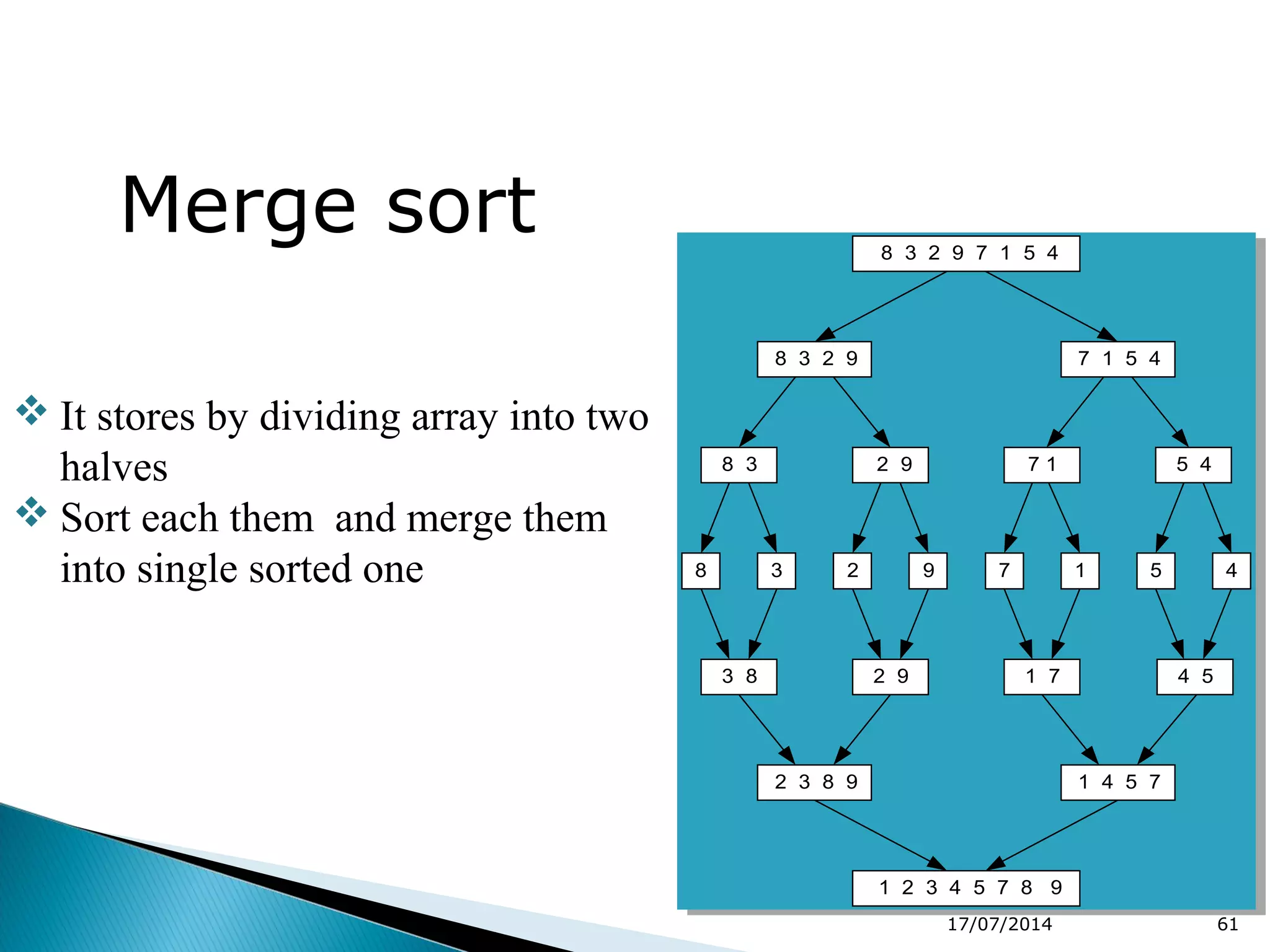
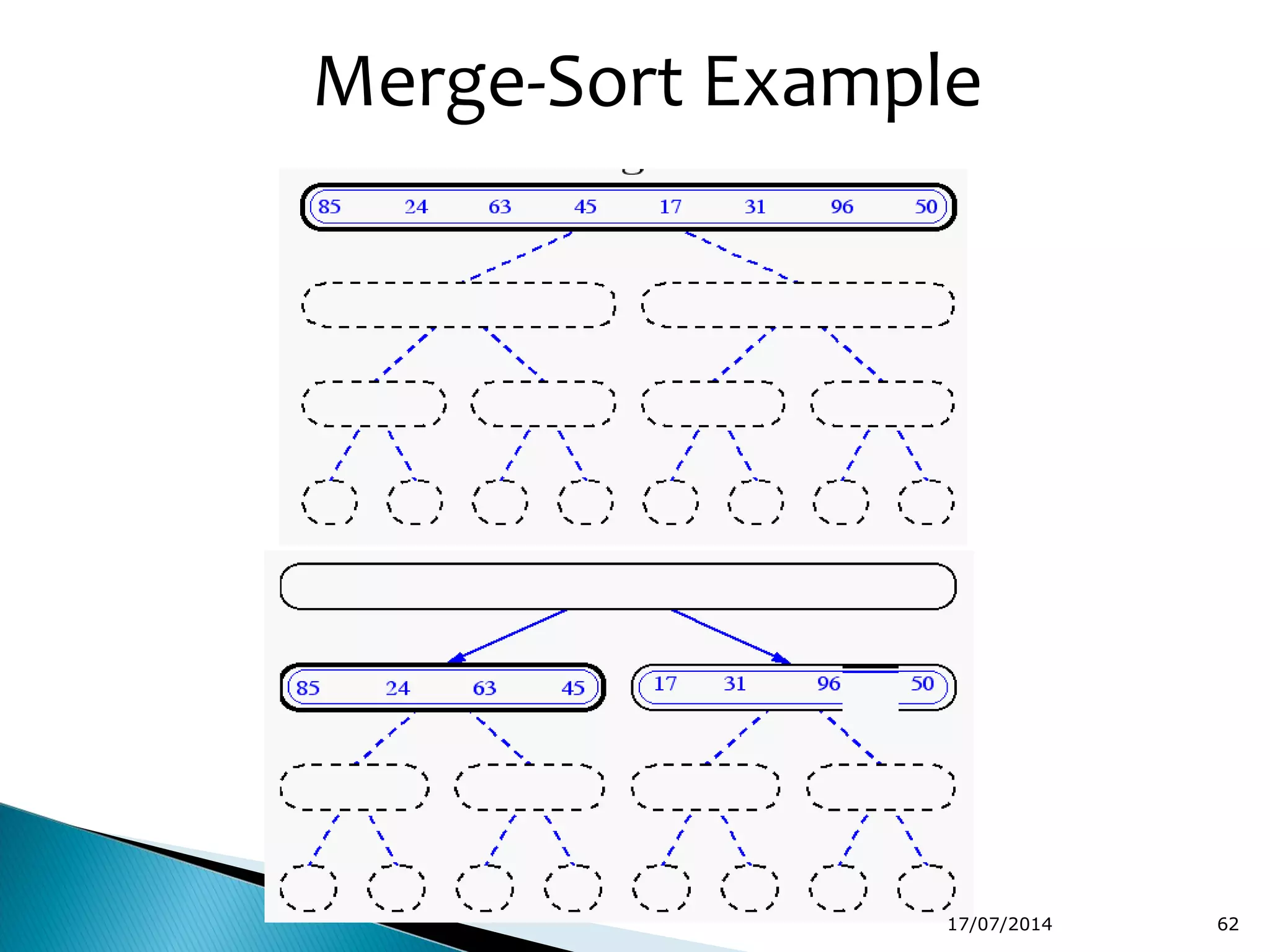
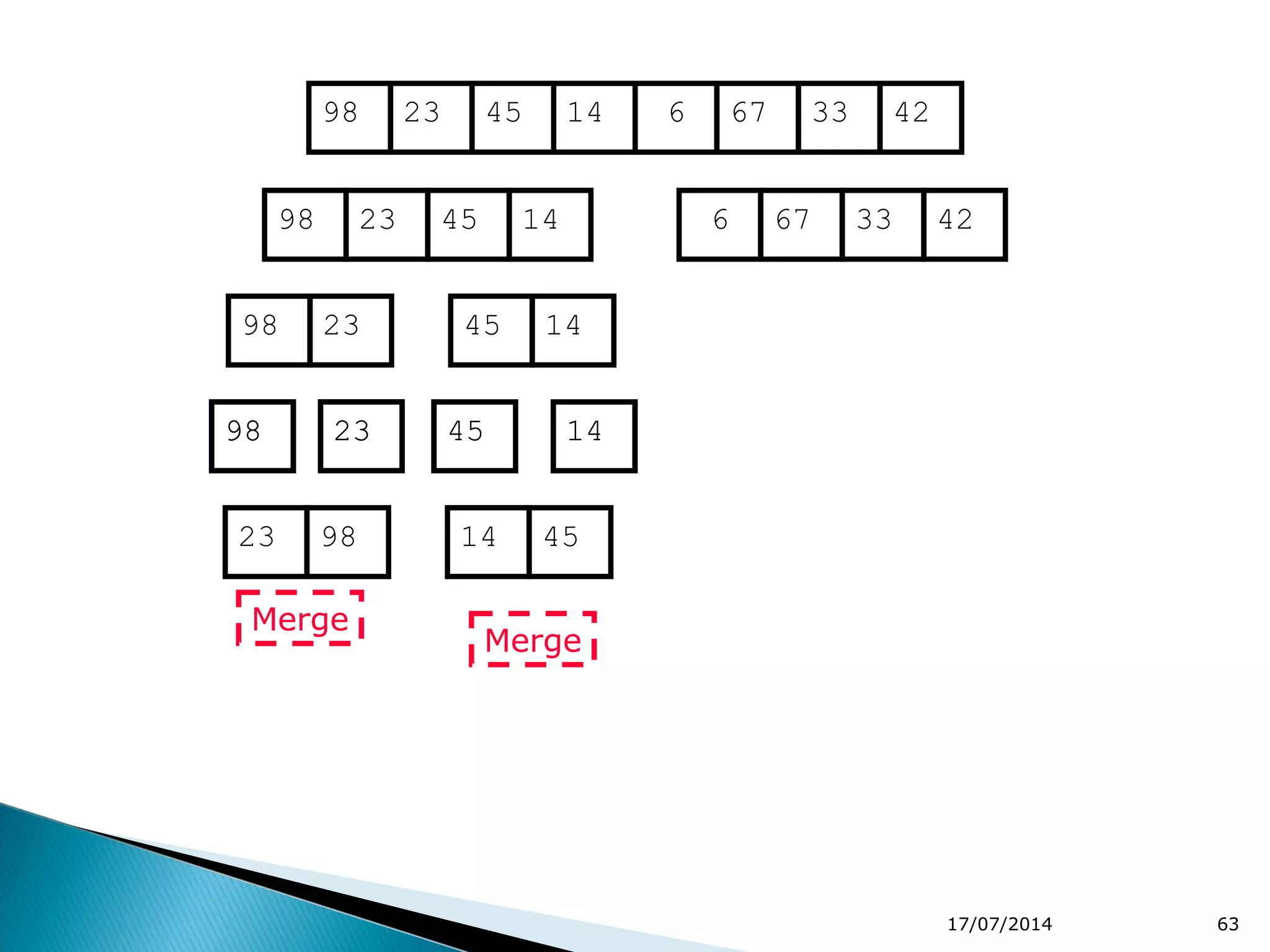
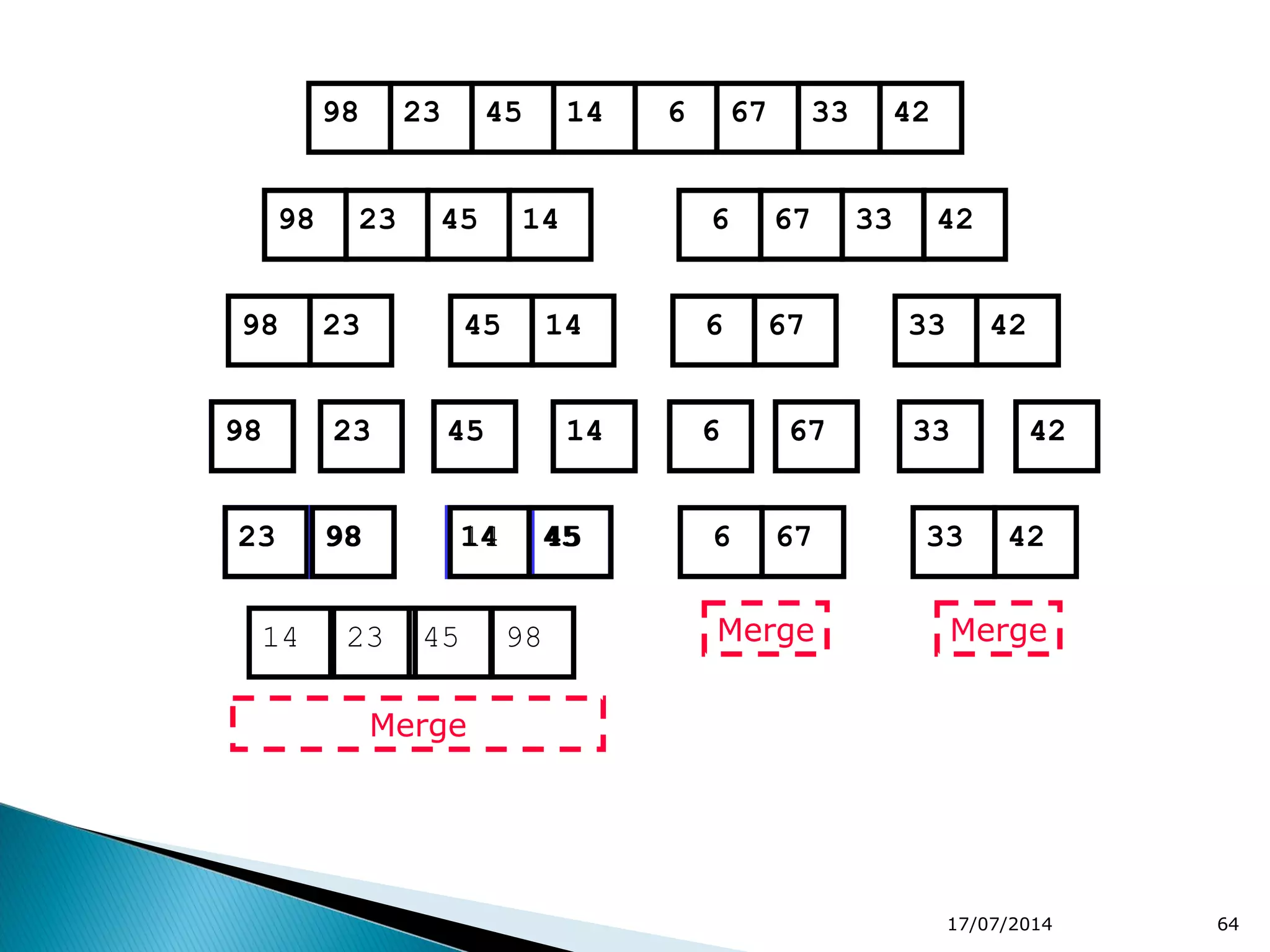
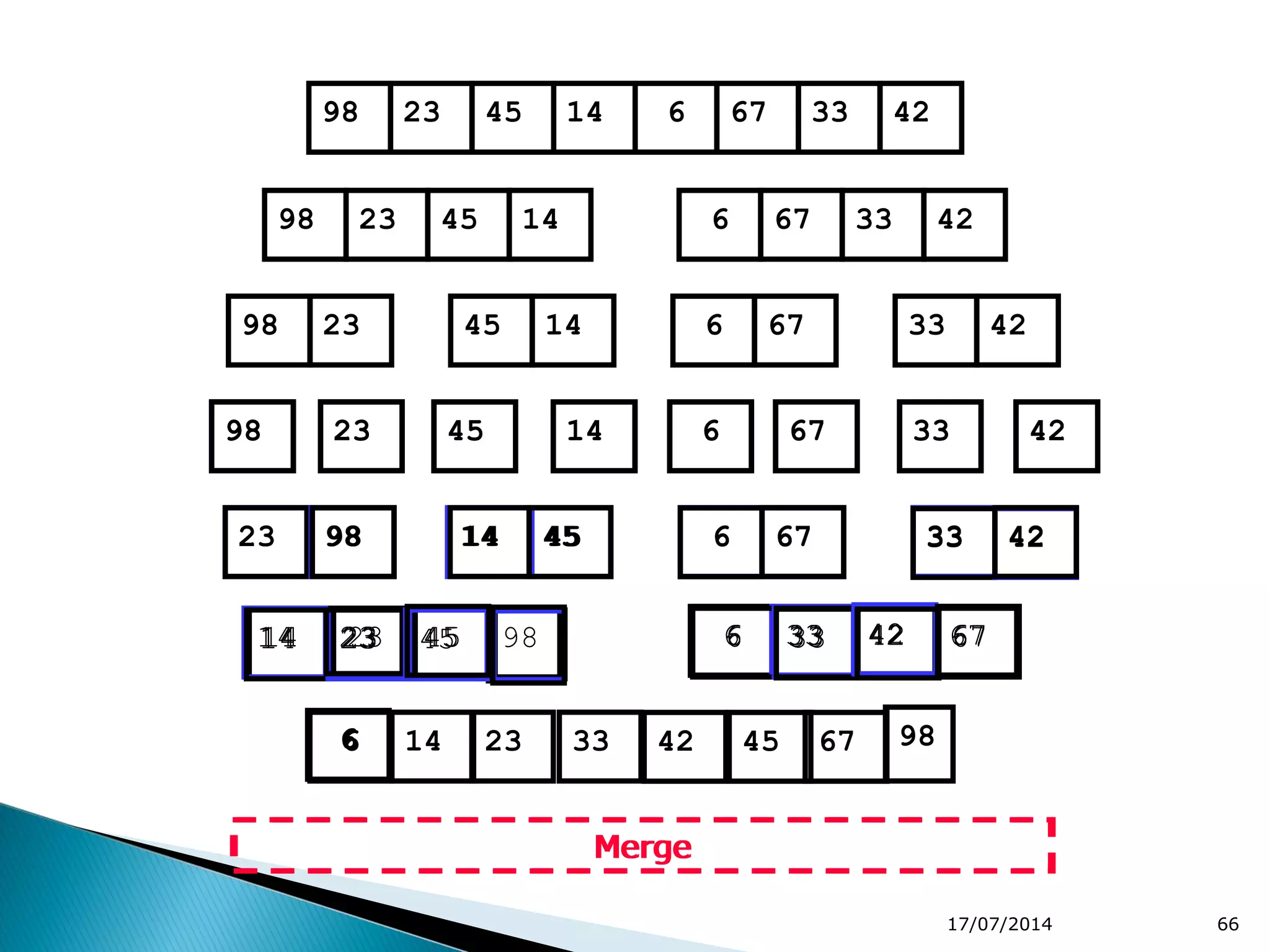
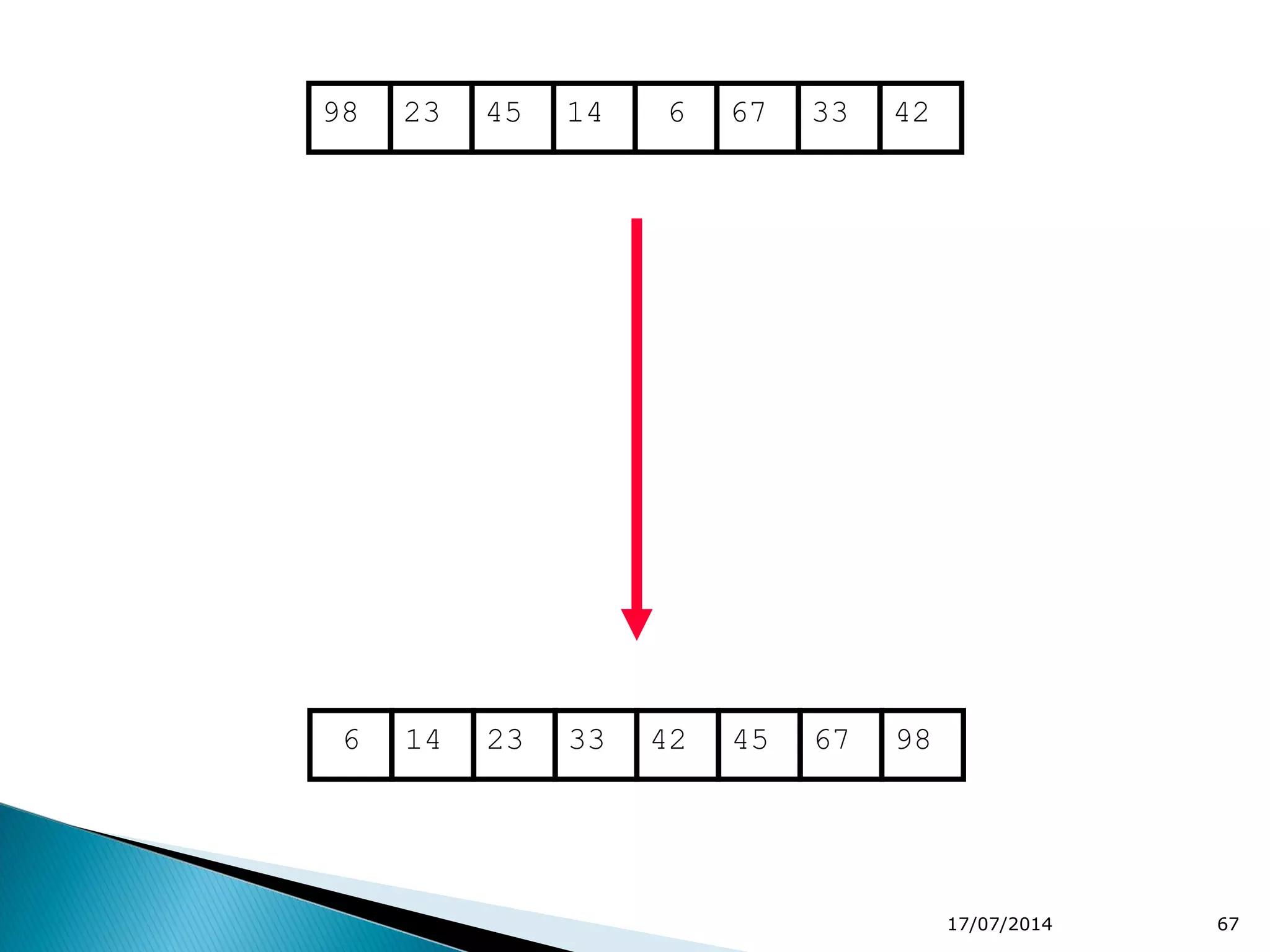
2. Divide and conquer algorithms like merge sort and quicksort are mentioned. Merge sort works by dividing the list into halves and then merging the sorted halves.
3. The document concludes by stating divide and conquer is a common algorithm design strategy that breaks problems into subproblems.































![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 73](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-73-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
17/07/2014 74](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-74-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
17/07/2014 75](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-75-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
17/07/2014 76](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-76-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
17/07/2014 77](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-77-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
17/07/2014 78](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-78-2048.jpg)
![40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
17/07/2014 79](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-79-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
17/07/2014 80](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-80-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 81](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-81-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 82](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-82-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 83](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-83-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 84](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-84-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 85](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-85-2048.jpg)
![40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
17/07/2014 86](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-86-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 87](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-87-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 88](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-88-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 89](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-89-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 90](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-90-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 91](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-91-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 92](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-92-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 93](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-93-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 94](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-94-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 95](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-95-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
5. Swap data[too_small_index] and data[pivot_index]
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 96](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-96-2048.jpg)
![1. While data[too_big_index] <= data[pivot]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]
4. While too_small_index > too_big_index, go to 1.
5. Swap data[too_small_index] and data[pivot_index]
7 20 10 30 40 50 60 80 100pivot_index = 4
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index
17/07/2014 97](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-97-2048.jpg)
![17/07/2014 98
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-98-2048.jpg)
![17/07/2014 99
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]](https://image.slidesharecdn.com/finalppt-140926092757-phpapp01/75/DESIGN-AND-ANALYSIS-OF-ALGORITHM-DAA-99-2048.jpg)

