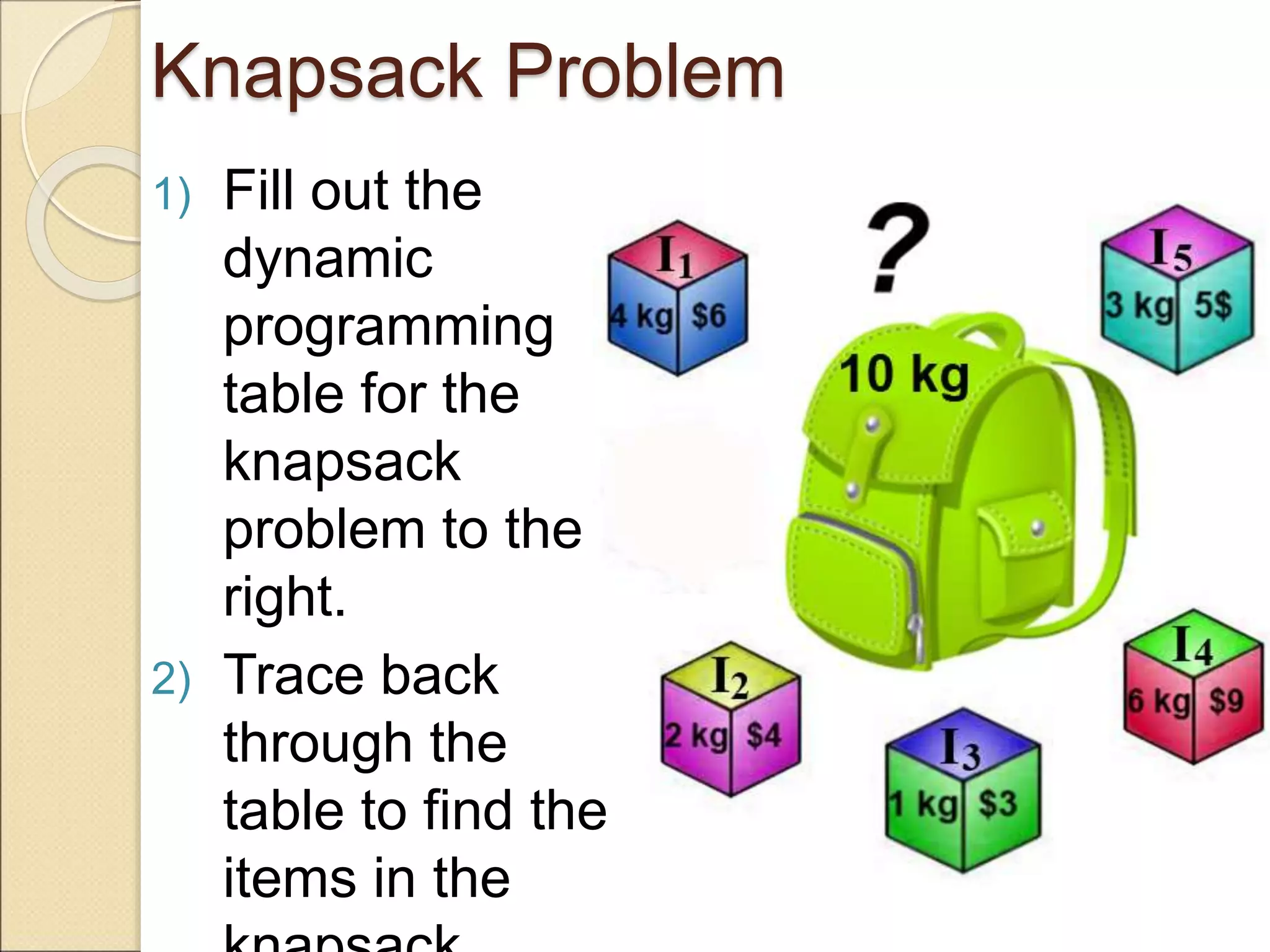
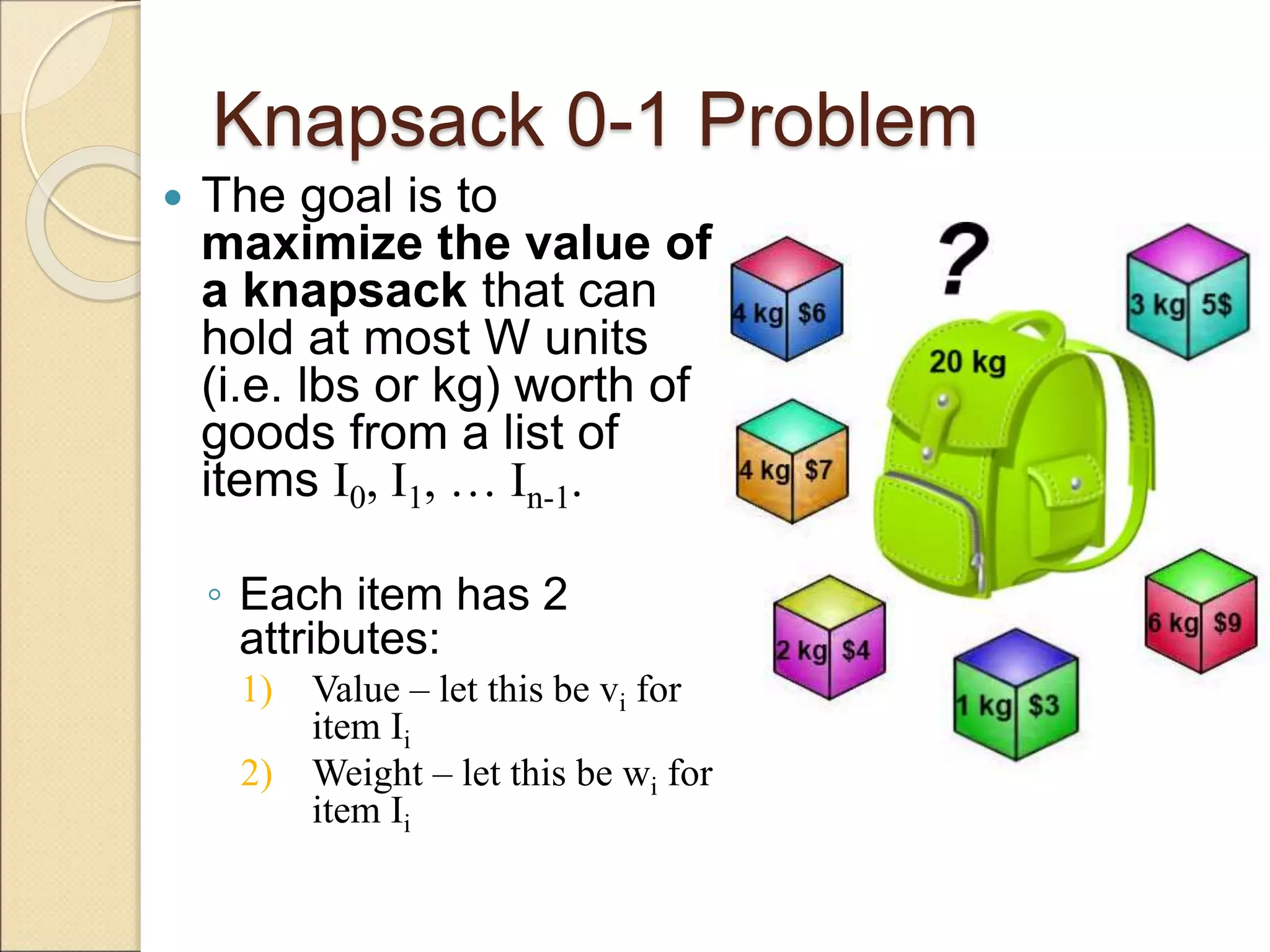
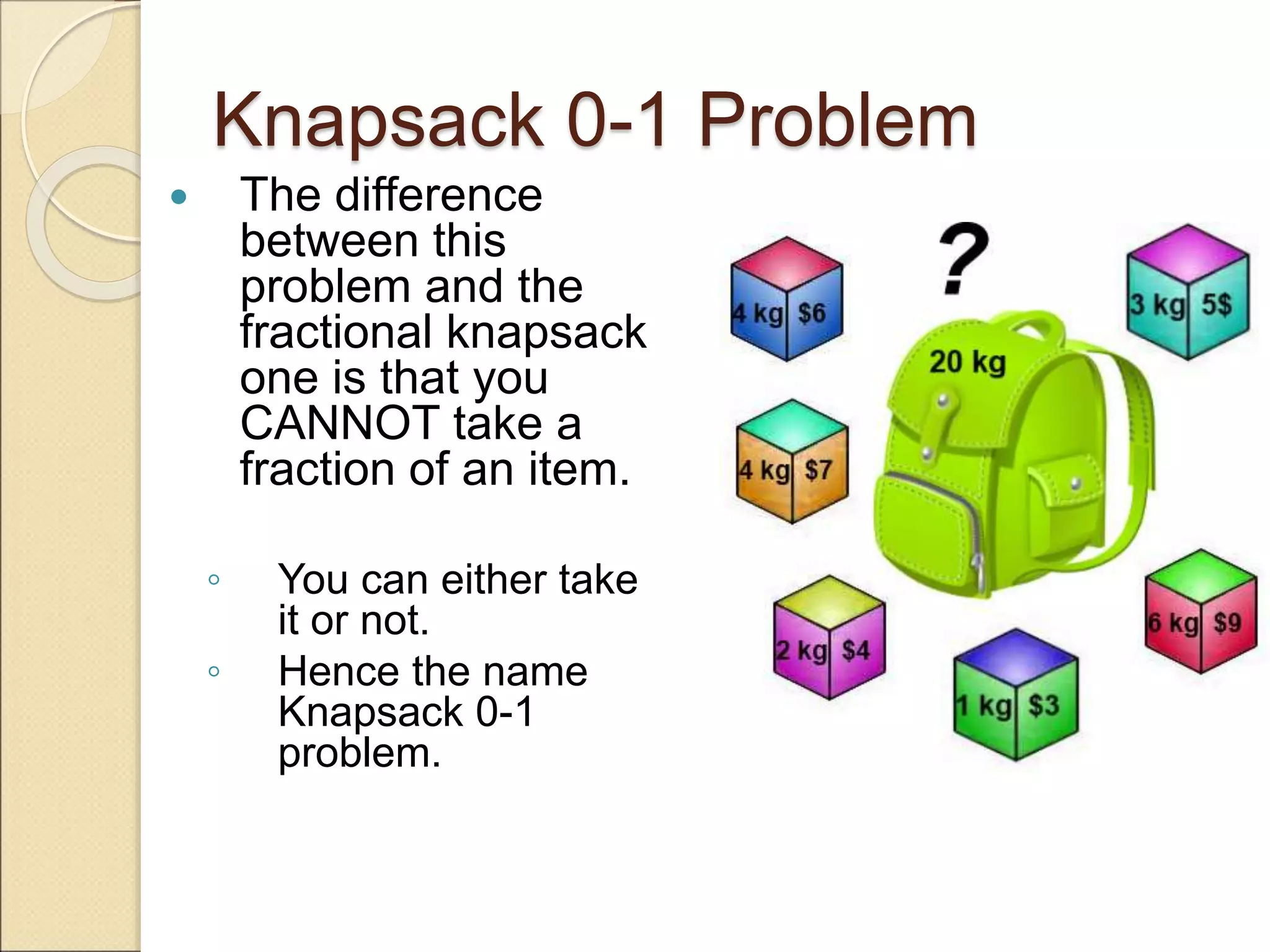
The document discusses the 0-1 knapsack problem and provides an example of solving it using dynamic programming. The 0-1 knapsack problem aims to maximize the total value of items selected from a list that have a total weight less than or equal to the knapsack's capacity, where each item must either be fully included or excluded. The document outlines a dynamic programming algorithm that builds a table to store the maximum value for each item subset at each possible weight, recursively considering whether or not to include each additional item.







![Knapsack 0-1 problem
So now we must re-work the way we build upon previous
sub-problems…
◦ Let B[k, w] represent the maximum total value of a subset Sk with
weight w.
◦ Our goal is to find B[n, W], where n is the total number of items
and W is the maximal weight the knapsack can carry.
So our recursive formula for subproblems:
B[k, w] = B[k - 1,w], if wk > w
= max { B[k - 1,w], B[k - 1,w - wk] + vk}, otherwise
In English, this means that the best subset of Sk that has
total weight w is:
1) The best subset of Sk-1 that has total weight w, or
2) The best subset of Sk-1 that has total weight w-wk plus the item k](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-10-2048.jpg)

![Knapsack 0-1 Algorithm
for w = 0 to W { // Initialize 1st row to 0’s
B[0,w] = 0
}
for i = 1 to n { // Initialize 1st column to 0’s
B[i,0] = 0
}
for i = 1 to n {
for w = 0 to W {
if wi <= w { //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
}
else B[i,w] = B[i-1,w] // wi > w
}
}](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-12-2048.jpg)

![Knapsack 0-1 Example
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0
2 0
3 0
4 0
// Initialize the base cases
for w = 0 to W
B[0,w] = 0
for i = 1 to n
B[i,0] = 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-14-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 1
vi = 3
wi = 2
w = 1
w-wi = -1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0
2 0
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-15-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 1
vi = 3
wi = 2
w = 2
w-wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-16-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 1
vi = 3
wi = 2
w = 3
w-wi = 1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3
2 0
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-17-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 1
vi = 3
wi = 2
w = 4
w-wi = 2
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3
2 0
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-18-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 1
vi = 3
wi = 2
w = 5
w-wi = 3
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-19-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 2
vi = 4
wi = 3
w = 1
w-wi = -2
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-20-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 2
vi = 4
wi = 3
w = 2
w-wi = -1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-21-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 2
vi = 4
wi = 3
w = 3
w-wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-22-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 2
vi = 4
wi = 3
w = 4
w-wi = 1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-23-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 2
vi = 4
wi = 3
w = 5
w-wi = 2
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0
4 0](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-24-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 3
vi = 5
wi = 4
w = 1..3
w-wi = -3..-1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-25-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 3
vi = 5
wi = 4
w = 4
w-wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-26-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 3
vi = 5
wi = 4
w = 5
w-wi = 1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-27-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 4
vi = 6
wi = 5
w = 1..4
w-wi = -4..-1
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-28-2048.jpg)
![Knapsack 0-1 Example
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w
i = 4
vi = 6
wi = 5
w = 5
w-wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
if wi <= w //item i can be in the solution
if vi + B[i-1,w-wi] > B[i-1,w]
B[i,w] = vi + B[i-1,w- wi]
else
B[i,w] = B[i-1,w]
else B[i,w] = B[i-1,w] // wi > w](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-29-2048.jpg)

![Knapsack 0-1 Algorithm
This algorithm only finds the max
possible value that can be carried in
the knapsack
◦ The value in B[n,W]
To know the items that make this
maximum value, we need to trace
back through the table.](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-31-2048.jpg)
![Knapsack 0-1 Algorithm
Finding the Items
Let i = n and k = W
if B[i, k] ≠ B[i-1, k] then
mark the ith item as in the knapsack
i = i-1, k = k-wi
else
i = i-1 // Assume the ith item is not in the knapsack
// Could it be in the optimally packed knapsack?](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-32-2048.jpg)
![Knapsack 0-1
Algorithm
Finding the Items
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i = 4
k = 5
vi = 6
wi = 5
B[i,k] = 7
B[i-1,k] = 7
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
i = n , k = W
while i, k > 0
if B[i, k] ≠ B[i-1, k] then
mark the ith item as in the knapsack
i = i-1, k = k-wi
else
i = i-1
Knapsac
k:](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-33-2048.jpg)
![Knapsack 0-1
Algorithm
Finding the Items
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i = 3
k = 5
vi = 5
wi = 4
B[i,k] = 7
B[i-1,k] = 7
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
i = n , k = W
while i, k > 0
if B[i, k] ≠ B[i-1, k] then
mark the ith item as in the knapsack
i = i-1, k = k-wi
else
i = i-1
Knapsac
k:](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-34-2048.jpg)
![Knapsack 0-1
Algorithm
Finding the Items
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i = 2
k = 5
vi = 4
wi = 3
B[i,k] = 7
B[i-1,k] = 3
k – wi = 2
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
i = n , k = W
while i, k > 0
if B[i, k] ≠ B[i-1, k] then
mark the ith item as in the knapsack
i = i-1, k = k-wi
else
i = i-1
Knapsac
k:
Item 2](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-35-2048.jpg)
![Knapsack 0-1
Algorithm
Finding the Items
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i = 1
k = 2
vi = 3
wi = 2
B[i,k] = 3
B[i-1,k] = 0
k – wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
i = n , k = W
while i, k > 0
if B[i, k] ≠ B[i-1, k] then
mark the ith item as in the knapsack
i = i-1, k = k-wi
else
i = i-1
Knapsac
k:
Item 1
Item 2](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-36-2048.jpg)
![Knapsack 0-1
Algorithm
Finding the Items
Items:
1:
(2,3
)
2:
(3,4
)
3:
(4,5
)
4:
(5,6
)
i = 1
k = 2
vi = 3
wi = 2
B[i,k] = 3
B[i-1,k] = 0
k – wi = 0
i / w 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
k = 0, so we’re DONE!
The optimal knapsack should contain:
Item 1 and Item 2
Knapsac
k:
Item 1
Item 2](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-37-2048.jpg)
![Knapsack 0-1 Problem – Run
Time
for w = 0 to W
B[0,w] = 0
for i = 1 to n
B[i,0] = 0
for i = 1 to n
for w = 0 to W
< the rest of the code >
What is the running time of this algorithm?
O(n*W)
Remember that the brute-force algorithm takes: O(2n)
O(W)
O(W)
Repeat n times
O(n)](https://image.slidesharecdn.com/dynprogknapsack-220907141709-795118bf/75/DynProg_Knapsack-ppt-38-2048.jpg)