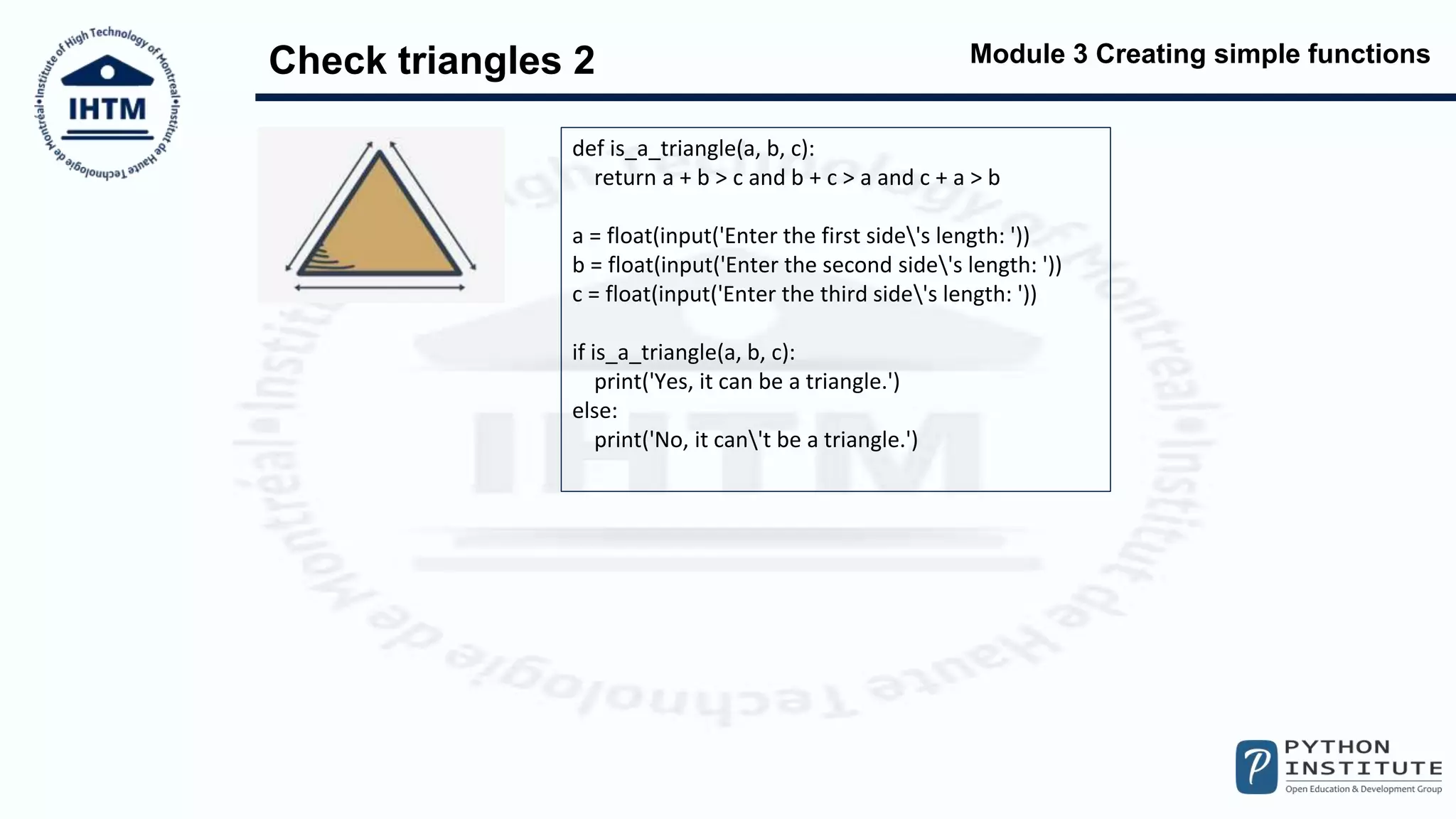
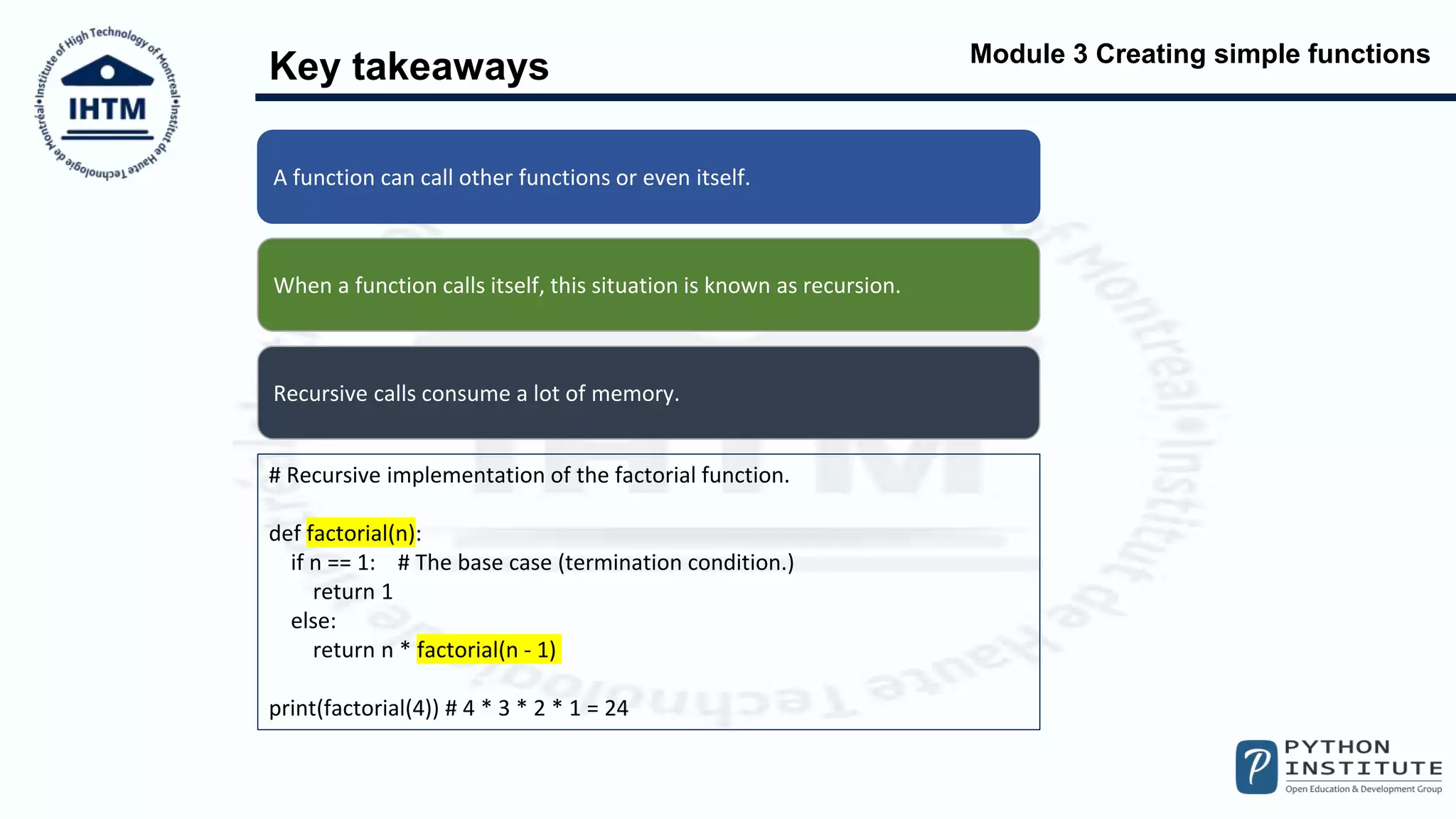
The document discusses creating simple functions in Python. It provides examples of functions to calculate BMI, convert between units of measurement, check properties of triangles, calculate factorials and Fibonacci numbers, and evaluate triangles using Heron's formula. Recursive functions are also demonstrated, including a recursive implementation of the factorial function. Key takeaways are that functions can call other functions or themselves recursively, but recursive calls consume significant memory.