Sorting

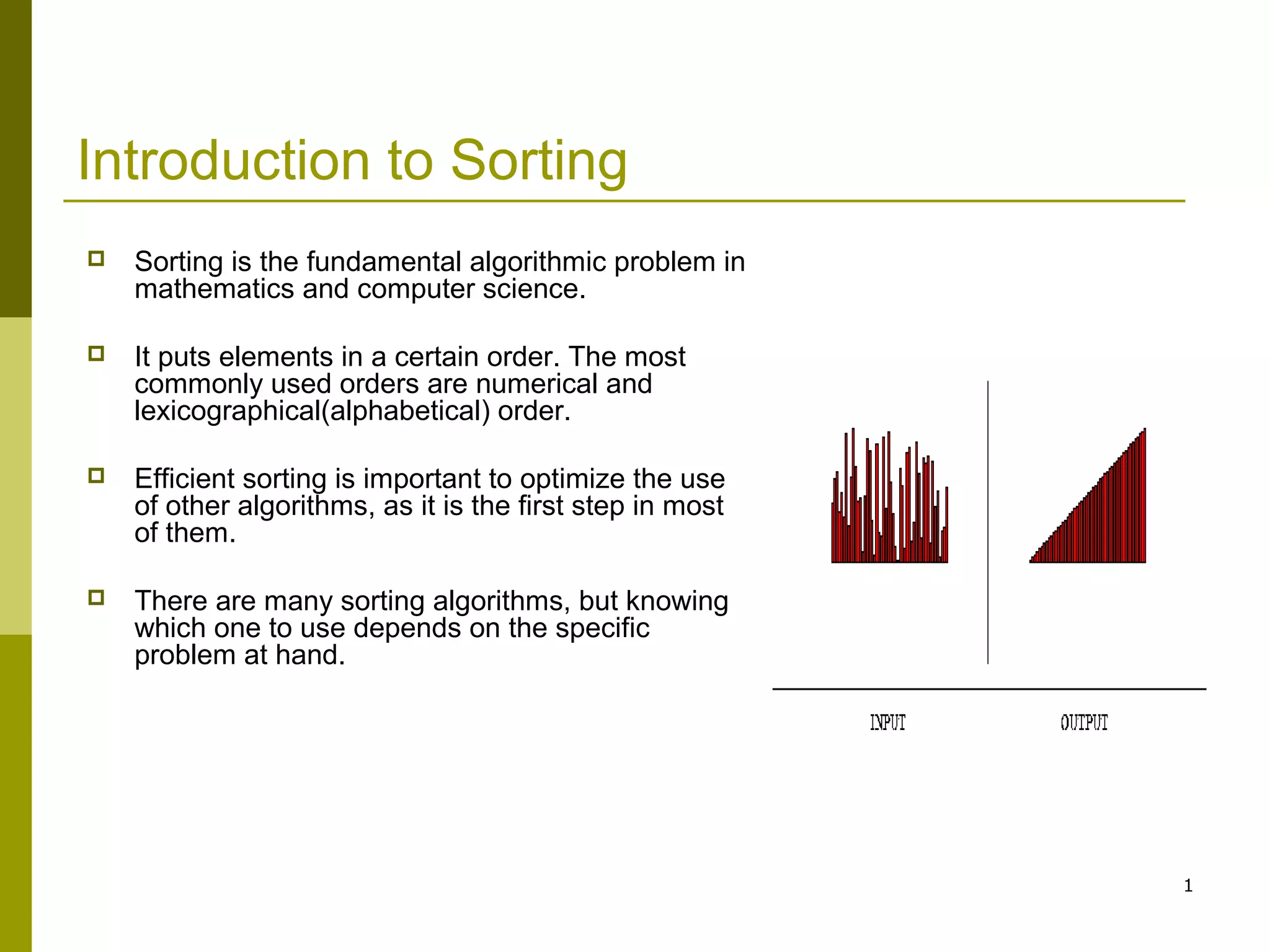
1
Introduction to Sorting
 Sorting is the fundamental algorithmic problem in
mathematics and computer science.
 It puts elements in a certain order. The most
commonly used orders are numerical and
lexicographical(alphabetical) order.
 Efficient sorting is important to optimize the use
of other algorithms, as it is the first step in most
of them.
 There are many sorting algorithms, but knowing
which one to use depends on the specific
problem at hand.

2
Classification of Sorting algorithms
Sorting algorithms are often classified using different metrics:
 Computational complexity: classification is based on worst, average and best
behavior of sorting a list of size (n).
 For typical sorting algorithms acceptable/good behavior is O(n log n) and
unacceptable/bad behavior is Ω(n^2).
 Ideal behavior for a sort is O(n).
 Memory usage (and use of other computer resources):
 Some sorting algorithms are “in place", such that only O(1) or O(log n) memory is
needed beyond the items being sorted.
 Others need to create auxiliary data structures for data to be temporarily stored.
We’ve seen in class that mergesort needs more memory resources as it is not an
“in place” algorithm, while quicksort and heapsort are “in place”. Radix and
bucket sorts are not “in place”.
 Recursion: some algorithms are either recursive or non-recursive.(e.g., mergesort is
recursive).
 Stability: stable sorting algorithms maintain the relative order of elements/records
with equal keys/values. Radix and bucket sorts are stable.
 General method: classification is based on how sort functions internally.
 Methods used internally include insertion, exchange, selection, merging,
distribution etc. Bubble sort and quicksort are exchange sorts. Heapsort is a
selection sort.

3
Classification of Sorting algorithms…contd
 Comparison sorts: A comparison sort examines elements with a comparison
operator, which usually is the less than or equal to operator(≤). Comparison sorts
include:
 Bubble sort
 Insertion sort
 Selection sort
 Shell sort
 Heapsort
 Mergesort
 Quicksort.
 Non-Comparison sorts: these use other techniques to sort data, rather than using
comparison operations. These include:
 Radix sort (examines individual bits of keys)
 Bucket sort (examines bits of keys)
 Counting sort (indexes using key values)

5
Divide and Conquer
1.Base Case, solve the problem
directly if it is small enough
2.Divide the problem into two or
more similar and smaller
subproblems
3.Recursively solve the subproblems
4.Combine solutions to the
subproblems

Quick sort
 A key step in the Quicksort algorithm is
partitioning the array
 We choose some (any) number p in the
array to use as a pivot
 We partition the array into three parts:
p
numbers
less than
p
numbers greater
than or equal to
p
p

Quick Sort(Partitioning )
 Choose an array value (say, the first) to
use as the pivot
 Starting from the left end, find the first
element that is greater than or equal to
the pivot
 Searching backward from the right end,
find the first element that is less than
the pivot
 Interchange (swap) these two elements
 Repeat, searching from where we left
off, until done

Example of partitioning
 choose pivot: 4 3 6 9 2 4 3 1 2 1 8 9 3 5 6
 search: 4 3 6 9 2 4 3 1 2 1 8 9 3 5 6
 swap: 4 3 3 9 2 4 3 1 2 1 8 9 6 5 6
 search: 4 3 3 9 2 4 3 1 2 1 8 9 6 5 6
 swap: 4 3 3 1 2 4 3 1 2 9 8 9 6 5 6
 search: 4 3 3 1 2 4 3 1 2 9 8 9 6 5 6
 swap: 4 3 3 1 2 2 3 1 4 9 8 9 6 5 6
 search: 4 3 3 1 2 2 3 1 4 9 8 9 6 5 6
(left > right)
 swap with pivot:1 3 3 1 2 2 3 4 4 9 8 9 6 5 6

Quick sort
 To sort a[left...right]:
1. if left < right:
1.1. Partition a[left...right] such that:
all a[left...p-1] are less than a[p], and
all a[p+1...right] are >= a[p]
1.2. Quicksort a[left...p-1]
1.3. Quicksort a[p+1...right]
2. Terminate

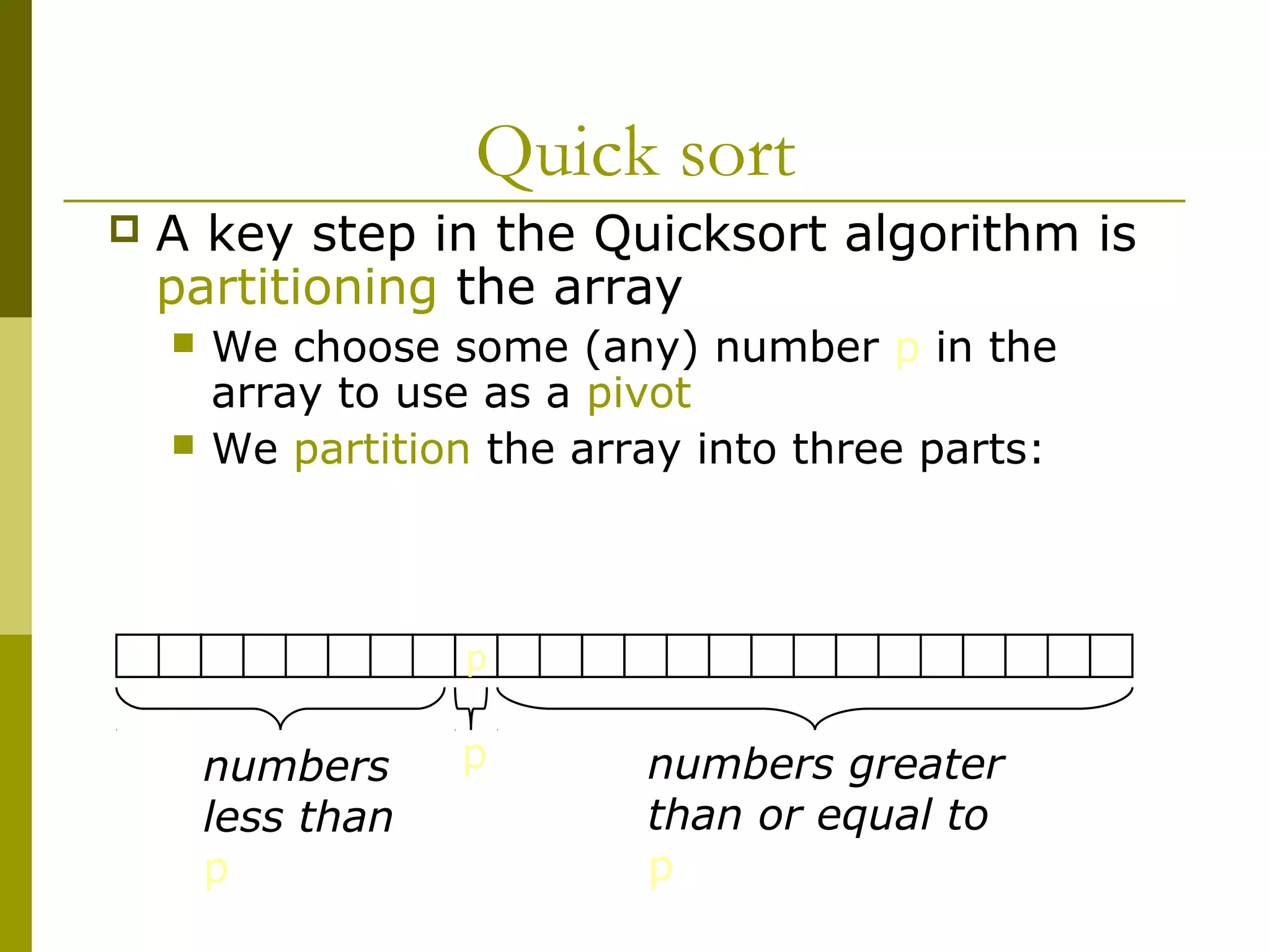
Partitioning
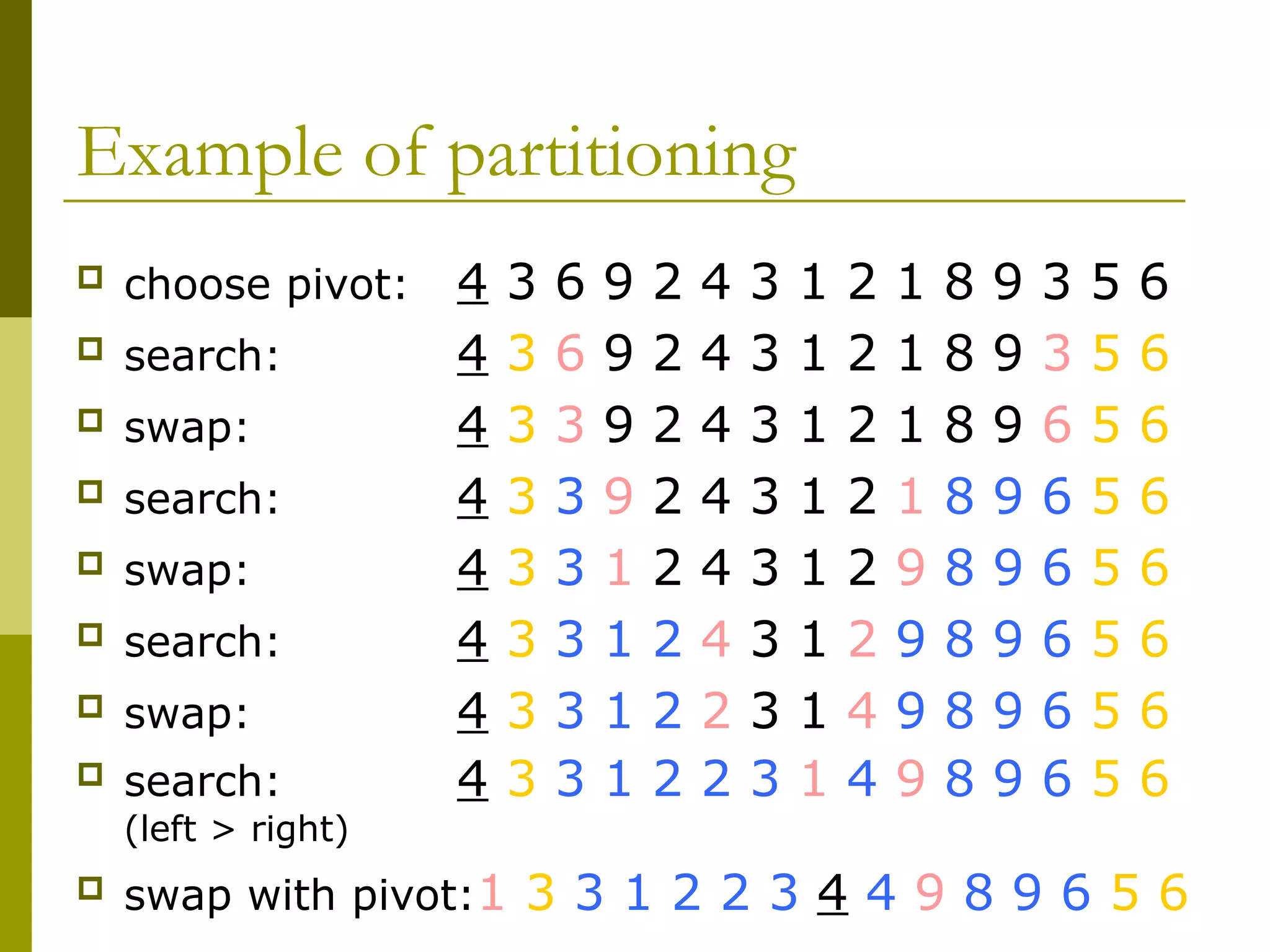
 To partition a[left...right]:
1. Set p = a[left], l = left + 1, r = right;
2. while l < r, do
2.1. while l < right && a[l] < p { l = l + 1 }
2.2. while r > left && a[r] >= p { r = r – 1}
2.3. if l < r { swap a[l] and a[r] }
3. a[left] = a[r]; a[r] = p;
4. Terminate

12
Merge Sort: Idea
Merge
Recursively
sort
Divide into
two halves
FirstPart SecondPart
FirstPart SecondPart
A
A is sorted!

13
A[middle]A[middle]A[left]A[left]
SortedSorted
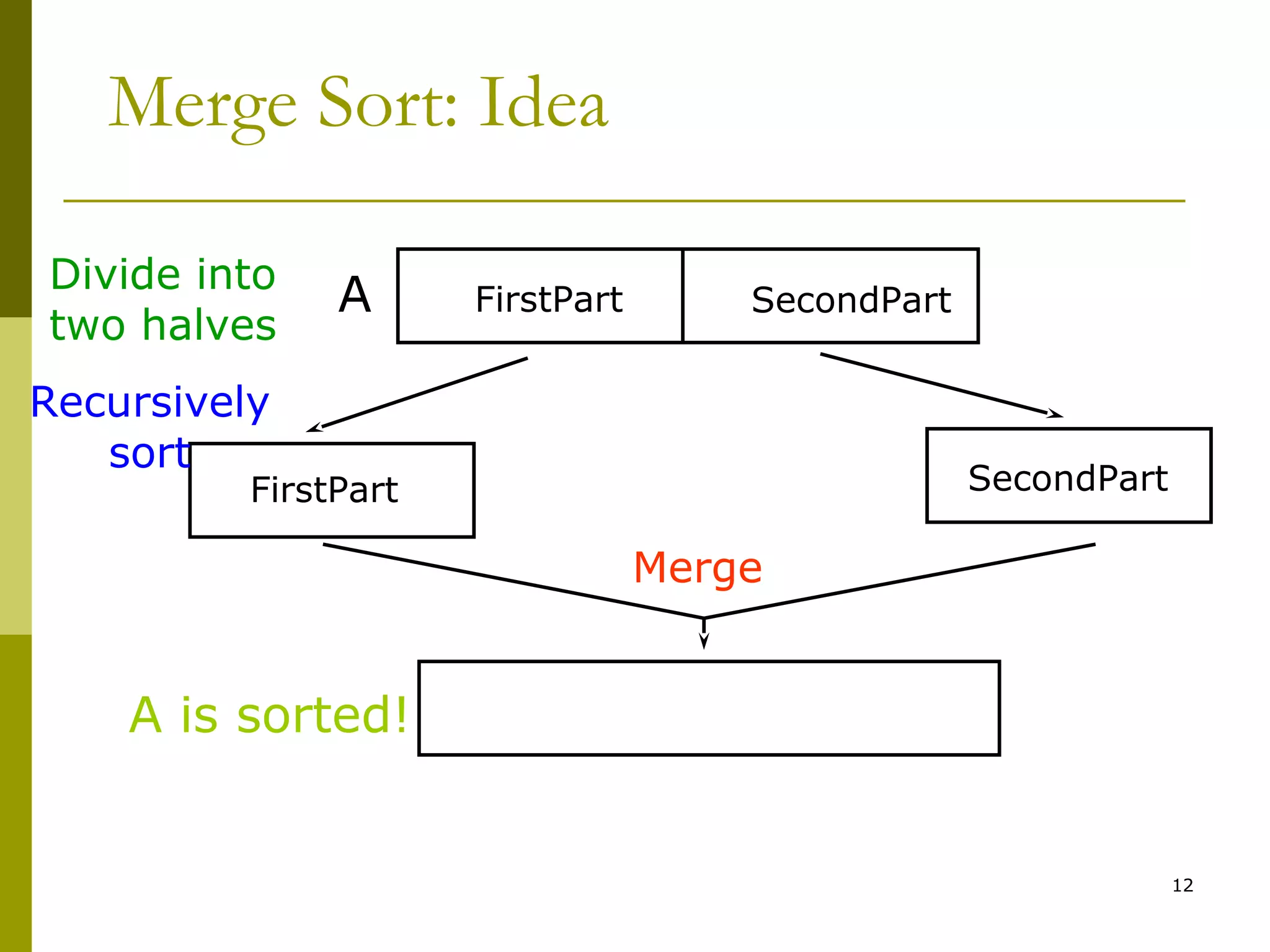
FirstPartFirstPart
SortedSorted
SecondPartSecondPart
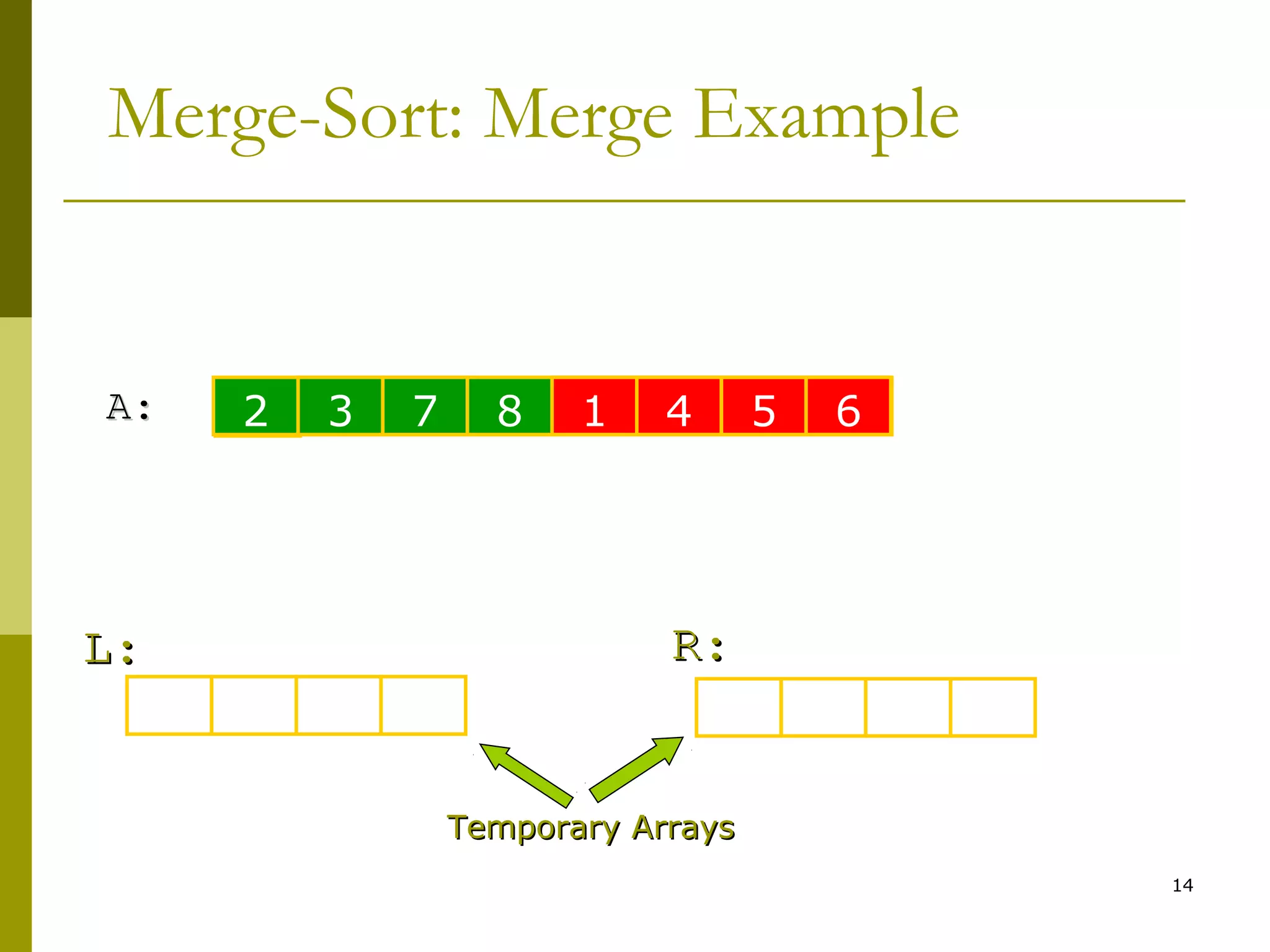
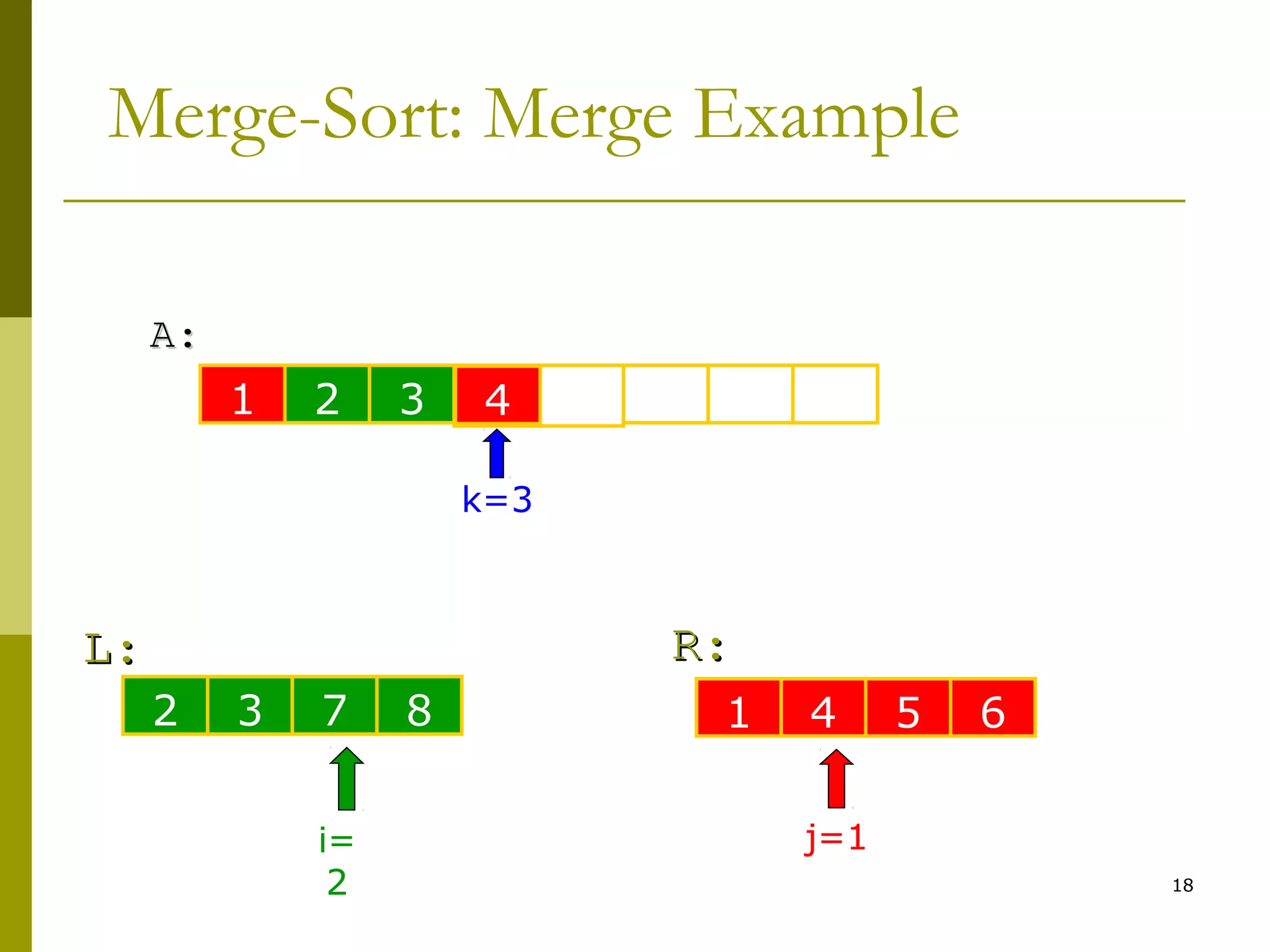
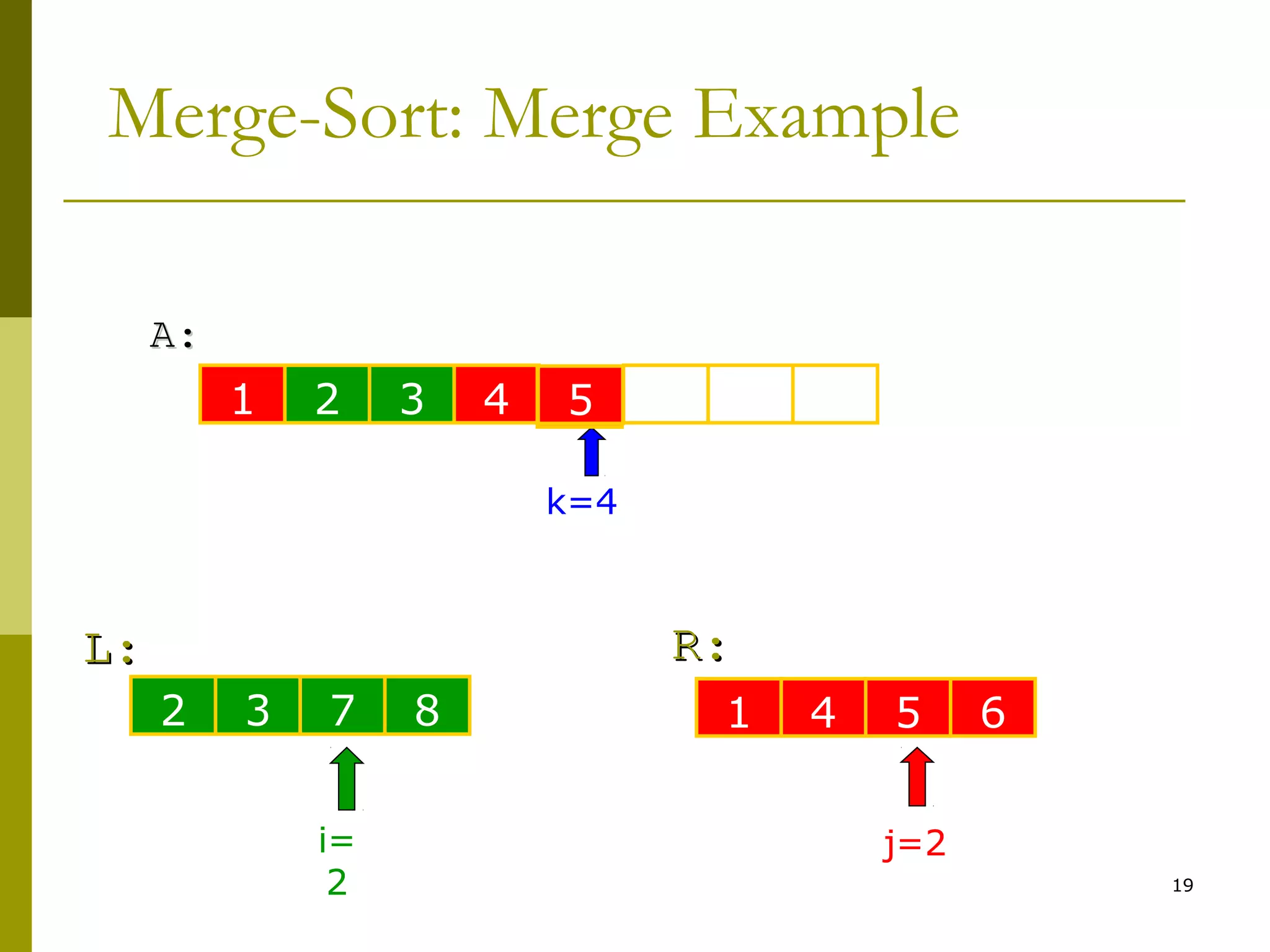
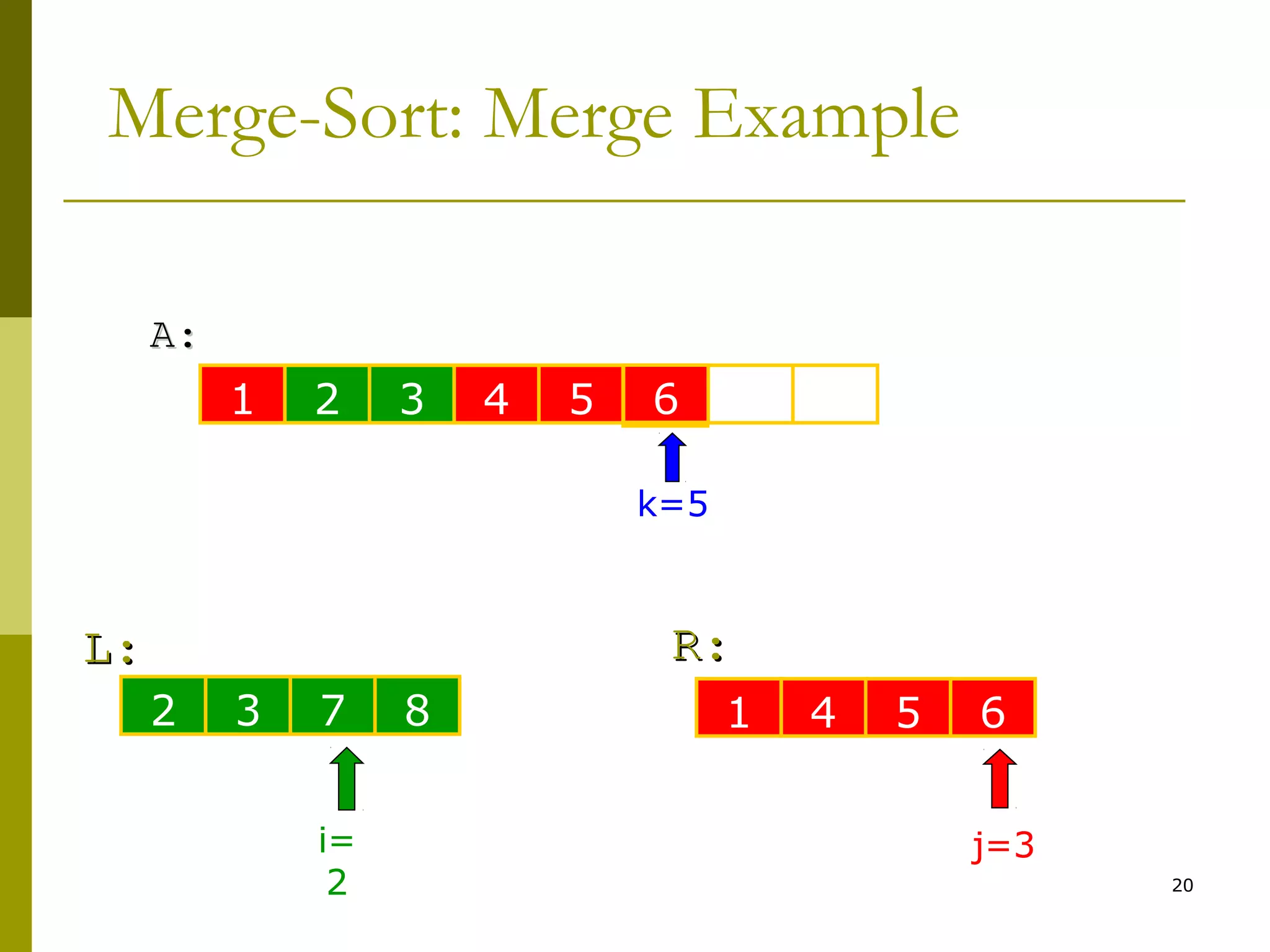
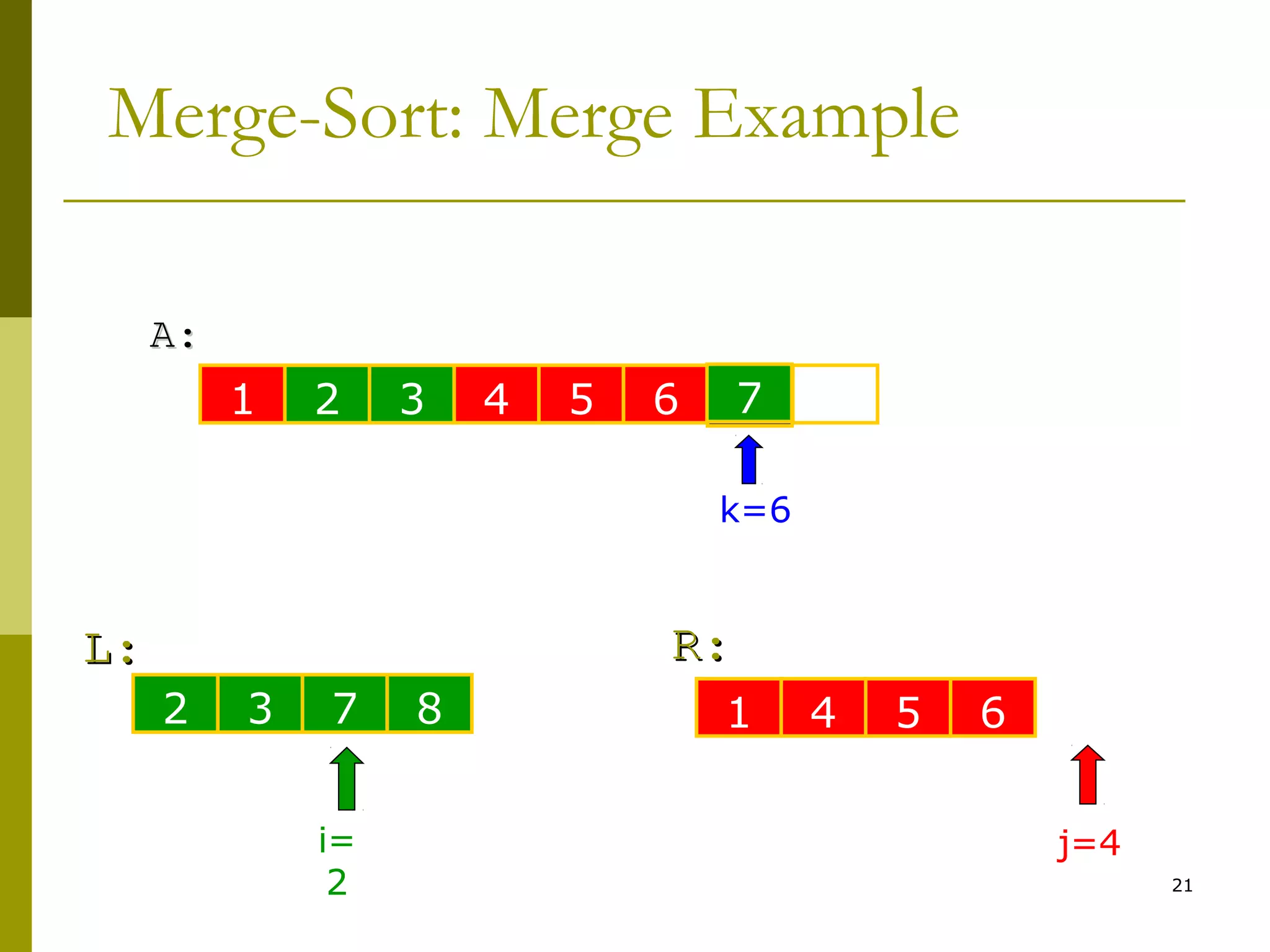
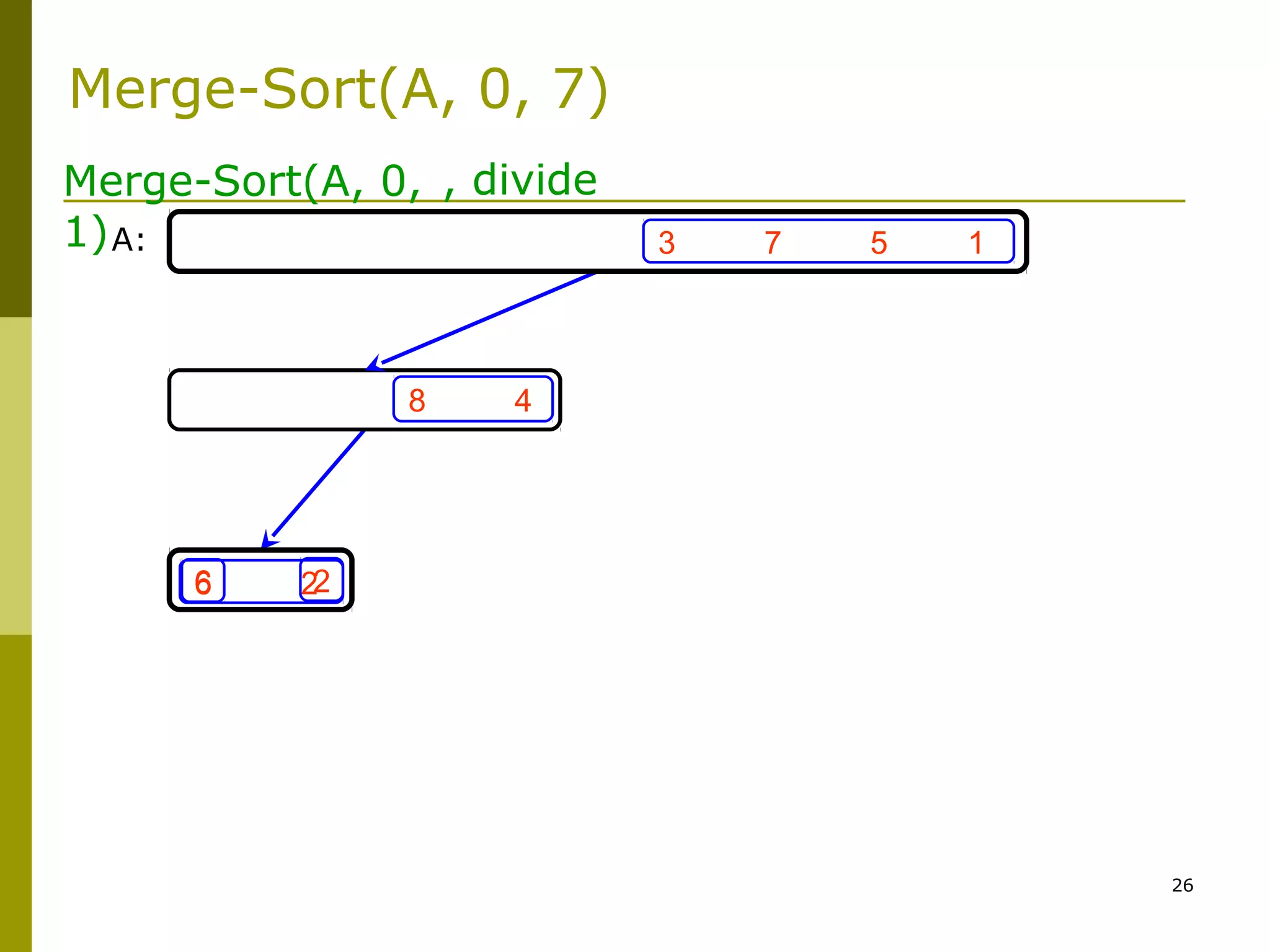
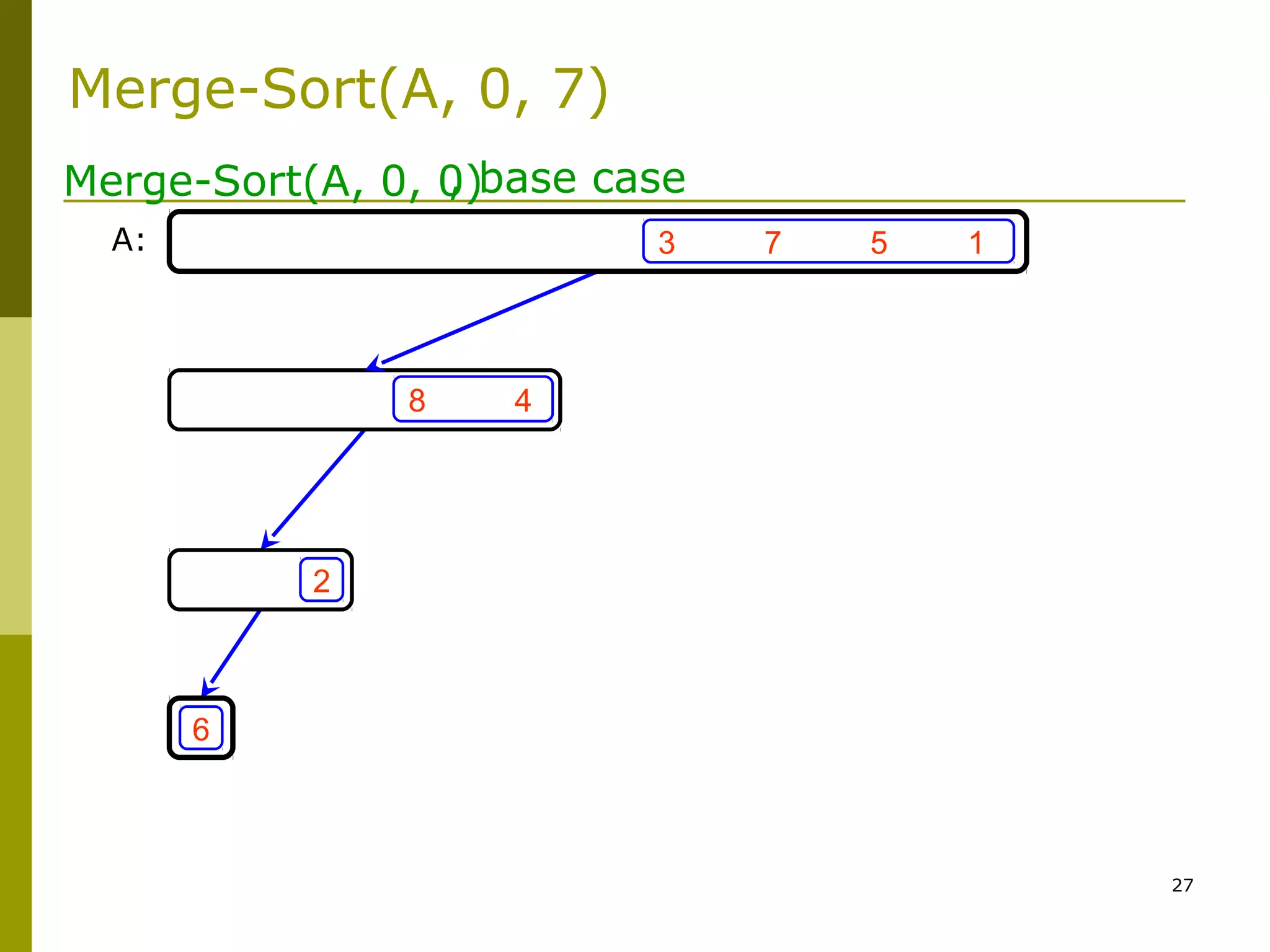
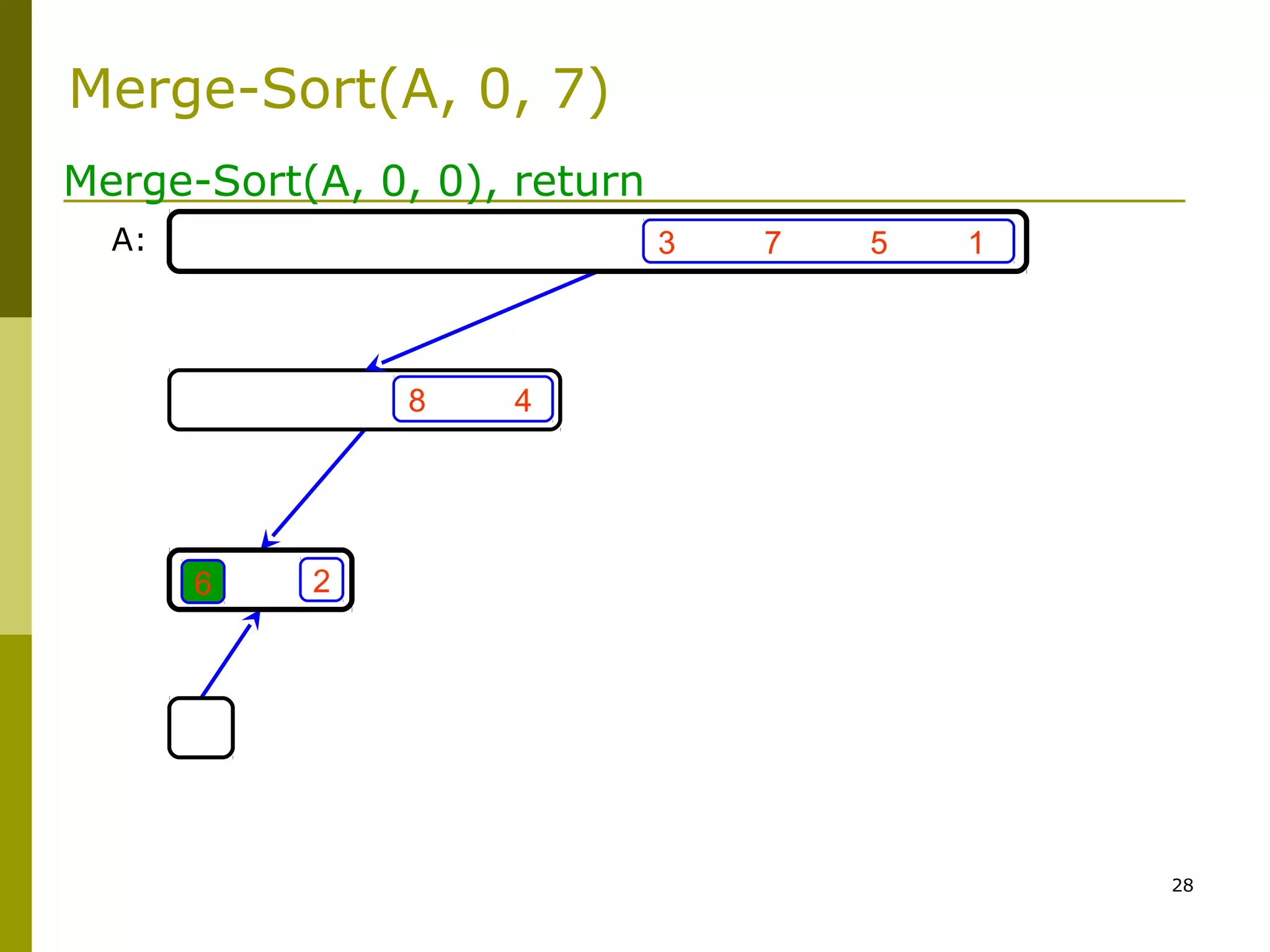
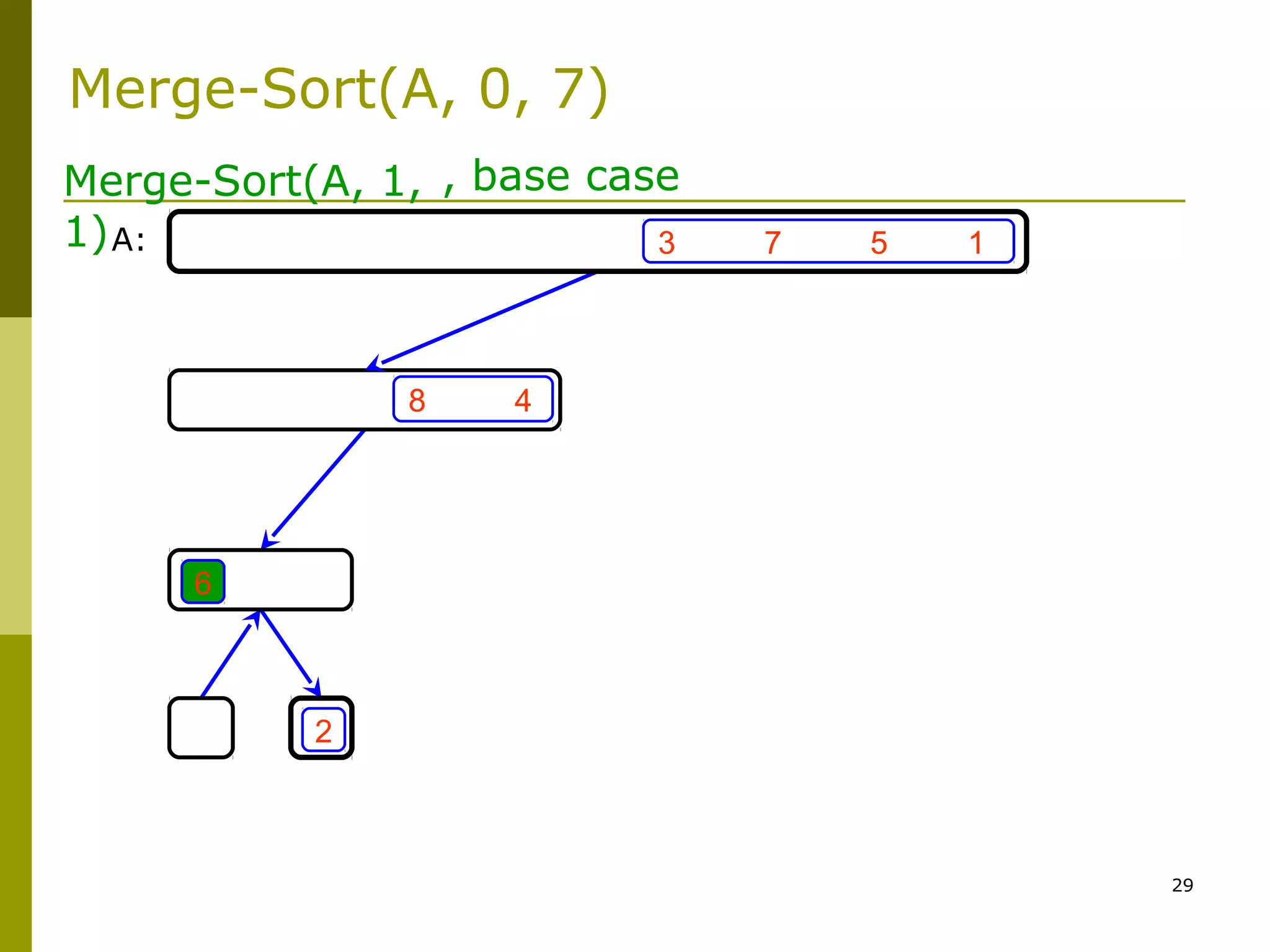
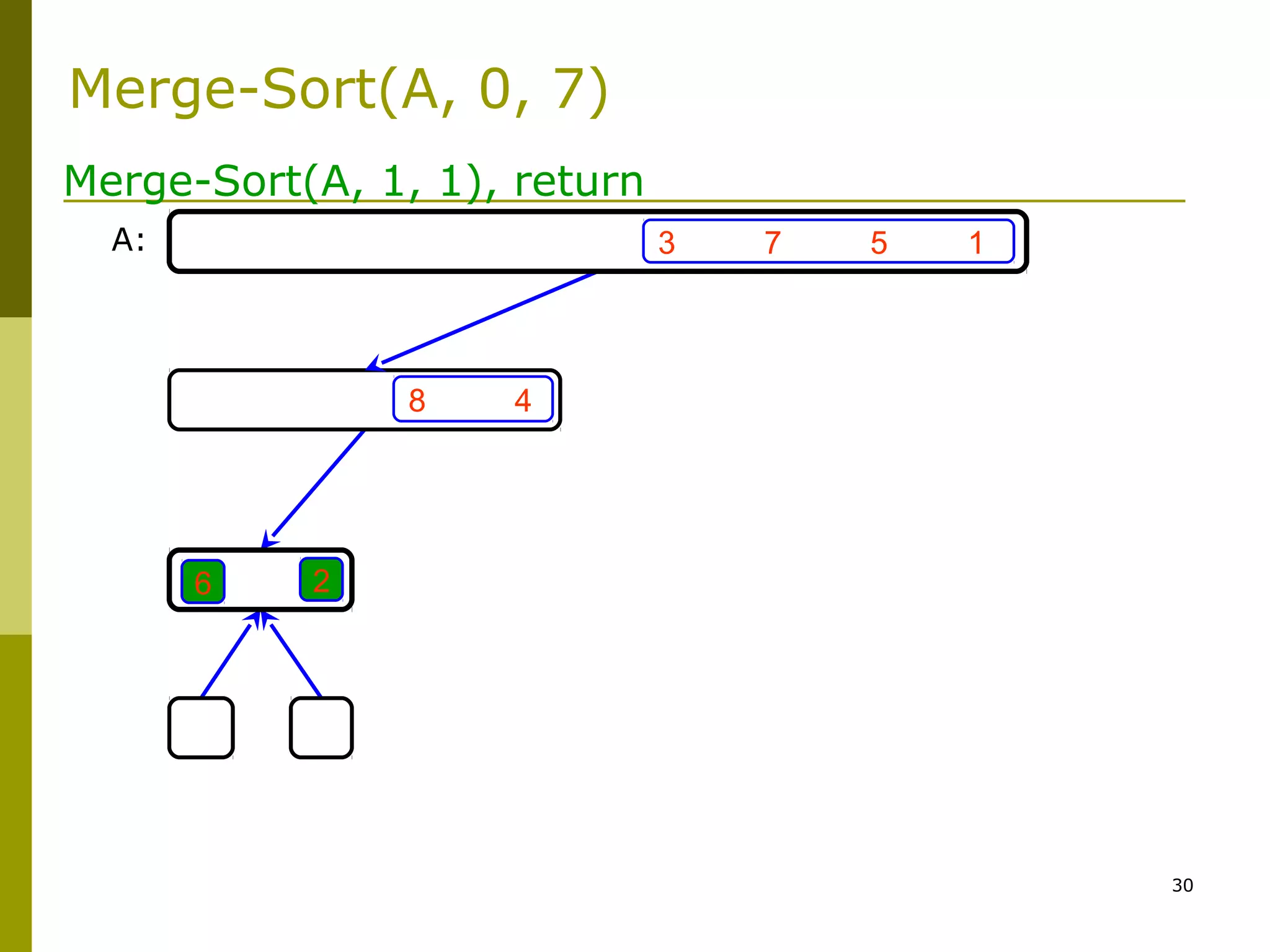
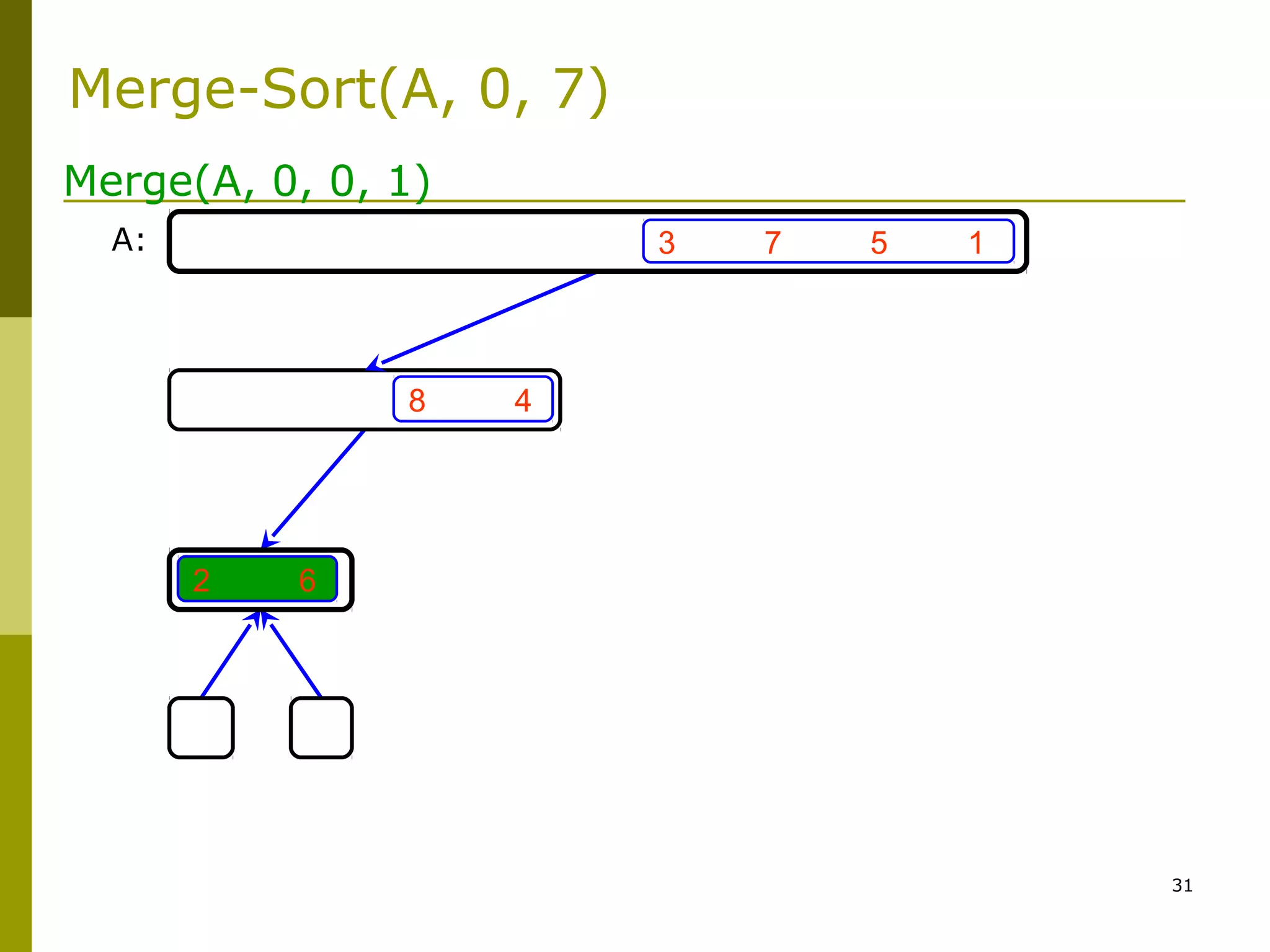
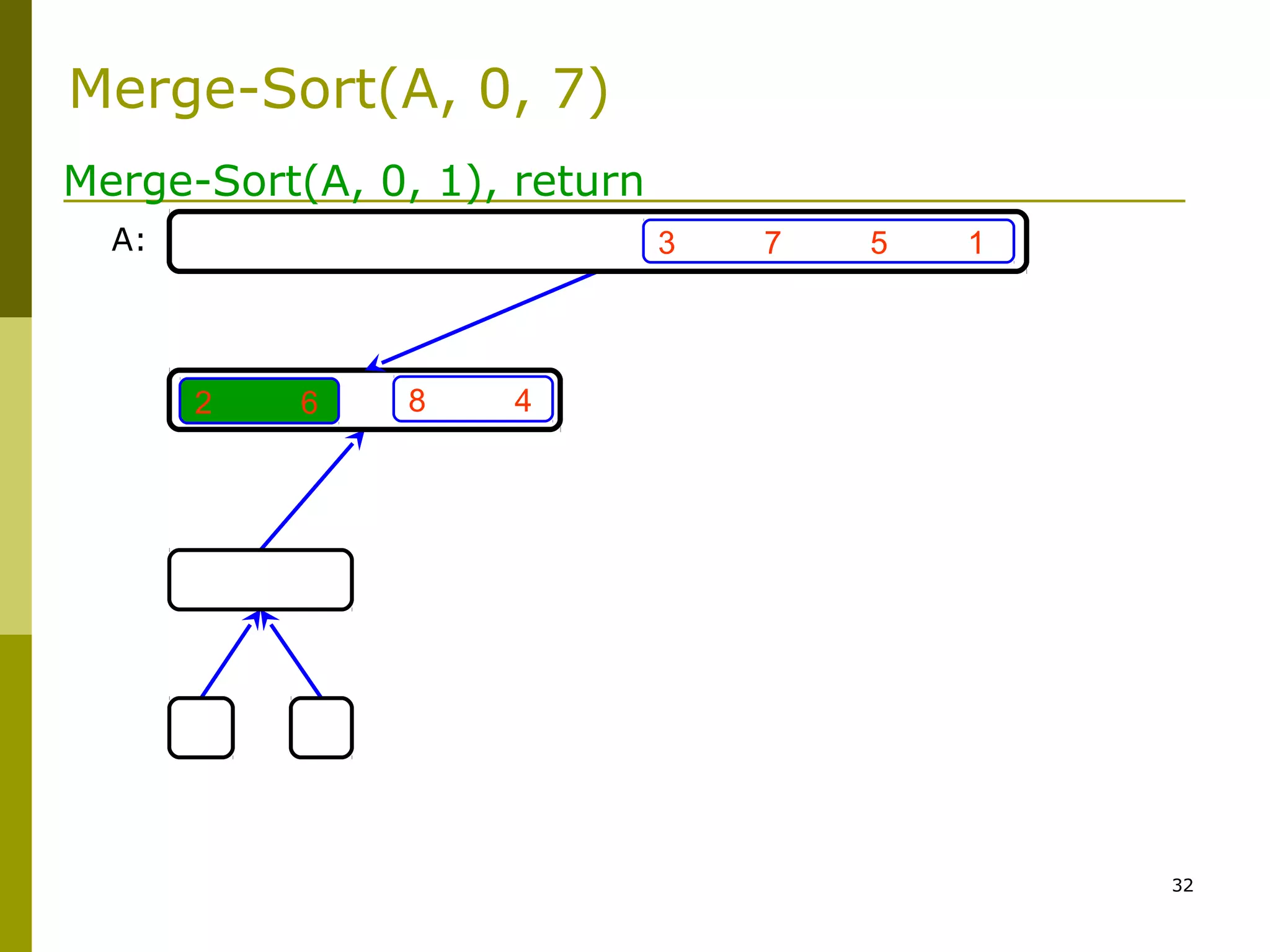
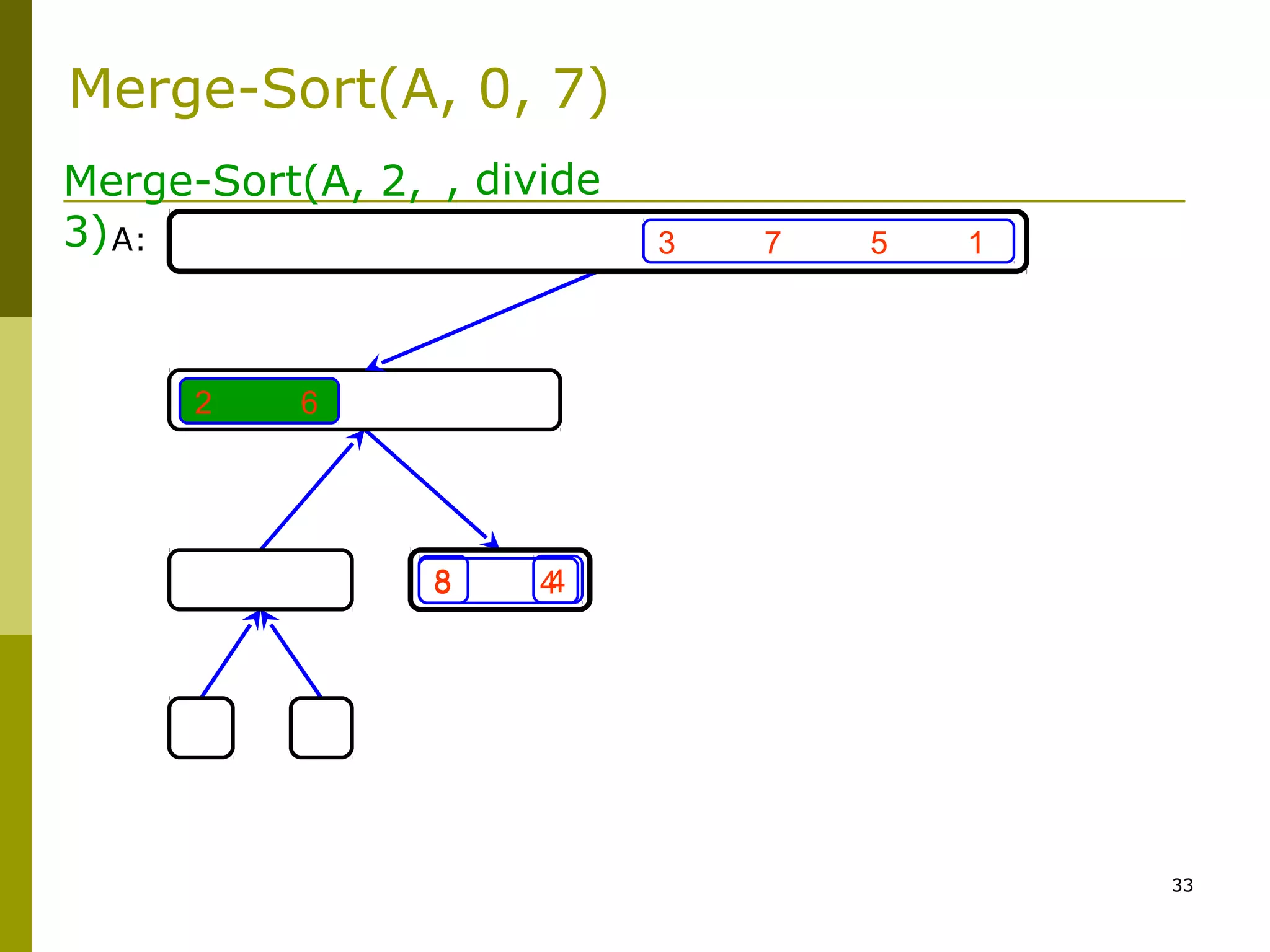
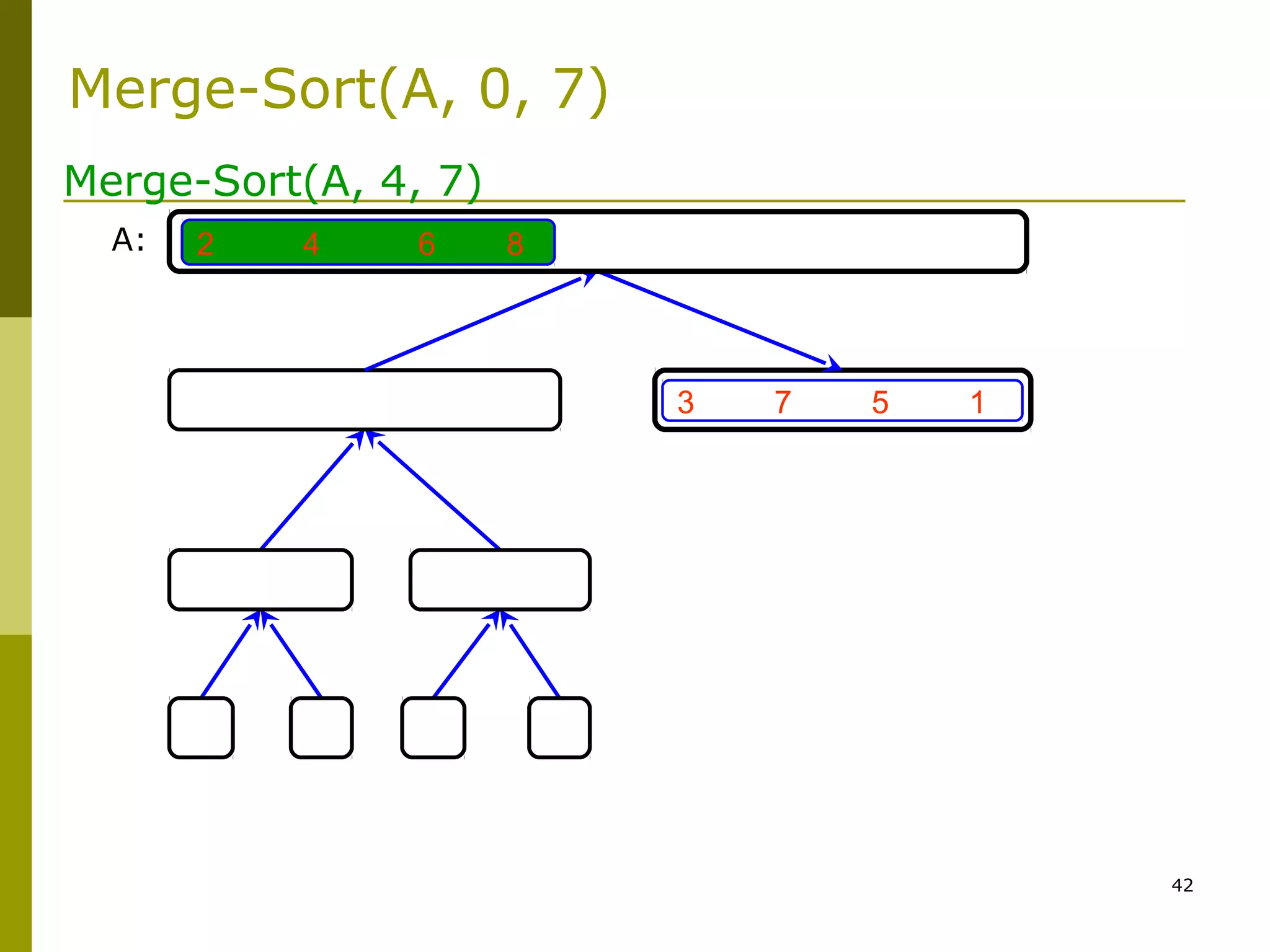
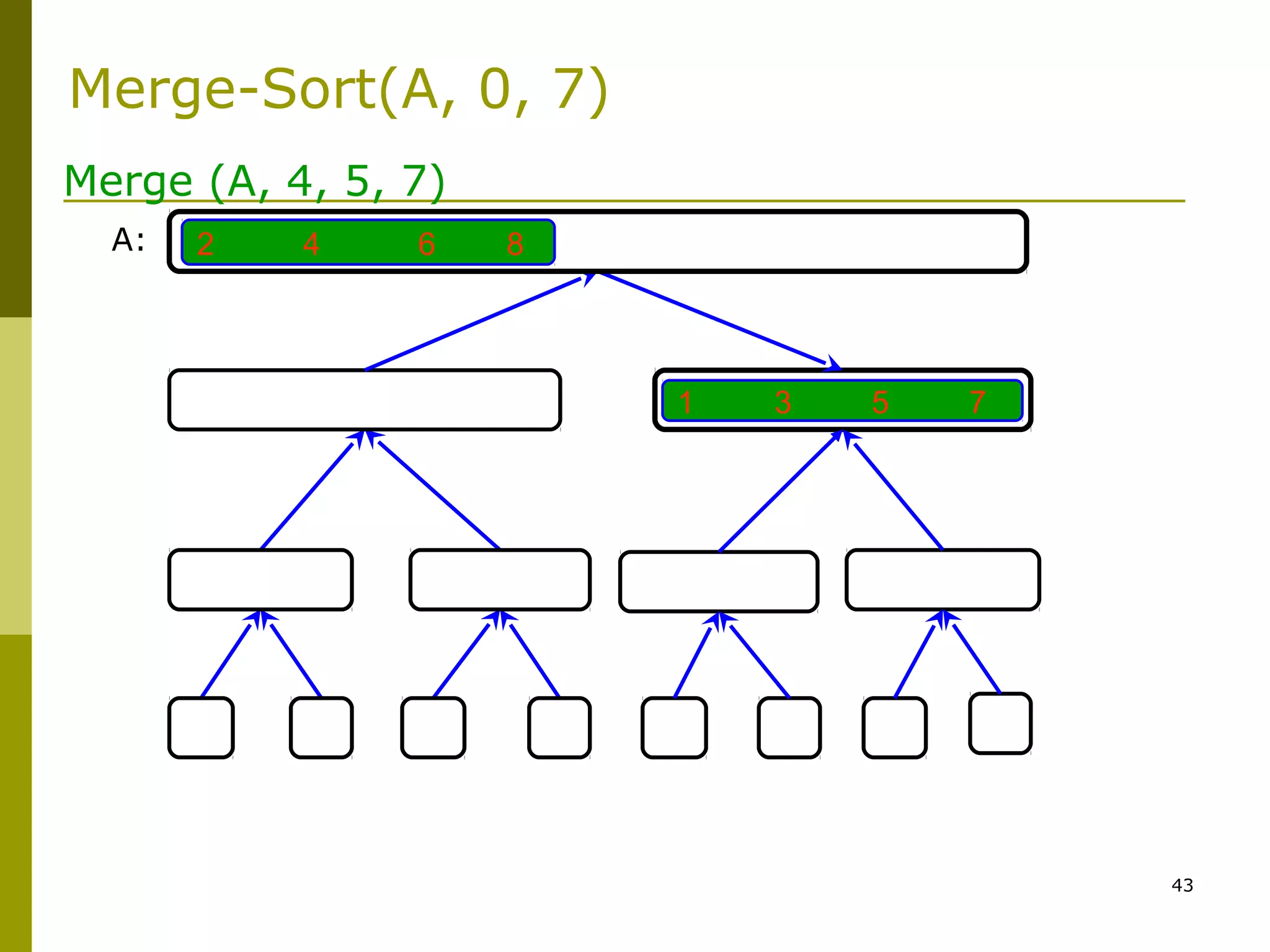
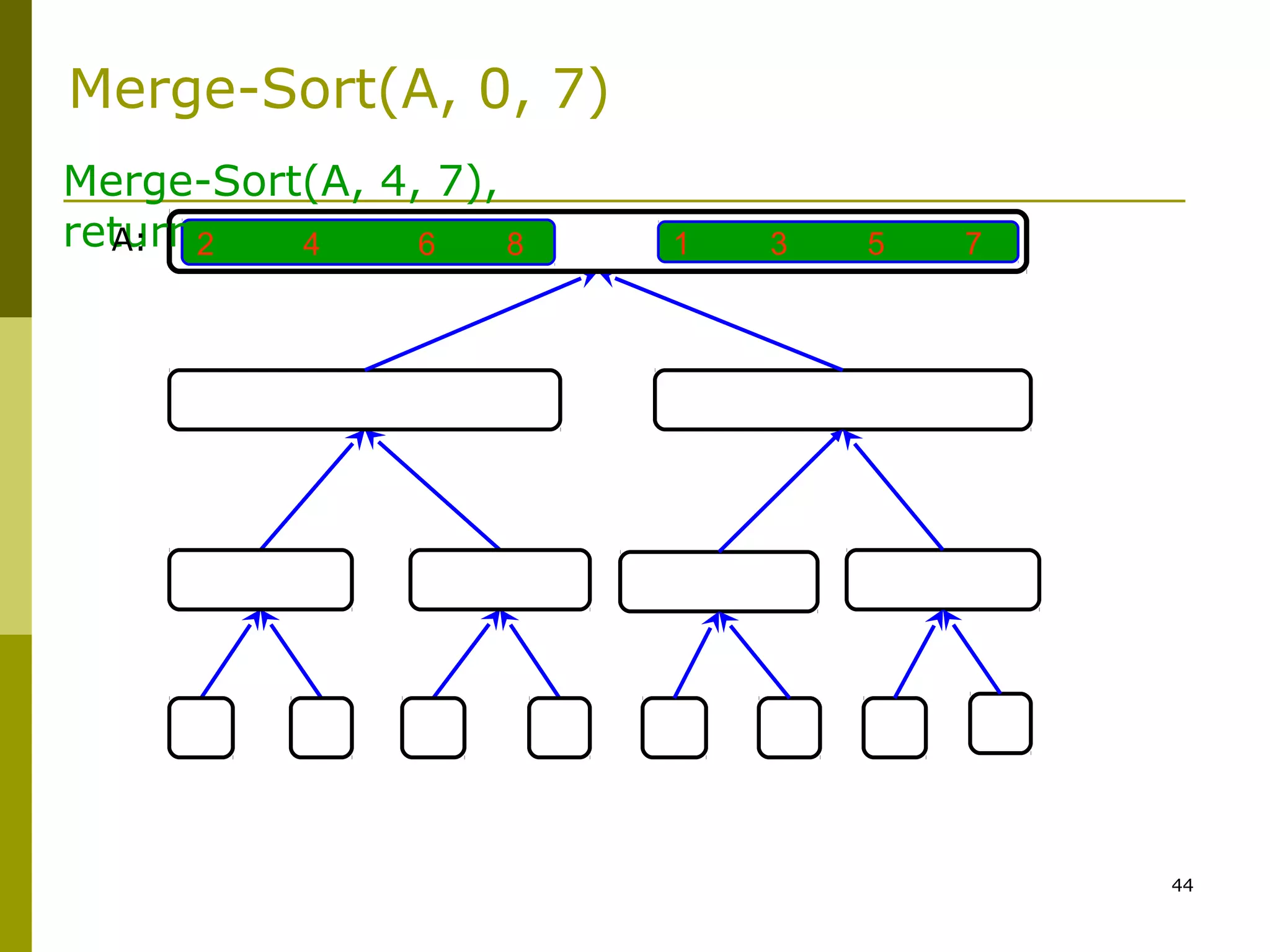
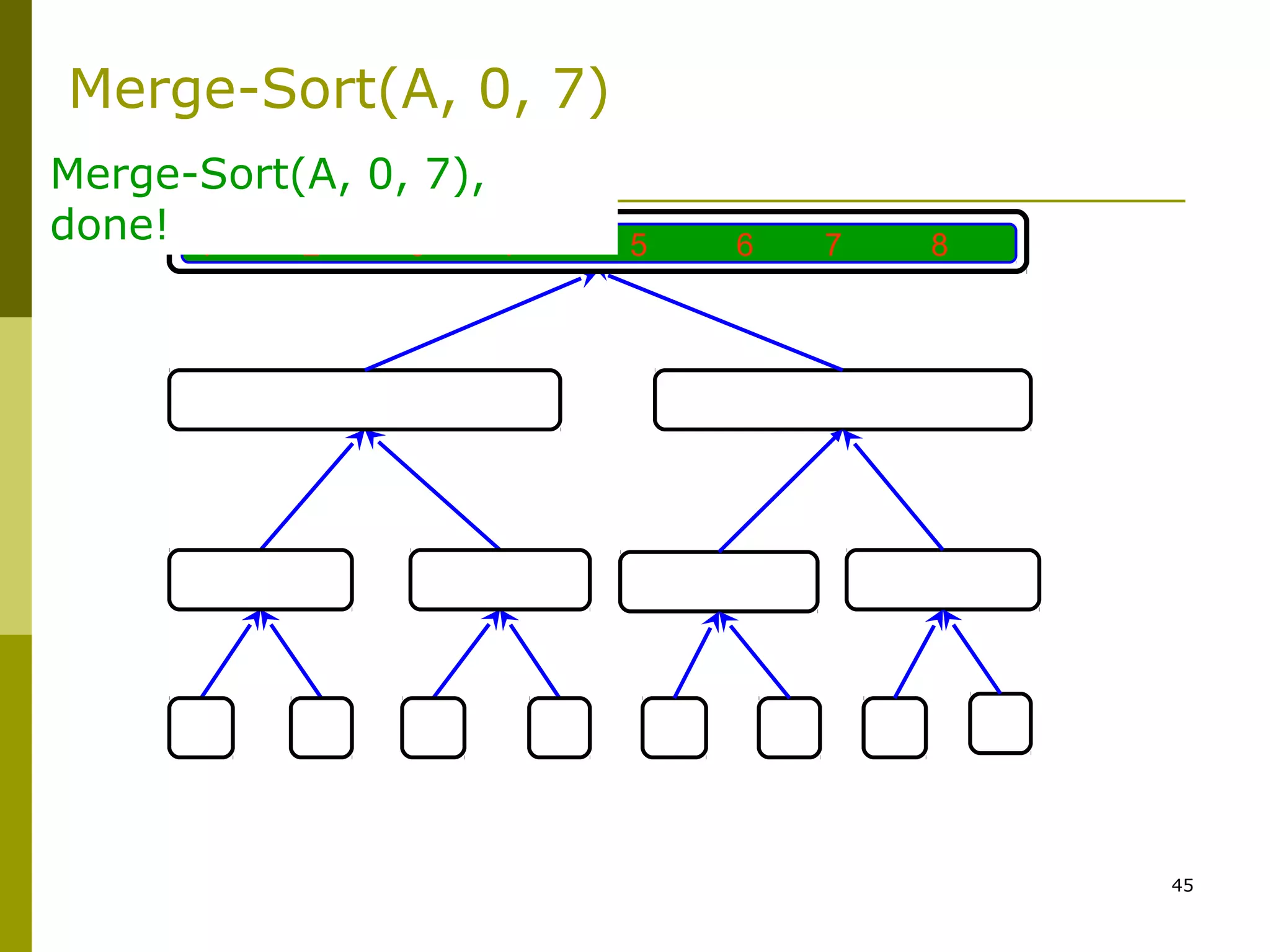
Merge-Sort: Merge
A[right]A[right]
mergemerge
A:A:
A:A:
SortedSorted

14
6 10 14 223 5 15 28
L:L: R:R:
Temporary ArraysTemporary Arrays
5 15 28 30 6 10 145
Merge-Sort: Merge Example
2 3 7 8 1 4 5 6A:A:

15
3 5 15 28 30 6 10 14
L:L:
A:A:
3 15 28 30 6 10 14 22
R:R:
i=
0
j=0
k=0
2 3 7 8 1 4 5 6
1

16
1 5 15 28 30 6 10 14
L:L:
A:A:
3 5 15 28 6 10 14 22
R:R:
k=1
2 3 7 8 1 4 5 6
2
i=
0
j=1

17
1 2 15 28 30 6 10 14
L:L:
A:A:
6 10 14 22
R:R:
i=
1
k=2
2 3 7 8 1 4 5 6
3
j=1

18
1 2 3 6 10 14
L:L:
A:A:
6 10 14 22
R:R:
i=
2
j=1
k=3
2 3 7 8 1 4 5 6
4

19
1 2 3 4 6 10 14
L:L:
A:A:
6 10 14 22
R:R:
j=2
k=4
2 3 7 8 1 4 5 6
i=
2
5

20
1 2 3 4 5 6 10 14
L:L:
A:A:
6 10 14 22
R:R:
i=
2
j=3
k=5
2 3 7 8 1 4 5 6
6

21
1 2 3 4 5 6 14
L:L:
A:A:
6 10 14 22
R:R:
k=6
2 3 7 8 1 4 5 6
7
i=
2
j=4

22
1 2 3 4 5 6 7 14
L:L:
A:A:
3 5 15 28 6 10 14 22
R:R:
2 3 7 8 1 4 5 6
8
i=
3
j=4
k=7

23
1 2 3 4 5 6 7 8
L:L:
A:A:
3 5 15 28 6 10 14 22
R:R:
2 3 7 8 1 4 5 6
i=
4
j=4
k=8

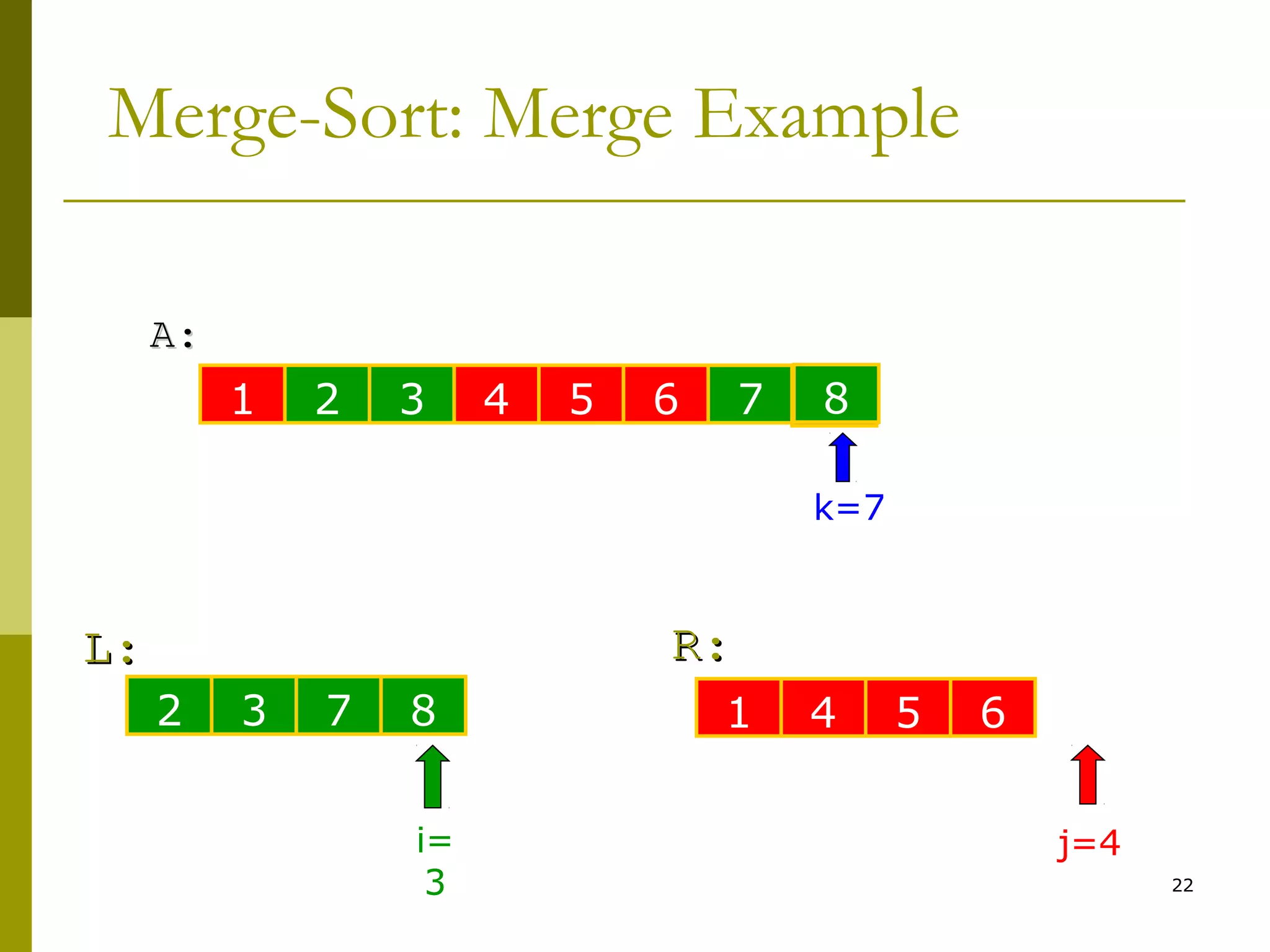
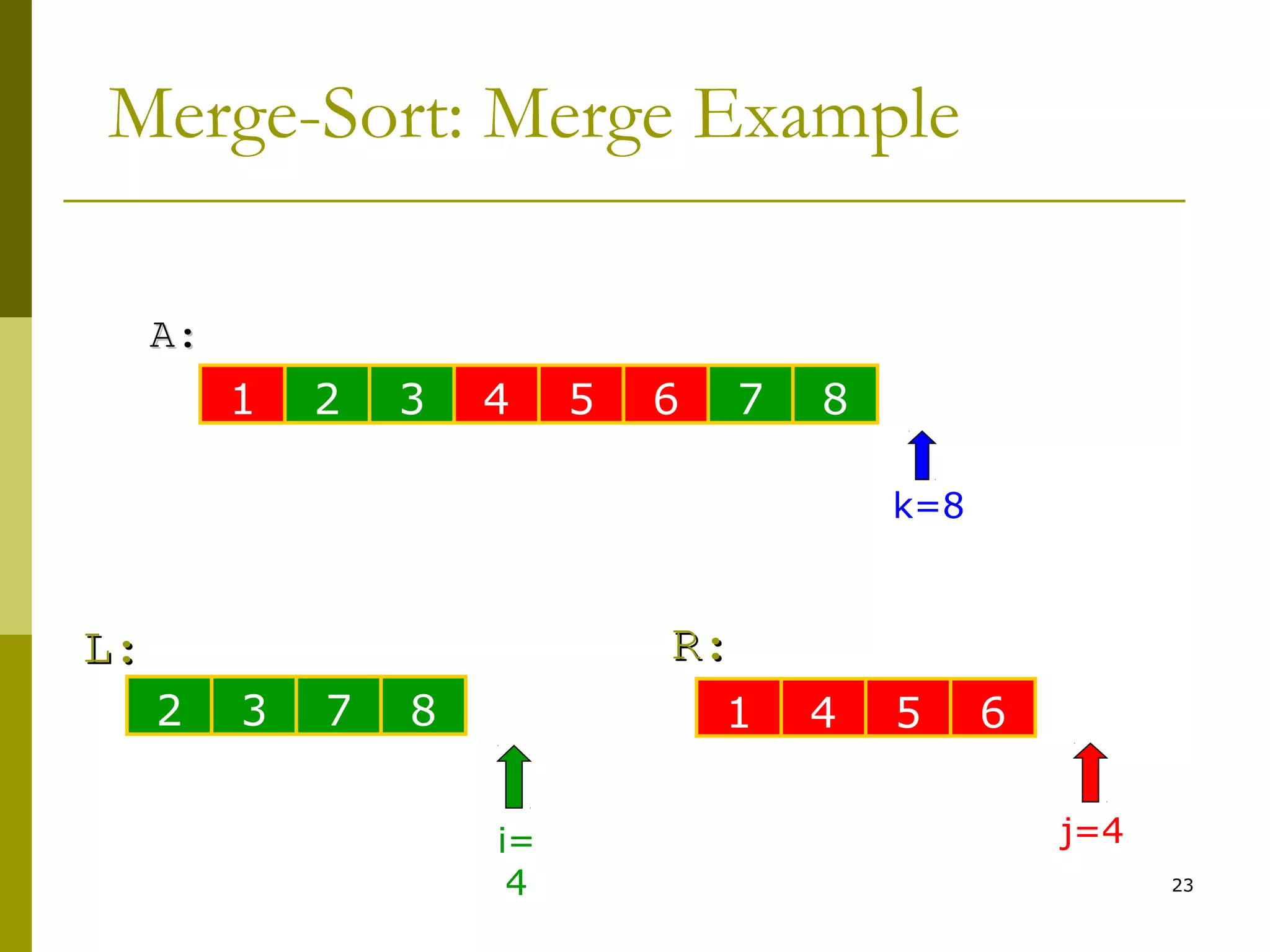
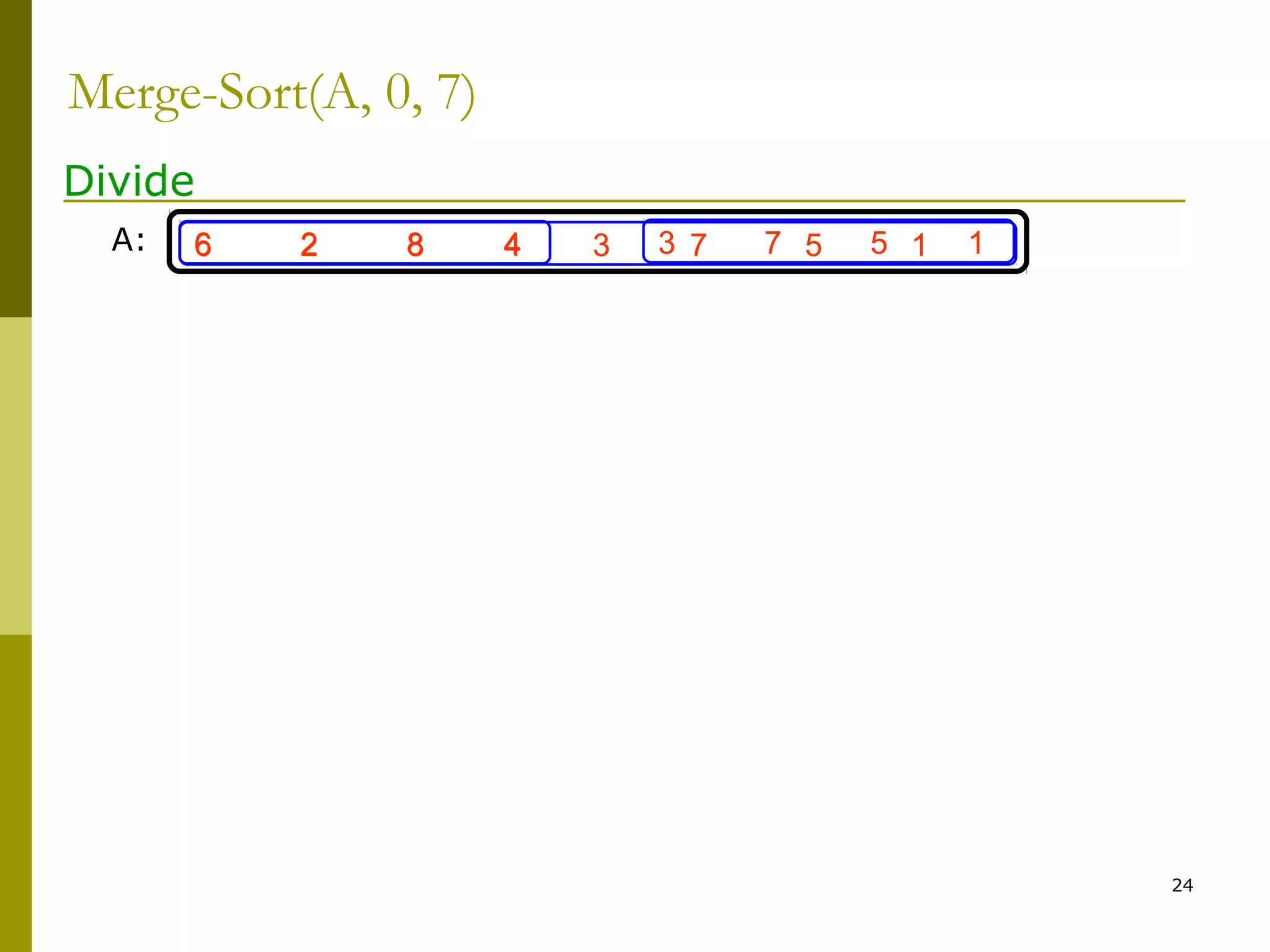
24
6 2 8 4 3 7 5 16 2 8 4 3 7 5 1
Merge-Sort(A, 0, 7)
Divide
A:

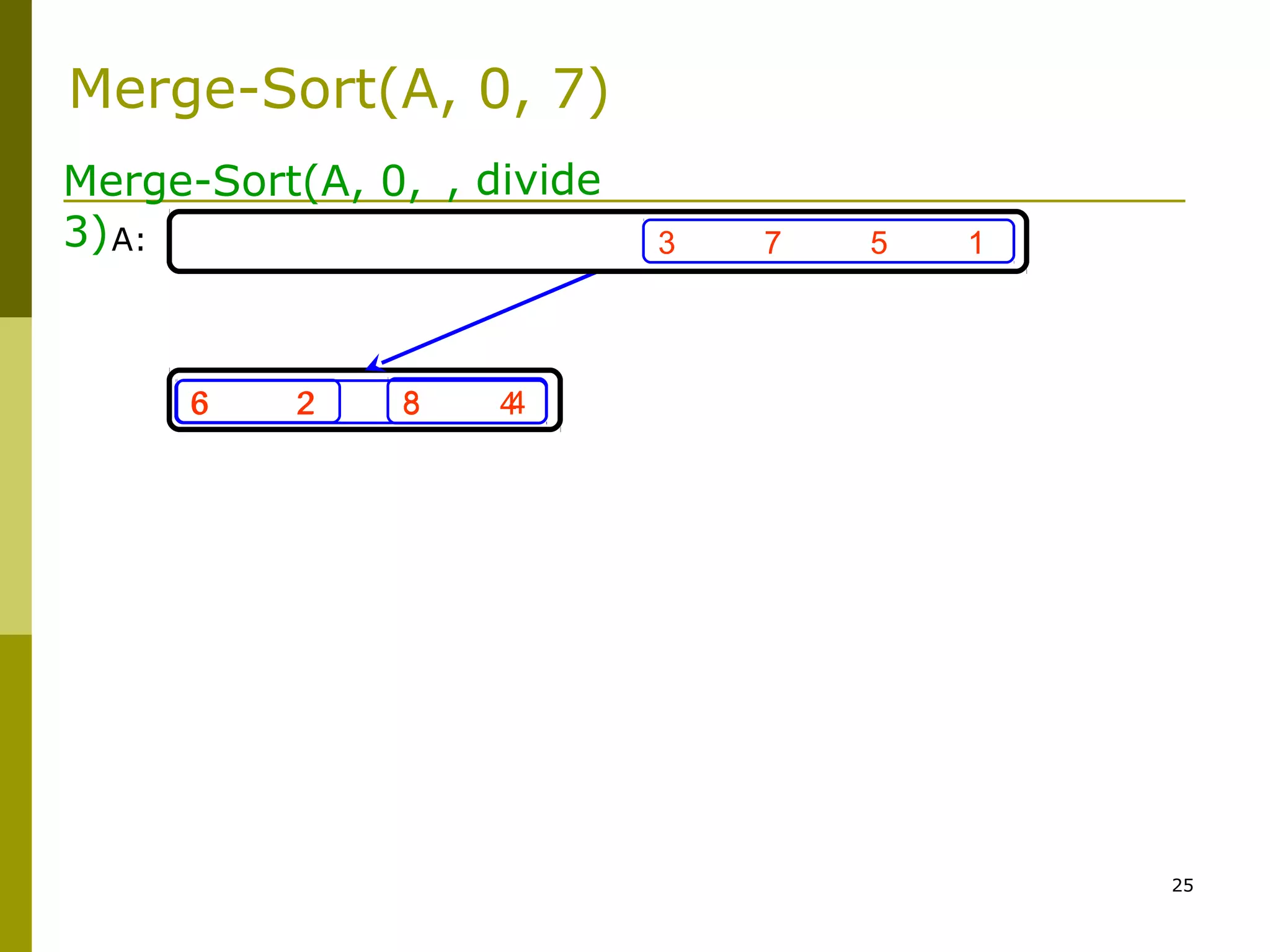
25
6 2 8 4
3 7 5 1
6 2 8 4
Merge-Sort(A, 0,
3)
, divide
A:
Merge-Sort(A, 0, 7)

26
3 7 5 1
8 4
6 26 2
Merge-Sort(A, 0,
1)
, divide
A:
Merge-Sort(A, 0, 7)

27
3 7 5 1
8 4
6
2
Merge-Sort(A, 0, 0), base case
A:
Merge-Sort(A, 0, 7)

28
3 7 5 1
8 4
6 2
Merge-Sort(A, 0, 0), return
A:
Merge-Sort(A, 0, 7)

29
3 7 5 1
8 4
6
2
Merge-Sort(A, 1,
1)
, base case
A:
Merge-Sort(A, 0, 7)

30
3 7 5 1
8 4
6 2
A:
Merge-Sort(A, 0, 7)

31
3 7 5 1
8 4
2 6
Merge(A, 0, 0, 1)
A:
Merge-Sort(A, 0, 7)

32
3 7 5 1
8 42 6
A:
Merge-Sort(A, 0, 7)

33
3 7 5 1
8 4
2 6
Merge-Sort(A, 2,
3)
48
, divide
A:
Merge-Sort(A, 0, 7)

34
3 7 5 1
4
2 6
8
A:
Merge-Sort(A, 0, 7)

35
3 7 5 1
4
2 6
8
A:
Merge-Sort(A, 0, 7)

36
4
2 6
8
A:
Merge-Sort(A, 0, 7)

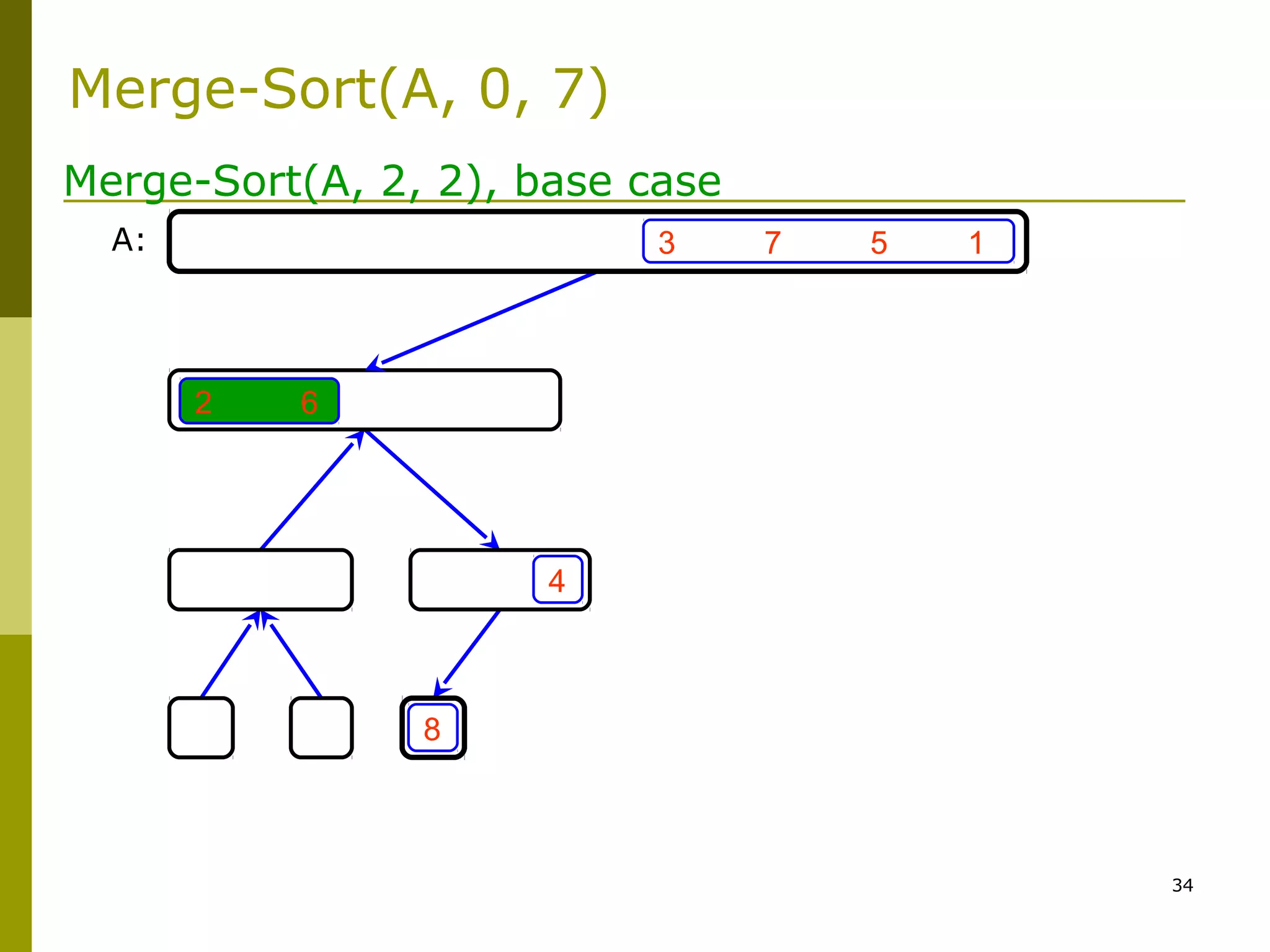
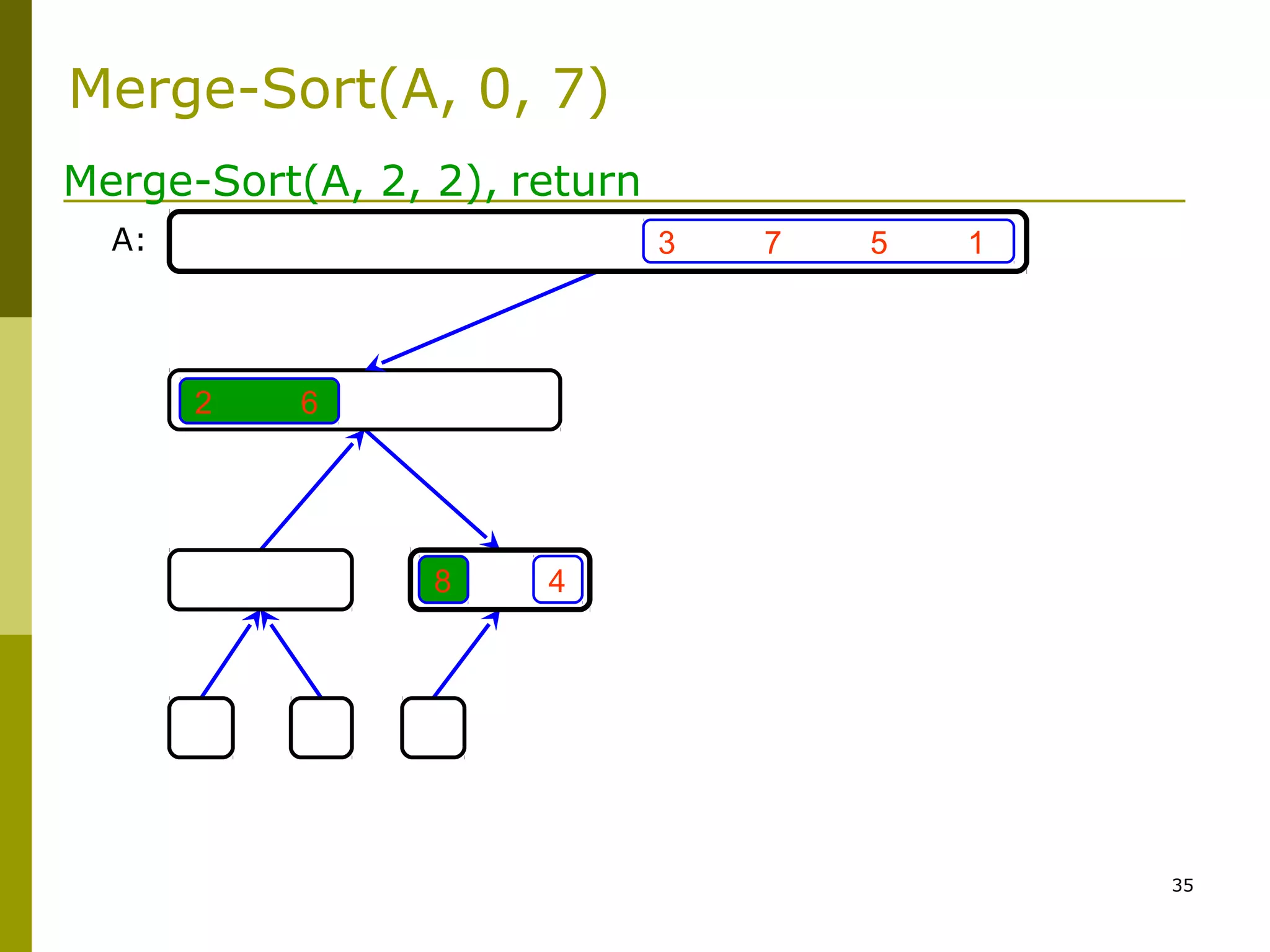
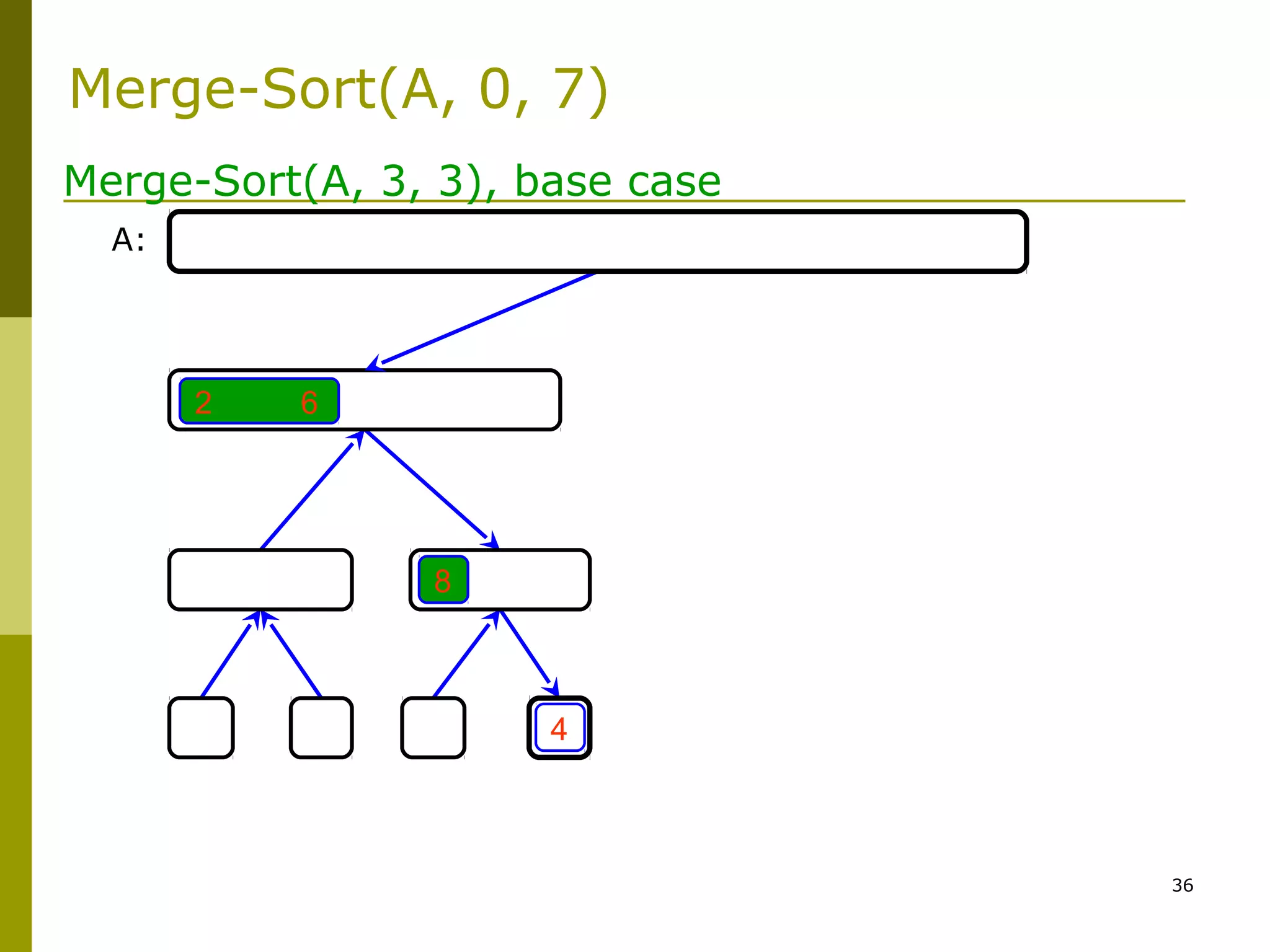
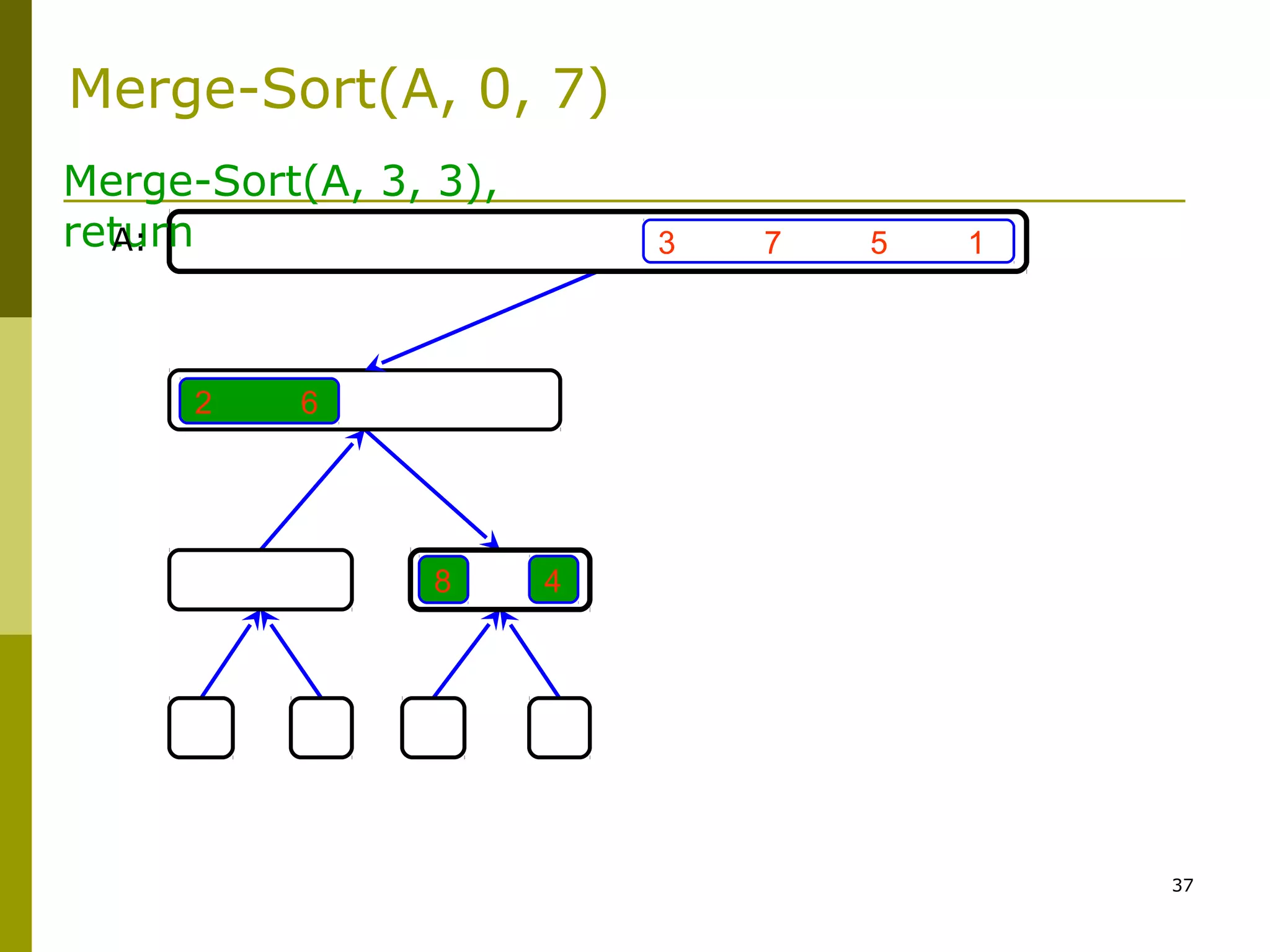
37
3 7 5 1
4
2 6
8
Merge-Sort(A, 3, 3),
returnA:
Merge-Sort(A, 0, 7)

38
3 7 5 1
2 6
4 8
Merge(A, 2, 2, 3)
A:
Merge-Sort(A, 0, 7)

39
3 7 5 1
2 6 4 8
returnA:
Merge-Sort(A, 0, 7)

40
3 7 5 1
2 4 6 8
Merge(A, 0, 1, 3)
A:
Merge-Sort(A, 0, 7)

41
3 7 5 12 4 6 8
returnA:
Merge-Sort(A, 0, 7)

42
3 7 5 1
2 4 6 8
Merge-Sort(A, 4, 7)
A:
Merge-Sort(A, 0, 7)

43
1 3 5 7
2 4 6 8A:
Merge (A, 4, 5, 7)
Merge-Sort(A, 0, 7)

44
1 3 5 72 4 6 8
returnA:
Merge-Sort(A, 0, 7)

45
1 2 3 4 5 6 7 8
Merge(A, 0, 3, 7)
A:
Merge-Sort(A, 0, 7)
done!

46
Merge Sort: Algorithm
Merge-Sort (A, left, right)
if left ≥ right return
else
middle ←(left + right)/2
Merge-Sort(A, left, middle)
Merge-Sort(A, middle+1, right)
Merge(A, left, middle, right)
Recursive Call

47
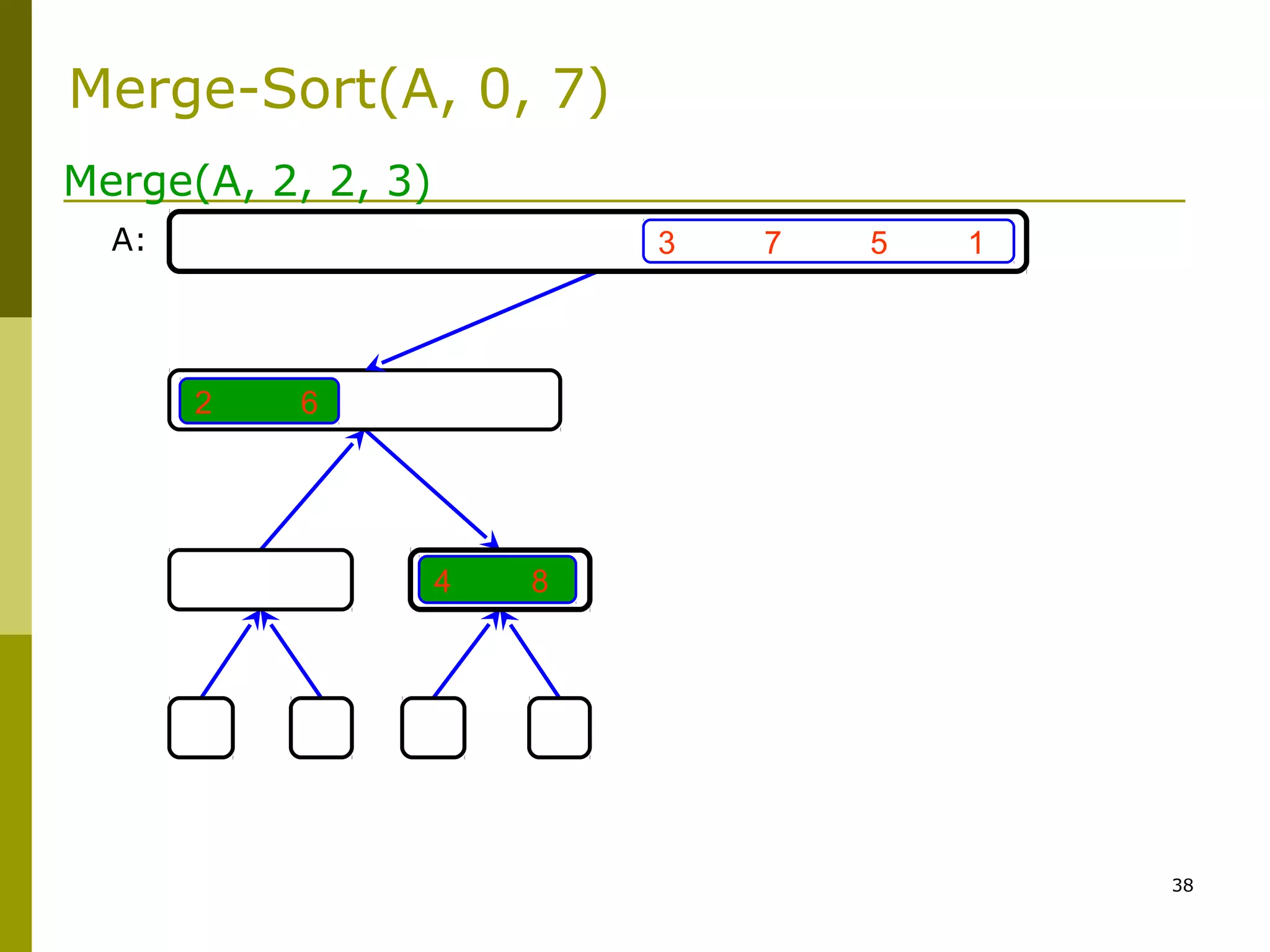
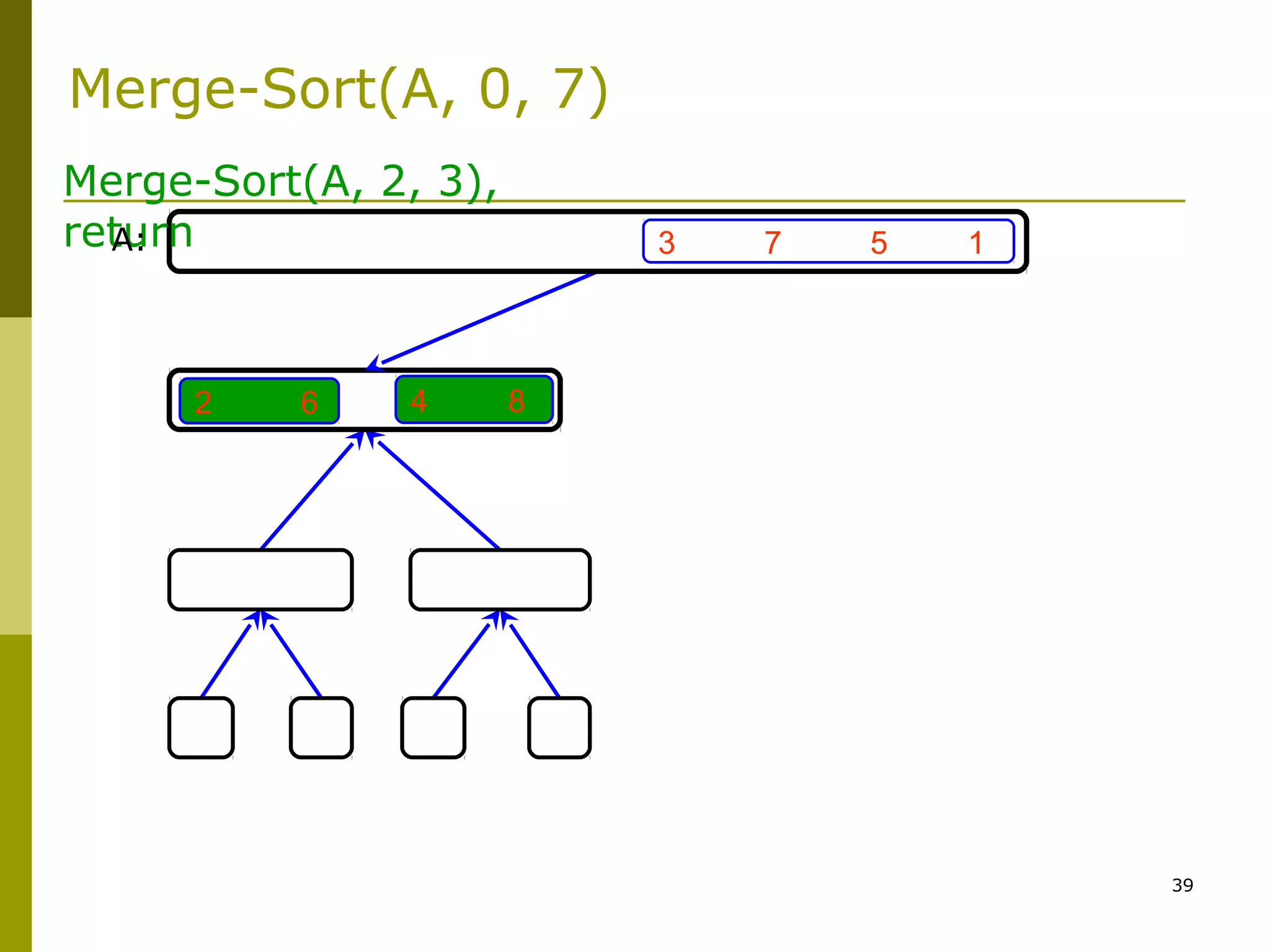
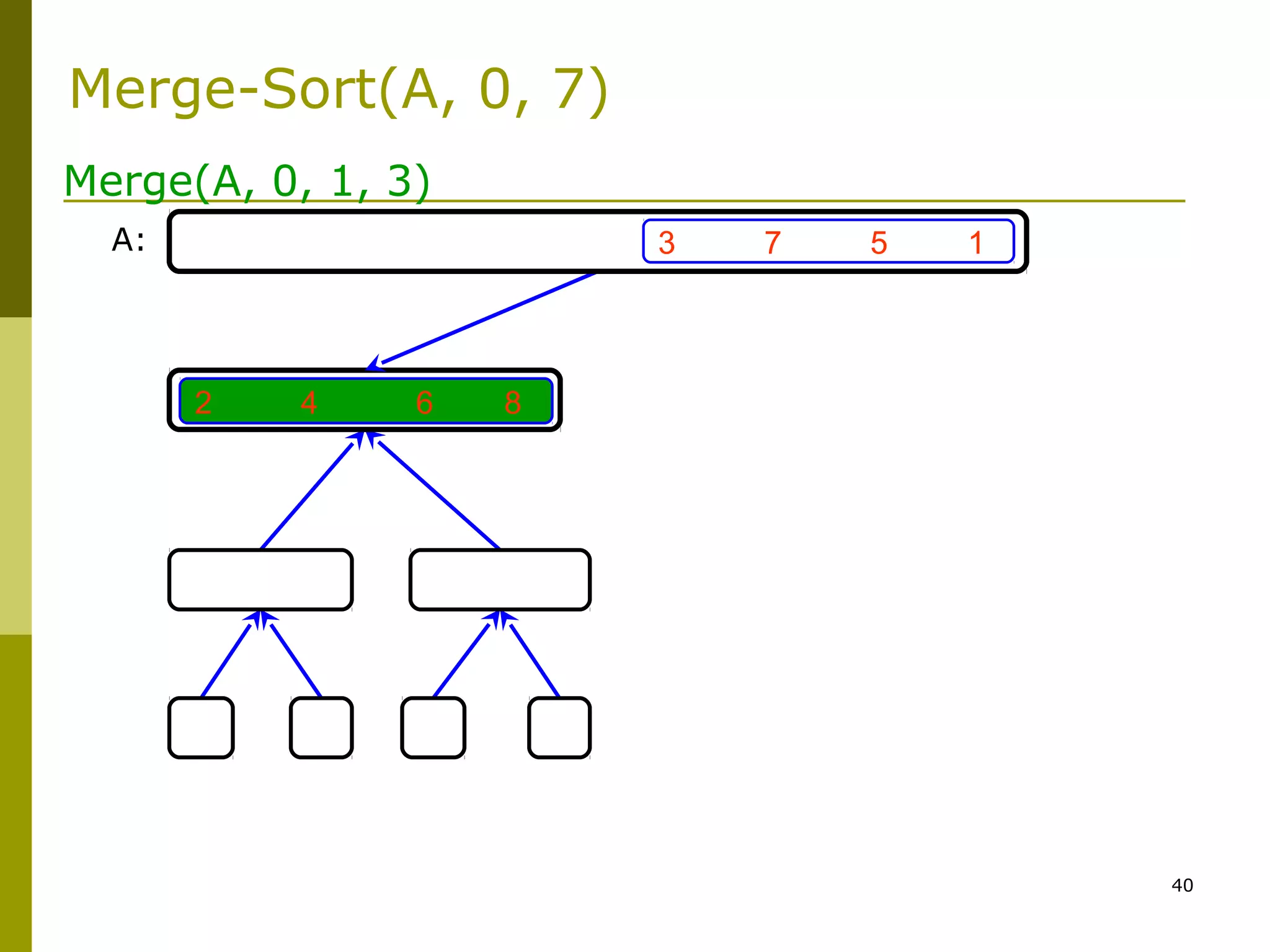
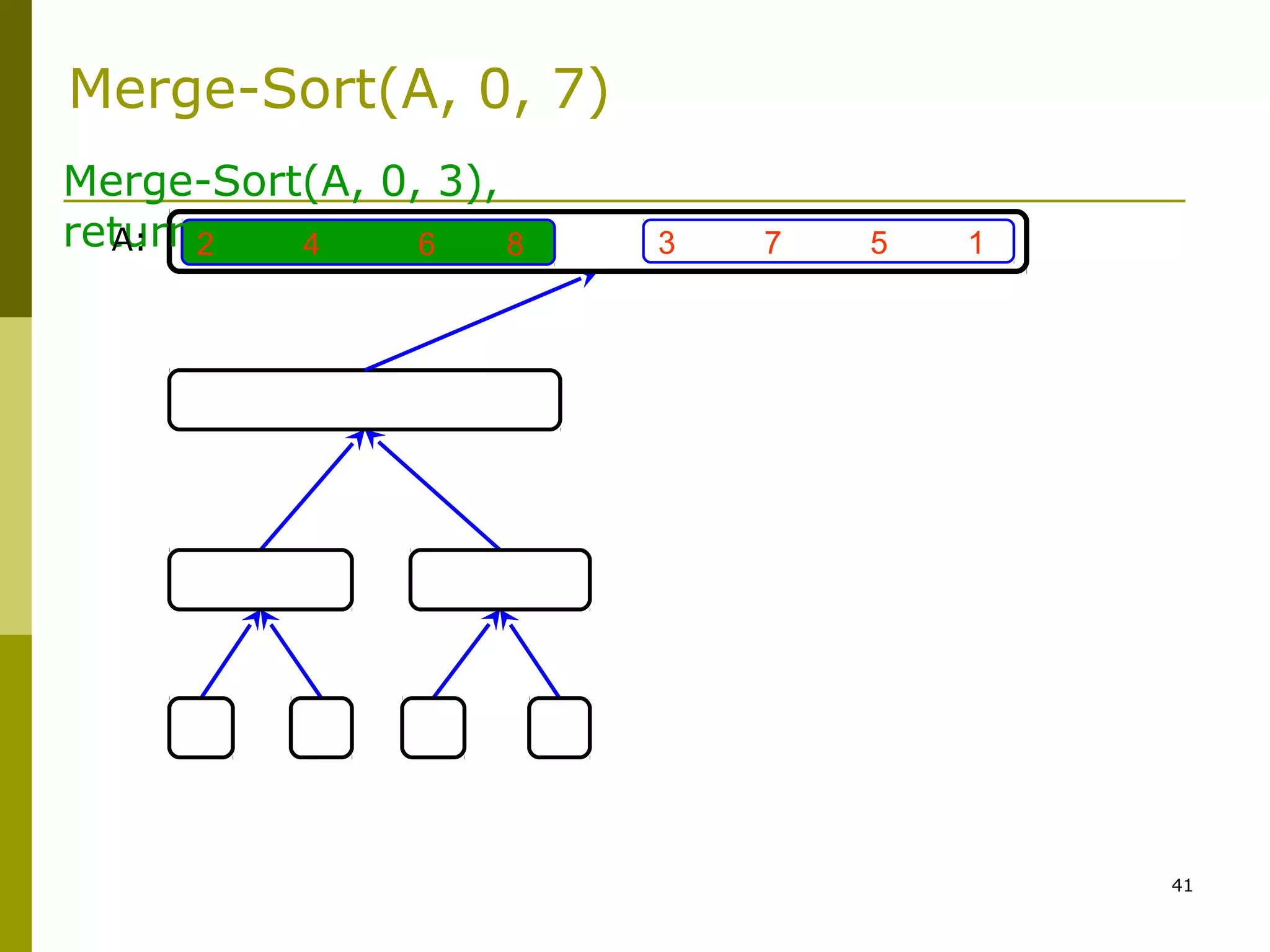
Merge(A, left, middle, right)
1. n1 ← middle – left + 1
2. n2 ← right – middle
3. create array L[n1], R[n2]
4. for i ← 0 to n1-1 do L[i] ← A[left +i]
5. for j ← 0 to n2-1 do R[j] ← A[middle+j]
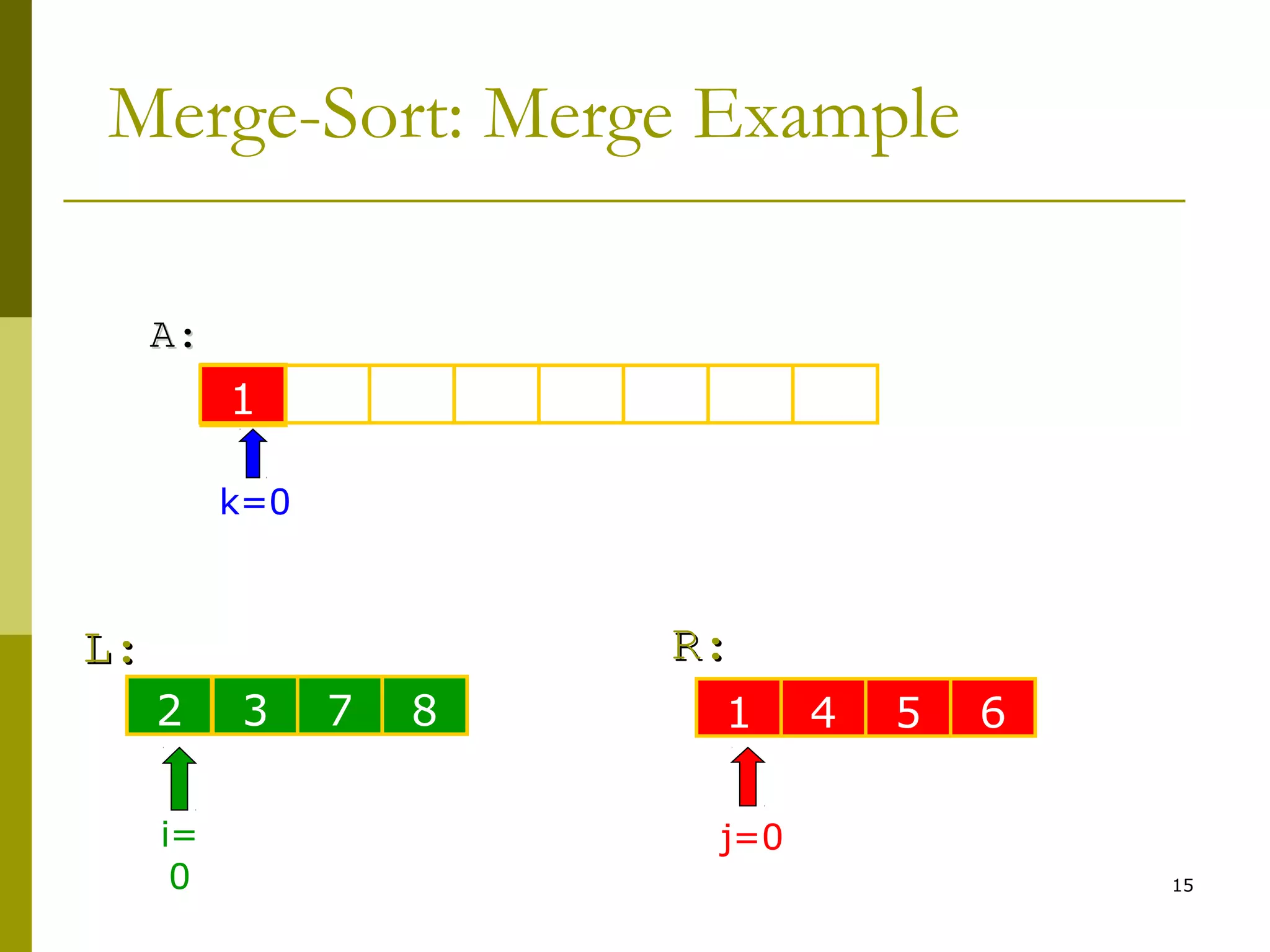
6. k ← i ← j ← 0
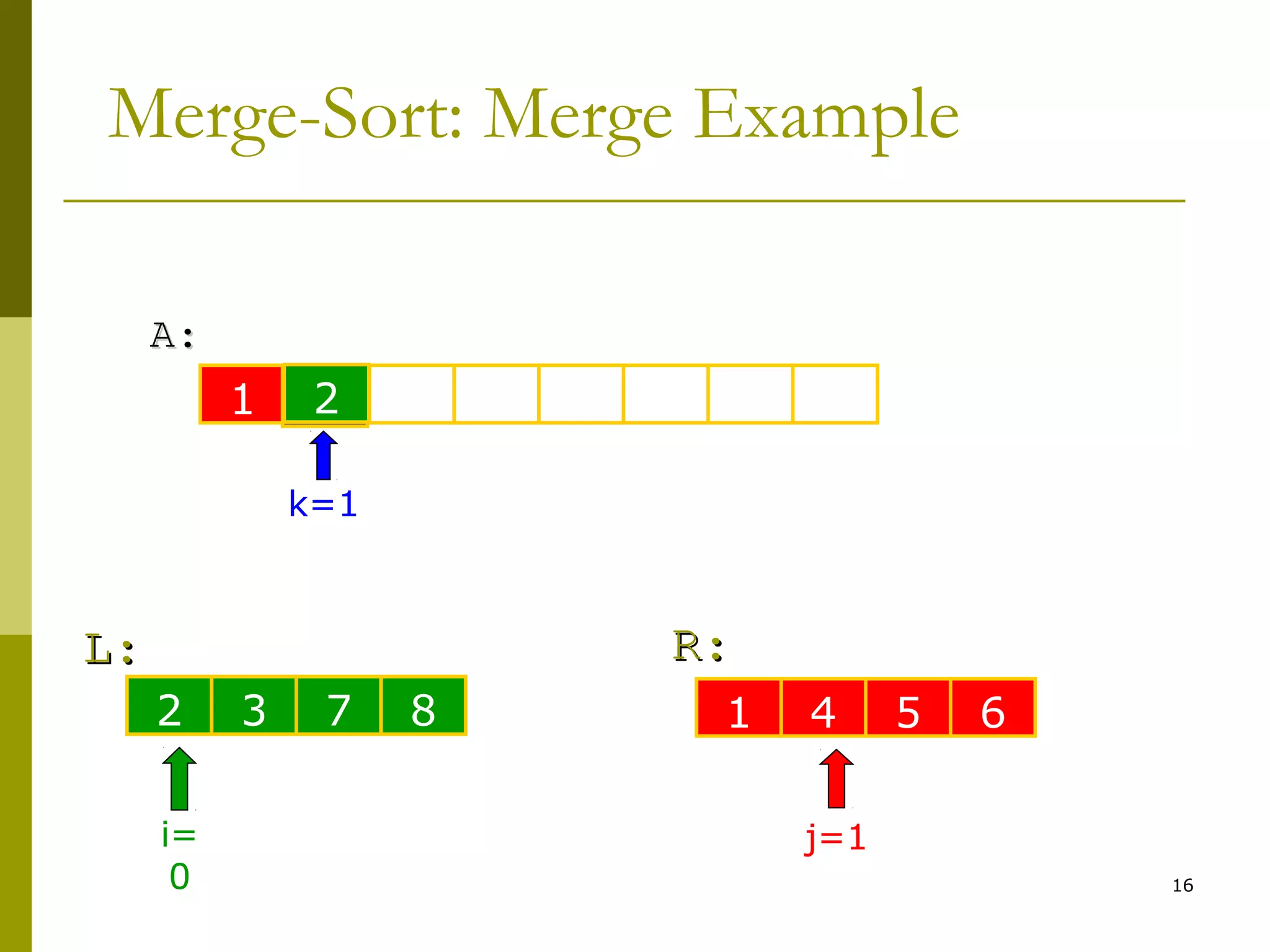
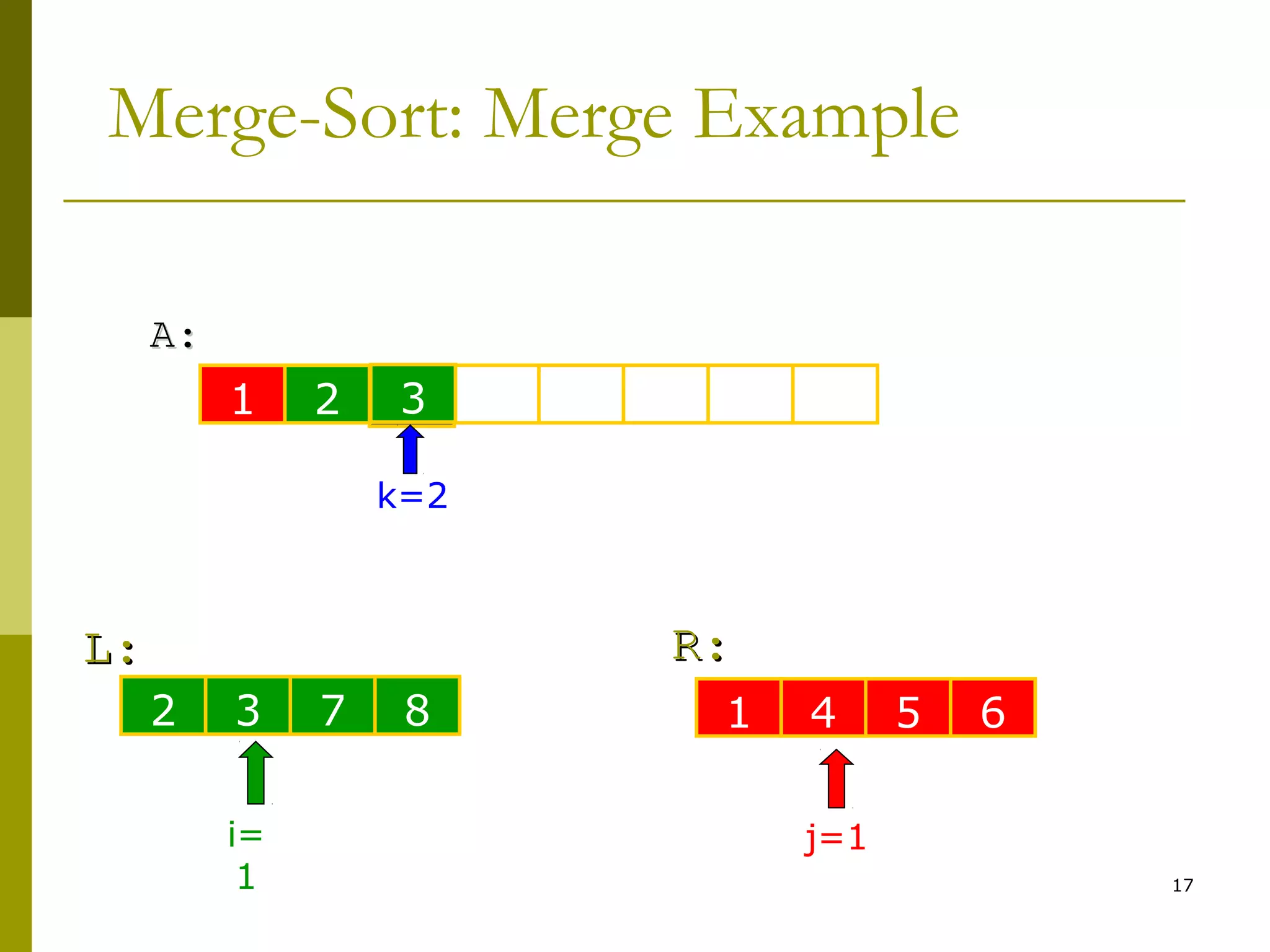
7. while i < n1 & j < n2
8. if L[i] < R[j]
9. A[k++] ← L[i++]
10. else
11. A[k++] ← R[j++]
12. while i < n1
13. A[k++] ← L[i++]
14. while j < n2
15. A[k++] ← R[j++]
n = n1+n2
Space: n
Time : cn for some constant c

Sorting

More Related Content

What's hot

Similar to Sorting

More from invertis university

Recently uploaded

Sorting

Editor's Notes