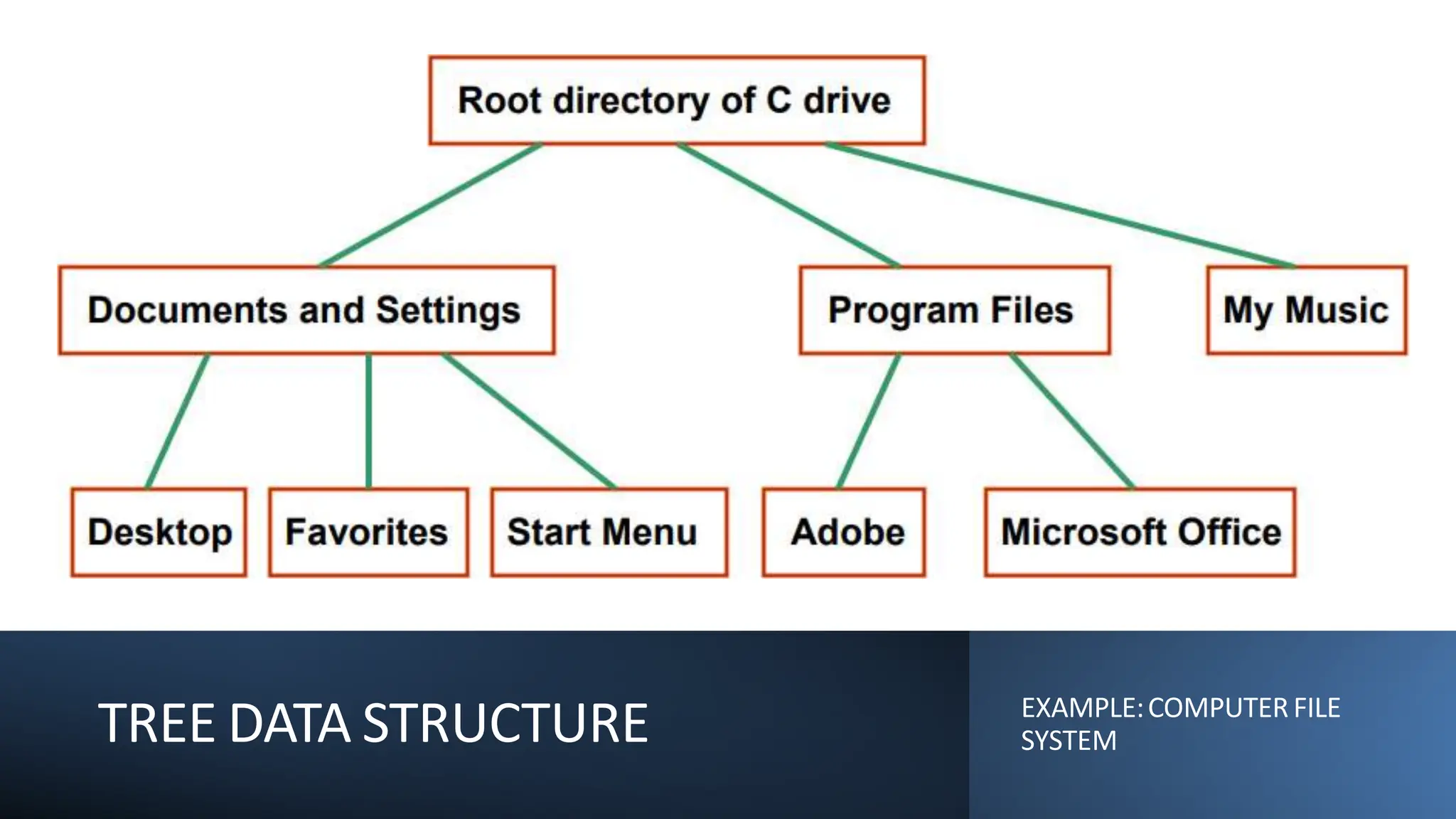
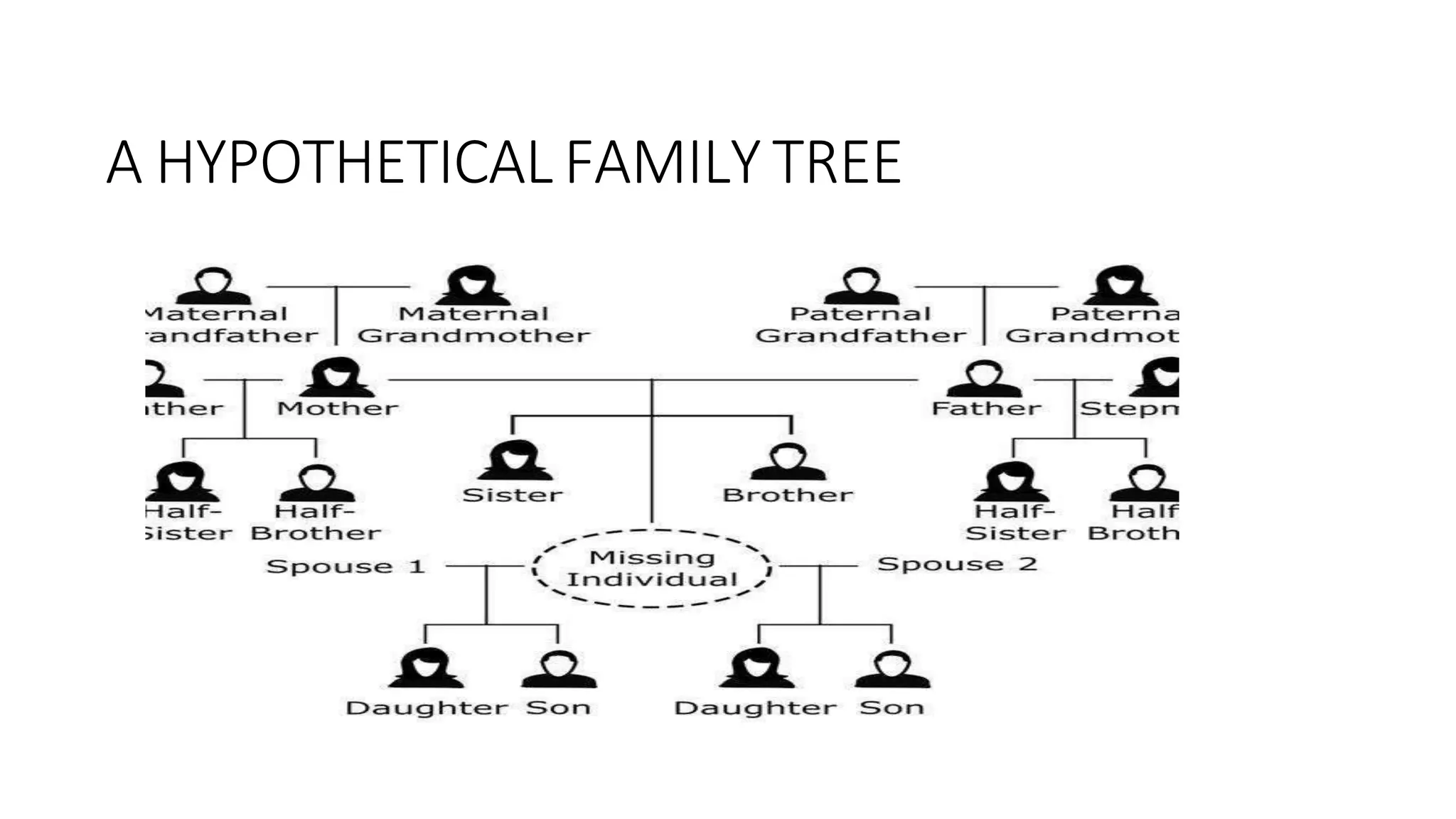
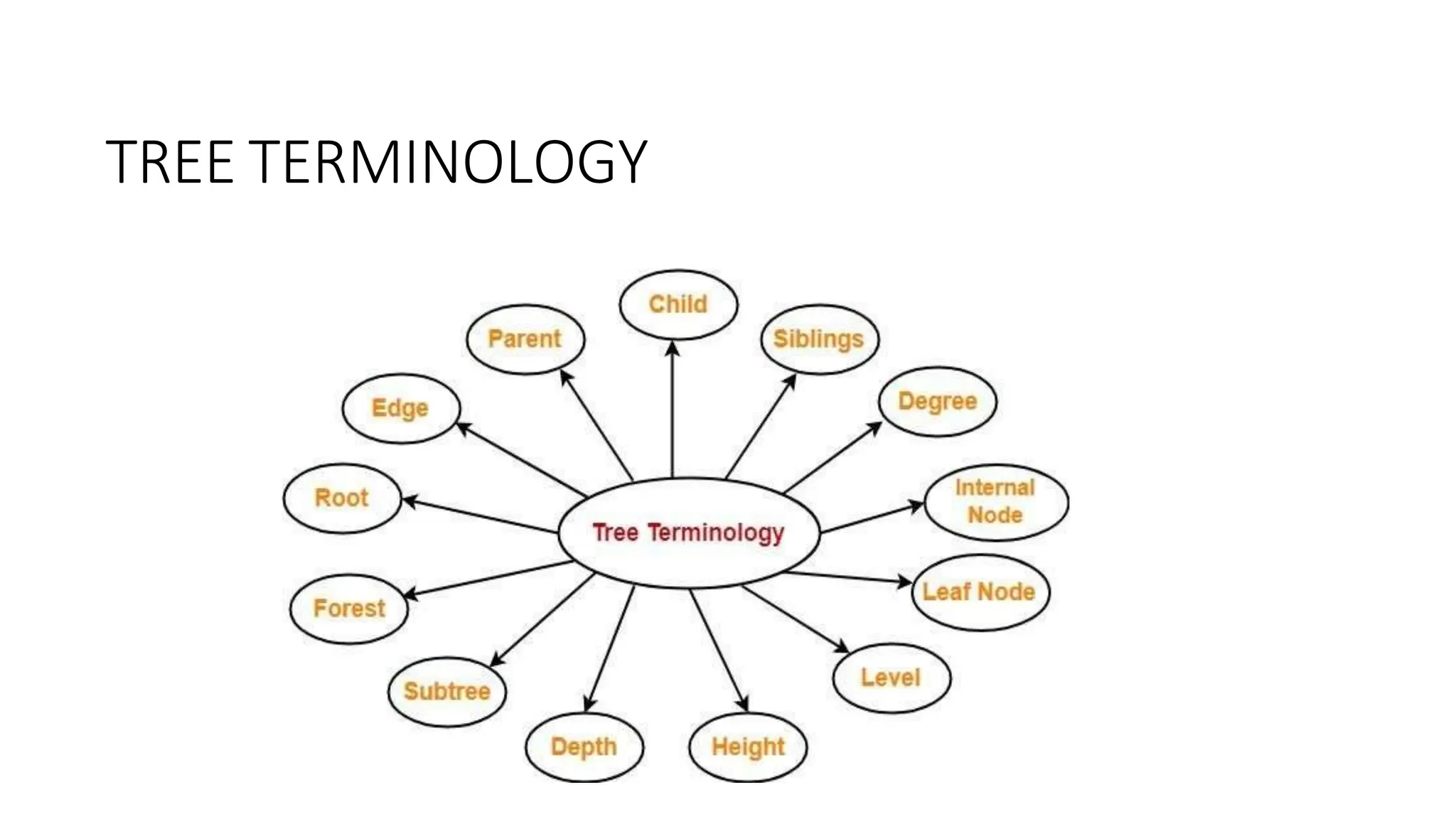
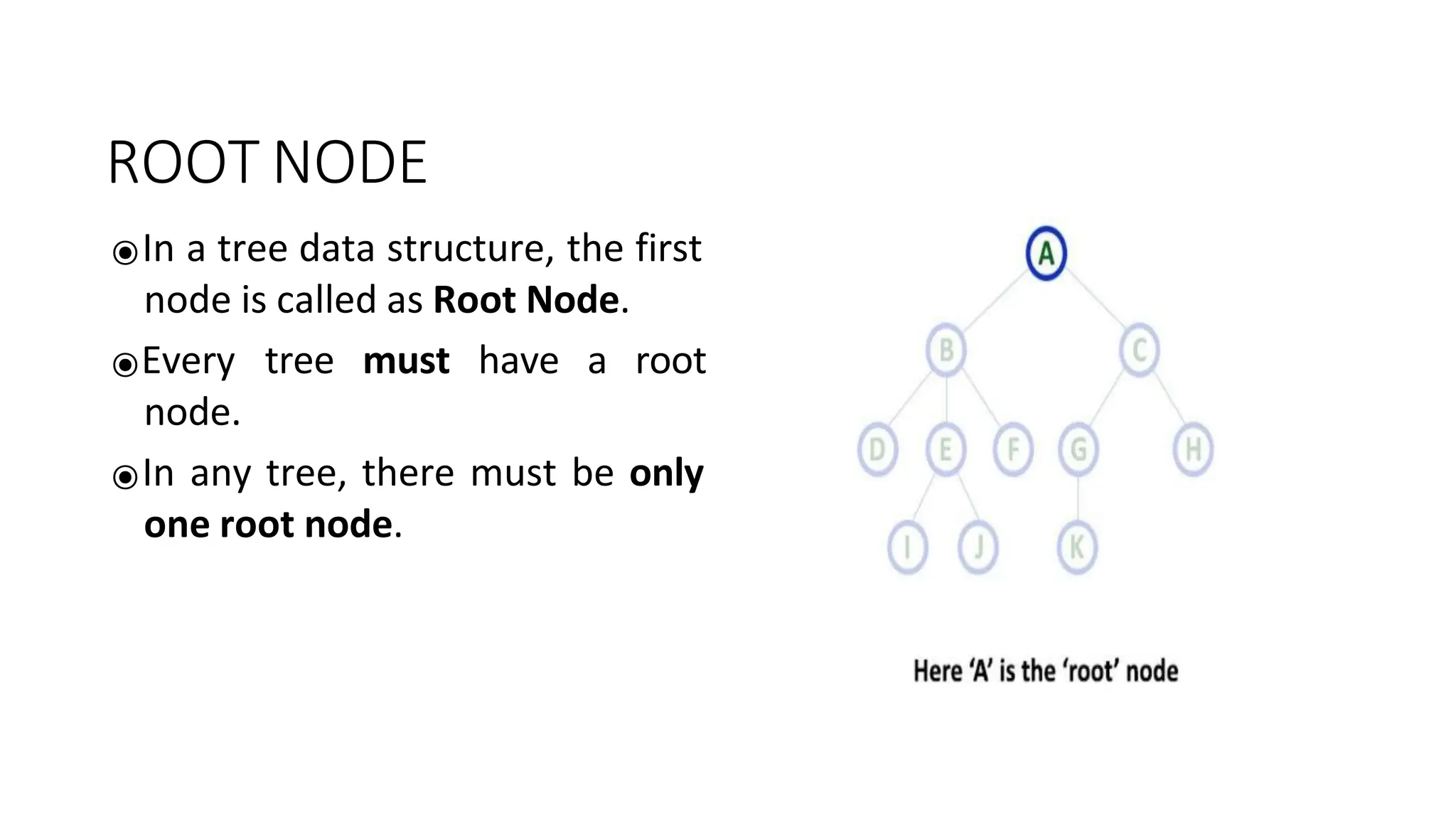
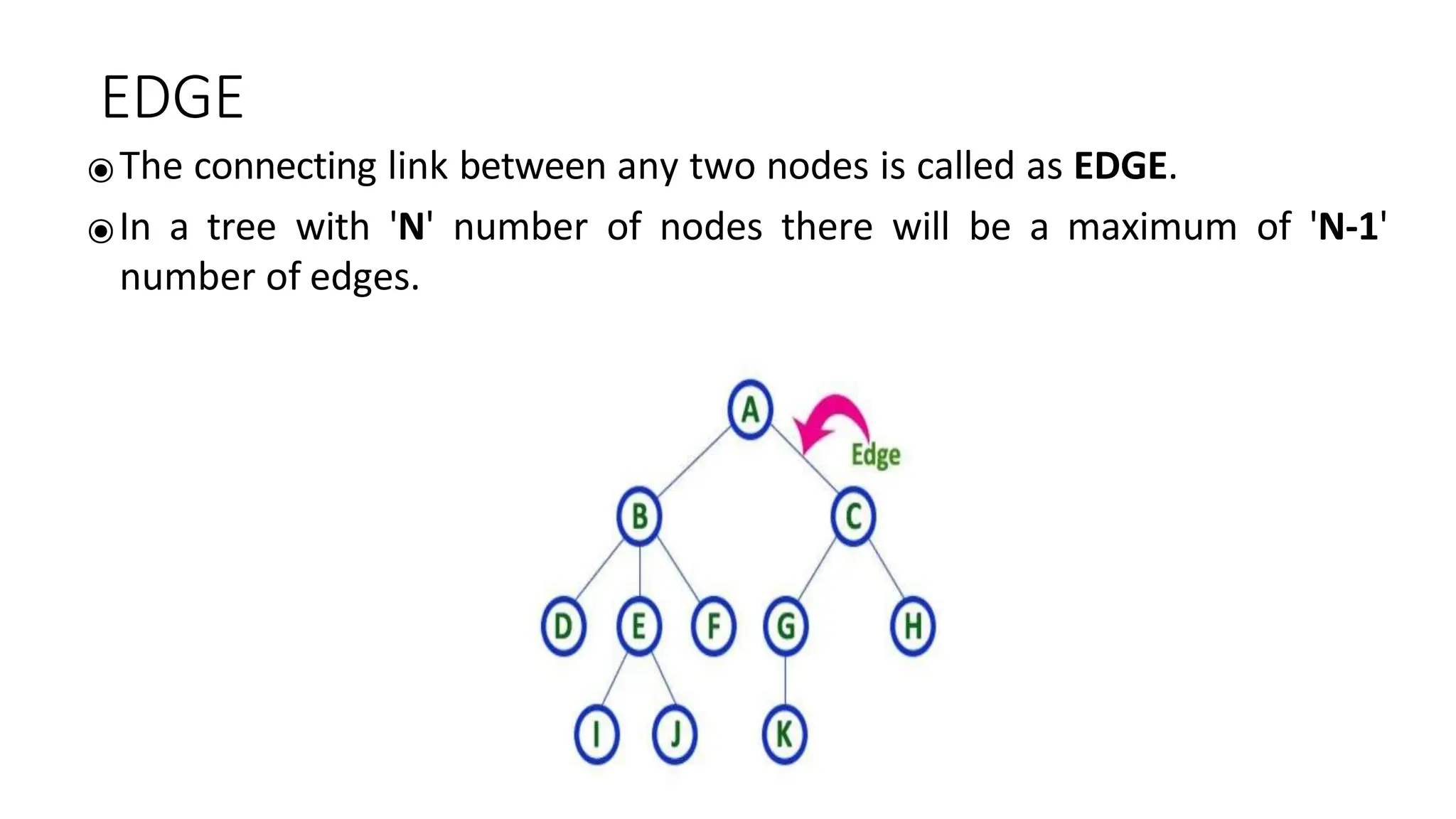
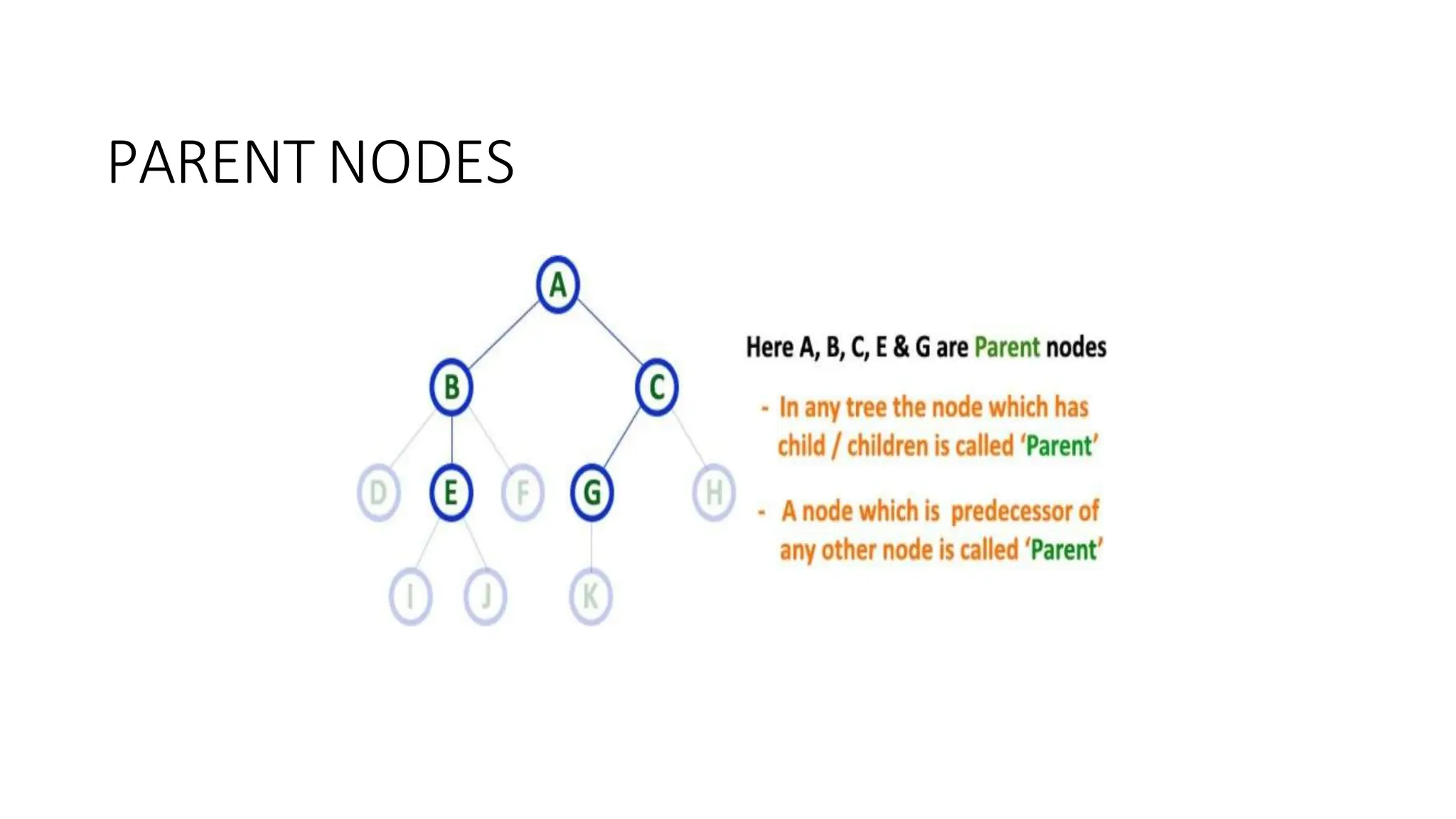
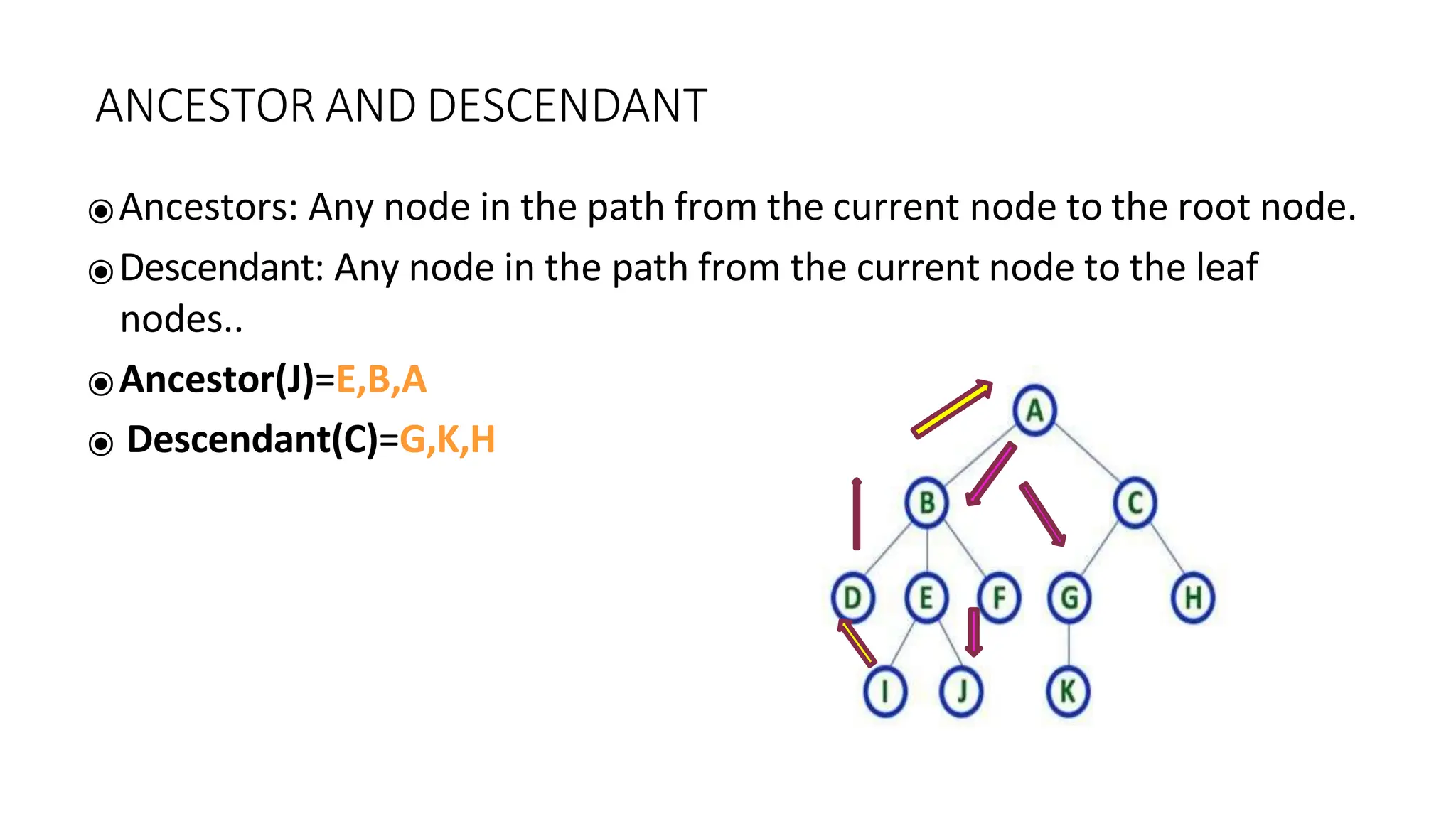
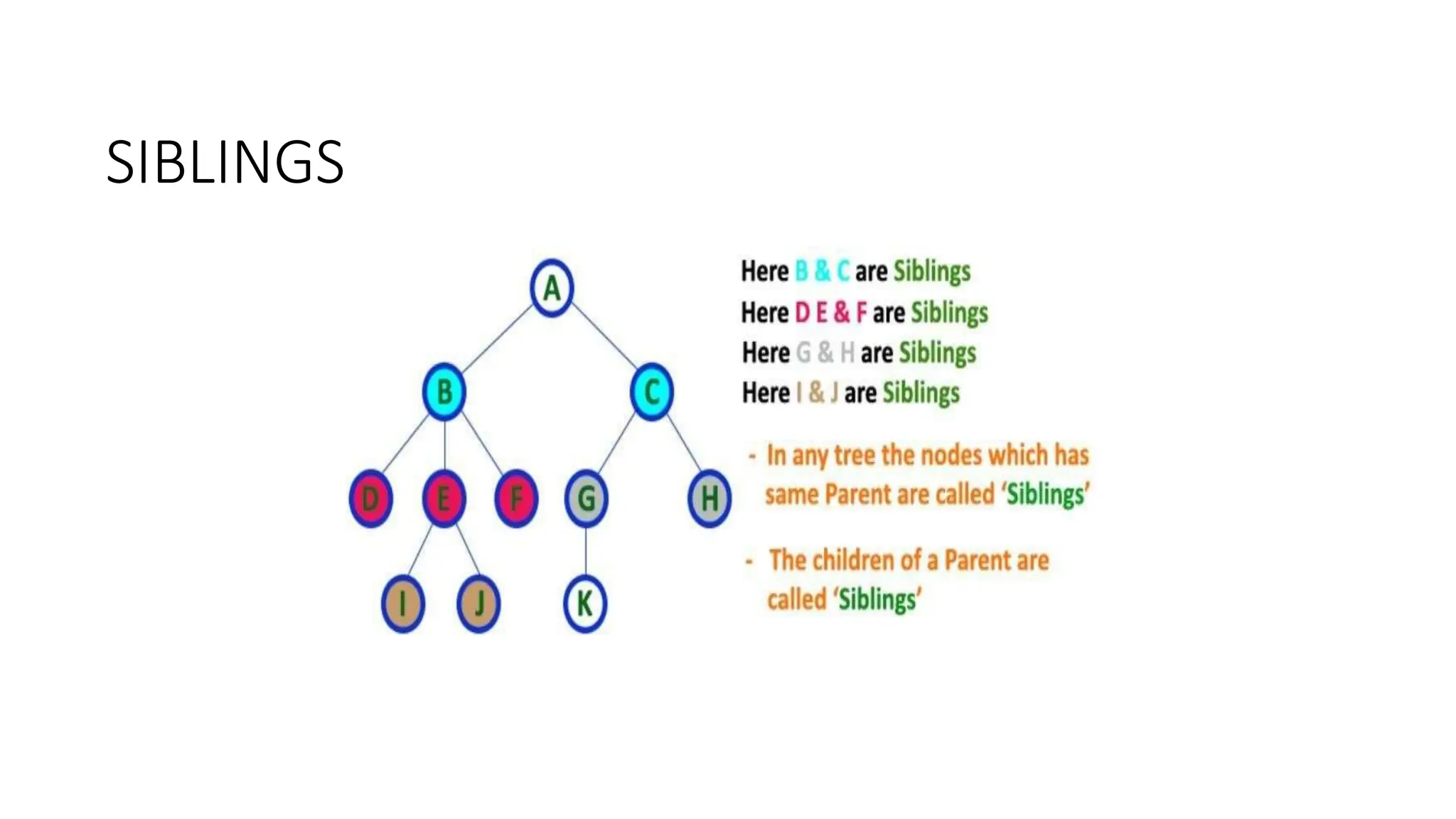
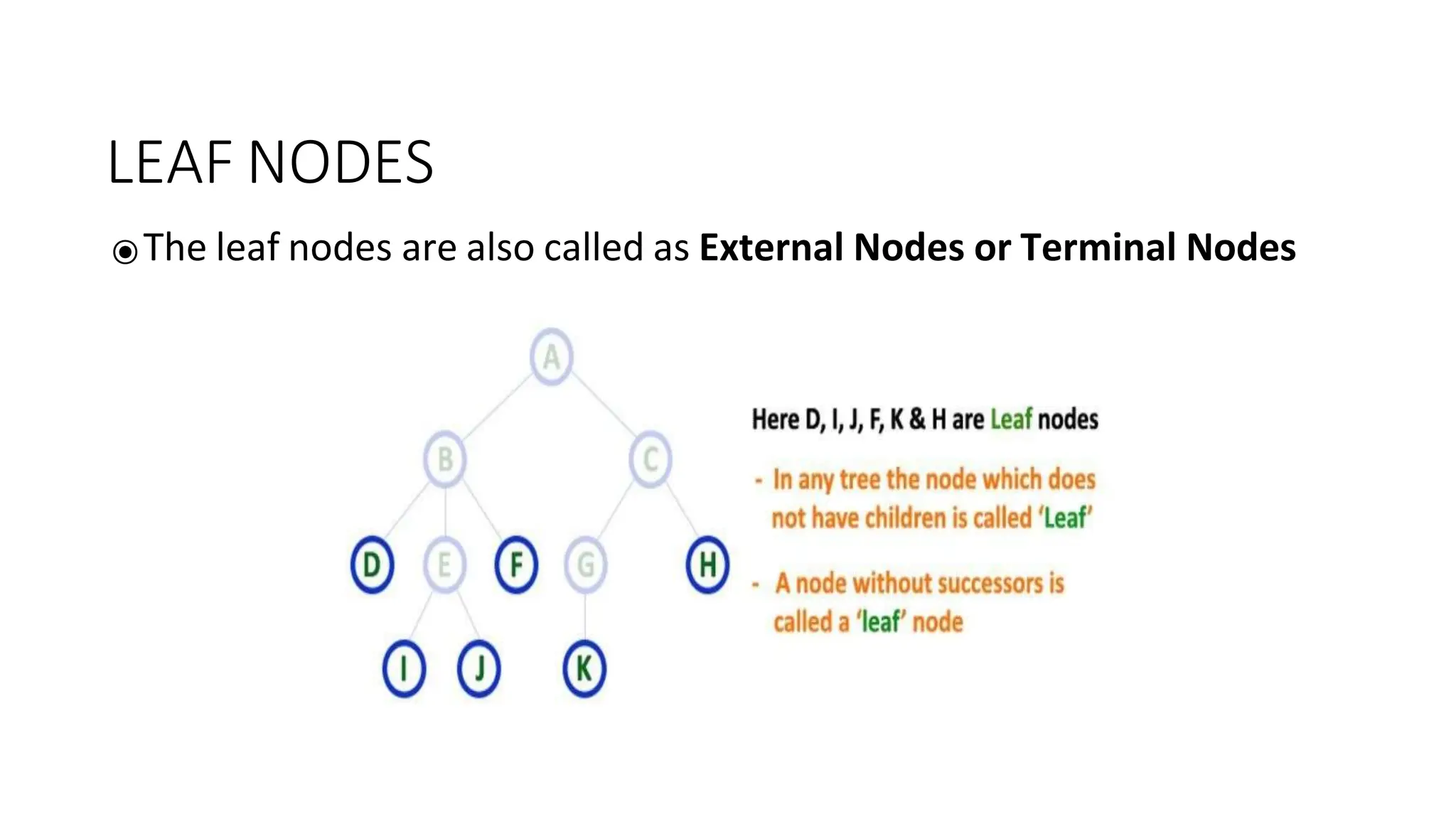
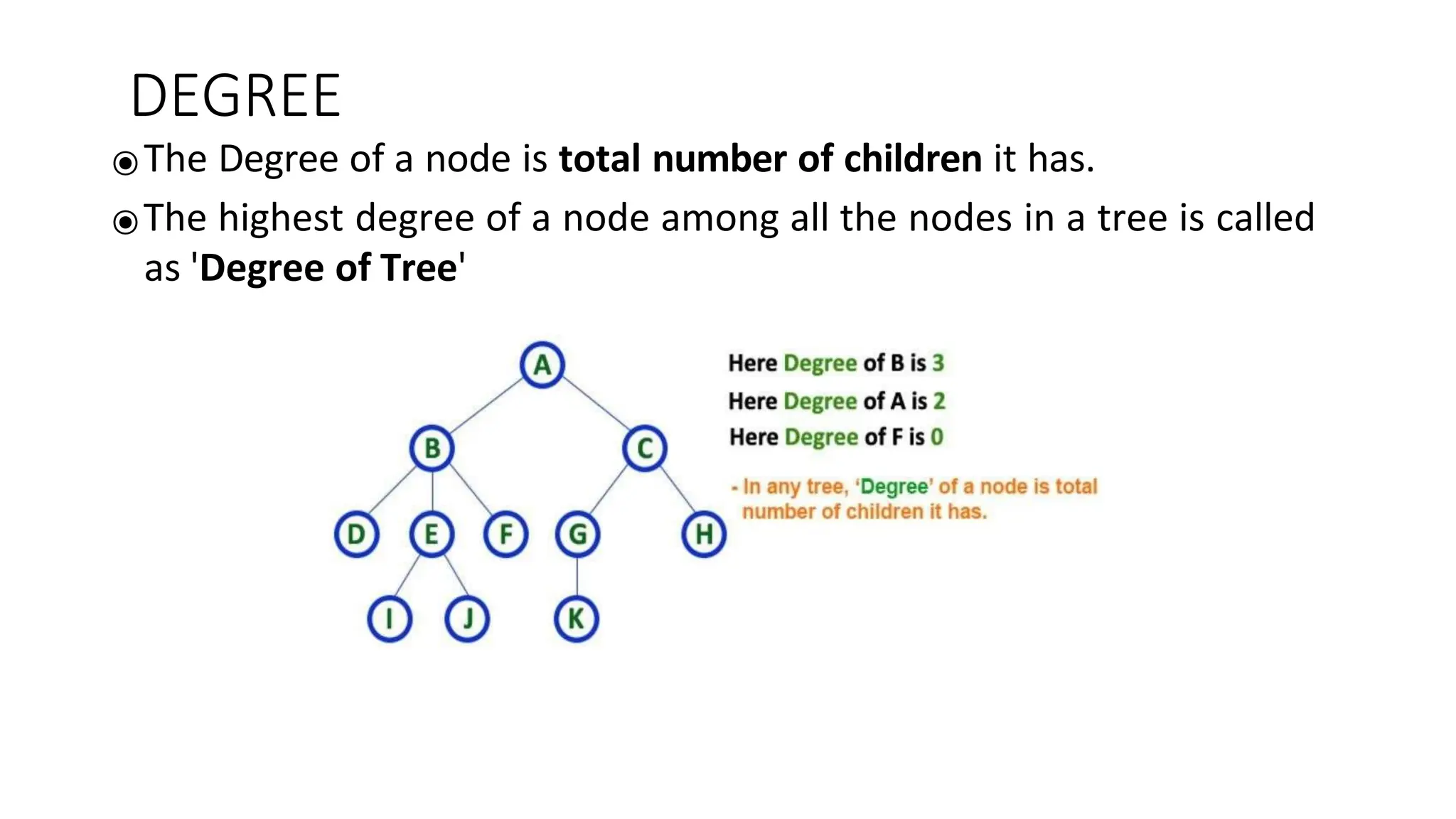
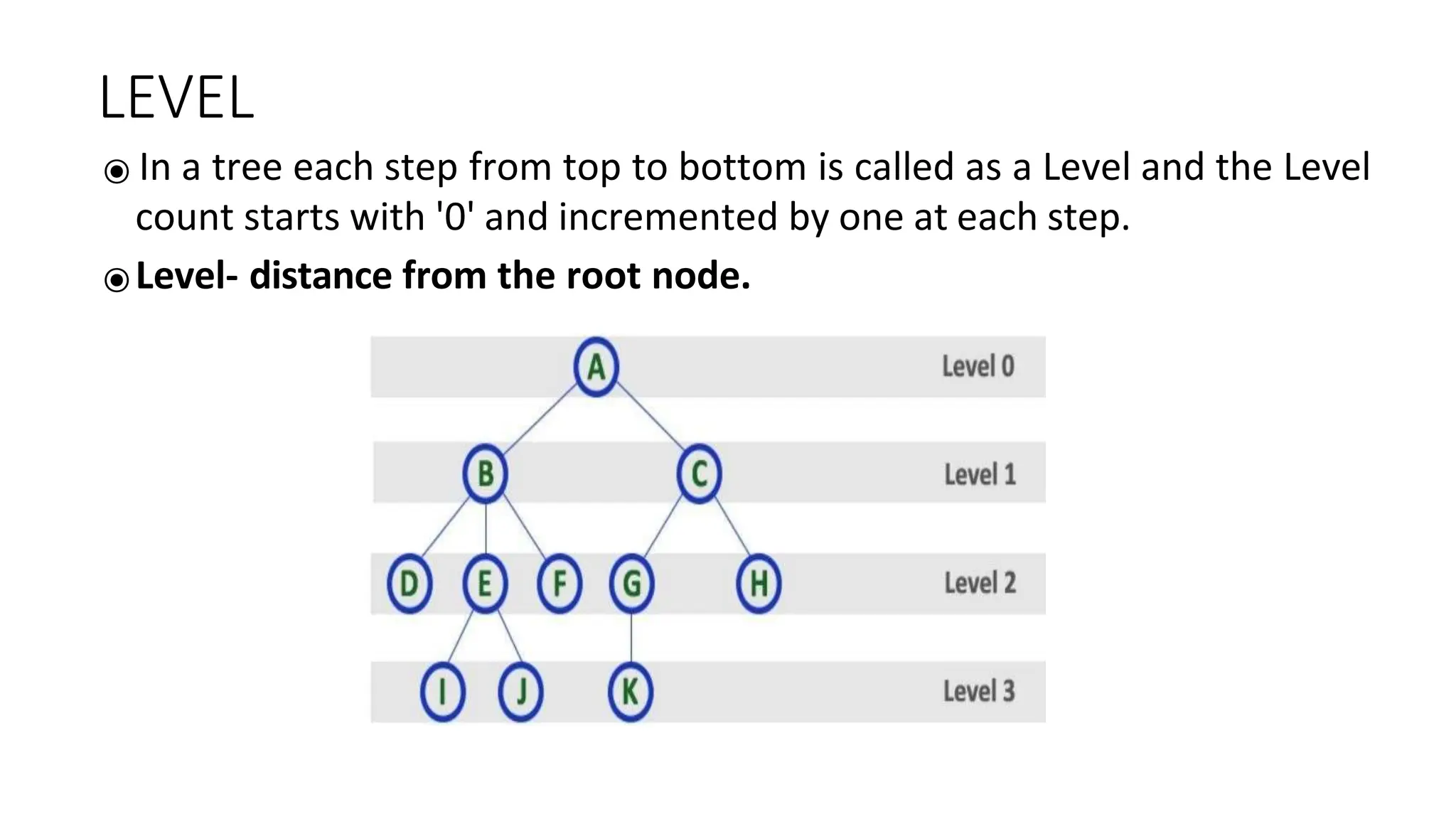
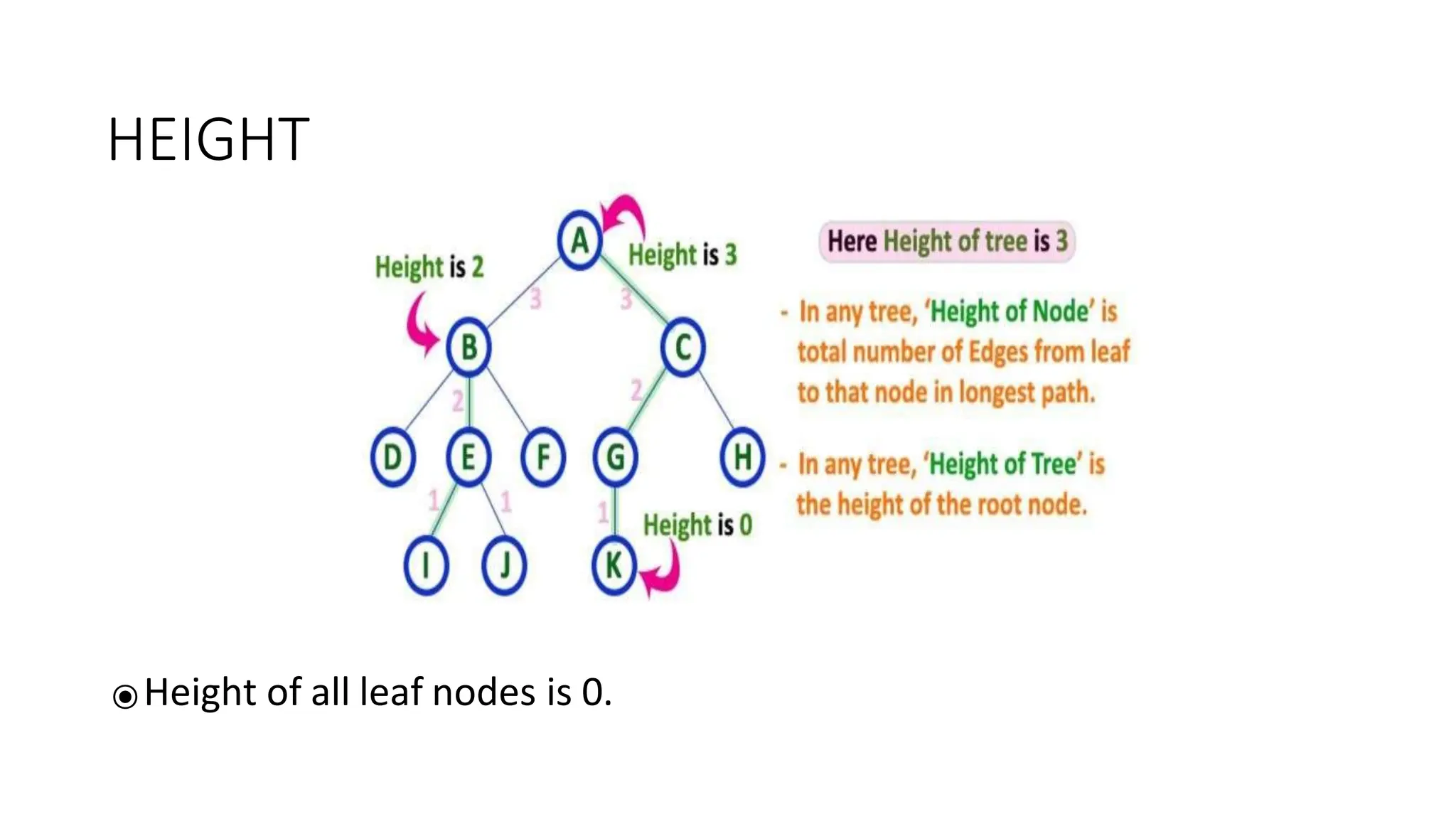
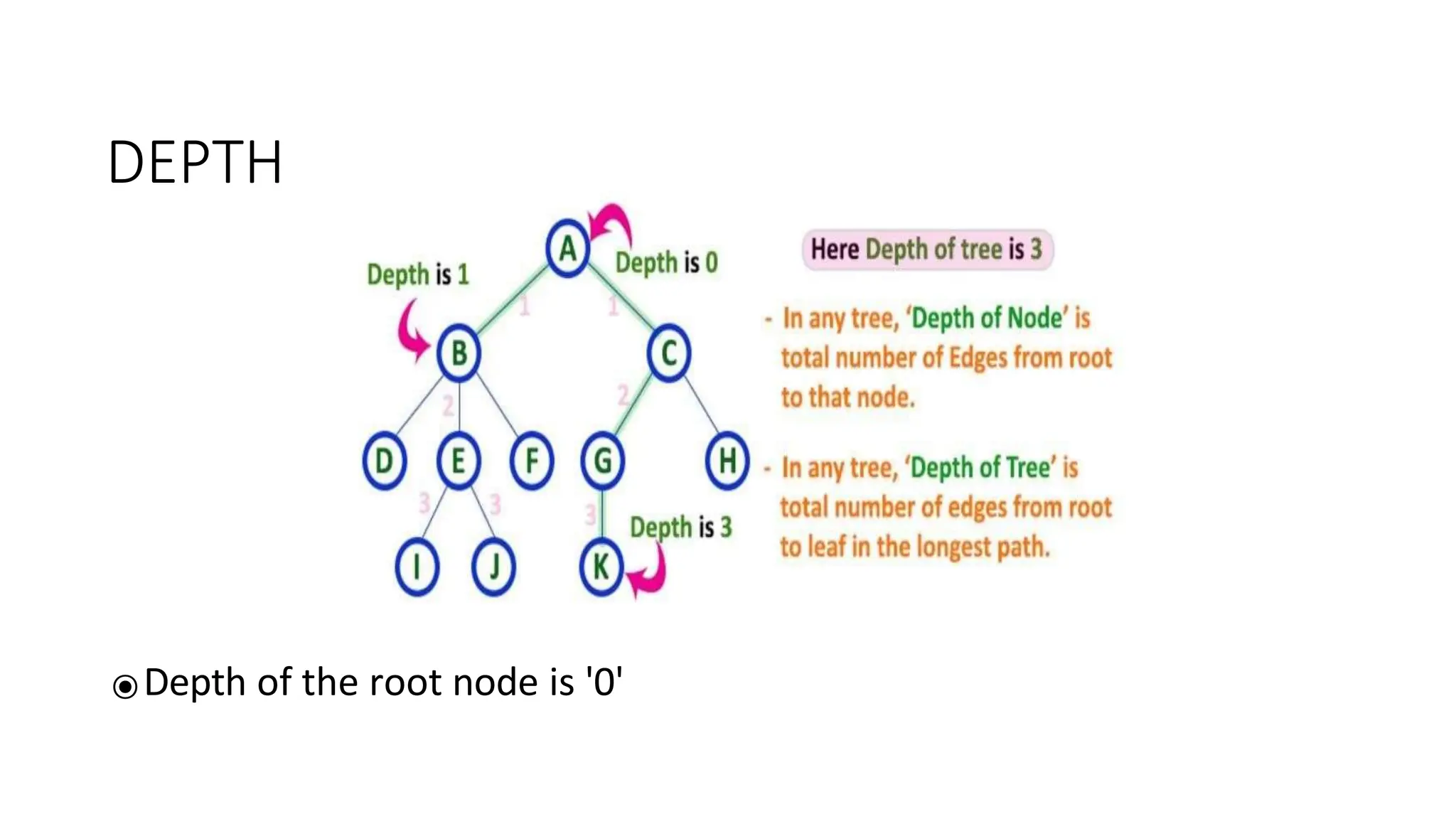
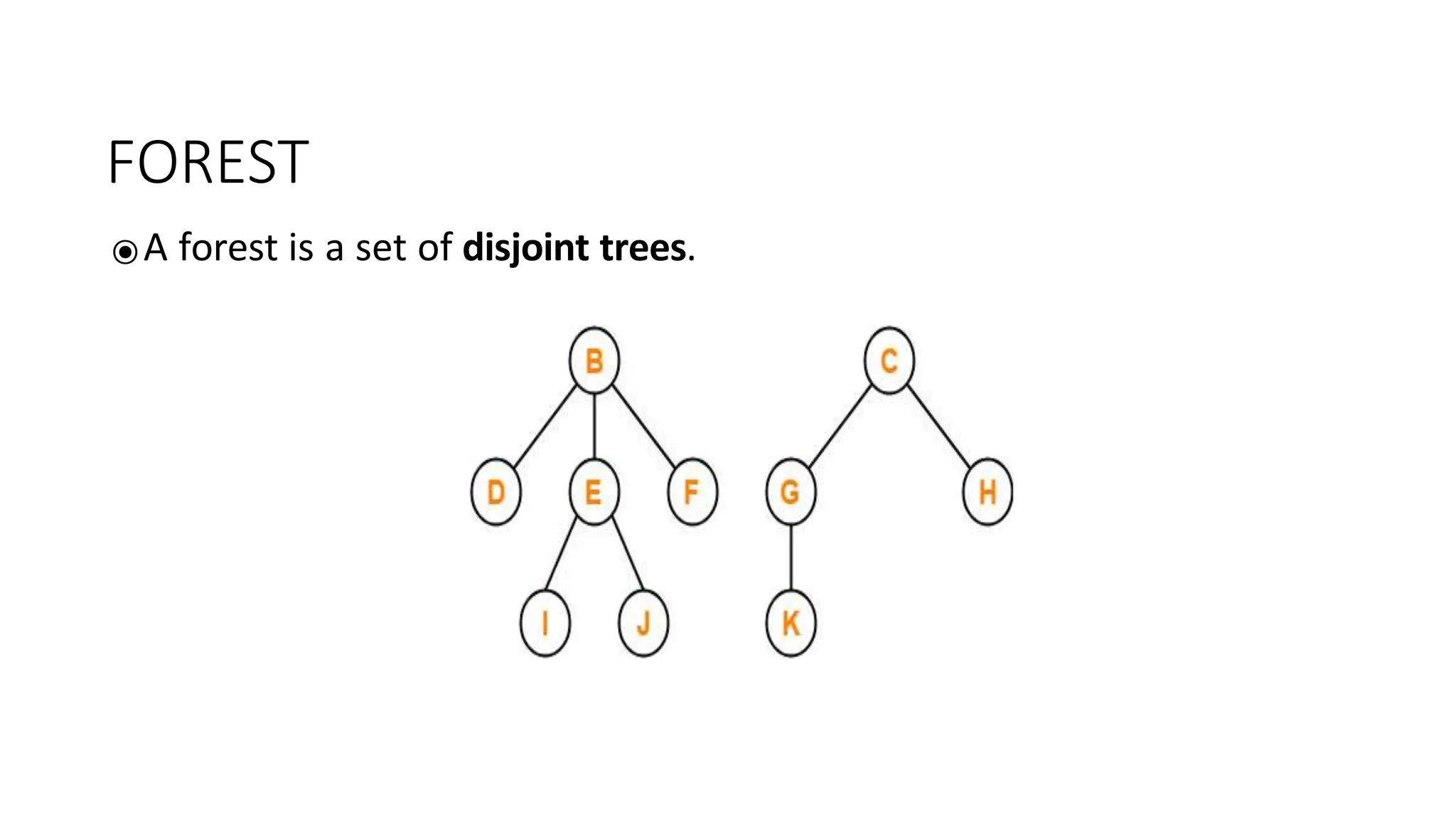
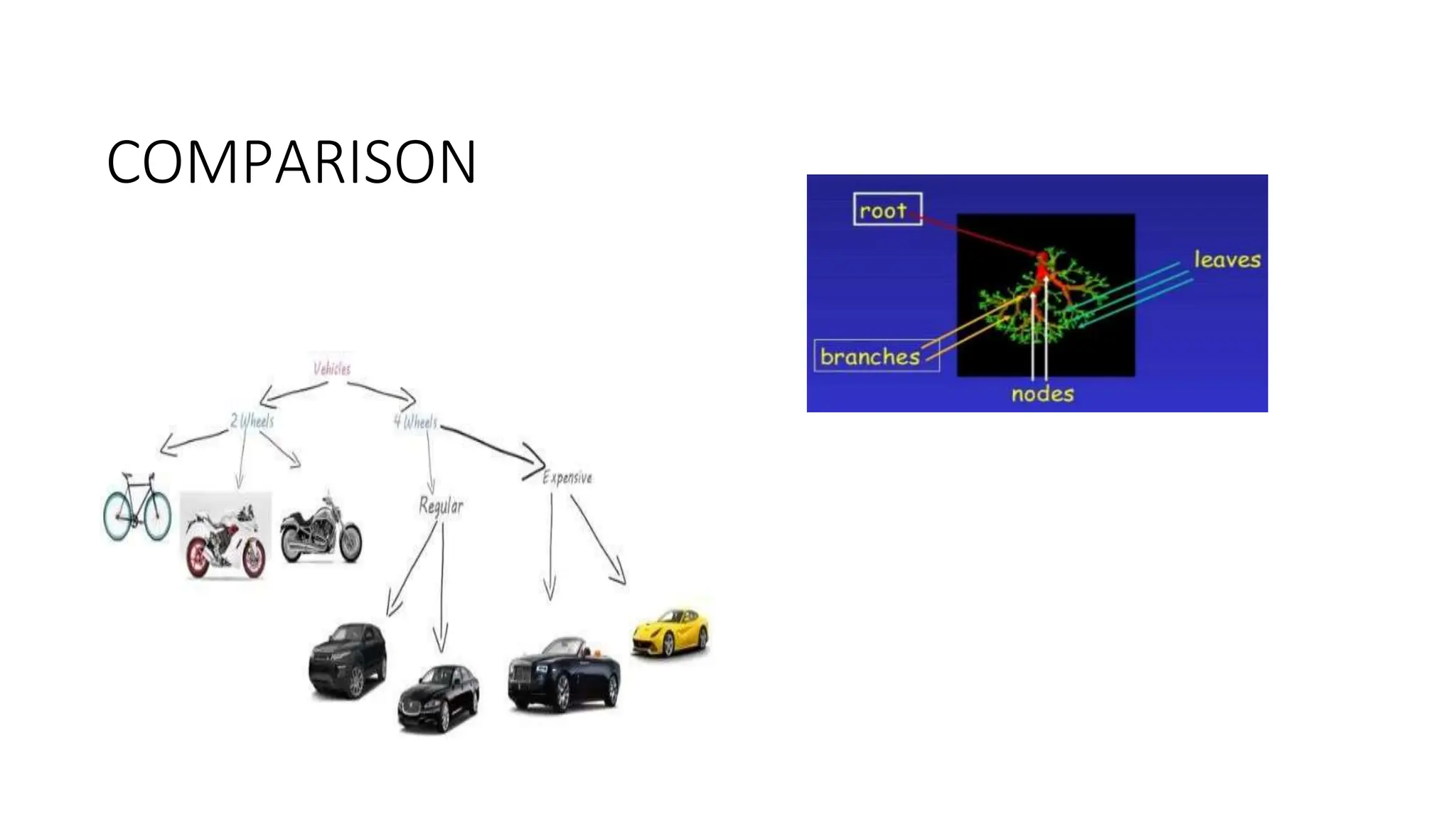
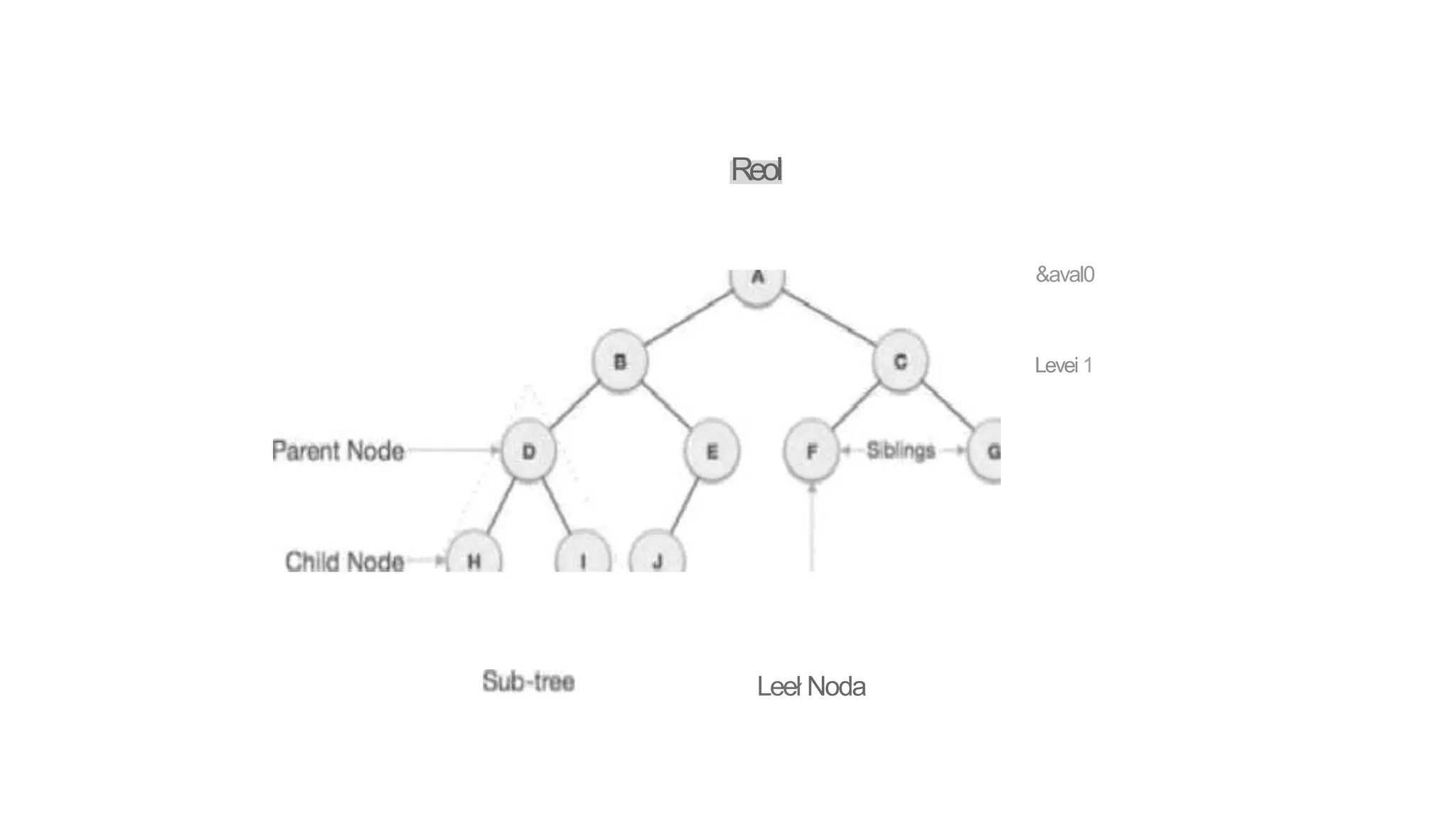
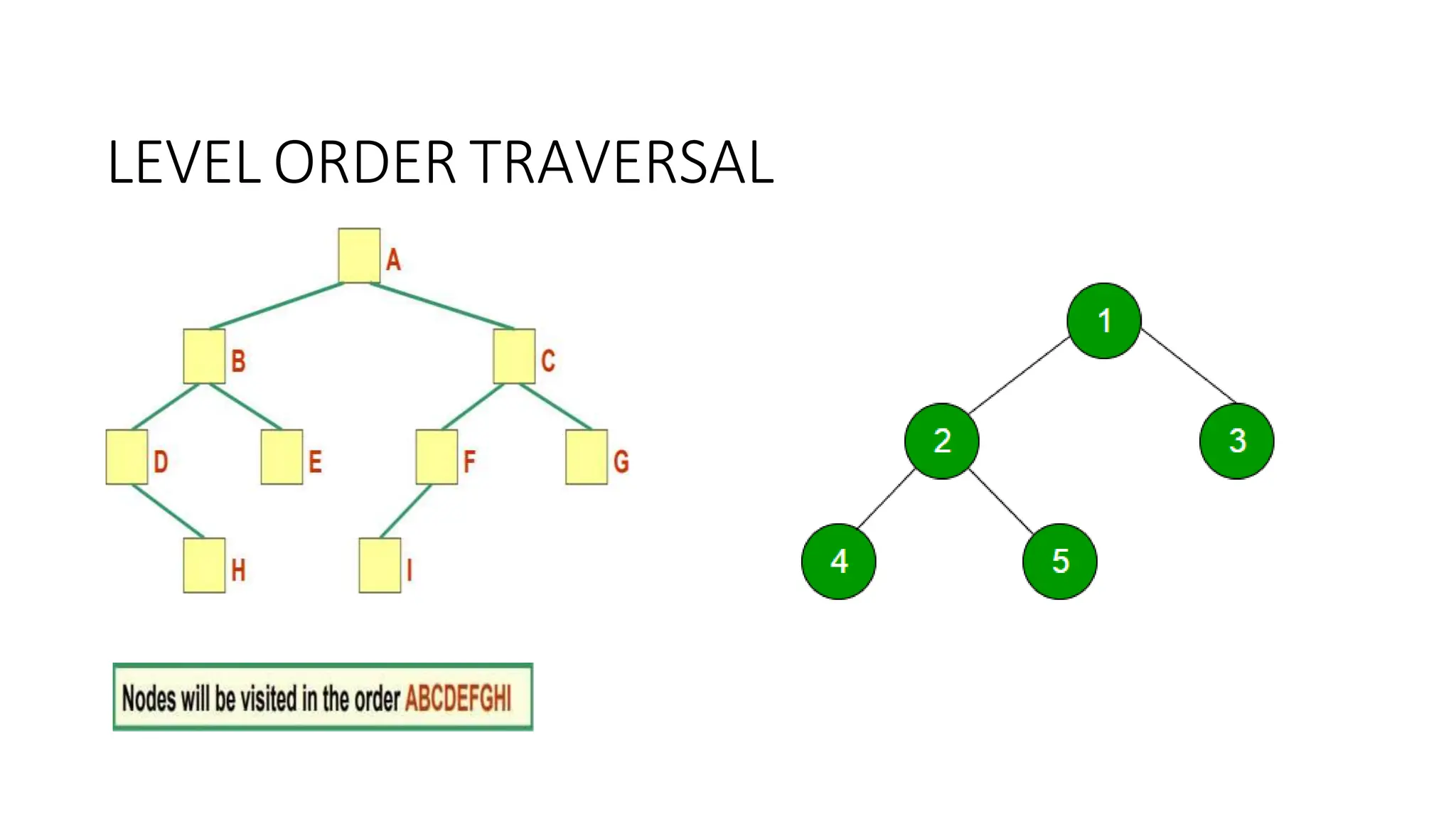
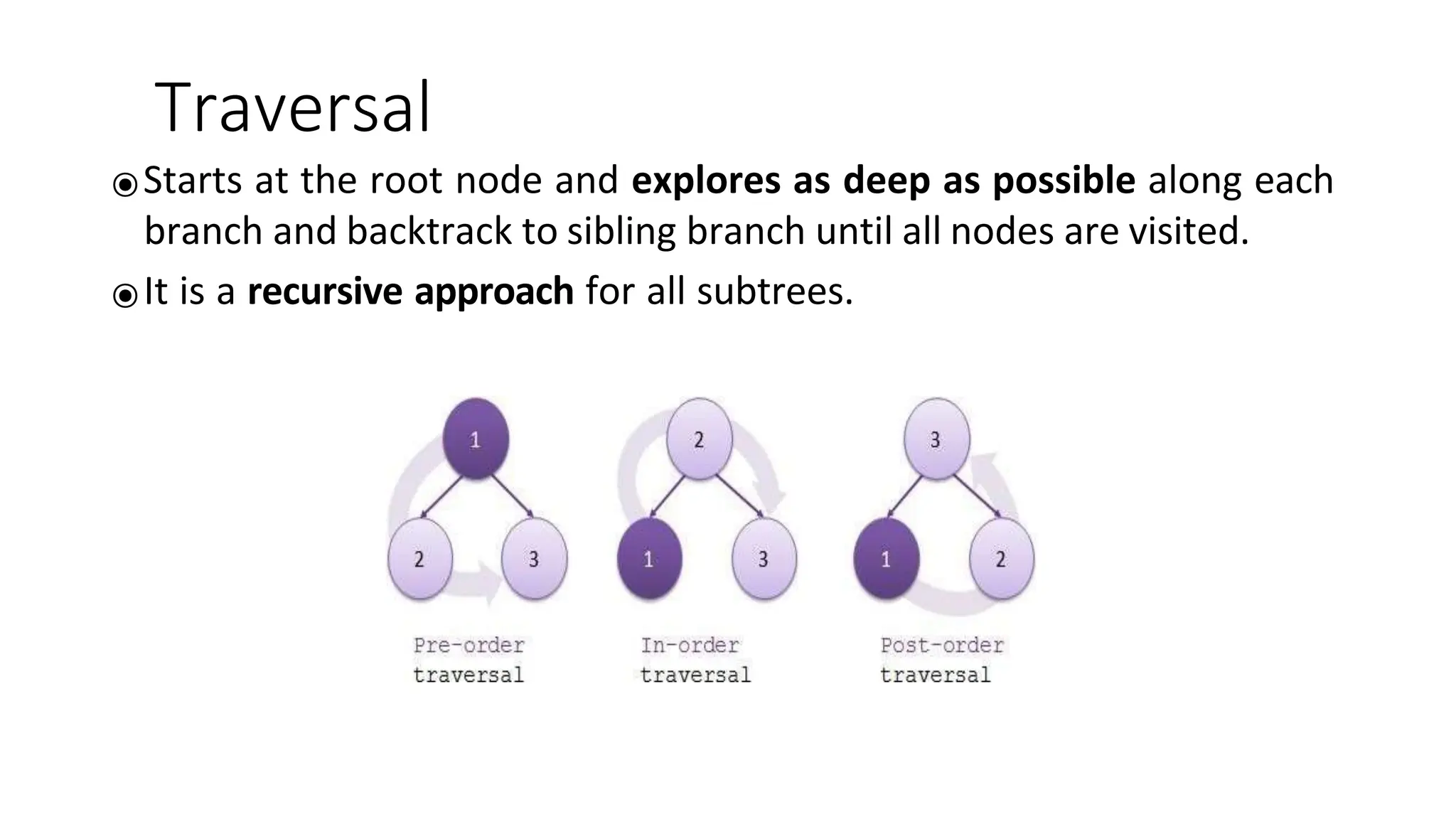
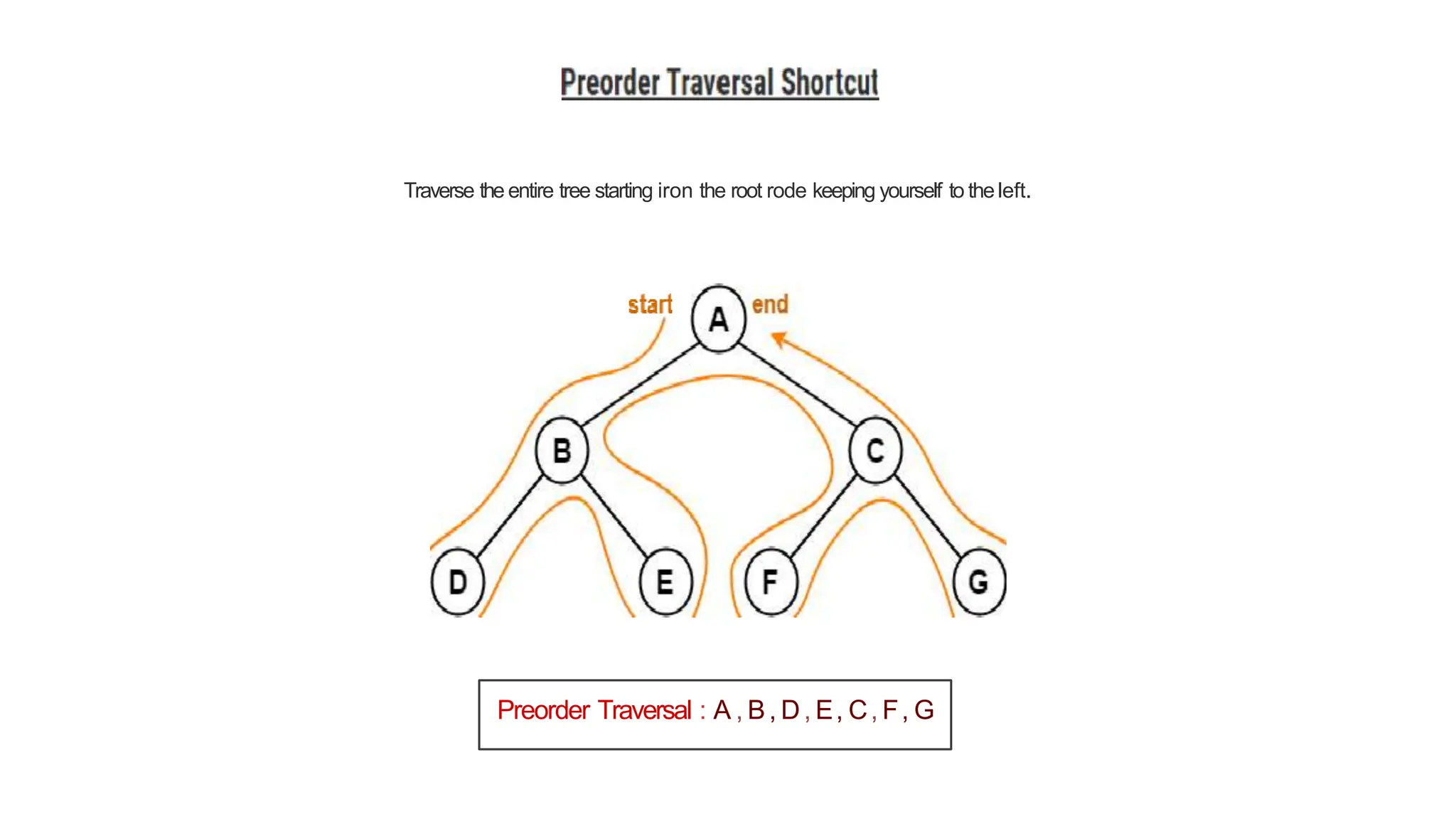
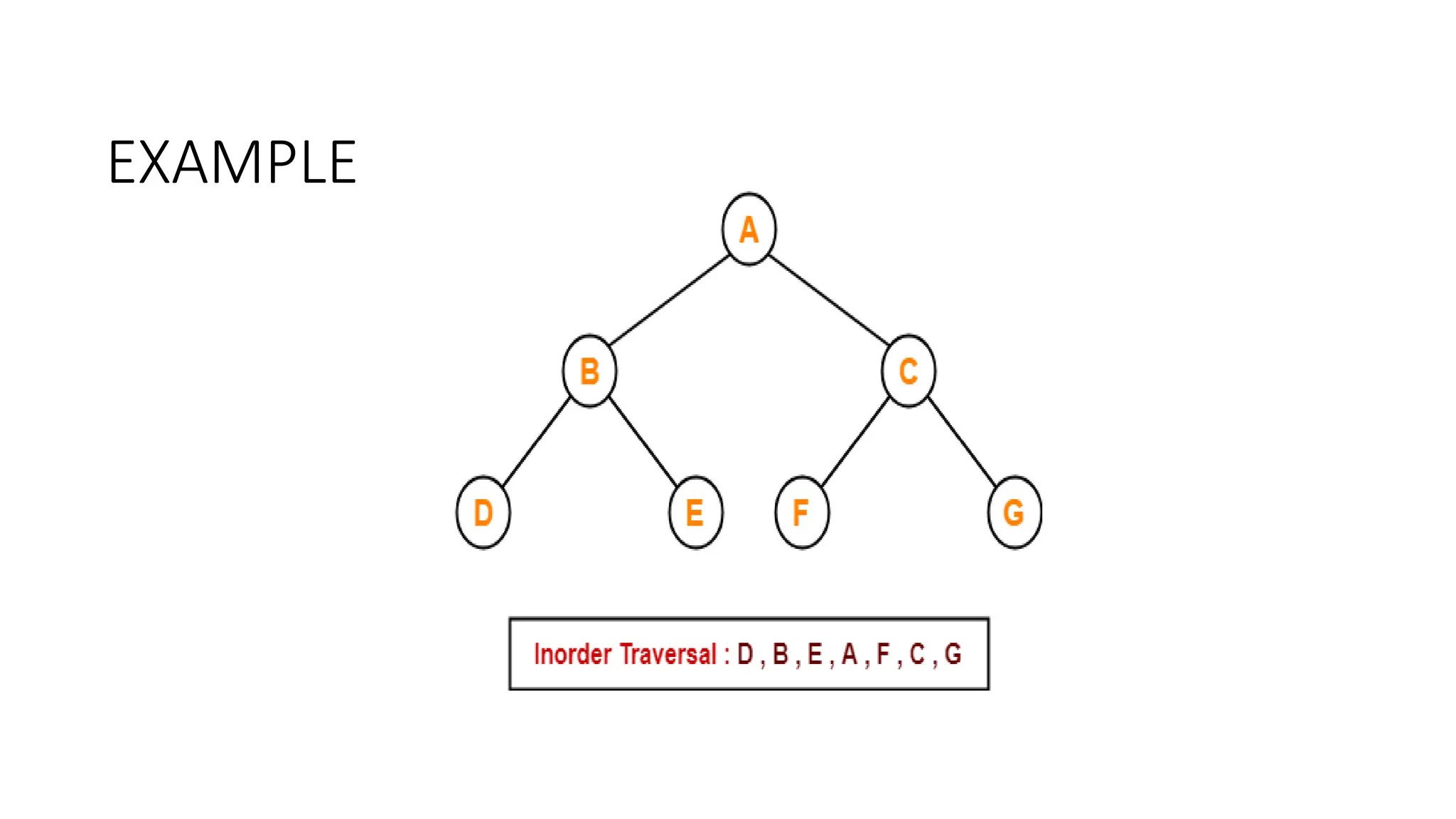
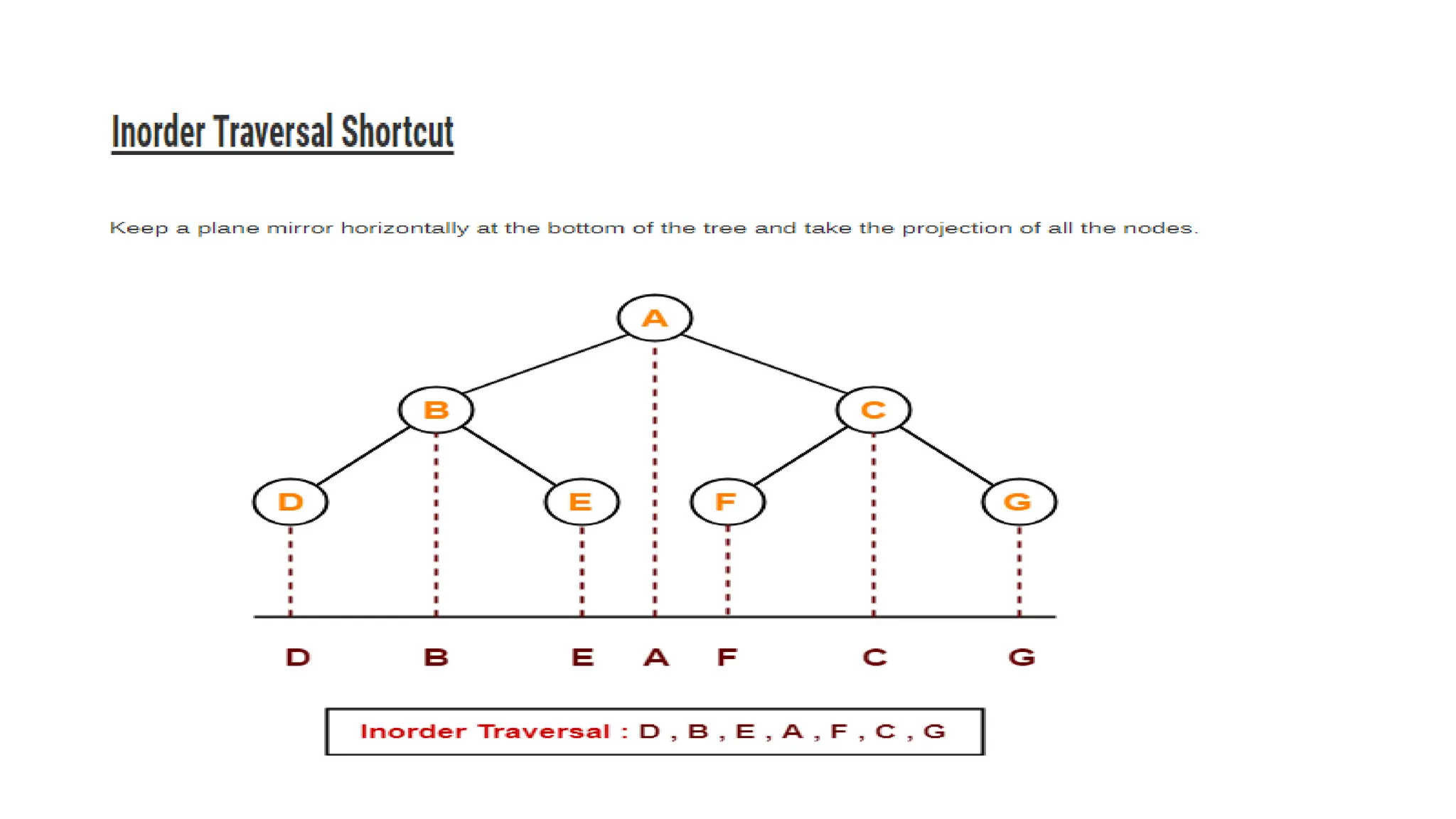
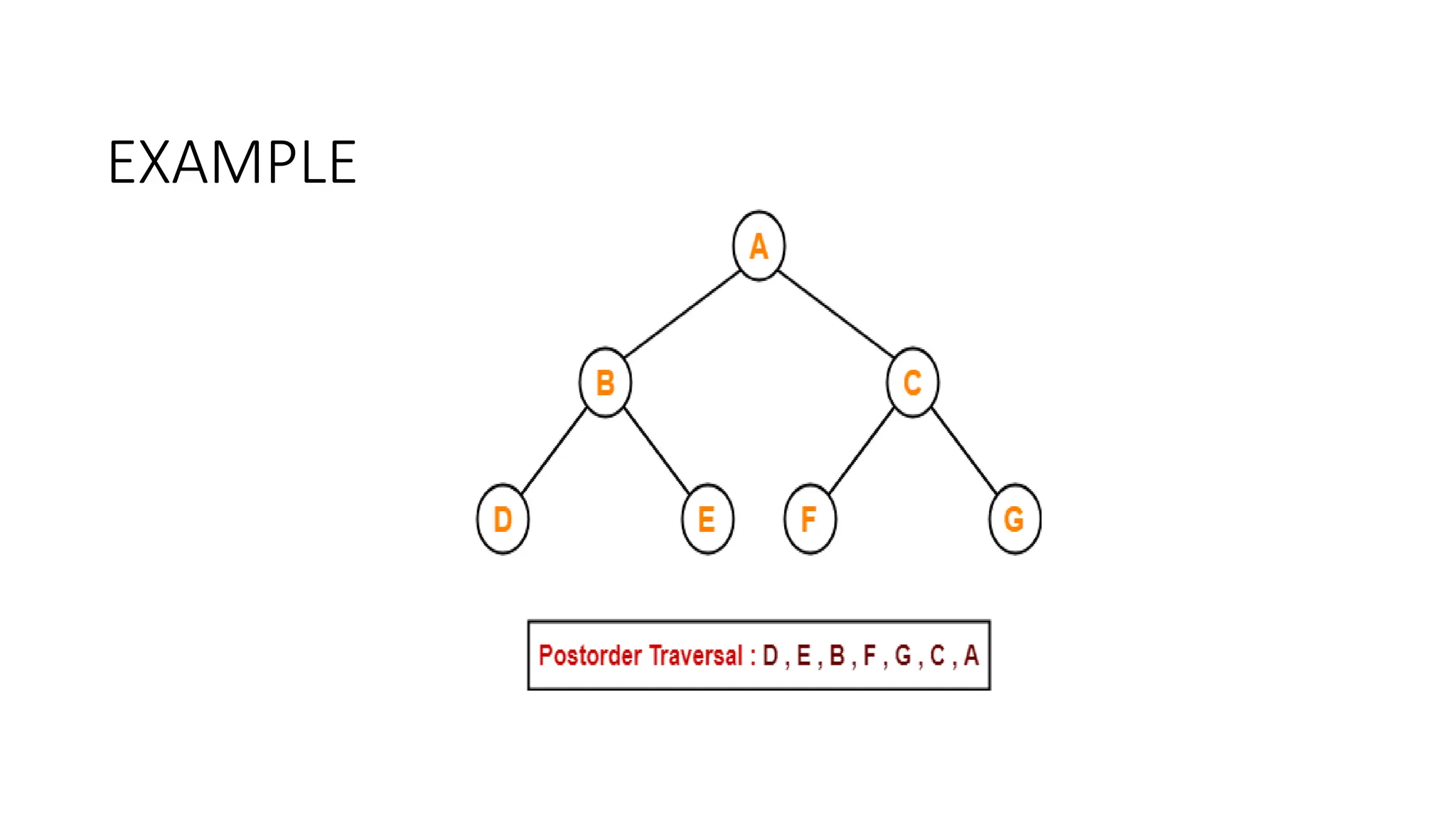
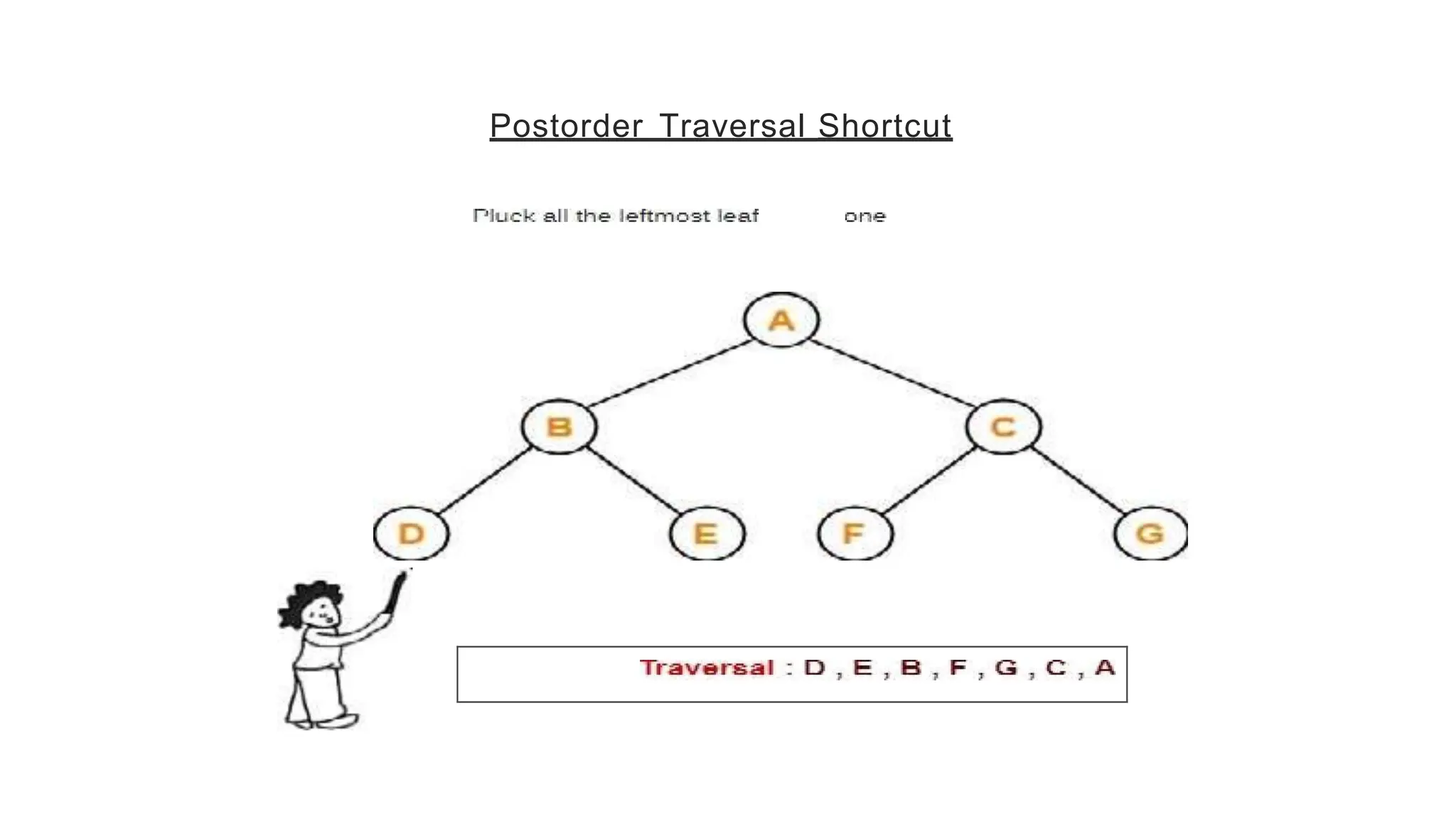
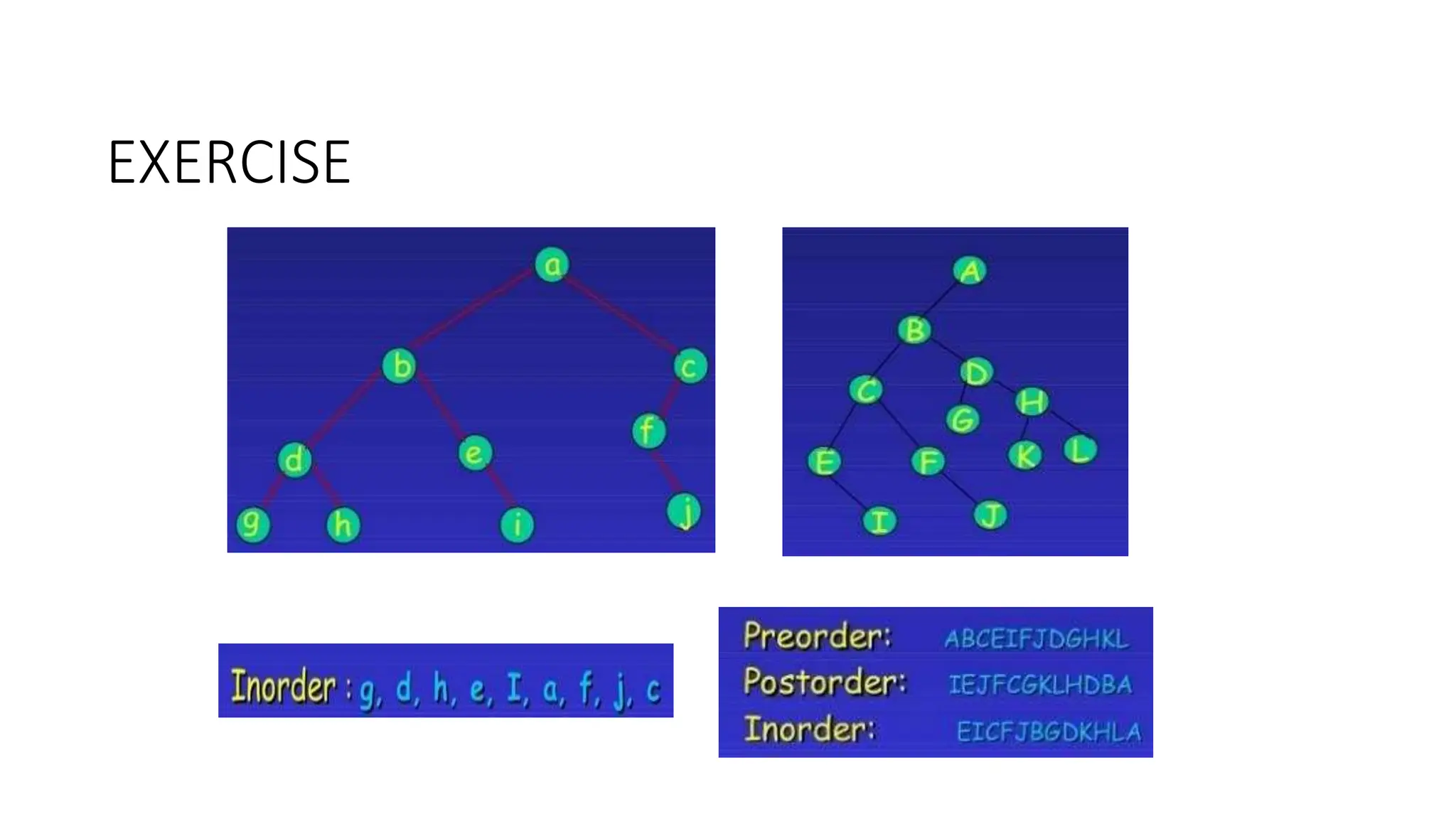
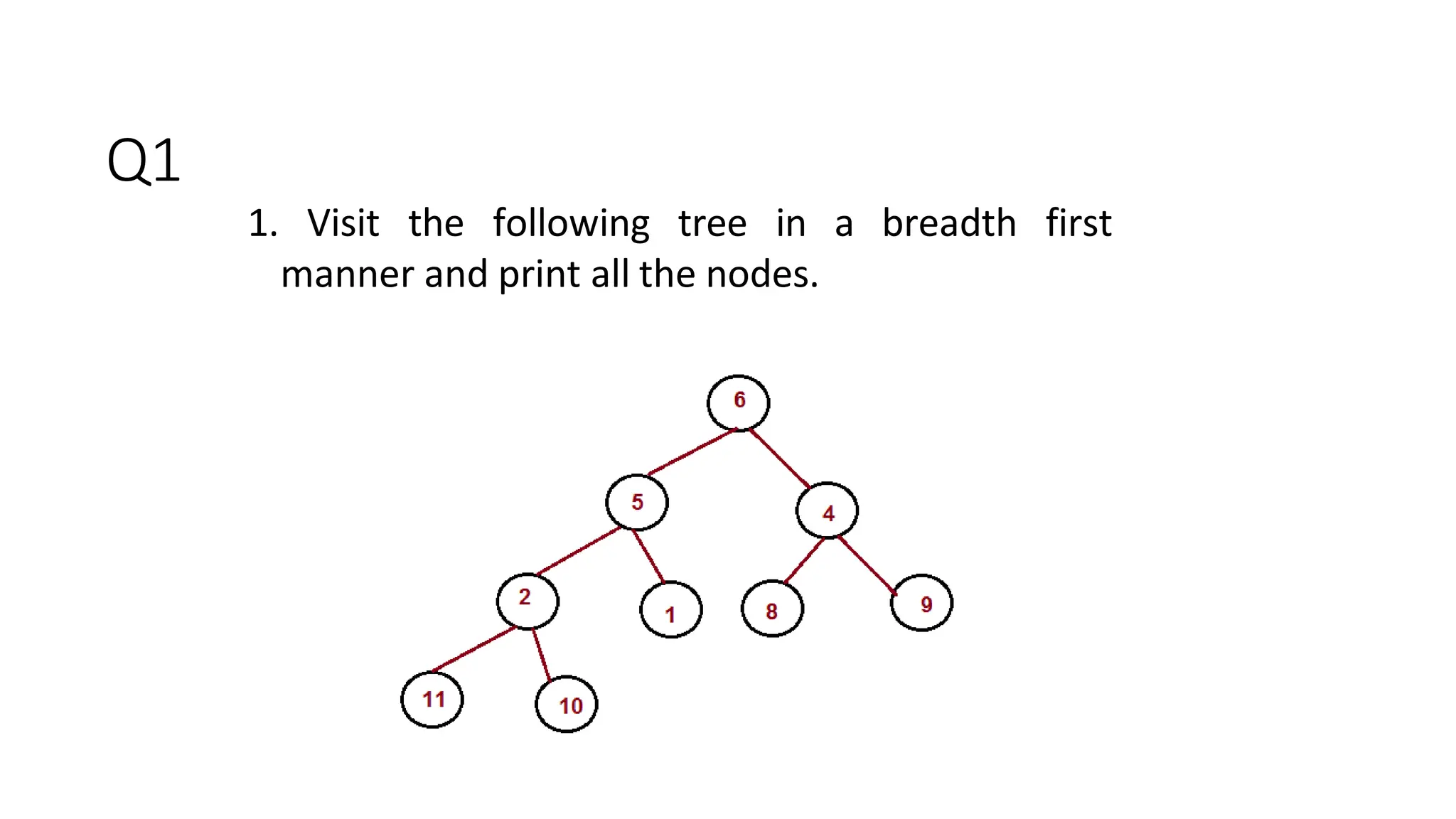
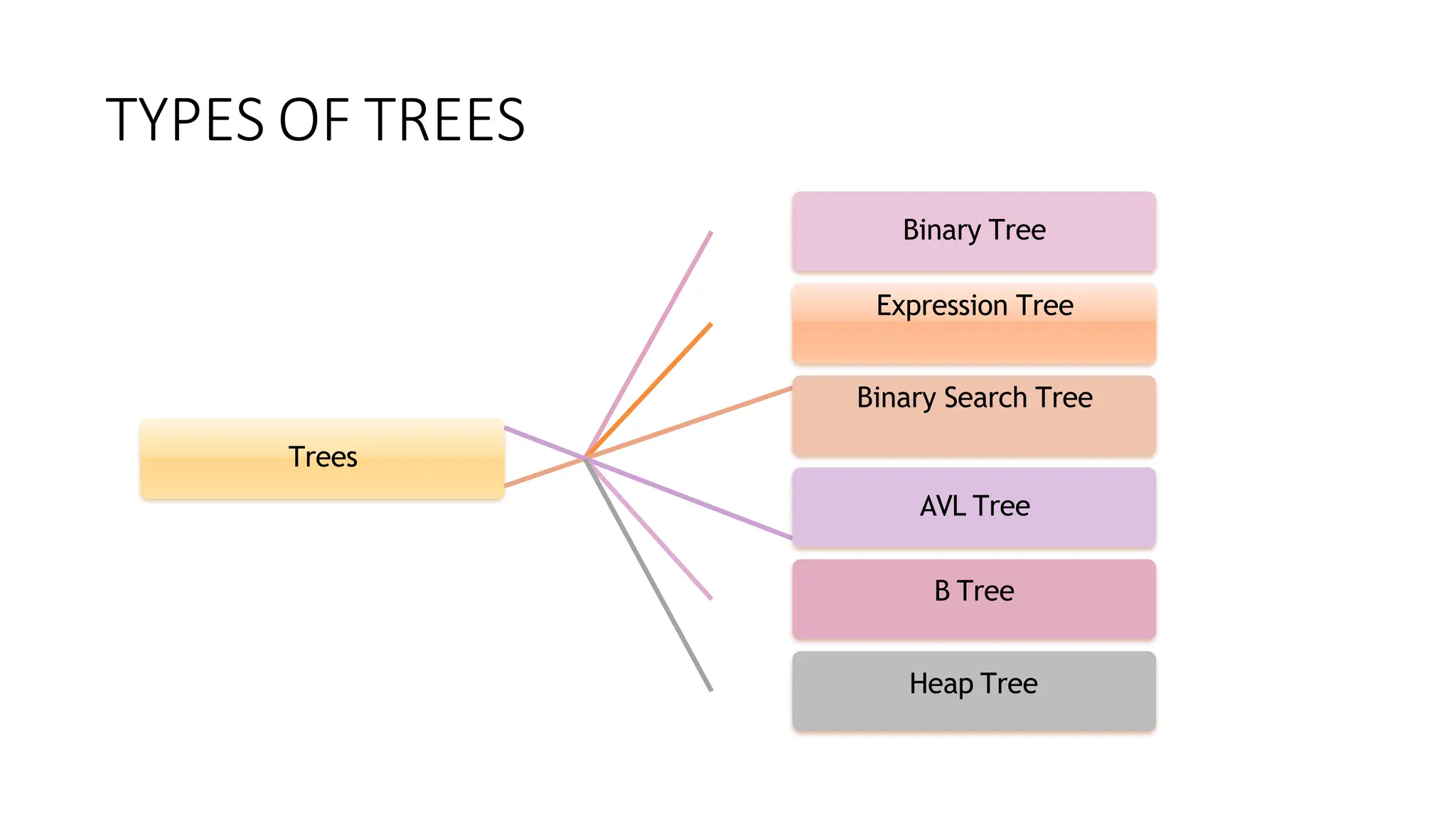
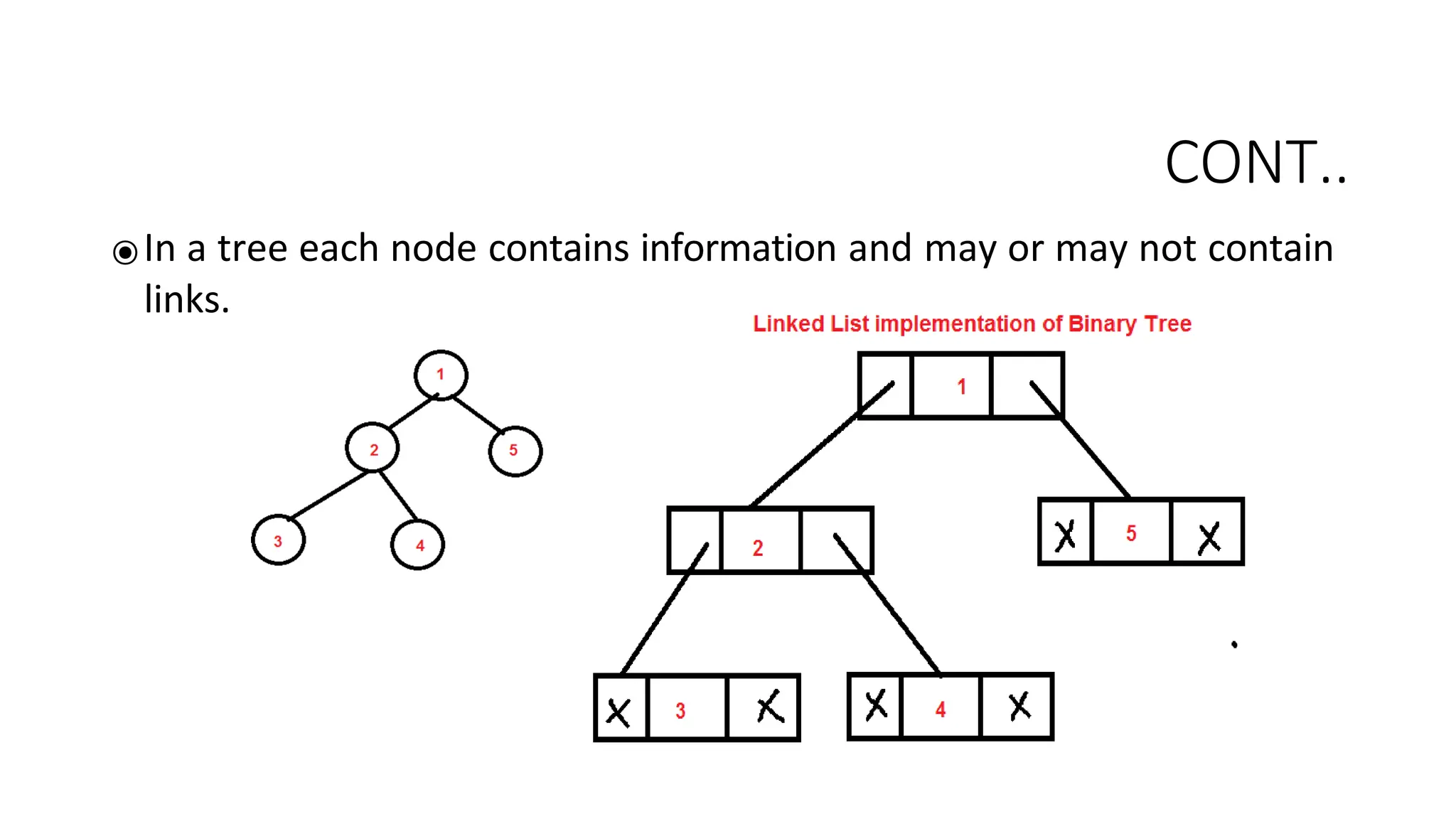
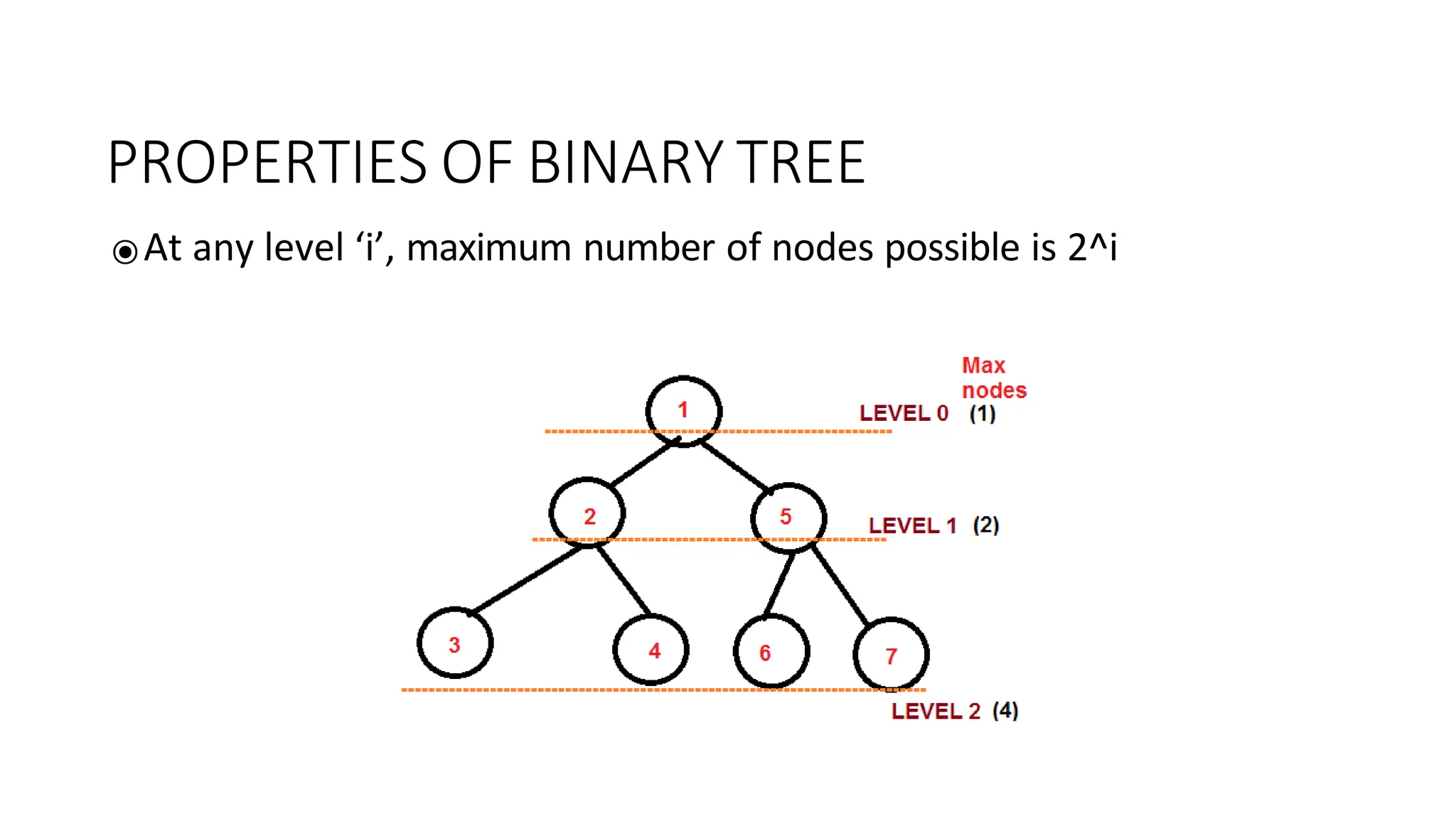
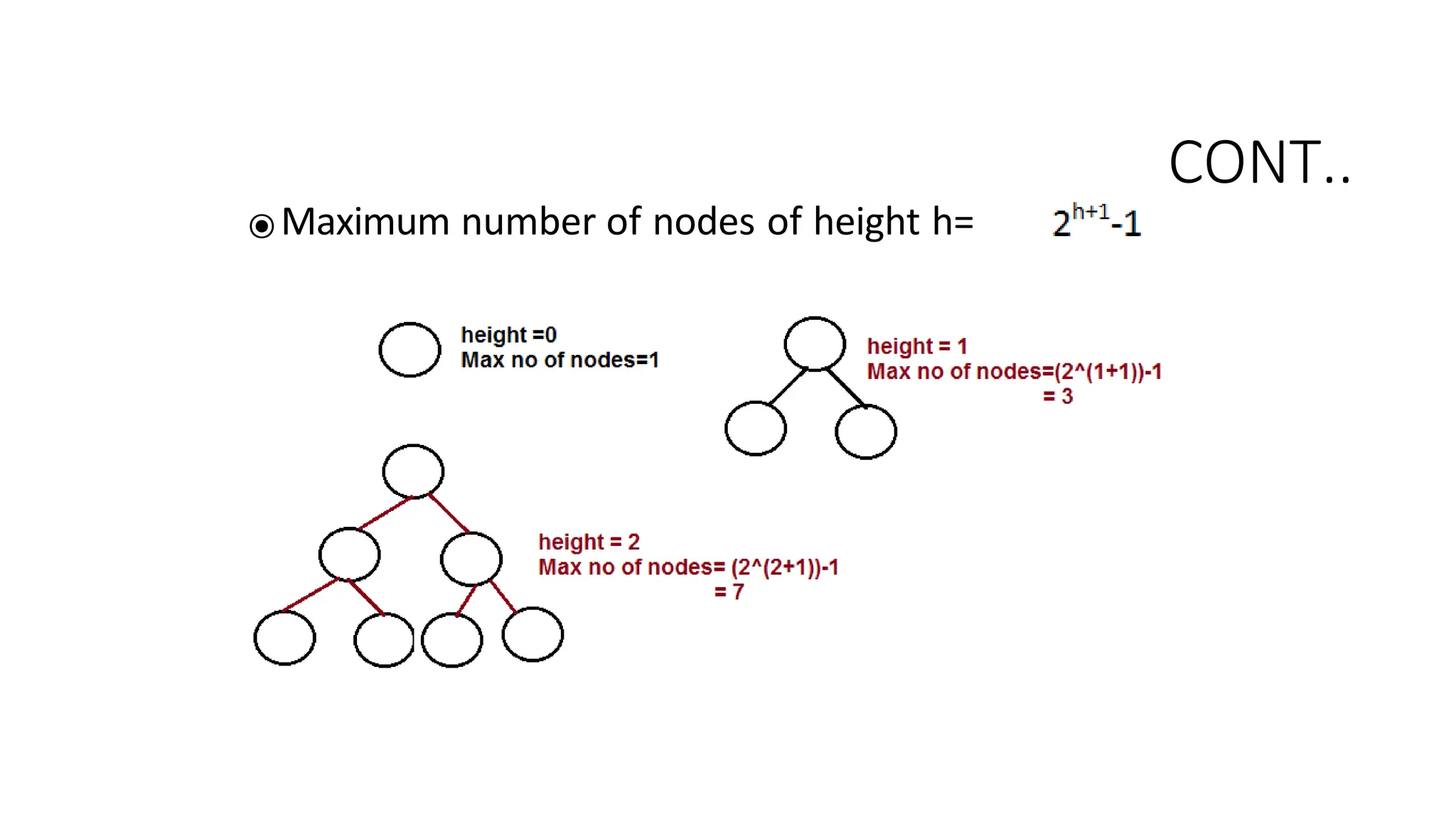
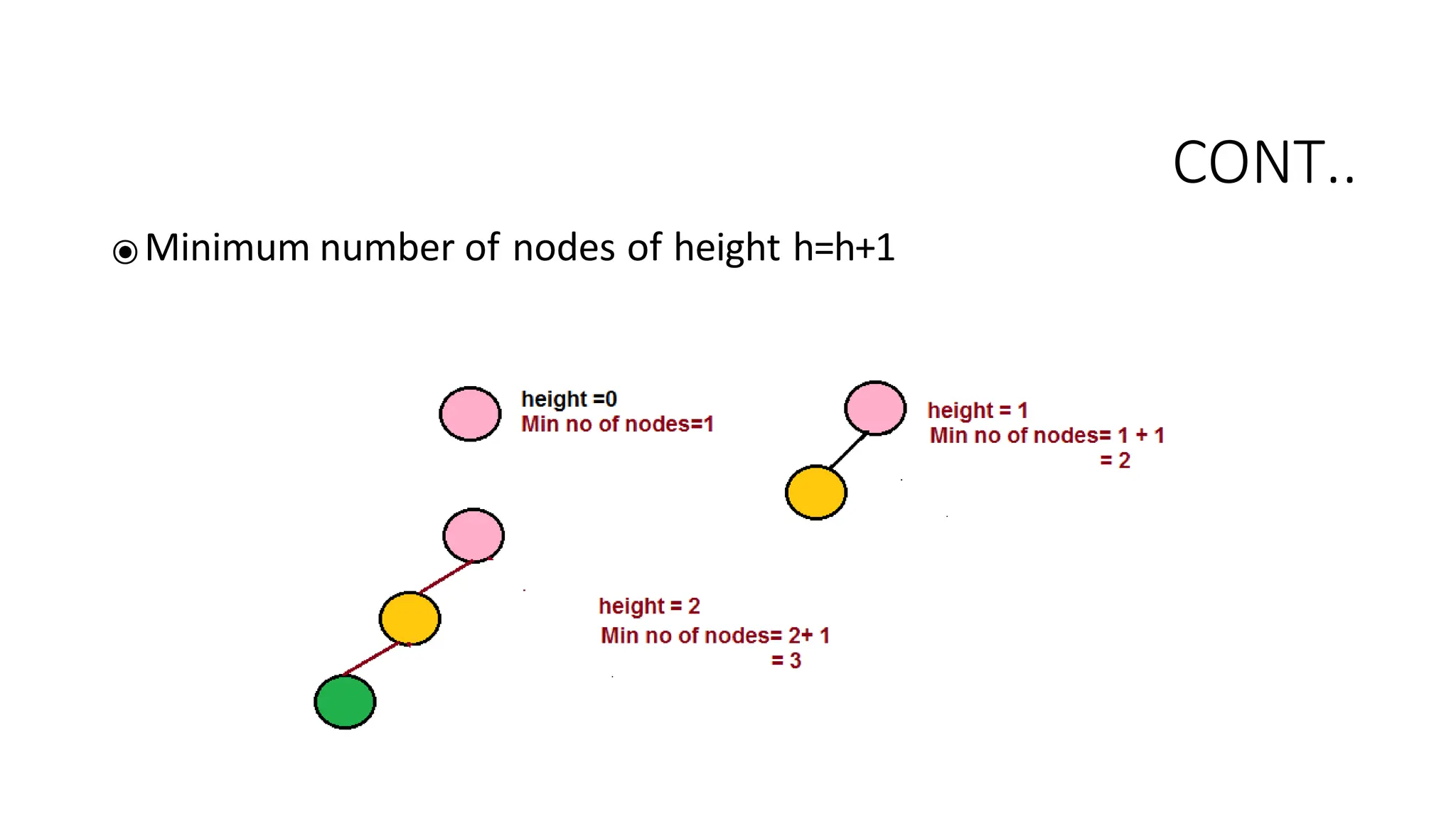
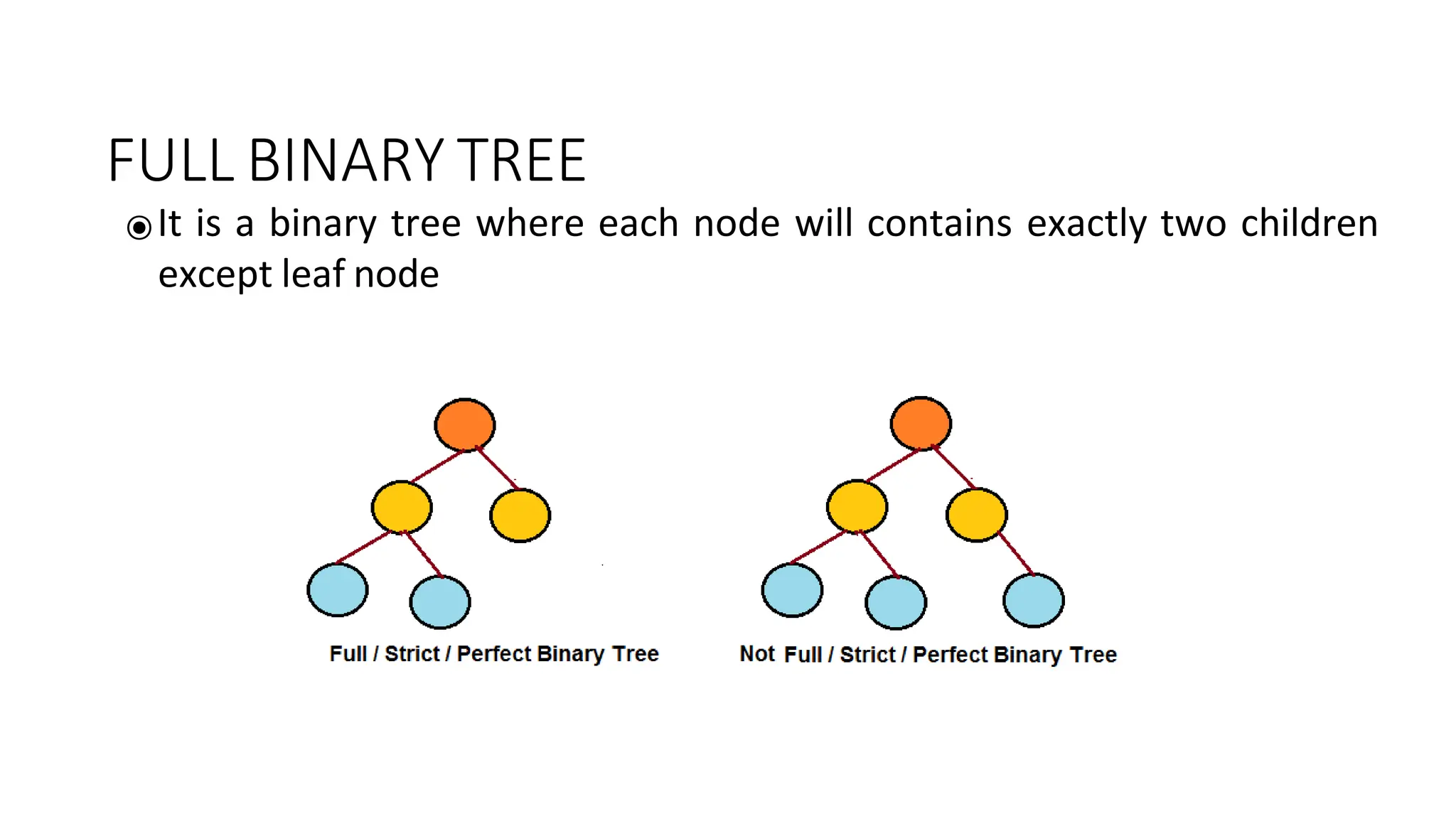
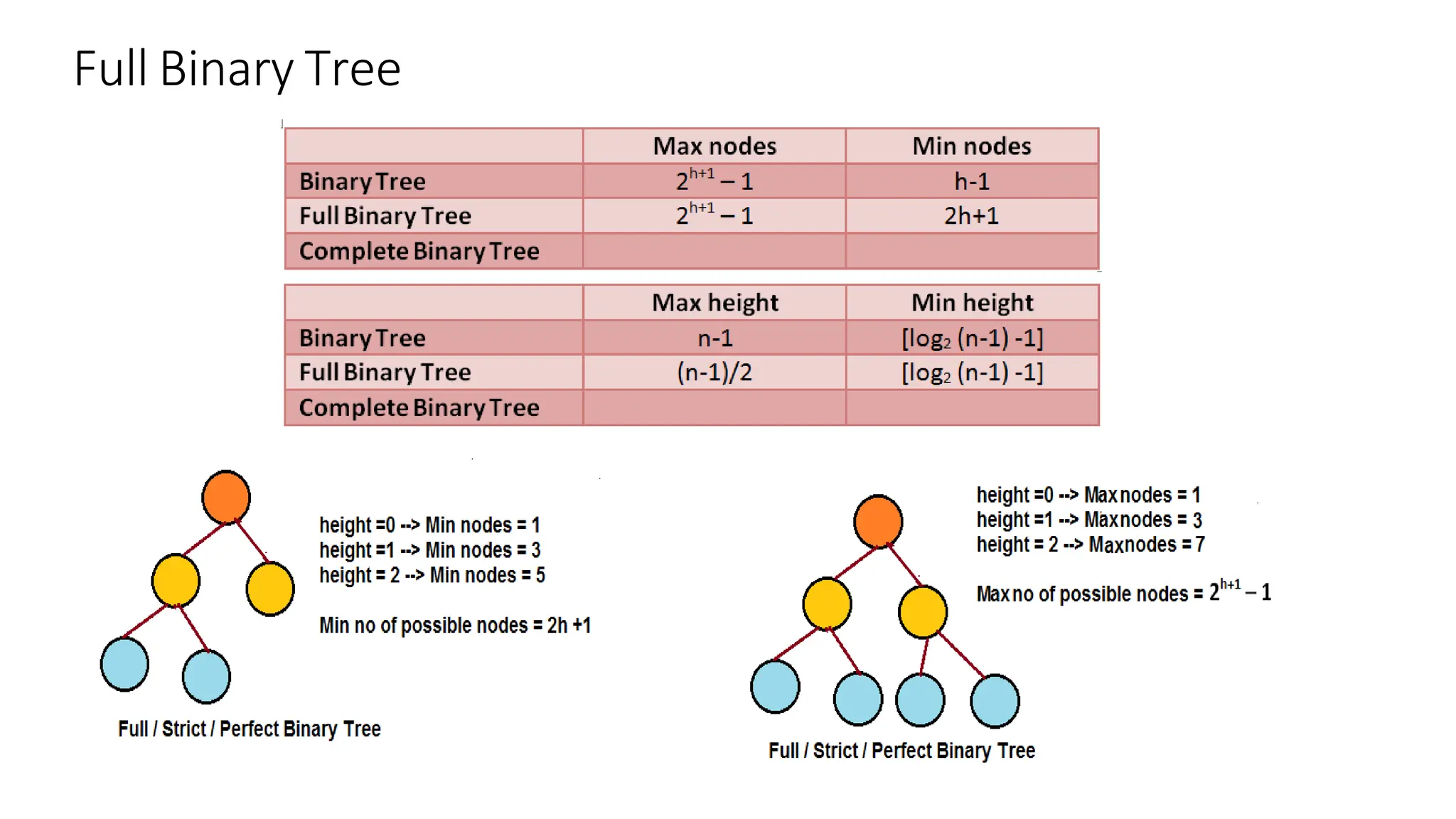
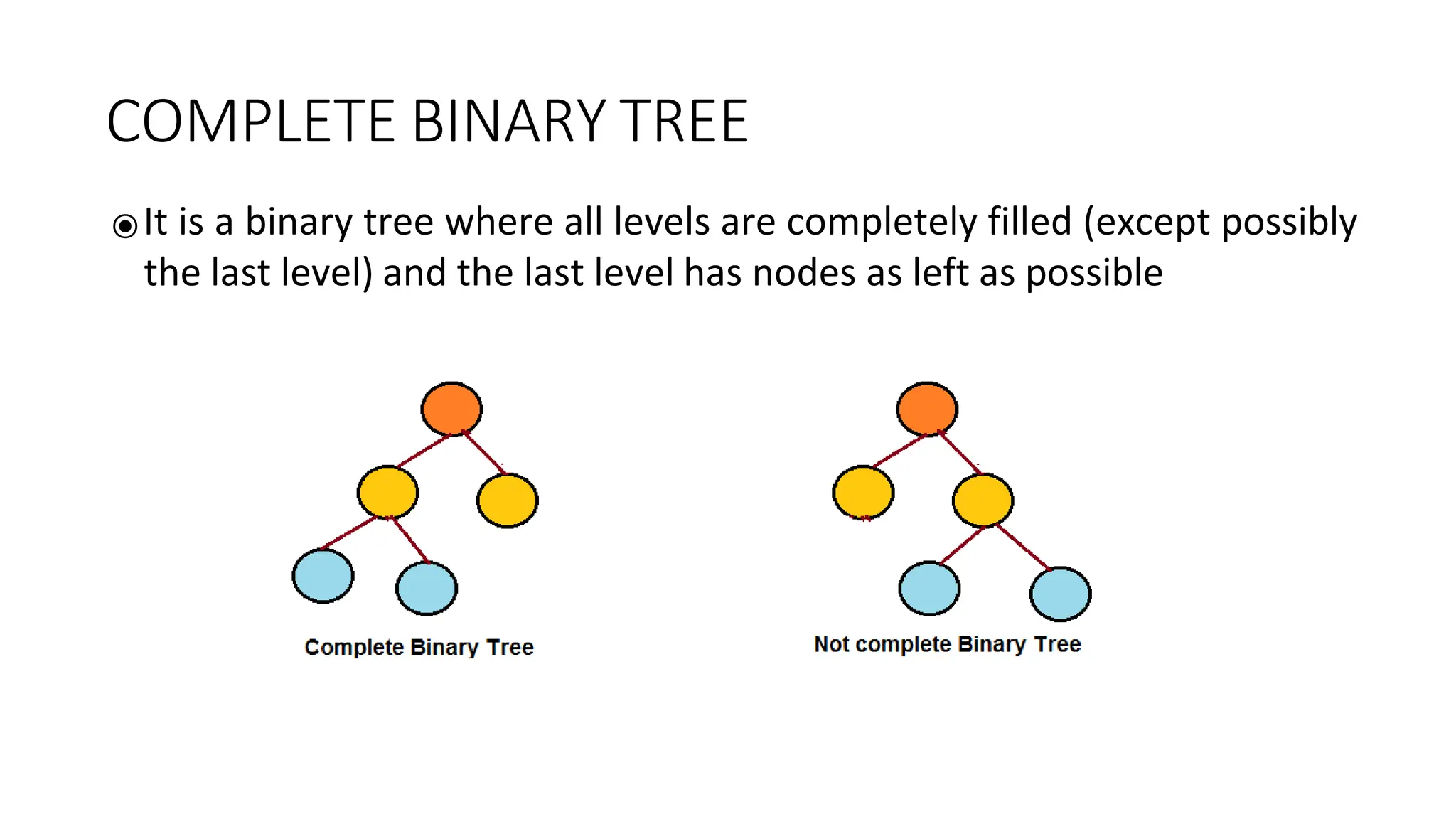
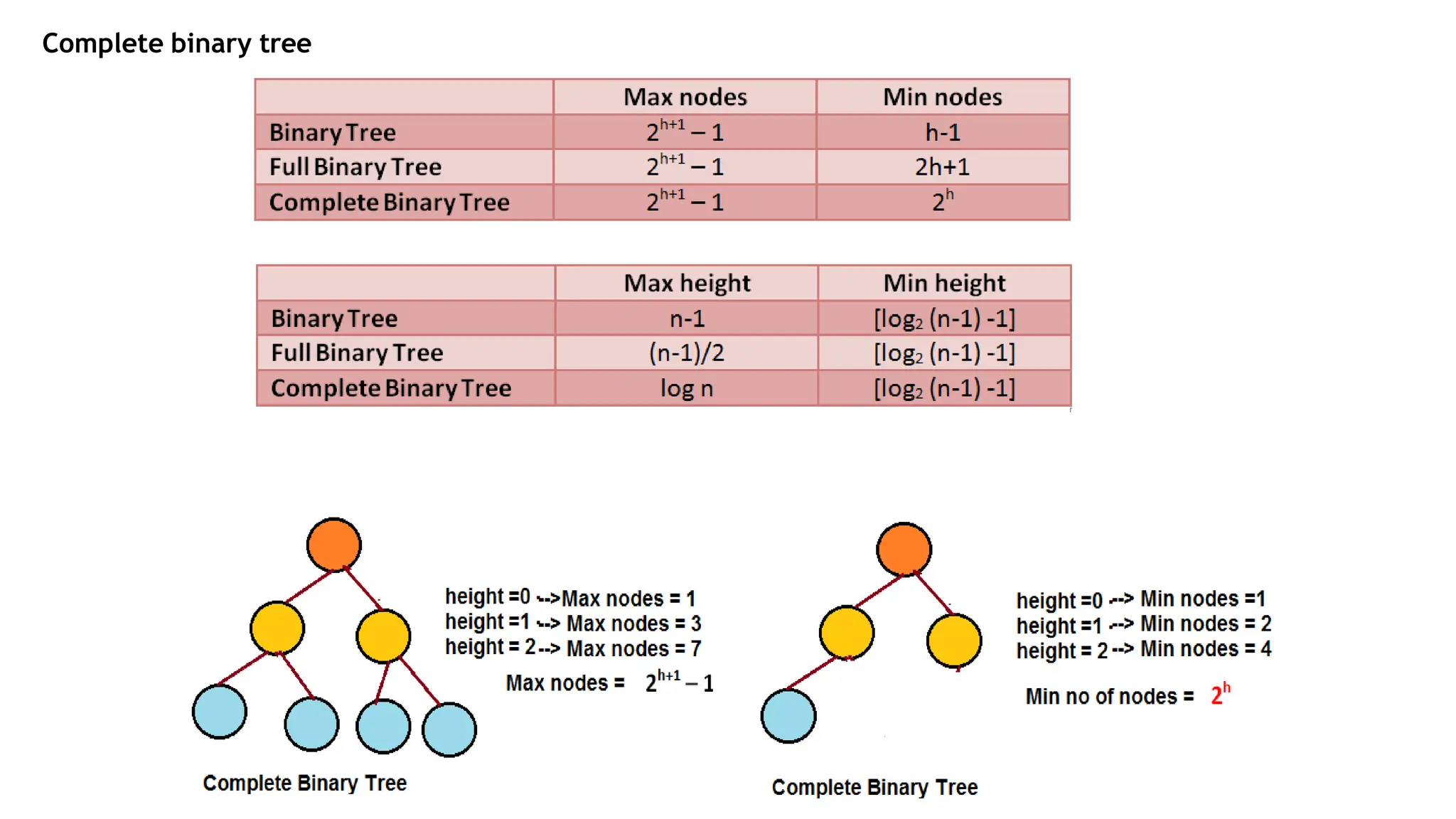
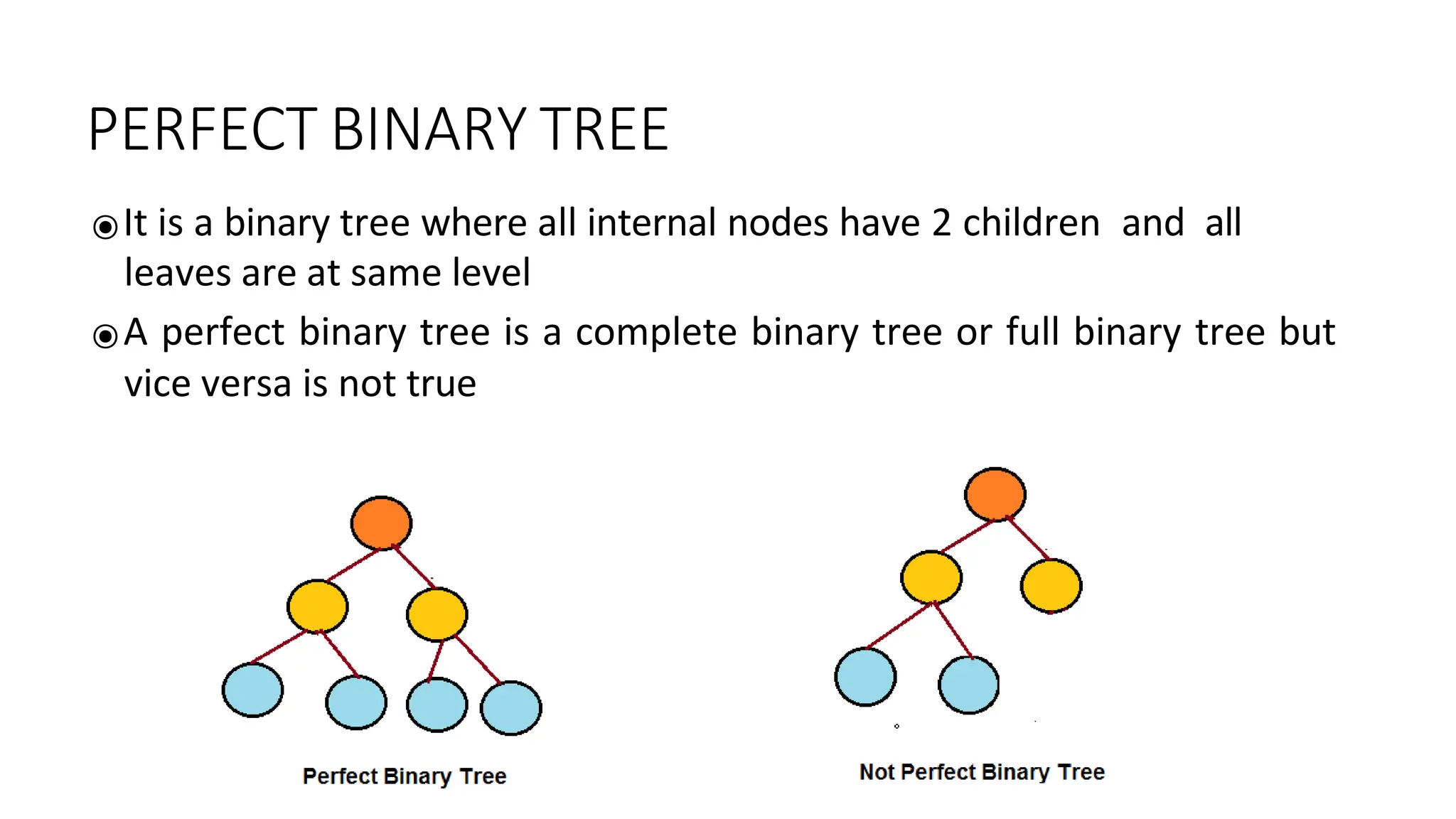
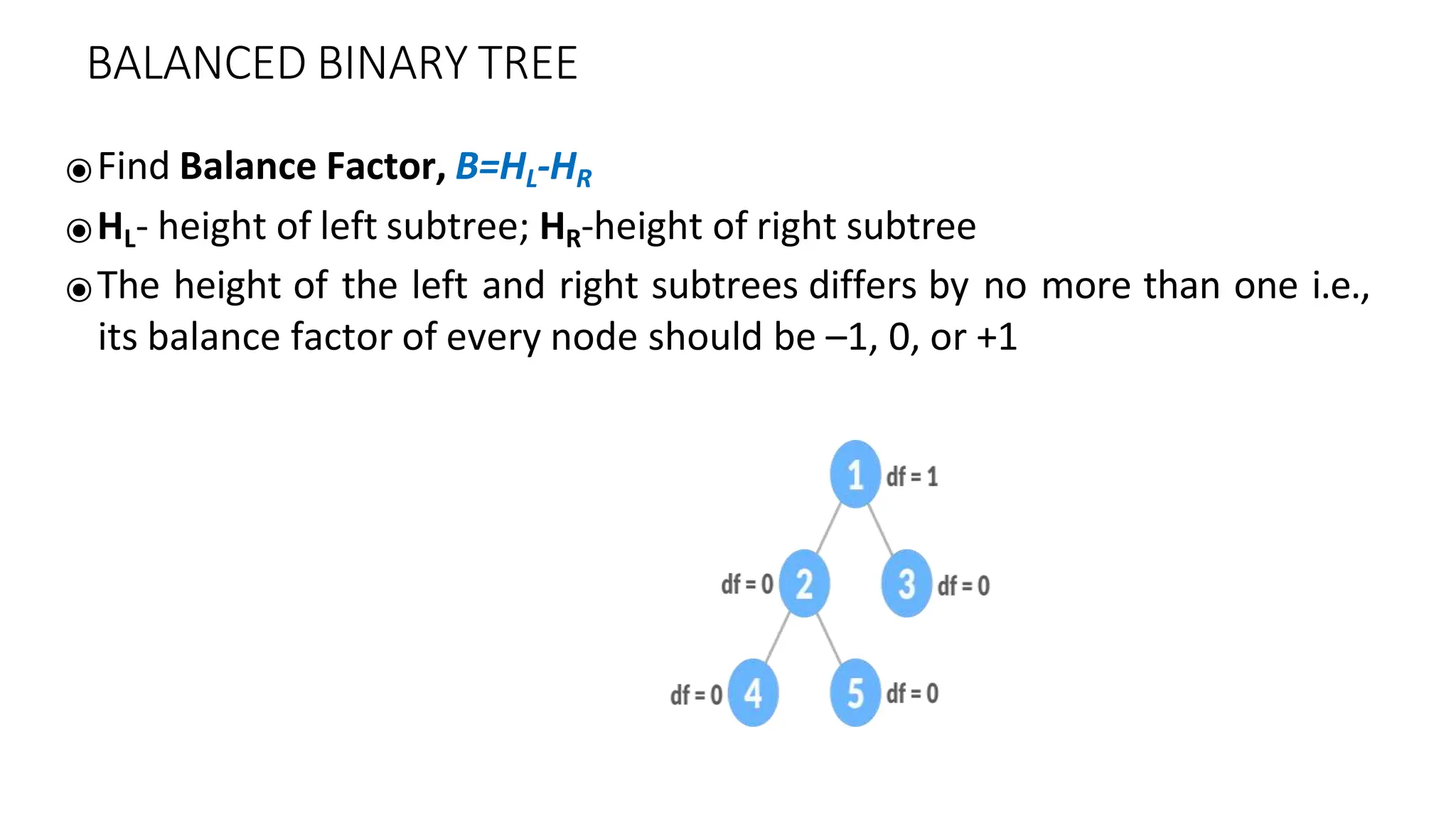
The document provides an overview of tree data structures, explaining key concepts such as nodes, edges, and terminology including root, leaf, and various types of trees. It describes traversal methods like preorder, inorder, and postorder, emphasizing their algorithms and applications. Additionally, it classifies binary trees and their properties, outlining distinctions between categories such as full, complete, and balanced binary trees.