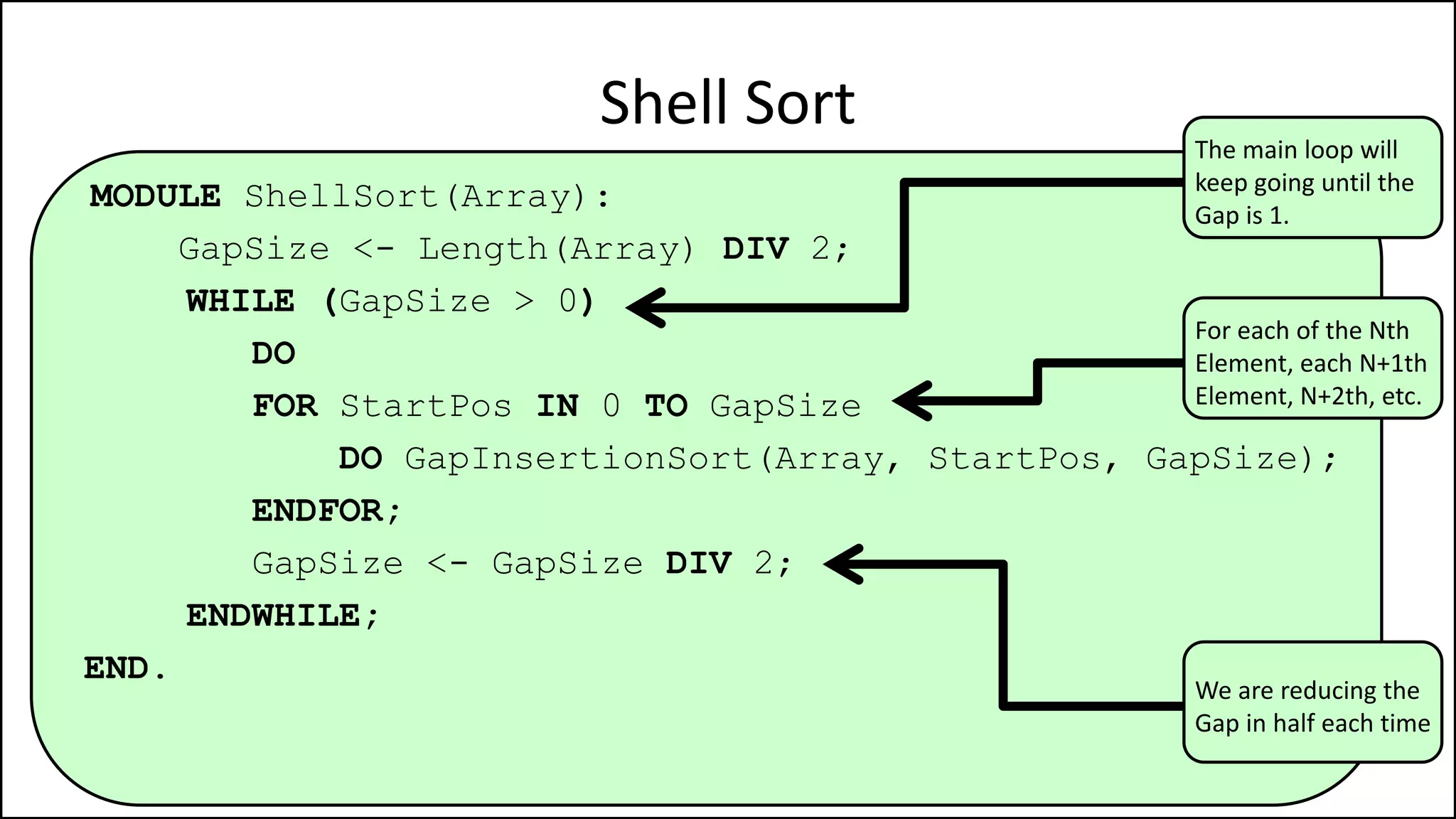
The document describes various sorting algorithms, including insertion sort, selection sort, and shell sort. It provides pseudocode examples and explanations of how each algorithm works to sort a list of numbers in ascending order. Insertion sort works by taking each element and inserting it into the sorted position within the growing sorted sublist. Shell sort improves on insertion sort by sorting elements spaced further apart before sorting adjacent elements.



![PROGRAM BubbleSort:
Integer Age[8] <- {44,23,42,33,16,54,34,18};
FOR Outer-Index IN 0 TO N-1
DO FOR Index IN 0 TO N-2
DO IF (Age[Index+1] < Age[Index])
THEN Temp_Value <- Age[Index+1];
Age[Index+1] <- Age[Index];
Age[Index] <- Temp_Value;
ENDIF;
ENDFOR;
ENDFOR;
END.
Sorting: Bubble Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-4-2048.jpg)
![PROGRAM SelectionSort:
Integer Age[8] <- {44,23,42,33,16,54,34,18};
FOR Outer-Index IN 0 TO N-1
MinValueLocation <- Outer-Index;
FOR Index IN Outer-Index+1 TO N-1
DO IF (Age[Index] < Age[MinValueLocation])
THEN MinValueLocation <- Index;
ENDIF;
ENDFOR;
IF (MinValueLocation != Outer-Index)
THEN Swap(Age[Outer-Index], Age[MinValueLocation]);
ENDIF;
ENDFOR;
END.
Sorting: Selection Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-5-2048.jpg)



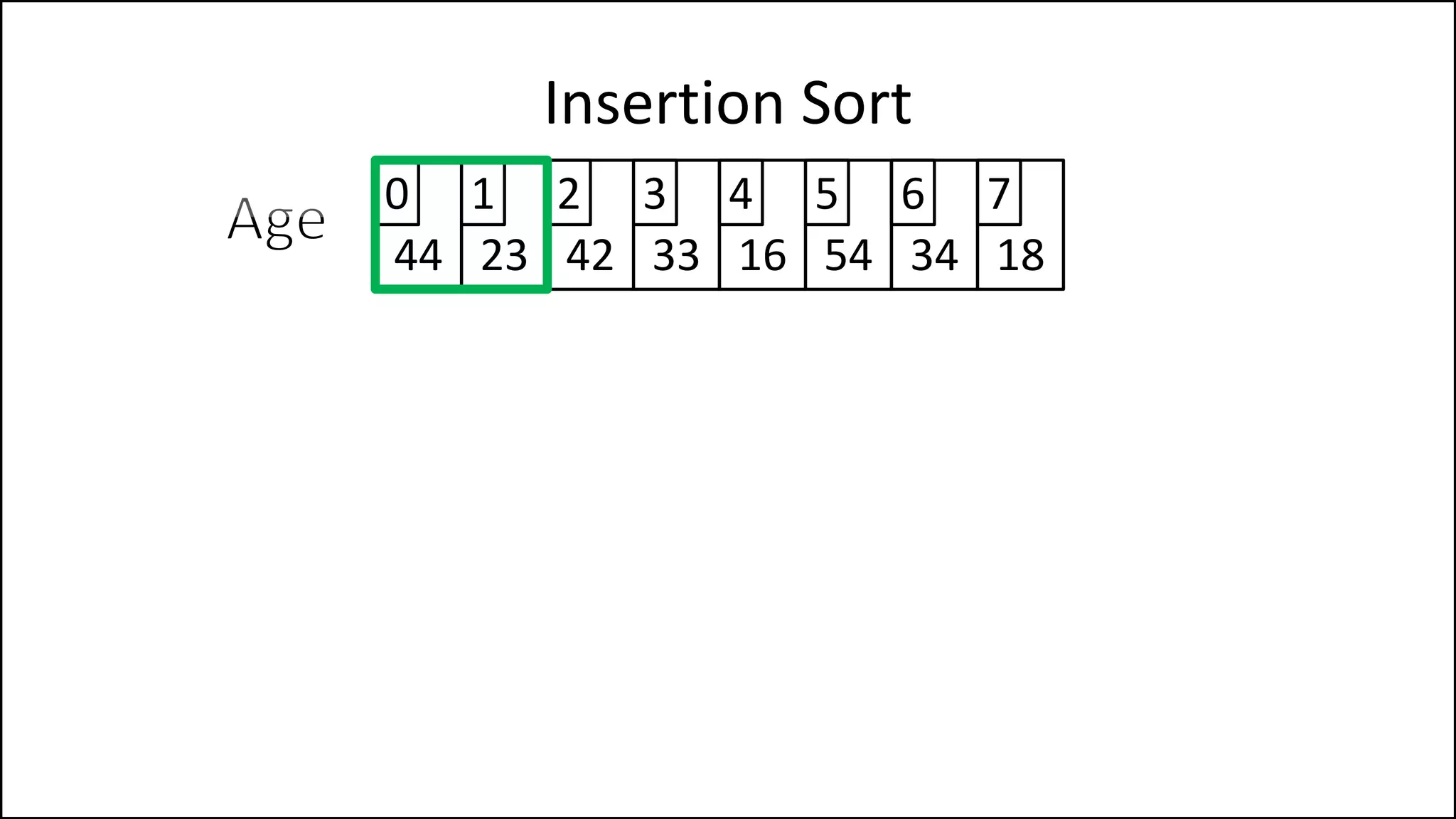
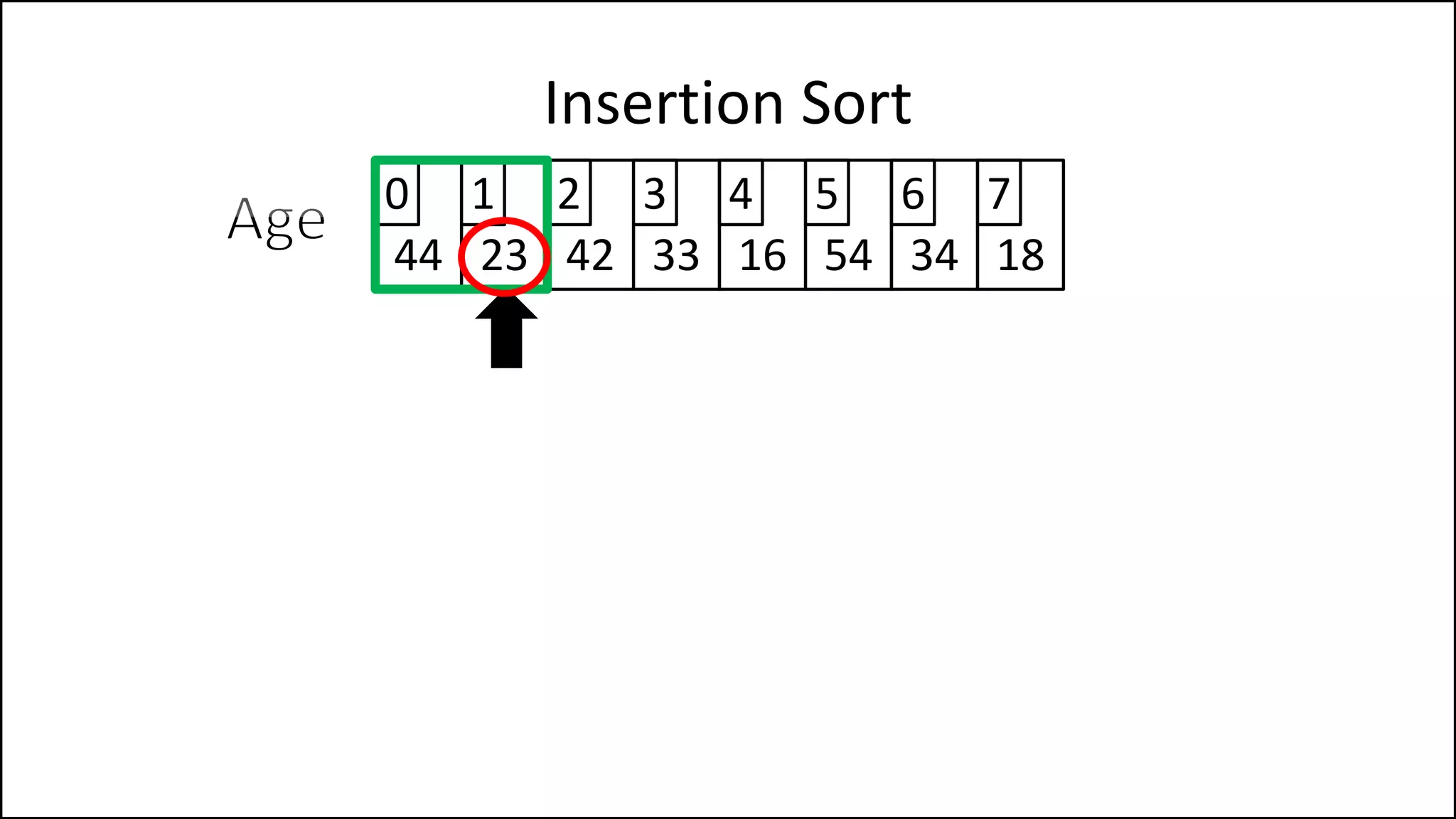

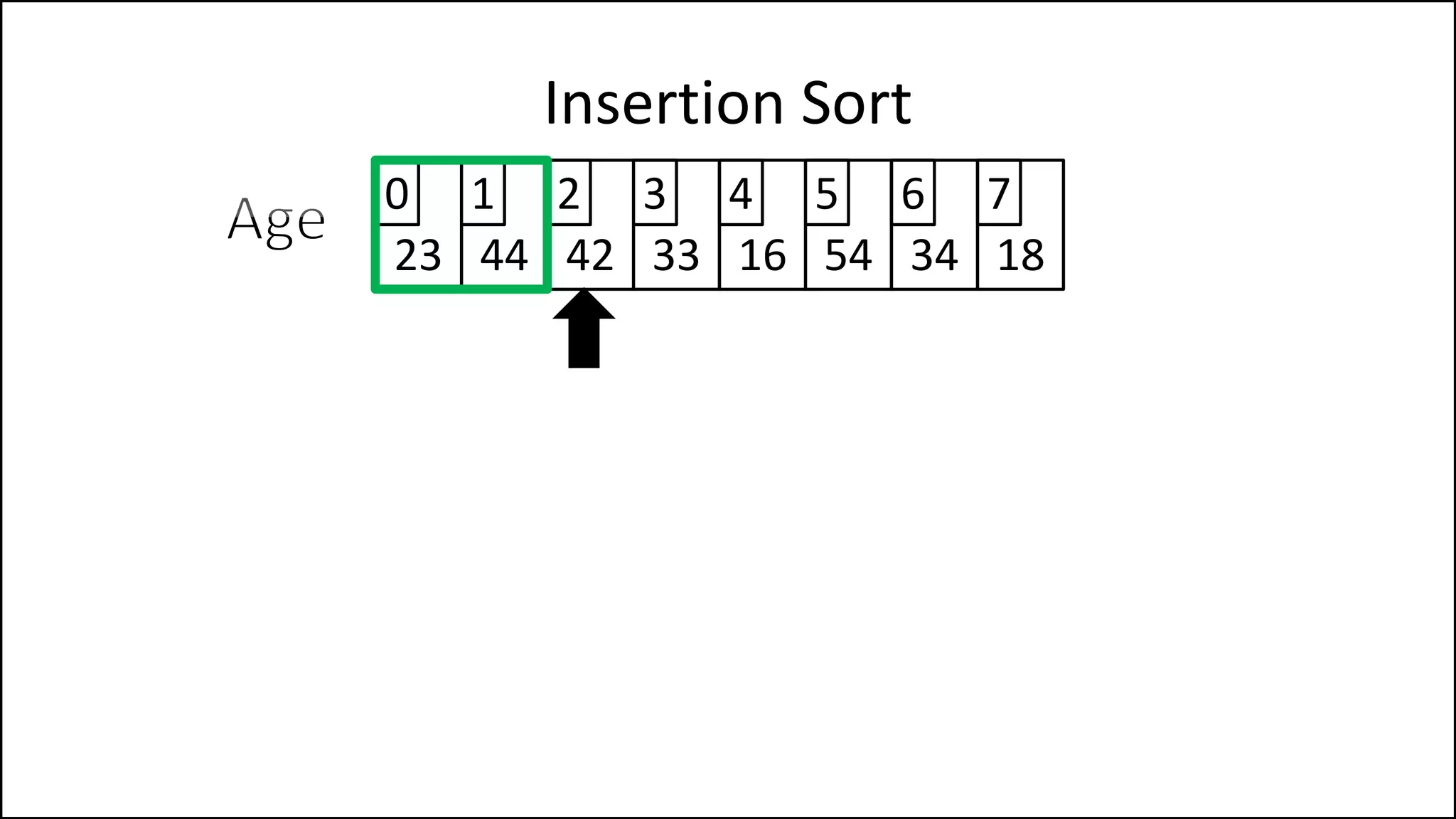
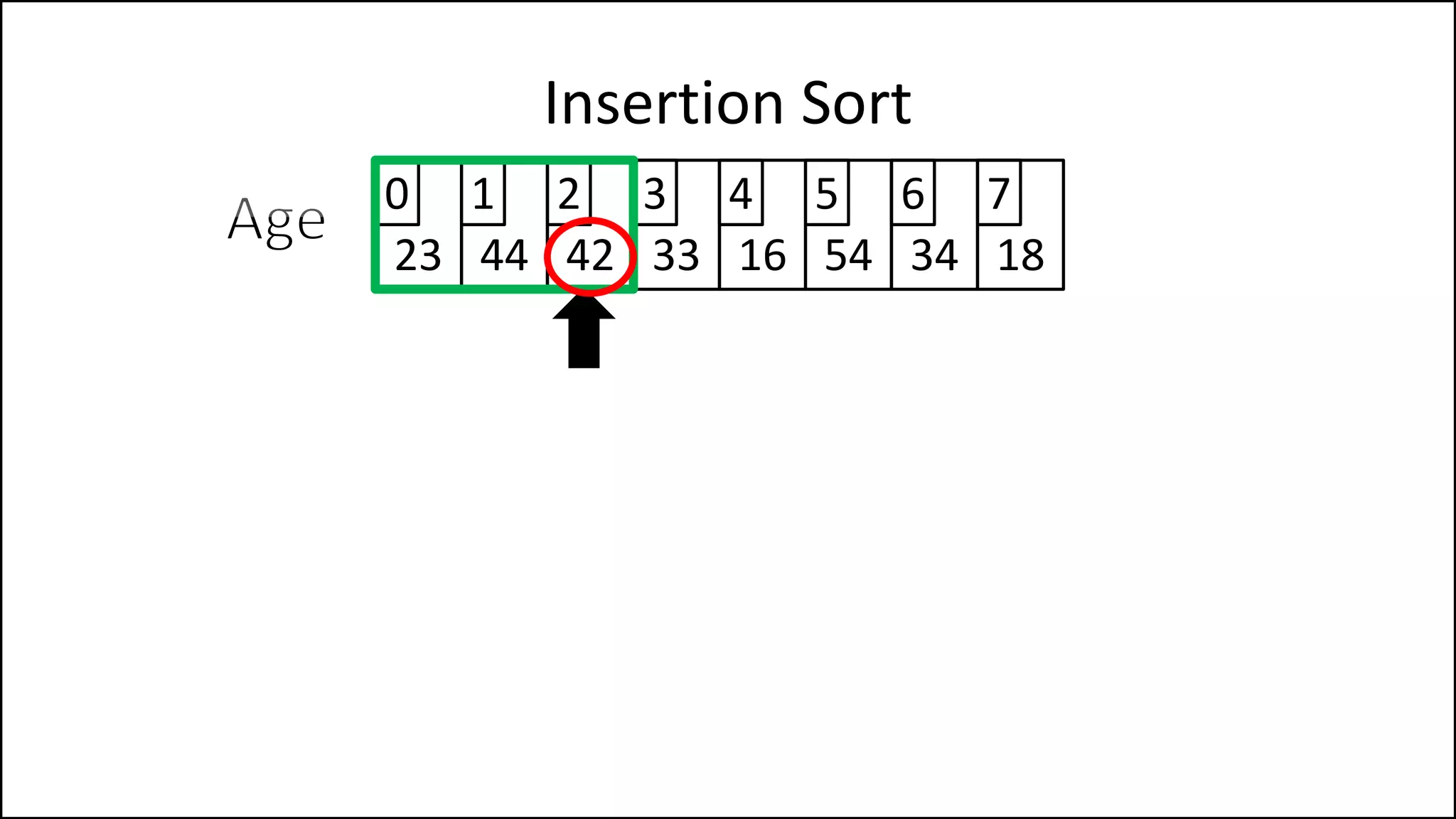
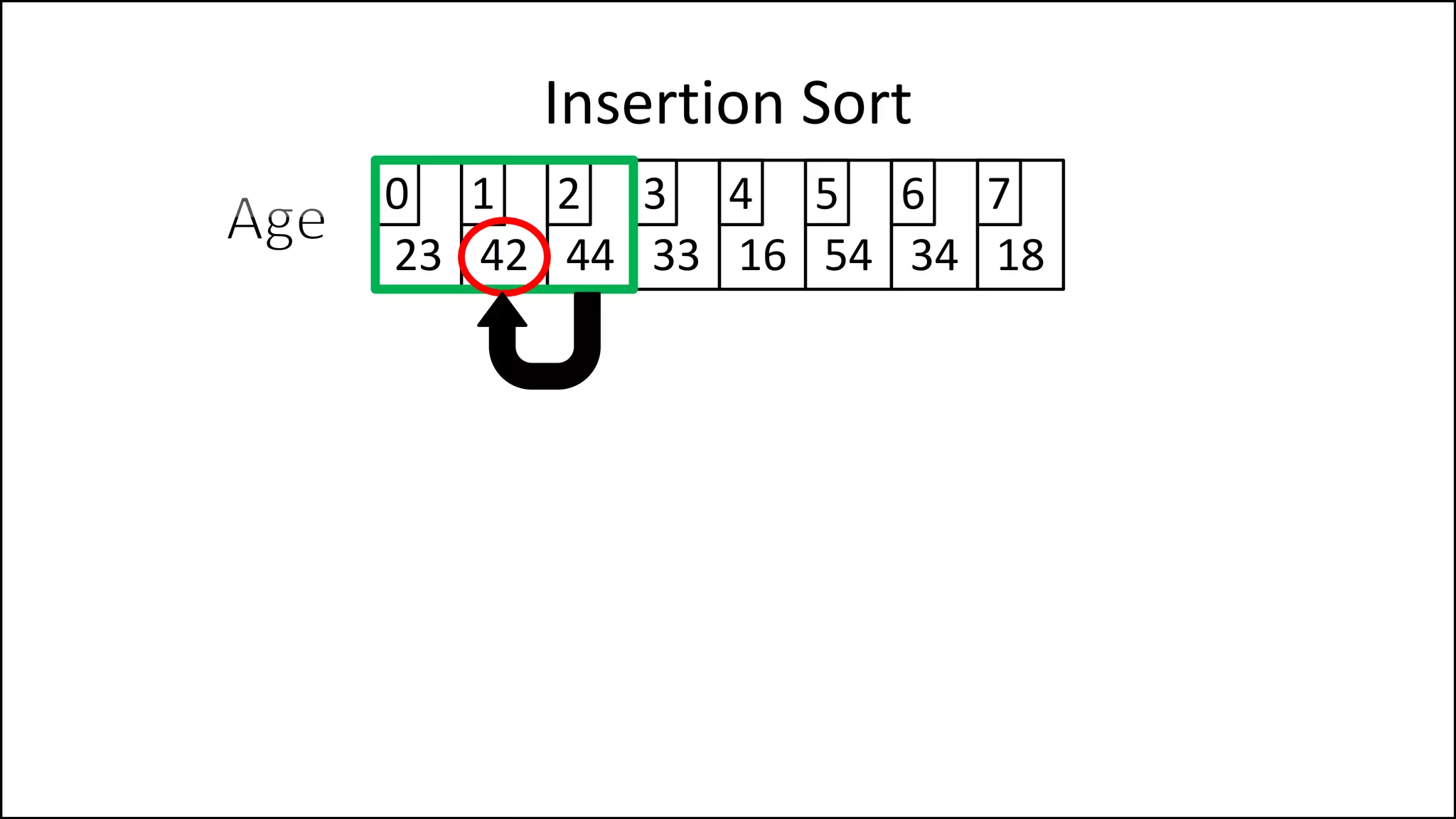
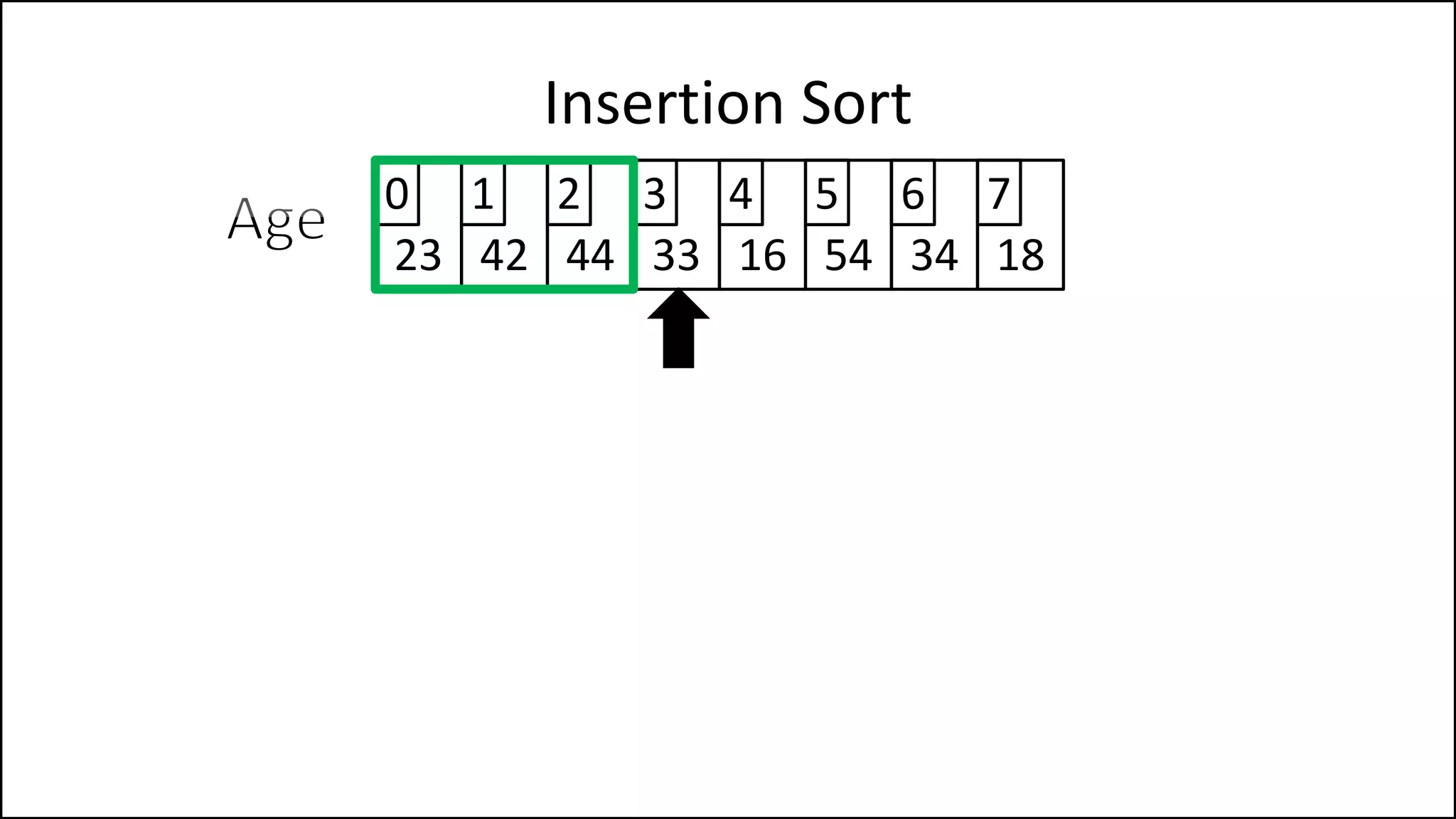
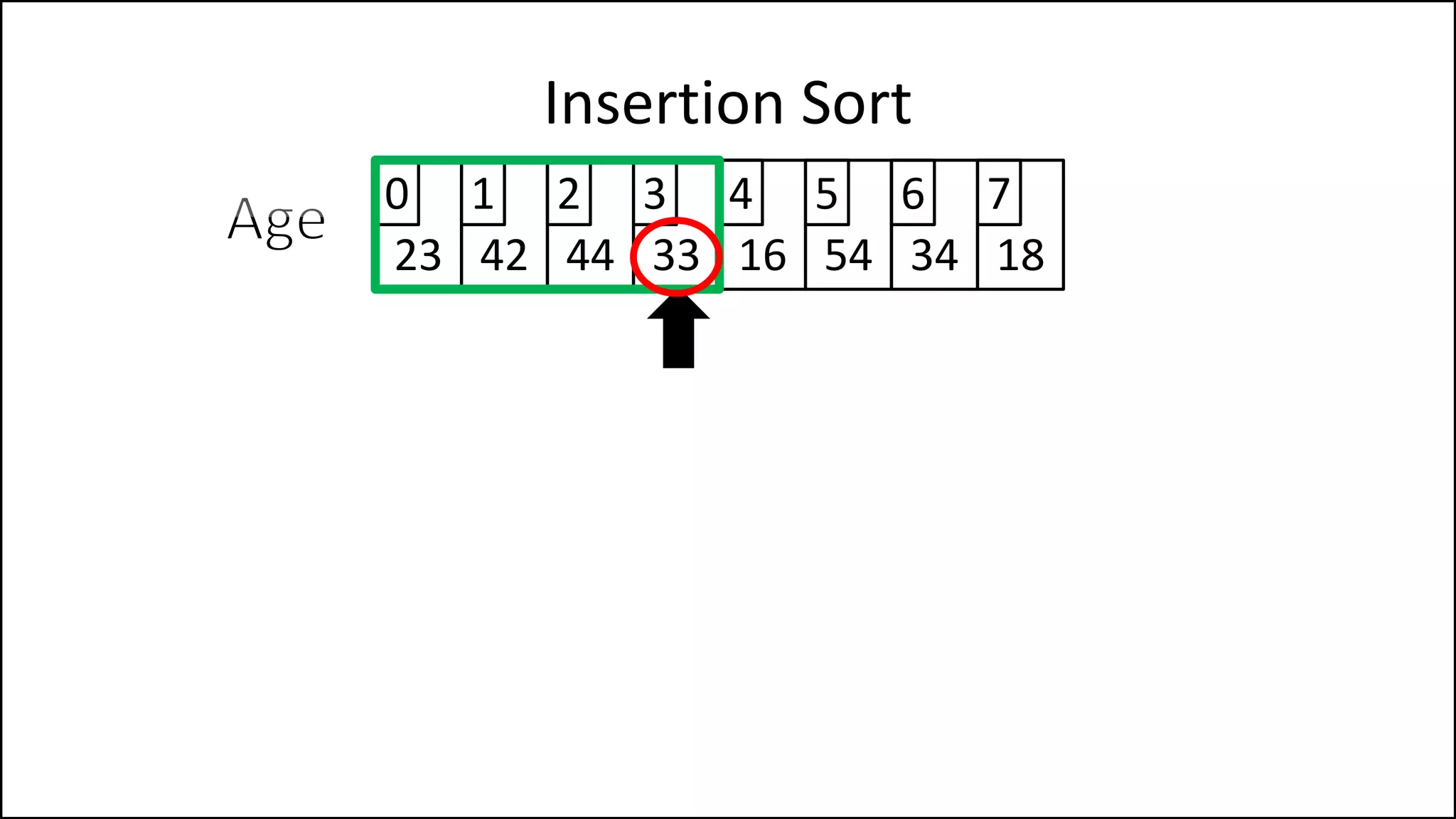
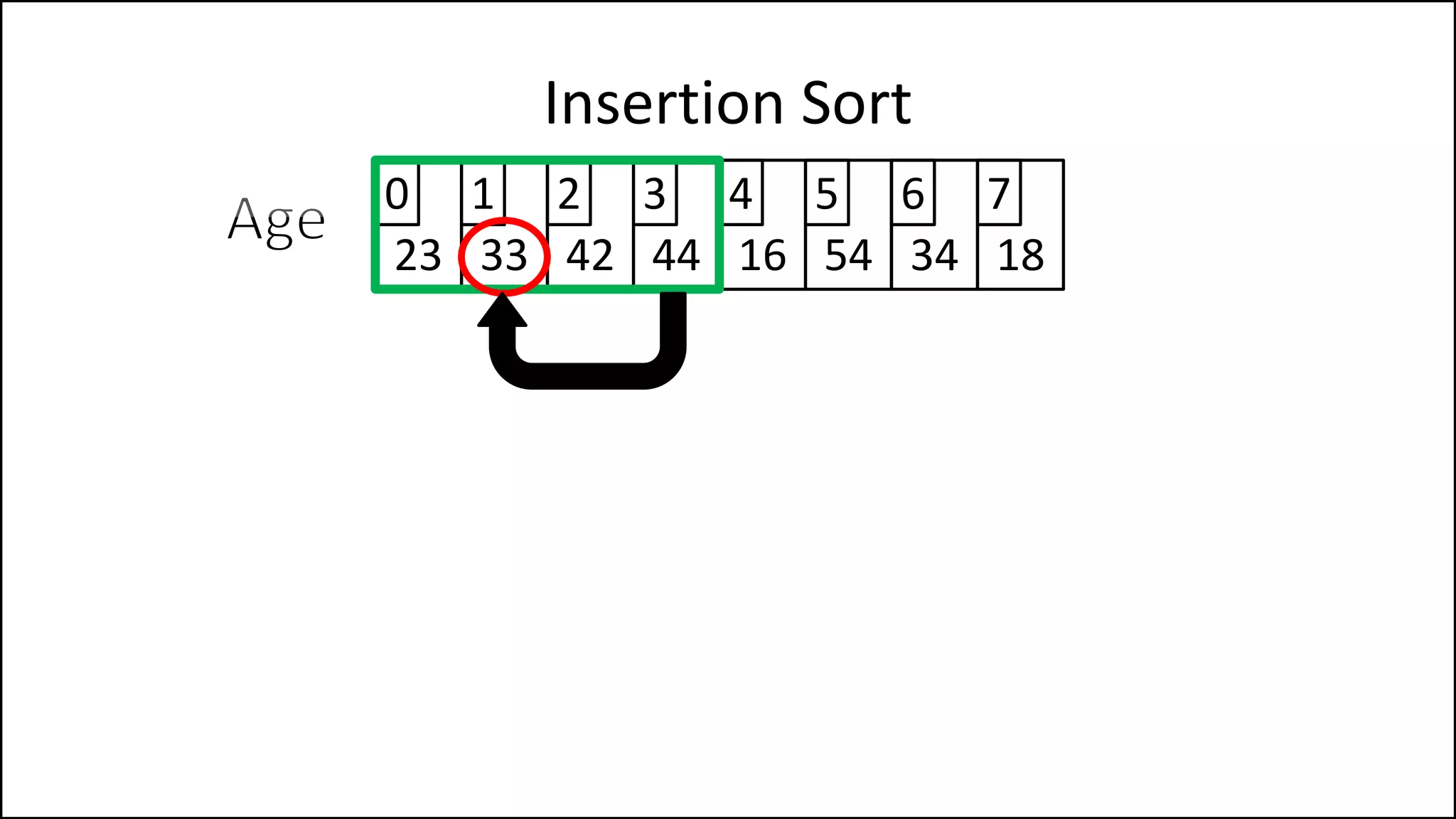
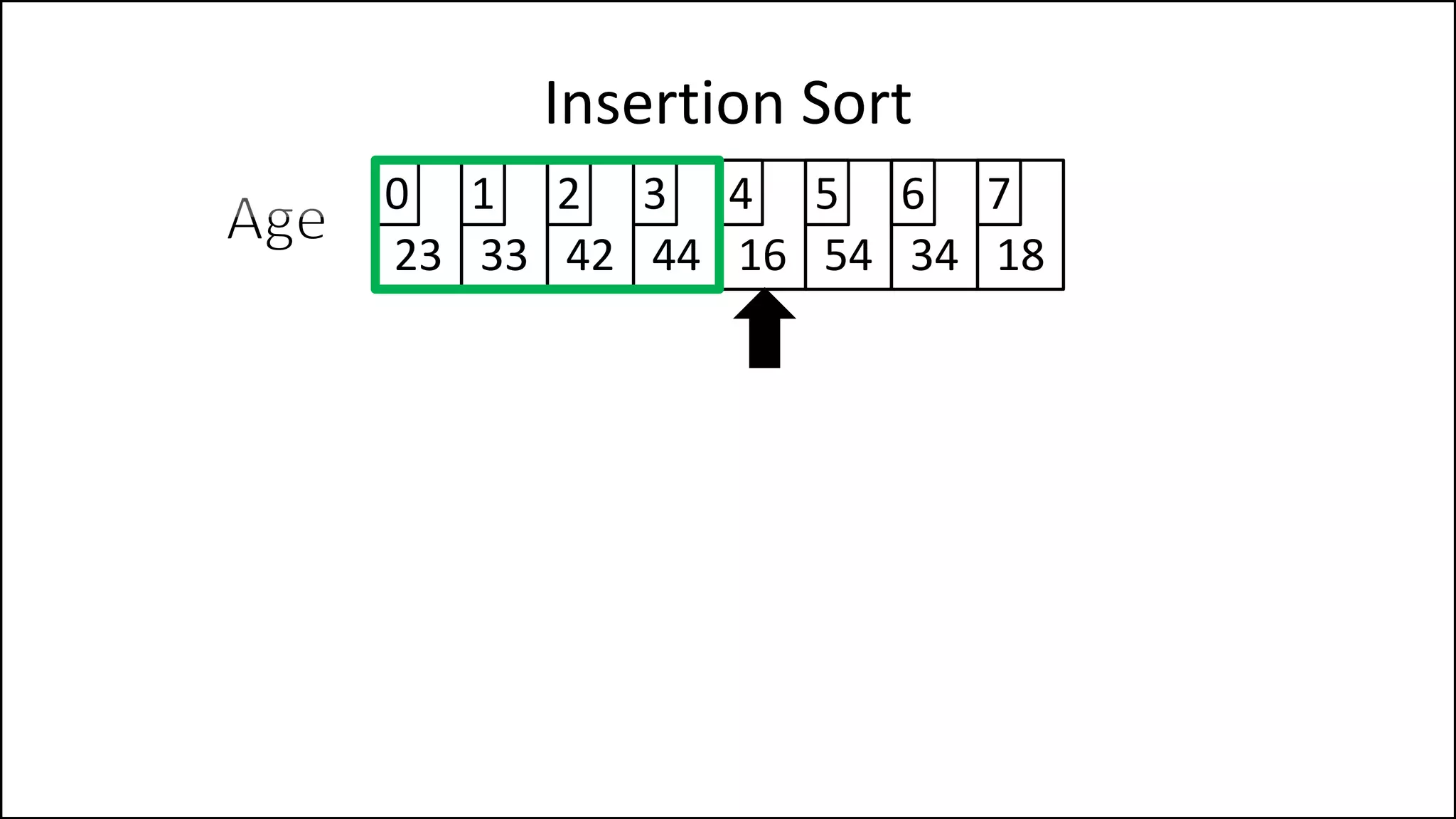
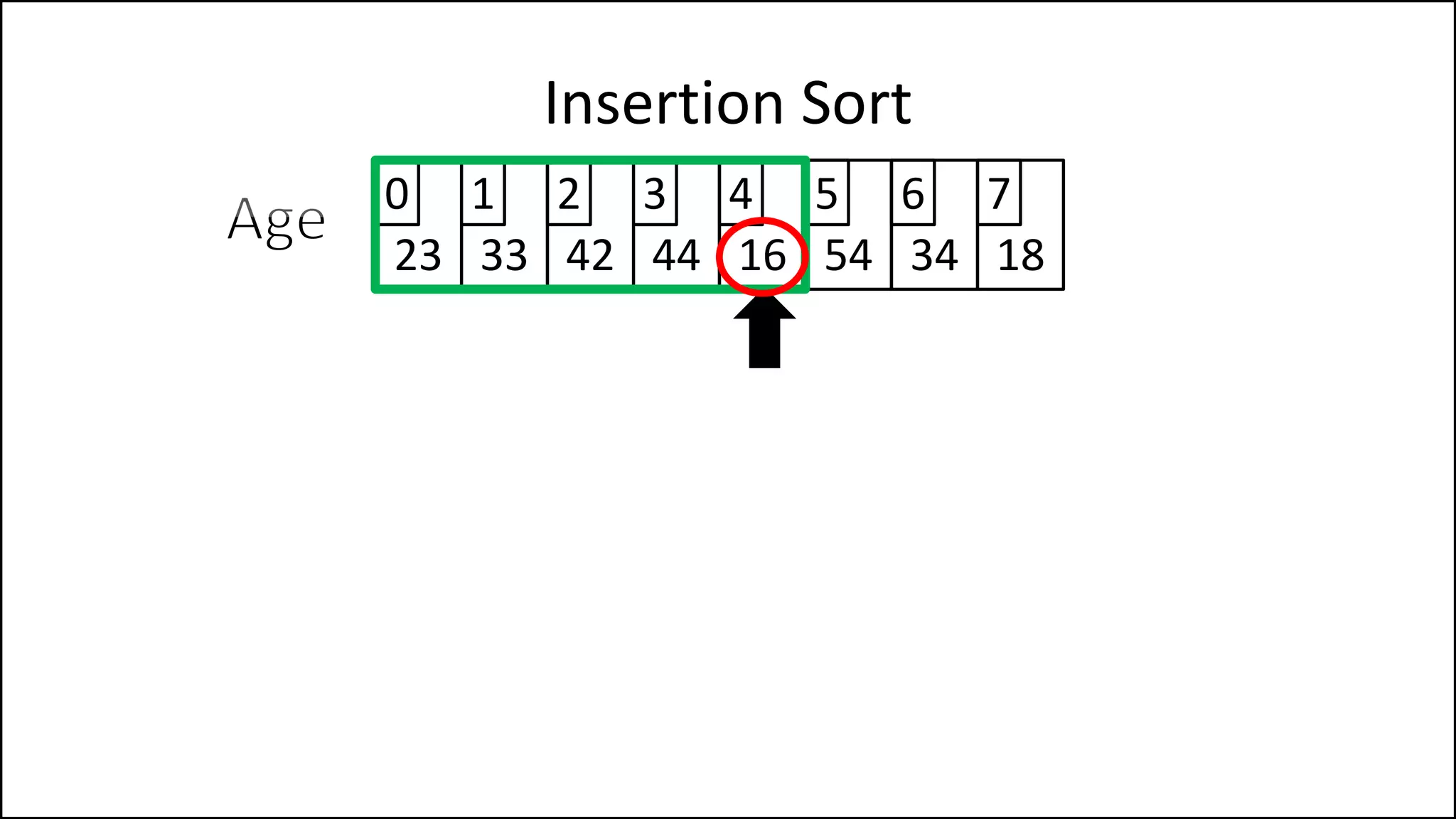
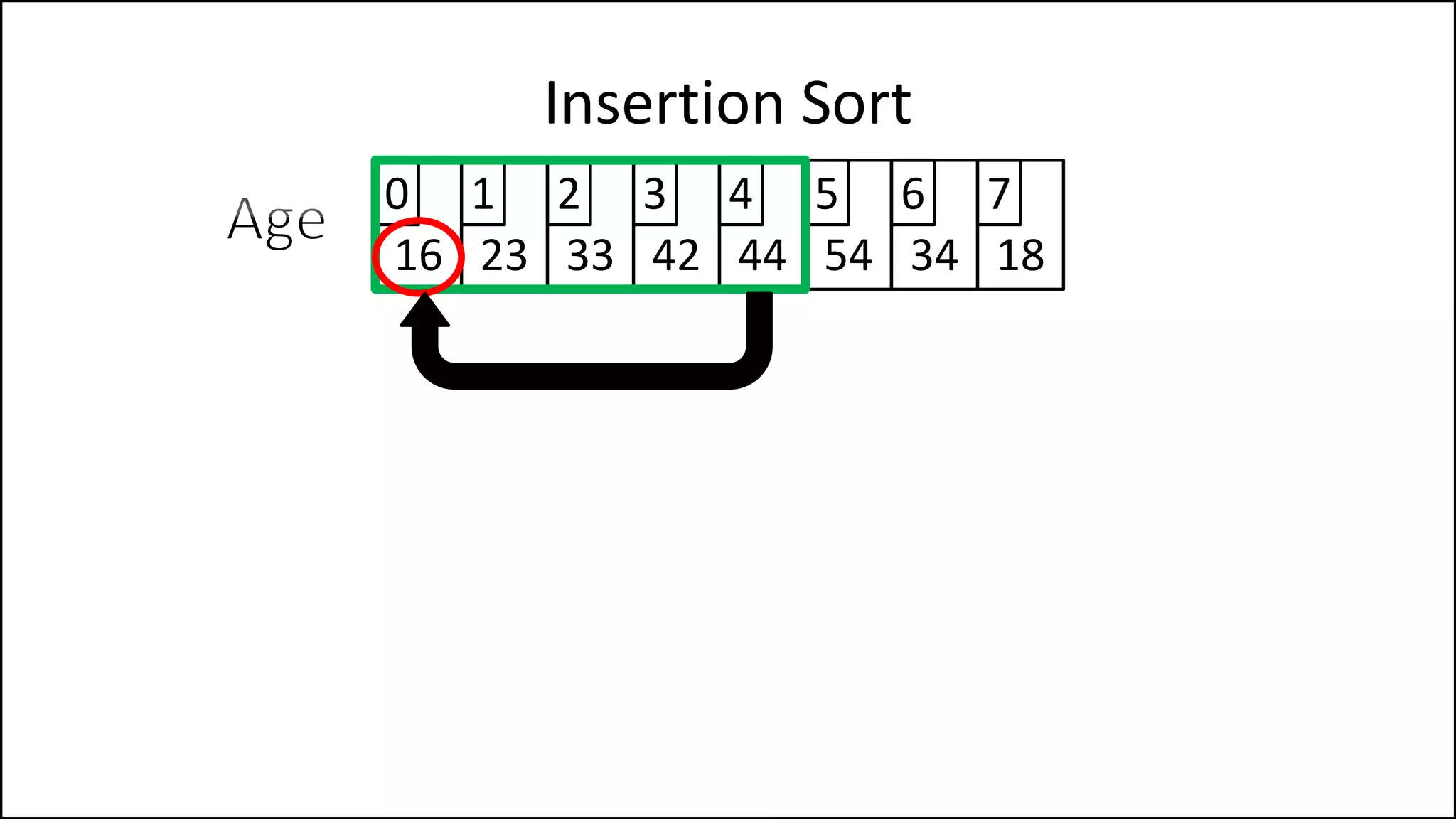
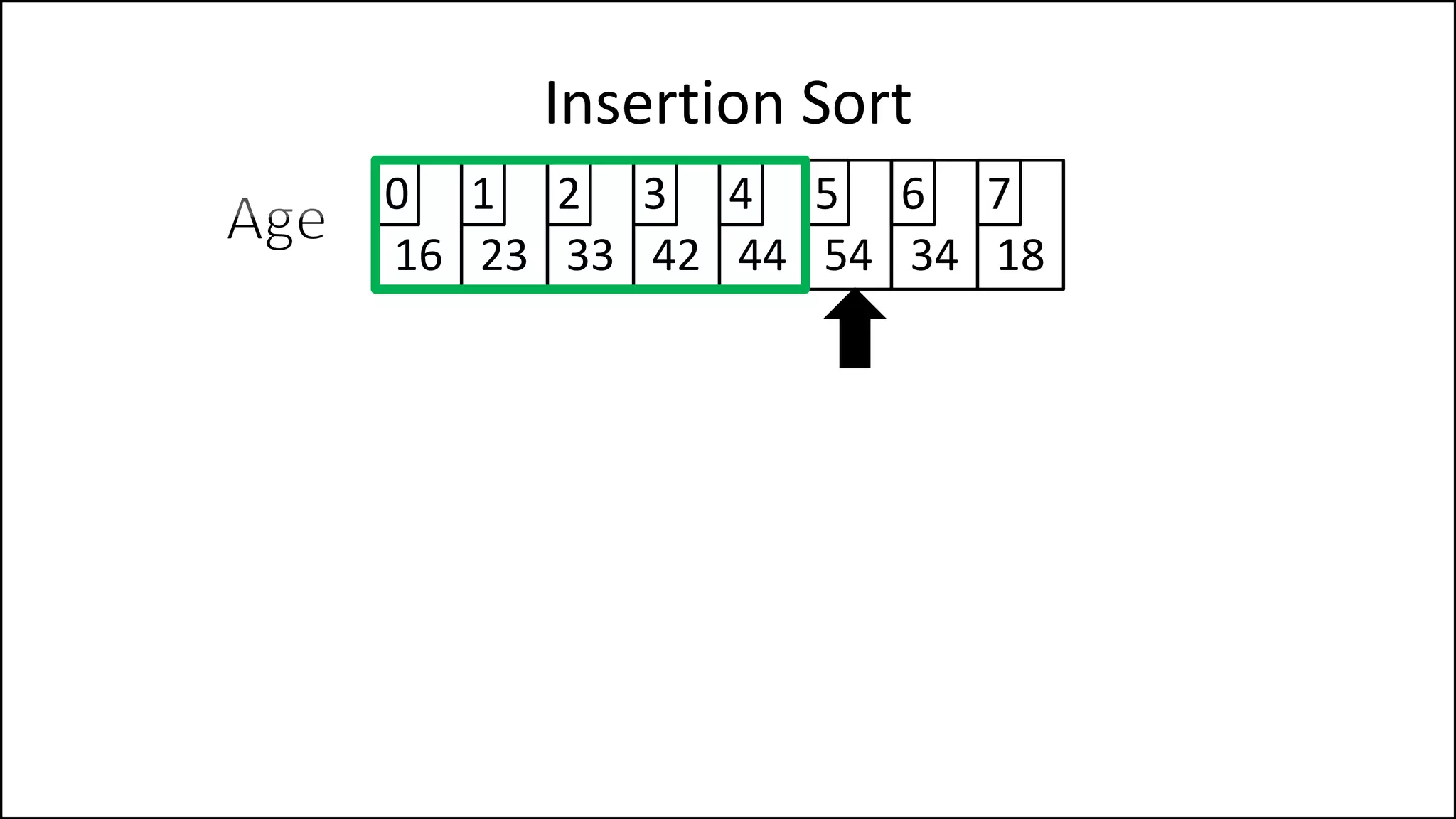

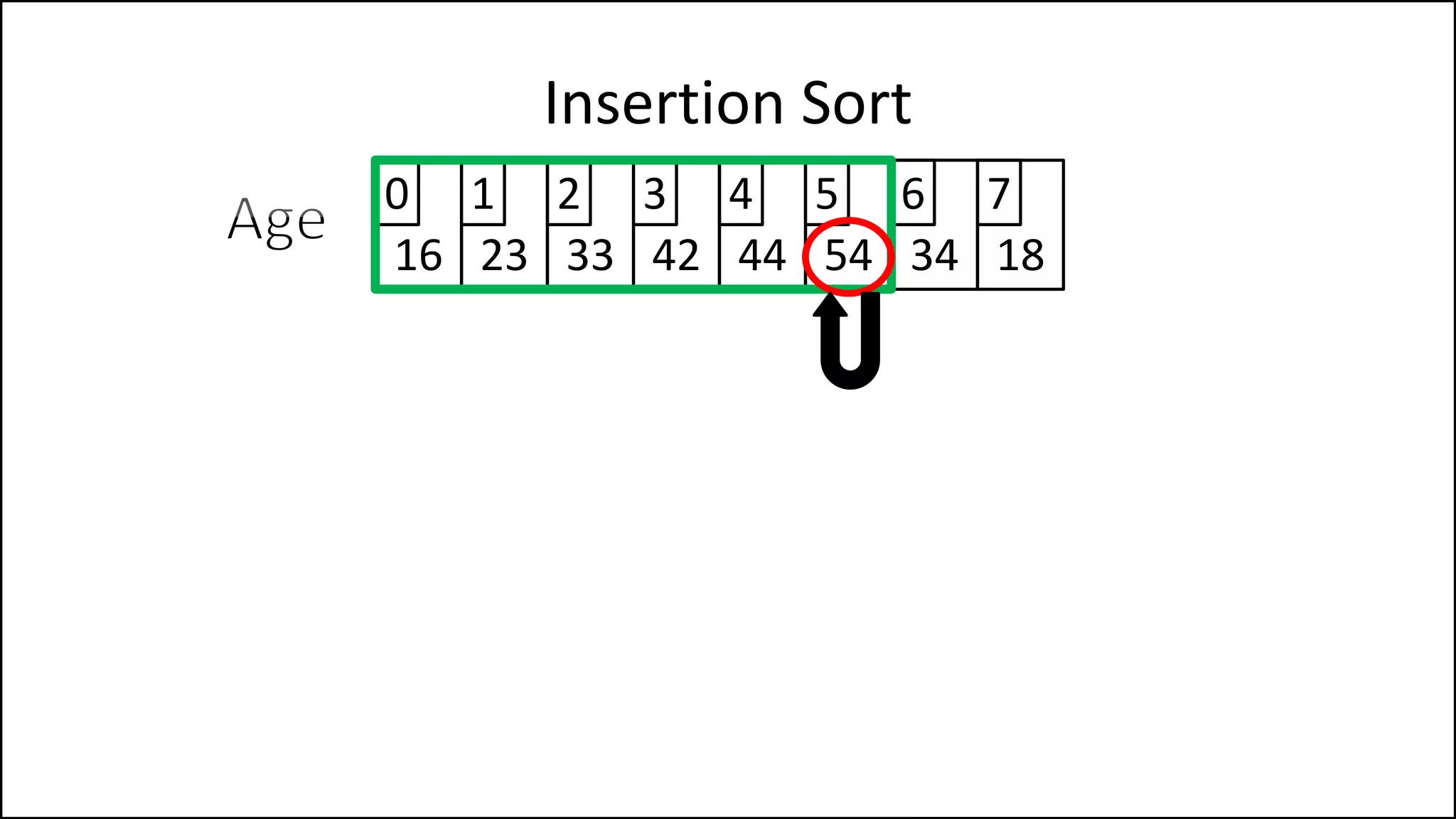

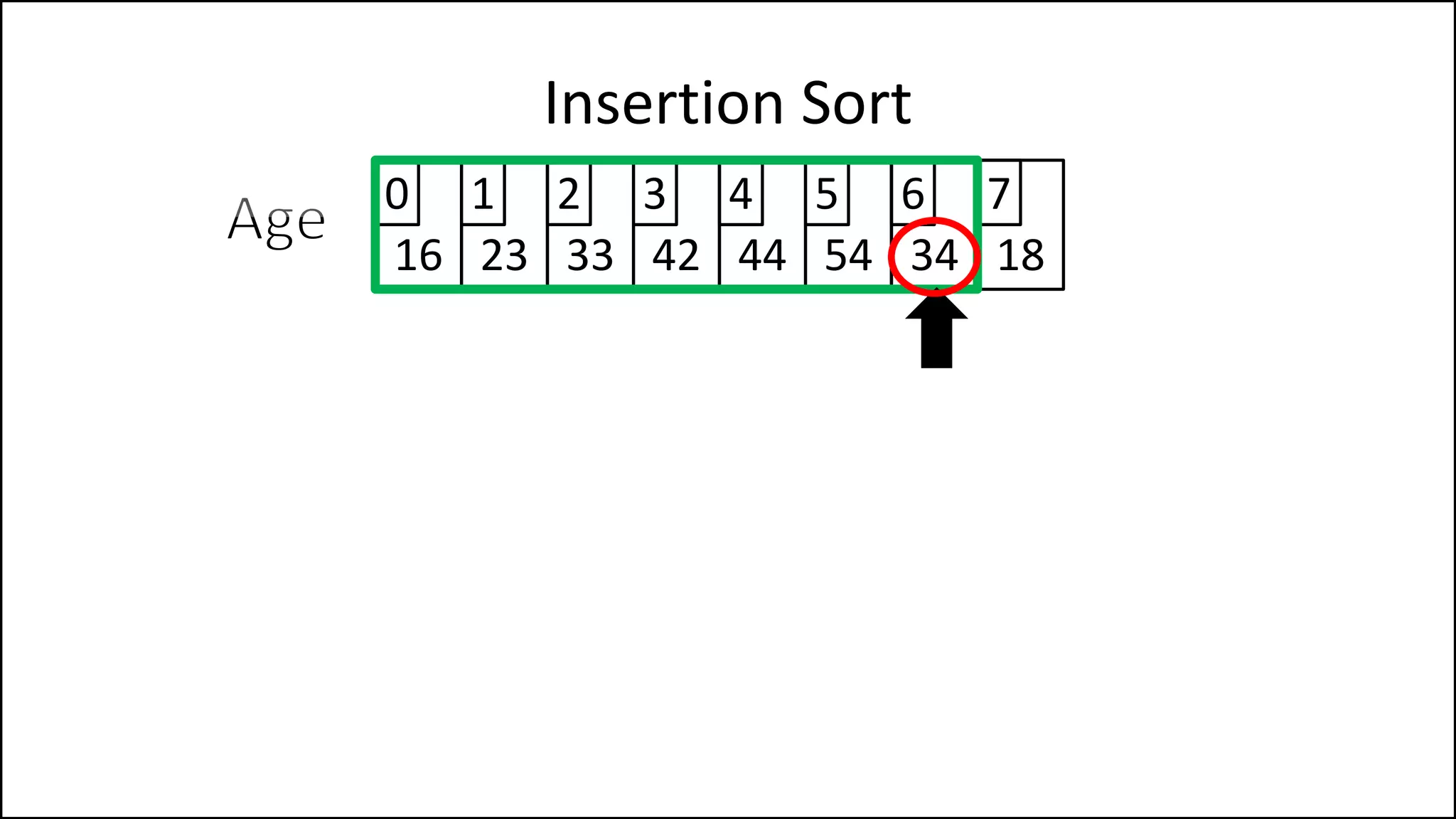
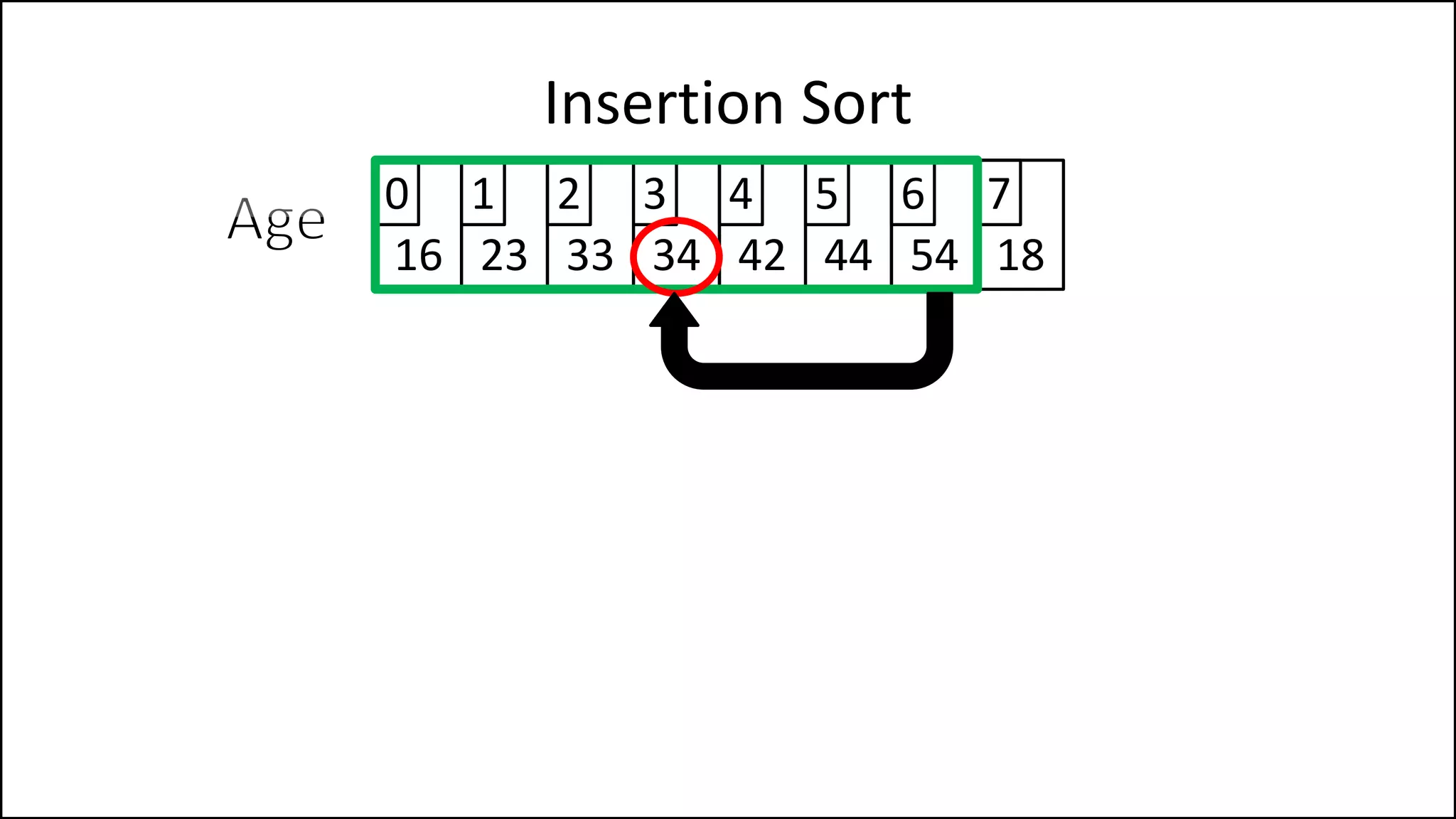
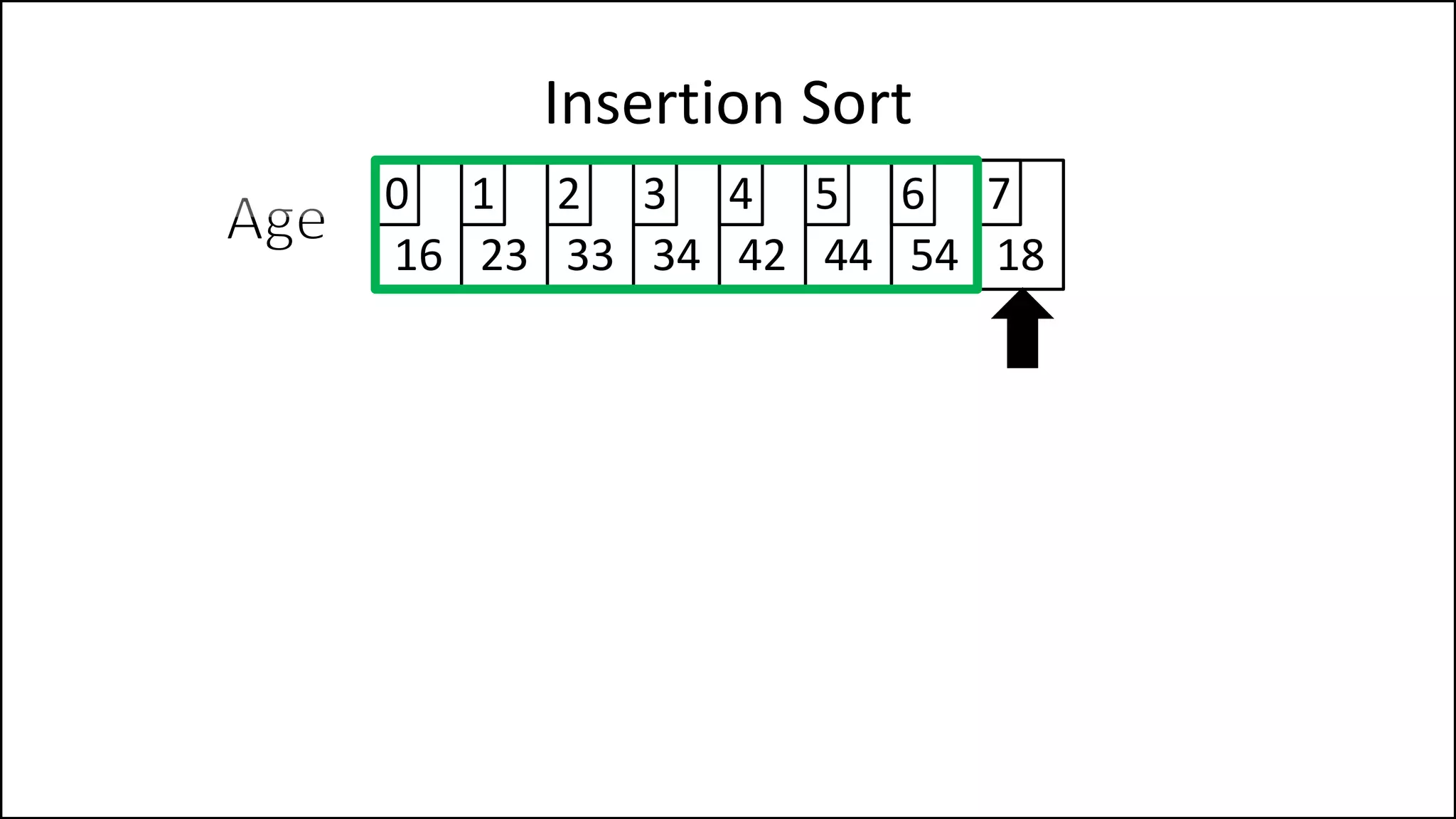
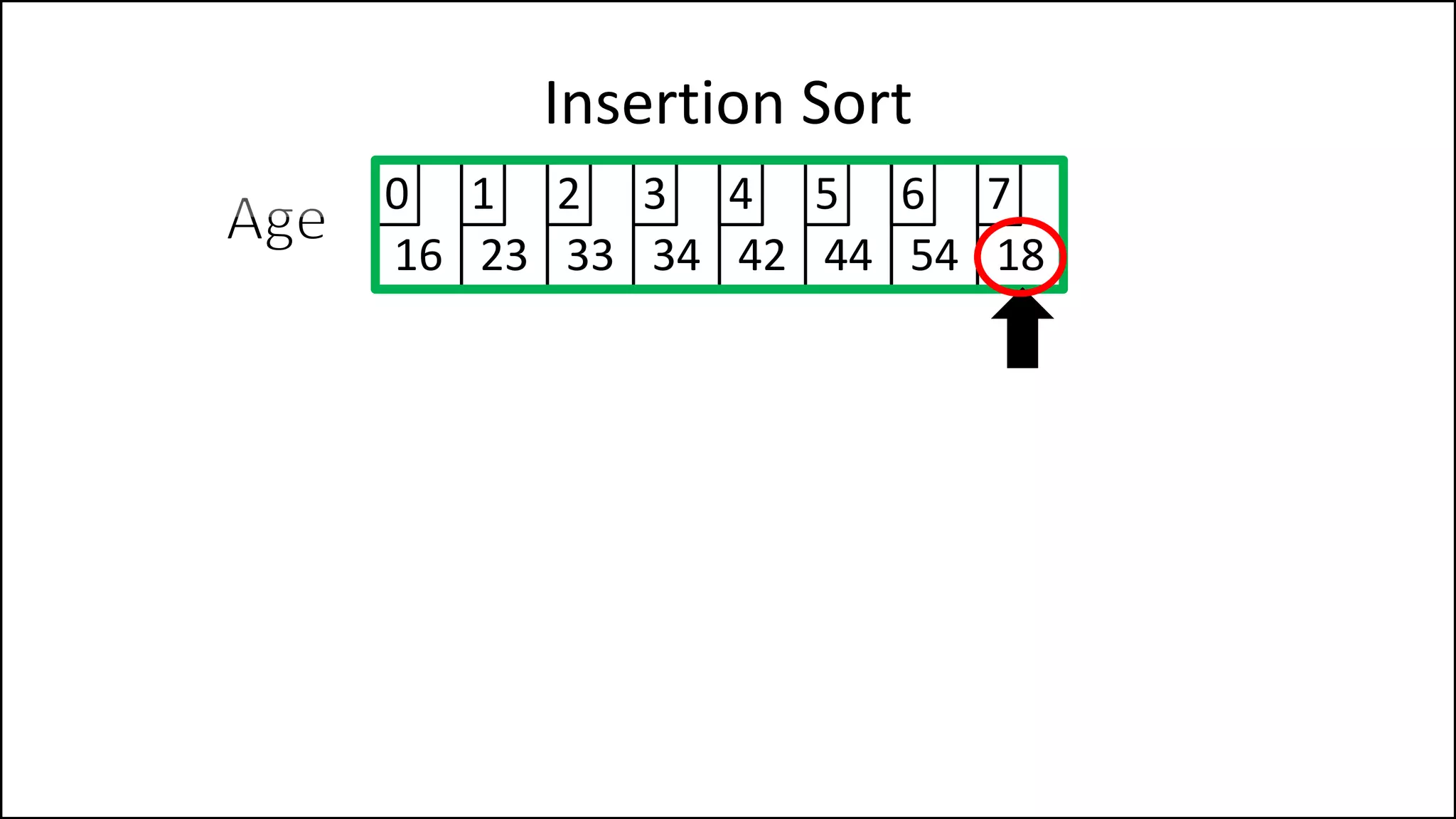
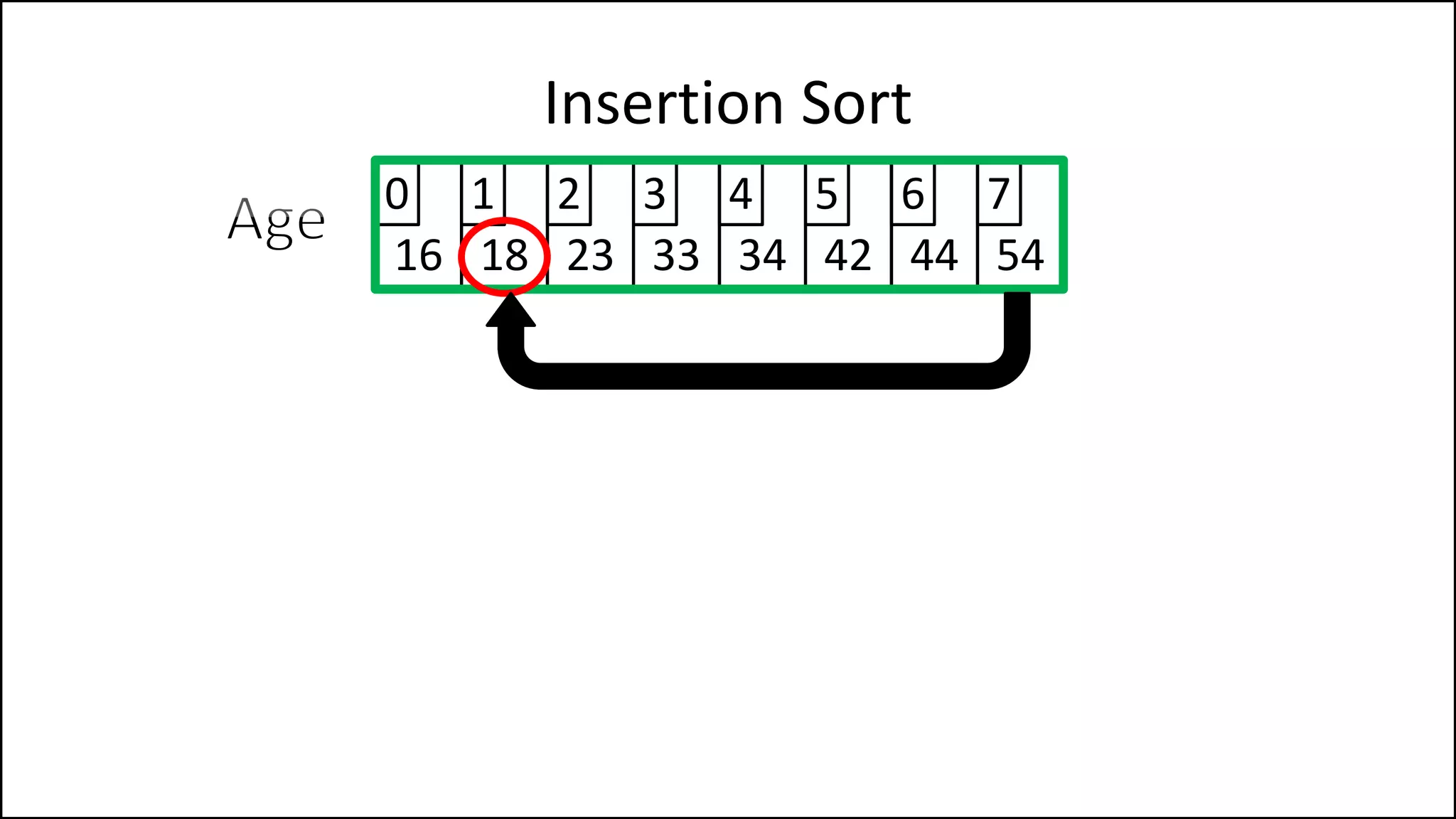
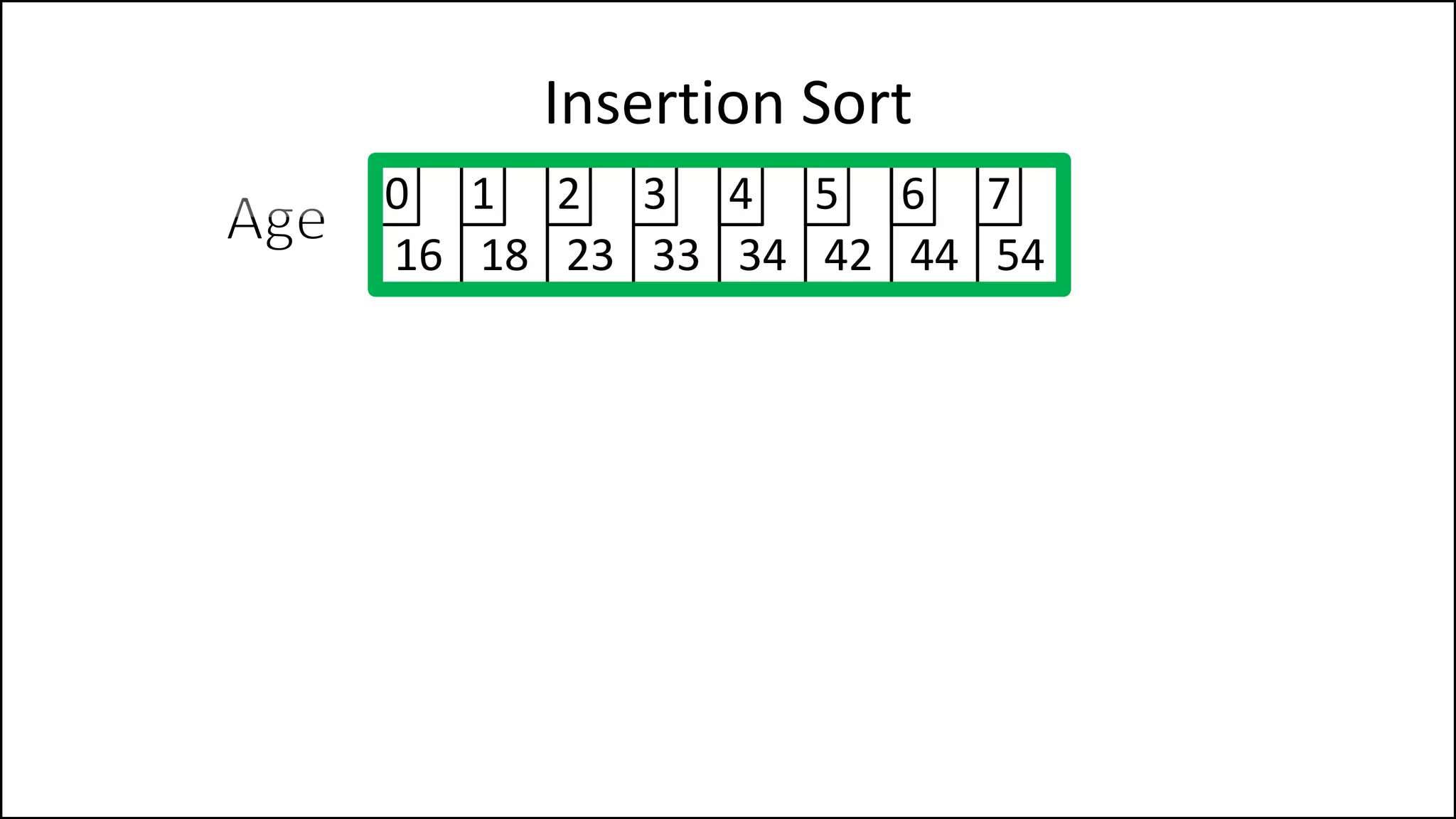
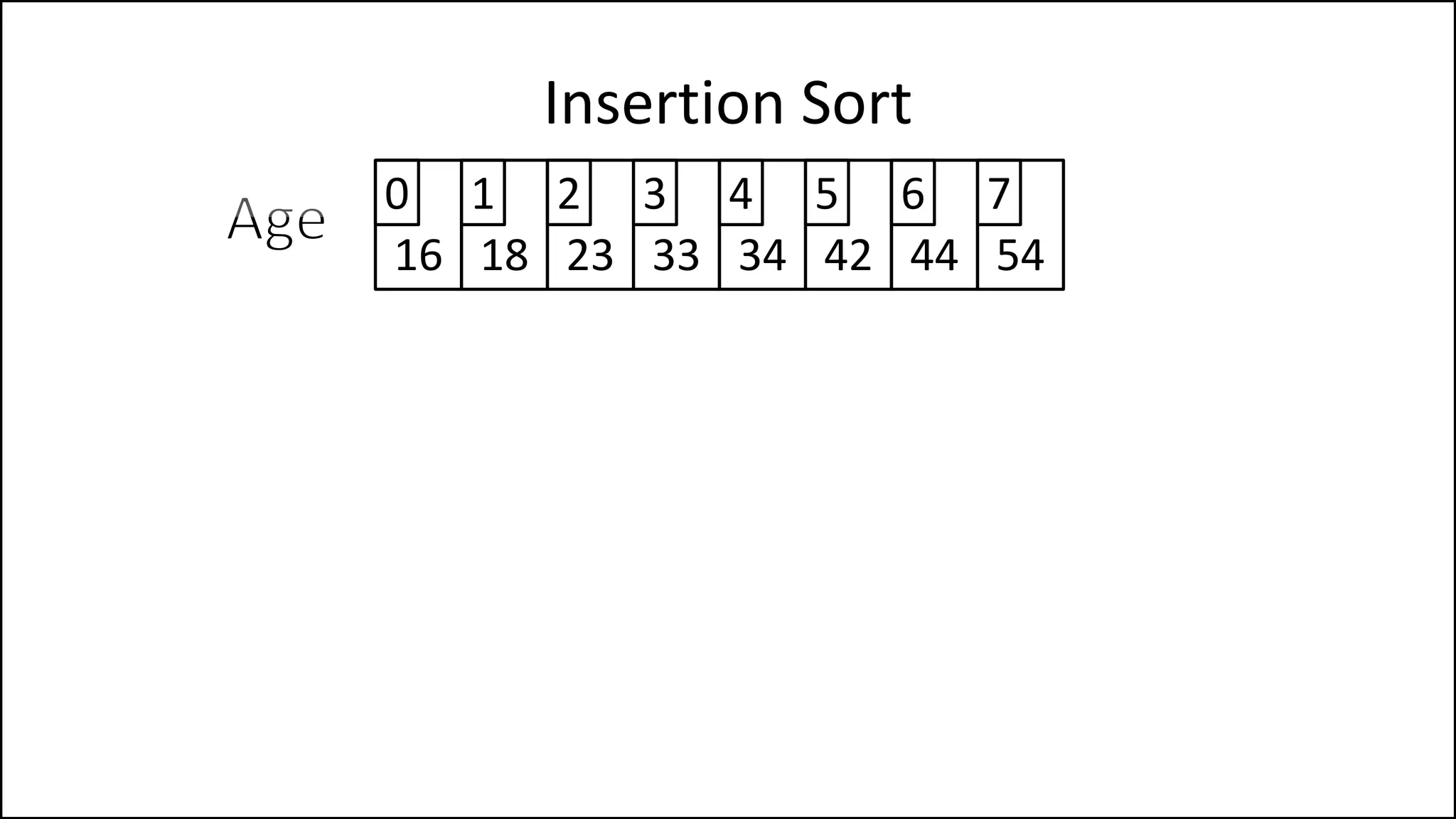

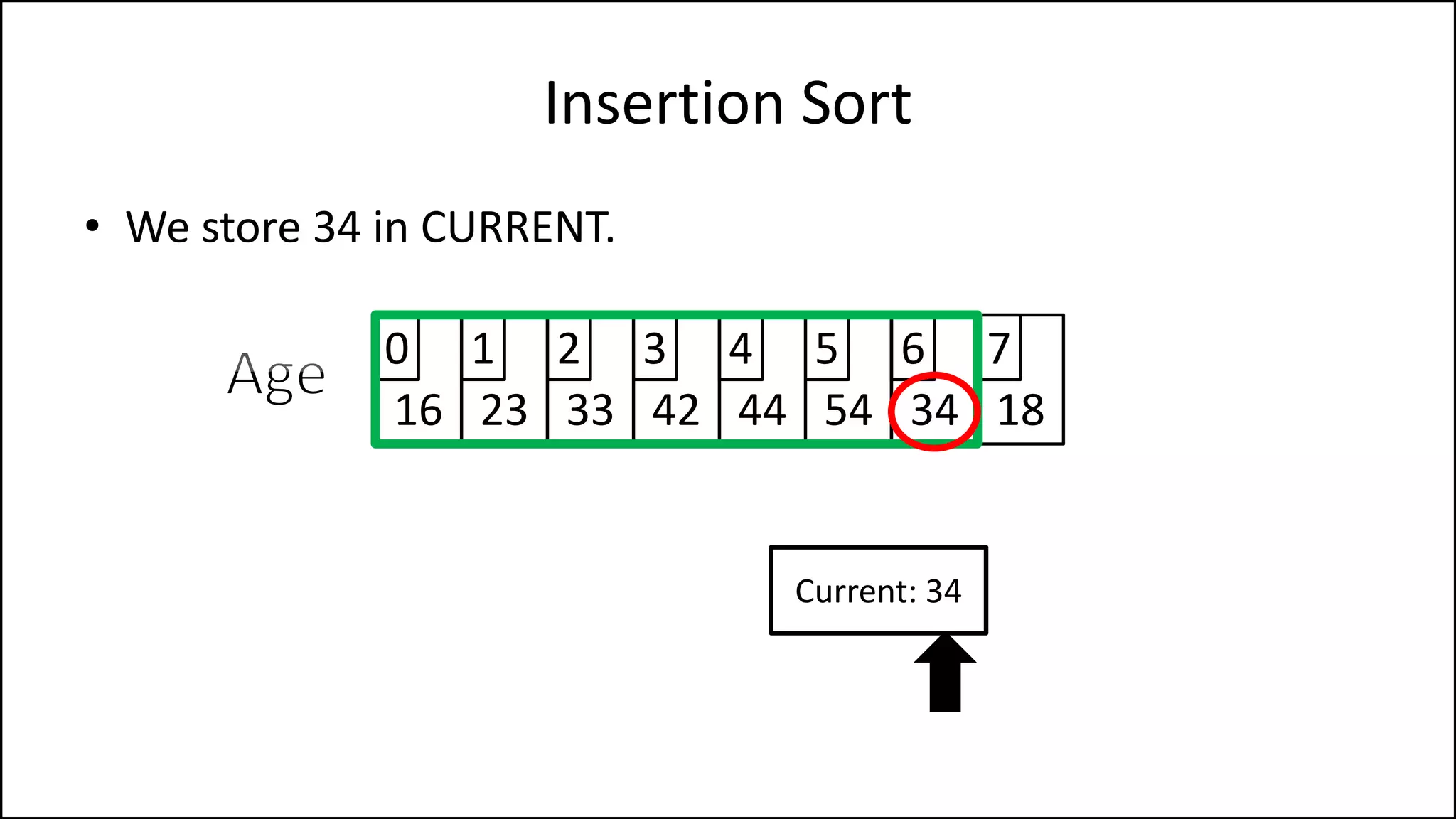
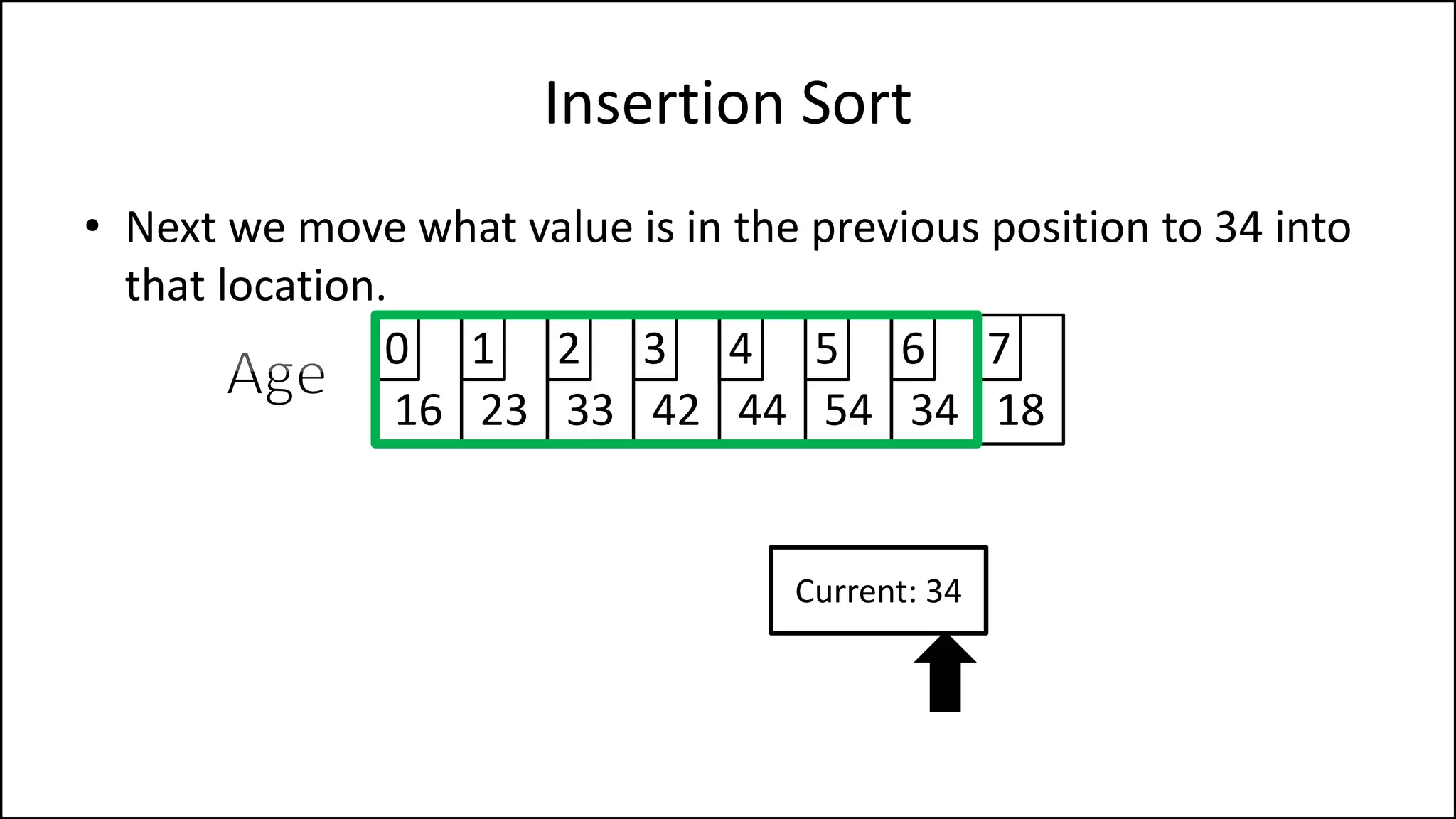
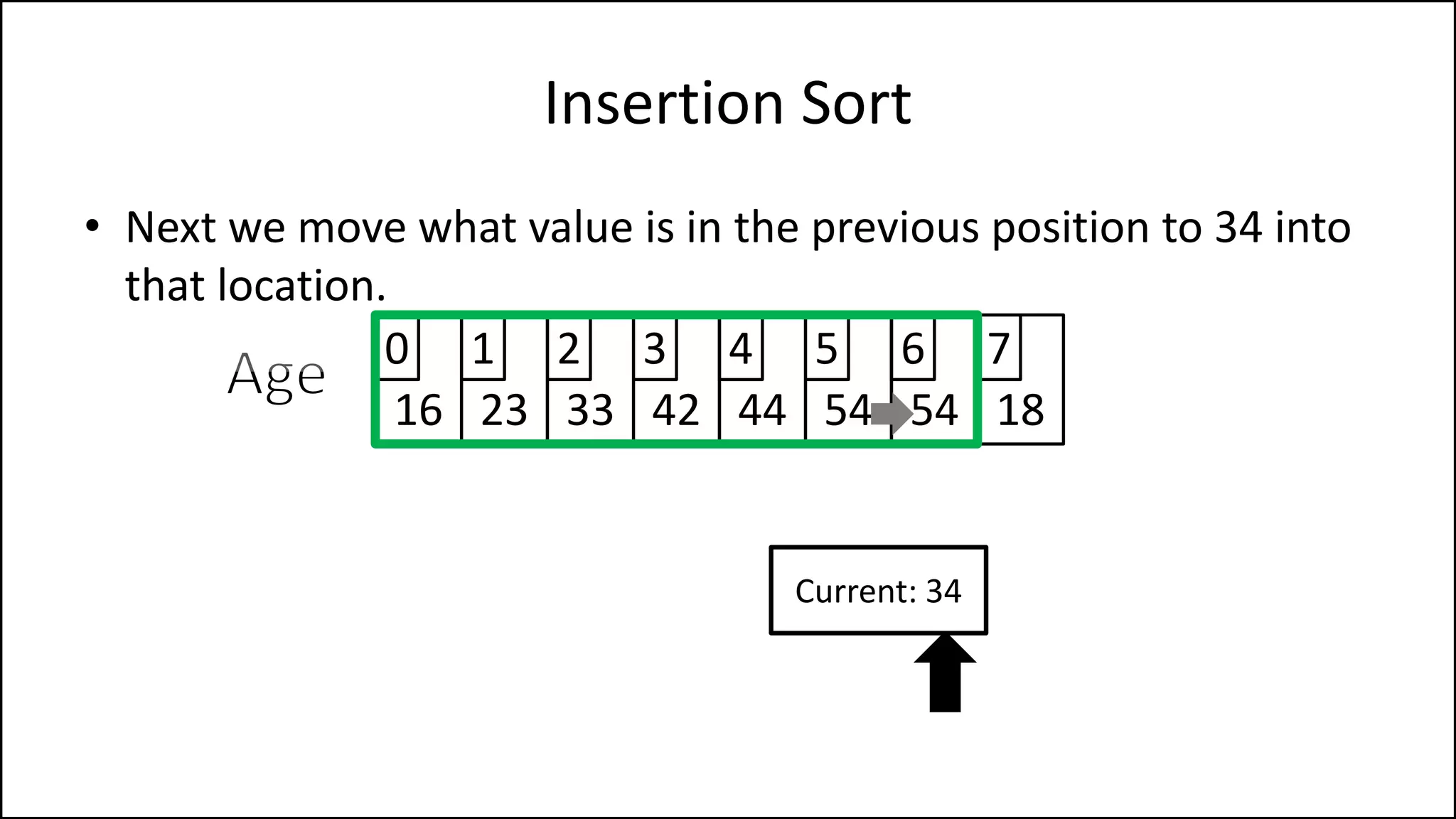
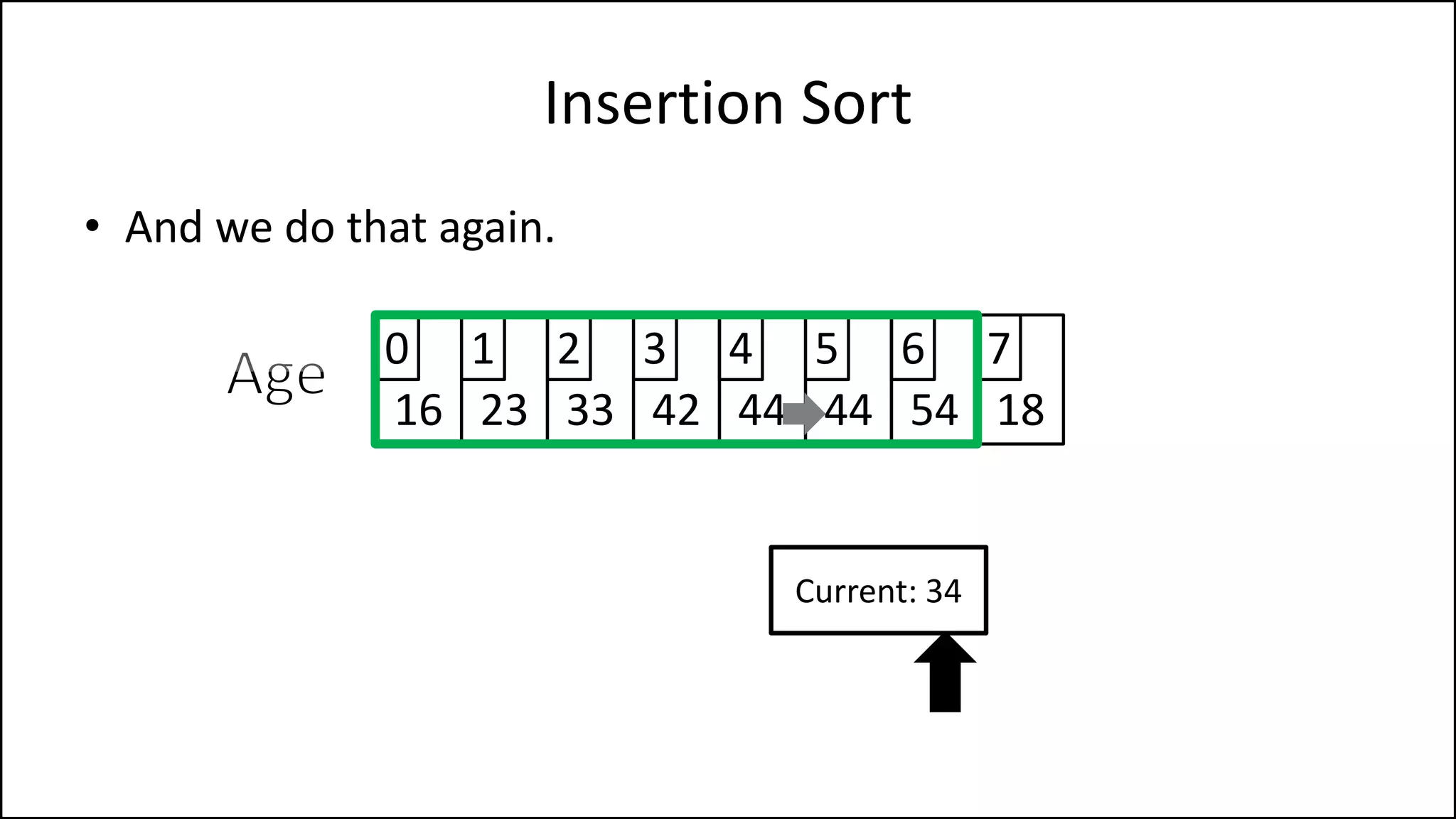
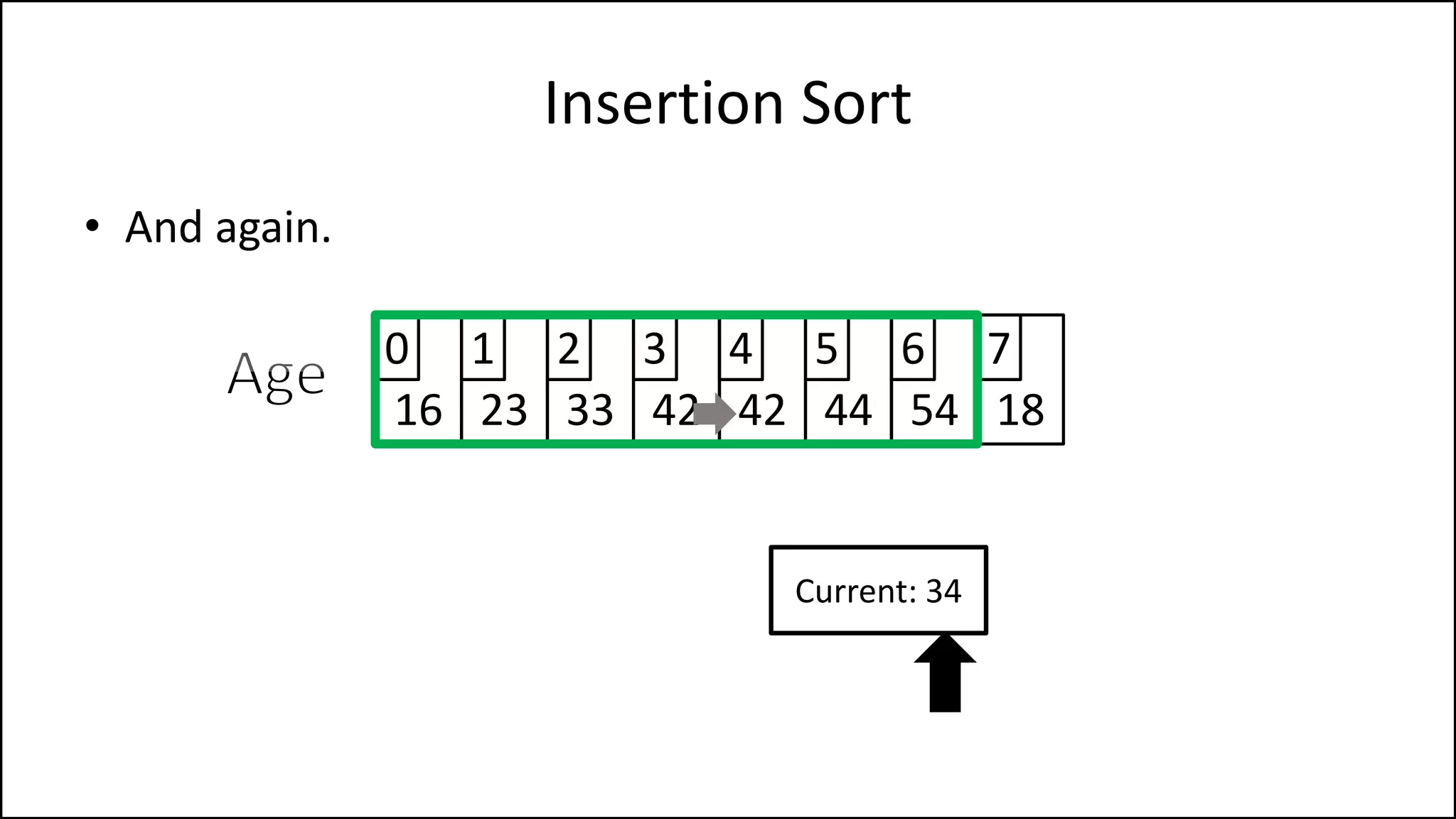
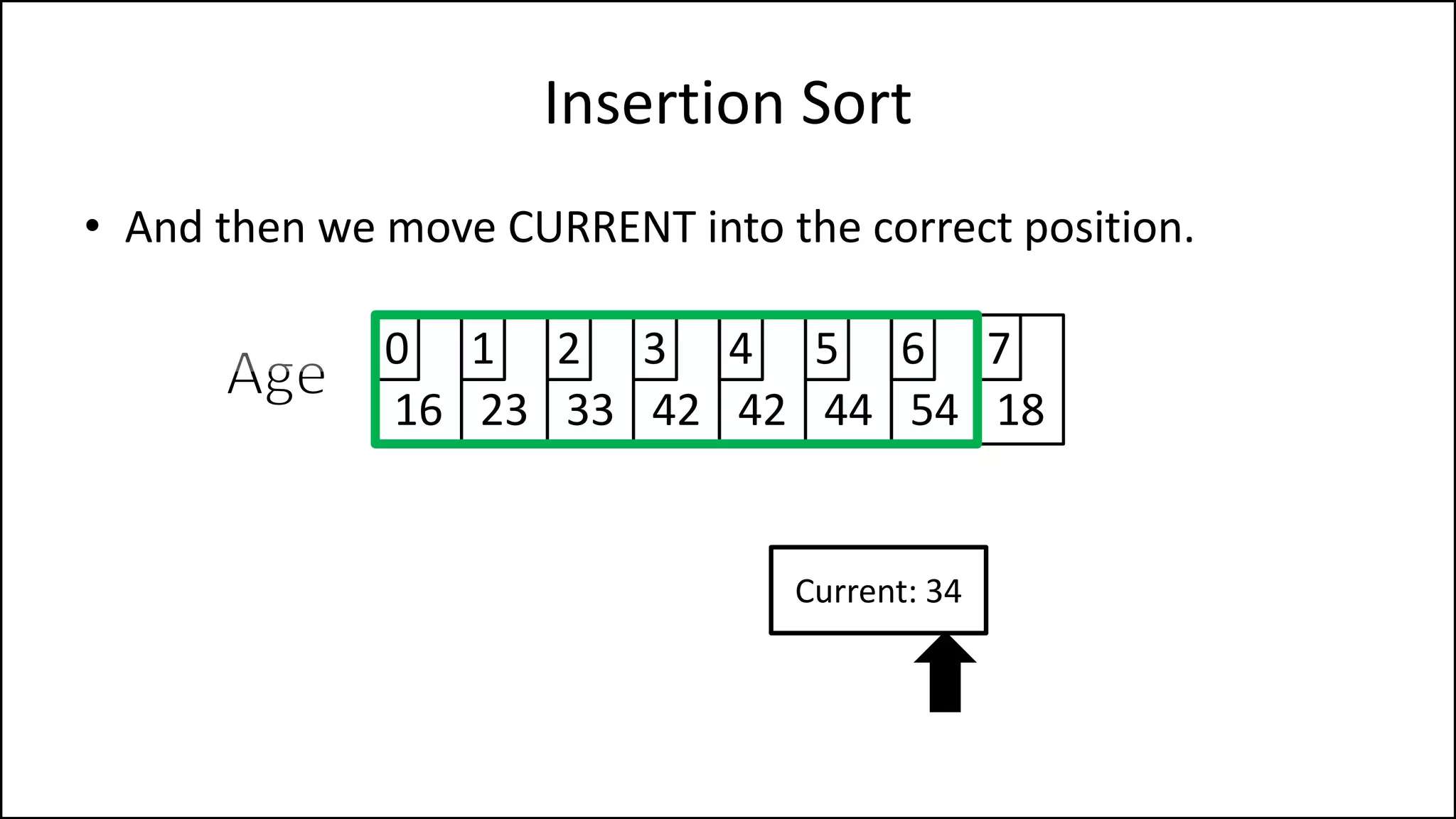
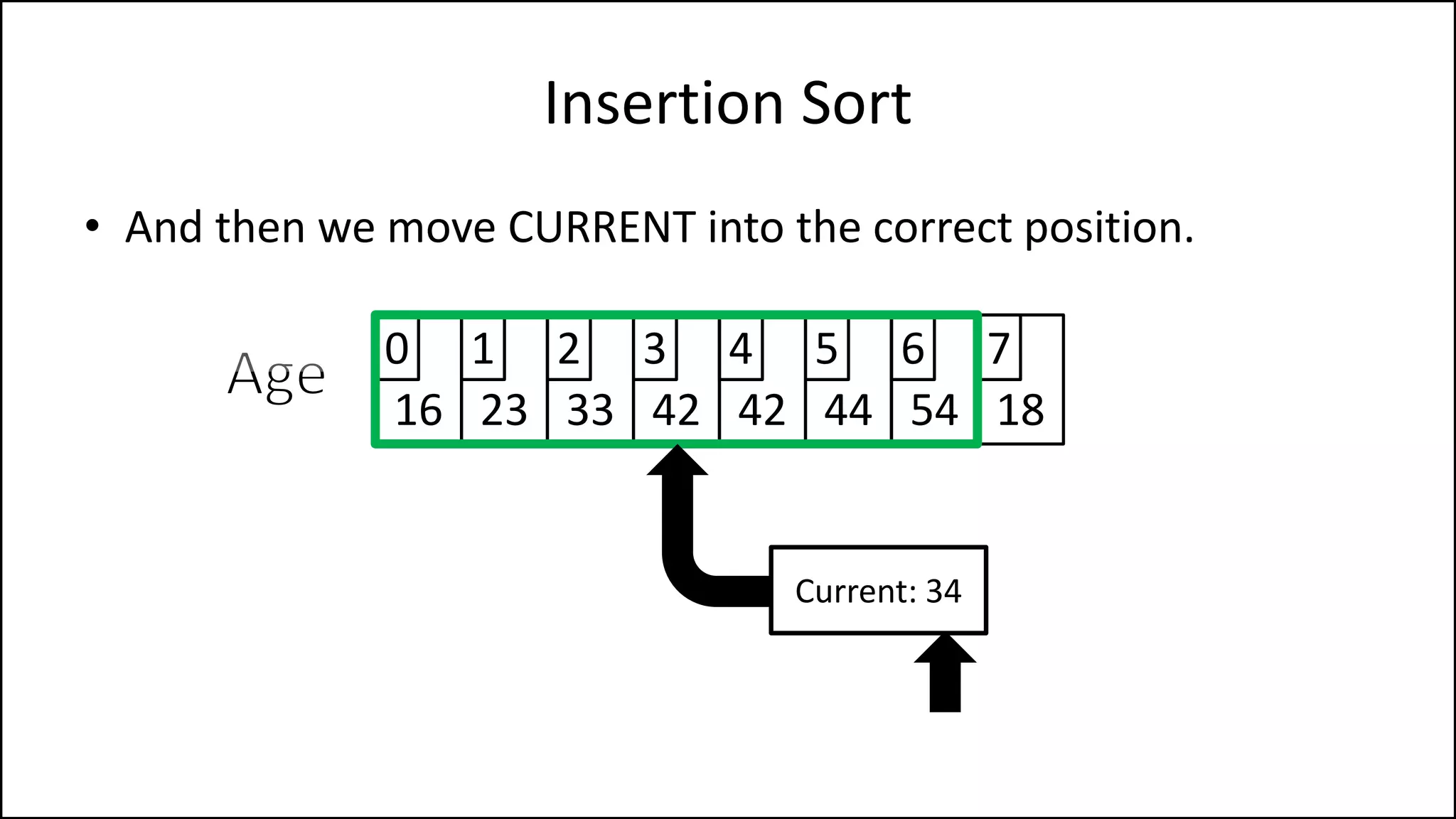
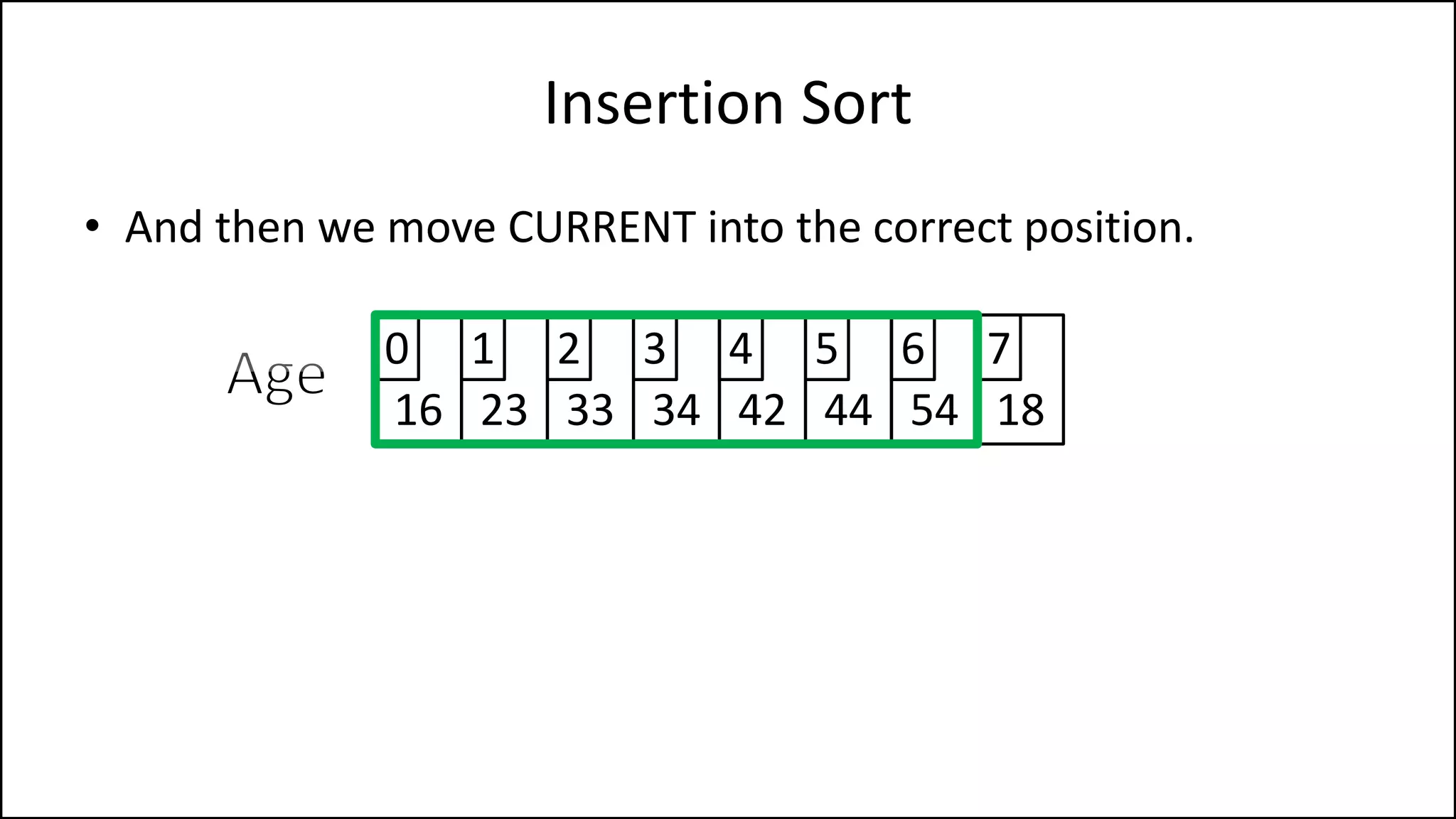


![PROGRAM InsertionSort:
Integer Array[8] <- {44,23,42,33,16,54,34,18};
FOR Index IN 1 TO N
DO current = Array[index];
pos = index;
WHILE (pos > 0 and Array[pos – 1] > current)
DO Array[pos] <- Array[pos - 1];
pos = pos - 1;
ENDWHILE;
Array[pos] = current;
ENDFOR;
END.
Insertion Sort
NOTE: If you have
reached the start of
the list, STOP!](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-43-2048.jpg)





![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-49-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-50-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-51-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-52-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-53-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-54-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-55-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54
– Third group: 42, 34](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-56-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54
– Third group: 42, 34](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-57-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54
– Third group: 42, 34
– Fourth group: 33, 16](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-58-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18
– Second group: 23, 54
– Third group: 42, 34
– Fourth group: 33, 16
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-59-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18 18, 44
– Second group: 23, 54 23, 54
– Third group: 42, 34 34, 42
– Fourth group: 33, 16 16, 33
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-60-2048.jpg)
![Shell Sort
• So, for example. Age = [44, 23, 42, 33, 18, 54, 34, 16].
• Let’s pick every 4th element:
– First group: 44, 18 18, 44
– Second group: 23, 54 23, 54
– Third group: 42, 34 34, 42
– Fourth group: 33, 16 16, 33
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-61-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Let’s pick every 4th element:
– First group: 44, 18 18, 44
– Second group: 23, 54 23, 54
– Third group: 42, 34 34, 42
– Fourth group: 33, 16 16, 33
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-62-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Let’s pick every 4th element:
– First group: 44, 18 18, 44
– Second group: 23, 54 23, 54
– Third group: 42, 34 34, 42
– Fourth group: 33, 16 16, 33
Sort these using
Insertion Sort
The data is not sorted, but a lot of the big numbers have been moved to the end of
the list, and a lot of the smaller numbers have been moved to the start.](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-63-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-64-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-65-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-66-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-67-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42
– Second Group: 23, 16, 54, 33](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-68-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42
– Second Group: 23, 16, 54, 33
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-69-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42 18, 34, 42, 44
– Second Group: 23, 16, 54, 33 16, 23, 33, 54
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-70-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 23, 34, 16, 44, 54, 42, 33].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42 18, 34, 42, 44
– Second Group: 23, 16, 54, 33 16, 23, 33, 54
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-71-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 16, 34, 23, 42, 33, 44, 54].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42 18, 34, 42, 44
– Second Group: 23, 16, 54, 33 16, 23, 33, 54
Sort these using
Insertion Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-72-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 16, 34, 23, 42, 33, 44, 54].
• Now let’s do every 2nd element:
– First Group: 18, 34, 44, 42 18, 34, 42, 44
– Second Group: 23, 16, 54, 33 16, 23, 33, 54
Sort these using
Insertion Sort
The data is almost completely sorted now.](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-73-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 16, 34, 23, 42, 33, 44, 54].
• Finally do one more Insertion Sort with all elements](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-74-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 16, 34, 23, 42, 33, 44, 54].
• Finally do one more Insertion Sort with all elements
• This will be very fast since the data is almost sorted](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-75-2048.jpg)
![Shell Sort
• So, for example. Age = [18, 16, 34, 23, 42, 33, 44, 54].
• Finally do one more Insertion Sort with all elements
• This will be very fast since the data is almost sorted
• Age = [16, 18, 23, 33, 34, 42, 44, 54].](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-76-2048.jpg)

![MODULE GapInsertionSort(Array, StartPos, Gap):
FOR Index IN StartPos TO N INCREMENT BY Gap
DO current = Array[index];
pos = index;
WHILE (pos > Gap and Array[pos – Gap] > current)
DO Array[pos] <- Array[pos - Gap];
pos = pos - Gap;
ENDWHILE;
Array[pos] = current;
ENDFOR;
END.
Shell Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-78-2048.jpg)
![MODULE GapInsertionSort(Array, StartPos, Gap):
FOR Index IN StartPos TO N INCREMENT BY Gap
DO current = Array[index];
pos = index;
WHILE (pos > Gap and Array[pos – Gap] > current)
DO Array[pos] <- Array[pos - Gap];
pos = pos - Gap;
ENDWHILE;
Array[pos] = current;
ENDFOR;
END.
Shell Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-79-2048.jpg)







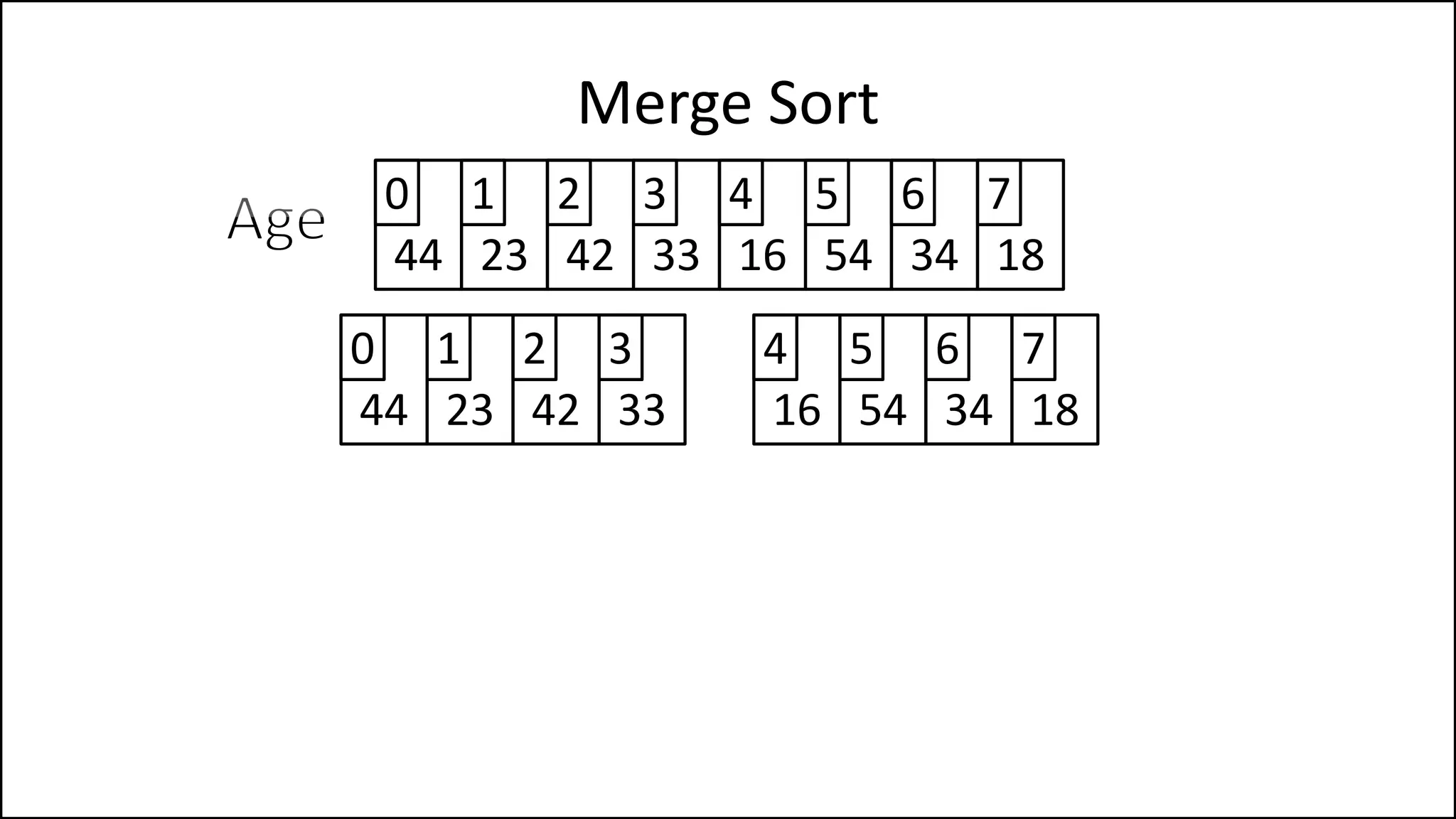
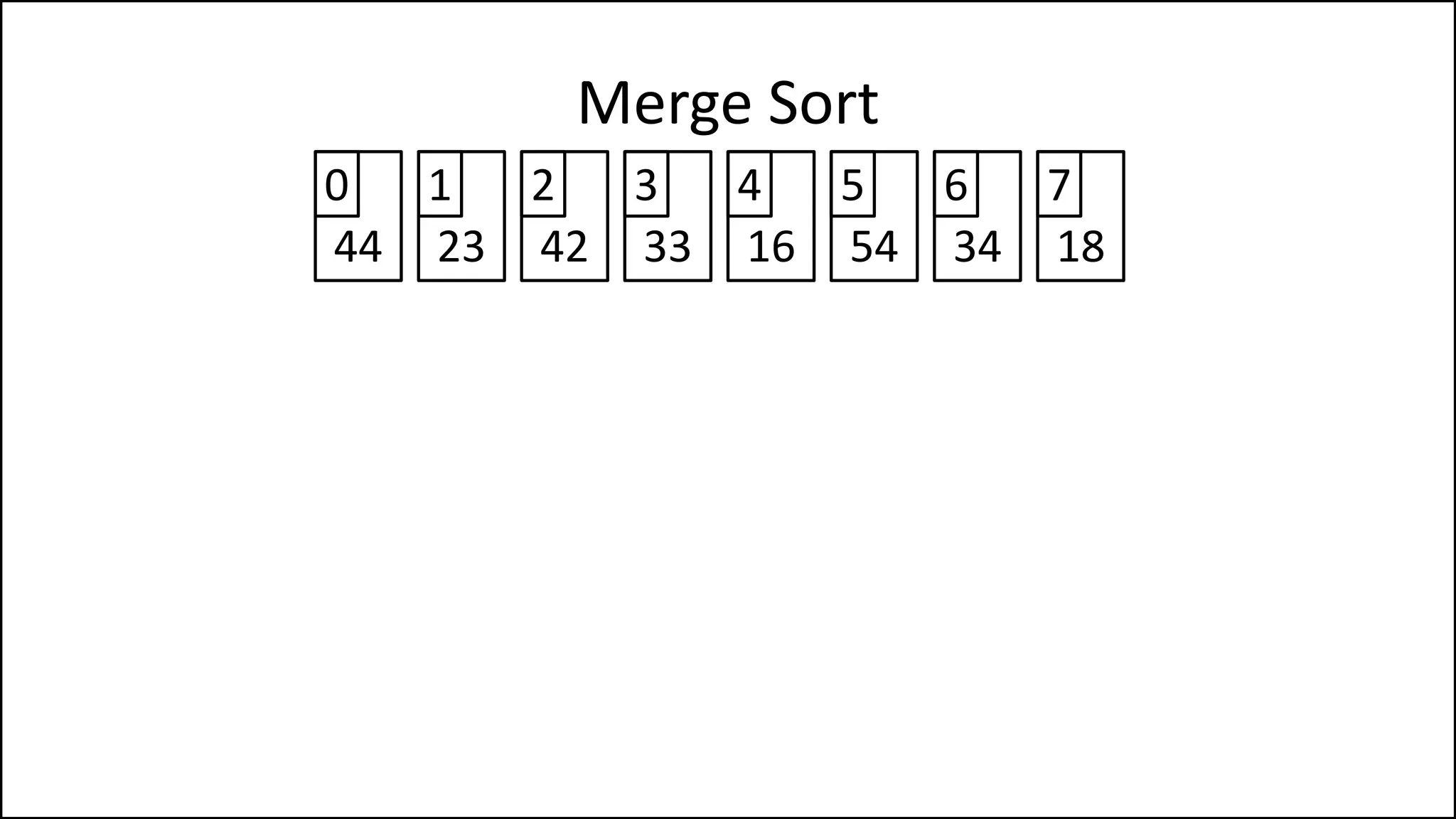
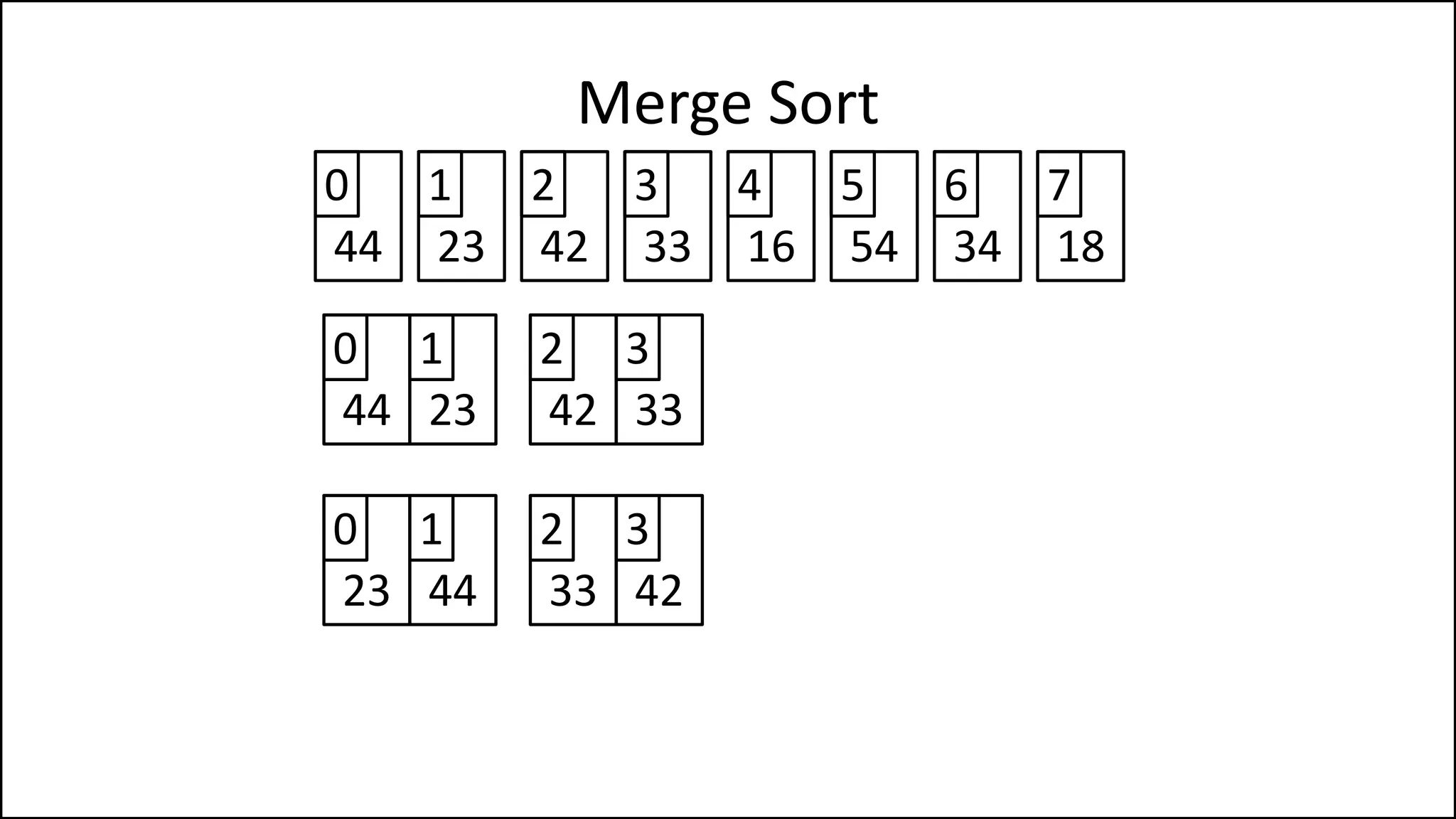
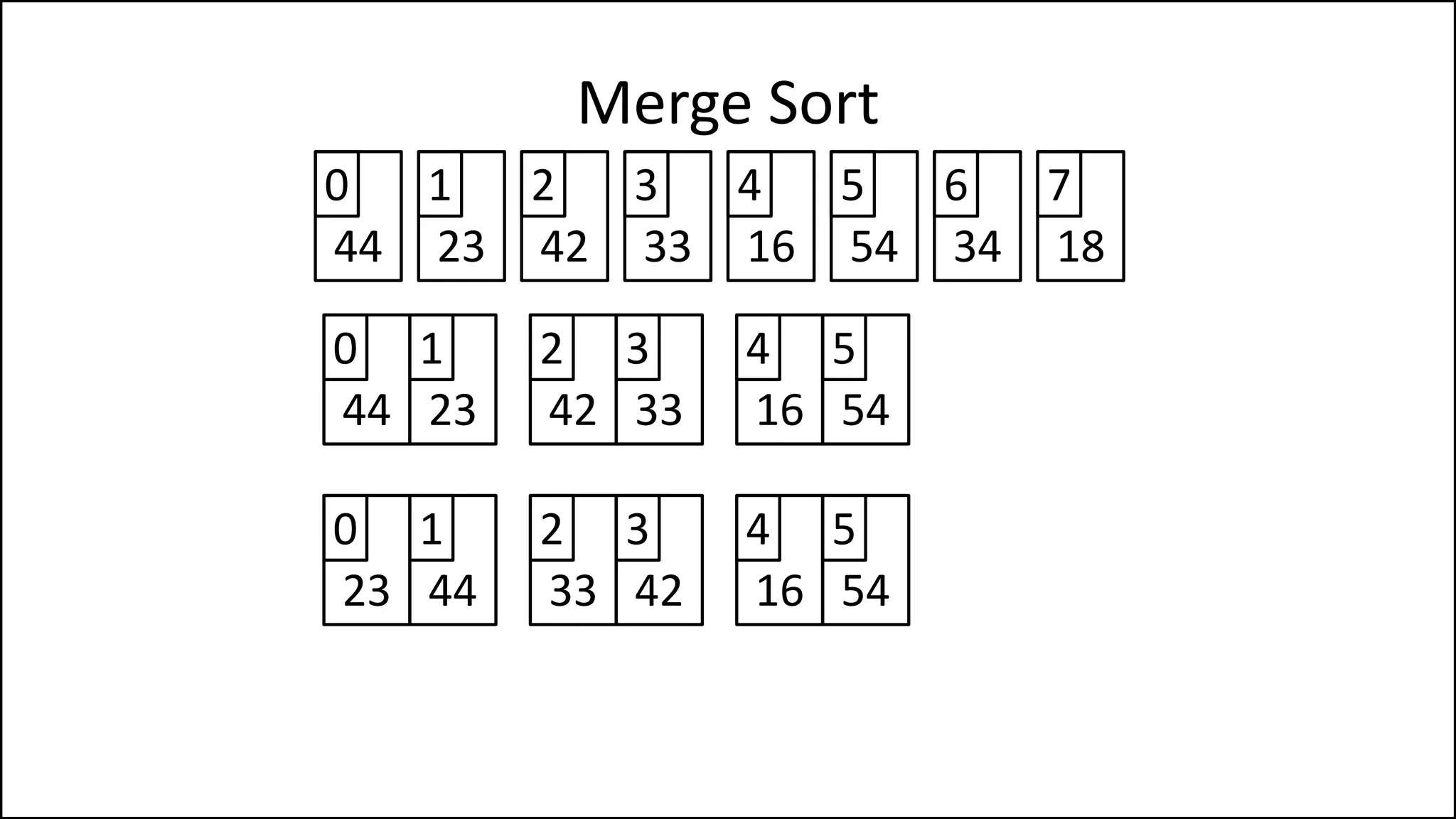

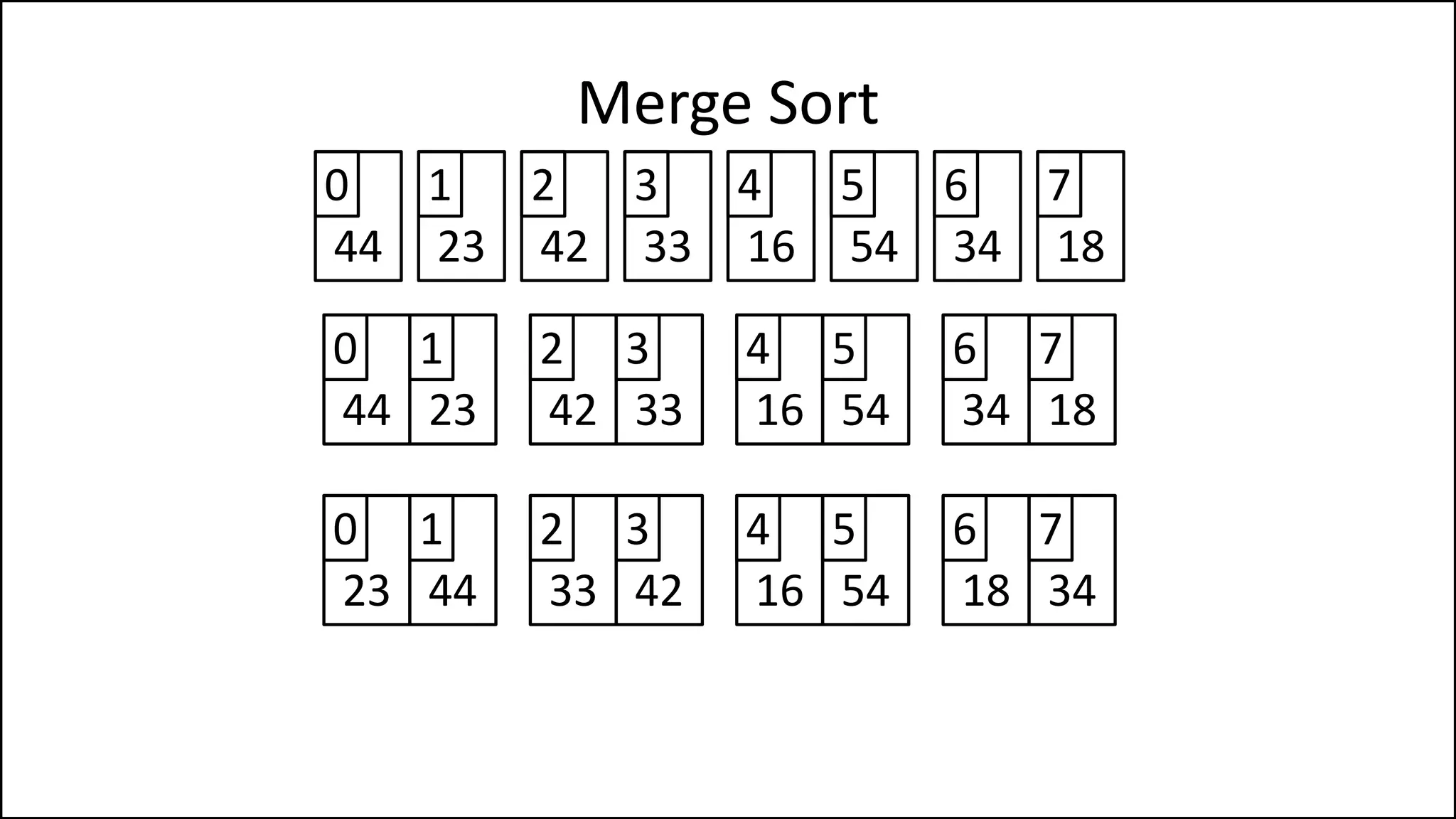
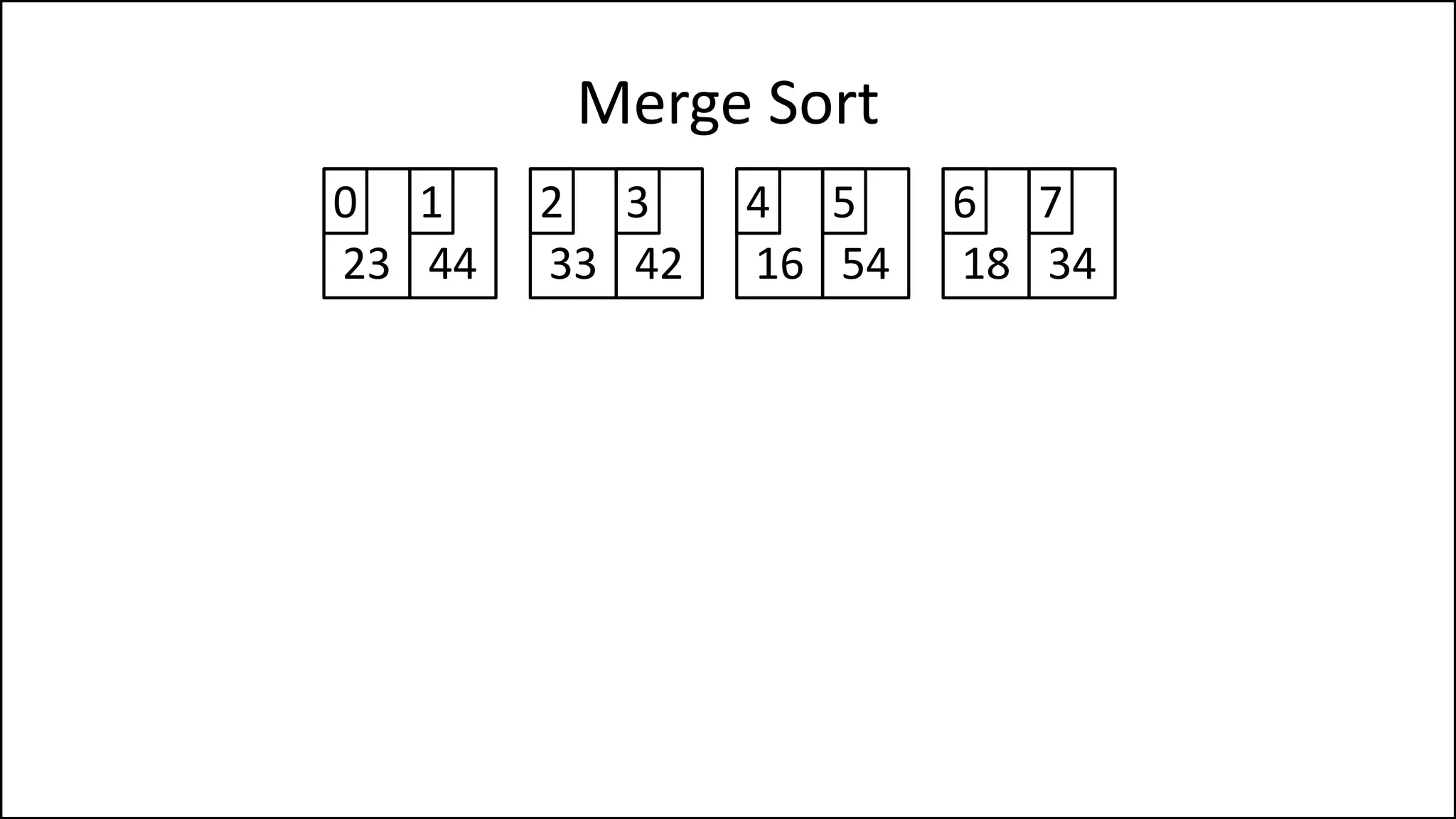
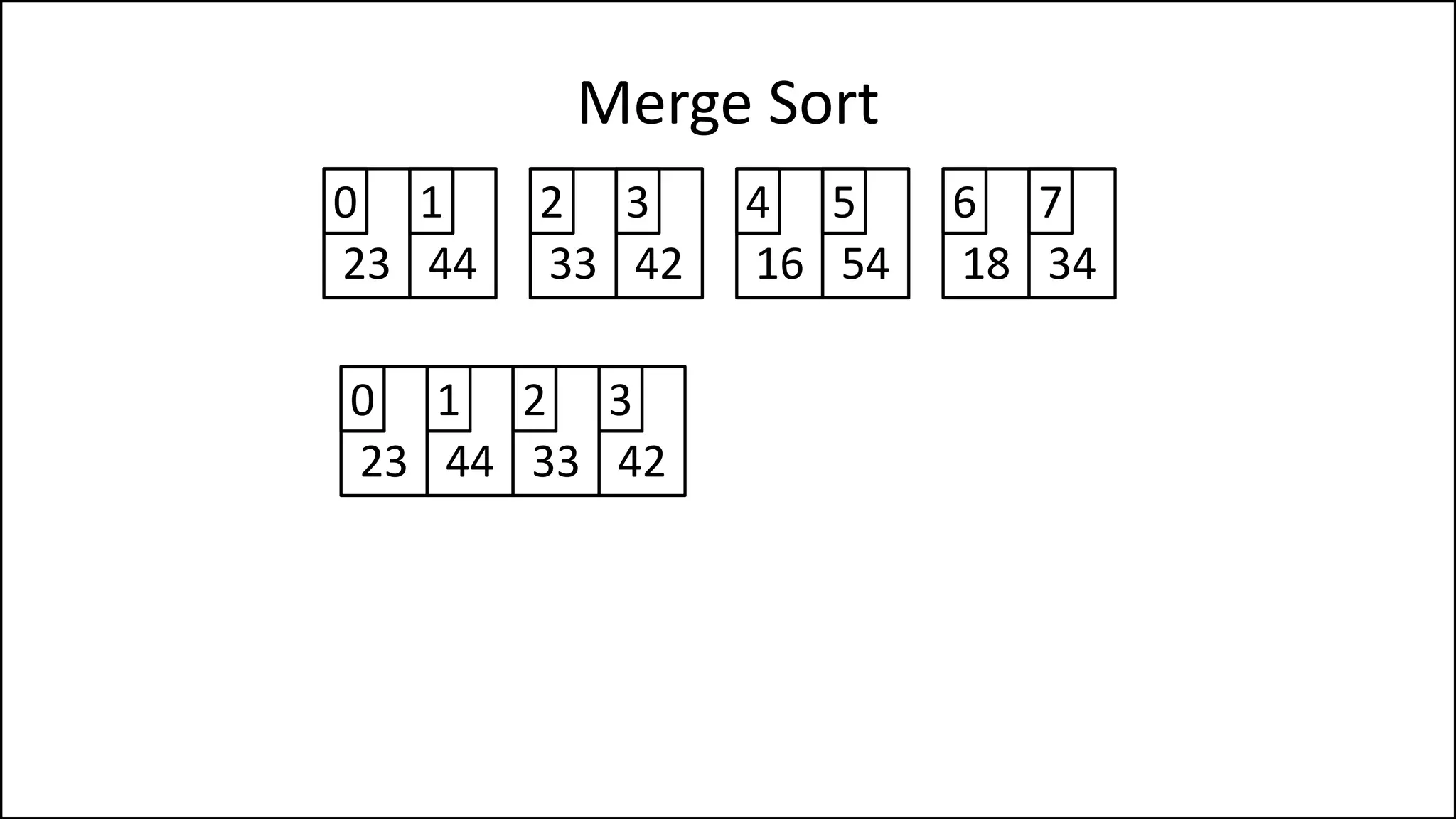

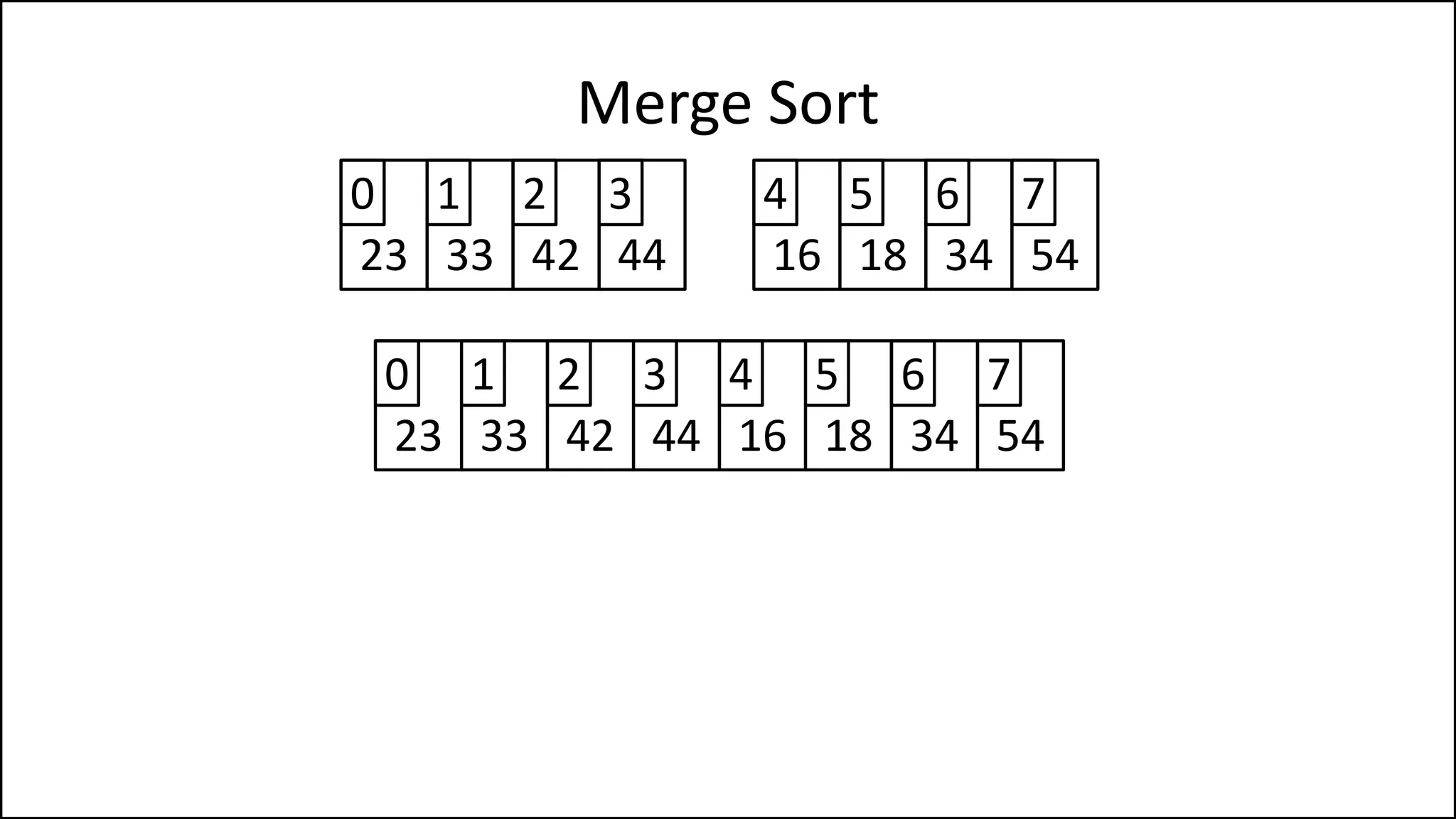
![PROGRAM MainMergeSort:
Array = [44,23,42,33,16,54,34,18];
MergeSort(Array);
PRINT Array;
END.
Merge Sort](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-107-2048.jpg)
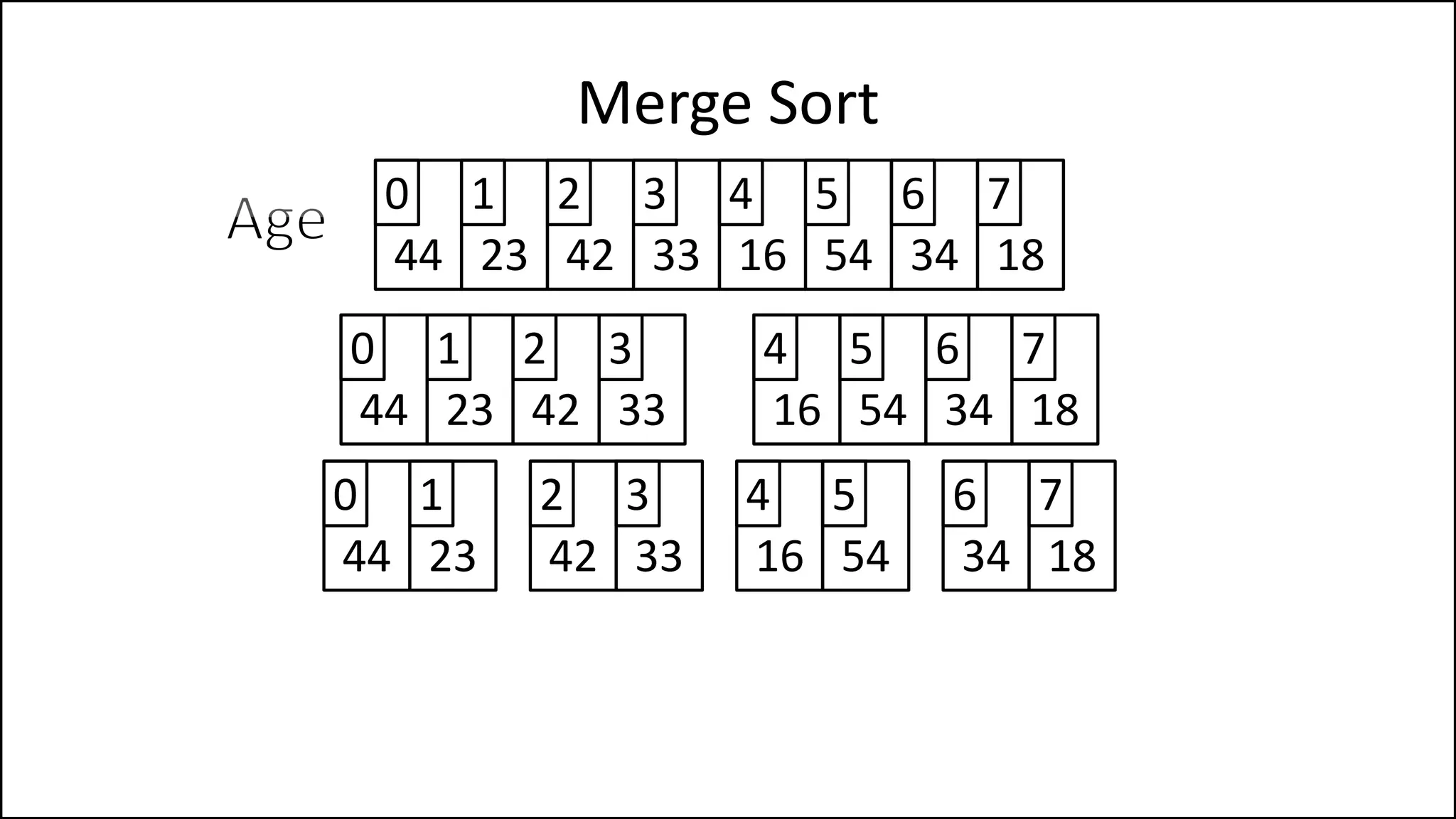
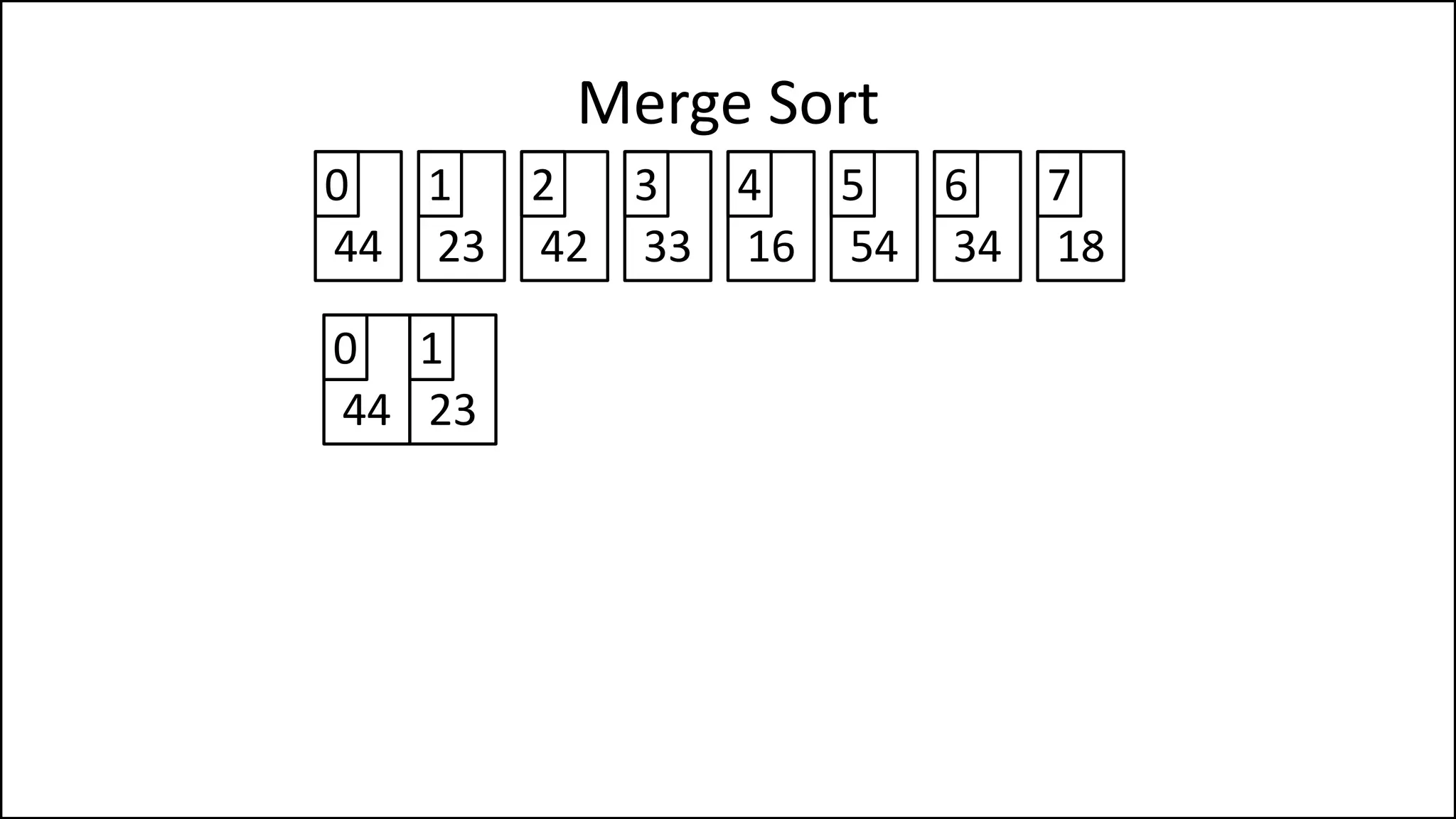
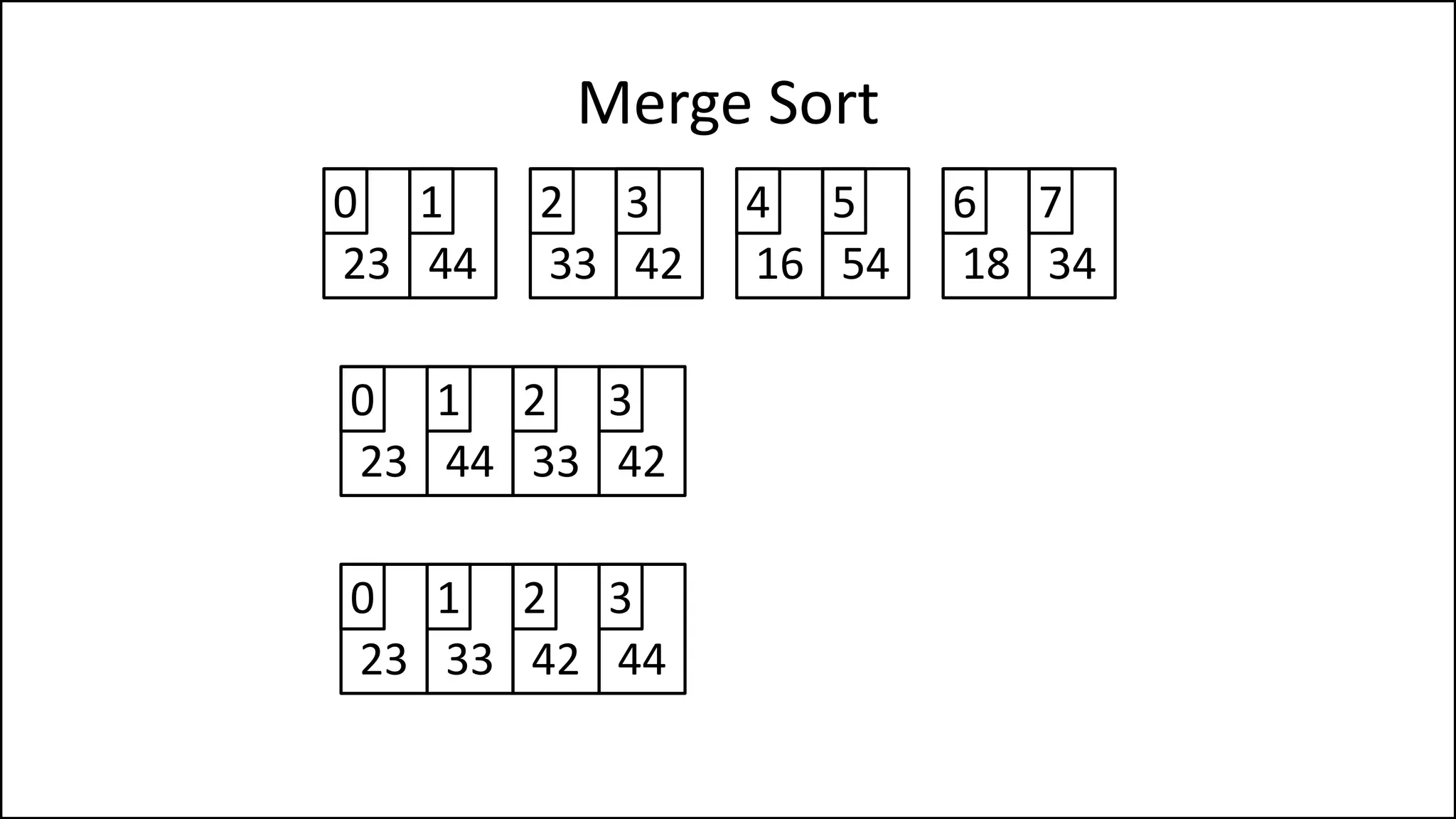
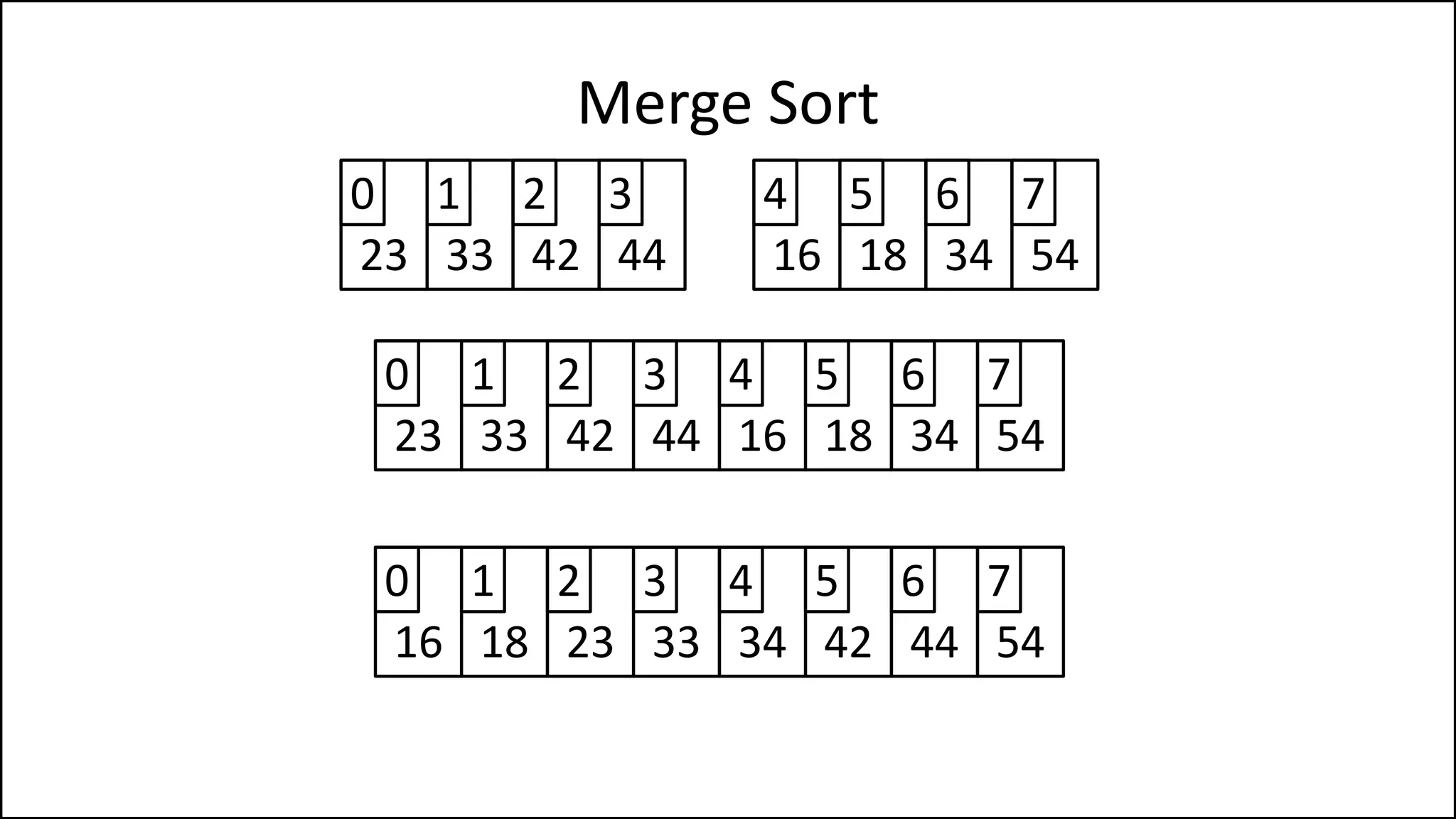
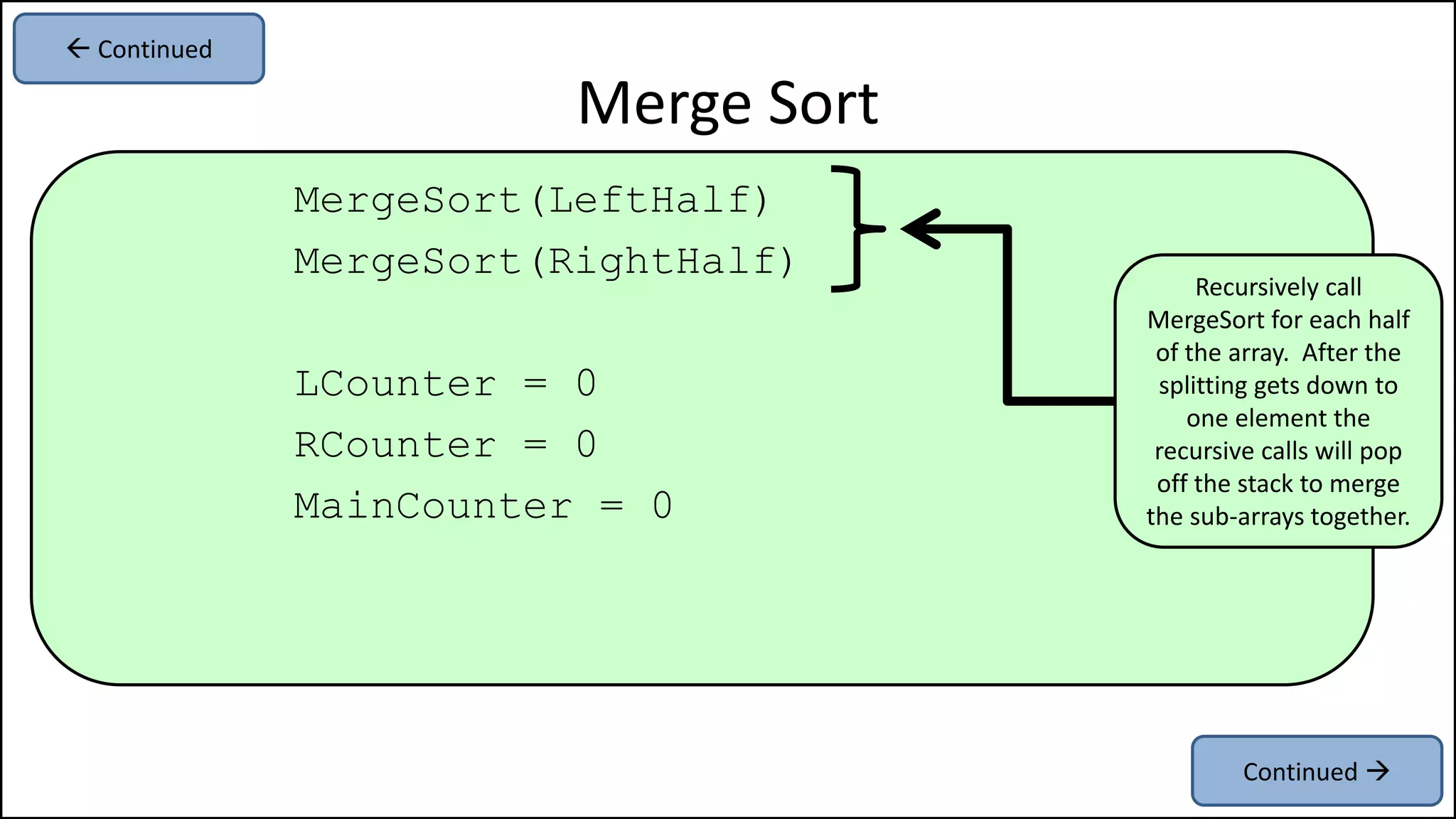
![PROGRAM MergeSort(Array):
IF (length(Array) > 1)
THEN MidPoint = len(Age)//2
LeftHalf = Age[:MidPoint]
RightHalf = Age[MidPoint:]
Merge Sort
Keep recursively
splitting the array
until you get down
sub-arrays of one
element.
Continued ](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-108-2048.jpg)
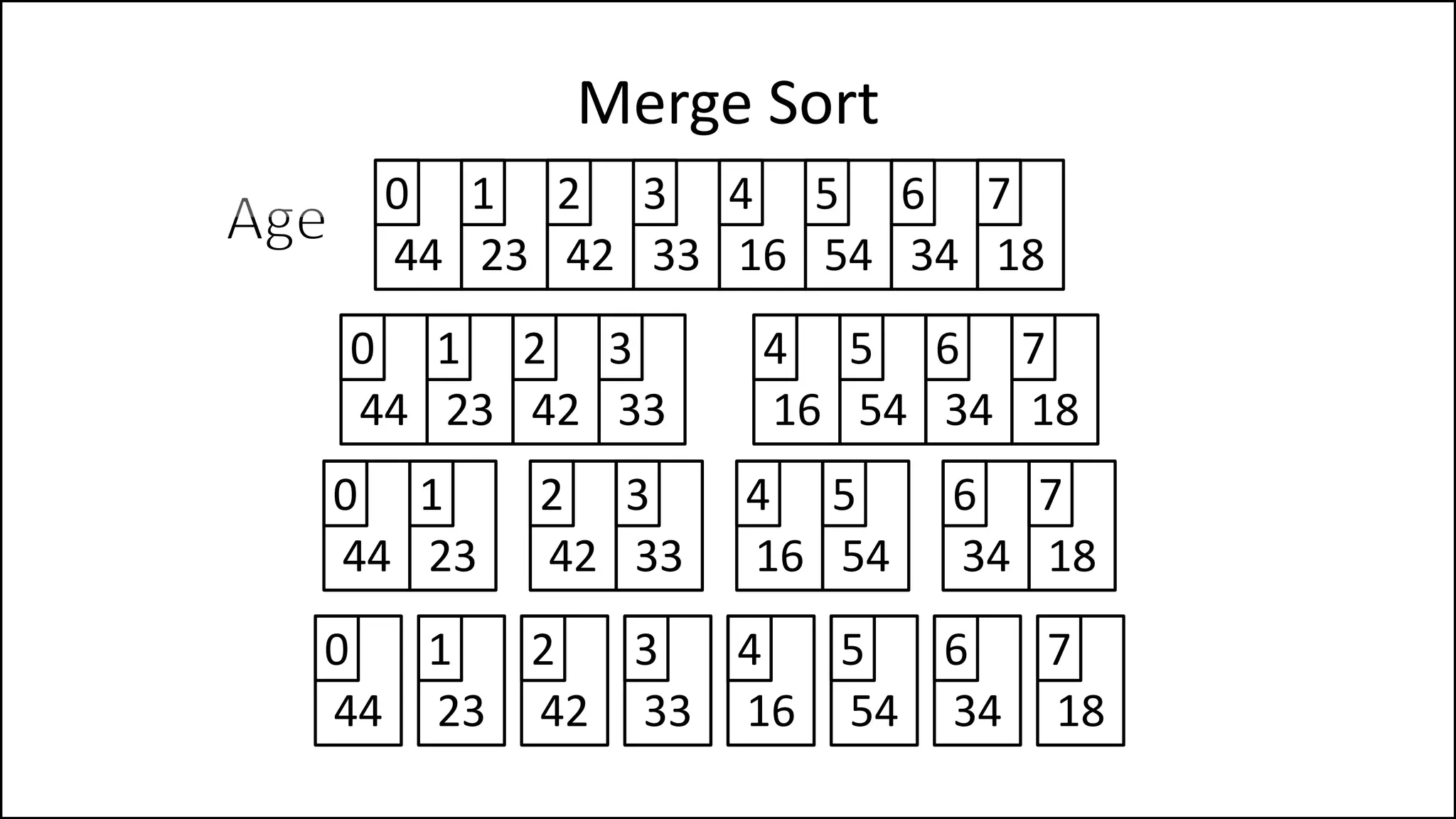
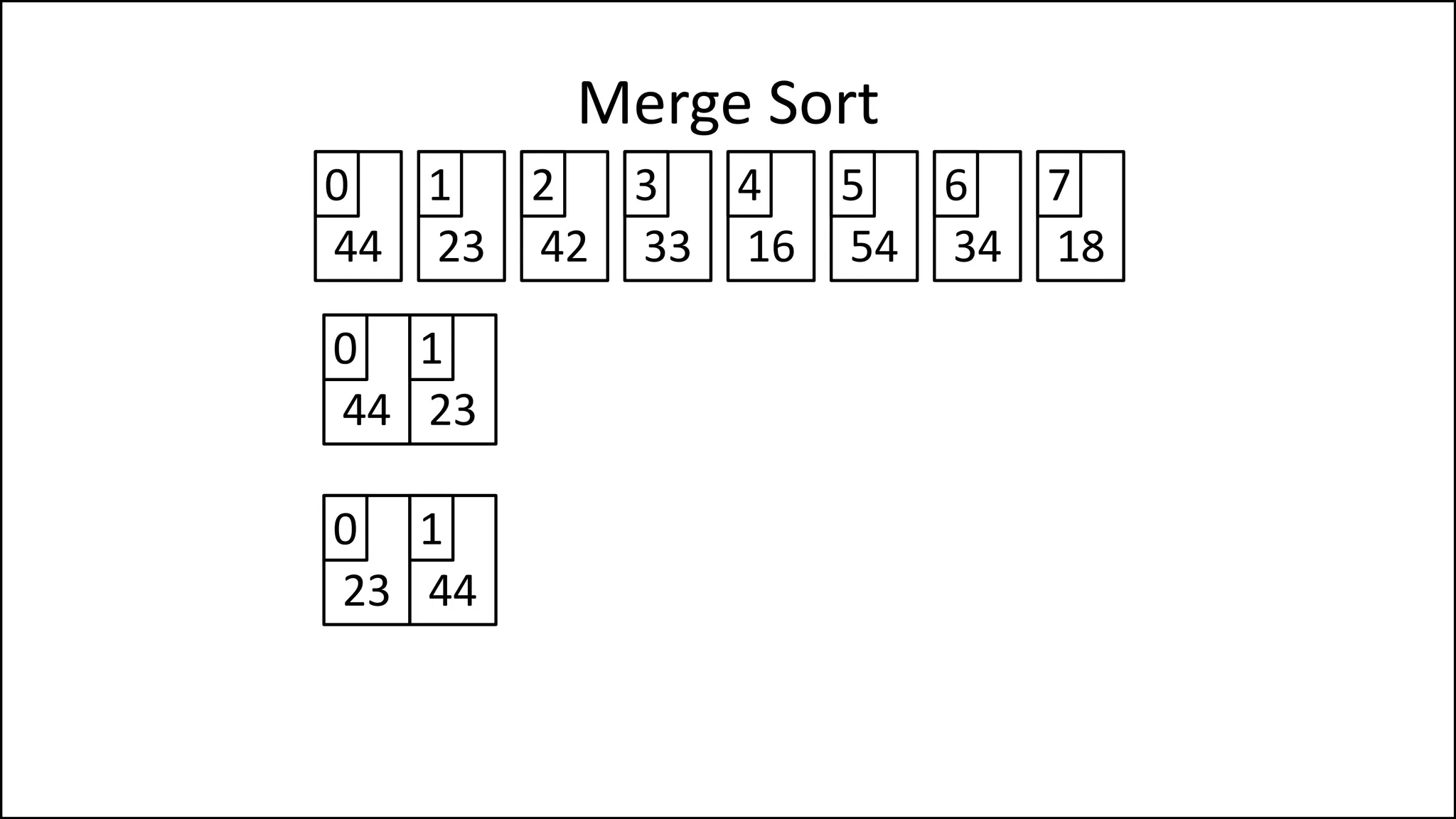
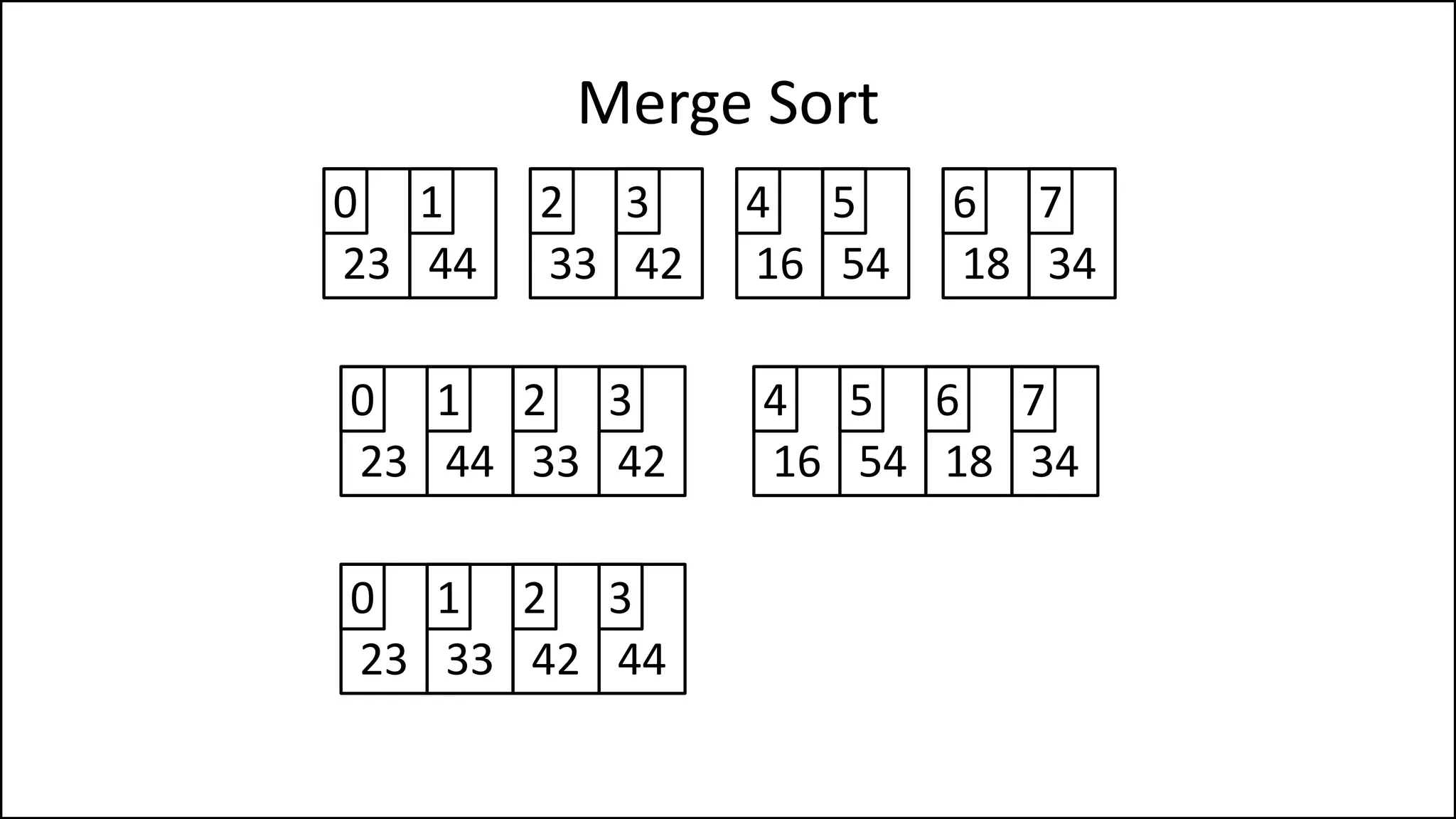
![WHILE (LCounter < len(LeftHalf) AND
RCounter < len(RightHalf))
DO IF LeftHalf[LCounter] < RightHalf[RCounter]
THEN Age[MainCounter] = LeftHalf[LCounter];
LCounter = LCounter + 1;
ELSE Age[MainCounter] = RightHalf[RCounter];
RCounter = RCounter + 1;
ENDIF;
MainCounter = MainCounter + 1;
ENDWHILE;
Merge Sort
Continued
Continued
Keep comparing each
element of the left and
right sub-array, writing
the smaller element
into the main array](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-110-2048.jpg)
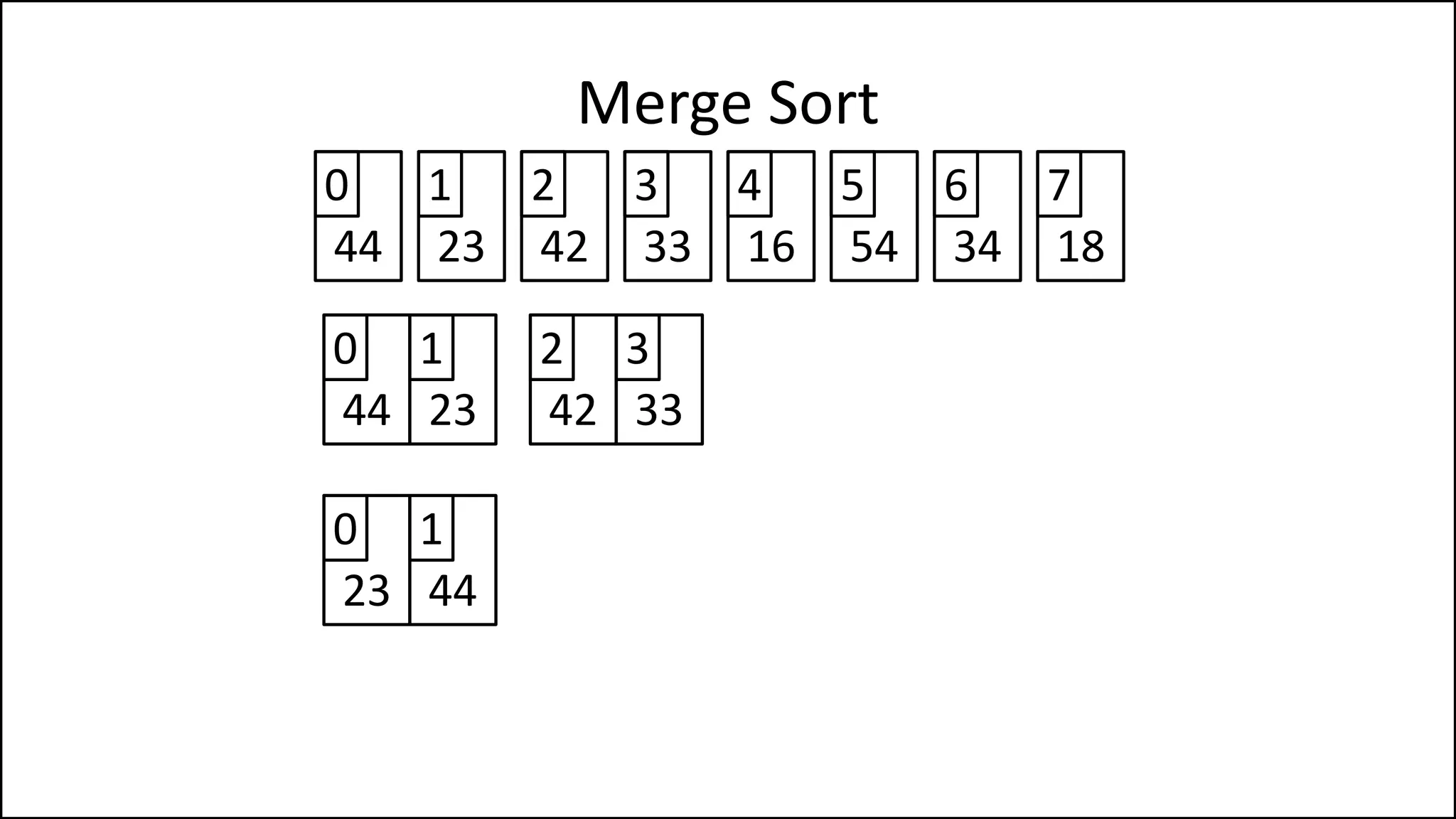
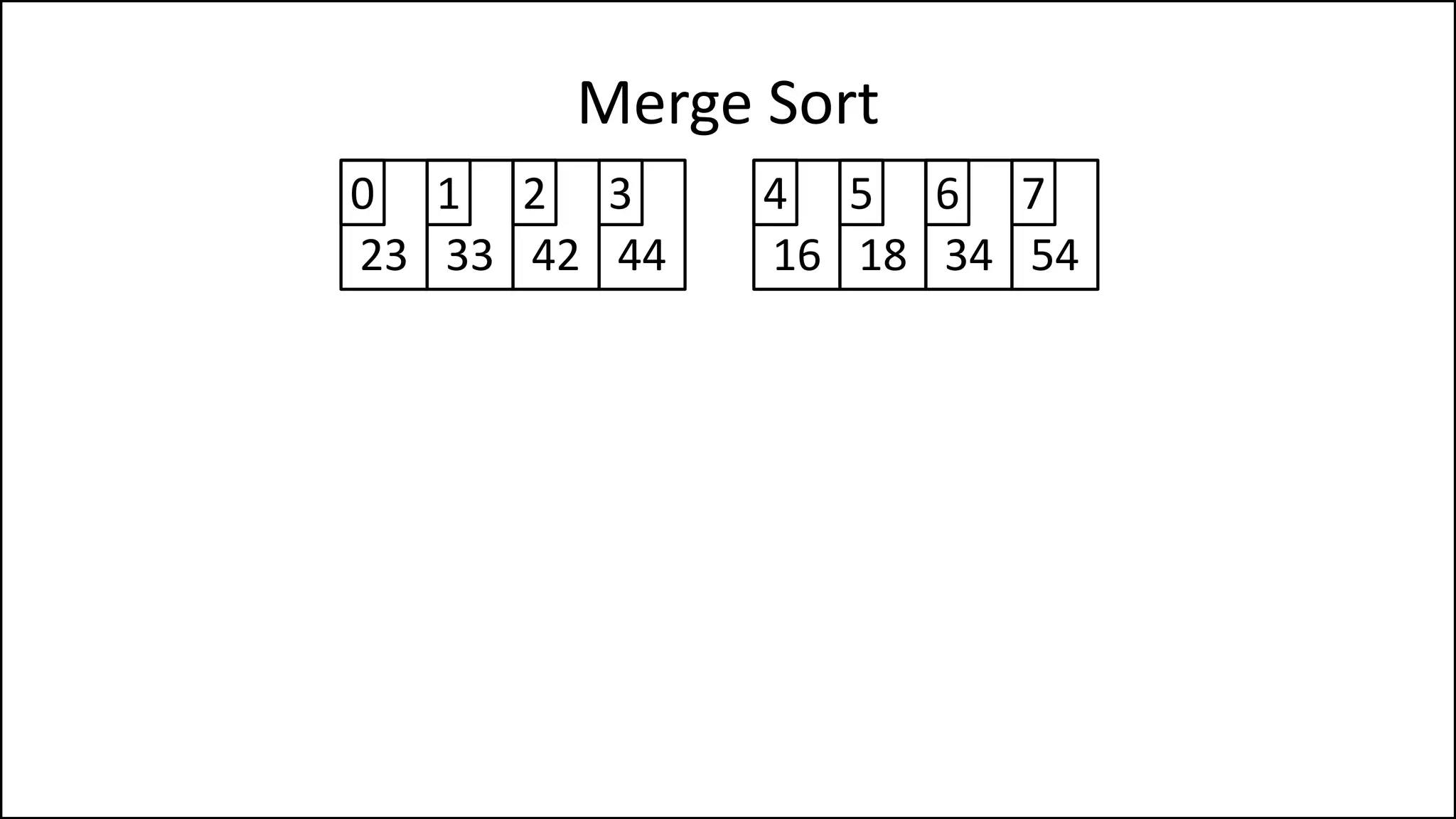
![WHILE LCounter < len(LeftHalf)
DO Age[MainCounter] = LeftHalf[LCounter];
LCounter = LCounter + 1;
MainCounter = MainCounter + 1;
ENDWHILE;
WHILE Rcounter < len(RightHalf)
DO Age[MainCounter] = RightHalf[RCounter]
RCounter = RCounter + 1
MainCounter = MainCounter + 1
ENDWHILE;
ENDIF;
Merge Sort
Continued
After the comparisons
are done, write either
the rest of the left array
or the right array into
the main array that](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-111-2048.jpg)






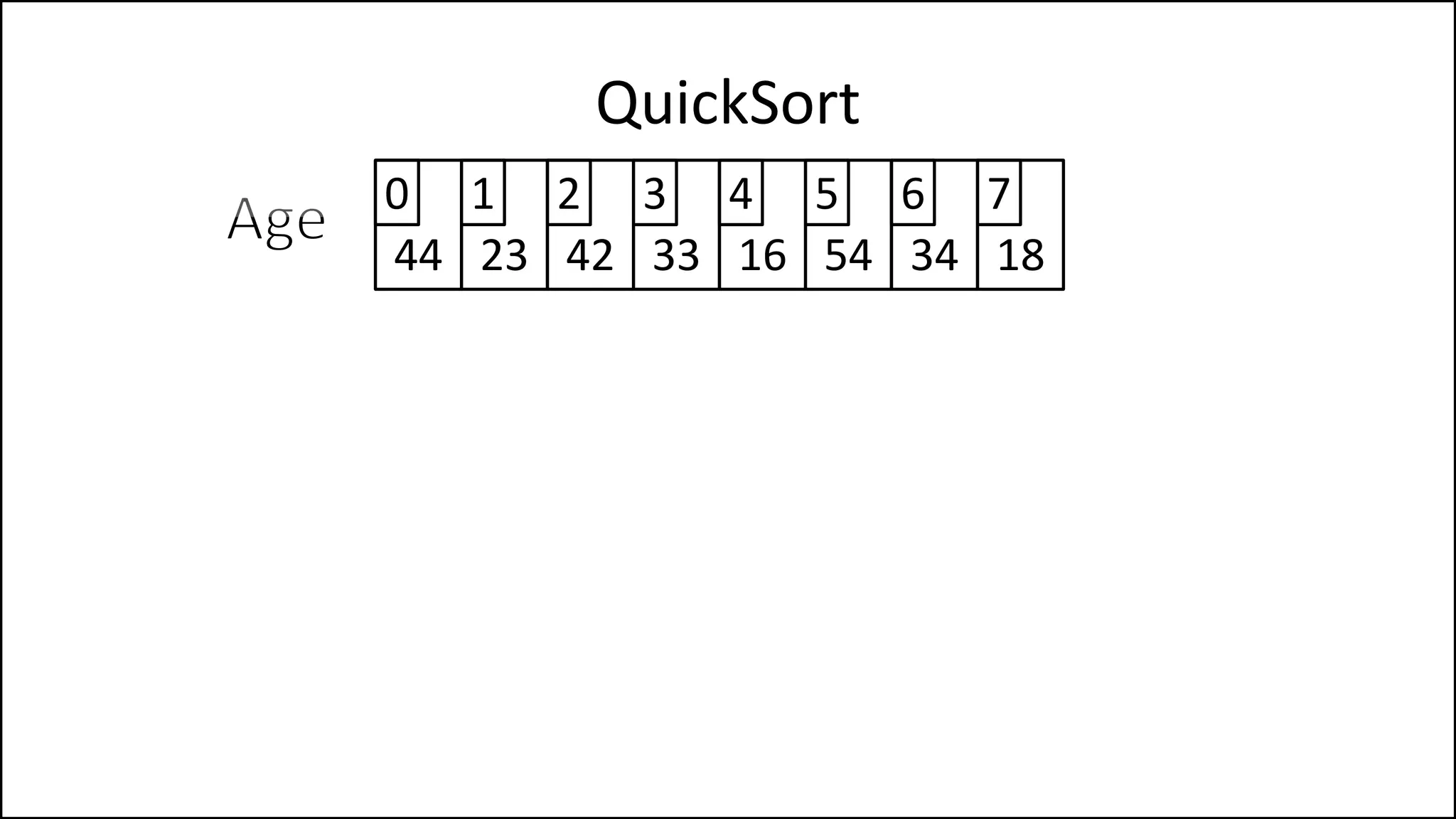
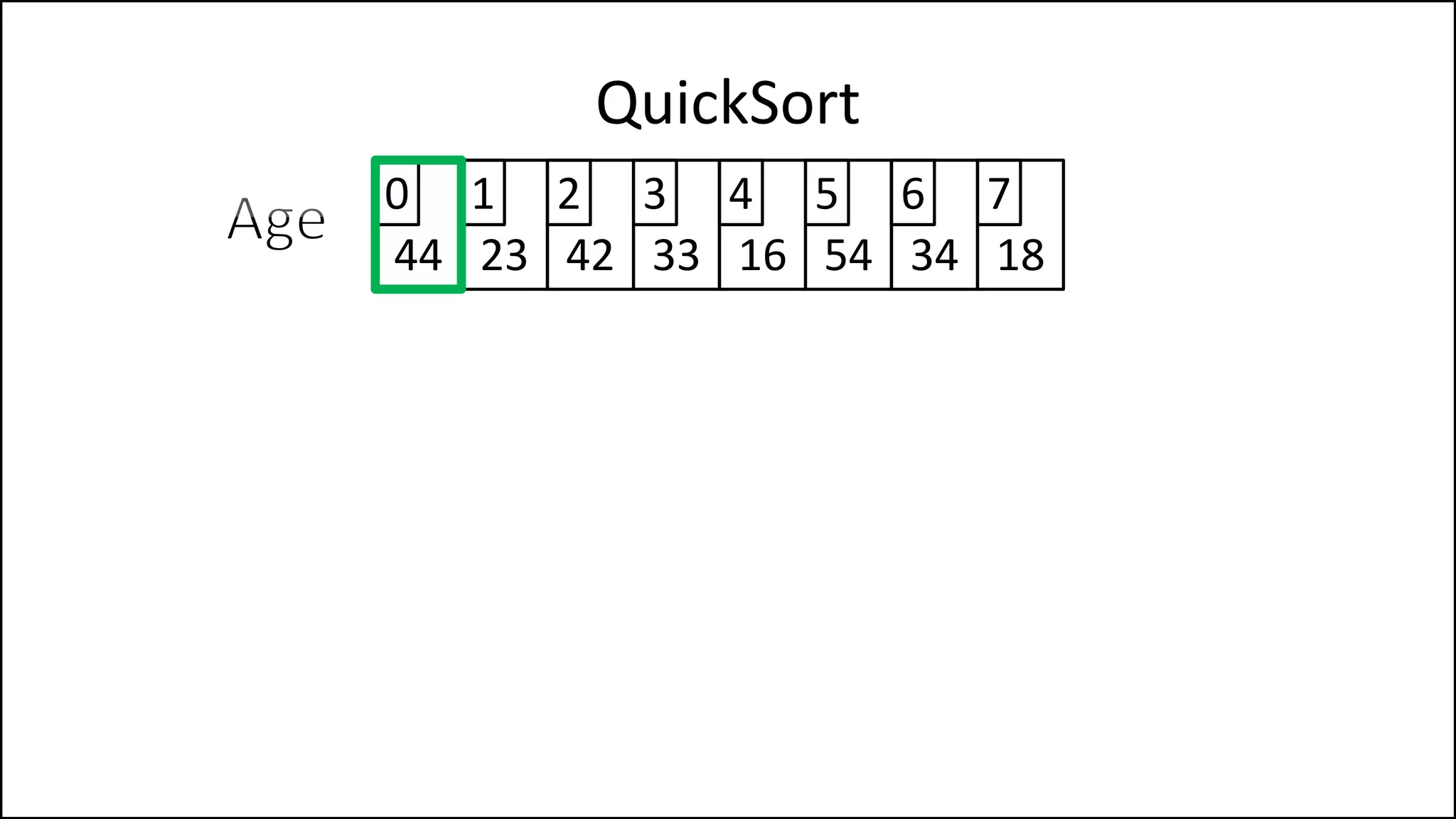


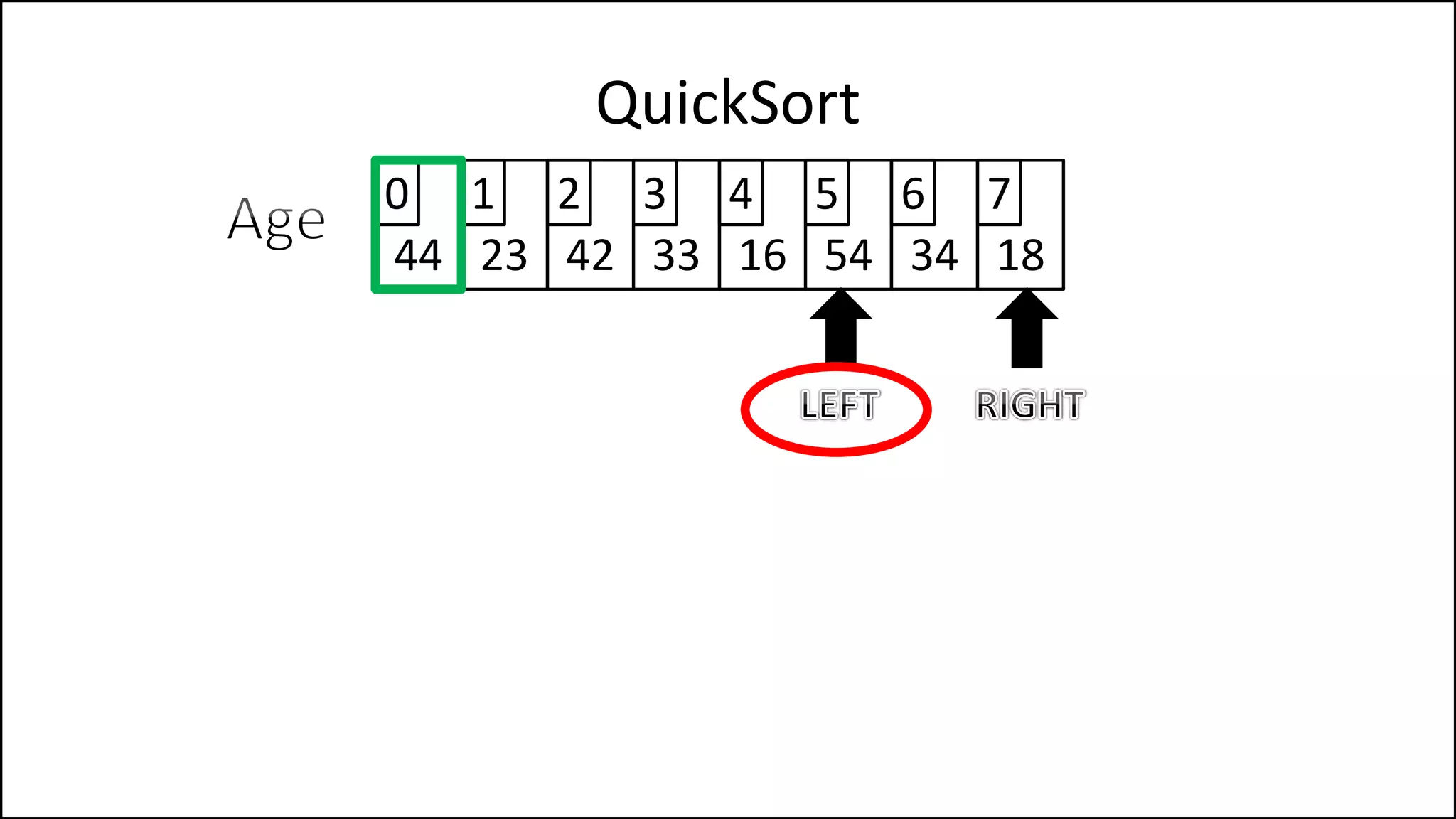



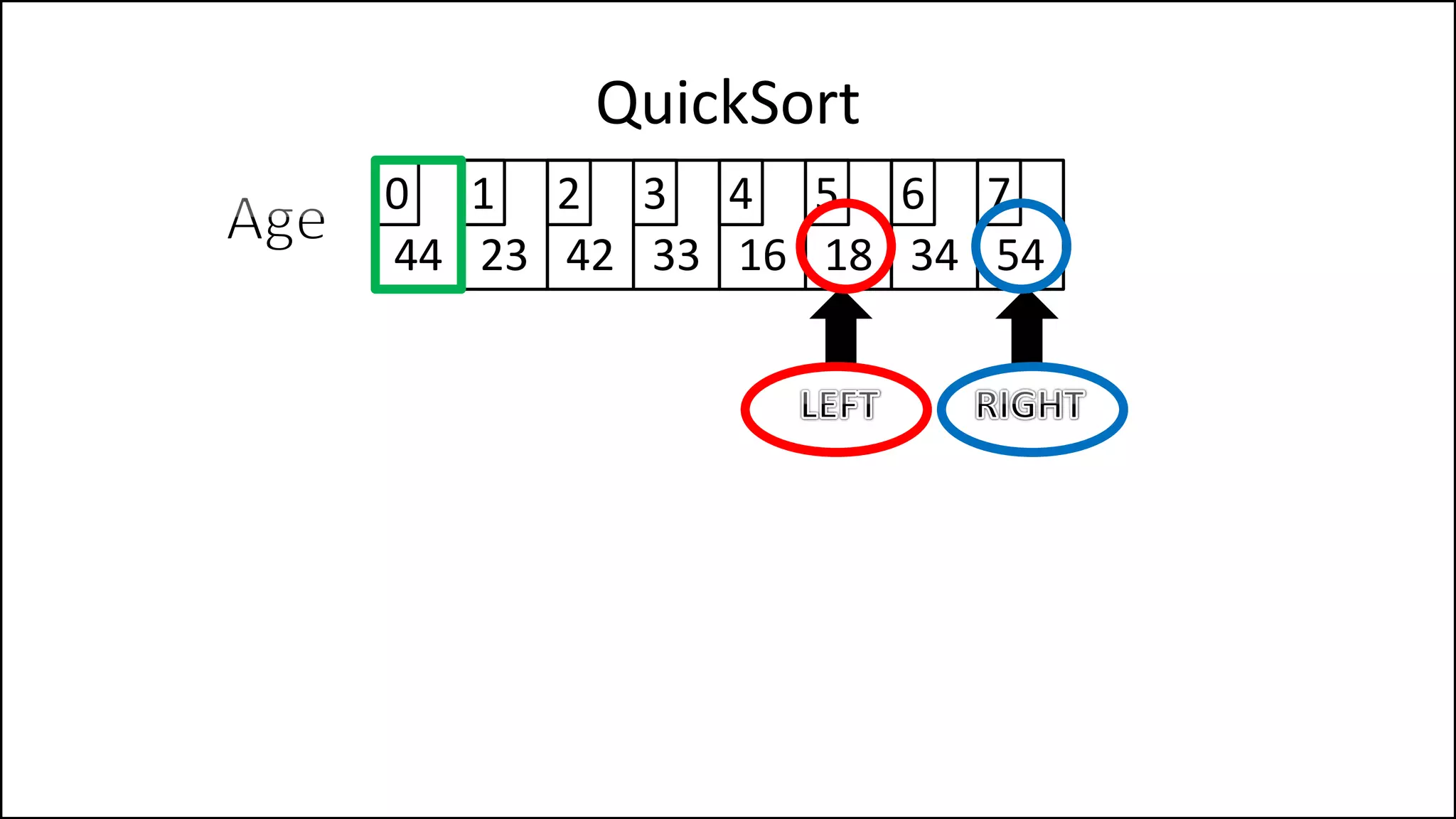
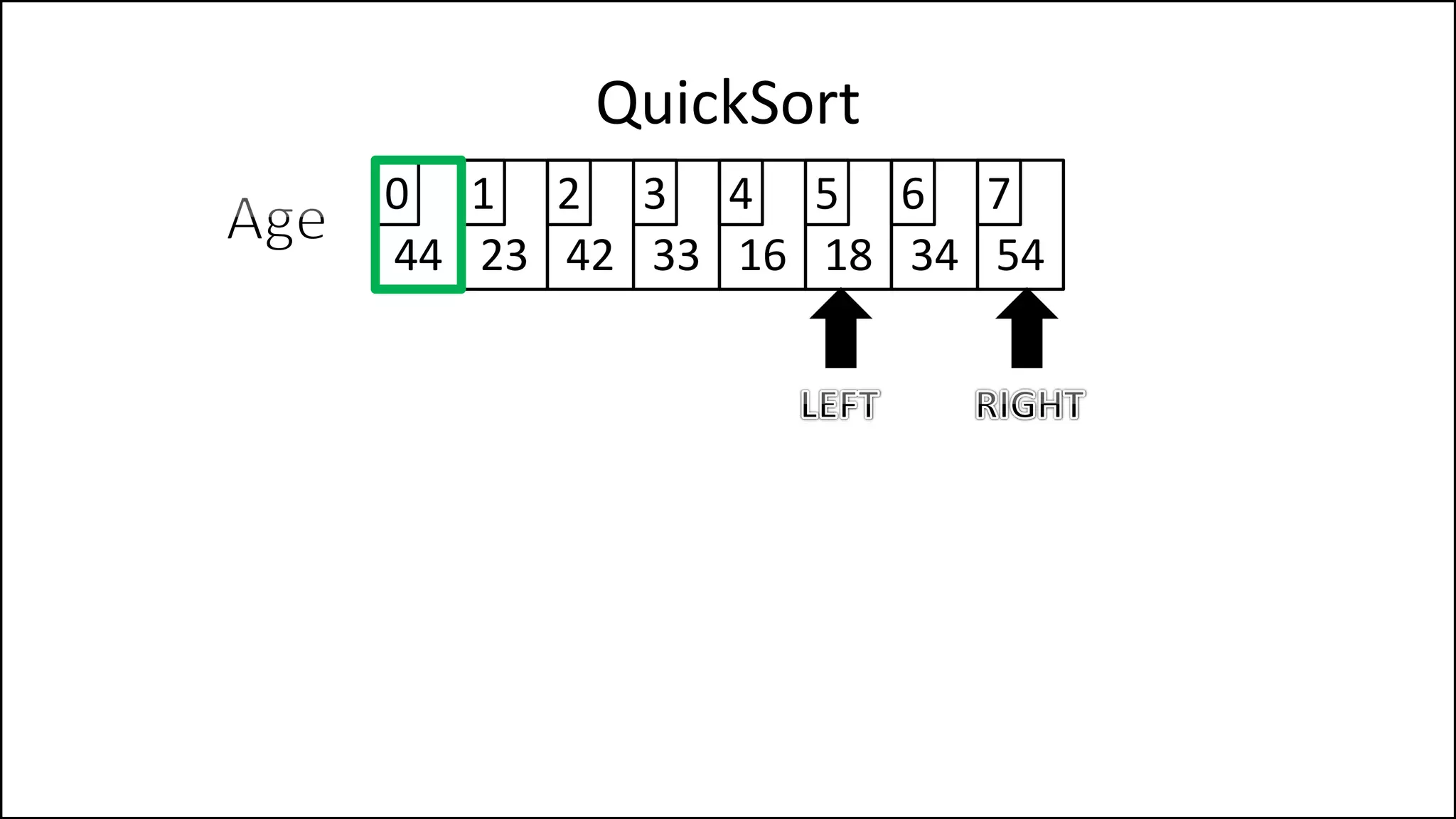
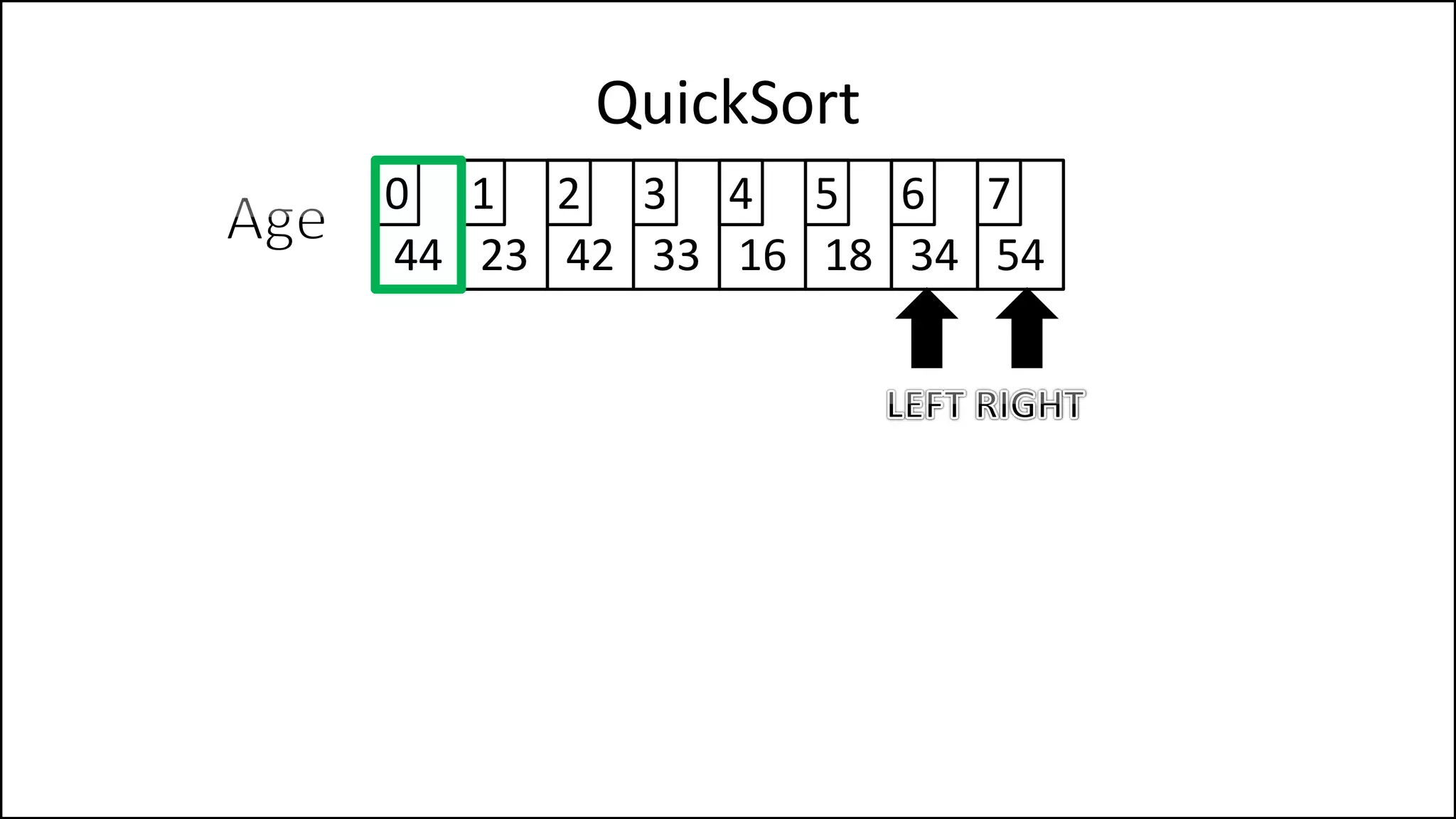
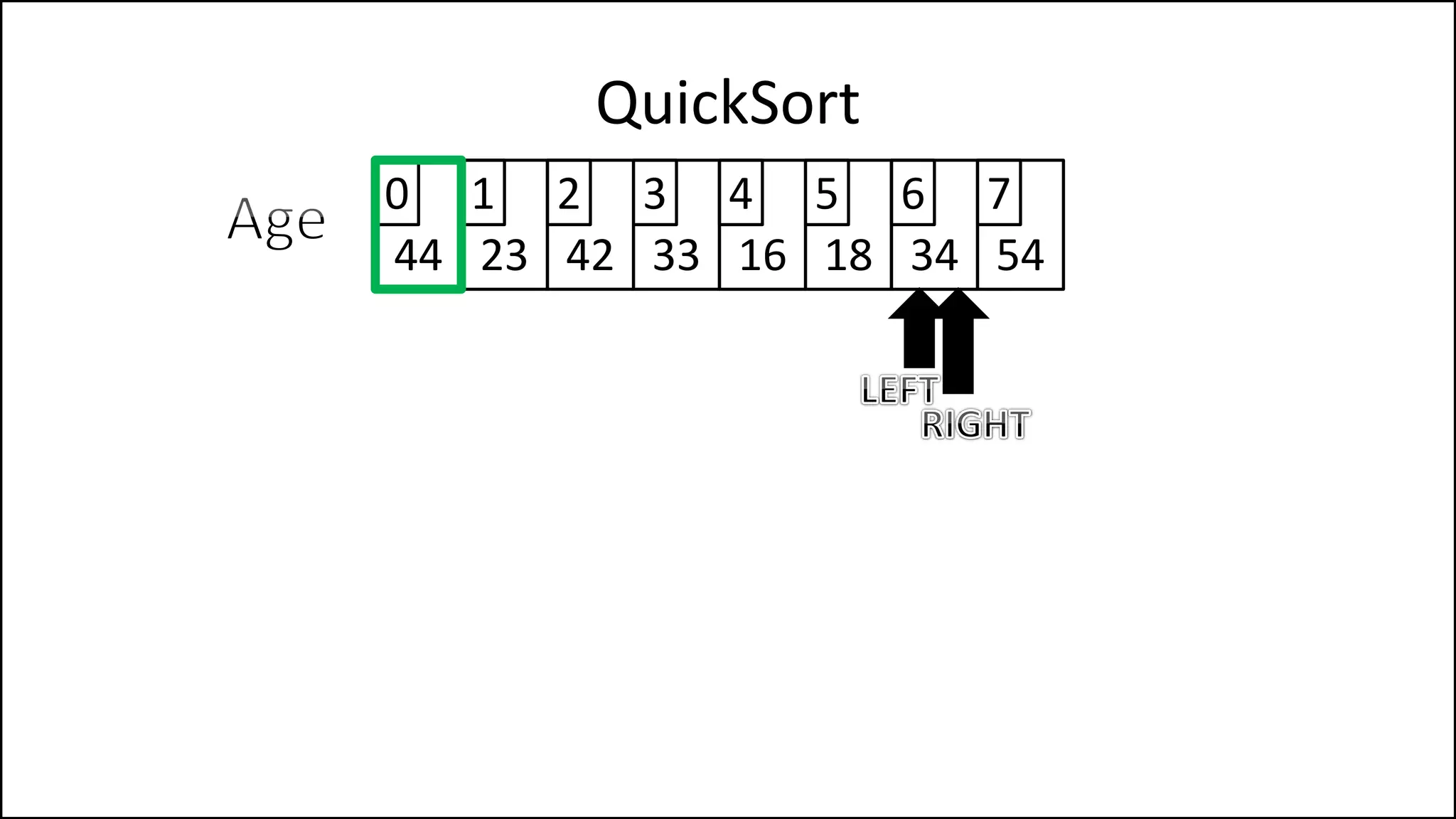
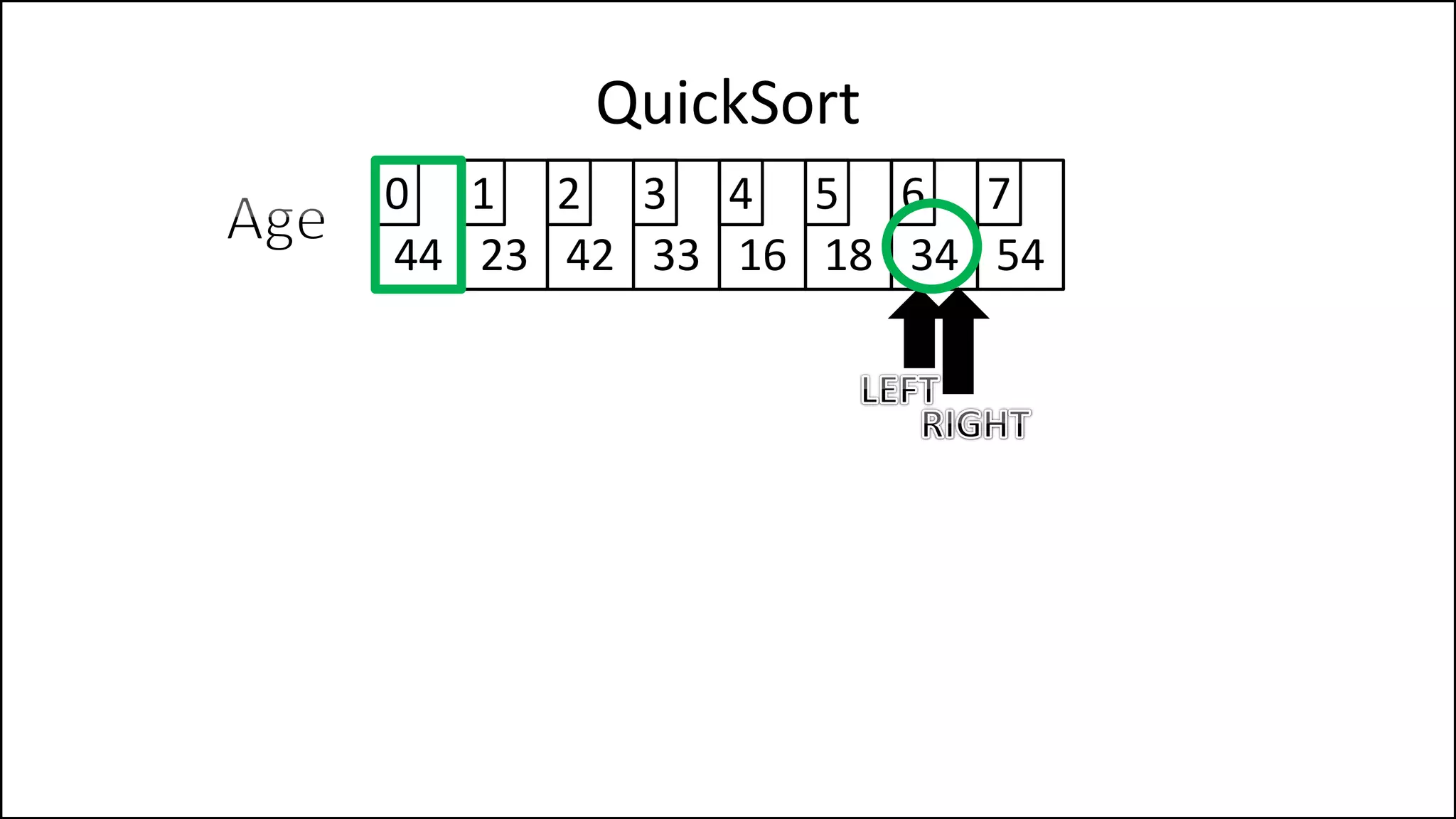

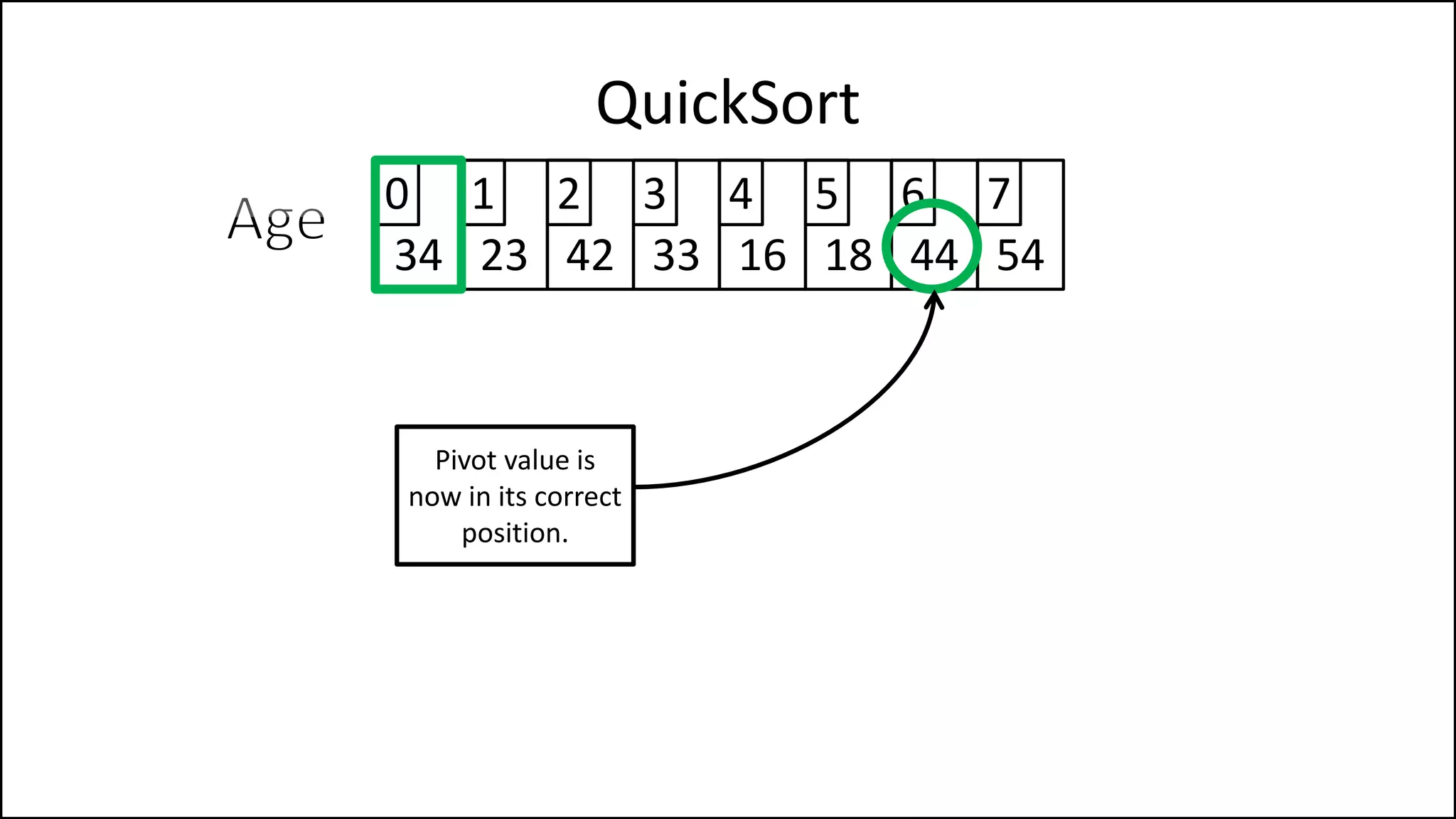
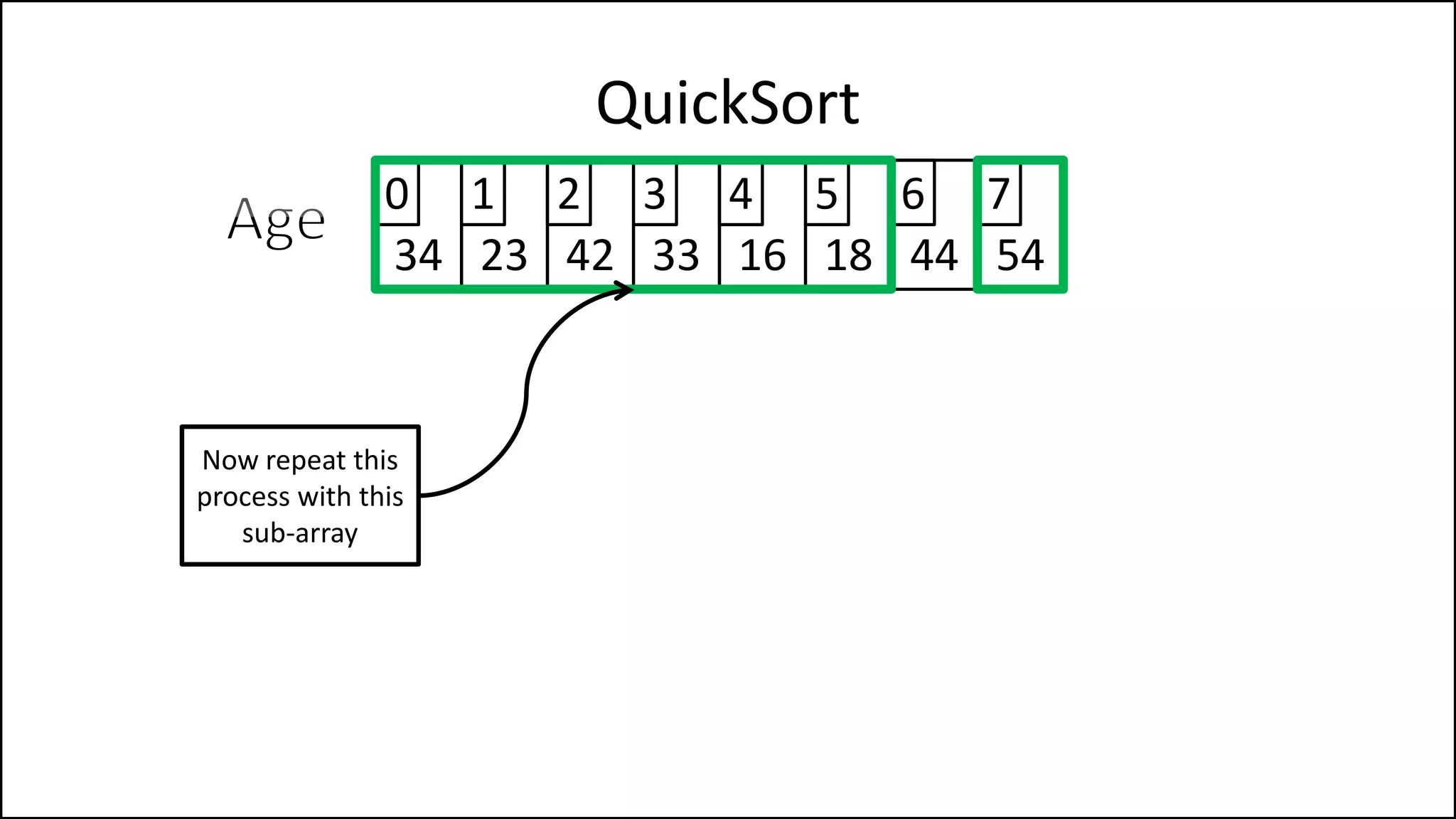
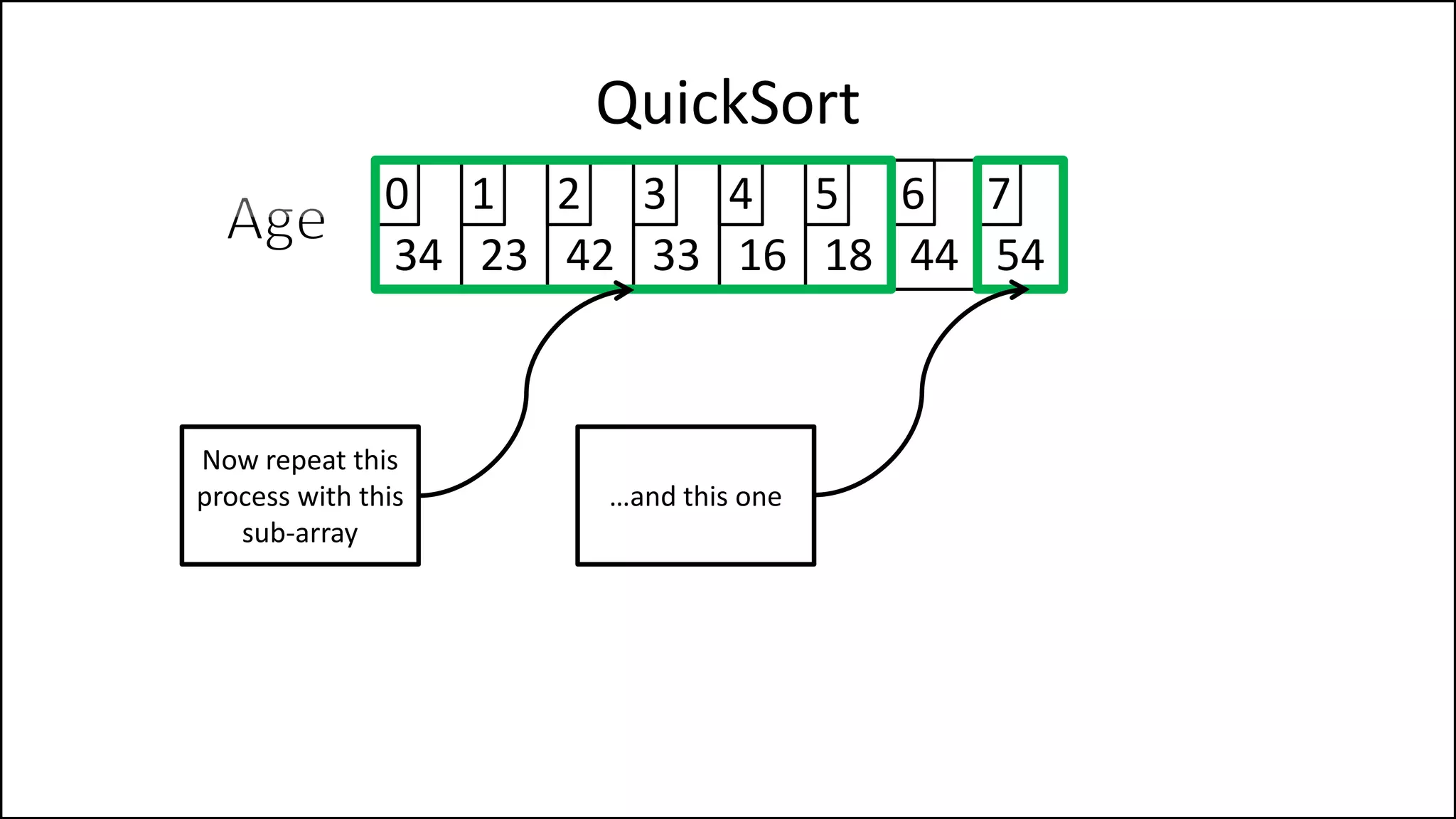

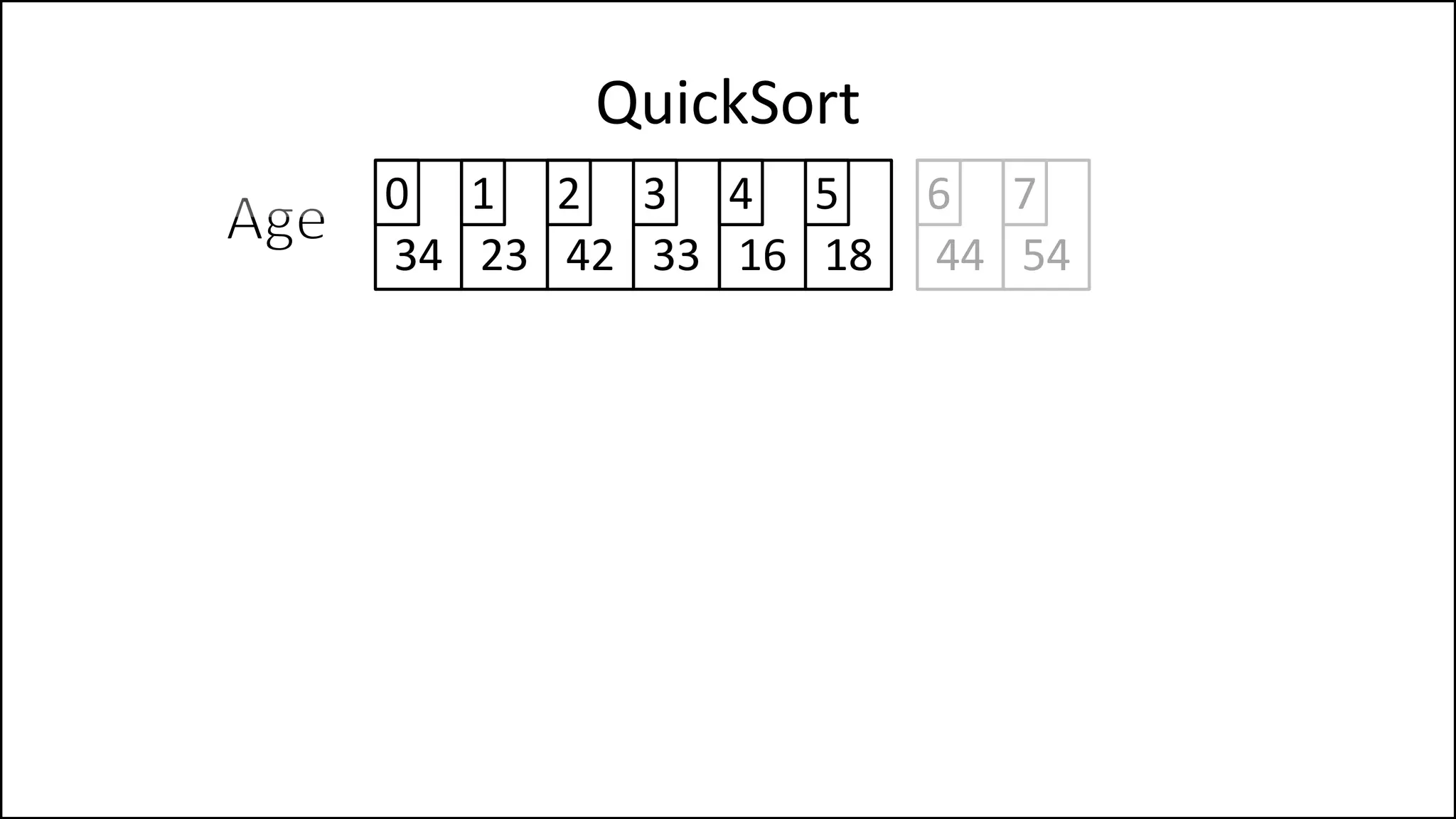

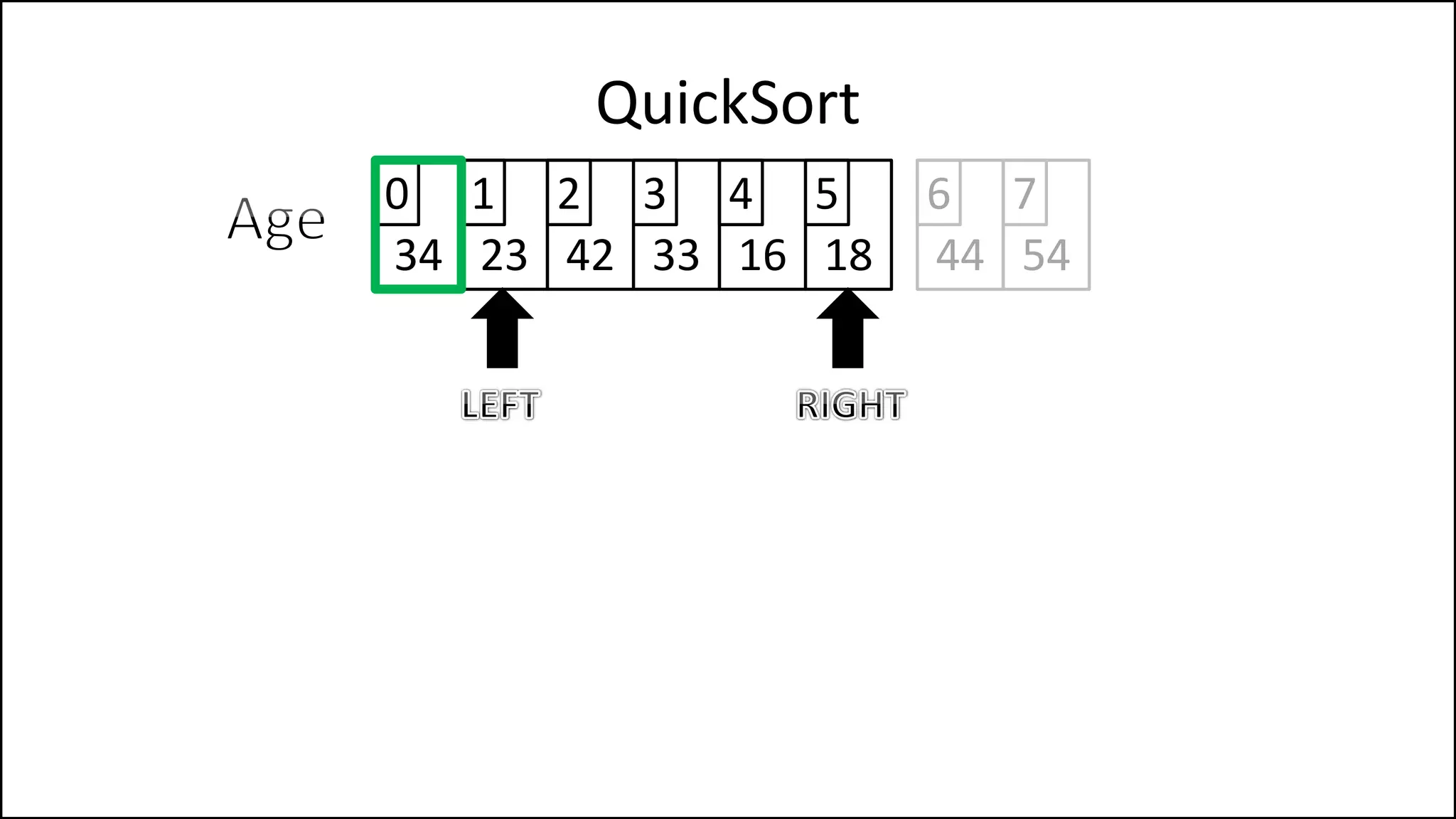
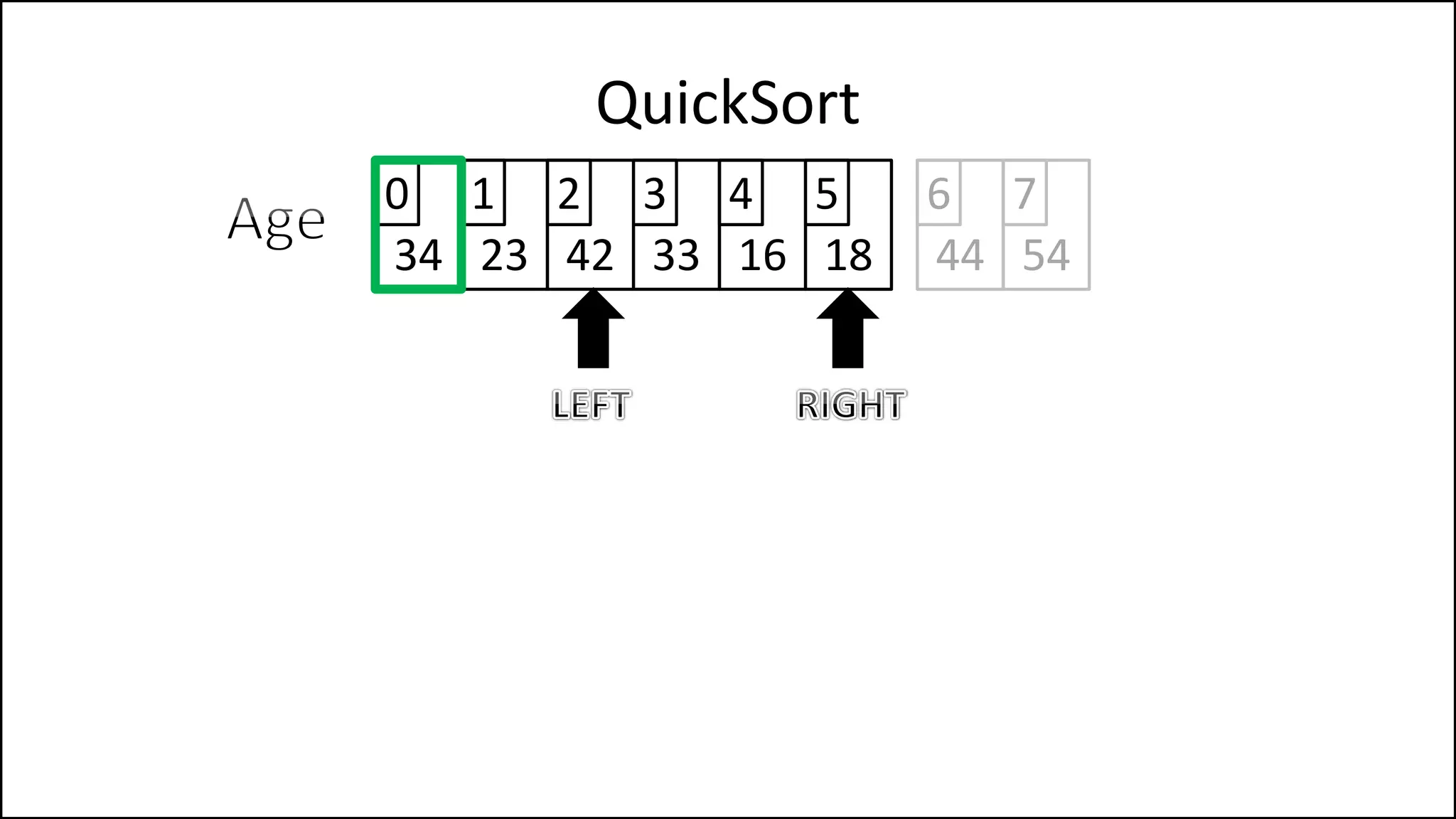
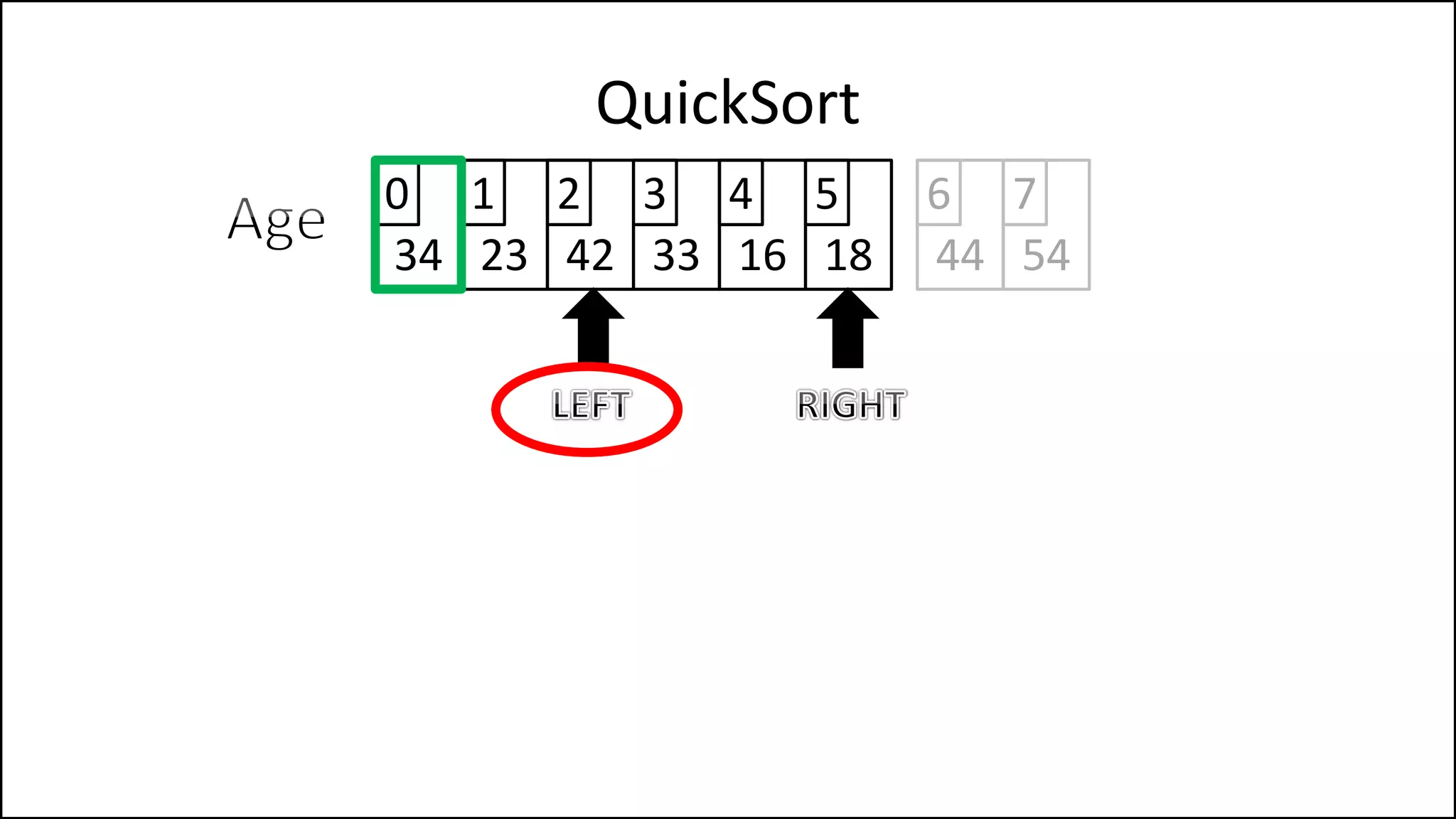
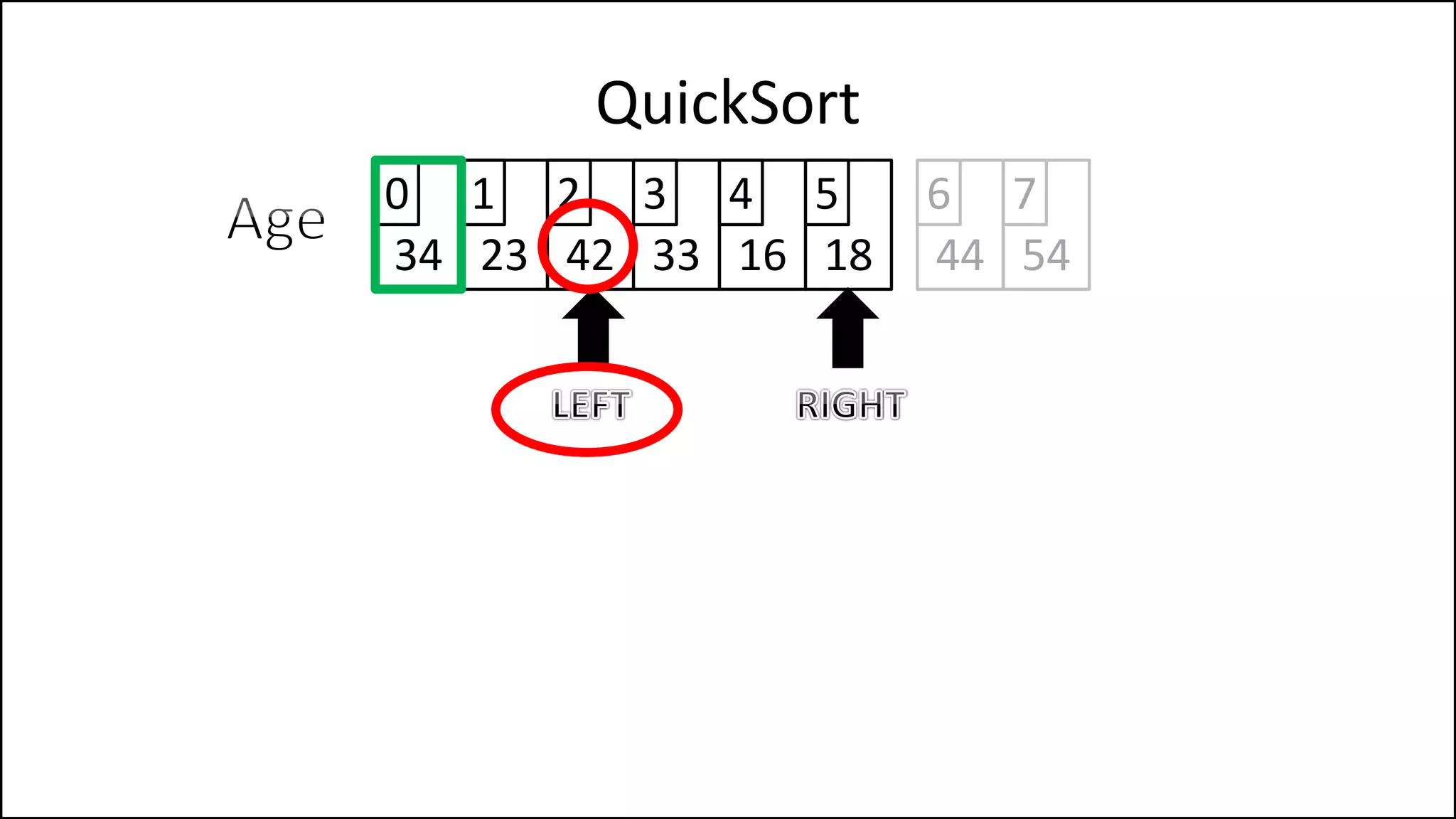

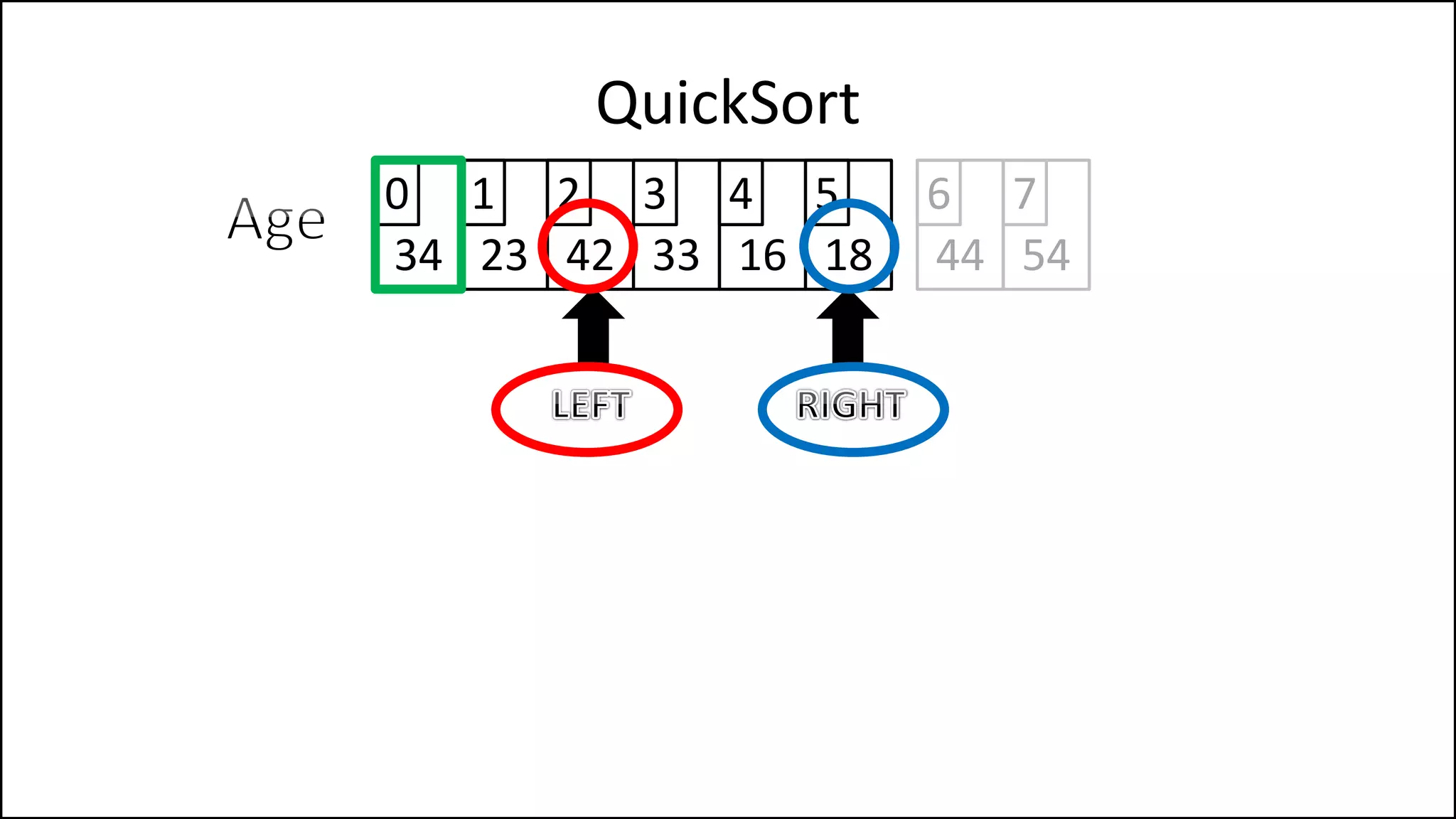
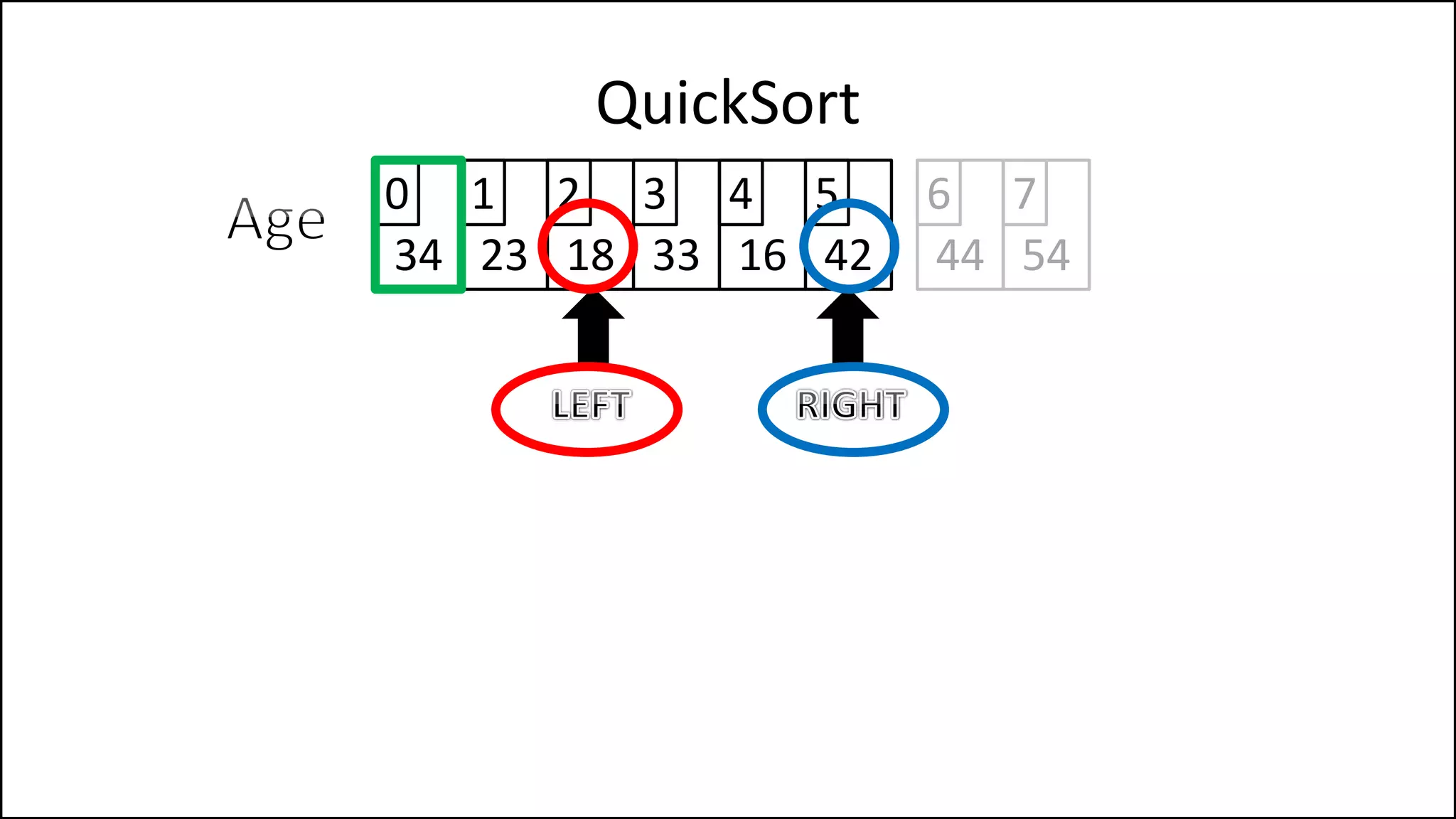
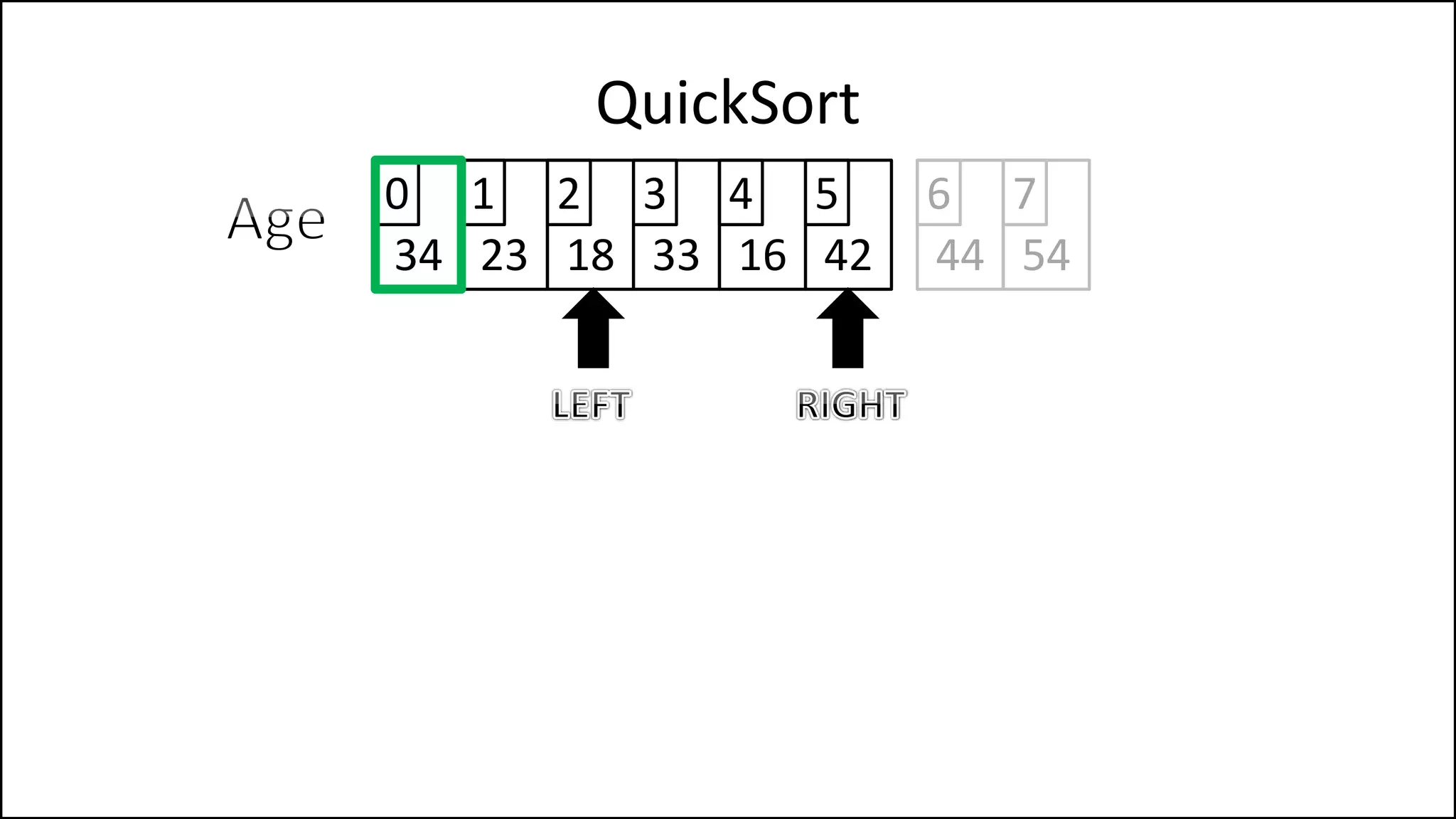

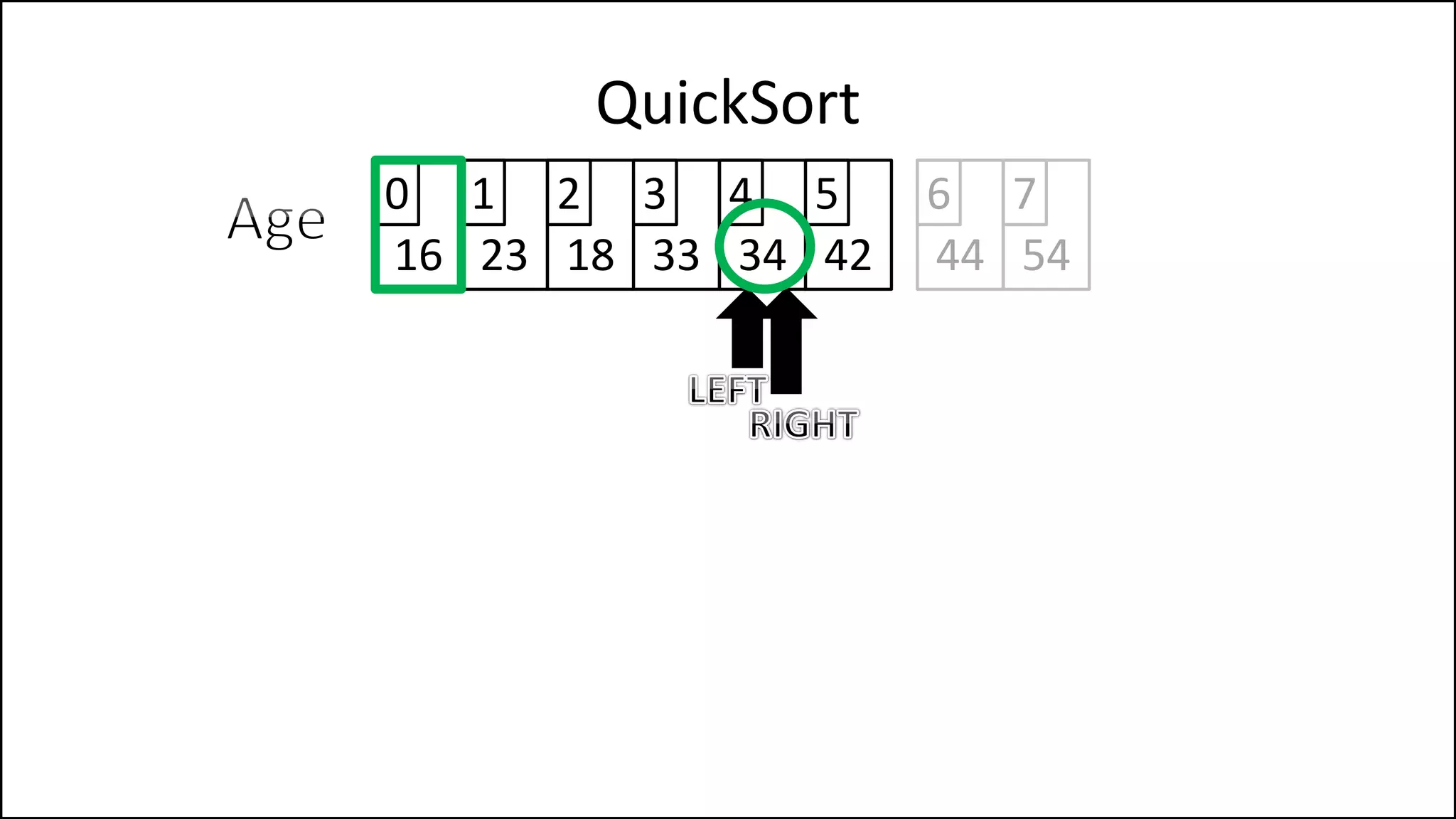
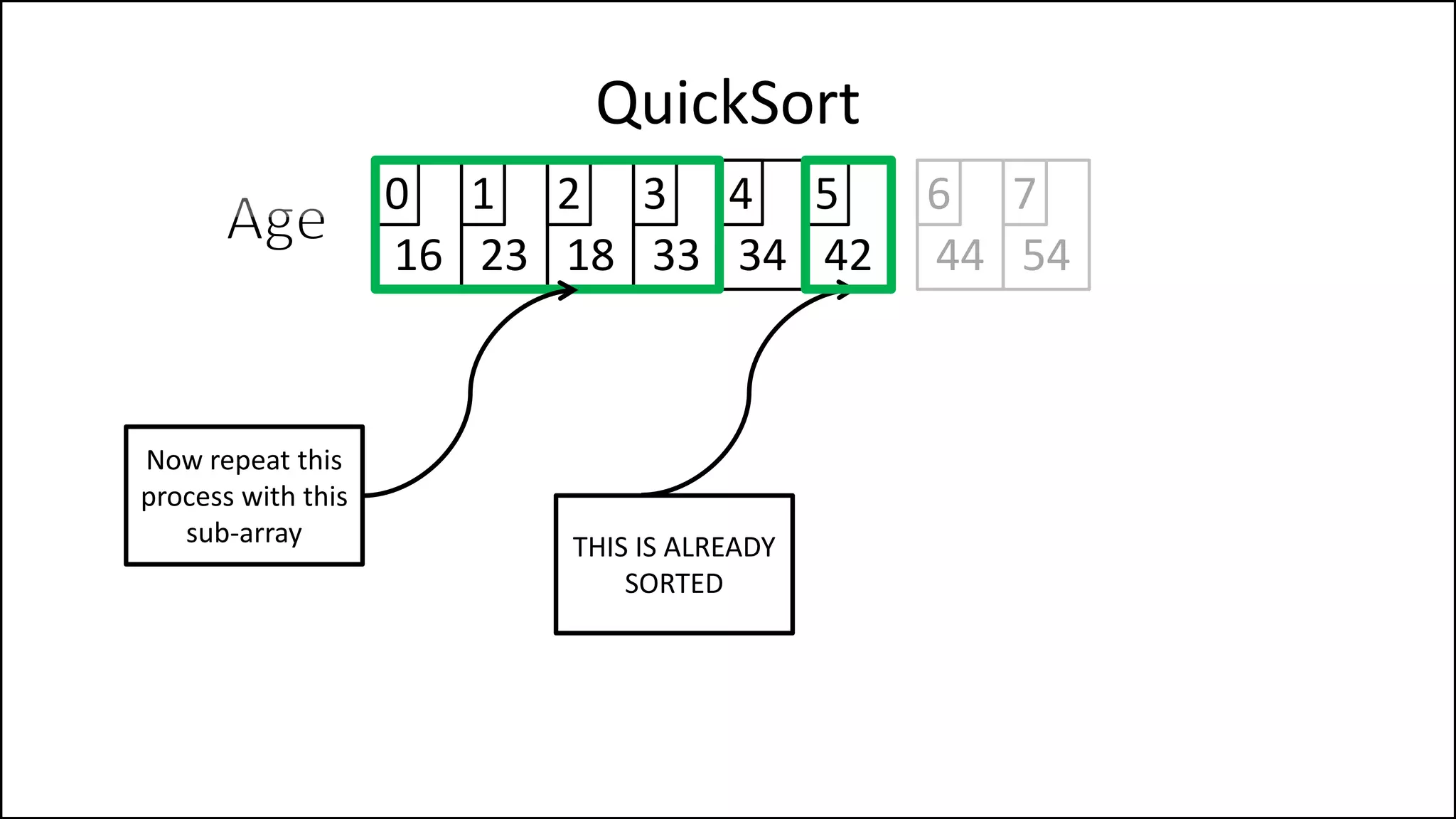
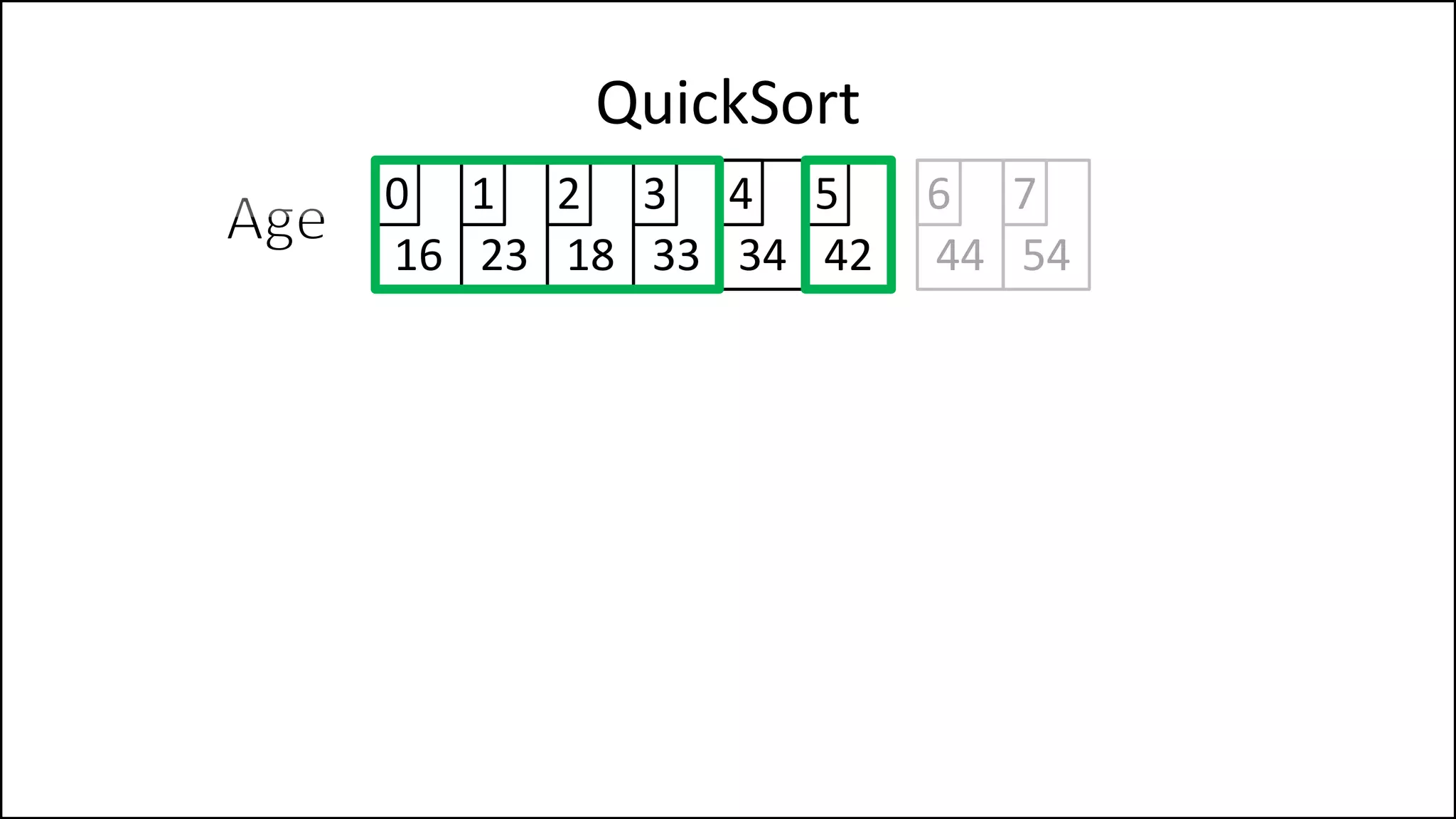
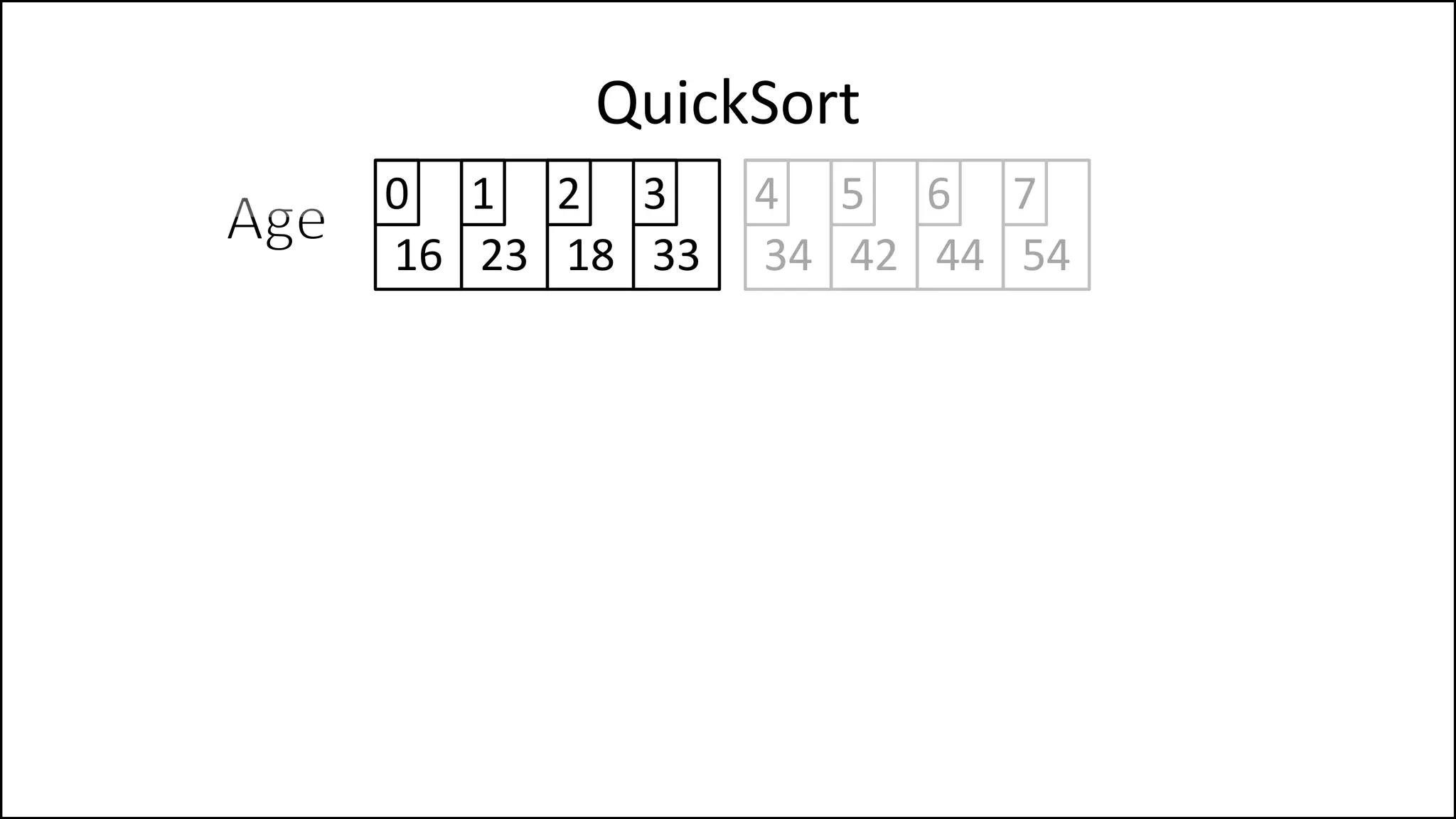


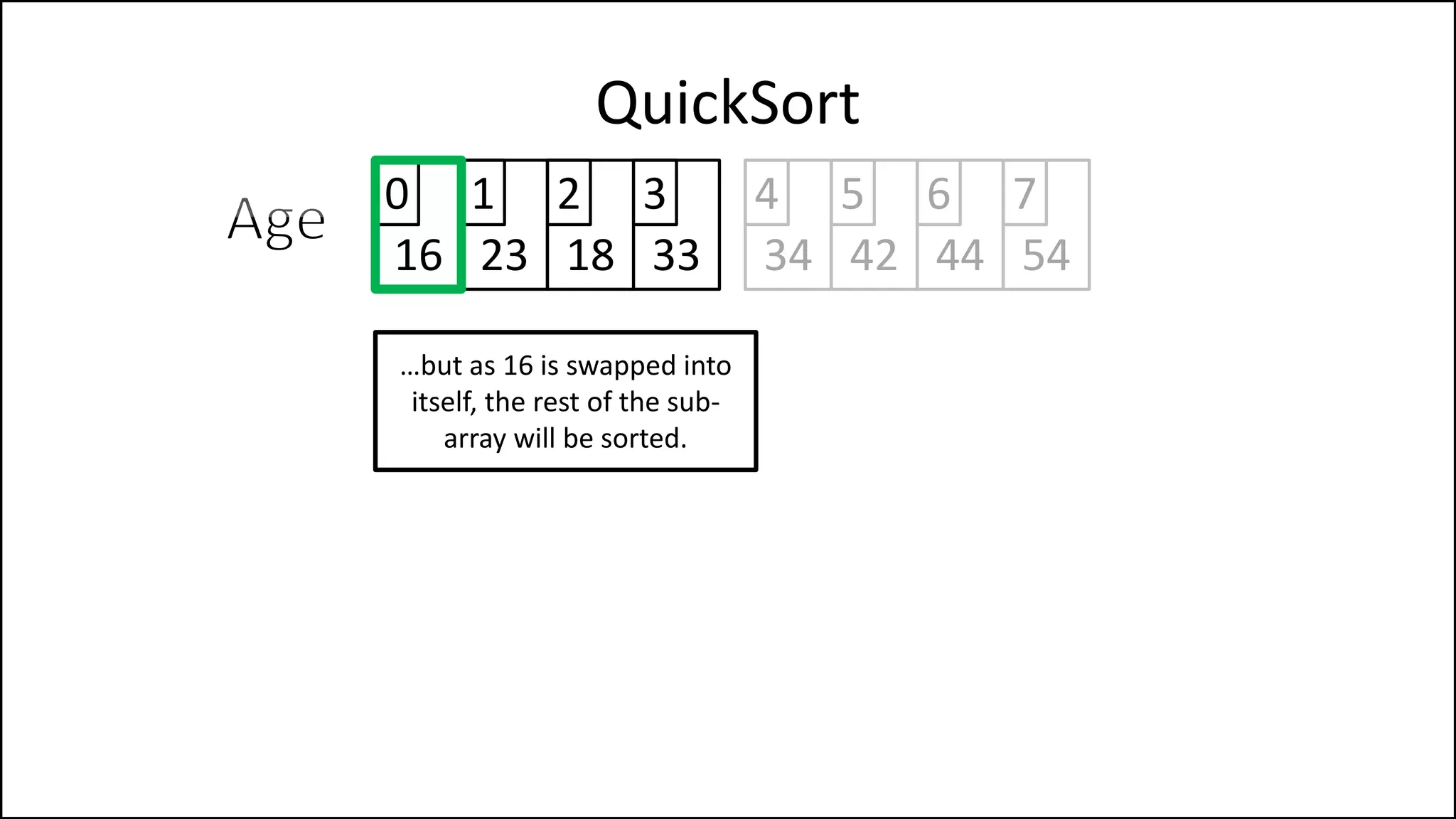
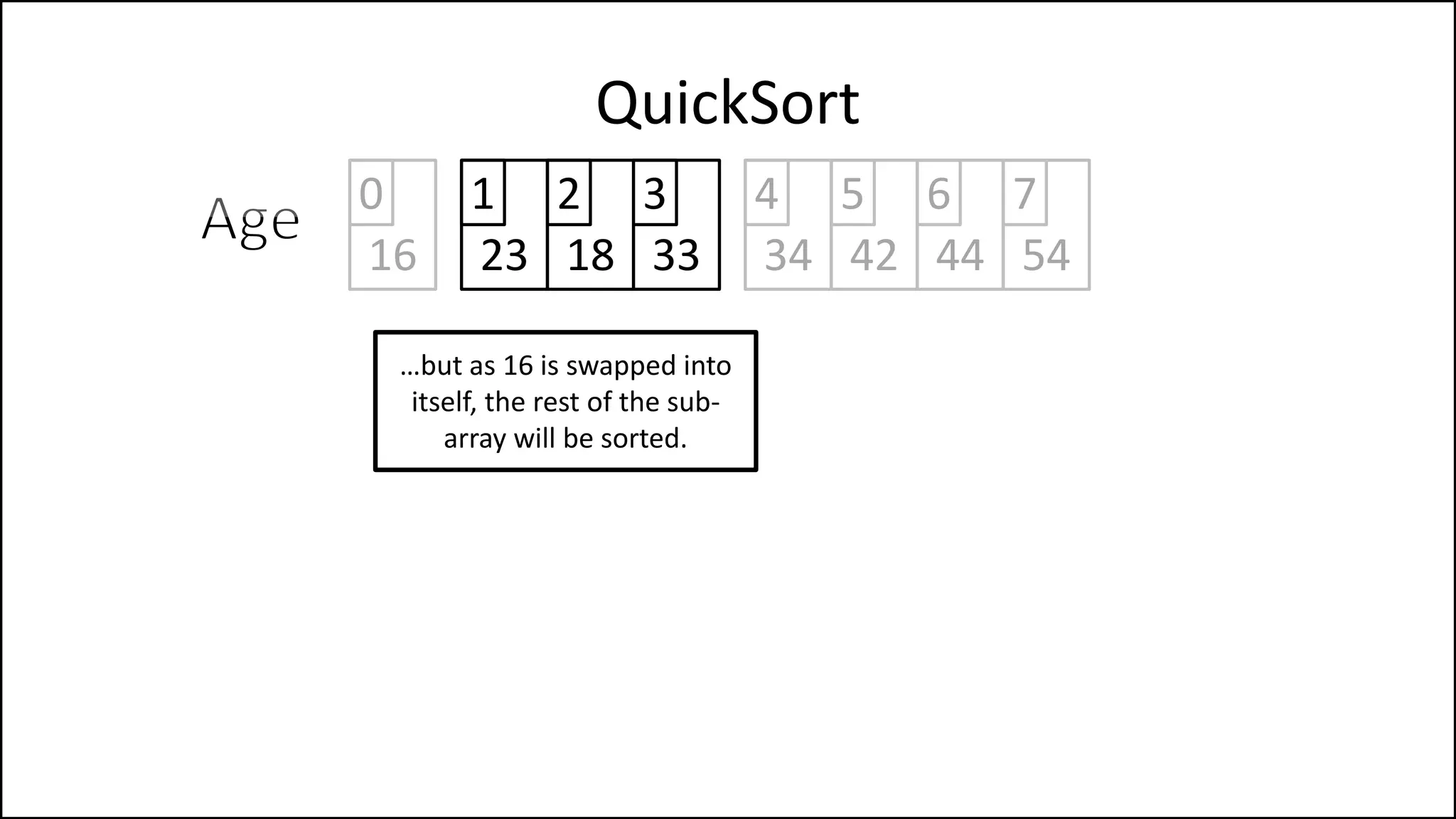
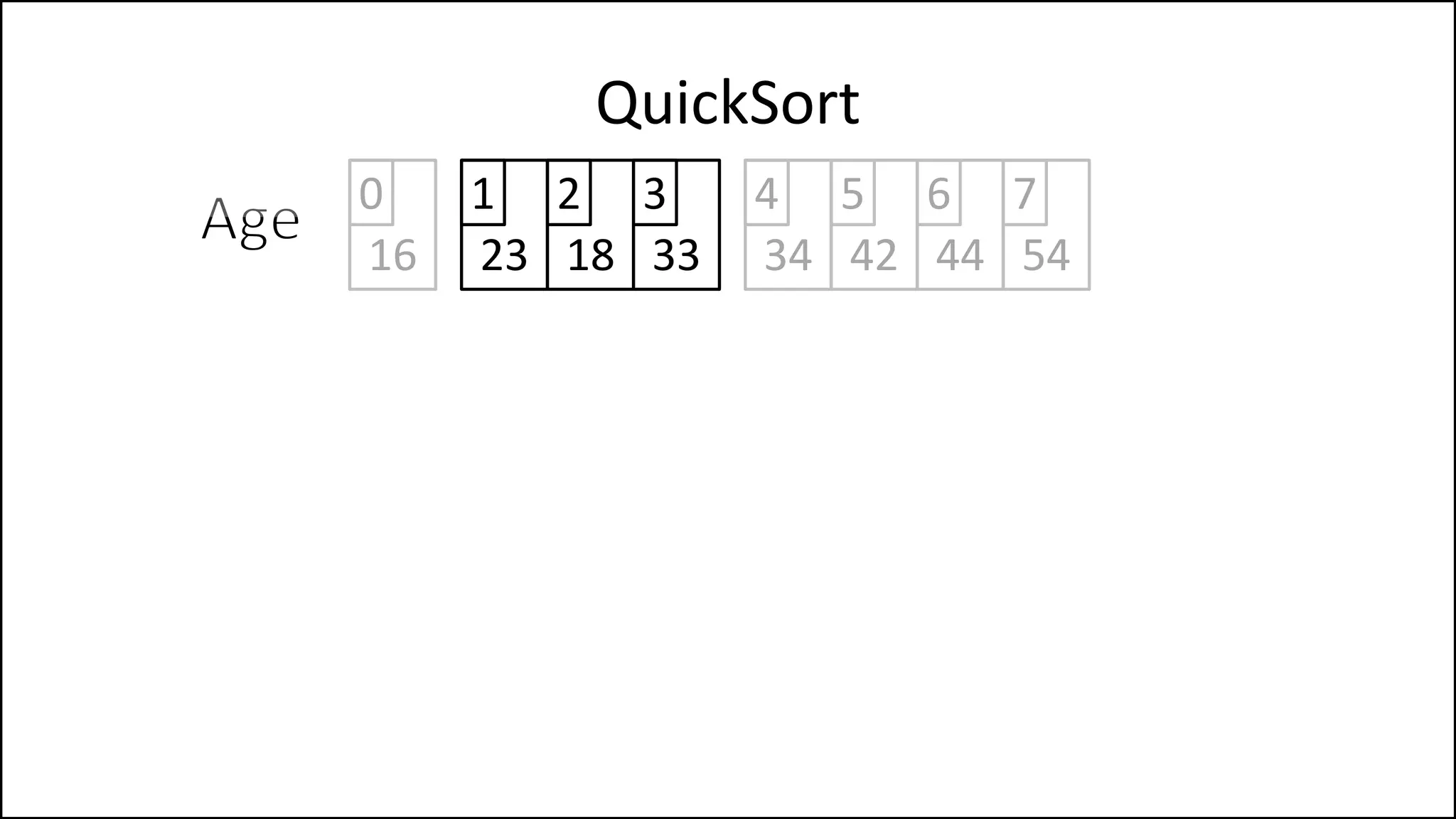

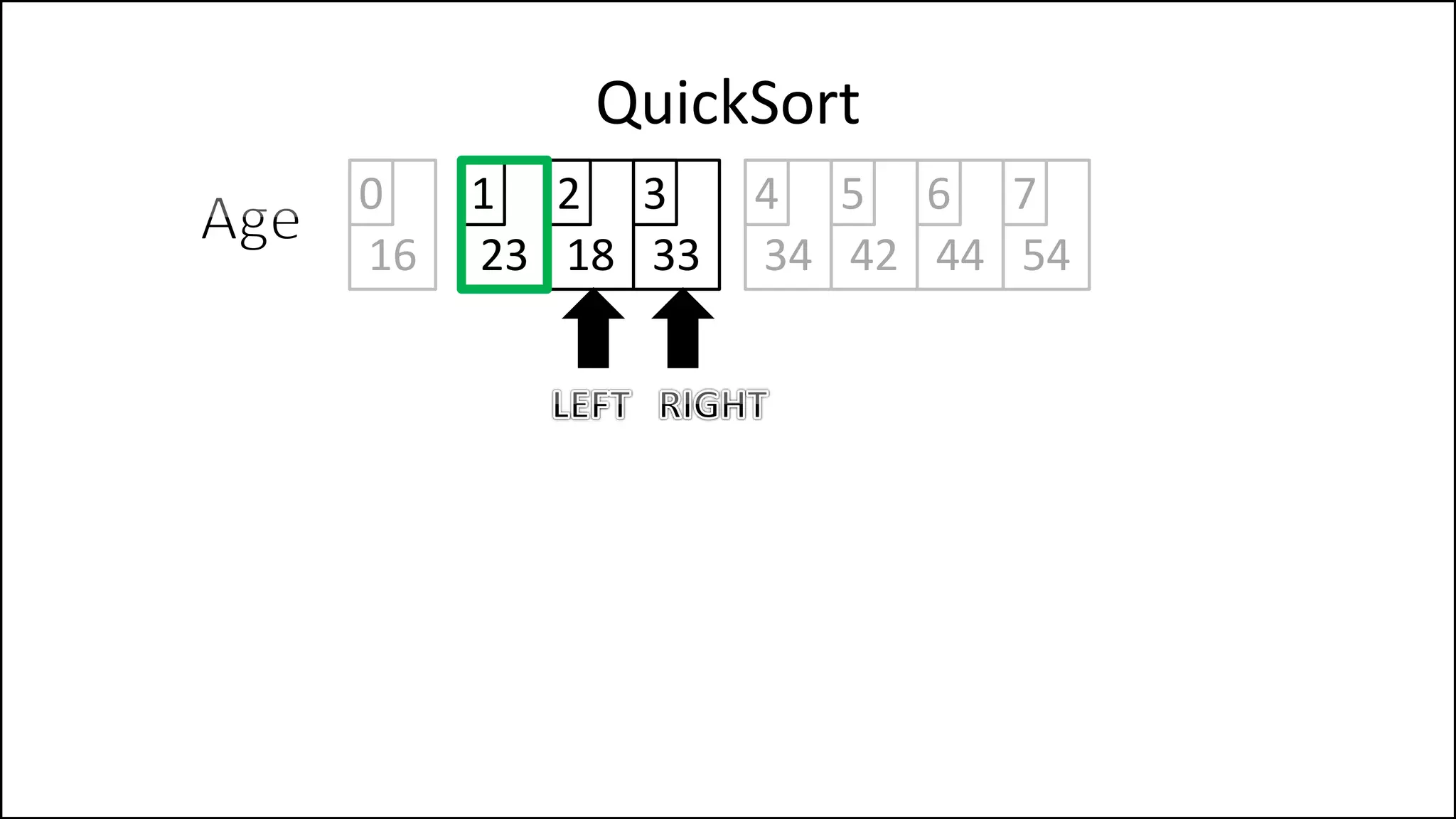
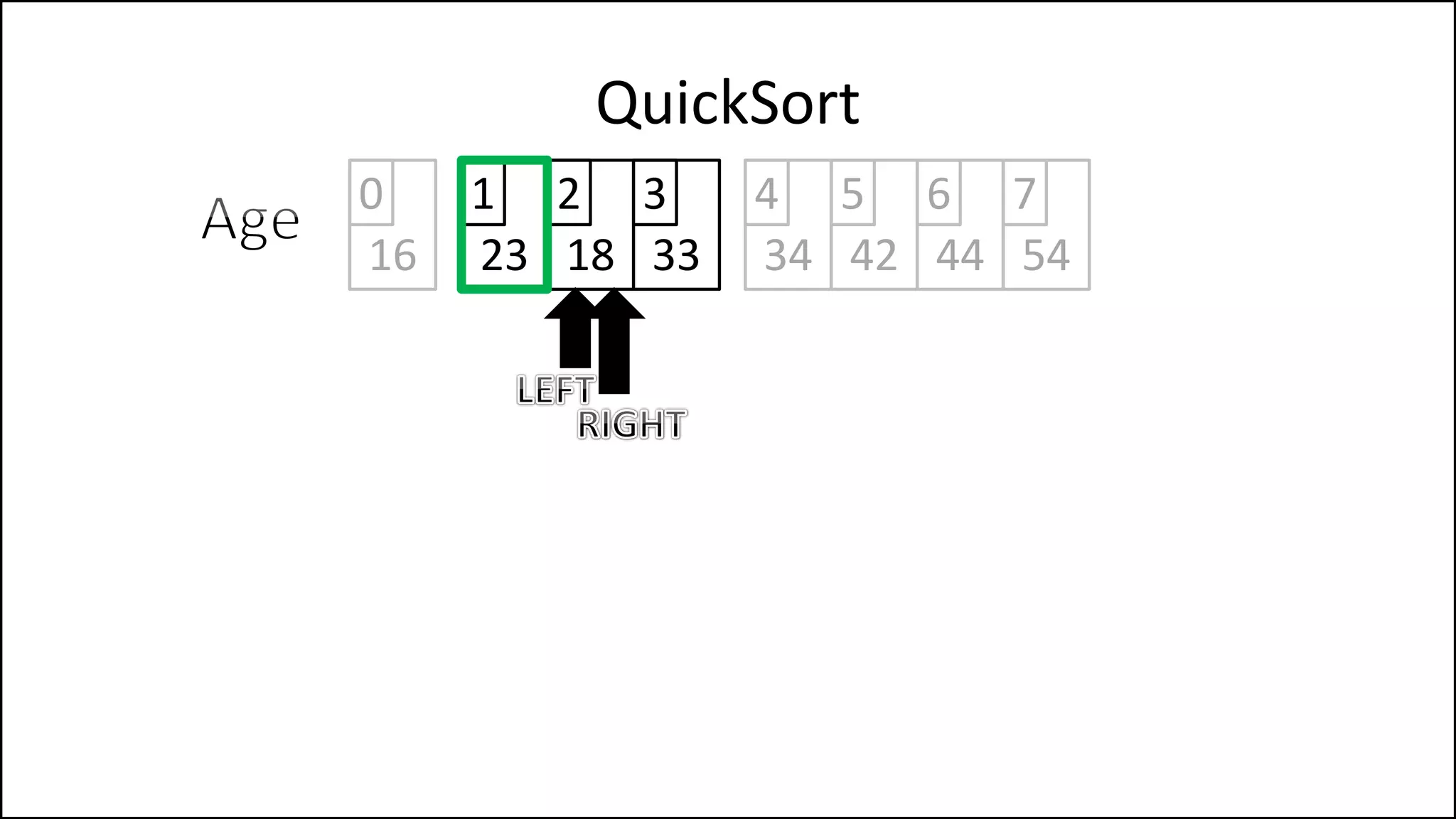
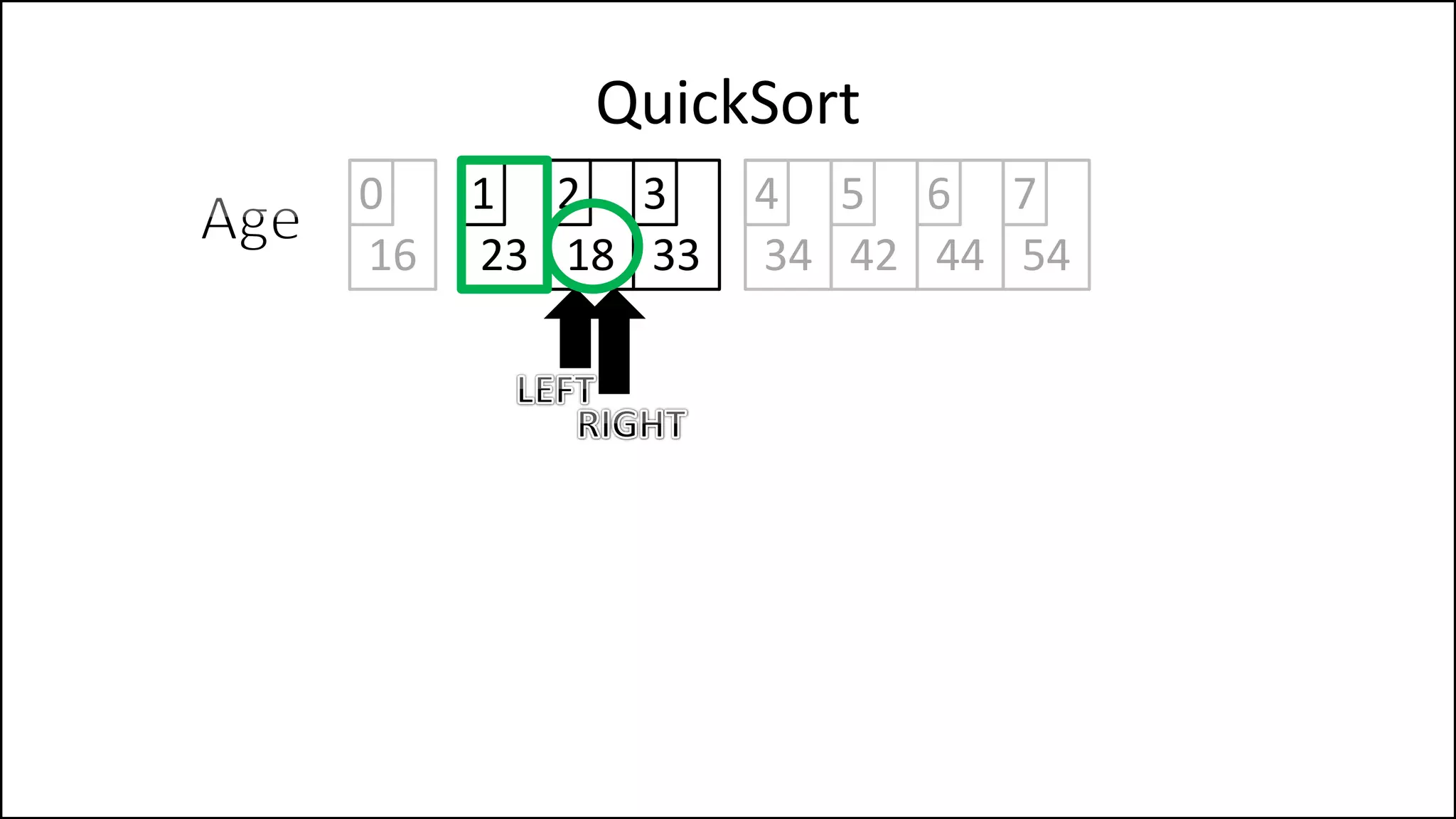
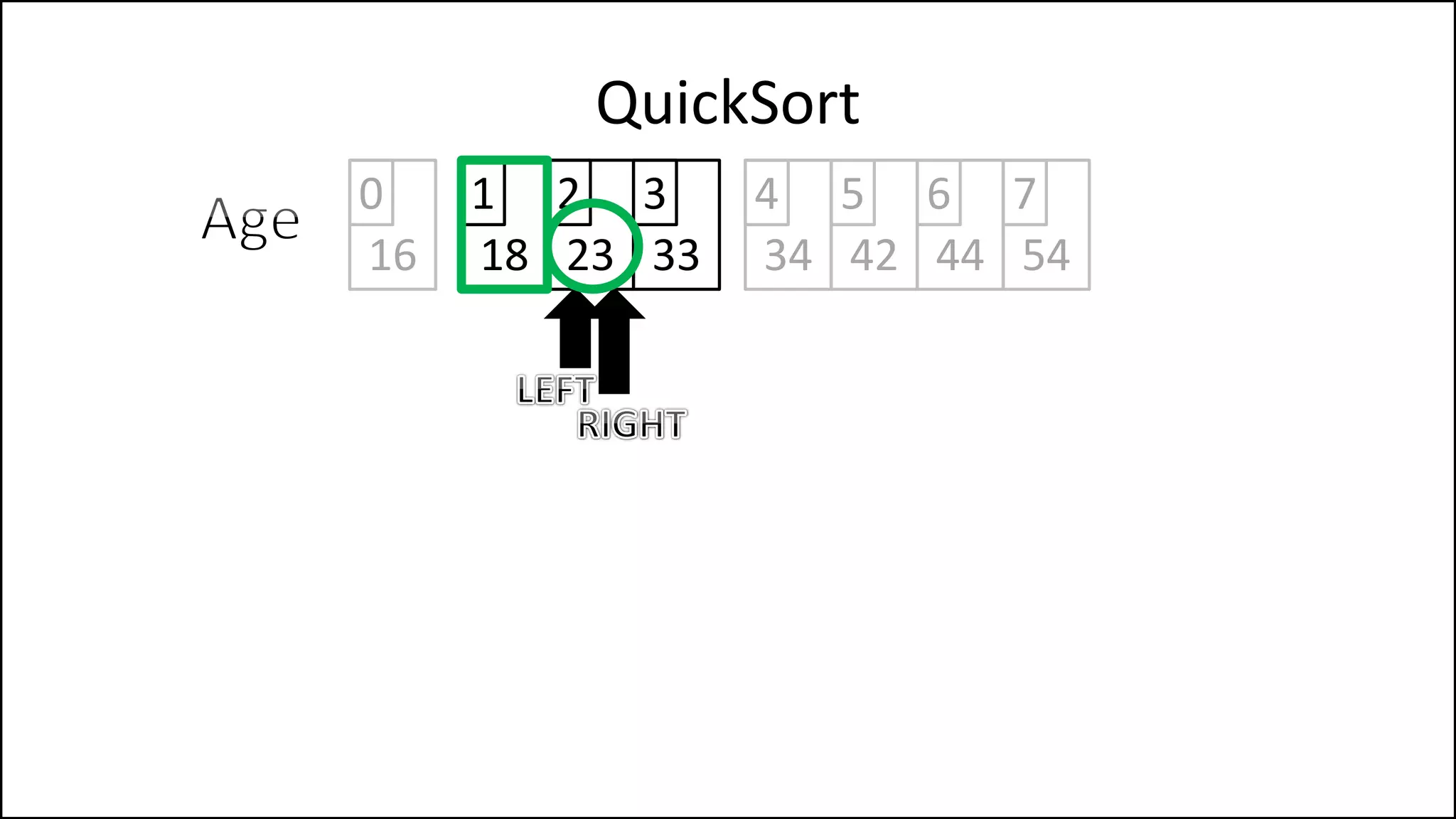
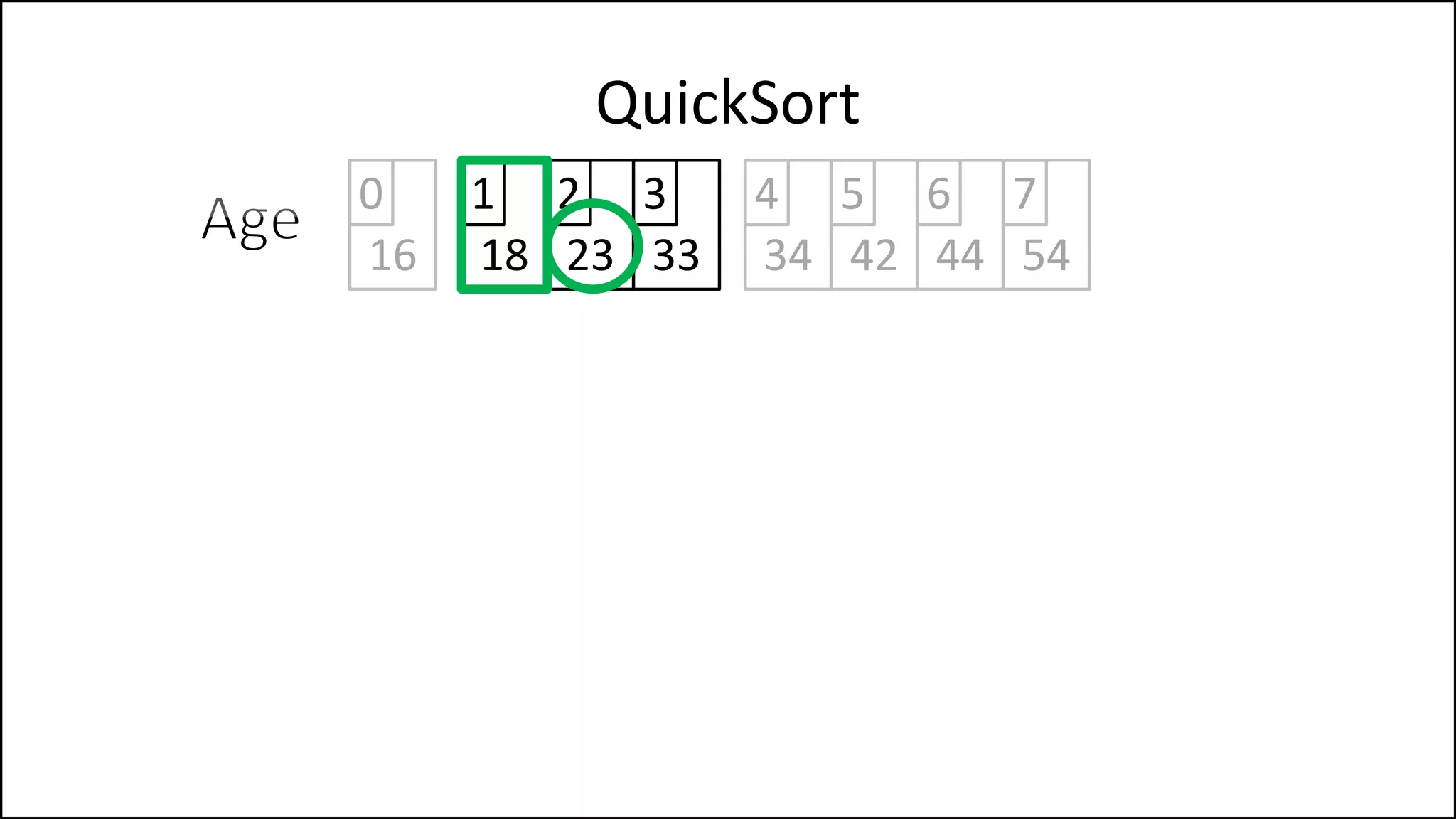
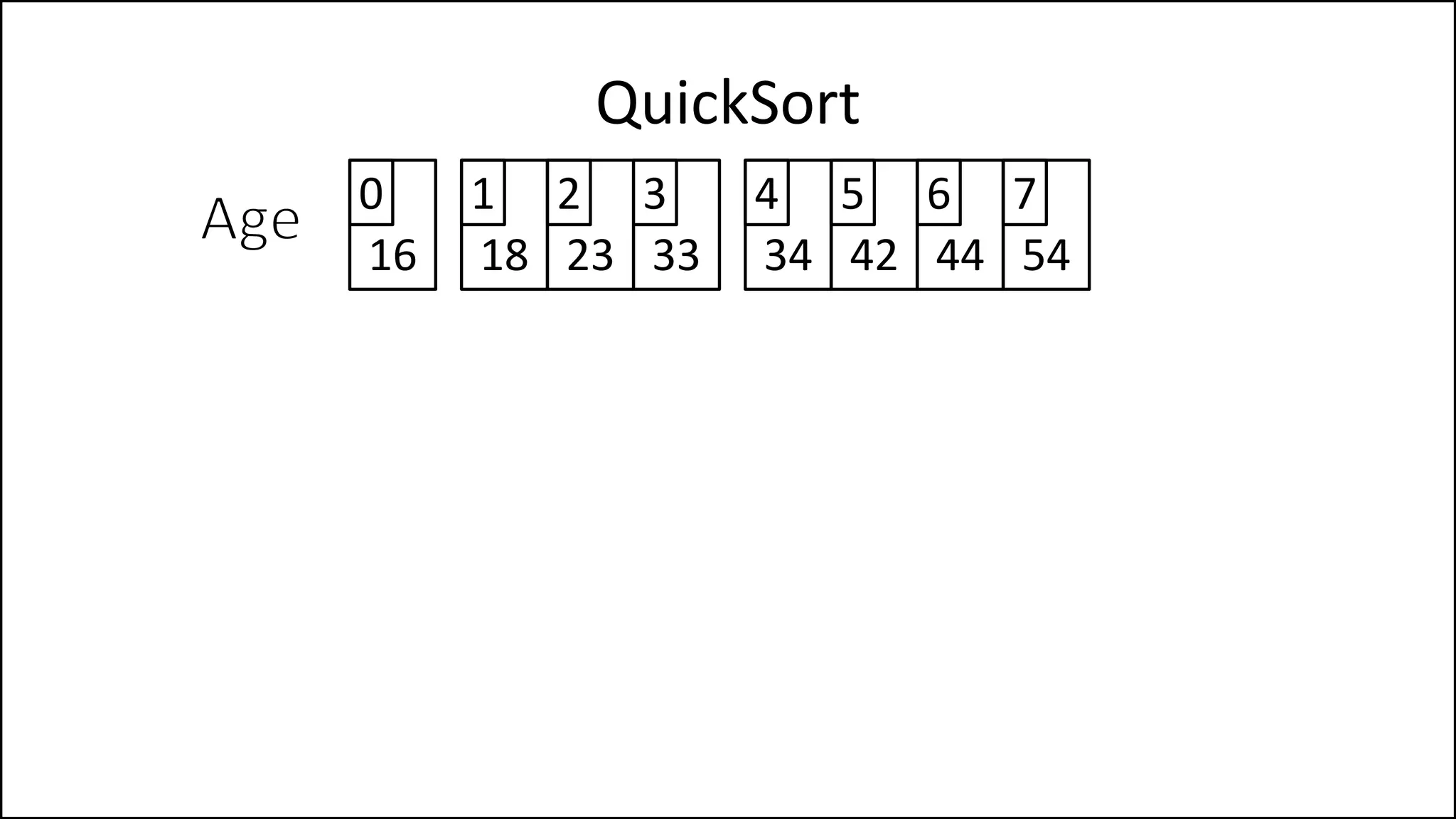

![PROGRAM Partition(Array, First, Last):
PivotVal = Array[First];
Finished = False;
LeftPointer = First + 1;
RightPointer = Last;
QuickSort
We randomly select
the pivot, in this case
we select the first
element. Since the
array isn’t sorted yet,
the value of the first
element could have
any value
Continued ](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-175-2048.jpg)
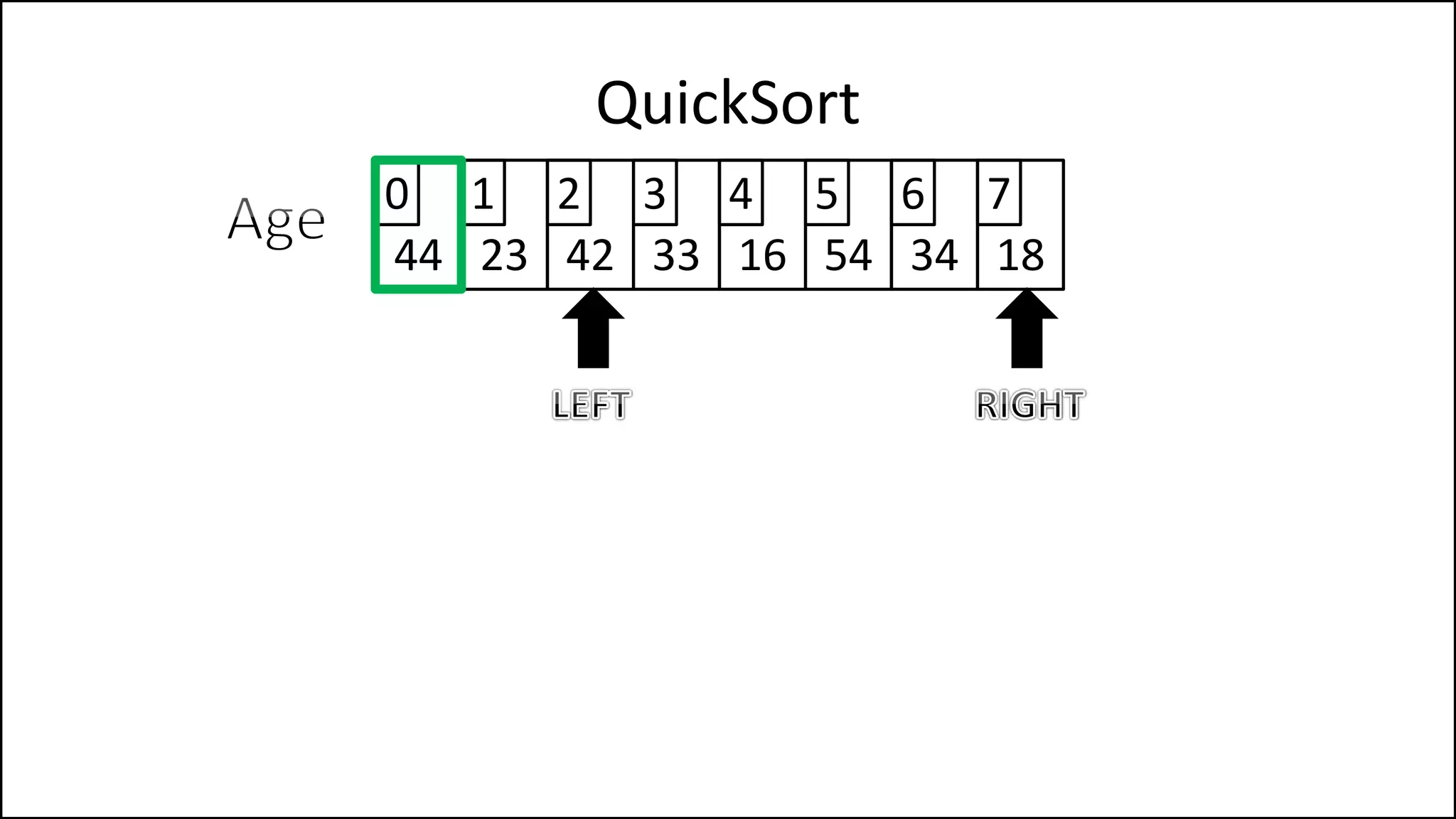
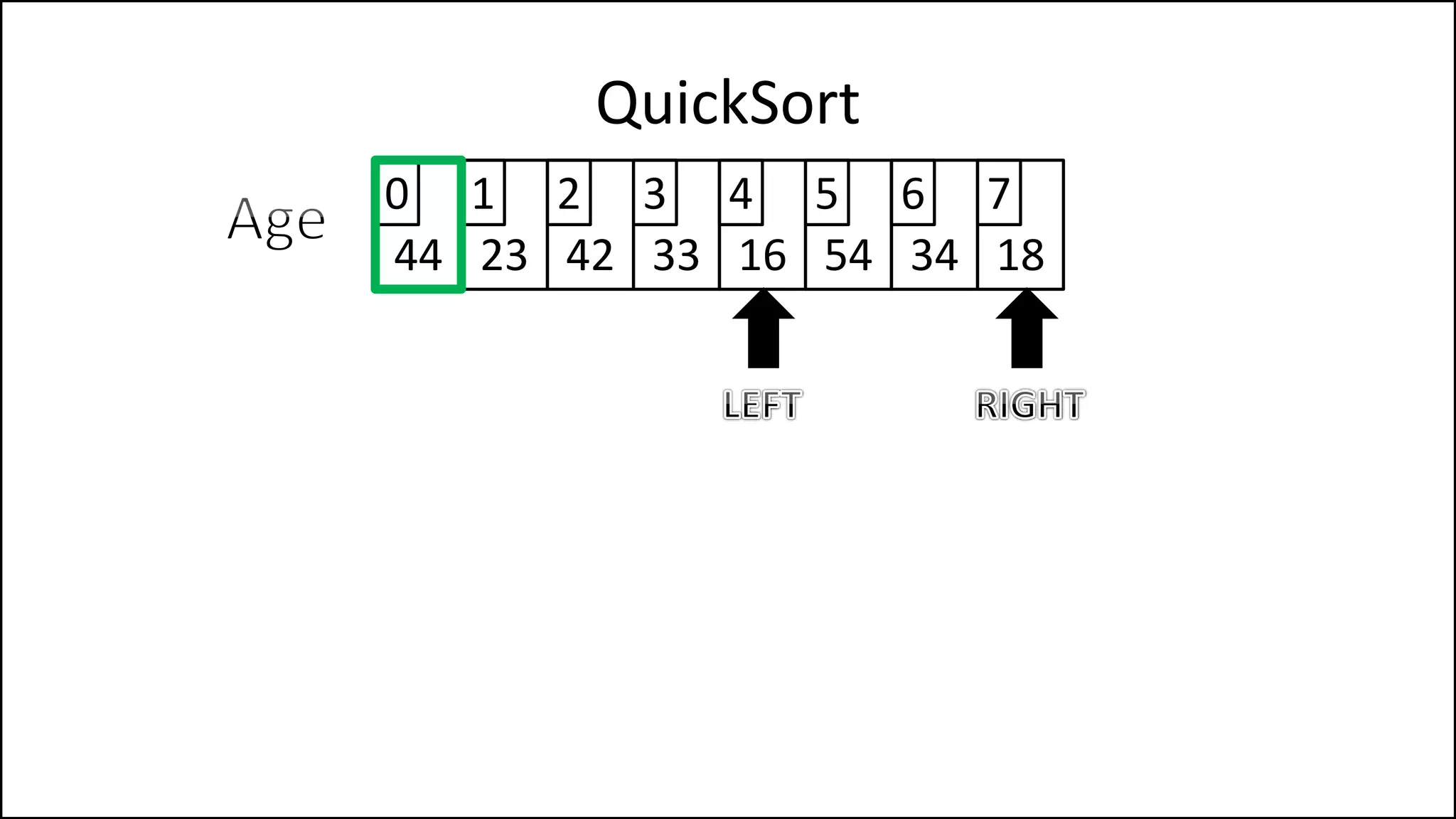
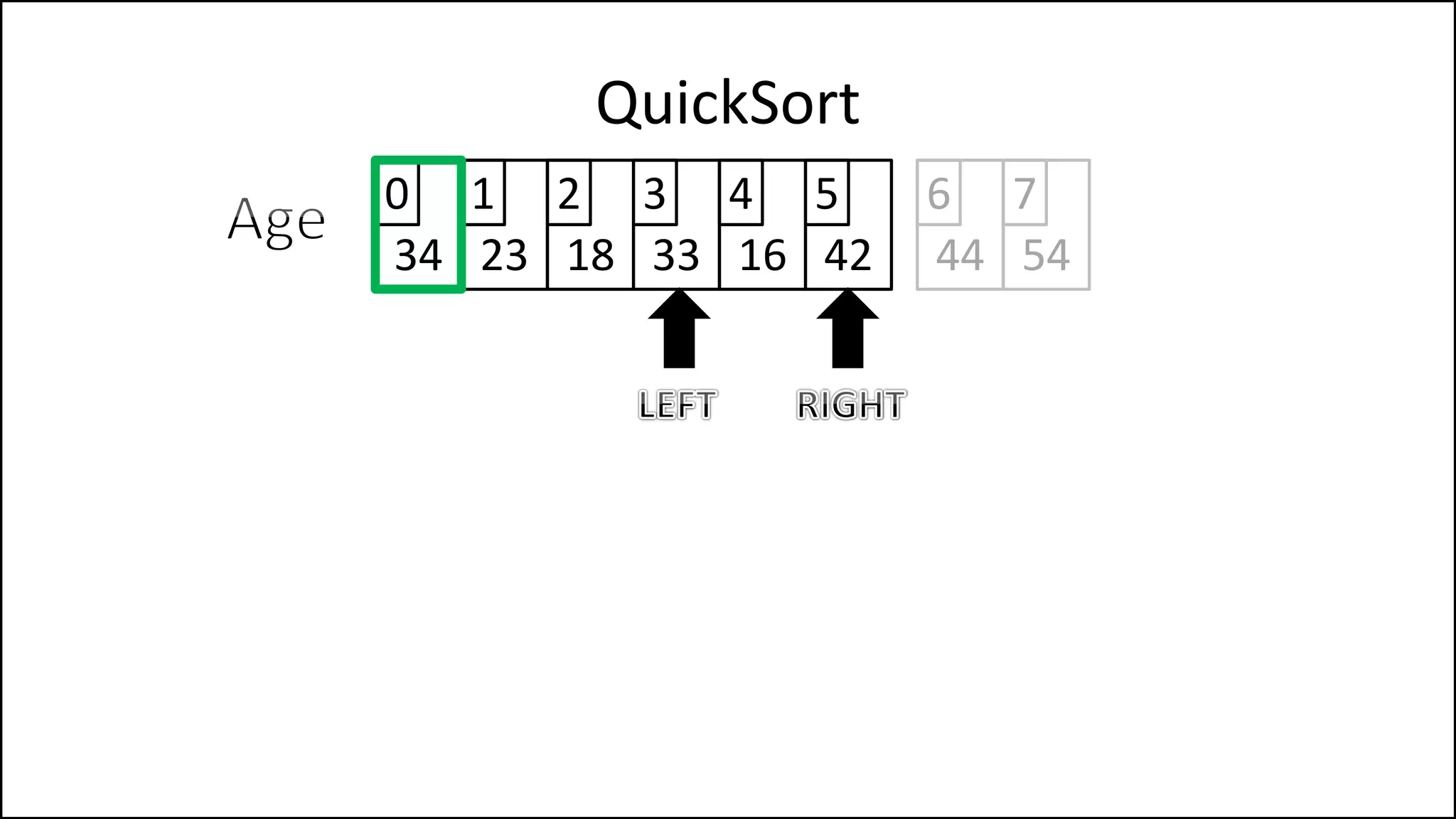
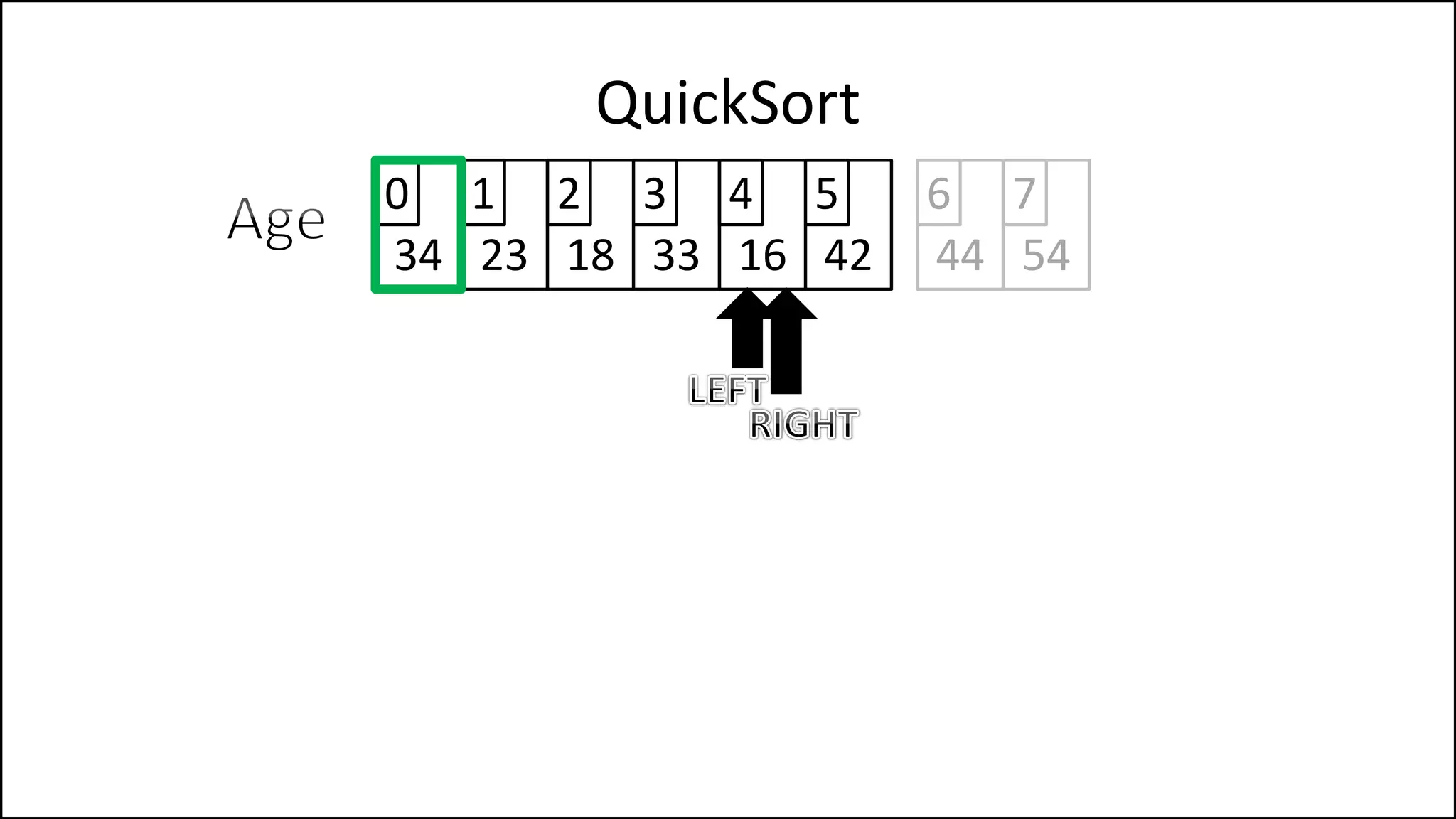
![WHILE NOT(Finished)
DO
WHILE (LeftPointer <= RightPointer) AND
(Age[LeftPointer] <= PivotVal)
DO LeftPointer = LeftPointer + 1
ENDWHILE;
WHILE (Age[RightPointer] >= PivotVal) AND
(RightPointer >= LeftPointer)
DO RightPointer = RightPointer - 1
ENDWHILE;
QuickSort
Continued
Continued
Keep moving left
until we find a
value that is less
than the pivot, or
we reach the Right
Pointer.
Keep moving right
until we find a
value that is
greater than the
pivot, or we reach
the left Pointer.](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-176-2048.jpg)
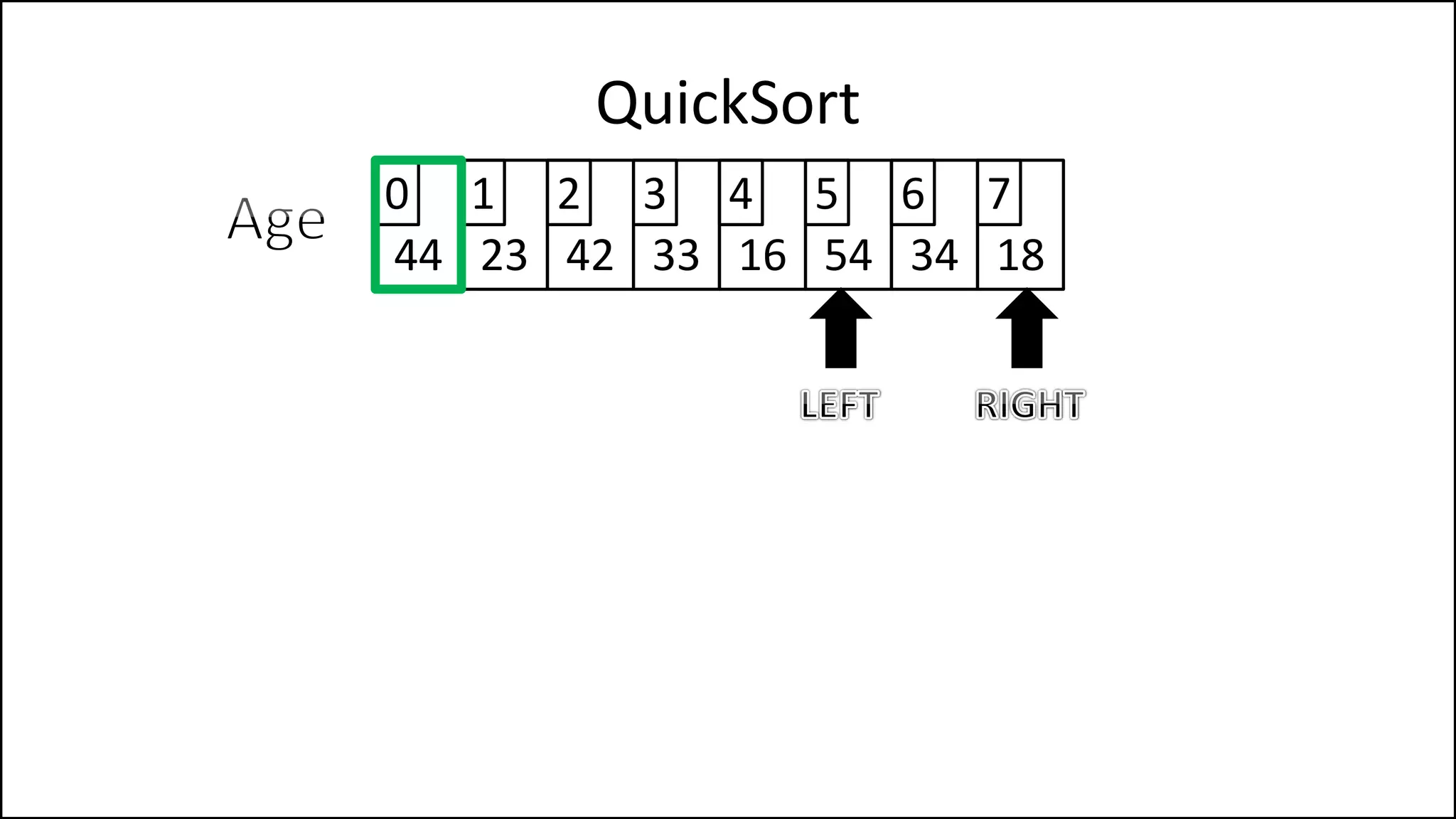
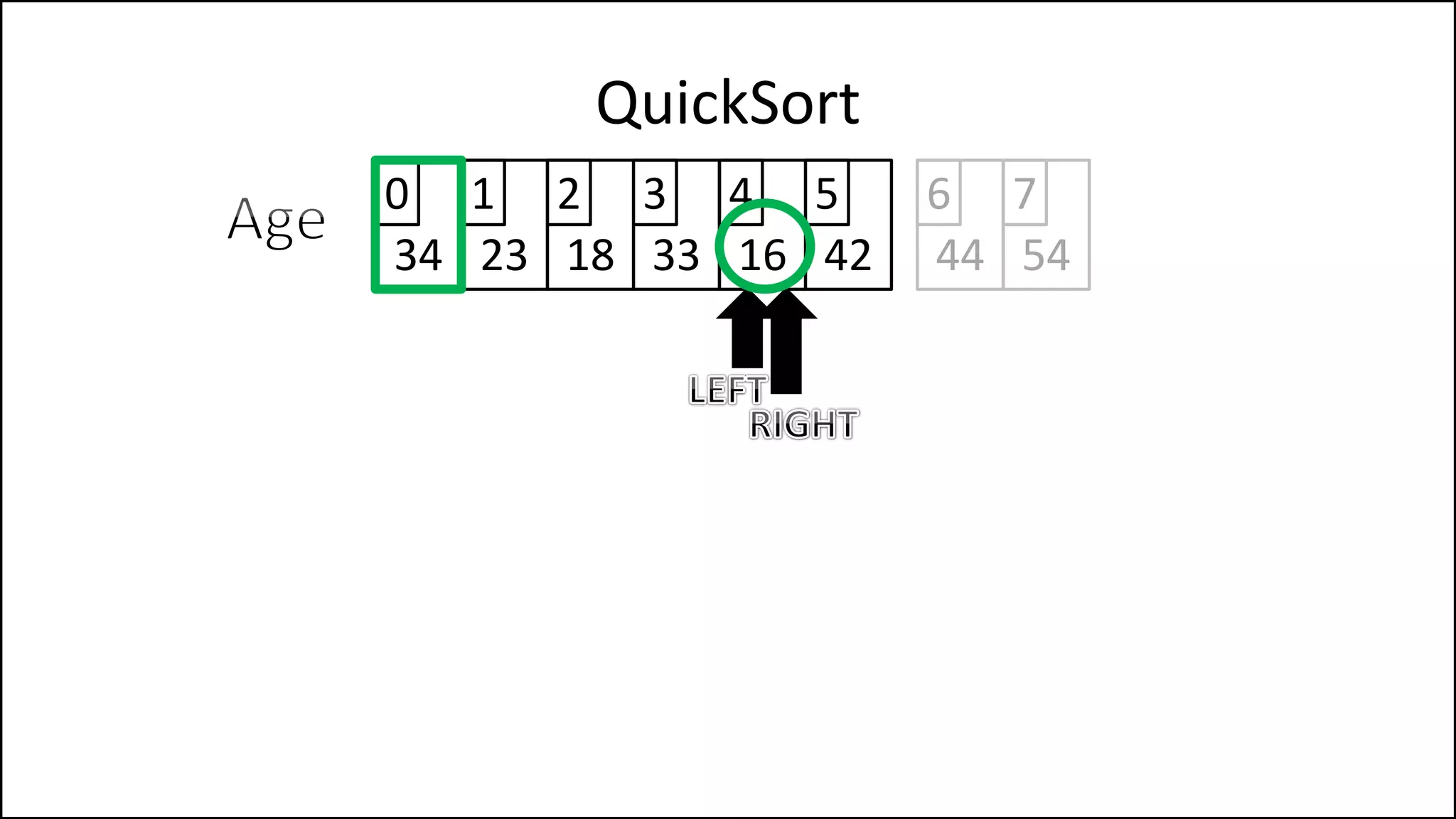
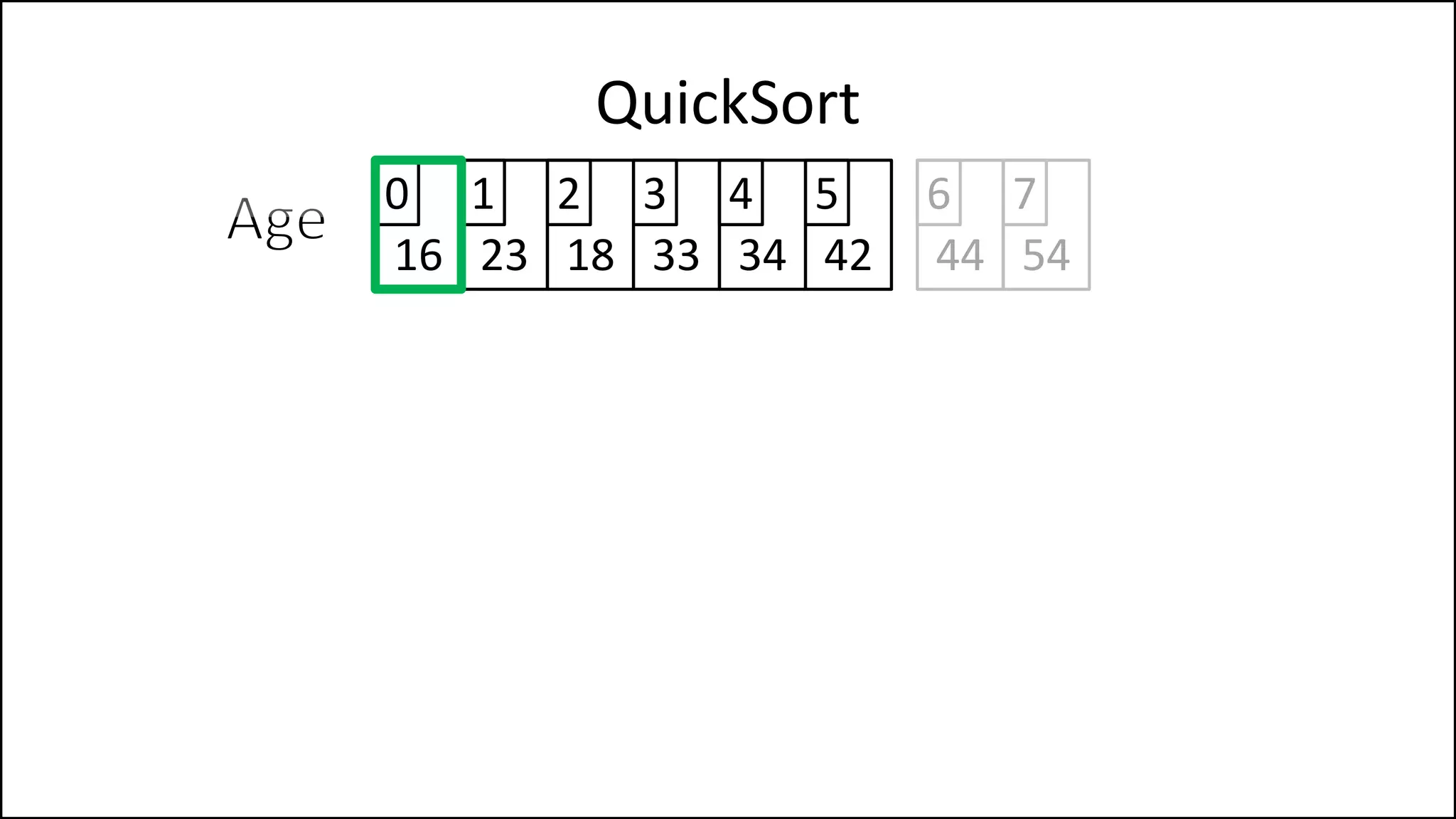
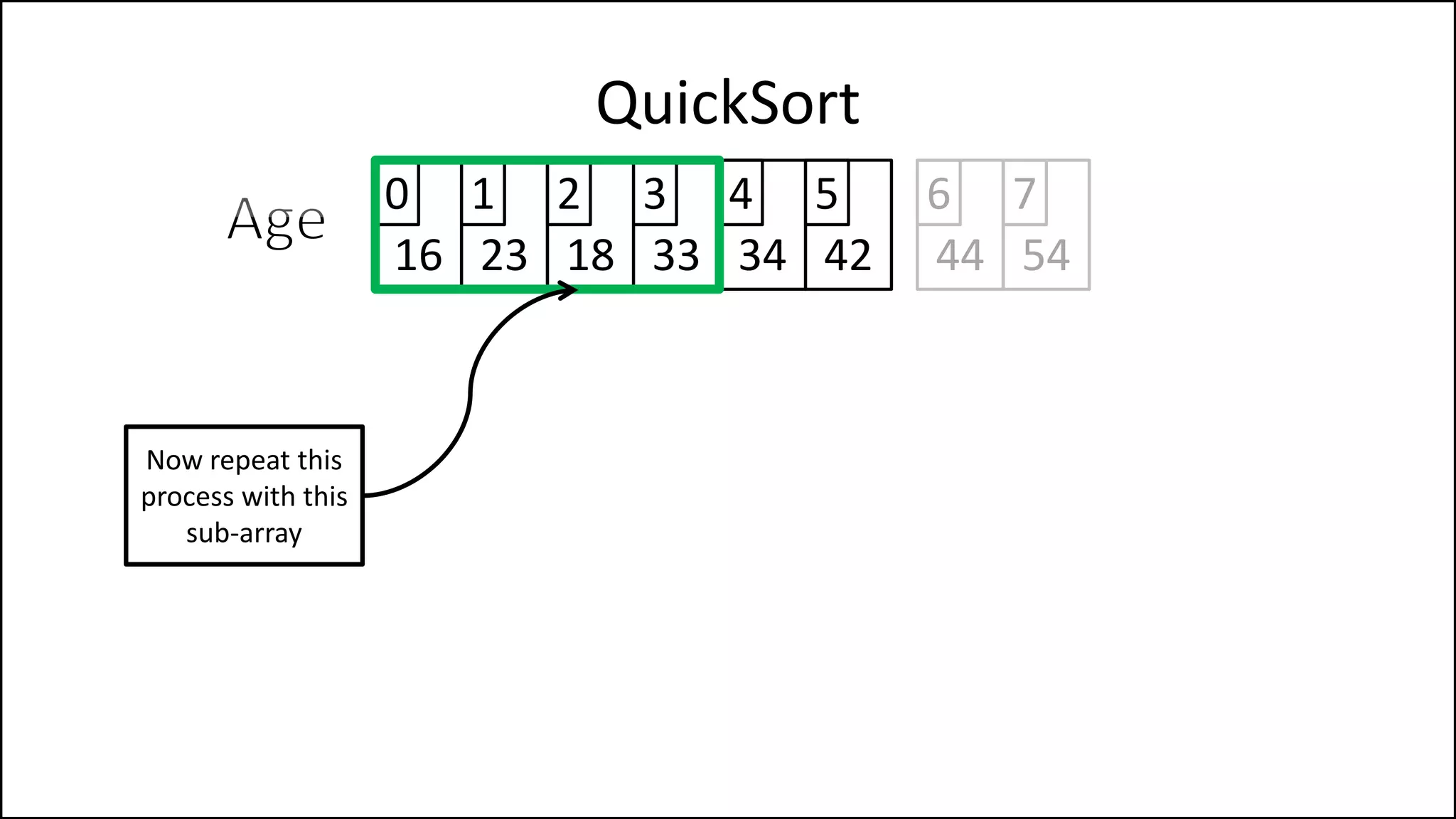
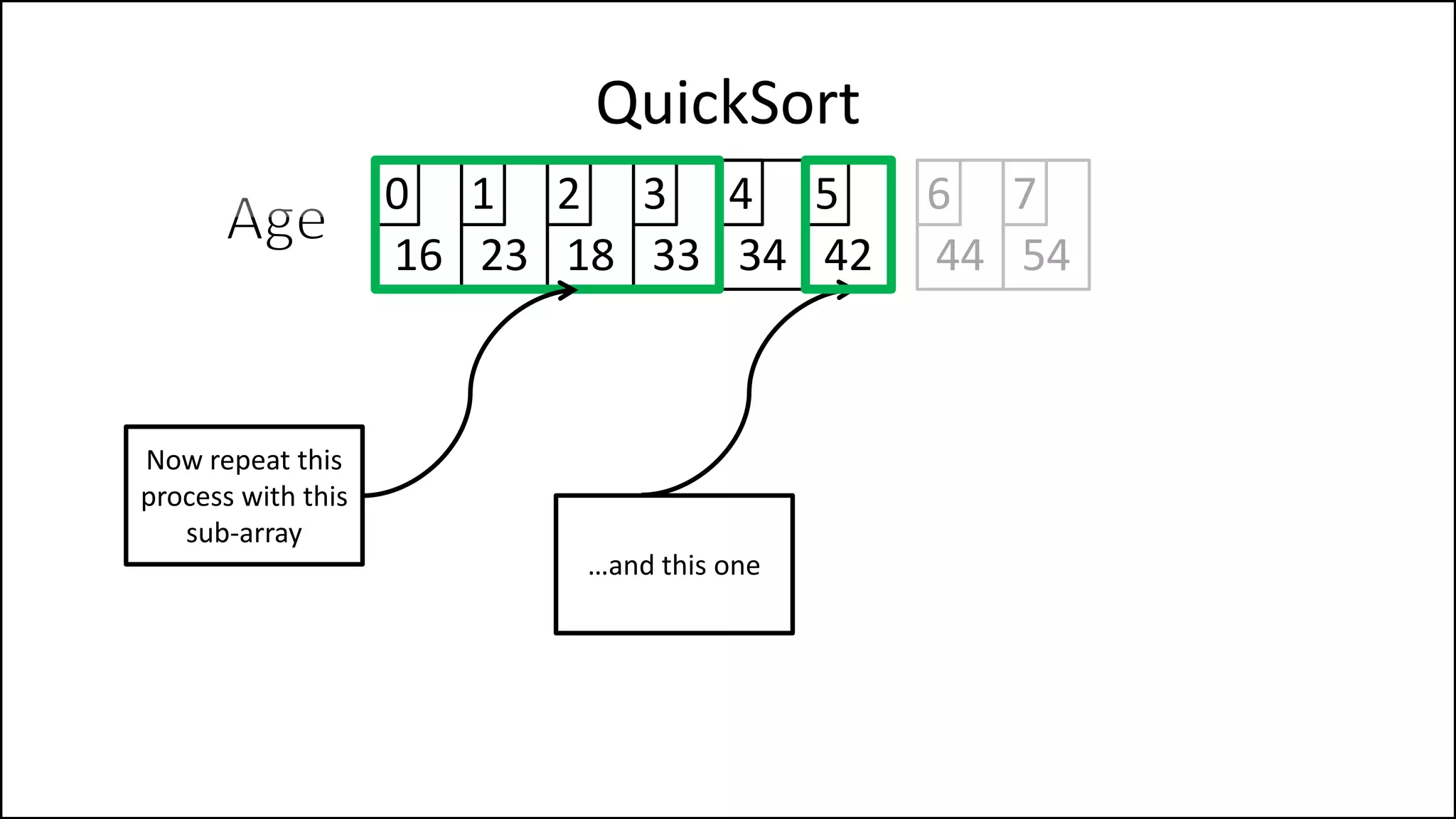
![IF (LeftPointer < RightPointer)
THEN Finished = False;
ELSE SWAP(Age[LeftPointer], Age[RightPointer]);
ENDIF;
SWAP(Age[First], Age[RightPointer]);
RETURN RightPointer;
END Partition.
QuickSort
Continued
We’ve a value
greater than the
pivot to the left,
and one less to the
right, swap them
Put the pivot in its
correct position](https://image.slidesharecdn.com/17a-advancedalgorithms-sorting-160222125148/75/Advanced-Sorting-Algorithms-177-2048.jpg)


