Downloaded 57 times
Uploaded byMadhu Bala
GRAPH APPLICATION - MINIMUM SPANNING TREE (MST)
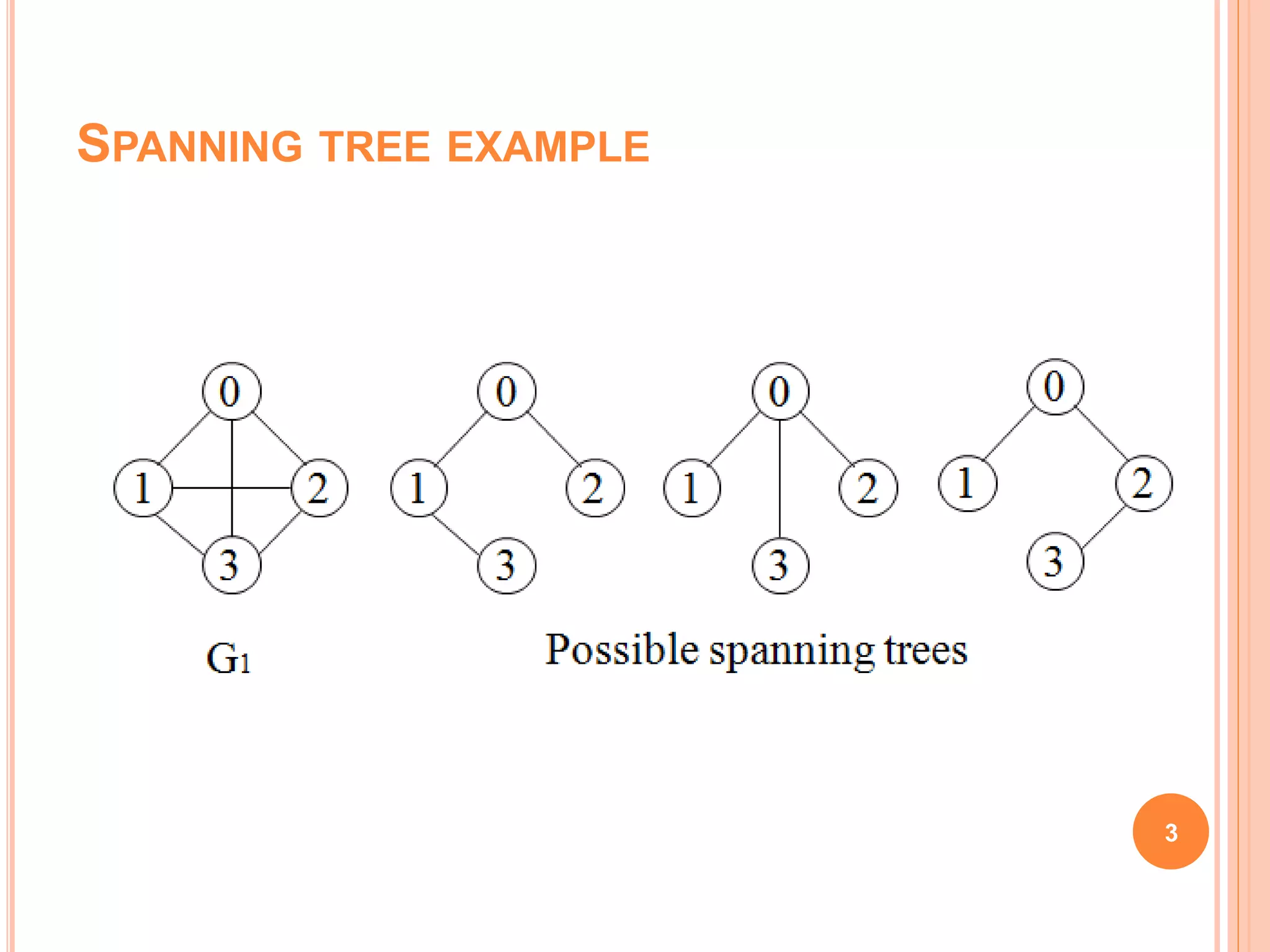
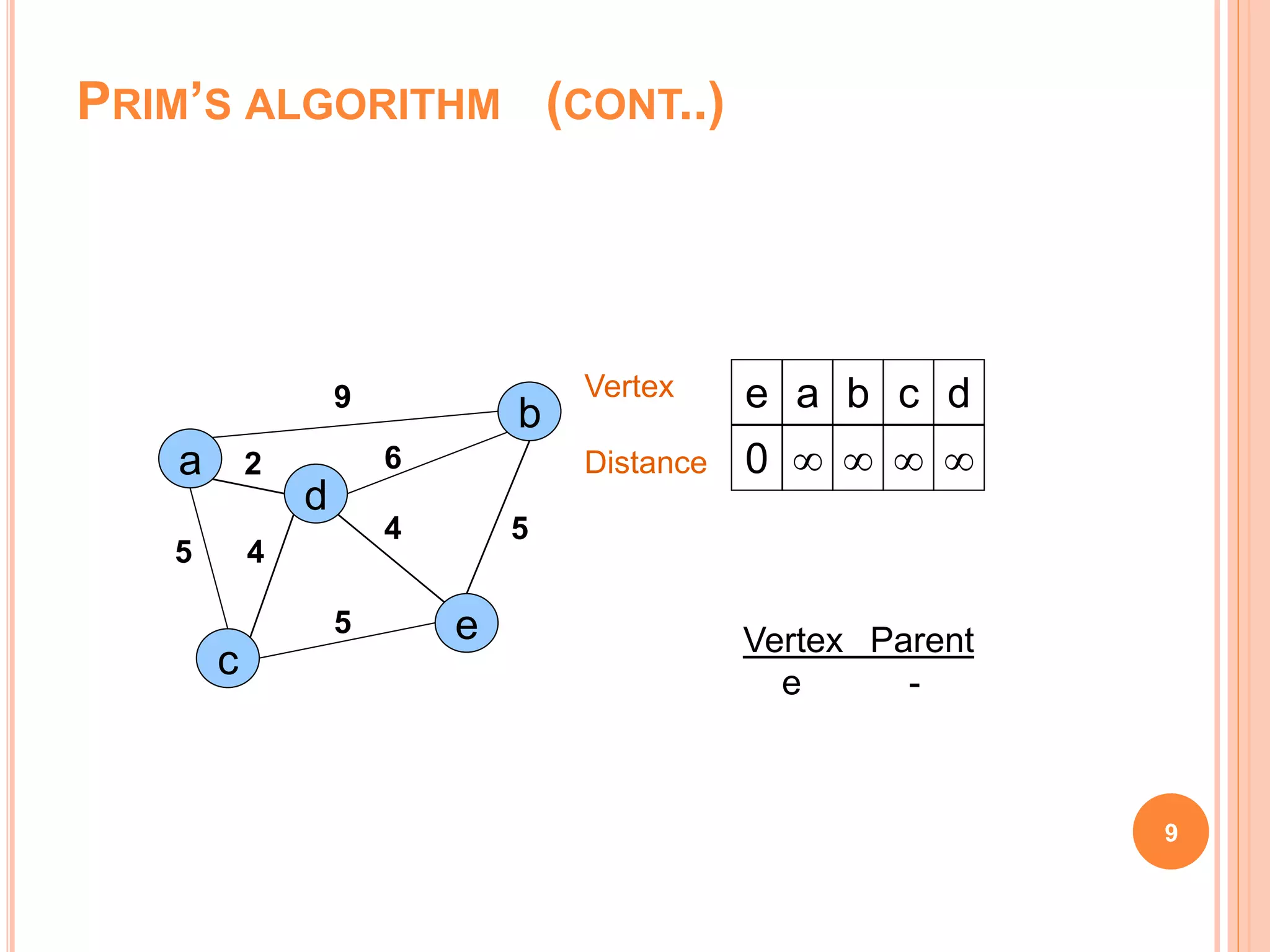
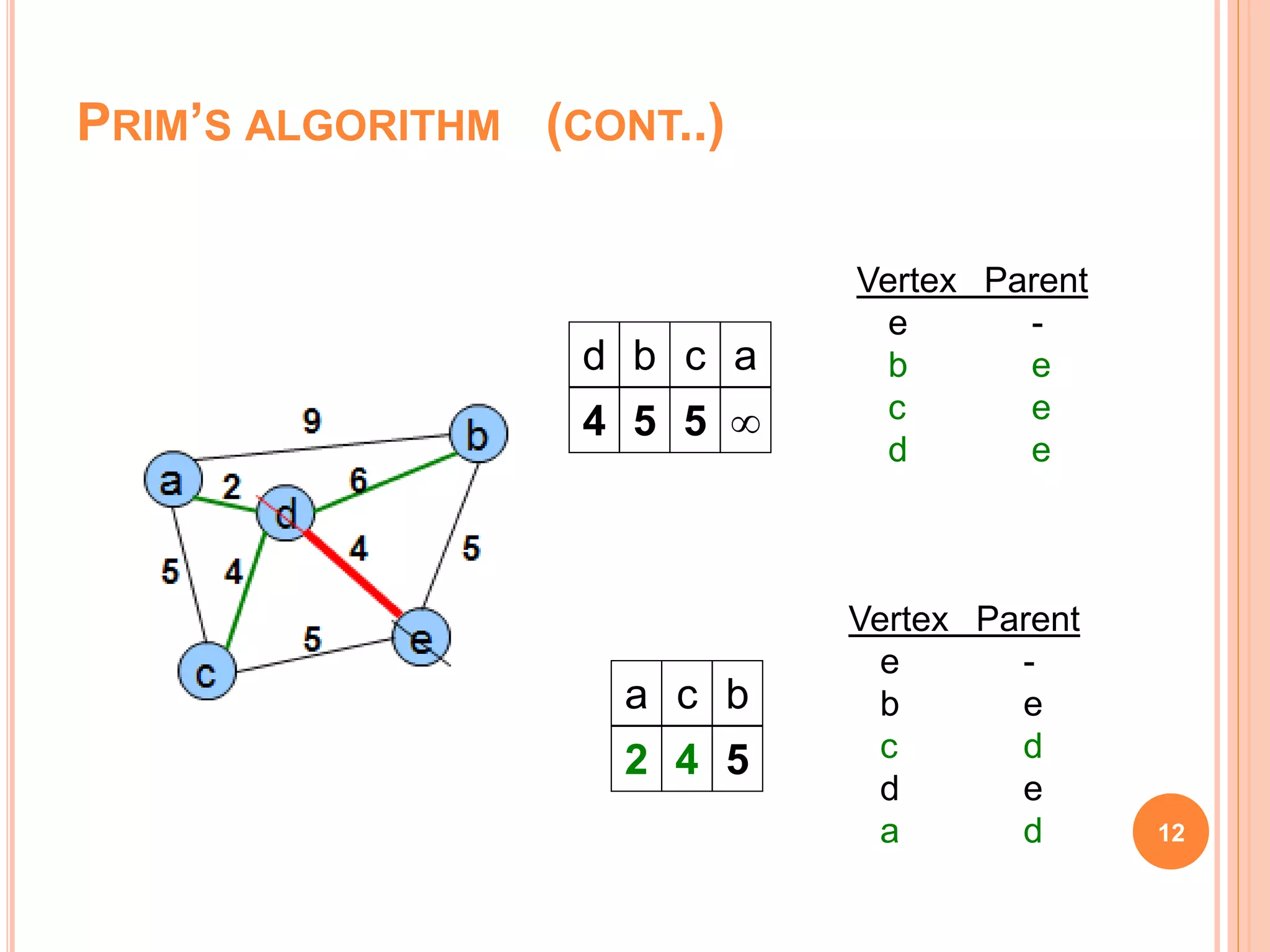
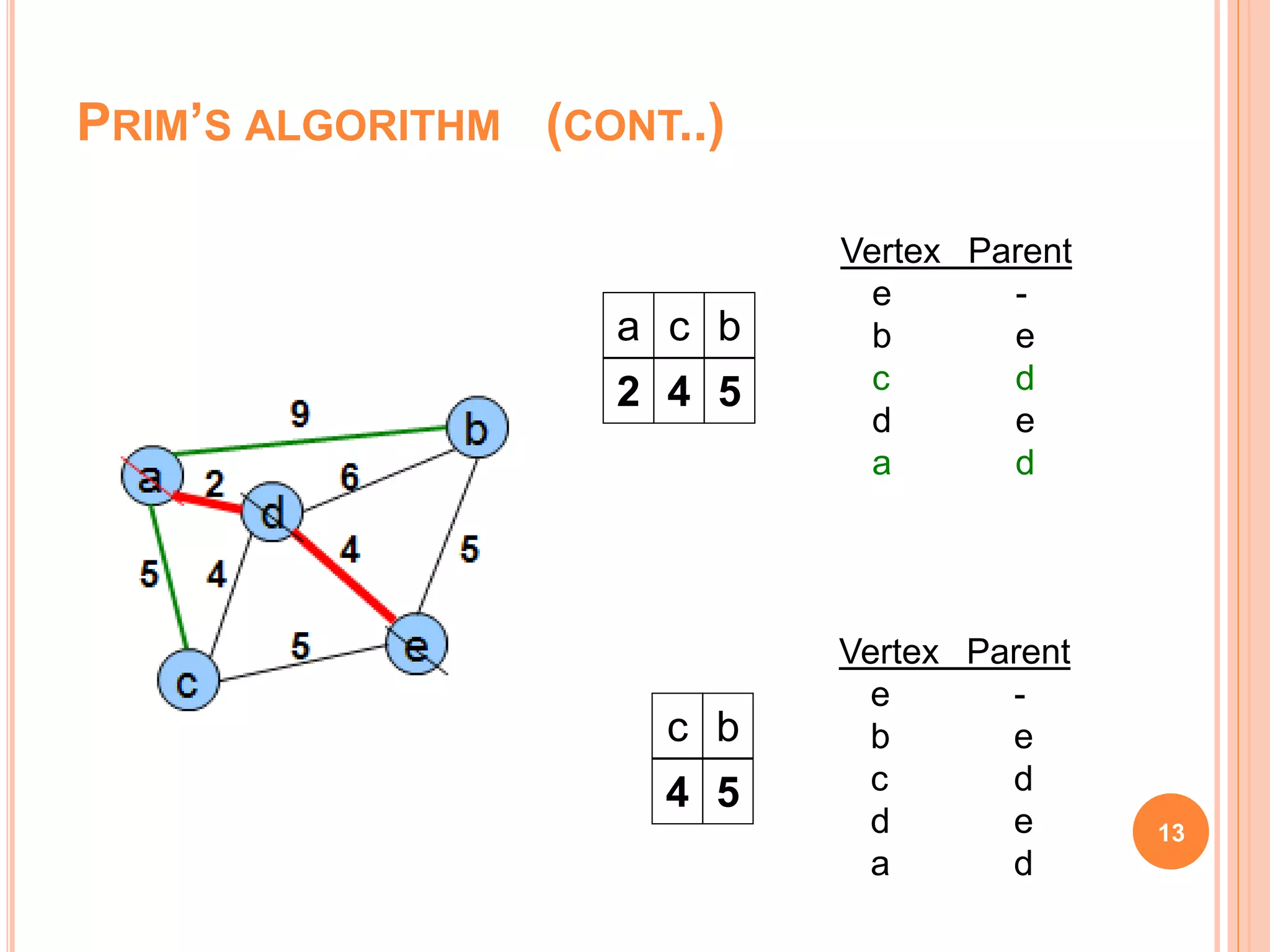
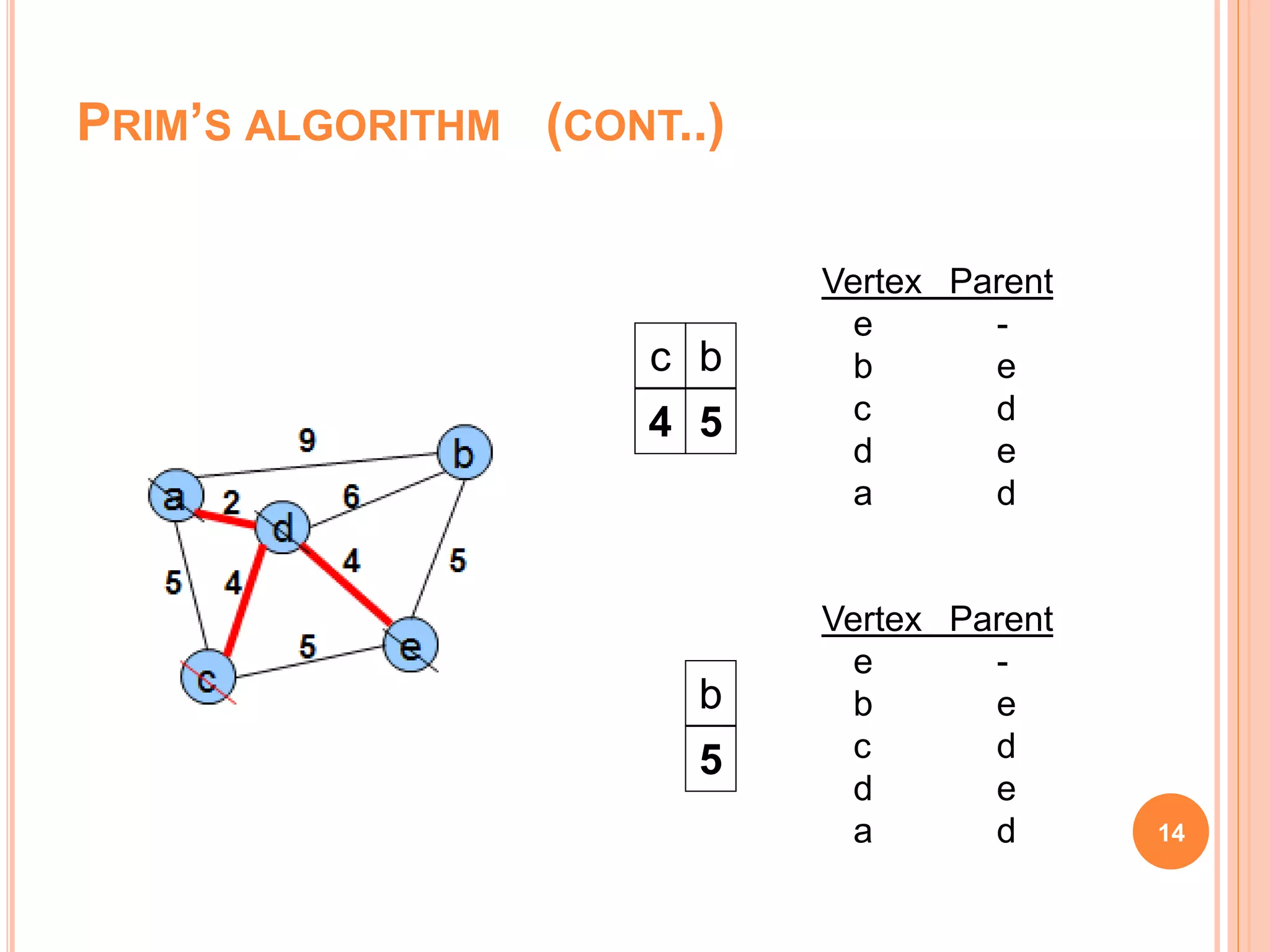
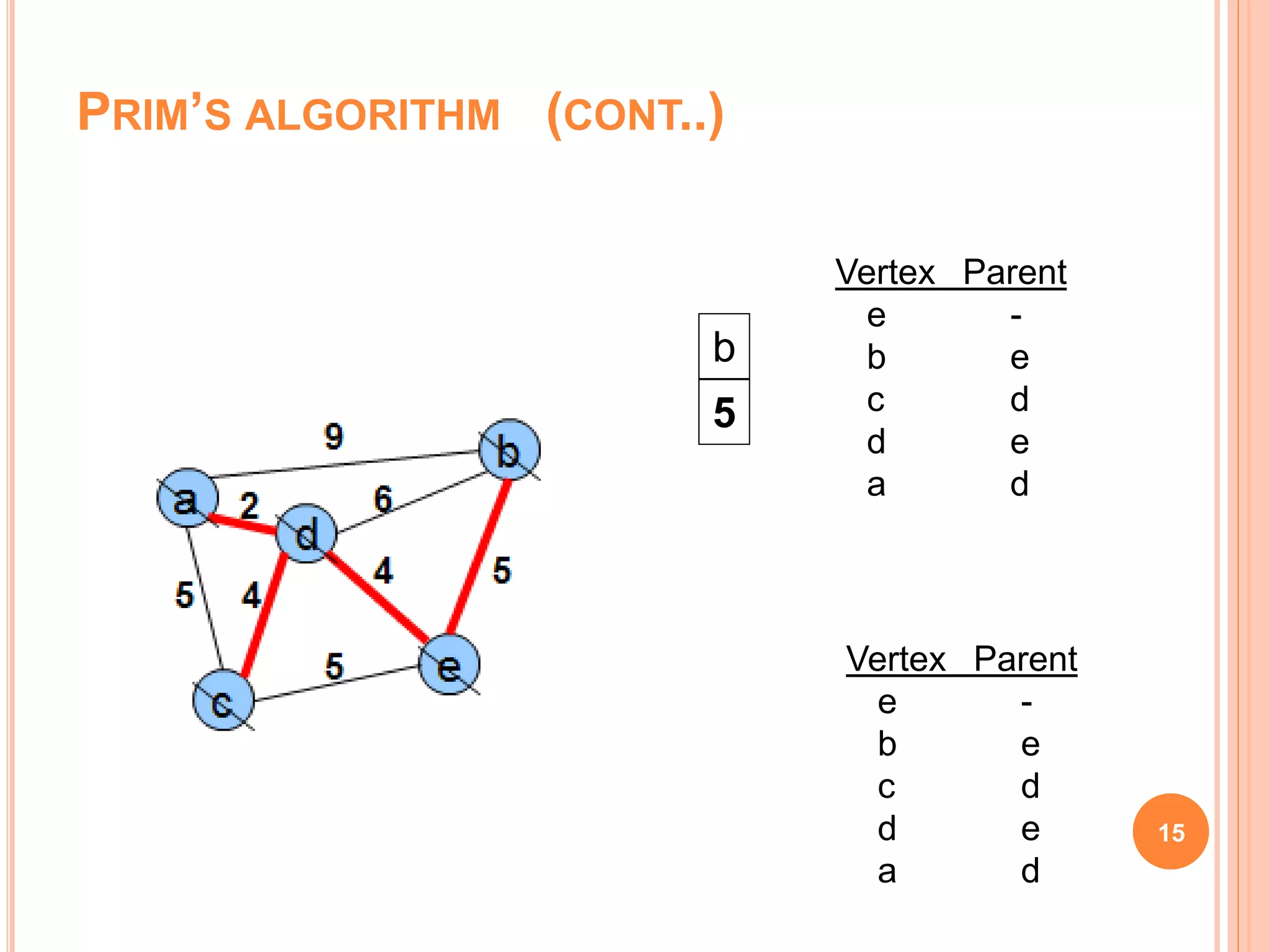
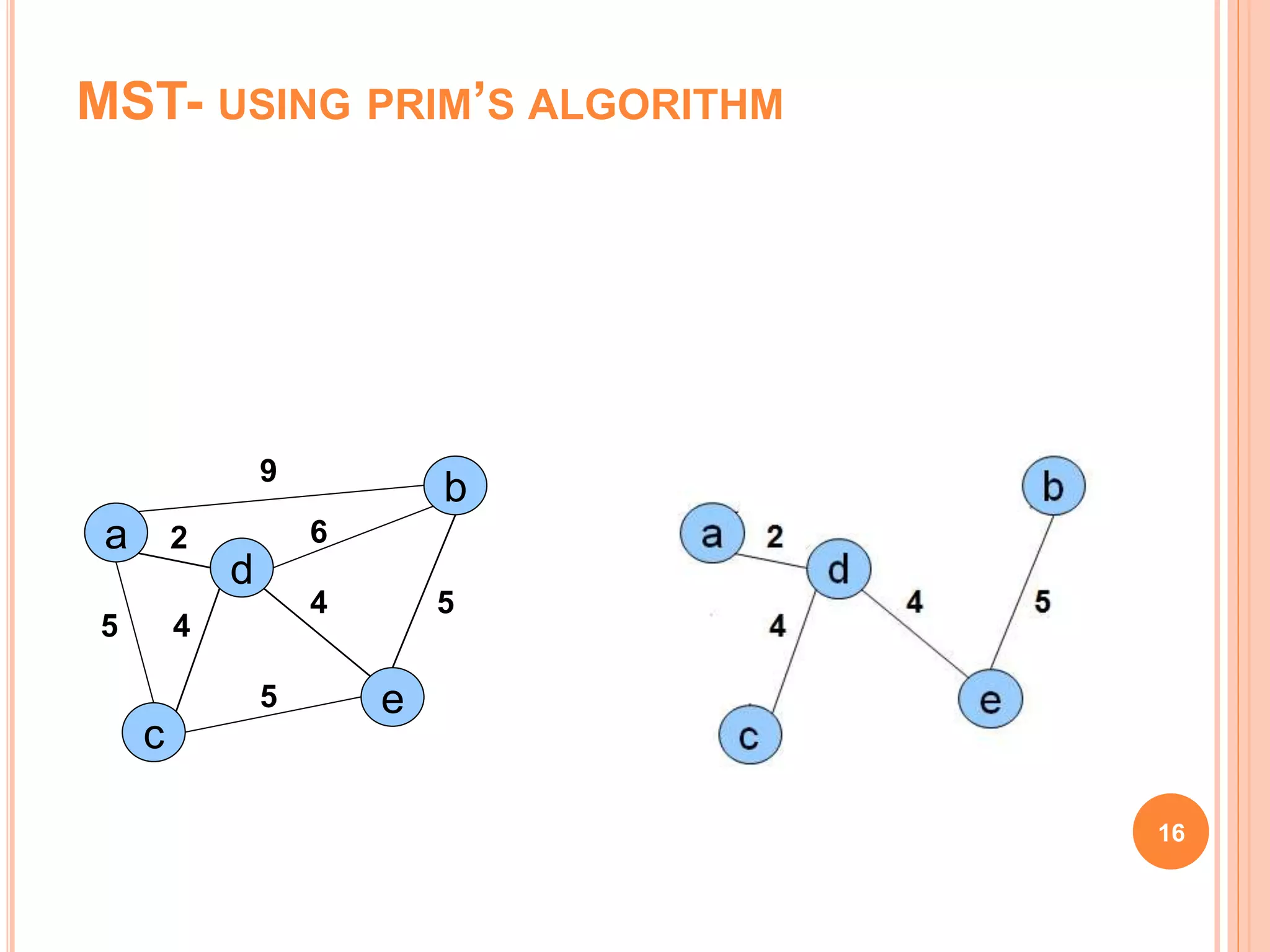
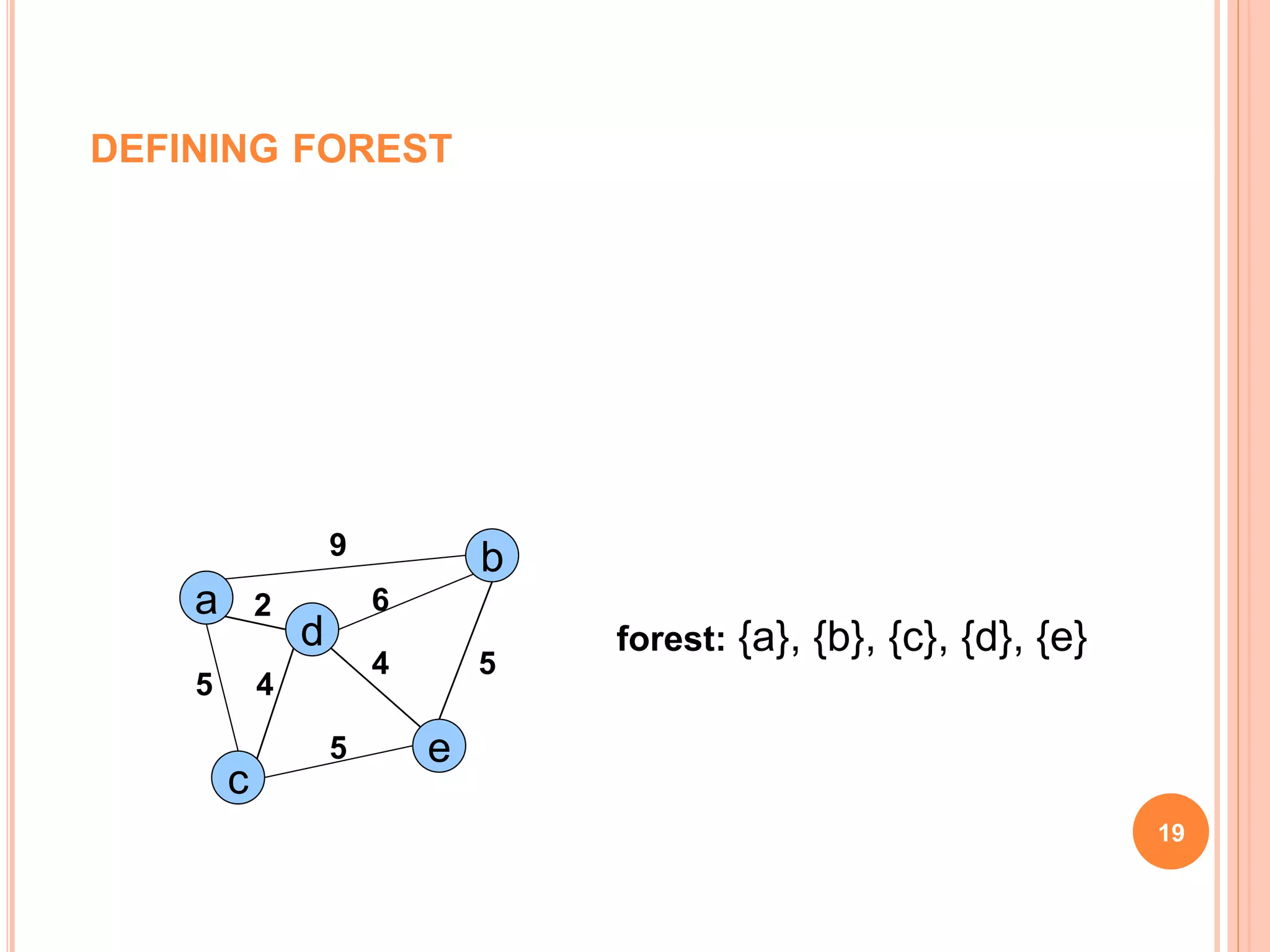
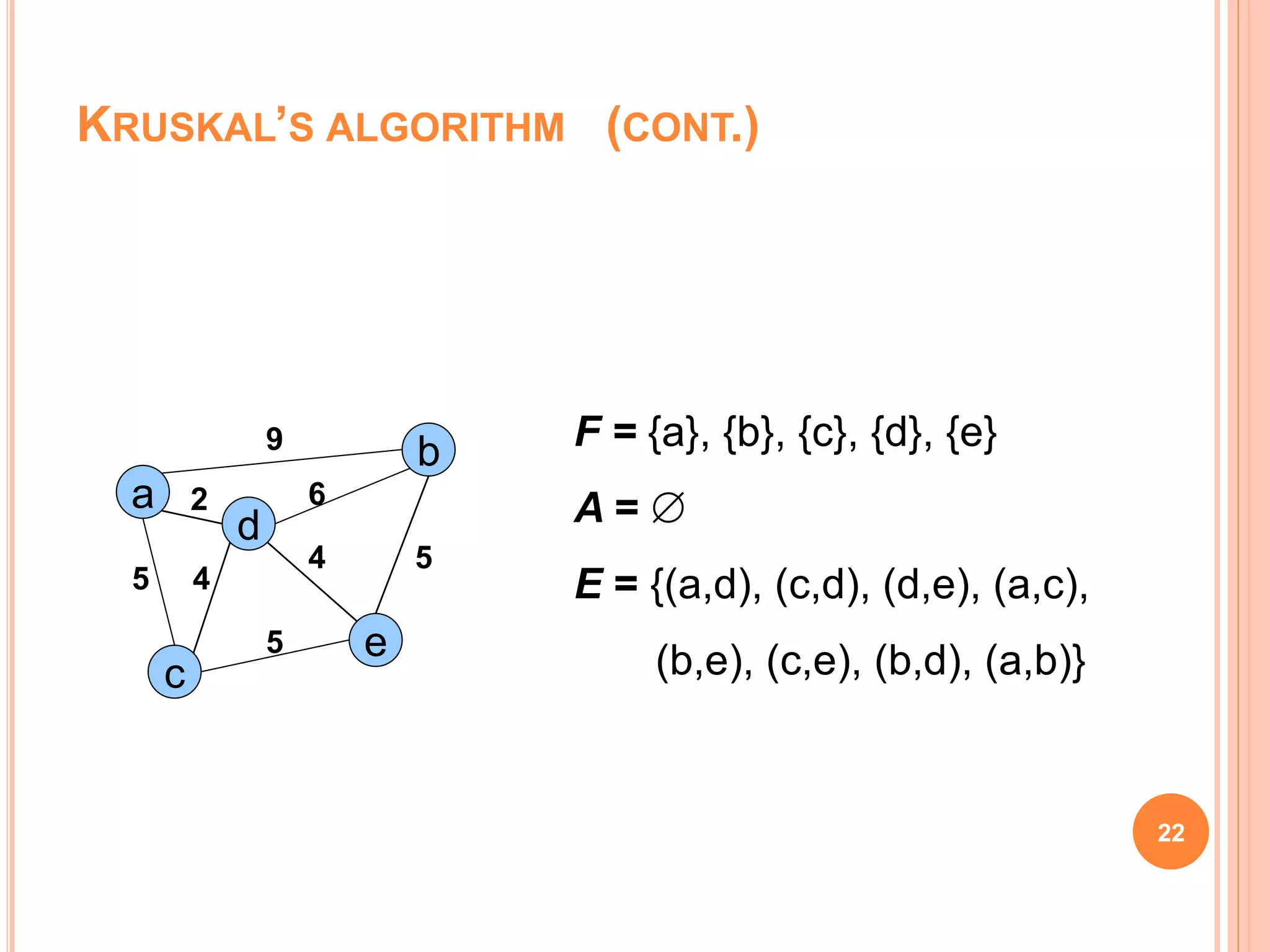
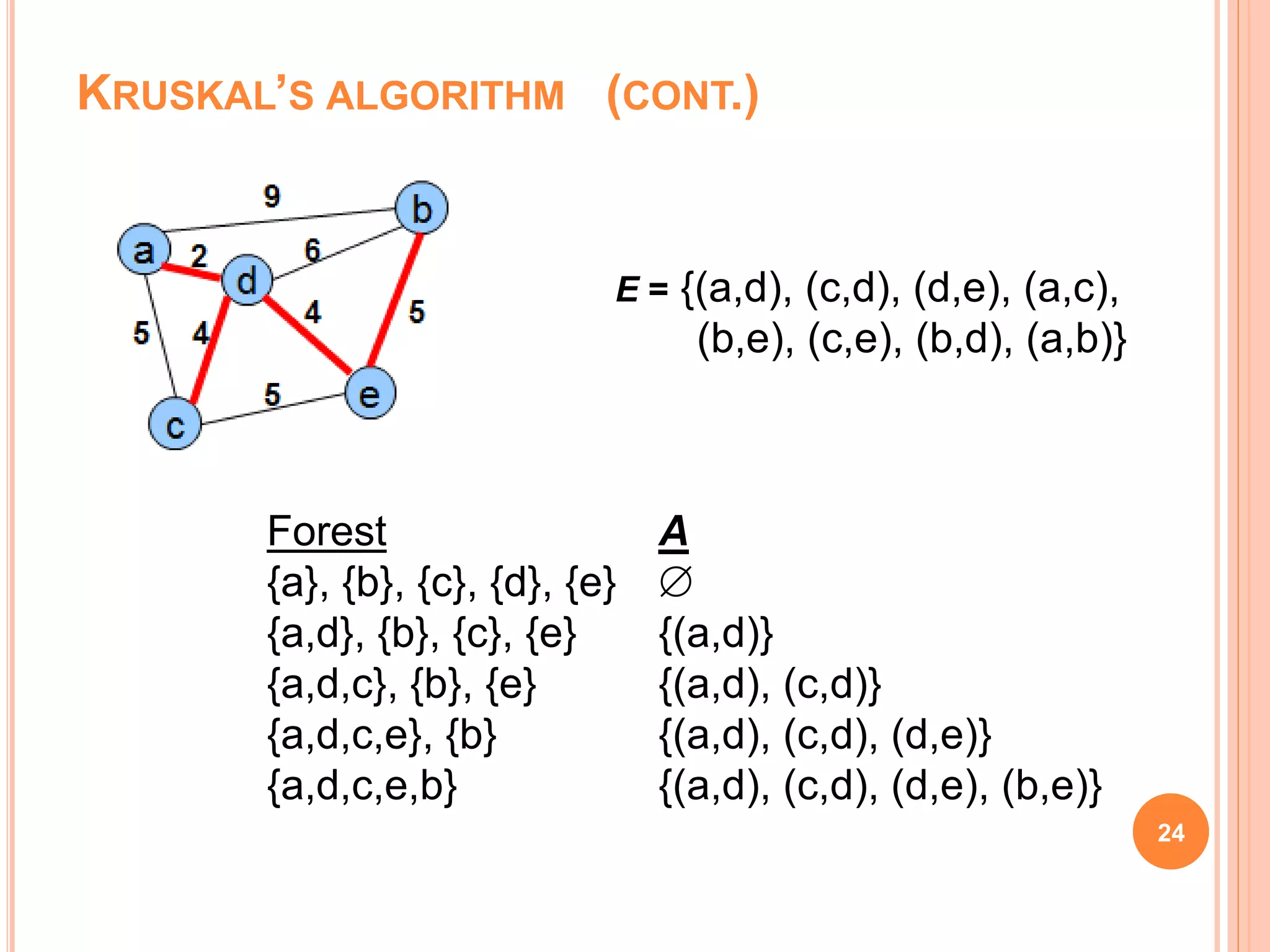
The document discusses spanning trees, particularly focusing on minimum spanning trees (MSTs) and two algorithms for their creation: Prim's algorithm and Kruskal's algorithm. It details the procedures for both algorithms, their initialization, and the steps to build the trees while avoiding cycles. Additionally, it highlights applications of MSTs, including cost-effective graph traversal for network layouts.
More Related Content
Similar to GRAPH APPLICATION - MINIMUM SPANNING TREE (MST)
GRAPH APPLICATION - MINIMUM SPANNING TREE (MST)
- 1. GRAPH APPLICATION - MST oPrim’s o Kruskal’s 1
- 2. WHAT IS SPANNINGTREE A spanning tree of a graph is a tree that has all the vertices of the graph connected by some edge A graph can have one or more number of spanning trees. If the graph has N vertices then the spanning tree will have n-1 edges 2
- 3.
- 4. SPANNING TREE -CREATION Either DFS or BFS can be used to create a spanning tree When DFS is used, the resulting spanning tree is known as a depth first spanning tree When BFS is used, the resulting spanning tree is known as a breadth first spanning tree While adding a non-tree edge into any spanning tree, this will create a cycle 4
- 5. MINIMUM SPANNING TREE A minimum spanning tree is a spanning tree that has the minimum weight than all other spanning trees of a graph Three different algorithms can be used Prim’s algorithm Kruskal’s algorithm 5
- 6. PRIM’S ALGORITHM -INTRODUCTION Prim's algorithm is a greedy algorithm. It finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. 6
- 7. PRIM’S STEPS 1.Select anyvertex 2.Select the shortest edge connected to that vertex 3.Select the shortest edge connected to any vertex already connected 4.Repeat step 3 until all vertices have been connected 7
- 8. PRIM’S ALGORITHM 8 Initialization: Picka vertex r to be the root Set D(r) = 0, parent(r) = null For all vertices v V, v r, set D(v) = Insert all vertices into priority queue P, using distances as the keys
- 9. PRIM’S ALGORITHM (CONT..) 9 a c e d b 2 45 9 6 4 5 5 ea b c d 0 Vertex Parent e - Vertex Distance
- 10. PRIM’S ALGORITHM (CONT..) WhileP is not empty: Select the next vertex u to add to the tree u = P.deleteMin() Update the weight of each vertex w adjacent to u which is not in the tree (i.e., w P) If weight(u,w) < D(w), a. parent(w) = u b. D(w) = weight(u,w) c. Update the priority queue to reflect new distance for w 10
- 11. PRIM’S ALGORITHM (CONT..) 11 db c a 4 5 5 Vertex Parent e - b e c e d e Vertex Parent e - b - c - d - d b c a e 0
- 12. PRIM’S ALGORITHM (CONT..) 12 ac b 2 4 5 Vertex Parent e - b e c d d e a d d b c a 4 5 5 Vertex Parent e - b e c e d e
- 13. PRIM’S ALGORITHM (CONT..) 13 cb 4 5 Vertex Parent e - b e c d d e a d a c b 2 4 5 Vertex Parent e - b e c d d e a d
- 14. PRIM’S ALGORITHM (CONT..) 14 b 5 VertexParent e - b e c d d e a d c b 4 5 Vertex Parent e - b e c d d e a d
- 15. PRIM’S ALGORITHM (CONT..) 15 VertexParent e - b e c d d e a d b 5 Vertex Parent e - b e c d d e a d
- 16. MST- USING PRIM’SALGORITHM 16 a c e d b 2 45 9 6 4 5 5
- 17. RUNNING TIME OFPRIM’S ALGORITHM Initialization of priority queue (array): O(|V|) Update loop: • Choosing vertex with minimum cost edge: O(|V|) • Updating distance values of unconnected vertices: each edge is considered only once during entire execution, for a total of O(|E|) updates Overall cost : 17 O(|E| + |V| 2)
- 18. KRUSKAL’S ALGORITHM -INTRODUCTION Create a forest of trees from the vertices Repeatedly merge trees by adding “safe edges” until only one tree remains A “safe edge” is an edge of minimum weight which does not create a cycle 18
- 19. 19 a c e d b 2 45 9 6 4 5 5 forest: {a}, {b},{c}, {d}, {e} DEFINING FOREST
- 20. 1. Select theshortest edge in a network 2. Select the next shortest edge which does not create a cycle 3. Repeat step 2 until all vertices have been connected 20 KRUSKAL’S STEPS
- 21. 21 Initialization a. Createa set for each vertex v V b. Initialize the set of “safe edges” A comprising the MST to the empty set c. Sort edges by increasing weight KRUSKAL’S ALGORITHM
- 22. 22 a c e d b 2 45 9 6 4 5 5 F = {a},{b}, {c}, {d}, {e} A = E = {(a,d), (c,d), (d,e), (a,c), (b,e), (c,e), (b,d), (a,b)} KRUSKAL’S ALGORITHM (CONT.)
- 23. 23 For eachedge (u,v) E in increasing order while more than one set remains: If u and v, belong to different sets U and V a. add edge (u,v) to the safe edge set A = A {(u,v)} b. merge the sets U and V F = F - U - V + (U V) Return A KRUSKAL’S ALGORITHM (CONT.)
- 24. 24 E = {(a,d),(c,d), (d,e), (a,c), (b,e), (c,e), (b,d), (a,b)} Forest {a}, {b}, {c}, {d}, {e} {a,d}, {b}, {c}, {e} {a,d,c}, {b}, {e} {a,d,c,e}, {b} {a,d,c,e,b} A {(a,d)} {(a,d), (c,d)} {(a,d), (c,d), (d,e)} {(a,d), (c,d), (d,e), (b,e)} KRUSKAL’S ALGORITHM (CONT.)
- 25. 25 Running timebounded by sorting (or findMin) O(|E|log|E|) , or equivalently, O(|E|log|V|) RUNNING TIME OF KRUSKAL’S ALGORITHM
- 26.
- 27. APPLICATION OF MST Any time you want to visit all vertices in a graph at minimum cost (e.g., wire routing on printed circuit boards, sewer pipe layout, road planning…) Internet content distribution Idea: publisher produces web pages, content distribution network replicates web pages to many locations so consumers can access at higher speed MST may not be good enough! content distribution on minimum cost tree may take a long time! 27