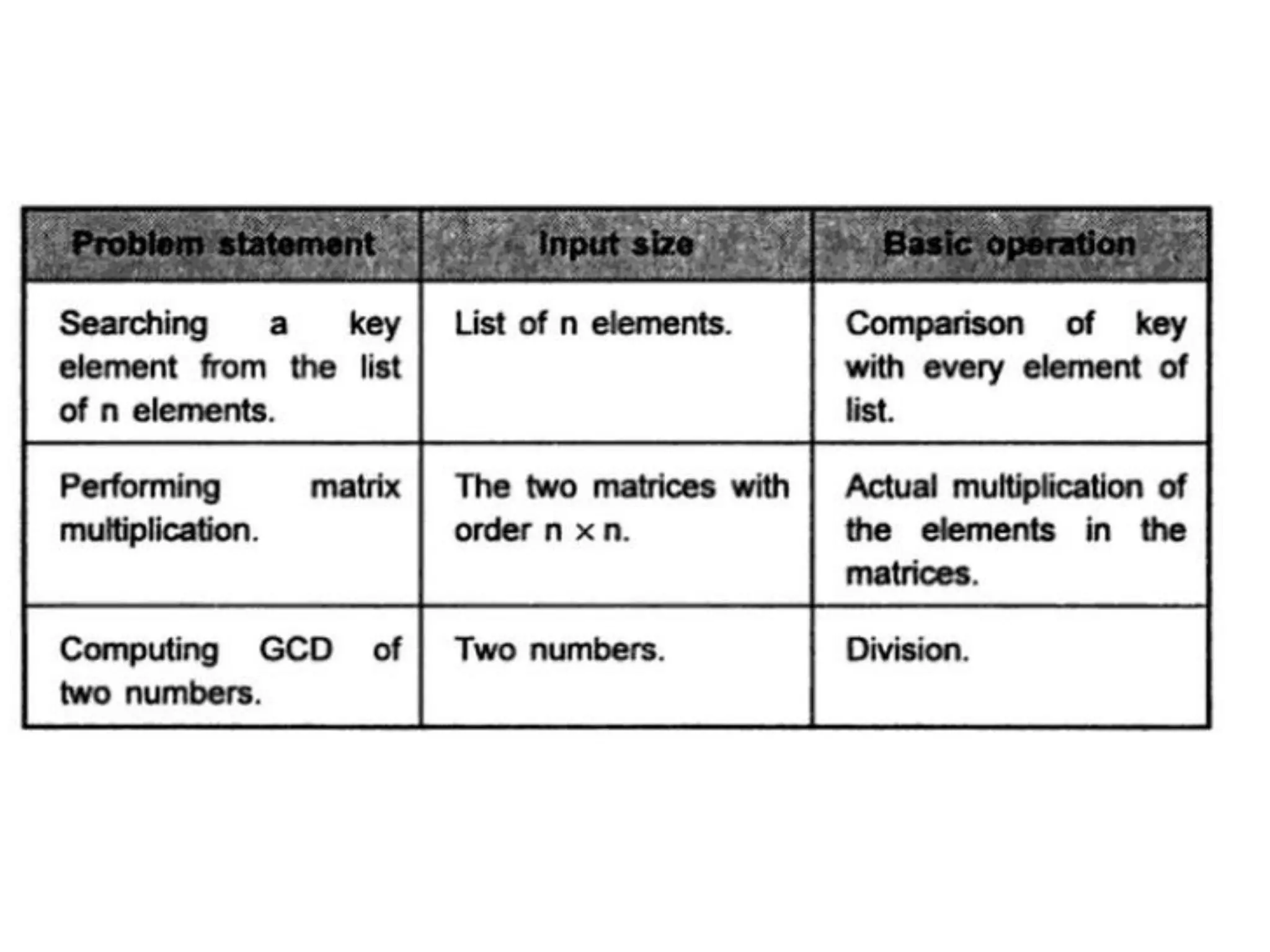
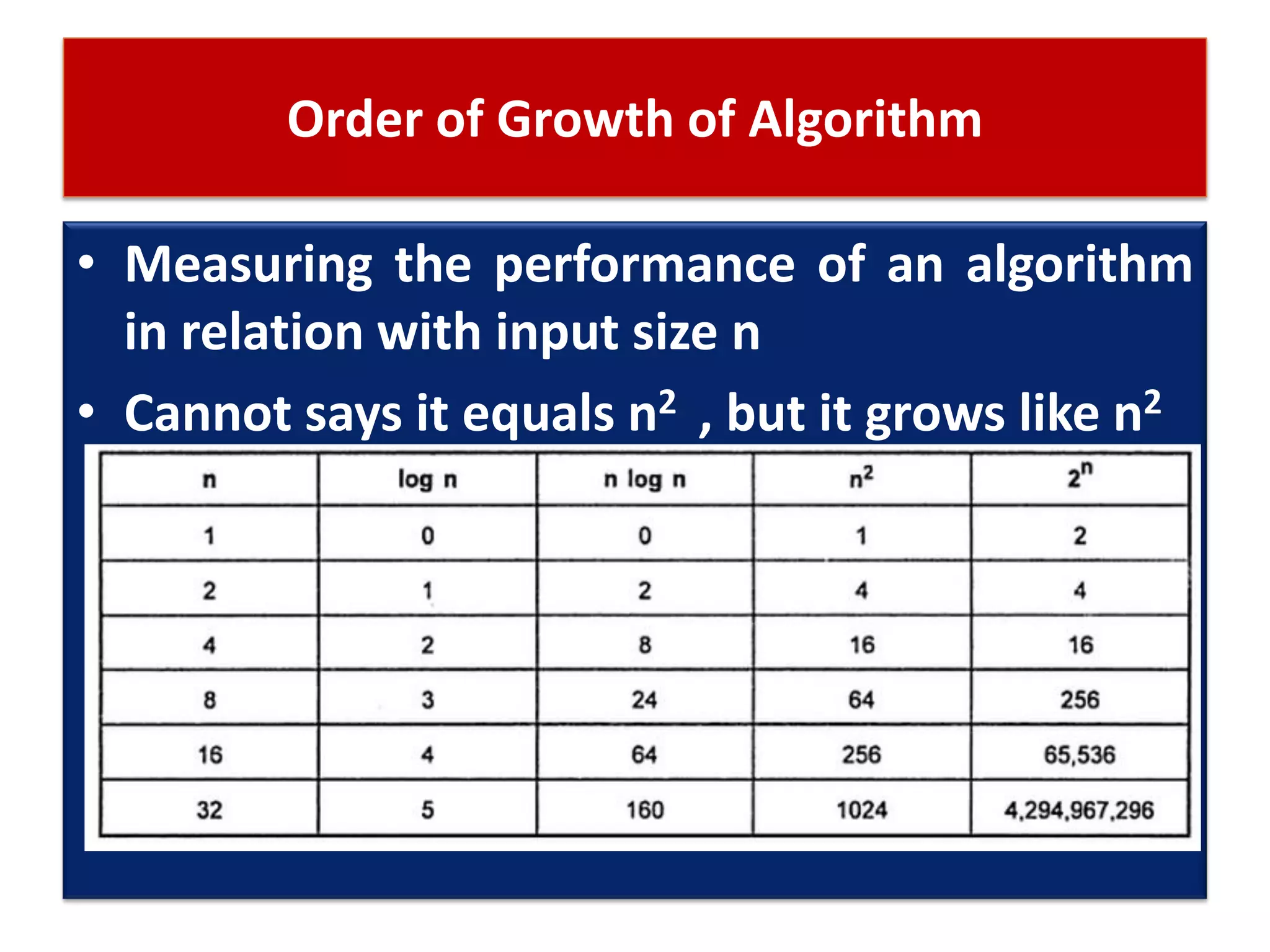
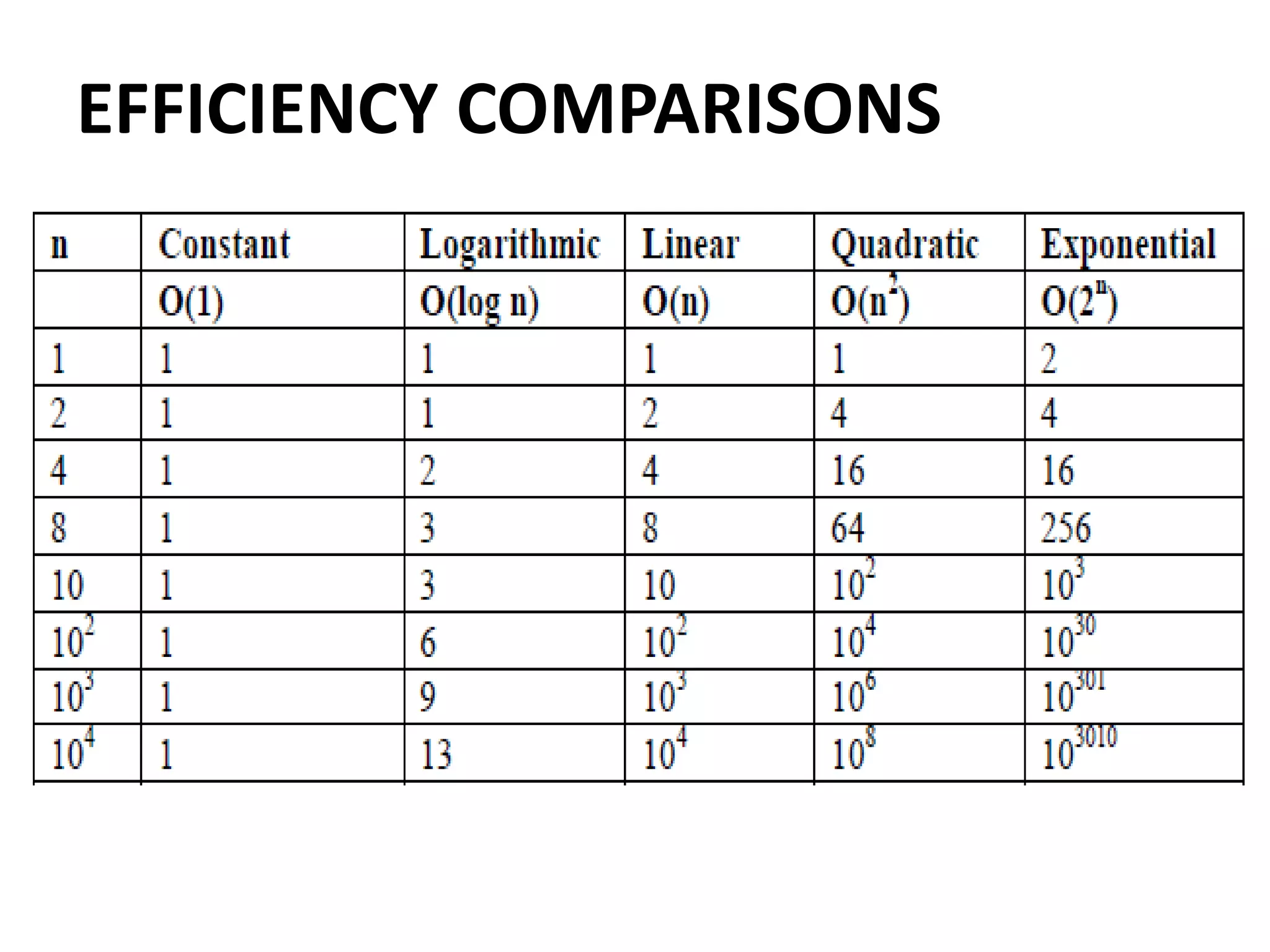
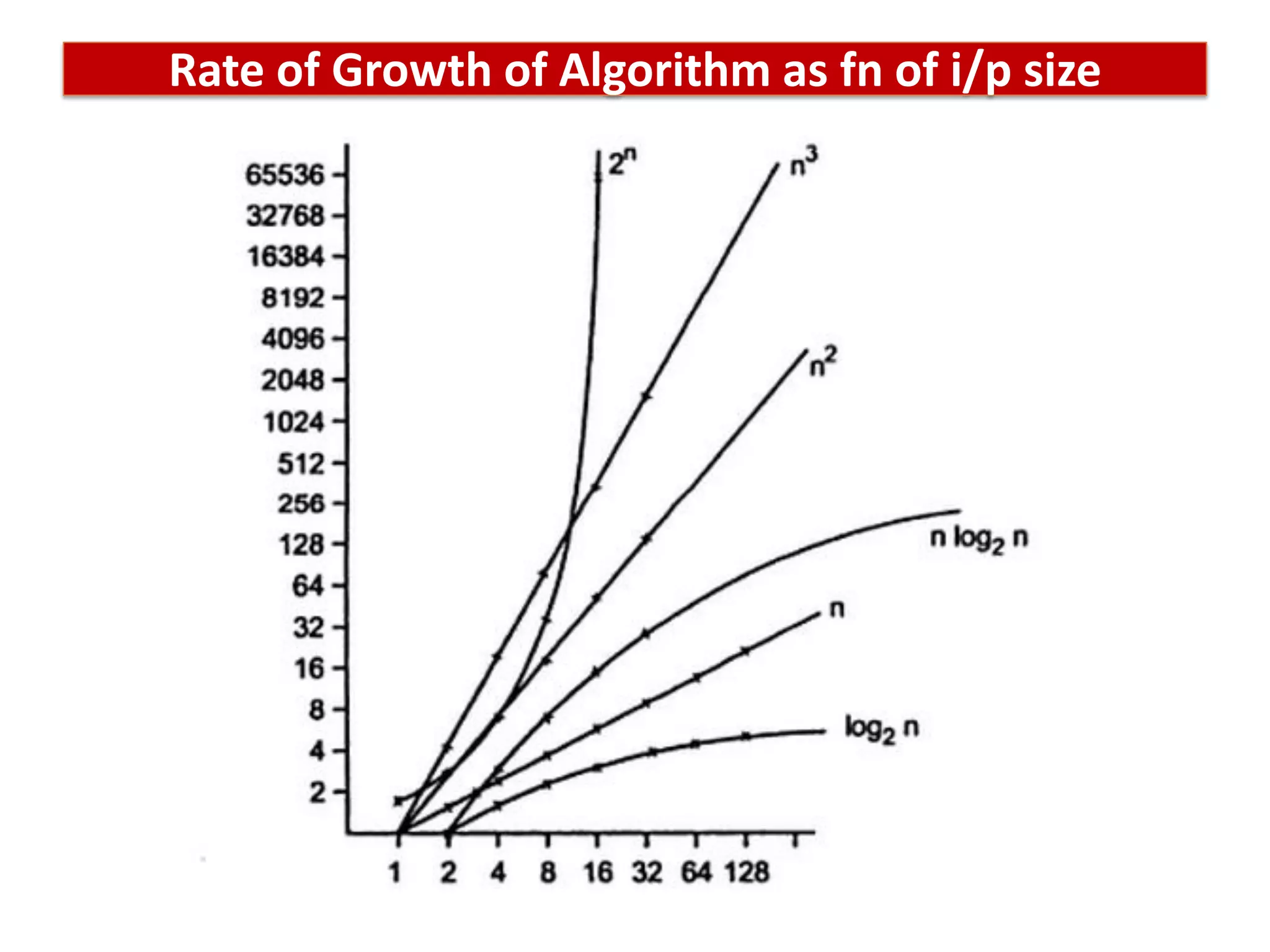
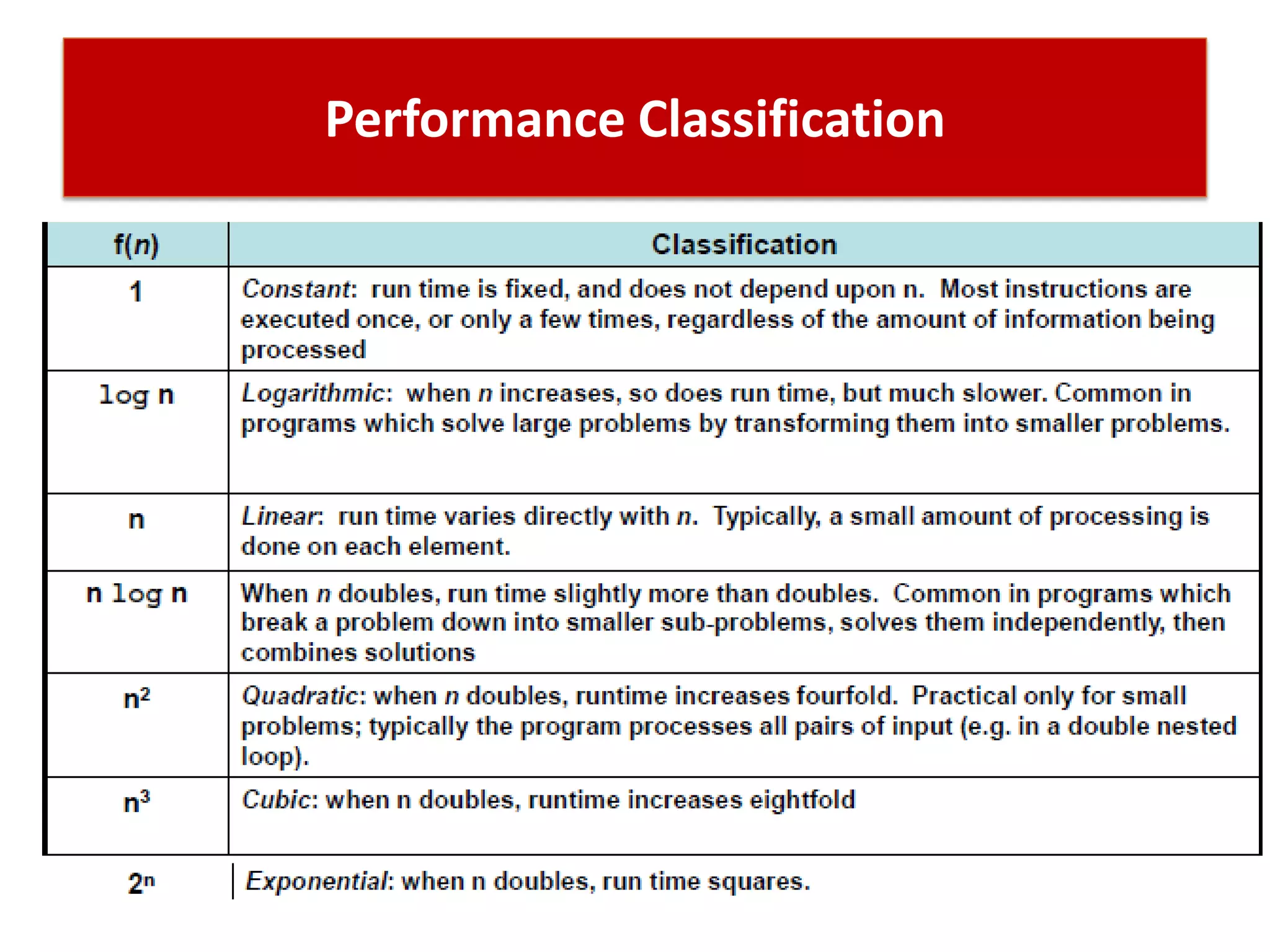
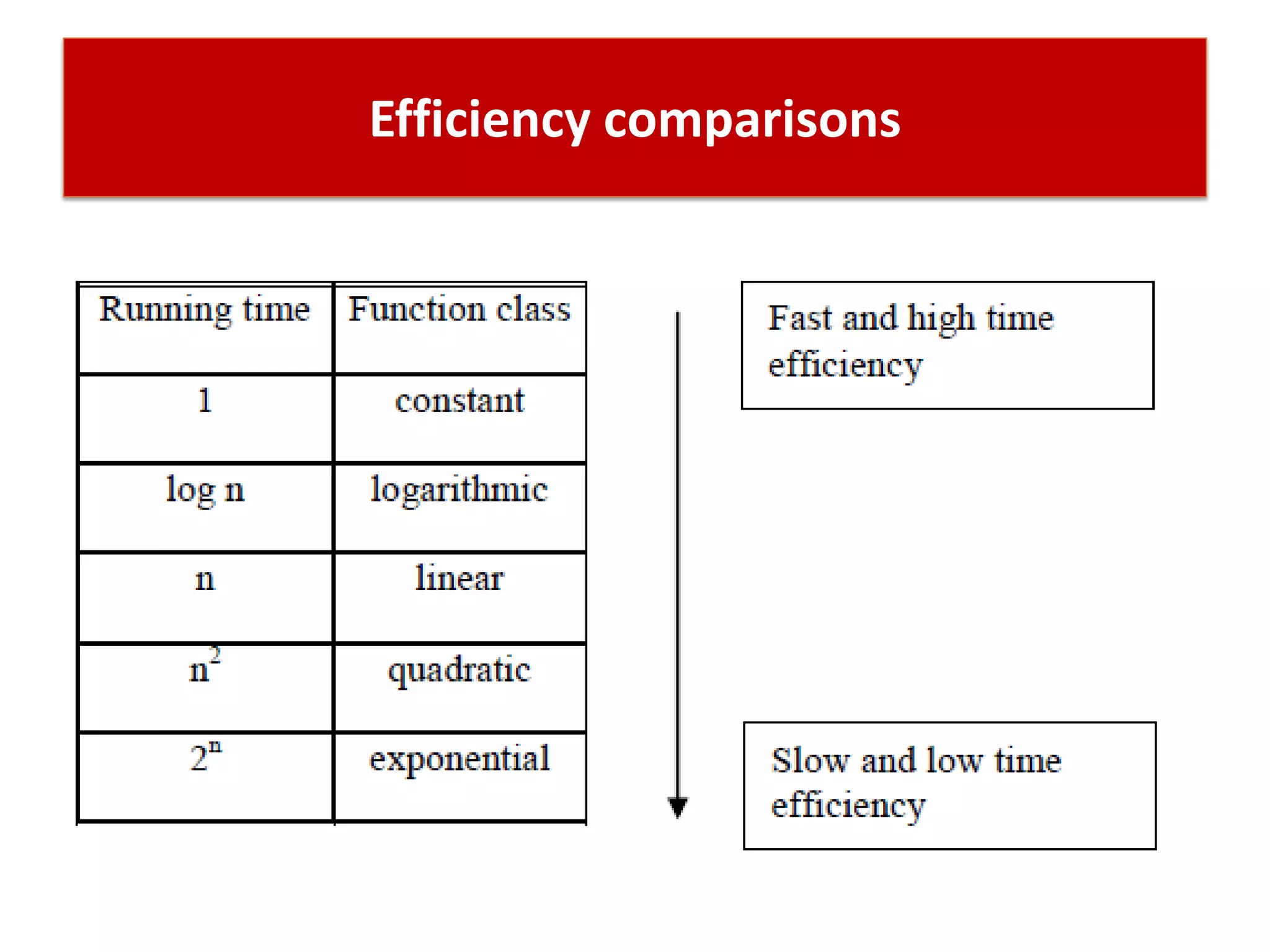
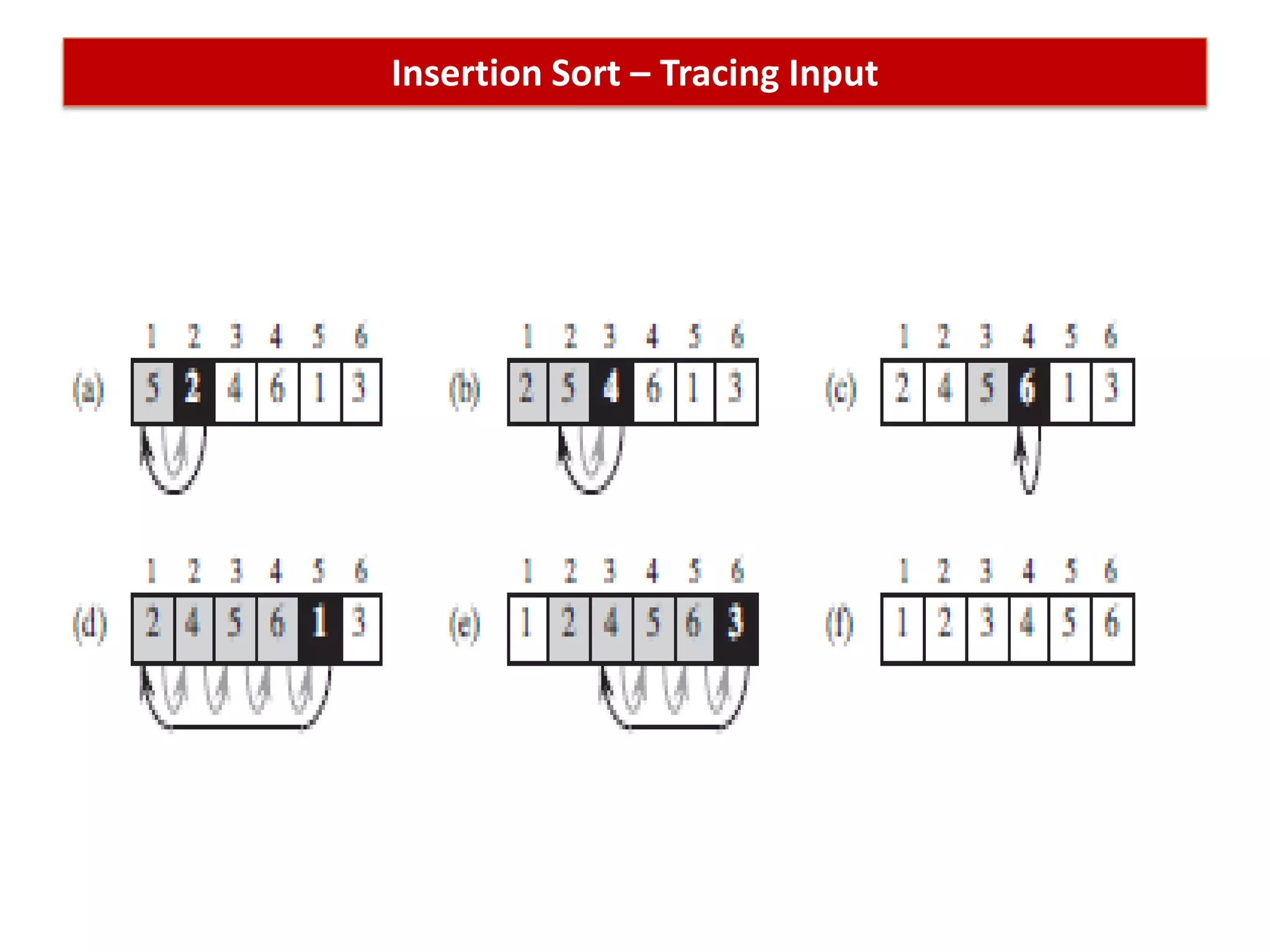
This document discusses algorithms and insertion sort. It begins by defining time complexity as the amount of computer time required by an algorithm to complete. Time complexity is measured by the number of basic operations like comparisons, not in physical time units. The document then discusses how to calculate time complexity by counting the number of times loops and statements are executed. It provides examples of calculating time complexities of O(n) for a simple for loop and O(n^2) for a nested for loop. Finally, it introduces insertion sort and divide-and-conquer algorithms.


![How to calculate running time then?
• Time complexity given in terms of FREQUENCY
COUNT
• Count denoting number of times of execution of
statement.
For (i=0; i <n;i++) { // St1 : 1, St 2 : n+1 , St 3 : n times
sum = sum + a[i]; // n times
}
3n + 2 ; O(n) neglecting constants and lower order terms](https://image.slidesharecdn.com/lecture3-insertionsortcomplexityanalysis-160326045646/75/Lecture-3-insertion-sort-and-complexity-analysis-3-2048.jpg)
![How to calculate running time then?
for (i=0; i < n ; i ++) // 1 ; n+1 ; n times
{
for (j=0; j < n ; j ++) // n ; n(n+1) ; n(n)
{
c[i][j] = a[i][j] + b[i][j];
}
}
3n2+4n+ 2 = O(n2)](https://image.slidesharecdn.com/lecture3-insertionsortcomplexityanalysis-160326045646/75/Lecture-3-insertion-sort-and-complexity-analysis-4-2048.jpg)