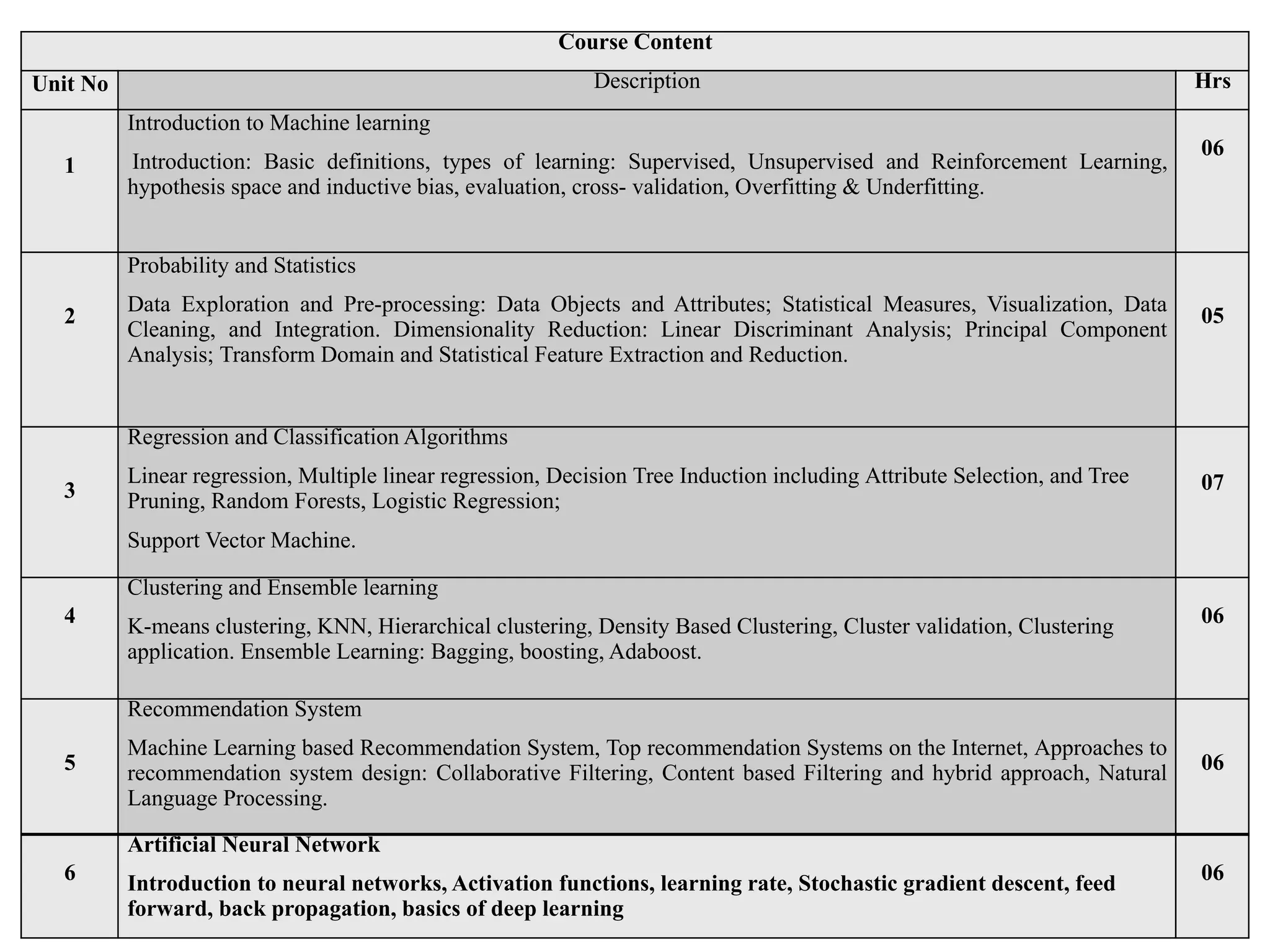
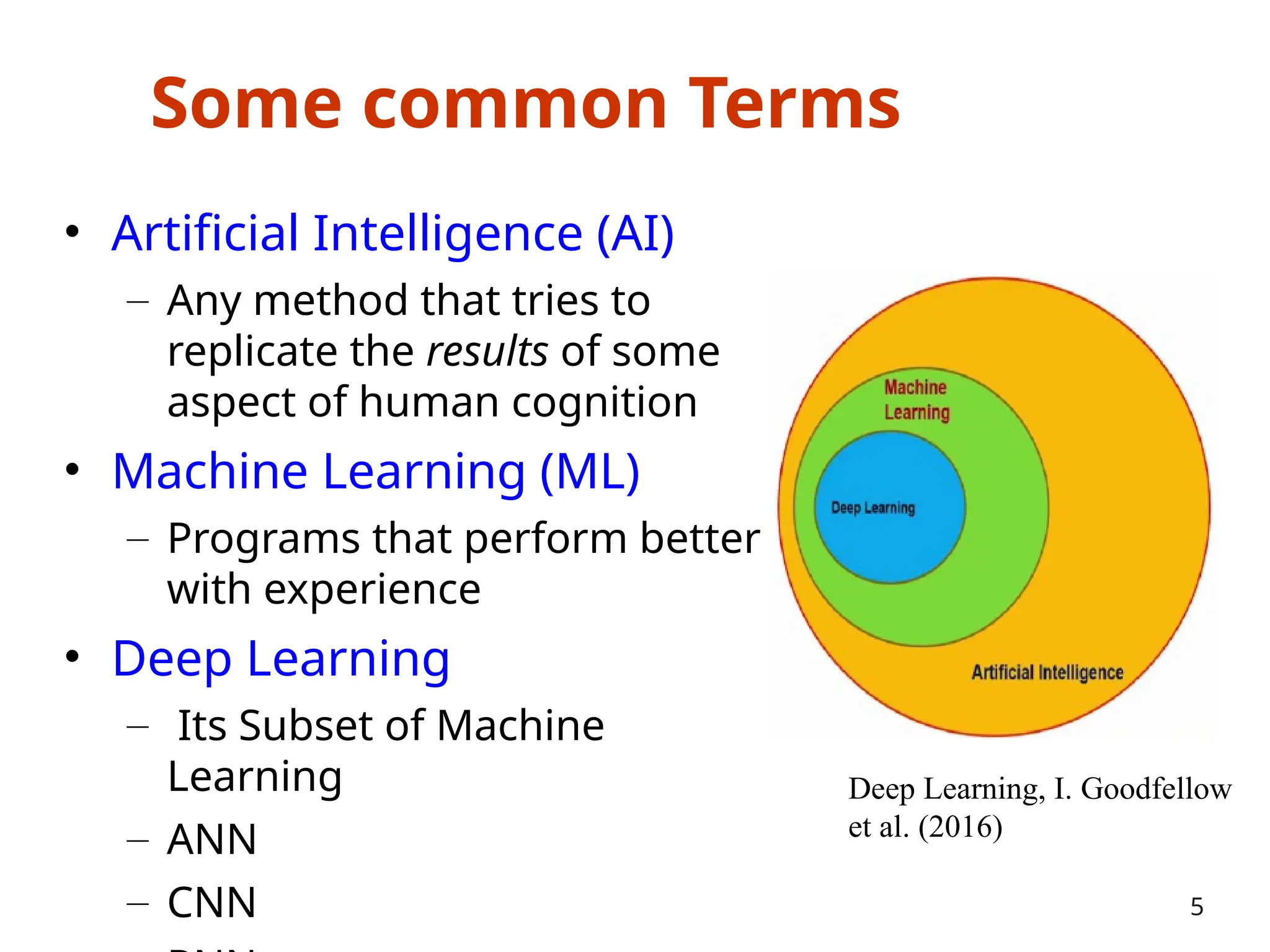
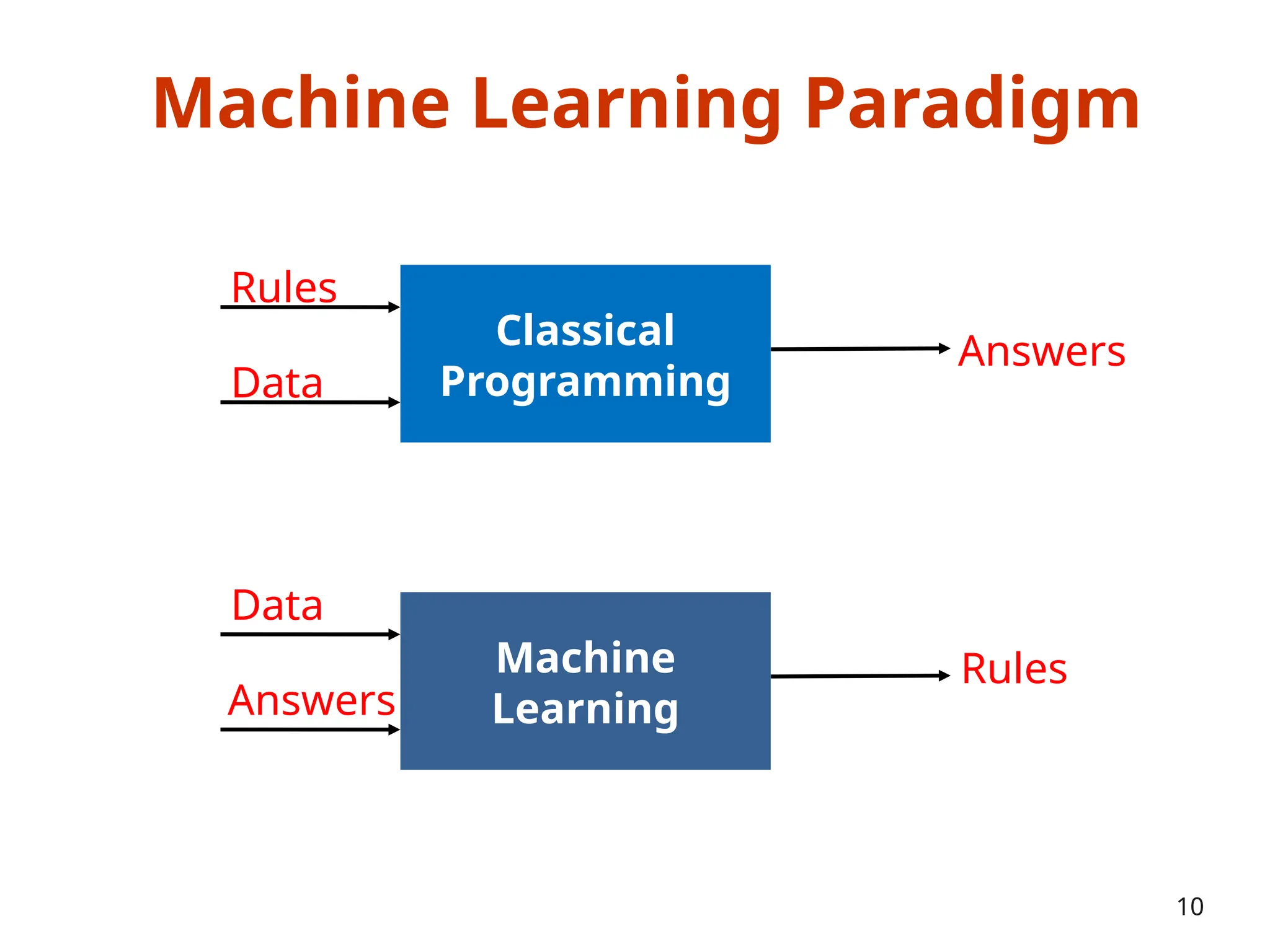
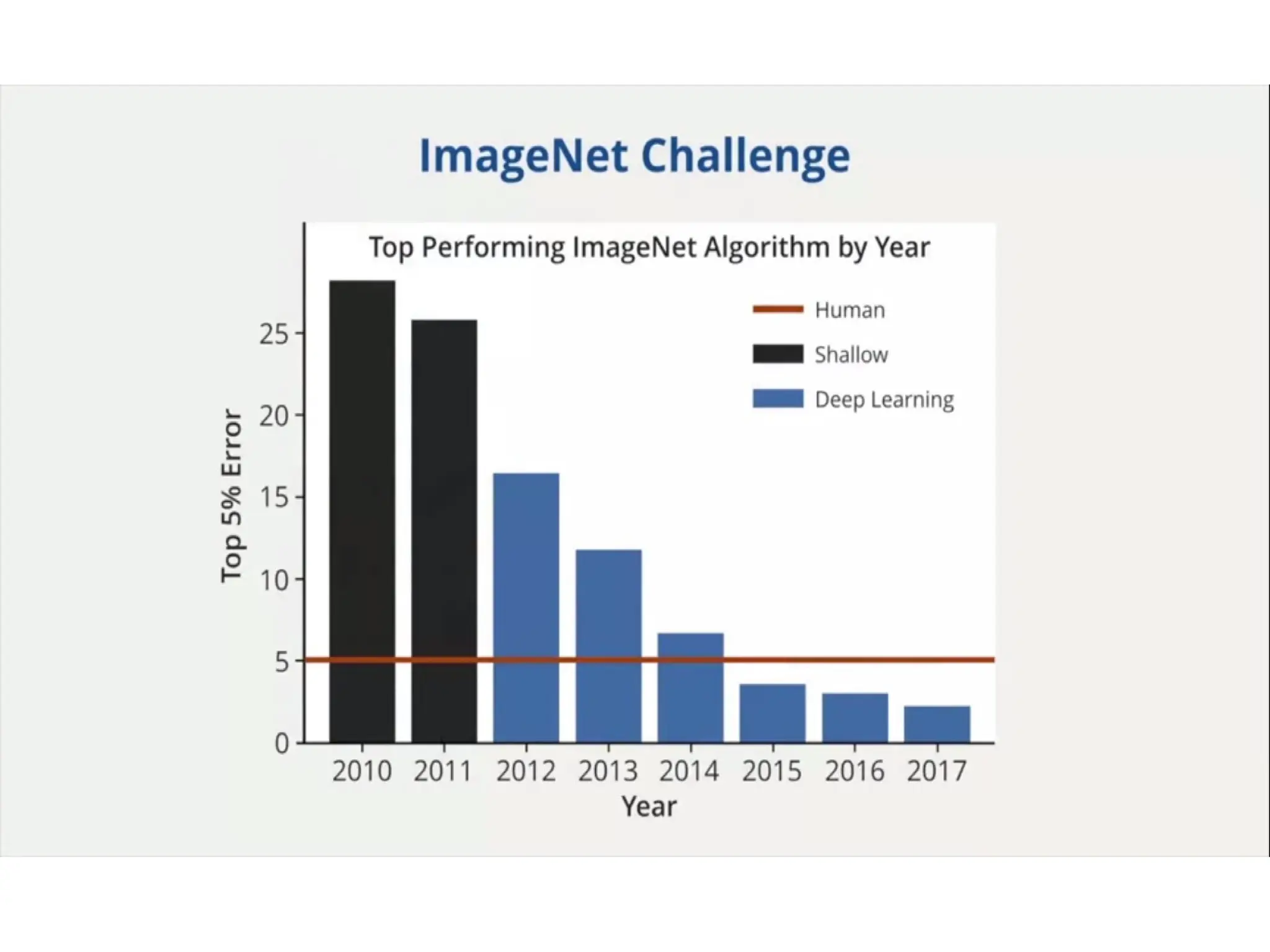
The document outlines a machine learning course (CS4013) taught by Mr. Taranpreet Singh, focusing on essential concepts and popular algorithms, including supervised and unsupervised learning techniques. Students will learn to identify real-world problems suited for machine learning, evaluate algorithm performance, and apply various ML methods such as regression, classification, and clustering. The course also addresses prerequisites, learning outcomes, and covers significant topics in machine learning, including deep learning and recommendation systems.















































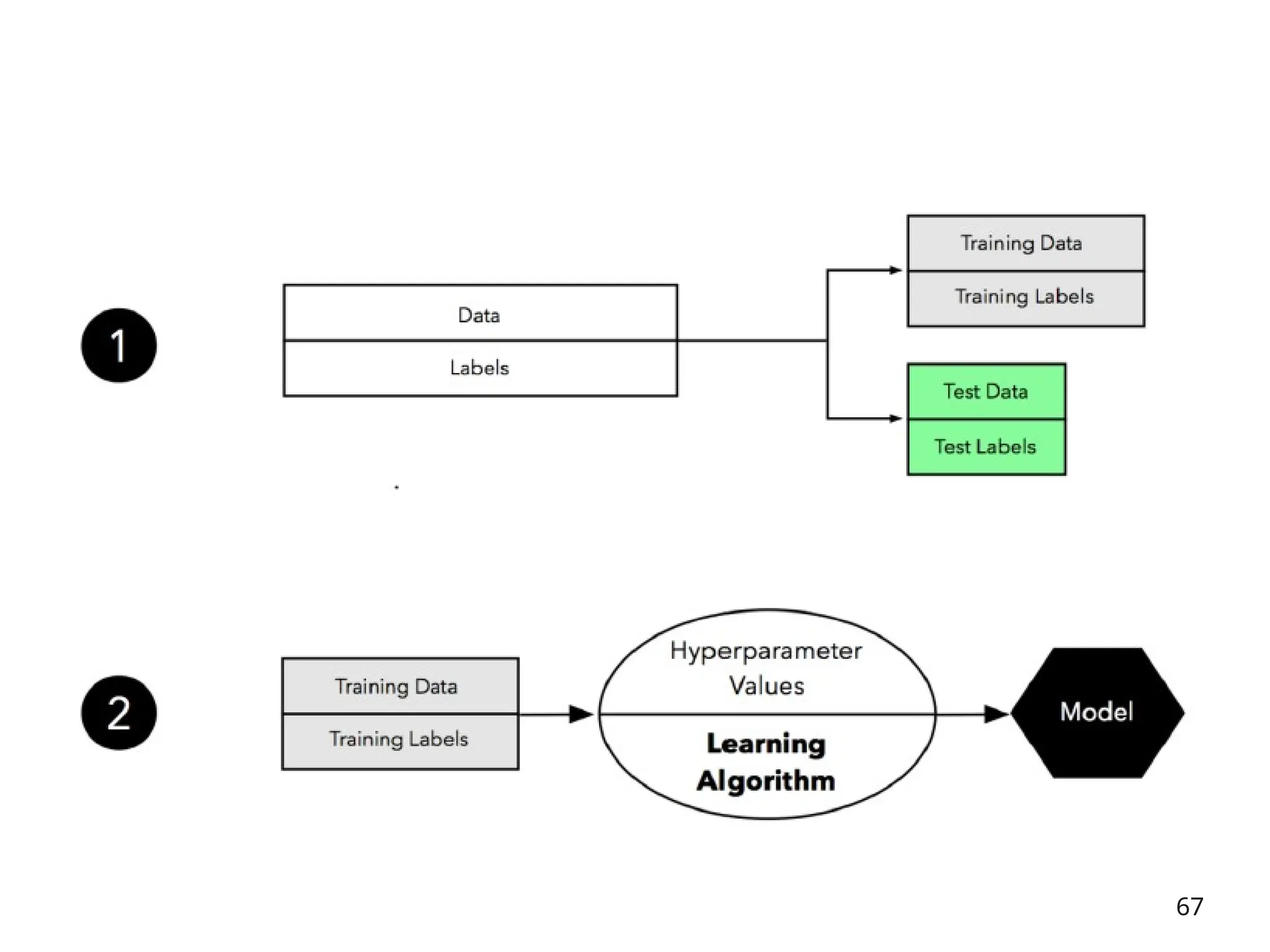
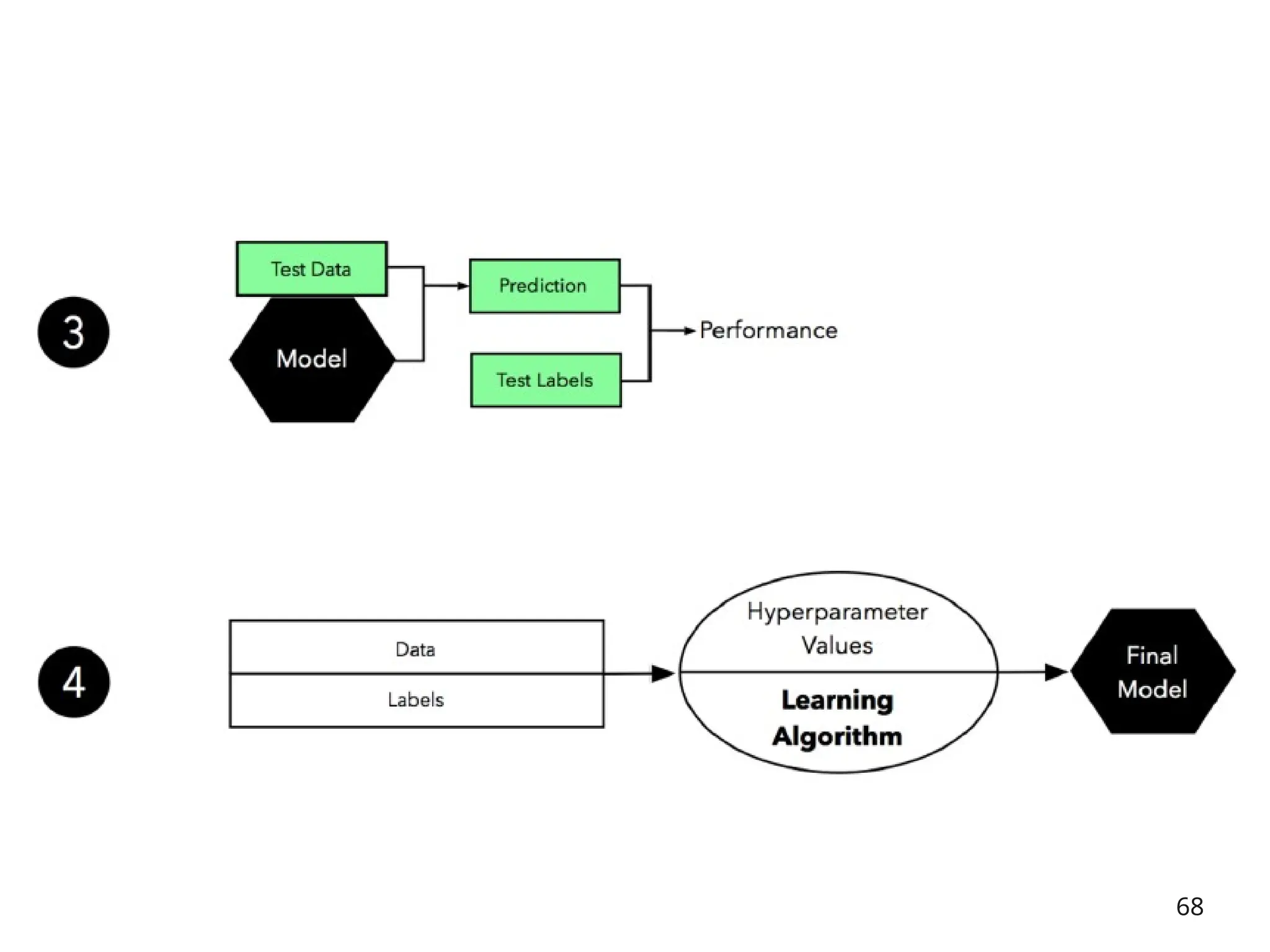





![Three-way data splits
• If model selection and true error estimates are to be
computed simultaneously, the data needs to be divided into
three disjoint sets [Ripley, 1996]
– Training set: a set of examples used for learning: to fit the parameters of the
classifier
– Validation set: a set of examples used to tune the parameters of a classifier
– Test set: a set of examples used only to assess the performance of a fully-
trained classifier
• Why separate test and validation sets?
– The error rate estimate of the final model on validation data will be biased
(smaller than the true error rate) since the validation set is used to select the
final model
– After assessing the final model on the test set, YOU MUST NOT tune the model
any further!
74](https://image.slidesharecdn.com/unit-1-introduction-250206152513-09c374ab/75/Unit-1-Introduction-of-the-machine-learning-72-2048.jpg)







